Comparison of electronic and mechanical Schmidt hammers in the context of exposure-age dating: are Q- and R-values interconvertible?
ABSTRACT
Application of Schmidt-hammer exposure-age dating (SHD) to landforms has substantially increased in recent years. The original mechanical Schmidt hammer records R-(rebound) values. Although the newly introduced electronic Schmidt hammer (SilverSchmidt) facilitates greatly improved data processing, it measures surface hardness differently, recording Q-(velocity) values that are not a priori interconvertible with R-values. This study is the first to compare the performance of both instruments in the context of field-based exposure-age dating with a particular focus on the interconvertibility of R-values and Q-values. The study was conducted on glacially polished pyroxene-granulite gneiss, Jotunheimen, southern Norway. Results indicate that mean Q-values are consistently 8–10 units higher than mean R-values over the range of values normally encountered in the application of SHD to glacial and periglacial landforms. A convenient conversion factor of ±10 units may, therefore, be appropriate for all but the softest rock types close to the technical resolution of the instruments. The electronic Schmidt hammer should therefore be regarded as a useful complement and potential replacement for the mechanical Schmidt hammer. Conversion of published R-values data to Q-values requires, however, careful control and documentation of instrument calibration. Copyright © 2014 John Wiley & Sons, Ltd.
Introduction
Boulder and bedrock surface hardness affected by subaerial surface weathering as a function of exposure time is the basic principle for geomorphologists applying the Schmidt hammer to the dating of landforms (Day and Goudie, 1977; McCarroll, 1994; Goudie, 2006; Shakesby et al., 2006, 2011). The technique has been used, for example, to date moraines and glacially sculptured bedrock (Matthews and Shakesby, 1984; Evans et al., 1999; Winkler, 2005, 2014; Owen et al., 2007; Matthews and Owen, 2010; Matthews and Winkler, 2011), rock glaciers and pronival ramparts (Frauenfelder et al., 2005; Kellerer-Pirklbauer et al., 2008; Matthews et al., 2011; Rode and Kellerer-Pirklbauer, 2011; Matthews et al., 2013), talus slopes and rock avalanches (Nesje et al., 1994; Aa et al., 2007), and fluvial terraces and flood berms (Matthews and McEwen, 2013; Stahl et al., 2013). Initially providing only relative age estimates, the past decade has seen the development of Schmidt-hammer exposure-age dating (SHD) as a calibrated-age dating technique (sensu Colman et al., 1987) constrained by the requirement of control points for known age of constructing high-precision age-calibration curves.
An electronic Schmidt hammer (named SilverSchmidt) was introduced by the manufacturer of the original mechanical Schmidt hammer (Proceq SA, Schwerzenbach) in 2007 as an improvement of mechanical Schmidt hammers (Proceq, 2007). It offers, in particular, facilities for easy data procession such as the initial storage and subsequent download of all measurements to a laptop and constitutes a potential complement if not replacement for the mechanical Schmidt hammer. However, its different approach to the measurement of surface hardness – based on Q-(velocity) values instead of R-(rebound) values – is a potential drawback. This difference means that measurements from the two instruments cannot be used interchangeably. Although Viles et al. (2011) compared the mechanical Schmidt hammer and SilverSchmidt (alongside two versions of another instrument, the Equotip) in a pilot study, they primarily focussed on their capabilities for investigating rock types of different surface hardness in relation to expected standard deviation and required sample size. Moreover, the manufacturers have failed to produce any guidelines on interconvertibility.
Furthermore, no comparison of mechanical versus electronic Schmidt hammers in terms of Q- and R-values has so far been conducted in the context of SHD. Given the increasing quantity of existing data and the increasing number of well-established regional age-calibration curves derived from mechanical Schmidt hammers, it seems vital to test whether the SilverSchmidt could, in future, be introduced within this field of research. To this end, the performance of both instruments was compared on glacially polished bedrock surfaces at various localities in Jotunheimen, southern Norway, previously utilized for the construction of age-calibration curves (Matthews and Owen, 2010). The performance of the SilverSchmidt during extensive field measurements on surfaces of different surface hardness was, in this context, tested for the first time. The overall aim was to compare the Q-values obtained by the SilverSchmidt with the R-values obtained with a mechanical Schmidt hammer on the same types of surfaces under controlled field conditions. By investigating the interconvertibility of Q- and R-values the possibility of establishing a numerical conversion factor for Q- and R-values was explored. In summary, this study assesses the potential of the SilverSchmidt as a future complement or even replacement for the mechanical Schmidt hammer.
Study Area
The sample localities for this study are located in the west-central part of the Jotunheimen mountain range of southern Norway (Figure 1) and constitute sites of known age previously investigated by Matthews and Owen (2010). Two localities lie within the boundaries of the Little Ice Age (LIA) glacier forelands of Leirbreen and Storbreen (both deglaciated c. ad 1900) and three localities lie beyond glacier-foreland boundaries: one in the lower part of Leirdalen to the east of the Smorstabbtindan massif and the remaining two close to the glacier forelands of Leirbreen and adjacent Bøverbreen to the west of the massif. These three ‘older’ localities became ice-free late in the Preboreal c. 9700 years ago (Dahl et al., 2002; Matthews and Dresser, 2008; Matthews and Owen, 2010). Age and altitude of all five sites are listed in Table 1. The impact of altitudinal differences between individual sites was neither specifically discussed by Matthews and Owen (2010), nor considered by them as a potential factor affecting the variability of mean R-values. For our study, this factor was considered not relevant as altitude is controlled in our comparative approach.

| Locality | Sample | R-Valuea | Q-Valuea | Δ | ∅ Δ |
|---|---|---|---|---|---|
| A - Leirbreen outside | NS 181.1x | 37.16 ± 2.37 | 47.22 ± 2.67 | 10.06 | |
| (1520 m a.s.l.; c. 9700 years) | NS 181.6x | 35.58 ± 1.92 | 43.94 ± 2.24 | 8.36 | 9.21 |
| B – Bøverbreen outside | NS 183.1x | 39.30 ± 2.58 | 49.55 ± 2.88 | 10.25 | |
| (1400 m a.s.l.; c. 9700 years) | NS 183.6x | 36.08 ± 3.06 | 43.78 ± 3.31 | 7.70 | 8.58 |
| C – Leirdalen outer valley | NS 185.1x | 42.12 ± 2.05 | 50.88 ± 2.29 | 8.76 | |
| (1050 m a.s.l.; c. 9700 years) | NS 185.2x | 43.32 ± 2.29 | 51.90 ± 2.37 | 8.58 | 8.67 |
| D – Leirbreen inside | NS 182.1x | 65.04 ± 0.97 | 73.03 ± 1.28 | 7.99 | |
| (1510 m a.s.l.; c. 100 years) | NS 182.7x | 66.74 ± 0.98 | 74.37 ± 1.38 | 7.63 | 7.81 |
| E – Storbreen inside | NS 184.1x | 69.08 ± 1.02 | 77.41 ± 1.05 | 8.33 | |
| (1260 m a.s.l.; c. 100 years) | NS 184.6x | 71.40 ± 0.94 | 79.76 ± 0.72 | 8.36 | 8.35 |
| A–C (old control points) | combined | 38.93 ± 1.03 | 47.88 ± 1.13 | 8.95 | |
| D–E (young control points) | combined | 68.07 ± 0.59 | 76.14 ± 0.67 | 8.07 | |
| A–E (all points) | combined | 50.58 ± 1.42 | 59.18 ± 1.42 | 8.60 | |
| Test anvil | 80.84 ± 0.29 | 89.38 ± 0.20 | 8.54 | ||
| Tarmac | NS 186.1x | 25.28 ± 1.35 | 28.97 ± 1.70 | 3.69 | |
| NS 186.2x | 22.28 ± 0.97 | 27.68 ± 1.66 | 5.40 | 4.55 |
- Note: Paired sampling approach is the comparison of R- and Q-value mean data for the five selected localities previously investigated by Matthews and Owen (2010; see also Figure 1). Matched pairs of Q- and R-values are used to calculate the mean difference, which is given for individual samples (Δ, n = 50) as well as for each locality (∅ Δ, n = 100). Differences are additionally given for all old and young sites, respectively, and for the whole data set. The test anvil and tarmac are included as additional test surfaces (see text).
- a Mean with standard error of the mean (SEM) at 95% confidence (α = 0.05; n = 50).
The bedrock at all localities is part of the early-Proterozoic Jotunheimen complex of predominantly pyroxene-granulite gneiss (Lutro and Tveten, 1996). Although within-site and within-locality lithological and mineralogical heterogeneity was identified by previous studies (Matthews and Owen, 2010; Matthews and Winkler, 2011), the bedrock is generally well suited to Schmidt hammer applications. The closest meteorological station Sognefjell [1413 m above sea level (a.s.l.)] has a mean annual air temperature of −3.1 °C (Aune, 1993). Annual precipitation is ~860 mm on the basis of the discontinued measurements at this station (Førland, 1993).
Methods
Both instruments used in this comparative study were N-type models with an identical impact energy of 2.207 Nm for the plunger (Proceq, 2004, 2012; see also Shakesby et al., 2006, Viles et al., 2011, for more technical details). The main difference regarding the measurement of compressive strength/surface hardness of a rock surface is that the mechanical Schmidt hammer displays a rebound distance value. It uses a rider with a guide rod to record the specific distance the plunger bounces back after it impacts the rock surface. The SilverSchmidt, in contrast, uses an inbuilt sensor to record the rebound velocity of the plunger and electronically displays and saves this Q-value. The Q-value has primarily been introduced because it is not influenced by the impact direction of the plunger. By contrast, R-values are slightly influenced by the impact direction and the mechanical Schmidt hammer should therefore ideally always be held vertical during sampling (Basu and Aydin, 2004; Proceq, 2007).
Due to this difference in measuring the rebound and its potential deviations the manufacturer Proceq SA refrains from providing a conversion factor for Q- and R-values with the latest versions of the SilverSchmidt. The first SilverSchmidts had an R-value unit conversion of unknown procedure in their software but that was eventually removed and the plunger modified (see later). There are two main differences with handling the instruments and sampling in the field: first, the SilverSchmidt is able to store up to 4000 impacts and calculate arithmetic mean and standard deviation values; second, the data can be easily downloaded after fieldwork and displayed either in the instrument's own software (Hammerlink) or exported into spreadsheets and statistical programmes (e.g. Microsoft Excel, IBM SPSS). Thus, there is no need for the operator to book individual readings, which improves efficiency both in the field and in subsequent processing.
To compare both instruments and explore interconvertibility, we used two different approaches. First, parallel sampling was conducted with both instruments with a high level of experimental control. For this approach, paired samples (n = 50) on glacially polished bedrock were collected so that the plunger impacts of both instruments were set close together on the rock surface (to avoid both the influence of minor lithological heterogeneity and modifications to the surface by consecutive impacts on the same spot; see Discussion section). In order to test their performance at the higher and lower end of surface hardness, similar paired sample tests were also made on a full-metal proprietary test anvil and soft tarmac, respectively. Second, resampling was carried out with the SilverSchmidt at five selected localities (see Table 1, Figure 2) previously sampled by Matthews and Owen (2010) with the mechanical Schmidt-hammer. The rationale for this second approach was to test whether also older archive data and/or previously published data could be utilized in this context. With a considerable amount of R-value data already available for some regions, this would in the end be important for the acceptance of the new instrument. Although this approach involved a lower level of experimental control, in order to achieve maximum comparability, we kept to a minimum sample size at each locality of n = 400 (25 impacts × 16 sites). The involvement of one author in both studies ensured, furthermore, that measurements were conducted under equal conditions (e.g. on dry bedrock surfaces; see Discussion section). An attempt was made to identify the same bedrock exposures previously tested at all localities and actually re-sample those.

 (1)
(1) = arithmetic mean, σ = standard deviation, and n = number of impacts for individual samples at 95% confidence (α = 0.05) following Shakesby et al. (2006). Standard statistical analysis included Kolmogorov–Smirnov tests for normality and paired t-tests for dependent samples (Sachs, 1999; Lehmann, 2002) using IBM SPSS Statistics software.
= arithmetic mean, σ = standard deviation, and n = number of impacts for individual samples at 95% confidence (α = 0.05) following Shakesby et al. (2006). Standard statistical analysis included Kolmogorov–Smirnov tests for normality and paired t-tests for dependent samples (Sachs, 1999; Lehmann, 2002) using IBM SPSS Statistics software.Results
Measuring Q-values with the SilverSchmidt was unproblematic. Data were downloaded on a daily basis, the internal memory cleared, and battery capacity checked and occasionally re-charged. Hence, even with more than 1300 impacts per day, the stated maximum memory capacity was far from being approached. With all impacts automatically registered by the instrument, inaccurate impacts (caused, for example, by small particles splintering away during impact or invisible cracks below the rock surface which only may be detected by an anomalous amphoric sound during the impact) needed to be individually deleted. After some practise this proved easy to perform during sampling without difficulty or delay. The SilverSchmidt was still perfectly calibrated after 3000 impacts and the plunger fully operational. The latter was initially a concern as, unlike the solid steel plunger of the mechanical Schmidt hammer, the SilverSchmidt has a bi-component plunger made of aluminium alloy with a steel head. During an earlier field test on hard and rough boulder surfaces of metamorphosed sandstone in the Southern Alps of New Zealand, an early version of the SilverSchmidt plunger (which is not purpose-built for such surfaces) did not last more than a few hundred impacts. But, with the plunger meanwhile improved by the manufacturer (personal communication, L. Raj, Proceq Singapore), this potential weakness has been overcome. With the field performance of the SilverSchmidt successfully completed, subsequent data processing was, as expected, considerably more efficient than with the mechanical Schmidt hammer.
The results of all paired samples for the five selected localities are plotted in Figure 3 and summarized along with comparable results from the test anvil and tarmac surface in Table 1. The data points for each Q-/R-value pair are closely clustered for the young surfaces (localities D and E) but more scattered for the older ones (localities A–C; see Table 1). When interpreting this plot, and the correspondingly moderate coefficients of determination (R2) for the calculated linear trend, one must be aware that the impacts could not be performed on exactly the same spot of the bedrock surface (as justified earlier; see also Discussion section). The greater variability of the older, weathered surfaces is reflected in the greater scatter and hence in higher standard deviations and broader confidence intervals. This effect has been recognized in numerous previous Schmidt-hammer studies and is most likely related to the effects of micro-scale lithological variability, which becomes a more pronounced influence with time exposed to subaerial weathering.
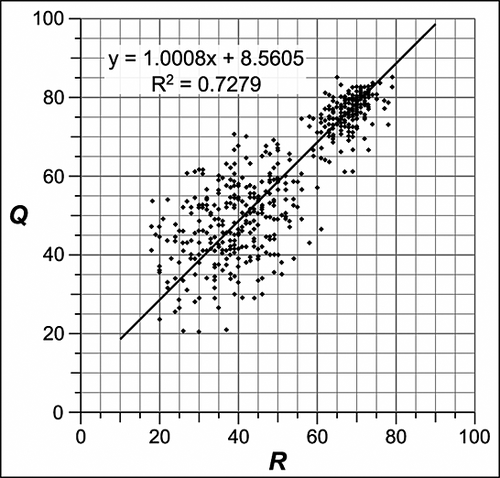
The numerical differences between mean Q- and R-values vary consistently in the range 7.70–10.25 for individual samples and 7.81–9.21 for whole localities (Table 1). The mean Q-value for samples is therefore in the order of 8 to 10 units higher than the corresponding mean R-value. Samples of Q-values tend to display higher standard deviations and consequently wider confidence intervals than R-value samples, which is most likely a consequence of the higher mean values of the former (see Discussion section). Paired t-tests were run for every sample involving paired sampling with the mechanical Schmidt hammer and the SilverSchmidt (except those on the test anvil). All samples showed mean paired differences that were statistically different at p < 0.05. All samples passed the Kolmogorov–Smirnov test and were normal distributed at a significance level of p < 0.05. Thus, the statistical analyses yielded no potential uncertainties about the validity of the obtained data or any subsequent interpretation. Although two samples (NS 181.1x, NS 183.1x) might be termed outliers, they were included in the summarizing overall calculations for older sites and all sites in Table 1. The final result of an average 8.60 numerical difference between mean Q- and R-values is almost identical to the difference on the test anvil (8.54) with its standardized impact conditions. An exception from this fit was the tarmac chosen to represent a surface even softer/weaker then the c. 9700 year old Preboreal bedrock surface. It should be noted that the difference between mean Q- and R-values for the tarmac surface is much less and can be interpreted as a consequence of both instruments approaching their lower limit of resolution.
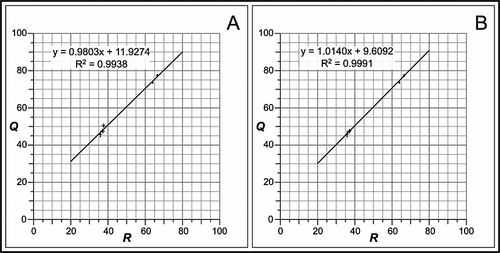
These results encouraged the attempt to calculate a conversion formula for Q- and R-values. Two sets of three different equations assuming a linear trend have been calculated using reduced major axis regression in the search for a conversion factor (Sachs, 1999; Smith, 2009). These are derived for (a) individual samples and (b) particular localities in Figures 4a–4c and Figures 4d–4f, respectively. Whereas the first equation of both sets includes rock surfaces at localities A–E only, the second equation additionally includes the data from the test anvil and the third equation from both, the test anvil and the tarmac surface. Coefficients of determination (R2) are uniformly high (> 99%), suggesting that, despite the small number of data points, the intercept of the regression line represents a potential conversion factor for Q-values from R-values. Inclusion of the test anvil data improved the fit and maintained this conversion factor yielding Q-values ~10 units higher than R-values. However, inclusion of the tarmac surface reduced the fit and produced an unacceptable conversion formula resulting in a lower conversion factor (only ~6.5 units higher Q-values), thus confirming that very soft rock surfaces should be avoided with both instruments.

The results of resampling the five localities with the SilverSchmidt and comparison of mean Q-values with mean R-values originally published by Matthews and Owen (2010) are summarized in Table 2. With the exception of the possibly anomalous locality C (where the rock outcrops used in the resampling may, despite all effort, have differed from those used originally by Matthews and Owen), the numerical differences between Q- and R-value means vary consistently between 9.06 and 11.32. Direct comparison of the differences in mean Q-values and mean R-values from the paired sampling (Table 1) and the resampling (Table 2) approaches are summarized in Table 3. The differences between the two approaches ranged between 0.74 and 3.21 for localities A–E with an overall average difference of 2.17. The difference between Q-values and R-values in the resampling approach averaged 10.57, which is almost exactly two units higher than the average difference obtained for all sites in the paired sampling approach (8.60) and between R-values and Q-values obtained on the test anvil (8.55). A supposed explanation for this offset may be a slight difference in the initial calibration of the mechanical Schmidt-hammer used in this study and that used by Matthews and Owen (2010) or, alternatively, an operational bias or differences in rock moisture during sampling (see Discussion section). The consistent nature of the difference allows nevertheless the calculation of individual retrospective conversion formulas for the inclusion/exclusion of locality C (see Figure 5).
| Locality | R-Valuea | nb | Q-Value | nc | Δ Ranged |
|---|---|---|---|---|---|
| A - Leirbreen outside | 35.78 ± 0.74e | 60 | 45.43 ± 1.48 | 16 | 9.65–10.12 |
| 35.21 ± 1.21 | 30 | 45.73 ± 1.45 | 15 | ||
| 36.35 ± 0.89 | 30 | 45.90 ± 1.53 | 14 | ||
| B – Bøverbreen outside | 37.12 ± 0.92e | 60 | 46.31 ± 1.88 | 16 | 9.19–10.38 |
| 38.37 ± 1.36 | 30 | 46.32 ± 1.82 | 15 | ||
| 35.88 ± 1.14 | 30 | 47.50 ± 1.08 | 14 | ||
| C – Leirdalen outside | 37.59 ± 0.78 | 30 | 51.97 ± 1.17 | 44 | 11.86–14.38 |
| 51.21 ± 1.02 | 40 | ||||
| 51.69 ± 1.22 | 30 | ||||
| 51.04 ± 1.20 | 30 | ||||
| 50.45 ± 1.02 | 30 | ||||
| D – Leirbreen inside | 63.91 ± 0.40 | 30 | 73.73 ± 1.07 | 20 | 9.06–10.06 |
| 72.97 ± 0.85 | 16 | ||||
| 73.65 ± 0.55 | 15 | ||||
| E – Storbreen inside | 66.43 ± 0.46 | 30 | 77.33 ± 0.69 | 20 | 10.90–11.32 |
| 77.64 ± 0.73 | 16 | ||||
| 77.75 ± 0.75 | 15 |
- Note: Resampling approach is the comparison of mean Q-values with previously published mean R-values (Matthews and Owen, 2010). Apart from the Q-value means using all individual samples obtained from each site (top value), a number of different selections have been calculated for each site in an attempt to minimize the variability reflected in the confidence intervals.
- a Original data taken from Matthews and Owen (2010).
- b Number of samples included (each sample with n = 25 impacts).
- c Number of samples included/selected (each sample with n = 25 impacts; cf. text).
- d For sites A and B only for the ‘combined’ values.
- e Data for combined sites (cf. Matthews and Owen, 2010).
| Locality | Δ Q-/R-values resampling approach | Δ Q-/R-values paired sampling approach | Difference |
|---|---|---|---|
| A - Leirbreen outside | 9.95a | 9.21 | 0.74 |
| (9.65–10.12) | (8.36–10.06) | ||
| B – Bøverbreen outside | 10.38 | 8.98 | 2.40 |
| (9.19–10.38) | (7.70–10.25) | ||
| C – Leirdalen outer valley | 11.86 | 8.67 | 3.21 |
| (11.86–14.38) | (8.58–8.76) | ||
| D – Leirbreen inside | 9.74 | 7.81 | 1.97 |
| (9.06–10.06) | (7.63–7.99) | ||
| E – Storbreen inside | 10.90 | 8.35 | 2.55 |
| (10.90–11.32) | (8.33–8.36) | ||
| Test anvil | 8.54 | ||
| Tarmac | 4.55 | ||
| (3.69–5.40) |
- a Value for the site-specific selection of Q-value samples with the lowest standard error of the mean (SEM) (cf. Table 2 and text).
Discussion
In their study focussed on a comparison of general applicability of mechanical and electronic Schmidt hammers (and additionally two Equotip devices) Viles et al. (2011) used an older version of the SilverSchmidt still yielding R-values. Unlike our study, they did not compare Q-values with R-values. Their reported strong positive correlation of R-values from both instruments is, however, in good agreement with our results. Viles et al. (2011) corrected their R-values for the mechanical Schmidt hammer for impact direction following Basu and Aydin (2004) prior to their comparison, a procedure impractical with our type of application. But as the bedrock surfaces at all localities tested were almost horizontal, the mechanical Schmidt hammer could be held nearly vertical with all impacts and any effect on the data should, therefore, be negligible. All means and standard deviations for Q-values were calculated using the same software as with all calculations of R-values parameters and not the instrument's own software to avoid any potential bias.
Viles et al. (2011) state that the SilverSchmidt tends to give more variable datasets than the mechanical instrument. This agrees with our findings that the Q-value means in generally yield slightly higher confidence intervals with few exceptions (one site at the young locality E and the test anvil) and seems to be at least partially related to the way the SilverSchmidt measures Q-values. Viles et al. (2011) suggest that their result might be influenced artificially by an instrumental difference as they used an N-type mechanical Schmidt hammer and an L-type SilverSchmidt, which had a three-time lower plunger impact energy. However, an artefact of operator handling of the SilverSchmidt also cannot be excluded. Unlike the mechanical Schmidt hammer where the operator needs to read the scale after each impact, with the SilverSchmidt there is no need to check individual readings as the instruments automatically stops recording when the pre-programmed sample size is reached and the operator needs to accept the sample to start a new one. Apart from those cases were an impact is discarded and subsequently deleted for obvious reasons as described earlier, all readings will be kept. With the mechanical Schmidt hammer experienced operators might, however, tend to question unexpected low (or high) R-values and eventually use a second impact to confirm the first reading. During data processing some Q-value samples included individual readings with the character of an outlier that might have been challenged (and re-tested) if they had been read in the field.
Although other Schmidt hammer studies have confirmed that the variability of individual readings tend to increase with older and more weathered rock surfaces (see Winkler, 2005, 2014; Shakesby et al., 2006, 2011; Matthews and Owen, 2010; Matthews and Winkler, 2011), one might think about strategies to reduce the scatter of the Q-/R-values pairs presented here for such older surfaces (see Figure 3). In theory, an ideal test design would see all mechanical and electronic Schmidt hammer impacts performed on exactly the same spot (as occurs on the test anvil with its negligible scatter). Comprehensive rock mechanics research into the application of the Schmidt hammer for its original purpose of concrete/rock testing clearly demonstrated, however, that R-values increase with multiple impacts on the same spot during field testing (Poole and Farmer, 1980; Aydin and Basu, 2005). As a consequence, guidelines are set in place to either (1) perform a certain minimum number of impacts on the same spot until the R-value reading stabilizes or (2) grind or clean the rock surface prior to the impact (Basu and Aydin, 2004; Aydin, 2009). The nature of weathered rock surfaces does not allow for such a test design as with both procedures the essential information about the degree of surface weathering (and, thus, exposure age) would be altered or destroyed. Therefore, this scatter cannot be avoided but is partly compensated for by a large number of paired test samples and multiple test sites at each locality, which reduce the standard errors of the means and the width of confidence intervals.
The slight difference between R-value means obtained during the paired sampling of this study and those reported by Matthews and Owen (2010) for the same localities may well be attributed to random error and/or operator bias during sampling (such as different treatment of apparent outliers). Another possibility is different rock moisture of the bedrock surfaces at the day of sampling because this factor influenced R-values as shown by Sumner and Nel (2002). But as Matthews and Owen (2010) did their sampling in 2008 on visually ‘dry’ surfaces on several different days in 2008 and sampling for this study was also performed on different days, one would expect a more random offset. The relatively consistent character of this difference could, however, also be influenced by minor differences with the calibration of the mechanical Schmidt hammers of those studies. According to the manufacturer, calibration of all Schmidt hammers is realized within a ±2 unit interval around the nominal reading on the test anvil (typically 81 ± 2 R-value for a N-type mechanical Schmidt hammer). Considered satisfactory for its original purpose of concrete testing (personal communication, L. Raj), the range of ±2 units may therefore be insufficient for exposure-age dating purposes using both, mechanical and electronic Schmidt hammers. Nevertheless, any difference in the range of two units as reported here does not compromise our conclusions on interconvertibility of both instruments. It underlines, however, the importance of comparable calibration of the instruments and of keeping records of test-anvil readings during fieldwork (rather than only checking if they pass the manufacturer's calibration requirements). The fact that the average difference between Q- and R-value means of all localities in the paired sampling of this study (8.60) is almost identical to the mean difference between the instruments on the test anvil (8.54) supports these considerations.
A final point for discussion is the reason for the breakdown of the conversion factor on the tarmac surface, which can be considered representative of relatively soft rock surfaces near the lower operational range of both of the instruments. Is the decrease in the numerical difference of between Q- and R-values for the tarmac gradual, what form does it take, and at what point on the scale does convergence begin? It currently seems most likely that there is a threshold in Q- and R-values below which the constant linear conversion no longer applies. The more-or-less constant conversion factor that applies to the test anvil (certainly representative of the hardest rocks that occur in nature) appears applicable to Q-values down to about 40 and R-values down to about 30. Within this acceptable range of operation, error margins of the conversion factor increase towards lower Q- and R-values appears to be the result of lithological heterogeneities becoming more pronounced as a result of long-term weathering (rather than instrumental differences). However, further investigations are necessary to draw definite conclusions in relation to the lower limit of the proposed conversion factor.
Conclusion
Our empirical comparative study of mechanical and electronic Schmidt hammers in the context of SHD based on pyroxene-granulite rock surfaces in Jotunheimen, southern Norway, has shown that the application of the electronic SilverSchmidt with extensive sampling under field conditions is unproblematic. Subsequent data processing was considerably less time-consuming and more efficient than with the mechanical Schmidt hammer. The Q-values from the SilverSchmidt and the R-values from the conventional mechanical N-type Schmidt hammer are closely related. However, Q-values are systematically higher than R-values by 7.70 to 10.25 units over most of the operational range of both instruments. Linear conversion equations indicate a conversion factor between +9.6 to +10.1 units is applicable when converting R-values to Q-values. These estimates agree well with data obtained on the standard test anvil, which yield Q-values that are, on average, 8.54 units higher than R-values. These numerical relationships are likely to break down only on very soft lithologies with Q-values of below 40 and R-values of below 30, respectively. The younger the surface, the more precise the conversion is due to tighter standard errors. Given the interconvertibility of the two instruments, the SilverSchmidt is regarded as an efficient complement and potential replacement for the mechanical Schmidt hammer. This enables, moreover, continuity in the use of existing R-value data. However, when comparing data sets of different age, adjustments may be necessary for different instrumental calibration values. Further testing of these conclusions in relation to different rock types, bedrock versus boulder surfaces and environmental conditions is advisable. Future research should also address the uncertainties regarding the shape of the conversion curve towards the lower end of the operational range of the instruments.
Acknowledgements
The authors thank Andreas Kellerer-Pirklbauer, Paul Sumner and the editors of this journal for their valuable comments on the manuscript. This paper is Jotunheimen Research Expeditions, Contribution No. 189.




