Optimizing the Microstructure and Processing Parameters for Lithium-Ion Battery Cathodes: A Use Case Scenario with a Digital Manufacturing Platform
Abstract
With increasing electrification in the automotive field, lithium-ion batteries are rapidly becoming an inseparable part of everyday life. To meet the various governmental goals regarding CO2 emissions, it has become imperative to rapidly optimize the manufacturing process to produce high-quality batteries at the least possible emissions and cost. Model-based methods provide a simple and efficient view on complex processes and on identifying best-case scenarios for production, since they require minimal material and time expenditure. In the authors’ recently published work, by Thomitzek et al., a digital modeling framework is initially described. It uniquely combines process chain and battery cell models. Herein, this digital framework is utilized to set up a numerical optimization routine. The routine helps to identify the best possible microstructure parameters in an NMC 622 cathode to maximize the resulting discharge volumetric energy density. Furthermore, the minimal energy expenditure for processing is determined. With the findings herein, an inexpensive method for identifying optimal battery manufacturing scenarios is presented, with the goal of producing high-quality battery cells at the lowest cost. The provided model framework and optimization routine is easily adaptable for other battery types and manufacturing lines.
1 Introduction
1.1 Motivation: The Need for Performance Improvement and Cost Reduction
The lithium-ion battery (LIB) is one of the most well-established energy storage technologies and has become a common part of everyday life.[1] However, to meet the expected gigantic demand for automotive applications, of around 1 TWh by 2028, product quality must be further enhanced and manufacturing costs need to be reduced.[2] Some of the focal performance aspects for the automotive field, which need improvement, are cyclability, lifetime, charge capability, and safety, all while keeping production costs at a minimum. For this reason, a great amount of research and development is currently being undertaken to tackle these challenges. Key factors for cost reduction include minimizing the scrap rate, which can apparently reach up to 14%, and optimizing the electrode processing steps.[3-6] Improving battery performance often involves the employment of new electrode and electrolyte materials, modifying established materials, or optimizing the electrode transport properties.[3, 7] Under the second point, modifying the electrode microstructure is a main issue since its properties, such as porosity or particle size distribution, play an important role on transport processes and chemical reactions.[8-10] For example, the diffusion of lithium ions through the electrolyte seems to be the limiting factor during discharge at higher current densities.[7] However, a large variety of optimal performance objectives exist, none of which are satisfied by a universal electrode design.[7] For this reason, finding an optimal electrode design under consideration of the exact scope of application is a critical factor for producing tailored battery cells with enhanced performance.[9, 10]
The microstructure of a battery electrode is directly determined by the manufacturing process, for example, the coating, drying, and calendaring process steps directly influence factors such as the mass loading and the density.[1, 11, 12] Hence, the performance of the final battery cell is tied to the manufacturing process to a great extent.[12] Furthermore, fluctuations in the processing steps could heavily influence the microstructure and could negatively impact the performance of the final product.[1, 2, 11] Such fluctuations could lead to undesirable product qualities and large scrap rates during production. For the sake of counteracting this, it becomes imperative to determine an electrode design, which does not only deliver desirable performance properties, but is also robust against production uncertainties.[2] Consequently, to achieve a cost-effective knowledge-based manufacturing, having knowledge of the processing parameters which bring about the desired microstructure is critical. Moreover, the processing parameters should preferably be advantageous for the production, for example, by allowing for maximum throughput, to achieve a lower production cost.
Accomplishing a fully optimized battery production line is a challenging task since improving one aspect may counteract other optimization goals. Furthermore, the manufacturing process chain is highly complex, so that the exact interdependencies between the steps are not entirely defined and are subject to speculation, which further complicates the matter. At the factory level, ascertaining the optimal electrode design and process parameters (PPs) typically involves an iterative process of incremental improvement, which is associated with the risk of production delays, as well as unnecessary consumption of materials and energy.[1, 2] This issue gives incentive for a model-based approach, through which optimal PPs can be predicted, which can bring about the desired performance properties.
In literature, approaches already exist to separately optimize electrode properties based on performance goals and to optimize the production process based on desired electrode properties and process costs. However, the link between these two separate optimization procedures is still missing.
In the study by Thomitzek et al., we established a model-based digital platform for cathode manufacturing, which combines mechanistic process chain and battery cell models.[1] This platform allows the model-based investigation of the effect of the production steps on the structural properties of the intermediate and final products and on the performance of the final cell. Herein, we build upon the previously presented platform and use it to determine optimal cathode structure parameters for a desired cell performance by means of simulations. An optimization routine was established for two separate discharge current densities. We further determine the optimal combination of processing parameters for the coating, drying, and calendaring steps which bring about the previously determined microstructure, while maximizing throughput. The process design parameters are the roll temperature, the line load, the volume flow during coating, and the foil velocity. With our approach, the missing link between cost-effective manufacturing scenarios and user-defined battery properties is established. At the industrial level, our approach acts as a guide to decision-making before and during production, to increases throughput, enhance product quality, and reduce costs.
1.2 Existing Approaches for Optimizing and Analyzing Cathode Structure and Processing
Several modeling approaches and frameworks have been published in literature on the investigation and optimization of cathode microstructure and processing. The objectives of such optimizations can be performance characteristics, such as safety and energy density or processing costs.[7] Liu et al. presented a machine learning approach to predict the effect of intermediate product properties and PPs on the final mass loading of the resulting electrode.[13] Similarly, Niri et al. implemented a machine learning model to analyze and quantify the influence of processing parameters of the coating step on the physical properties of the anode and cathode coatings and on the discharge capacity. They concluded that the comma bar gap in the coating process has the highest influence on the resulting mass loading and thickness of the produced electrodes, in comparison to the coating ratio and web speed and therefore on the discharge capacity.[2] While such data-driven approaches deliver accurate results at low computational costs, they are only valid within the range of the training data and do not provide a clear understanding of physiochemical phenomena.[1, 7] Furthermore, they would require many experiments, especially when exploring a large number of design parameters.
Mechanistic models, on the other hand, represent physical processes and enable an exploration of the parameters space, beyond that which was used for model parameterization. Ngandjong et al. investigated the effect of slurry drying and calendaring on the electrochemical performance of cathodes. They used mechanistic models for the drying and calendaring steps using grain molecular dynamics and discrete element methods, respectively. For the electrochemical simulations they used the finite-element method. Even though their approach produces highly accurate and validated results, they reported a great computational expense for single evaluations of their process and electrochemical models.[14] Thus implementing their approach with a numerical optimization algorithm, which often requires many model evaluations, would not provide results within reasonable time.[15]
When it comes to electrochemical battery models, the Doyle–Fuller–Newman pseudo-2D model offers a balance between computational expense and simulation accuracy.[1, 7] Furthermore, this model can be extended to include further effects, such as degradation, or can be coupled directly with battery-processing models. Liu et al. implemented a genetic optimization algorithm for such an extended P2D model, where they optimized battery design parameters and charging strategies for reduced charging time and degradation mitigation during fast charging.[16] However, the Bruggeman relation was used to estimate the effective transport parameters of the electrodes, such as the effective electric and ionic conductivity.[17] While simple from an implementation standpoint, the Bruggeman relation only takes into account the electrode porosity as a physical parameter and neglects other important factors, such as particle size or the ratio of active material (AM) to conductive additive. To allow a more detailed analysis of structure–property relations, employing 3D microstructure models may be implemented.[8, 18] Laue et al. introduced such a model, which uses stochastically generated 3D microstructures to evaluate the effective electrical conductivity, the effective tortuosity, and the active surface area.[8] In a further study, the same authors coupled a P2D model with surrogate polynomials, representing the microstructure model, to investigate the effect of calendaring on the discharge capacity. They evidenced more accurate results than with the classical Bruggeman relation, relative to experimental data. They also determined that an optimal porosity for high current densities was around 35%.[19] Witt et al. implemented a similar approach to carry out a comprehensive parameter screening and optimization, using both half-cell and full-cell P2D models.[7] They highlighted the absence of a universal optimum for cell design, which would fulfill all optimization objectives. As a result, optimizing a cell for a particular objective, such as minimizing lithium plating, may yield less desirable characteristics in a different aspect, such as a lower capacity during fast charging. So far, the presented modeling approaches focused on analyzing and optimizing particular processes or the structural properties of the battery cell. Carrying out the proposed optimization with such modeling approaches would allow the determination optimal settings of only single processes; however, they do not reveal how the optimized parameters could interact with further processes down the chain. Few modeling frameworks exist in literature, which allow a comprehensive analysis of the manufacturing chain and its interaction with the battery cell. Schmidt et al. implemented a multilevel approach to quantify the propagation of production uncertainties along the process chain and their effect on the achievable discharge energy density.[11] They employed physical models of three successive cathode processing steps: coating, drying, and calendaring to represent a process chain. The resulting structural parameters (SPs) were passed on to a pseudo-2D battery model to evaluate the energy density. With a sensitivity analysis, they identified the impact of PP uncertainty on the performance properties of the final product. In the work by Thomitzek et al., we presented a modeling framework, which builds upon the approach from Schmidt et al.[1, 11] and allows a qualitative prediction of process impact on the battery cell performance. In the current work, we employ the established framework to carry out the optimization of the electrode structure parameters and to determine the corresponding PPs. Further studies could include other target properties for the optimization as well as could be expanded to other battery cell chemistries.
2 Methodology
2.1 The Digital Platform in Condensed Form
Our modeling framework, which is illustrated in Figure 1, will be revisited briefly. An extensive description can be found in our other publications.[1, 20] The framework consists of three modules: 1) the process chain model, 2) the battery cell model, and 3) analysis. The process chain model (1) combines mechanistic process models, whose interfaces are defined by intermediate structure and material parameters and receive PPs as input. To reduce computational expense, surrogate algebraic equations for expensive models were preferred. The final output of the process chain model (1) is the input for (2) the battery cell model, which consists of a P2D model with a structure surrogate extension, which is similar to the approach by Witt et al. and Laue et al.[7, 19] With the battery model, simulations such as charge and discharge can be carried out to analyze the influence of the input SPs on the performance. Further extensions to the P2D model could allow the analysis of more effects such as aging and thermal degradation. The (3) analysis module is a bundle of mathematical methods, which can be implemented to acquire awareness of the simulation results of (1) and (2). In our previous work,[1] we implemented the sensitivity analysis method from (3) to quantify the sensitivities between process and SPs and performance properties.
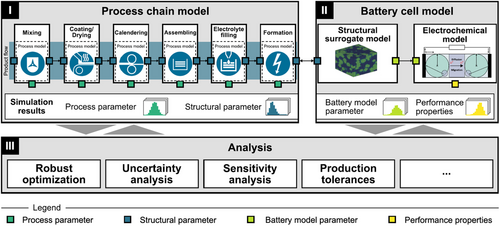
The digital platform similarly allows for the implementation of a numerical optimization procedure on both the process chain and battery cell models. With the battery cell model, the optimization can be carried out to determine the optimal cell design for attaining desirable performance properties. On the other hand, optimizing the process chain model would involve identifying the best combination of PPs to bring about the optimal cell design and deliver favorable production conditions, for example, maximizing throughput.
2.2 Battery Cell Model
The battery cell model, the second module of the presented framework (Figure 1), is used to evaluate the electrochemical performance of the digitally manufactured electrode. It consists of two submodels: the structural surrogate model and the electrochemical model, which will be briefly described in the next two subsections.
2.2.1 Structural Surrogate Model
The electrochemical performance of a LIB is determined by the microstructure of its electrodes. This microstructure is already formed during different manufacturing processes such as coating, drying, calendaring, and electrochemically during the formation process. Parameters, which may highly influence the performance of the final cell, are porosity, tortuosity, mass fractions of the materials, or the thickness of the electrodes. To represent these properties a structural model is needed.[19]
One possibility is the Bruggeman model. The Bruggeman model is based on a simplified calculation of the electric and ionic conductivity by assuming transport processes inside homogeneous bodies with isotropic components of the AM and the electrolyte. In addition, particles are supposed to be spherical and are not in contact with each other. Laue et al. developed a 3D voxel-based microstructural model. This model simulates a cathode microstructure consisting of the AM, an electron-conducting additive (ECA), and an electrolyte, representing the volumetric ratios of the individual materials.[8] To enhance computational efficiency, a surrogate model was implemented, which was parameterized with data from the actual model.[19]
2.2.2 Electrochemical Model
The electrochemical model is a Doyle–Fuller–Newman pseudo-2D cathode half-cell model.[1, 21, 22] It receives as input: the active surface area as, the effective tortuosity , and the effective electrical conductivity of the solid phase from the structural surrogate model, as well as further electrode SPs (i.e., porosity and thickness). Subsequently, simulations such as charge or discharge can be carried out to analyze the electrochemical performance of a given set of SPs.
2.3 Optimization Procedure
In this section, the implemented optimization procedure is presented. The procedure consists of three overarching steps, which are presented visually in Figure 2. The first step, which is the formulation of the optimization problem, involves defining the optimization goals, the design variables, and the optimization constraints.[23, 24] In this step an initial point is also defined. In the second step of the procedure, the optimization is carried out with the battery cell model, with the electrode SPs as the design variables and the objective as some indicator of electrochemical performance, such as the achievable energy density. After determining the optimal SPs in step 2, step 3 is carried out, which involves identifying the processing parameters, which correspond to the optimal electrode structure parameters. Furthermore, the processing parameters are optimized to fulfill a certain level of production efficiency, such as maximizing throughput or profit. The formulations of the optimization problems in this work are described in Section 2.3.1 and 2.3.2 for the battery cell and process chain models, respectively.
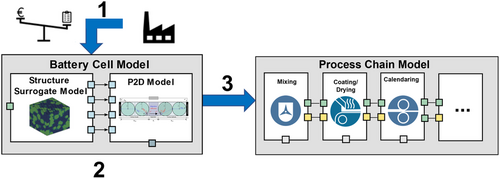
2.3.1 Optimization with the Battery Cell Model
In this section, the optimization problem is formulated, and the applied procedure for the battery cell model will be described. For this study, the volumetric energy density was chosen as the target performance metric, since it considers both voltage and capacity and thus allows to evaluate the energy conversion efficiency. A second reason for choosing the volumetric energy density is its relevance to electric vehicle applications, since increasing it allows for a larger travel distance without further increase in the battery size.[25] The most modified electrode SPs for enhancing performance properties are layer thickness, porosity, and particle size.[7] Decreasing the porosity, through, for example, calendaring, enhances the electrical conductivity of the electrode, since it allows percolation networks to form in the conductive additive and binder matrix. On the other hand, increasing the porosity also decreases the tortuosity, which improves ionic transport in the electrolyte phase.[8] Herein, the chosen electrode design variables were chosen to be mass loading and density, which are more intuitive values from a processing point of view and can be directly translated into cathode thickness and porosity. Also, the sensitivity analysis in our previous work, by Thomitzek et al., revealed that the postcalendaring density and mass loading have a great influence on the achievable discharge capacity and volumetric energy density, since these two values directly affect the layer thickness and porosity.[1] The parameterization of the model was accomplished using discharge voltage curves, which were experimentally obtained from a coin cell. The cathode of the cell consisted of 95.5 wt% NMC 622 as the AM, 2.25 and 0.75 wt% of SuperC45 and SFG6L as the conductive additives, respectively, and 1.5 wt% PVDF as the binder. The parameterization was carried out by defining it as an optimization problem, where the objective was to minimize the difference between the simulated and experimental discharge curves with the model parameters as the design variables. The initial and maximum concentrations of lithium ions c0 and cmax were obtained using the formation curve, whereas the reaction rate constant for the Butler–Volmer equation, ke, solid diffusion coefficient, Ds, and the intrinsic electronic conductivity of the AM, , were determined by simultaneously minimizing the difference between simulated and experimental discharge curves for different current densities, that is, a single set of parameters was obtained, which reproduces multiple discharge curves at different C-rates. The values of the obtained model parameters can be found in our previous study, by Thomitzek et al.[1]
The optimization and parameter study were carried out in MATLAB. As an optimization constraint, it was set that fluctuations in ω due to a 2% fluctuation in mL and ρ should be minimized. To allow for faster model evaluations, a surrogate model based on 50 points from the battery cell model was generated. Both the optimization and generating the surrogate model were accomplished using UQLab, which is an open-source MATLAB-based framework for uncertainty quantification (UQ).[26] The optimization was set up as a reliability-based design optimization (RBDO) problem and the surrogate models were generated using the Kriging method.[27, 28]
2.3.2 Optimization of the Process Chain Model
The process chain model is based on the concept of coupled process models to describe the process–structure relation in individual process steps and along the process chain.[1] Optimizing the process chain model requires defining single or multiple performance, in indicators of production to be either maximized (e.g., throughput, process capability, machine utilization) or minimized (e.g., scrap rate, energy demand, manufacturing cost). Many performance indicators influence each other, for example, process capability might impact throughput and scrap rate, which can hinder a joint optimization. Consequently, it is preferable to establish superordinate performance indicators, which allow to relate and effectively balance the individual performance indicators.
The profit of production combines a variety of relevant performance indicators such as throughput, process capability, machine utilization, scrap rate, energy demand, and manufacturing costs in a single value and thus is suited as a superordinate performance indicator. In order to maximize profit, either the manufacturing costs are reduced or production capacity, that is, number of battery cells, is increased so that economies of scale can be exploited.
While the price per cell, pu, can be approximated by current market prices in order to ensure a competitive production, the number of cells produced is a direct consequence of the process chain configuration, that is, number of machines per process, shift system, waiting times, and PPs affecting machine throughput. It should include variable and fixed costs, an additional markup and taxes. The price should be reasonably balanced in order to achieve a sufficient markup for long-term success on the one hand and to remain competitive in the market on the other.
Similarly, manufacturing costs must be clearly defined and should be divided into variable and fixed costs in order to assess possible economies of scale. The profit model parameters are to be linked to the PPs of the process chain model to allow a joint optimization. For example, the roll temperature of the calender impacts the coating thickness during the calendering process and simultaneously causes variable costs due to the energy requirement.
In the optimization of the process chain model, the profit model serves as the objective function and the process models are set as equality constraints. The optimal design parameters of the process models are determined with the goal of achieving the optimal SPs from the battery cell optimization as well as maximizing the profit. To enable an efficient optimization, initial process and SPs should be selected within common ranges. The profit approach focuses on optimization in terms of nominal values of process and SPs, but does not allow for consideration of production uncertainty. While uncertain parameters can be easily considered by the process models using deviated parameters, parameter uncertainty regarding revenue, manufacturing cost, and thus profit requires a high level of detail of the respective models, for example, capital expenditure for machines as a function of machine precision (see also Thomitzek et al.[29]).
Similarly, greenhouse gas emissions, that is, CO2 equivalents, could serve as another superordinate performance indicator to optimize the production process. However, CO2 emissions are currently more intangible and require a deep understanding and modeling of not only the foreground (i.e., factory with its production system) but also the background system (i.e., emissions related to energy system and raw materials). While optimization via CO2 equivalent emissions is more challenging at present, it could play a more important role in the not too distant future due to ambitious CO2 targets and resulting rising cost of tons of CO2.
3 Use Case
After defining the optimization problems in Section 2.3.1 and 2.3.2, the results of the optimization procedure for the process chain and battery cell models as well as the parameter study with the battery cell model are presented. The overarching goal is to determine the optimal setting for the coating/drying and calendaring steps to achieve battery cells with a high volumetric energy density while maximizing the manufacturing profit.
3.1 Optimization, Parameter Study, and Uncertainty Analysis
As described in Section 2.3.1, the volumetric discharge energy density, ω, was chosen as a performance metric with design variables being the cathode mass loading, mL, and density, ρ.
For the optimization, two parameter spaces were considered: the first one, to which is referred as the global parameter space, represents a range for the mass loading and density, which is interesting from a research point of view, as indicated by Kremer et al., and is defined by the validity range of the structure surrogate model as well; the second one, introduced herein as the industrial parameter range, represents values, which are typically applied in industry.[30, 31] The spaces were defined by setting the optimization boundaries to the limits of the applied parameter spaces, which are shown in Table 1. The use of two design spaces was done to be able to distinguish between optimal electrode designs on research level and on industry level. The initial point for the optimization was chosen to be the center point of the industrial parameter range, as shown in Table 2.
| Parameter | Lower limit | Upper limit |
|---|---|---|
| m L (global) [mg cm−2] | 20 | 60 |
| ρ (global) [g cm−3] | 2.0 | 3.8 |
| m L (industrial) [mg cm−2] | 25 | 35 |
| ρ (industrial) [g cm−3] | 2.7 | 3.3 |
| Point | C/2 | 1C |
|---|---|---|
| Initial point | m L = 30.00 mg cm−2, ρ = 3.00 g cm−3 | m L = 30.00 mg cm−2, ρ = 3.00 g cm−3 |
| Global optimum | m L = 51.28 mg cm−2, ρ = 2.46 g cm−3 | m L = 31.33 mg cm−2, ρ = 2.25 g cm−3 |
| Industrial optimum | m L = 35.00 mg cm−2, ρ = 2.70 g cm−3 | m L = 35.00 mg cm−2, ρ = 2.70 g cm−3 |
In order to analyze the exact influence of the cathode mass loading and density on the discharge energy density and better understand the optimization results, a parameter study was carried out, where ω was calculated for 400 different combinations of mL and ρ from the global parameter space.
The results of the optimization and parameter study with the battery cell model are visualized in Figure 3, where the graphs show the achieved volumetric discharge energy density, which was normalized with respect to the maximum value of the energy density to give . Figure 3a shows the results for C/2 and Figure 3b for 1C. The areas with light shades of yellow represent higher energy density, whereas dark shades represent lower energy density. The trends for both discharge rates show larger areas with lighter shades at lower cathode densities, that is, at ρ between 2.0 and ≈3.5 g cm−3. In contrast, higher cathode densities predominantly yield lower energy densities. The impact of the mass loading, mL, on differs depending on the applied discharge current density. While a higher mass loading increases the achievable energy density at C/2, the same can not be observed for 1C. In fact, at 1C, a cathode mass loading above 40 mg cm−2 leads to a decrease in , which is more pronounced at lower cathode densities. Generally, Figure 3b shows larger dark areas than 3 a), indicating that high energy densities are achievable over a larger parameter space at C/2 compared to 1C.
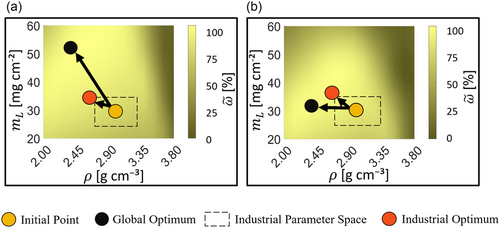
The first observation, which can be highlighted from the parameter study, is that is highly dependent on the microstructure parameters (ρ and mL) and applied current density. The reason behind the aforementioned dependence is that the cathode mass loading and density directly determine its thickness and porosity, which in turn affect the reaction kinetics and transport processes. A high porosity, which is usually achieved at a lower cathode density, translates to a lower effective electrical conductivity and also to a lower tortuosity, as can be seen in the Supporting Information. A less tortuous electrode allows for higher effective ionic conductivity and diffusivity, which improve the transport efficiency of lithium ions.[8, 19] Higher cathode densities lower the porosity, which increases the tortuosity and decreases the active surface area, both of which have a disadvantageous effect on ion transport and reaction kinetics. A higher areal mass loading signifies a larger mass of AM per unit area and thus a thicker cathode, assuming constant density. Thicker cathodes are theoretically advantageous, since they can enhance energy density and reduce production costs simultaneously.[7] However, thicker electrodes also tend to suffer from ionic transport limitations, especially at higher discharge current density. The concentration profiles of lithium ions across the cathode thickness at the end of discharge, which can be seen in the Supporting Information, show that higher concentration gradients exist for higher values of mass loading at higher discharge current densities. This could be a cause of electrolyte depletion, which is why lower capacities are attained for the thicker electrodes. Similar results were reported in the simulation study with a P2D battery cell model, which was done by Du et al.[32] Ionic transport limitations also lead to a smaller parameter range with higher energy density at 1C than at C/2. This relation implies that a battery cell, with the purpose to have high energy density for high current applications, has a narrower design space for the manufacturer.[7, 30, 32]
Similarly, the optimization delivered different results for each of the current densities, especially in the global parameter space, that is, the black dots in the figures. At C/2, the global optimum is at a relatively high mass loading of mL = 51.28 mg cm−2 and low density of ρ = 2.46 g cm−3. This combination of parameters represents a cathode with a relatively high thickness and high porosity. On the other hand, the global optimum at 1C is at a relatively low mass loading of mL = 31.33 mg cm−2 and low density of ρ = 2.25 g cm−3, which can be attributed to a cathode with lower thickness and higher porosity. For both current densities, a lower density and thus higher porosity was reached at the optimum. A high porosity lowers the tortuosity of the electrode, which enhances the ionic transport properties. A higher mass loading was optimal at C/2 in comparison to 1C. At C/2, the discharge process benefits from the presence of more AM per unit area and delivers a higher capacity. In contrast, the transport limitations at 1C imply a lower mass loading, meaning a lower thickness and shorter diffusion pathways, being optimal for achieving a higher capacity. Optimization in the industrial parameter space indicates the same point at both current densities at mL = 35 mg cm−2 of ρ = 2.7 g cm−3. In both cases, the industrial optimum yields electrodes with a lower energy density than the global optimum. However, since it was the optimal result within its parameter space for C/2 and 1C, it can be seen as the more versatile design.
The reason behind the disparity between the global and industrial optima could be the optimization objective itself. Since maximizing the energy density was the only objective in the presented use case, other aspects, such as safety, aging, or charge behavior, were not taken into account. Implementing a multiobjective optimization could assist in determining an electrode design which offers a balance between multiple performance goals.
One further aspect, which is highly relevant for cell manufacturing, is the robustness of a certain electrode design against fluctuations in the design parameters. Since the manufacturing process can be prone to uncertainties, for example, due to machine tolerances, it is desirable that the electrode design has high robustness against process fluctuations. For this reason, an UQ is carried out for each of the three points (initial point, global optimum, and industrial optimum). The results are achieved by generating normal distributions of 10 000 samples for the cathode mass loading mL and density, ρ. The mean values of the distributions are the values of mL and ρ at the initial point, the global optimum, and industrial optimum. The standard deviation is defined as 2%. The generated values from the distributions are then passed to the battery cell model and the resulting energy densities are evaluated.[11, 33] An example for the generated distributions for the initial point is shown in the Supporting Information. The results of the UQ are shown in Figure 4 for C/2 in (a) and 1C in (b).
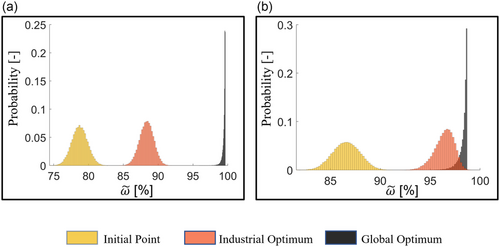
Figure 4 shows histograms with the probability distributions of normalized volumetric discharge energy density . In Figure 4a, where the UQ results for C/2 are shown, the histograms for the initial point (yellow) and industrial optimum (red) have symmetrical and relatively wider distributions than for the global optimum (black). In Figure 4b, where the UQ results for 1C are shown, the initial point has a symmetric and wider distribution, whereas the industrial optimum has a narrower distribution, which is slightly skewed to the right. In both (a) and (b), the global optimum (black) exhibits a very narrow distribution next to two other points.
The distribution shapes of the histograms reveal the differences in the robustness of the discharge energy density at the investigated points against fluctuations in mL and ρ. The very narrow distribution of the black point in both Figures 4a,b, means that the global optimum exhibits the lowest sensitivity or the highest robustness of design under the considered parameter fluctuations. In comparison, the relatively wider distributions of the red and yellow points indicate a higher sensitivity, although the industrial optimum is slightly less sensitive than the initial point in Figure 4b. In conclusion, the UQ for the global optimum shows the highest level of robustness against uncertainties in cathode mass loading and density at both current densities. At C/2, the UQ for the initial point and the industrial optimum show a similar response to uncertainties, whereas at 1C the industrial optimum was slightly more robust than the initial point.
The parameter study and optimization show that enhancing the achievable energy density of a manufactured cell can be done just by adjusting and optimizing the electrode design. As was seen, the global optima differed significantly, depending on the applied current density. This statement reaffirms the importance of taking the application scope into account when optimizing cell design. Furthermore, the UQ showed that different electrode designs respond differently to structural fluctuations with respect to their achievable energy density. In the next section, the optimal processing scenarios will be determined for obtaining the optimized electrode designs, while maximizing profit.
3.2 Optimized Process Parameters
The goal of the process chain optimization is to determine the combination of PPs, which leads to an optimal electrode design and maximizes profit at the same time. The industrial optimum from Section 3.1 (35 mg cm−2 for mass loading and 2.7 g cm−3 calendered coating density) was chosen as the target electrode design. This design provides an optimal volumetric energy density for both C/2 and 1C and thus has a wider range of application than either global optima. In the presented use case, the main focus of the manufacturing chain will be on the coating/drying and calendering processes.
Establishing the objective function requires defining the profit as a difference between revenue and cost, as shown in Equation (2). First, in order to calculate the revenue, R, the price per cell, pu, is set based on a target price of 100 € kWh−1 and a standard BLB cell format with ten anode–separator–cathode compartments and a total of 37 Wh energy storage capacity, that is, pu = 3.70 € cell−1. The throughput or the number of produced cells, n, is determined by the production speed of the roll-to-roll coating/drying and calendering process, that is, foil speed, which is assumed to be equal for both process steps. Similarly, it is assumed that both processes are the bottleneck of production, which implies that the two processes limit the total output of production along the process chain. Production scrap is neglected in the present scenario.
Now that the cost, C, and the revenue, R, have been defined, the profit can be calculated using Equation (2) and the optimization can be carried out.
To assure that the optimal SPs, that is, the optimal mL and ρ from Section 3.1, are obtained, an optimization constraint was set using the process models for the coating/drying and calendering processes. The bounds for the input parameters, that is, PPs and SPs, are set to reasonable values, which are the respective design spaces of the data-based models. The data-based models for the electricity demand are only applicable within their original parameter design space and thus are not viable for extrapolation. The optimization was performed with the SciPy library in Python for the industrial optimum at mL = 35 mg cm−2 of ρ = 2.7 g cm−3 as well as the global optimum for C/2 and 1C at mL = 51.28 mg cm−2 of ρ = 2.35 g cm−3, respectively, and mL = 31.33 mg cm−2 of ρ = 2.25 g cm−3. The optimization results for the PPs and SPs as well as the revenue and manufacturing cost can respectively be found in Table 3 and 4.
| Parameter | Unit | Type | Industrial optimum | Global optimum C/2 | Global optimum 1C |
|---|---|---|---|---|---|
| Calendering line load | N mm−1 | PP | 324.1 | 213.6 | 94.9 |
| Roll temperature | °C | PP | 30.0 | 30.0 | 30.0 |
| Volume flow during coating | mL h−1 | PP | 3 403.5 | 4 986.7 | 3 046.7 |
| Foil velocity | m min−1 | PP | 2.0 | 2.0 | 2.0 |
| Coating thickness after calendering | μm | SP | 129.6 | 218.2 | 139.2 |
| Porosity after calendering | % | SP | 37.3 | 45.4 | 47.8 |
| Porosity after drying | % | SP | 55.2 | 55.2 | 55.2 |
| Wet mass loading | mg cm−2 | SP | 50.0 | 73.3 | 44.8 |
| Coating thickness after coating | μm | SP | 226.9 | 332.4 | 203.1 |
| Parameter | Unit | Industrial optimum | Global optimum C/2 | Global optimum 1C |
|---|---|---|---|---|
| Number of cells produced | – | 1 001 143 | 1 001 143 | 1 001 143 |
| Power demand coating/drying | W | 87 681 | 87 681 | 87 681 |
| Energy demand coating/drying | kWh | 768 082 | 768 082 | 768 082 |
| Energy cost coating/drying | € | 204 617 | 204 617 | 204 617 |
| Power demand calendaring | W | 4 954 | 4 993 | 5 036 |
| Energy demand calendering | kWh | 43 403 | 43 743 | 44 113 |
| Energy cost calendering | € | 11 563 | 11 651 | 11 752 |
| Revenue | € | 3 704 229 | 3 704 229 | 3 704 229 |
| Manufacturing cost | € | 216 180 | 216 268 | 216 369 |
| Profit | € | 3 488 049 | 3 487 961 | 3 487 860 |
Table 3 shows the PPs and SPs, which result from the process chain optimization. Here it can be seen that the coating volume flow velocity and the calendering line load are the sole PPs, which vary between the different points, whereas the roll temperature and foil velocity remain constant. The highest volume flow velocity is required for the global optimum at C/2, which can be justified through its relatively high mass loading. The same trend for the volume flow velocity follows for the other two points. The highest calendering line load is needed for the industrial optimum, since it has the lowest porosity. The roll temperature remains constant at 30 °C for all three points so as to minimize the energy demand and cost. In practice, the roll temperature is operated at higher temperatures (≈80 °C) due to its beneficial impact on the coating. However, further model extensions are needed to include the impact of temperature on the resulting SPs. Similarly, the foil velocity is set to the maximum value in each scenario, that is, to increase throughput and thus revenue.
In Table 4, it is shown that if 1 001 143 battery cells are produced over a year with the desired design, a profit of 3 487 663 € can be expected for the defined boundary conditions at the industrial optimum. The results for the other two points differ only slightly from the industrial optimum. The revenue for all three points is identical, since the same number of cells is produced, whereas the manufacturing costs differ only slightly. In fact, the only cost, which varies across all three points, is that of the calendering process. As shown in Table 3, only the volume flow velocity and the calendering line load varied between the points. Both of these processing parameters are very small contributors to the energy demand of the process chain. The roll temperature has a larger impact on the energy demand and cost. However, as previously stated, the process models would require extensions, which include additional process–product interdependence such as binder migration during drying, to consider such effects. Thus, the interpretation of the results must be done based on the considered simplifications and assumptions.
In conclusion, the presented optimization of processing parameters successfully yielded the required calendering line load and temperature as well as coating volume flow and foil velocity to achieve the defined electrode structures. Furthermore, the procedure managed to predict the settings which also maximize the profit, by reducing the manufacturing costs. While the results are limited to the presented assumptions made for the BLB, that is, focus on coating/drying and calendering processes as bottleneck as well as electricity as manufacturing cost, the approach can be transferred to other battery cell production lines to identify optimal PP settings.
4 Conclusion and Outlook
Using our previously established digital platform in ref. 1, which couples process chain and battery cell models, an optimization approach was presented for determining the best possible manufacturing scenario for producing NMC622 cathodes with predefined performance properties. We implemented our approach in a use case. In the first step, the optimization objectives for the battery cell and process chain models were defined: maximizing the volumetric discharge energy density and the profit, respectively. The design variables for the battery cell were the cathode areal mass loading and postcalendering density, since these govern the transport processes during discharge; for the process chain model, the design variables were the PPs for the coating/drying and calendering steps: line load, roll temperature, foil velocity, and volume flow during coating. Furthermore, a parameter study and an UQ revealed the impact of the design parameters on the achievable energy density. In the second step, the optimization was carried out using the battery cell model to determine the cathode design for maximum volumetric energy density. Here two design spaces were considered: a larger one, which represents designs currently under research (global), and a smaller space, which represents typical values from industry (industrial). The results showed that the optimal cathode design in the global space was dependent on the applied discharge current density, where a lower mass loading was preferable at 1C in contrast to C/2, where a higher mass loading was favorable. The optimization for industry-relevant parameter sets delivered the same result for both C/2 and 1C. Despite the fact that the industrial optimum delivered less energy density than the global optima, it made up for it in versatility, since it offered an optimal design for both investigated C-rates and thus a wider application range. The UQ showed that the global optimum had the highest level of robustness against fluctuations in the design parameters. The third and final step was to determine the optimal parameters for the coating/drying and calendering processes, which can maximize the profit and realize, while realizing the determined optima from the battery cell model optimization. The profit was defined as the difference between revenue and cost. The revenue was calculated based on a price of 3.70 € cell−1. The cost was defined as the electricity consumption of the coating/drying and calendering machines, based on a price of 0.27 € kWh−1. The power demand for the machines was calculated using regression models based on experimental data from the Battery LabFactory Braunschweig (BLB). The optimization routine managed to determine the best combination for the PPs, which allowed for the manufacturing of ≈1 000 000 cells with the desired design, while achieving a profit of ≈3 500 000 €.
With the presented routine, a framework is established to determine the most profitable setting for the coating/drying and calendering processes for producing battery cells with high volumetric discharge energy density at different current ratings. The presented method is adaptable to other battery cell types, performance objectives, and processing steps, in order to determine optimal machine settings and assist with decision-making before and during production. Future work will focus on adapting the routine to different battery types and on including a multiobjective optimization to simultaneously consider multiple design goals. Furthermore, extensions shall be added to the process chain optimization, in order to include further physical effects, such as binder migration.
Acknowledgements
The authors thank the German Federal Ministry for Research and Education for funding Sim4Pro (grant number 03XP0242B) within the ProZell Cluster. Furthermore, the authors gratefully acknowledge Ulrike Krewer, Fridolin Röder, and Oke Schmidt for their previous work, which was the inspiration for this article. Finally, the authors would like to thank Sören Scheffler of the Institute for Particle Technology for generating and providing the necessary data from the calendering of the electrodes.
Open Access funding enabled and organized by Projekt DEAL.
Conflict of Interest
The authors declare no conflict of interest.
Open Research
Data Availability Statement
Research data are not shared.