Contingency and Emergency Manual Procedures for Calculation Firing Data Using Direction and Distance Coefficients
Funding: This work was supported by Ministry of Education, Youth and Sports (SV23-FVL-K107-PEK and SV24-FVL-K107_DRA).
ABSTRACT
This paper presents an analytical method for calculating artillery firing elements under contingency and emergency conditions, where reliance on automated systems may be compromised due to electronic warfare or system failure. The method introduces direction (Cdir) and distance (Cdis) coefficients, enabling accurate and efficient computation of firing data using only basic tools such as a calculator or tabulated values. These coefficients are derived through a geodetic approach involving auxiliary angles and coordinate transformations within the MGRS and UTM systems. The method addresses a critical gap in NATO's PACE (Primary, Alternative, Contingency, Emergency) framework by offering a time-efficient, low-error alternative to traditional graphical techniques. An experimental study compared the proposed analytical approach with graphical methods, involving expert artillery teams from Czech and Slovak forces. Results demonstrated that the analytical method significantly reduces errors in both direction and distance while maintaining comparable or shorter computation times. The study confirms the method's effectiveness in degraded operational environments and recommends its integration into artillery training and doctrine. This solution enhances the resilience and operational readiness of artillery units, particularly in multidomain operations where technology denial is a growing threat.
1 Introduction
Providing accurate and timely fire support is one of the key responsibilities of artillery, often serving as a decisive factor in the success of military missions. To ensure this capability, it is vital to maintain continuity and accuracy in all operational situations, including degraded environments where primary technological systems may fail. Recent conflicts, such as the war in Ukraine, have highlighted the vulnerability of modern systems to enemy interference, including jamming, spoofing, and electromagnetic disruption. Overreliance on automated systems for fire control can expose operational weaknesses, leading to a need for alternative solutions. In the North Atlantic Treaty Organization (NATO) context, the PACE (Primary, Alternative, Contingency, Emergency) framework provides multiple layers of redundancy for preparing firing elements. Nevertheless, current contingency and emergency measures rely heavily on graphical methods, which can be time-consuming and error-prone under operational stress. This need for systemic resilience is also reflected in broader defense planning models, such as the fair insurance-based national defense budgeting proposed by Šlouf et al. [1], who argue that defense expenditure should reflect political commitments, societal wealth, and expected threat levels. Additionally, adversaries capable of disrupting technologies can exploit dependence on automation, making it essential for NATO forces to develop robust, technology-independent procedures such as Karben [2], Markov [3], Ivan et al. [4], Świętochowski [5]. Furthermore, according to Rashid et al. [6], using artificial intelligence (AI) in fire control introduces additional vulnerability to cyber-attacks and electronic warfare. However, it also presents opportunities to automate compensations for degraded conditions if properly integrated. These dual aspects of AI require a balanced approach in doctrine and development to prevent over-dependence and maintain operational flexibility. As Najgebauer [7] points out, electronic warfare's growing influence significantly affects operational capabilities' development, making it essential to incorporate counter-EW measures into both system architecture and tactical planning.
This paper addresses these challenges by proposing an analytical approach to complement existing contingency and emergency procedures in the PACE framework. The authors introduce the use of the direction coefficient () and range coefficient () for the MGRS (Military Grid Reference System) and UTM (Universal Transverse Mercator) coordinate systems, enabling accurate and efficient calculation of firing elements without relying on automated systems. The objective is to enhance operational resilience in degraded environments by offering an alternative method that reduces dependency on graphical tools. The study further evaluates the proposed approach through experiments, comparing its accuracy and efficiency to traditional methods, demonstrating its potential for broader adoption across NATO artillery and related specializations.
2 Literature Review
Degraded operational environments are an emerging trend in modern military operations, including artillery activities. This shift is informed by lessons learned from the Russia-Ukrainian war and the expansion of operational domains into space called multidomain operations (MDO). The key topics are, in particular, the planning of multidomain operations in the context of the military decision-making process (MDMP), the capabilities of individual elements in the area of operations in the context of all considered domains, and the conduct of combat operations. Artillery operations, its fire control system, and thus the determination of elements for artillery fire are also integral parts of the process [8].
Blaha et al. [9] comprehensively discuss linear and angular challenges in fire control systems, highlighting the importance of accurate angular measurements in artillery fire planning under complex conditions. Mathematical modeling and simulation of artillery fire processes are essential for developing effective fire control procedures. Song et al. [10] provide a thorough overview of military simulation data frameworks that can support this kind of modeling, even in degraded conditions. Operations in a multidomain environment and interactions between domains are addressed by Najgebauer [11]. Kyu [12] analyzes the success of implementing MDO issues within the South Korean military.
Multidomain operations appear as a central theme in articles dealing with the technical aspects of the combat set elements and the technology of the assets employed. At the same time, it is clear that multi-domain operations are not only a prerogative of the military environment, but also of the civilian sphere, where people are involved in spreading fake news and exposing it within individual domains. Degradation of operations and assets and adaptation of military units to scenarios where access to modern technologies is limited or compromised has become a frequent topic of research. For instance, Leinberger [13] examines the potential of units in D3SOE (Denied, Degraded, Disrupted Space Operations Environment), while Stepanoff [14] emphasizes the importance of maintaining command and control capabilities under such conditions. Similarly, Withington [15] highlights the critical role of electromagnetic spectrum control, particularly in ensuring reliable radio communication, as a cornerstone for coordinating units in degraded environments.
Nelson [16] provides a strategic perspective on optimizing artillery operations under such challenges, while Świętochowski [17] and Repík et al. [18] point out the importance of learning from recent conflicts and adapting to evolving threats. Zahradníček et al. [19] link these operational demands to the necessity of integrating them into military education and leadership training, and Varecha [20] as well as Turaj et al. [21] emphasize the importance of education and prioritize the simulation technologies for the quality of acquiring practical skills. This approach is fully applicable for artillery fire direction education. Specific studies address practical solutions for degraded environments, such as the use of High Mobility Artillery Rocket Systems (HIMARS) Yang [22], communication tools Lapic [23], navigation systems and their protection Griffioen [24], or reconnaissance of artillery firing positions Ivan et al. [25].
The necessity of preparing an artillery battery to provide joint fire support in a degraded operational environment while maintaining the ability to execute accurate computational procedures is addressed by Beatty [26], but at the same time he cites the need to maintain “charts and darts,” the increase in human error during computations, and the increase in the time required to execute computations. The conclusions state the necessity to increase the time allocation of teaching and training for manual procedures and the need to equip the unit with the means to perform manual calculations. From a training accuracy perspective, Serhienko et al. [27] emphasize the need for scientifically grounded methodologies for assessing artillery fire accuracy during training under both optimal and degraded conditions, highlighting practical shortcomings in traditional evaluation approaches. Artillery firing is also dealt with by Boltenkov et al. [28], but they concentrate on the overall effectiveness of artillery fire, particularly in the context of the unit's time in firing position and ammunition consumption. Zhang et al. [29] present the possibility of refining artillery fire by increasing the accuracy of the data in the firing tables. Firing tables are an integral part of manual procedures for determining elements to fire and thus are part of the PACE plans of units within the means used to prepare elements for firing.
The growing importance of degraded operations and PACE methodologies across various military specialties is underscored by papers addressing the rapid evolution and modernization of technologies used on the battlefield, such as unmanned ground vehicles Nohel et al. [30], UAVs (unmanned aerial vehicles) Stodola et al. [31, 32], software solutions for operational support Sedláček et al. [33], automated systems of command, fire control, and target acquisition Mušinka et al. [34] and advanced algorithms for artillery operations Klima et al. [35]. Despite this growing interest, there remains a notable lack of scientific literature on calculating firing elements for artillery within the PACE methodology under degraded conditions. While manual methods for determining firing elements have been discussed in Šustr [36] and Vajda [37, 38], these models are typically proposed as alternatives to graphical procedures or automated fire control systems (AFCS) without addressing the use of distance and direction coefficients or providing detailed assessments of calculation accuracy and efficiency. Varecha et al. [39] orient their work on the effectiveness and errors of calculations of indirect fire systems. Mušinka et al. [40] focus on the accuracy standards achieved by the modern devices or tools used to measure input data for predicted artillery fire. Ivan [41] focuses on emergency artillery procedures for meteorological modeling. Blaha [42] describes control methods for artillery units based on operational experiences of the Czech Armed Forces abroad, aiming to improve efficiency under restricted conditions. Švehlík [43] uses alternative approaches for artillery operations during fire missions, though his focus lies in tactical considerations rather than the calculation of firing elements. Similarly, Blaha [44] discusses firing element calculations using the miles rule but emphasizes its use as a contingency for AFCS failure.
New approaches such as intelligent visual systems for battlefield analysis and targeting have also been reviewed, showing promise for degraded environments where traditional sensors may fail according to Wu et al. [45]. Majstrenko et al. [46] deal with the mathematical model of full preparation and component calculations for AFCS. Du [47] presents element calculations for artillery firing using a new approach based on the impact triangle and an improved ballistic algorithm. Virtual simulation environments for testing battlefield concepts, including the use of expendable ground vehicles in support of artillery, offer valuable insight into real-time degraded operations scenarios, Andersson et al. [48]. The relevance of this topic is confirmed by contributions from other military fields that deal with manual and alternative procedures for degraded environments, such as Sedláček [49]. These requirements are gradually integrated into national and NATO doctrines, including STANAG standards and degraded environment manuals such as AArtyP-5 [50]. MDO and degraded operations environment represent a modern and topical issue. At the same time, the combat use of artillery is a highly topical issue, even in an ongoing war. The need to provide the key requirement for the ability to continuously, accurately, and timely compute elements for artillery firing is critical. This study presents only one possible option to diversify and structure PACE in preparing elements for firing. The method of distance and direction coefficients in degraded operations is a very accurate method that fits into the broader context of current military challenges and complements current knowledge in the artillery field.
3 Theoretical Derivation of Range and Direction Coefficients for Determining the Firing Elements of Artillery
- Automated Systems—Utilizing hardware and software components of Automated Fire Control Systems (AFCS);
- Backup Systems—Employing spare hardware and software resources for AFCS;
- Graphical Methods—Using fire control instruments, maps, or emergency graphic templates;
- Analytical Methods—Applying mathematical formulas through programmable calculators with predefined calculation macros, standard calculators with step-by-step manual formula entry, direction and distance coefficients, and mathematical tables (though rarely used in practice) [51].
- pendant CA corresponds to ΔE = EC–EB (difference of E coordinates);
- pendant BA corresponds to ΔN = NC–NB (difference of N coordinates);
- hypotenuse BC is the topographic range of the target;
- The angle ABC between the direction of the N-axis and the direction of the target is the (topographic) bearing (direction) of the target.
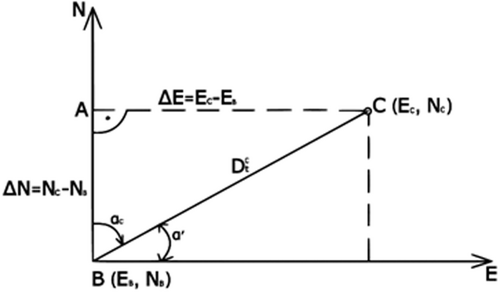
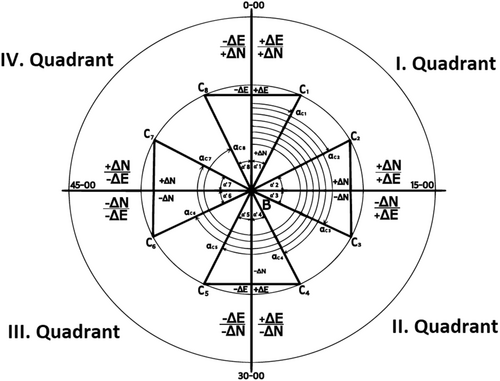
The tangent of the angle can be used to determine its magnitude conveniently with a calculator or by referencing trigonometric function tables. Figure 2 illustrates the values of the tangent of alpha prime (), with examples provided for II. Quadrant, such as and , among others, corresponding to different target positions relative to the firing position. The relationship between the coordinate differences and their respective signs enables the identification of the quadrant in which the angle lies, as well as its adjacency to a specific coordinate axis . Once the angle is determined, it can be used to calculate the target bearing as shown in Table 1.
| Quadrant | I | II | III | IV | |
|---|---|---|---|---|---|
| Coordinate difference signs | + | − | − | + | |
| + | + | − | − | ||
| Target direction (bearing) | 15−00− | 15−00 + | 45−00− | 45−00 + | |
| 30−00− | 30−00 + | 60−0− | |||
Given the value of the auxiliary angle , the topographic distance to the target can be determined based on the following principles, as illustrated in Figure 2:
To facilitate the calculation of the target bearing without the use of a calculator, a specialized table can be constructed to provide the direction coefficients () and distance coefficients (), as shown in Table 2. Table 2 includes pre-calculated values of the target directivity and the secant of the auxiliary angle sec . The rows and columns of the Table 2 are organized to simplify reference: the hundreds of parts are placed in the top and bottom rows, while the tens and units are listed in the leftmost and rightmost columns. The corners of Table 2 indicate the ratios of the coordinate differences, including their signs, with the smaller coordinate difference divided by the larger one, arranged according to the respective quadrants.
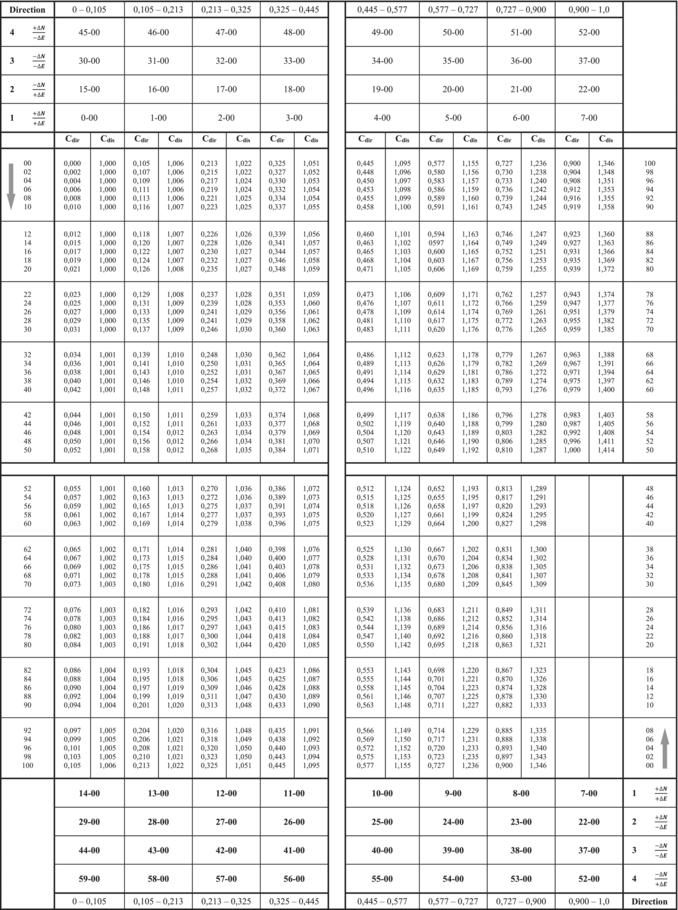 |
Table 2 takes the as its input. The columns with absolute values of are denoted as (direction coefficient). The values of spans from 0 to 1 (; ; ; because there will always be ).
Němec et al. [52] demonstrate the principle of using accessible computational tools to solve complex problems, such as location optimization using spreadsheet-based solvers. This also supports the rationale behind designing manual calculation tables for artillery applications.
Figure 2 illustrates that each value of the auxiliary angle (and its corresponding tangent) corresponds to eight potential values of the target's directional line, depending on the signs and ratios of the coordinate differences. However, only one value of target directivity is valid for a given combination of tan and coordinate difference ratios. These relationships have been carefully incorporated into the construction of Table 2.
To determine (the target bearing) it is necessary to add the value of the hundreds of segments corresponding to the ratio of the coordinate differences with their signs and the value of the complement of the angle corresponding to the tangent in the column, which can be read in the left or rightmost column of Table 2. If the corresponding ratio of the coordinate differences with their signs is in the upper header of Table 2, read the corresponding value of the complement of angle in the leftmost column; if the corresponding ratio of the coordinate differences with their signs is in the lower header of Table 2, read the corresponding value of the complement of angle in the rightmost column. For example, the target bearing with the ratio of coordinate differences and is 48−00 + 0−22 = 48−22, with the ratio and the same the target bearing will be 11−00 + 0−78 = 11−78.
In the same way, the target bearing from the observation post and the target's observation range can be calculated using the coordinates of the observation post instead of the firing position coordinates.
The reverse procedure is then used to determine the target's orthogonal coordinates (firing position or of the observatory) from the target's bearing (topographic or observatory) and range (topographic or observatory).
4 Experiment to Compare the Accuracy and Time of Determining Topographic Features by Graphical and Analytical Methods (CDIR, CDIS)
This concept of using direction and distance coefficients is not entirely new in the artillery of the Eastern armies. It was used for map bases within the S1942 coordinate system [53]. After joining NATO, the Czech artillery started to use standardized NATO map bases, and it was necessary to establish new coefficients for new conditions (for the new global coordinate system WGS84). At the same time, it was necessary to verify the ability to integrate into the PACE system under new conditions and the ability to produce the necessary data accurately and promptly so that, among other things, it would support the operational tempo of the supported task force, reduce collateral damage, and reduce the ammunition consumption needed to shoot targets.
- Graphic method—process of preparing elements for firing (PUO type artillery protractor)
- Graphic tool—artillery protractor set (set of AK-3 type)
- Graphic resource—emergency resource (map, topographic template)
- Analytical tool (distance and direction coefficients)
- Determination of topographic distance
- Determination of topographic lateral deviation
- Accuracy of topographic distance determination
- Accuracy of topographic lateral deviation determination
- Time-consuming determination of topographic features
For the purposes of this experiment, four expert teams comprising personnel from the Czech Artillery and the Armed Forces of the Slovak Republic were assembled. The Czech and Slovak artillery have experience with manual procedures other than those used within the alliance. Thus, they represent ideal test subjects, participants in the experiment. It is not necessary to carry out lengthy training on calculation procedures. The sample is sufficiently representative for the purposes of the pilot study. These teams collectively performed 500 calculations based on predefined combat scenarios and specific methods for preparing firing elements. Due to the specialized nature of the training, achieving a high number of repetitions with the required number of participants posed logistical challenges. Furthermore, repeating identical calculations multiple times was avoided to prevent memorization effects, which could bias the results. To address this, input data for the calculations were varied, resulting in tasks of differing complexity across quadrants and specific areas of the combat assembly. The experiment represents a first step to validate the possibility of using range and direction coefficients in determining firing elements in the conditions of alliance armies. The execution of live combat fires using all elements of a combat formation is economically challenging and in realistic conditions it is not possible to execute a set of fires in a short period of time under otherwise unchanged conditions. Random factors are present during firing that randomly affect the shot and the flight of the missile, causing dispersion of missile impacts. This phenomenon is called shot dispersion. Testing under laboratory conditions is thus an important step toward setting up follow-up specific experiments under near realistic conditions. Further investigation will need to include psychological factories based on lack of time or information.
Data reliability was ensured through the rigorous preparation and calibration of all instruments, equipment, and methods used by the fire control specialist teams (FCS) under peacetime conditions. Time for preparation of this equipment for readiness was not included in the overall evaluation. Validation of these processes was supported by field survey data. However, the experiment did not attempt to simulate combat conditions or combat-induced stress, as these factors cannot be reliably replicated. Even advanced stress testing simulations fail to recreate the psychological and physiological responses of individuals in life-threatening scenarios. As such, the effects of actual combat stress would only manifest in a real conflict situation.
Other requirements for accurate artillery fire, such as the accuracy of determining the coordinates of the combat formation, the accuracy of ballistic, meteorological, and technical preparations, and the accuracy of determining the target's position, are not part of the experiment. These requirements and the resulting errors occur depending on the methods used, available resources, and other variables, constituting the total error. The experiment focuses only on one step: determining the elements for firing, calculating the elements for firing, and its accuracy and time consumption.
The experimental design adhered to established standards for research while accounting for the unique aspects of the military environment and the complexity of preparing firing elements. Testing used clearly defined procedures and sub-steps to determine topographic elements. Variable conditions were applied across all tested methods to ensure uniformity and consistency of implementation within all experimental groups.
Participants were selected to ensure the representation of various levels of expertise, taking into account their education, military rank, and length of service. The resulting group included experts with many years of experience, academics, instructors from various units, long-term and new members of fire control platoons, and cadets from the fire support department. Each participant was required to complete five tasks using all available methods. The results were then analyzed to derive averages for minimum, maximum, and overall performance across the various tasks.
5 Results
Tables 3, 4, and Figure 3 comprehensively summarize the experimental results. Table 3 evaluates the accuracy and time required to determine topographic features using the coefficients and . It details the computation times (minimum, maximum, and average) and the associated errors in determining topographic features (minimum, maximum, and average).
| Summary tables of the results of the experiment on the time and accuracy of the determination of topographic features | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Min. average time (s) | Max. average time (s) | Average time (s) | Min. average error in direction (dc) | Max. average error in direction (dc) | Average error in direction (dc) | Min. average distance error (m) | Max. average distance error (m) | Average distance error (m) | |
| Analytical tools (calculator) | 1:04 | 3:58 | 1:48 | 0–00 | 0–01 | 0–01 | 0 | 1 | 0 |
| Analytical methods (I and II MTG) | 1:16 | 4:26 | 2:51 | 0–00 | 0–02 | 0–01 | 0 | 0 | 0 |
| Analytical resources (Cdir, Cdis) | 1:35 | 4:41 | 3:07 | 0–00 | 0–00 | 0–01 | 2 | 3 | 2 |
| Emergency methods of preparing elements for firing | 1:59 | 5:59 | 3:31 | 0–02 | 0–18 | 0–03 | 9 | 68 | 19 |
| Graphic tools (AK-3) | 1:15 | 4:21 | 2:51 | 0–01 | 0–23 | 0–04 | 5 | 83 | 15 |
| Graphic tools (PUO-9M) | 0:48 | 2:50 | 1:14 | 0–00 | 0–12 | 0–01 | 1 | 41 | 9 |
| Tools and methods of preparing elements for firing | Maximum individual error of determination of topographic lateral deviation (dc) | Maximum individual error of determination of topographic distance (m) | Maximum individual determination time for topographic features (min) |
|---|---|---|---|
| PUO-9M | 0–27 | 114 | 3:50 |
| AK-3 | 0–33 | 184 | 6:27 |
| Emergency methods of preparing elements for firing | 0–84 | 409 | 6:14 |
| Analytical methods of preparation of elements for shooting (I and II MTG) | 0–64 | 2 | 5:02 |
| Analytical tools for preparing elements for shooting (calculator) | 0–05 | 78 | 5:46 |
| Analytical resources for preparing elements for shooting (Cdir, Cdis) | 0–01 | 6 | 5:50 |
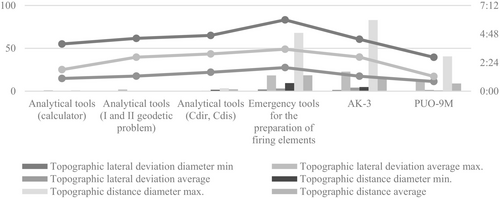
Table 4 highlights the maximum individual errors in determining topographic elements using various methods for preparing firing elements and the maximum individual computation times required for each method.
Figure 3 visualizes the data from Tables 3 and 4 in graphical form. The x-axis represents the different methods of preparing firing elements, while the primary y-axis displays errors (in parts), and the secondary y-axis shows the computation time required.
Participants in the experiment achieved average errors of 0.01 (dc) for determining topographic lateral deviation and 2 m for determining topographic distance when using and . The average computation time for these coefficients was recorded at 3 min and 7 s. Notably, the maximum error rates (as shown in Table 4) were lowest when using and . Additionally, the maximum individual computation time for and was 5 min and 50 s, which is lower than the time required for emergency graphical methods and procedures.
The results of the experiment validate the effectiveness of and coefficients as a method for preparing firing elements, demonstrating their ability to produce accurate and timely data. When compared to graphical methods, the analytical approach using and is significantly more precise, with participants achieving substantially lower individual errors. Moreover, the time required for calculations with and is comparable to that of graphical methods currently employed in practice.
6 Discussion
The results of this initial study demonstrate the efficiency of using the analytical coefficients and for determining topographic features in artillery operations, particularly under degraded operational conditions in MDO. Compared to traditional graphical methods, the analytical approach showed significantly higher accuracy while maintaining computation times that were competitive with or shorter than emergency graphical procedures. Specifically, the average errors in determining topographic lateral deviation (0.01 dc) and topographic distance (2 m) using and were substantially lower than those observed with graphical methods. Additionally, the maximum individual computation time for the analytical approach was shorter than that required for graphical methods, further reinforcing the suitability of this technique in time sensitive scenarios.
The experimental design ensured the reliability of the results by varying input data and incorporating a diverse set of tasks across all quadrants. However, it is important to acknowledge that this experiment was conducted under controlled, peacetime conditions. The absence of combat stress and other operational variables, such as equipment failures or adverse environmental factors, may limit the generalizability of the findings to actual combat situations. Nevertheless, the rigorous calibration of tools and the consistency of the results across multiple teams support the robustness of the proposed analytical method.
The study also highlights the importance of integrating analytical methods into the PACE framework. While the reliance on automated systems remains a key component of modern artillery operations, the vulnerability of these systems to jamming, spoofing, and other forms of disruption underscores the need for robust contingency and emergency solutions. By providing a method that is both accurate and relatively simple to implement using basic tools, the and coefficients offer a valuable alternative for artillery units operating in degraded environments.
Palasiewicz et al. [54] have also demonstrated this principle of adapting field procedures under constraints, particularly in terms of resource availability and simplicity of assembly, in the field of explosive engineering, where improvised shaped charges are tested for effectiveness under limited operational conditions.
This analytical approach reflects broader decision-making methodologies that balance operational efficiency with resource rationalization, as also demonstrated by Hujer et al. [55] in optimizing air defense structures using utility-based models.
Future research could explore the application of this method under simulated combat conditions to assess its effectiveness in scenarios involving combat stress and environmental challenges. Additionally, it will be necessary to identify ways to incorporate other sources of error inherent in the entire process of preparing firing elements, and consequently in the delivery of fire support, into the experimental framework. Future studies could investigate the integration of these coefficients into training programs and operational doctrine to enhance the resilience of artillery units further.
7 Conclusions
This study validates the use of analytical coefficients and as an effective method for preparing firing elements in artillery operations, particularly within the contingency and emergency layers of the PACE framework. The results indicate that the analytical approach provides significantly greater accuracy than traditional graphical methods while maintaining comparable computation times. This makes it a reliable and efficient solution for operations in degraded environments where automated systems may be compromised.
The proposed method enhances the operational flexibility of artillery units by offering a robust, technology-independent alternative for calculating firing elements. Furthermore, its implementation requires minimal equipment-relying only on a calculator or, in some cases, paper-based tables-making it highly adaptable to a wide range of operational scenarios.
By addressing a critical gap in the preparation of firing elements for degraded conditions, this research contributes to the ongoing development of resilient artillery practices. The integration of analytical methods into training and doctrine represents a valuable step toward ensuring the continuity and effectiveness of fire support in future conflicts.
Author Contributions
Jan Drábek: conceptualization, funding acquisition, writing – review and editing, resources. Michal Šustr: writing – original draft, writing – review and editing, resources. Ladislav Potužák: supervision, methodology, writing – review and editing. Jan Ivan: methodology, writing – review and editing, formal analysis. Richard Liška: visualization, resources, data curation.
Acknowledgments
This article resulted from research supported by the Ministry of Education, Youth and Sports of the Czech Republic, University of Defence, Faculty of Military Leadership Project “SV23-FVL-K107-PEK” and “SV24-FVL-K107_DRA.”
Conflicts of Interest
The authors declare no conflicts of interest.
Open Research
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.




