Volume 7, Issue 5 e70185

RESEARCH ARTICLE

Open Access

Enhanced Automatic Generation Control in Multiarea Power Systems: Crow Search Optimized Cascade FOPI-TIDDN Controller With Integrated Renewable Solar Thermal Models and HVDC Lines

Naladi Ram Babu,

Corresponding Author

Naladi Ram Babu

[email protected]

Department of Electrical and Electronics Engineering, Aditya University, Kakinada, India

Correspondence: Naladi Ram Babu ([email protected])

Wulfran Fendzi Mbasso ([email protected])

Contribution: Conceptualization, Methodology, Writing - review & editing

Search for more papers by this author

Pamarthi Sunitha,

Pamarthi Sunitha

Department of Electronics and Communication Engineering, Aditya University, Kakinada, India

Contribution: Investigation, Validation, Writing - original draft

Search for more papers by this author

Ganesh Pardhu B. S. S.,

Ganesh Pardhu B. S. S.

Department of Electrical and Electronics Engineering, Aditya University, Kakinada, India

Contribution: Investigation, Validation, Formal analysis

Search for more papers by this author

Sanjeev Kumar Bhagat,

Sanjeev Kumar Bhagat

Department of Electrical Engineering, Sandip University, Madhubani, India

Contribution: Methodology, Visualization, Formal analysis

Search for more papers by this author

Adireddy Ramesh,

Adireddy Ramesh

Department of Electrical and Electronics Engineering, Aditya University, Kakinada, India

Contribution: Validation, Data curation, Resources

Search for more papers by this author

Arindita Saha,

Arindita Saha

Department of Electrical Engineering, Regent Education and Research Foundation Group of Institutions, Kolkata, India

Contribution: Visualization, Formal analysis, Resources

Search for more papers by this author

Wulfran Fendzi Mbasso,

Corresponding Author

Wulfran Fendzi Mbasso

[email protected]

orcid.org/0000-0002-4049-0716

Technology and Applied Sciences Laboratory, U.I.T. of Douala, University of Douala, Douala, Cameroon

Department of Biosciences, Saveetha School of Engineering, Saveetha Institute of Medical and Technical Sciences, Chennai, India

Applied Science Research Center, Applied Science Private University, Amman, Jordan

Correspondence: Naladi Ram Babu ([email protected])

Wulfran Fendzi Mbasso ([email protected])

Contribution: Writing - review & editing, Project administration, Supervision

Search for more papers by this author

Pradeep Jangir,

Pradeep Jangir

University Centre for Research and Development, Chandigarh University, Gharuan Mohali, India

Department of CSE, Graphic Era Hill University, Dehradun, India

Department of CSE, Graphic Era Deemed to be University, Dehradun, India

Centre for Research Impact & Outcome, Chitkara University Institute of Engineering and Technology, Chitkara University, Rajpura, Punjab, India

Department of Electrical and Electronics Engineering, J.J. Technology, Tiruchirappalli, Tamilnadu, India

Contribution: Supervision, Validation, Visualization

Search for more papers by this author

Ahmed Hossam-Eldin,

Ahmed Hossam-Eldin

Department of Electrical Power and Machines, Faculty of Engineering, Alexandria University, Alexandria, Egypt

Contribution: Writing - review & editing, Project administration, Supervision

Search for more papers by this author

Naladi Ram Babu,

Corresponding Author

Naladi Ram Babu

[email protected]

Department of Electrical and Electronics Engineering, Aditya University, Kakinada, India

Correspondence: Naladi Ram Babu ([email protected])

Wulfran Fendzi Mbasso ([email protected])

Contribution: Conceptualization, Methodology, Writing - review & editing

Search for more papers by this author

Pamarthi Sunitha,

Pamarthi Sunitha

Department of Electronics and Communication Engineering, Aditya University, Kakinada, India

Contribution: Investigation, Validation, Writing - original draft

Search for more papers by this author

Ganesh Pardhu B. S. S.,

Ganesh Pardhu B. S. S.

Department of Electrical and Electronics Engineering, Aditya University, Kakinada, India

Contribution: Investigation, Validation, Formal analysis

Search for more papers by this author

Sanjeev Kumar Bhagat,

Sanjeev Kumar Bhagat

Department of Electrical Engineering, Sandip University, Madhubani, India

Contribution: Methodology, Visualization, Formal analysis

Search for more papers by this author

Adireddy Ramesh,

Adireddy Ramesh

Department of Electrical and Electronics Engineering, Aditya University, Kakinada, India

Contribution: Validation, Data curation, Resources

Search for more papers by this author

Arindita Saha,

Arindita Saha

Department of Electrical Engineering, Regent Education and Research Foundation Group of Institutions, Kolkata, India

Contribution: Visualization, Formal analysis, Resources

Search for more papers by this author

Wulfran Fendzi Mbasso,

Corresponding Author

Wulfran Fendzi Mbasso

[email protected]

orcid.org/0000-0002-4049-0716

Technology and Applied Sciences Laboratory, U.I.T. of Douala, University of Douala, Douala, Cameroon

Department of Biosciences, Saveetha School of Engineering, Saveetha Institute of Medical and Technical Sciences, Chennai, India

Applied Science Research Center, Applied Science Private University, Amman, Jordan

Correspondence: Naladi Ram Babu ([email protected])

Wulfran Fendzi Mbasso ([email protected])

Contribution: Writing - review & editing, Project administration, Supervision

Search for more papers by this author

Pradeep Jangir,

Pradeep Jangir

University Centre for Research and Development, Chandigarh University, Gharuan Mohali, India

Department of CSE, Graphic Era Hill University, Dehradun, India

Department of CSE, Graphic Era Deemed to be University, Dehradun, India

Centre for Research Impact & Outcome, Chitkara University Institute of Engineering and Technology, Chitkara University, Rajpura, Punjab, India

Department of Electrical and Electronics Engineering, J.J. Technology, Tiruchirappalli, Tamilnadu, India

Contribution: Supervision, Validation, Visualization

Search for more papers by this author

Ahmed Hossam-Eldin,

Ahmed Hossam-Eldin

Department of Electrical Power and Machines, Faculty of Engineering, Alexandria University, Alexandria, Egypt

Contribution: Writing - review & editing, Project administration, Supervision

Search for more papers by this author

First published: 16 May 2025

https://doi.org/10.1002/eng2.70185

Share a link

Email
Wechat
Bluesky

ABSTRACT

As renewable energy sources (RES) are increasingly unified into multiarea power systems, automatic generation control (AGC) faces challenges such as frequency instability, longer settling times, and higher overshoot. While existing optimization techniques like Firefly (FF) and gray wolf (GW) suffer from slow convergence and local optima trapping, conventional controllers like FOPI, PIDN, TIDN, and TIDDN struggle to maintain stability under fluctuating load conditions. Fractional-Order Proportional-Integral with Tilt Integral Double Derivative and Filter (FOPI-TIDDN), a novel cascade controller optimized using the crow search (CS) algorithm, is proposed in this paper to overcome these issues. Furthermore, a two-area AGC framework incorporates realistic dish-Stirling solar thermal systems (RDSTS) and parabolic trough solar thermal plants (PTSTP), and the effects of these systems are examined under different patterns of solar insolation. Additionally, the study assesses how high voltage direct current (HVDC) tie-lines contribute to increased system stability. According to simulation data, the FOPI-TIDDN controller works noticeably better than others in terms of improved frequency regulation, faster settling time, and less overshoot. Compared to FF and GW approaches, the CS algorithm guarantees faster convergence. An ideal fixed-random solar insolation method and HVDC integration also improve system performance. The suggested method enhances renewable-integrated power systems' resilience, efficiency, and stability.

1 Introduction

Power systems (PS) experience abrupt fluctuations in demand that cause a disparity between generation and load, leading to frequency and power value variations. This can be mitigated by AGC [1]. The main goal of AGC is to establish a reliable control system that ensures a consistent frequency profile, and that can be achieved by effectively distributing power among generation and load sides. AGC aims to maintain stability by carefully managing the power flow [2, 3]. The single-area thermal works are foundation works and later expanded to multiarea systems [4]. Physical constraints like generation rate constraints (GRC) and time delays are considered [4, 5]. An AGC analysis on a multiarea thermal system encompassing hydro and gas units is studied by Parmar et al. [6].

The gradual decline in fossil fuel use and increased CO₂ emissions have led to the use of renewable sources (RS). The idea of RS inclusion in AGC studies was first introduced in [7]. The most advanced methods can boost energy conversion efficiency while lowering their adverse environmental effects [8]. The RS is dominated by solar-wind energies [9]. The AGC study incorporating solar PV was presented by Bervani et al. [7]. The solar grid connection with thermal was demonstrated by Wang et al. [8]. The frequency parameter of a fusion inaccessible system with a parabolic trough collector-based solar thermal plant (PTSTP) was investigated by Das et al. [9], and its control strategy was demonstrated by Sharma et al. [10]. The concept of a dish-stirling solar thermal system (DSTS) with various solar insolations was presented by Rahman et al. [11]. Li et al. [12-14] suggested the narrow-speed operation of SCIG with energy devices for frequency regulation. Nonetheless, the PTSTP and RDSTS are not considered with conventional generation considering various types of solar insolation.

A rise in population causes a sharp increase in systems demand and can be overcome by interarea PS [15]. Also, an enhancement in interarea power transfer capability is necessary to accommodate the systems growing demand and this can be compensated by HVDC [16]. HVDCs offer effective power transfer capabilities and can be placed with existing systems [17, 18]. The AGC focus has historically been on two areas and further facilitates multiarea PS control. Moreover, the multiarea AGC studies with RDSTS and PSTSP integration, considering HVDC, have not been carried out.

There has been a significant emphasis on the secondary controller design in AGC. This focus led to the advance of secondary controllers. Classical IO controllers like I, PI, PID [19]; fractional such as FOPI and FOPID [20]; cascade such as FOPI − (1 + TD) [21], FOPID − (1 + TD) [22], fuzzy-IDD [23]; fuzzy-PID [24]; tilt controllers [25, 26]; adaptive fuzzy [27]; deep neural networks [28]; degree of freedom (DOF) controllers [29]; sliding mode [30] and so on, have been successfully implemented for the AGC study. A new cascade controller named FOPI-TIDDN has not been studied under AGC; thus, providing scope for further investigations.

To improve the AGC performance, various optimization techniques have been implemented. Conventional and heuristic algorithms optimize controller gains. Traditional techniques like gradient search and random search stick at local optima, and heuristic techniques like bacterial foraging [4, 23], genetic [5, 9], gray wolf [10], biogeography [11], sine-cosine [31], firefly [19, 32], flow direction [21], teaching learning [25], cuckoo search [29], flower pollination [33], barnacle optimizer [34], adopting jaya optimizer [35], global neighborhood algorithm [36], particle swarm [37, 38], salp swarm [39, 40], stochastic fractal search [41], Aquila [42], dragon fly [43] and learner behavior [44] provide global optima. A recent technique named crow search (CS) [45] works with the brainy behavior of crows, such as face recognition, tool usage, food search, effective communication, and so on. However, the CS technique is not utilized for the FOPI-TIDDN controller optimization.

The objectives are:

To demonstrate the effect of PTSTP and RDSTS with thermal systems.
To apply the CS algorithm to optimize controller parameters in PIDN, TIDN, and FOPI-TIDDN controllers.
To study the effect of various solar insolations.
Convergence comparison with gray wolf, firefly, and proposed CS technique.
To validate the impact of the HVDC.

1.1 Novelty and Contributions

From the above, the novelties are:

Evaluation performance of RDSTS and PTSTP in a two-area thermal system (TATS).
Designing a new FOPI-TIDDN controller for AGC studies of TATS.
Performance of thermal-RES system with a combination of various solar insulations.
Utilization of CS algorithm for synchronized enhancement of RDSTS parameter and FOPI-TIDDN controller.

The main contributions are:

A study was conducted in a TATS considering RDSTS and PTSTP.
A new controller termed FOPI-TIDDN was proposed by integrating RDSTS and PTSTP.
RDSTS and controller parameters are successfully optimized by the CS technique for the first time.
Efforts are made to analyze the impact of RDSTS and PTSTP at various solar insolations.

2 System Description

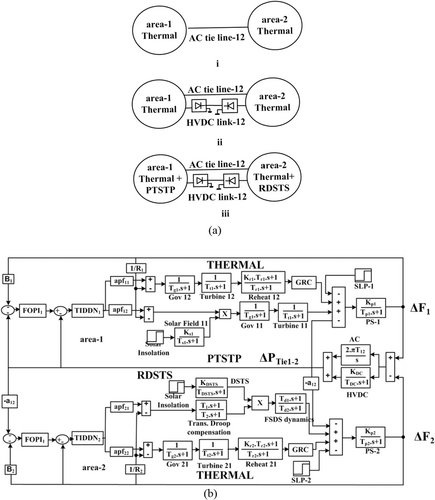
Investigations were carried out on a system with a capacity of 1:4 comprising thermal-RES units with HVDC integration. Area-1 comprises the PTSTP unit, and area-2 comprises RDSTS units with fixed and random solar insolations. The nominal values of the RDSTS, thermal, PTSTP, and HVDC tie-line models are from [4, 12, 23], respectively. The study and transfer function models of the investigated two-area systems comprising thermal, RDSTS, PTSTP, and HVDC units are in Figure 1a,b, respectively.

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

(a) Study system model. (b) Study system's transfer function model.

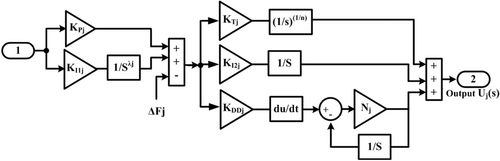
3 The Proposed FOPI-TIDDN Controller

The FOPI-TIDDN controller aims to overcome the challenges associated with traditional fractional order and tilt controllers in handling complex power systemPS dynamics. Also, this controller is of cascade type with two loops that enhance dynamics over single loop control systems. The transfer functions of FOPI and TIDDN considering the real order of the integrator (λ), differentiator (μ), and a real number (n) are from [6, 7] and represented in Equations (1) and (2), respectively. The transfer function block diagrams are in Figure 2.

{G}_{FOPI}(s)\kern0.5em =\kern0.5em {K}_{Pj}+\frac{K_{Ij}}{s^{\lambda j}}

(1)

{G}_{TIDDN}(s)\kern0.5em =\kern0.5em \frac{K_{Tj}}{(s)^{1/{n}_j}}+\frac{K_{Ij}}{s}+{K}_{DDj}{s}^2\left(\frac{N_j}{s^2+{N}_j}\right)

(2)

CS algorithm optimizes the FOPI-TIDDN controller gains–RDSTS parameters. The Simulink model is developed in a MATLAB environment considering integral squared error (ISE) with constraints in Equations (3) and (4), respectively.

{\upeta}_{\mathrm{ISE}}=\int_0^{\mathrm{T}}\left\{{\left({\Delta F}_{\mathrm{j}}\right)}^2+{\left({\Delta P}_{\mathrm{j}\hbox{-} \mathrm{k}}\right)}^2\right\}.\mathrm{dt}

(3)

\begin{array}{cc}& \le {\mathrm{K}}_{\mathrm{Pj}}\le 1,0\le {\mathrm{K}}_{\mathrm{Ij}}\le 1,0\le {\lambda}_{\mathrm{j}}\le 1,\\ {}0& \le {\mathrm{K}}_{\mathrm{Tj}}\le 1,0\le {\mathrm{n}}_{\mathrm{j}}\le 7,0\le {\mathrm{K}}_{\mathrm{TIj}}\le 1,0\le {\mathrm{K}}_{\mathrm{DDj}}\le 1,\mathrm{and}\kern0.5em 0\le {\mathrm{N}}_{\mathrm{j}}\le 100\end{array}

(4)

4 Crow Search (CS) Algorithm

A Askarzadeh [45] proposed CS grounded on the intelligence of crow's behavior, and its flow diagram is in Figure 3. It can recognize face tools usage and is greedy. They also steal, store food, and recall their hiding place. The hiding location (m) in position (p), size (n), and iteration (iter) are given by Equation (5).

\left[{\mathrm{X}}^{\mathrm{p},\mathrm{iter}}={\mathrm{X}}_1^{\mathrm{p},\mathrm{iter}},{\mathrm{X}}_2^{\mathrm{p},\mathrm{iter}},..\dots, {\mathrm{X}}_{\mathrm{d}}^{\mathrm{p},\mathrm{iter}}\right]

(5)

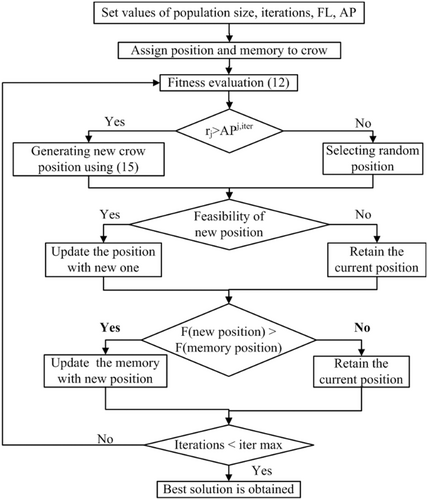
Two possibilities occur in food search:

Crow-q does not recognize that crow-p is subsequent, and its walloping place is given by Equation (6).

Crow-q knows that crow-p is subsequent and flies to a random position, as in Equation (7).

{\mathrm{X}}^{\mathrm{p},\mathrm{iter}+1}=\left.\begin{array}{l}{\mathrm{X}}^{\mathrm{p},\mathrm{iter}}+{\mathrm{r}}_{\mathrm{p}}\times {\mathrm{FL}}^{\mathrm{p},\mathrm{iter}}\times \left({\mathrm{m}}^{\mathrm{q},\mathrm{iter}}\hbox{-} {\mathrm{X}}^{\mathrm{p},\mathrm{iter}}\right)\\ {}\kern3.4em {\mathrm{r}}_{\mathrm{q}}\ge {\mathrm{AP}}^{\mathrm{q},\mathrm{iter}}\end{array}\right\}

(6)

{\mathrm{X}}^{\mathrm{p},\mathrm{iter}+1}=\mathrm{random}\ \mathrm{position}

(7)

where flight length (FL), random (r), and awareness probability (AP). The tuned CS technique parameters are noted in the Appendix A. The FOPI-TIDDN controller gains and RDSTS parameters are optimized by the CS technique considering ISE as the performance index and are in Equations (4) and (8).

0\le {\mathrm{T}}_1\le 1,1\le {\mathrm{T}}_2\le 4,0\le {T}_{\mathrm{ds}1}\le 1,\mathrm{and}\ 1\le {T}_{\mathrm{ds}2}\le 10

(8)

5 Simulation Results

The two-area thermal system with RDSTS, PTSTP, and HVDC lines considering CS optimized FOPI-TIDDN controller is regarded for the investigations and is in Figure 1b.

5.1 System Dynamics With PIDN, TIDN, and FOPI-TIDDN Controllers

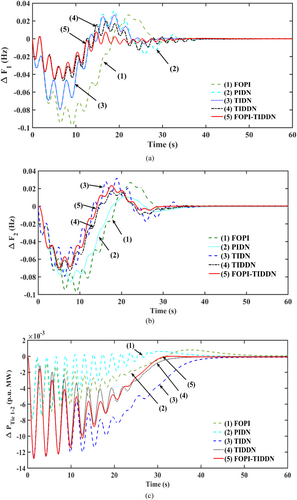
Figure 1a (i) with thermal units are considered and are provided with secondary controllers like FOPI [8], PIDN [19], TIDN [25], TIDDN [41], and FOPI-TIDDN. Their values are simultaneously augmented using CS and are in Table 1a. The system dynamics corresponding to every controller are illustrated in Figure 4. The performance indices are listed in Table 1b. With the keen observation of the numerical values in Table 1b, and from Figure 4, it is apparent that the responses with the proposed FOPI-TIDDN controller outperform other controllers.

TABLE 1a. CS augmented PIDN, TIDN, and FOPI-TIDDN controller values considering SLP.

With FOPI controller	K_P1 = 0.8547	K_I1 = 0.4758	λ₁ = 0.9978	K_P2 = 0.4751	K_I2 = 0.8757	λ₂ = 0.9785
With PIDN controller	K_P1 = 0.5161	K_I1 = 0.6383	K_D1 = 0.7868	N₁ = 10.6597	K_P2 = 0.3299	K_I2 = 0.0936
With PIDN controller	K_D2 = 0.1096	N₂ = 21.9706
With TIDN controller	K_T1 = 0.6514	n₁ = 3.5842	K_I1 = 0.5812	K_D1 = 0.9150	N₁ = 19.5652	K_T2 = 0.1096
With TIDN controller	n₂ = 6.3435	K_I1 = 0.2622	K_D2 = 0.3299	N₂ = 45.8975
With TIDDN controller	K_T1 = 0.5674	n₁ = 4.7824	K_I1 = 0.7584	K_DD1 = 0.7584	N₁ = 99.1425	K_T1 = 0.4157
With TIDDN controller	n₁ = 7.5416	K_I1 = 0.8324	K_DD1 = 0.9745	N₁ = 65.7412
With FOPI-TIDDN controller	K_P1 = 0.6661	K_I1 = 0.7542	λ₁ = 0.9856	K_T1 = 0.3567	n₁ = 3.5647	K_I1 = 0.9652
	K_DD1 = 0.9364	N₁ = 36.4585	K_P2 = 0.4578	K_I2 = 0.7745	λ₂ = 0.9981	K_T2 = 0.7714
	n₂ = 6.0125	K_I2 = 0.5378	K_DD2 = 0.4463	N₂ = 57.2450

TABLE 1b. Performance indices of responses in Figure 4.

Response	Controller	Settling time (s)	Peak overshoot	Peak undershoot (−ve)
ΔF₁	FOPI [8]	45	0.042	0.099
	PIDN [19]	42	0.040	0.0965
	TIDN [25]	38	0.027	0.0965
	TIDDN [41]	36	0.026	0.0800
	FOPI-TIDDN	34	0.025	0.0794
ΔF₂	FOPI [8]	44	0.024	0.090
	PIDN [19]	42	0.022	0.085
	TIDN [25]	40	0.016	0.072
	TIDDN [41]	36	0.0154	0.070
	FOPI-TIDDN	32	0.010	0.068
ΔPtie_1-2	FOPI [8]	47	0.002	0.0130
	PIDN [19]	45	0.002	0.0128
	TIDN [25]	42	0.001	0.0127
	TIDDN [41]	40	0.001	0.0125
	FOPI-TIDDN	38	0.001	0.0124

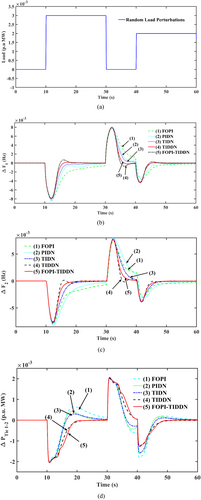
5.2 System Dynamics With Random Load Pattern (RLP) Considering PIDN, TIDN, and FOPI-TIDDN Controllers

The controllers in Section 5.1 are utilized for the study with RLP in Figure 5a CS technique optimizes the gains and is in Table 2. Responses with RLP are plotted in Figure 5b–d. Upon thorough examination of system dynamics in Figure 5b–d, it is evident that dynamics with FOPI-TIDDN controller exhibit superior performance compared to those of other controllers.

TABLE 2. CS augmented PIDN, TIDN, and FOPI-TIDDN controller values considering RLP.

With FOPI controller	K_P1 = 0.5538	K_I1 = 0. 4596	λ₁ = 0. 9217	K_P2 = 0. 9234	K_I2 = 0. 2781	λ₂ = 0. 2623
With PIDN controller	K_P1 = 0. 1942	K_I1 = 0. 6356	K_D1 = 0. 2471	N₁ = 34.5782	K_P2 = 0. 8327	K_I2 = 0. 2927
With PIDN controller	K_D2 = 0. 3896	N₂ = 21.9706
With TIDN controller	K_T1 = 0.6514	n₁ = 5.7245	K_I1 = 0. 9516	K_D1 = 0. 6341	N₁ = 98.9601	K_T2 = 0. 2172
With TIDN controller	n₂ = 4.4097	K_I1 = 0. 6767	K_D2 = 0.9004	N₂ = 64.5482
With TIDDN controller	K_T1 = 0. 4446	n₁ = 6.0502	K_I1 = 0. 2908	K_DD1 = 0. 1325	N₁ = 83.2482	K_T1 = 0. 9261
With TIDDN controller	n₁ = 3.7603	K_I1 = 0. 0381	K_DD1 = 0. 1804	N₁ = 32.4983
With FOPI-TIDDN controller	K_P1 = 0. 8324	K_I1 = 0. 3016	λ₁ = 0. 9613	K_T1 = 0. 6624	n₁ = 5. 3426	K_I1 = 0. 7410
	K_DD1 = 0. 979	N₁ = 68.5478	K_P2 = 0. 5863	K_I2 = 0. 8082	λ₂ = 0. 9504	K_T2 = 0. 4864
	n₂ = 5. 9058	K_I2 = 0. 2331	K_DD2 = 0. 8948	N₂ = 29.6547

5.3 Comparisons of Convergence Characteristics Among Algorithms Like Firefly, Gray Wolf, and CS

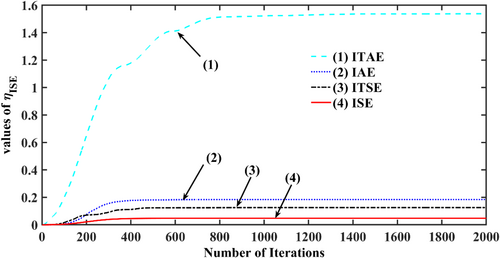
The unequal thermal system is considered to examine the convergence characteristics of CS, firefly [29] and gray wolf [4] techniques. The FOPI-TIDDN values are augmented by the algorithms mentioned above and are in Table 3, and their respective convergence features are in Figure 6. In Figure 6, the convergence curves of firefly [29] and gray wolf [4] are produced and analyzed with CS. The η_ISE values of every algorithm are examined, and it is witnessed that CS has a lower η_ISE value. Critical observations expose the system with the CS technique converging over firefly and gray wolf algorithms.

TABLE 3. Optimized FOPI-TIDDN controller values considering firely, gray wolf, and CS algorithms.

With firefly [29]	K_P1 = 0.5686	K_I1 = 0.5648	λ₁ = 0.8956	K_T1 = 0.4500	n₁ = 4.2150	K_I1 = 0.2180
	K_DD1 = 0.5018	N₁ = 65.1245	K_P2 = 0.7789	K_I2 = 0.6485	λ₂ = 0.9978	K_T2 = 0.9601
	n₂ = 5.1245	K_I1 = 0.3345	K_DD2 = 0.9013	N₂ = 21.0356
	ISE = 0.006
	Simulation Time = 284 s
With gray wolf [4]	K_P1 = 0.4856	K_I1 = 0.8945	λ₁ = 0.8555	K_T1 = 0.7580	n₁ = 4.2105	K_I1 = 0.5241
	K_DD1 = 0.6645	N₁ = 84.0125	K_P2 = 0.8820	K_I2 = 0.7456	λ₂ = 0.8585	K_T1 = 0.5463
	n₂ = 5.8231	K_I1 = 0.7814	K_DD2 = 0.8798	N₂ = 66.1470
	ISE = 0.004
	Simulation Time = 255 s
With CS	K_P1 = 0.8521	K_I1 = 0.7845	λ₁ = 0.7425	K_T1 = 0.3567	n₁ = 3.5647	K_I1 = 0.9652
	K_DD1 = 0.9364	N₁ = 36.4585	K_P2 = 0.7845	K_I2 = 0.5485	λ₂ = 0.9142	K_T1 = 0.0.7714
	n₂ = 6.0125	K_I1 = 0.5378	K_DD2 = 0.4463	N₂ = 57.2450
	ISE = 0.0028
	Simulation Time = 240 s

5.4 Selection of Performance Indices

System in Section 5.2 is considered and is provided with the best controller from Section 5.1 (FOPI-TIDDN) and the best algorithm from Section 5.2 (CS). CS optimizes the controller gains with ISE, ITSE, IAE, and ITAE as performance indices, considering one at a time, and responses are plotted in Figure 7. Results suggest that ISE exhibits better convergence with fewer error values over other indices.

5.5 Integration of HVDC

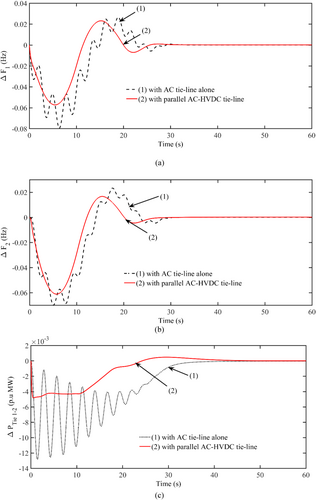
Figure 1a (ii) considers the unequal thermal system unified with the HVDC and FOPI-TIDDN controller. The CS technique augments its gains. Table 4 lists optimum values and their responses are related to the AC system in Figure 8. From Figure 8, the dynamics with AC-HVDC clearly show their prominence over the AC tie-lines. Further, an interconnected HVDC system enhances system dynamics significantly. This improvement is because HVDC tie-lines are less susceptible.

TABLE 4. CS-optimized FOPI-TIDDN values with parallel AC-HVDC.

With AC-HVDC tie-lines	K_P1 = 0.7584	K_I1 = 0.3213	λ₁ = 0.9875	K_T1 = 0.4723	n₁ = 7.0251	K_I1 = 0.6211
	K_DD1 = 0.7347	N₁ = 20.1521	K_P2 = 0.9952	K_I2 = 0.4252	λ₂ = 0.9685	K_T1 = 0.2116
	n₂ = 6.4990	K_I1 = 0.8469	K_DD2 = 0.4351	N₂ = 64.1150

5.6 System Dynamics Under Various Patterns of Solar Insolation Considering RES

The unequal thermal-HVDC system is unified with RS like PTSTP and in area-1, 2, which are taken for investigation and are in Figure 1a (iii). The area participation factors (apf)s of RES-thermal systems are chosen as 0.45 and 0.55, respectively. The input for PTSTP and RDSTS is intermittent solar insolation in Figure 9.

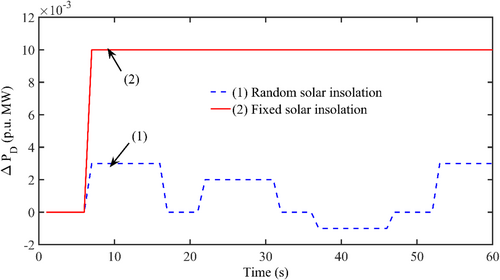
The thermal-RES system is exposed to various groupings of insolations:

Case (a): Random and random.

Case (b): Random and fixed.

Case (c): Fixed and fixed.

Case (d): Fixed and random.

The FOPI-TIDDN controller is used, and CS augments its gains and RDSTS parameters in the above combinations and its values in Table 5. The corresponding dynamics with various combinations of solar insolations are compared in Figure 10 and show that the solar insolation combination of fixed and random in area 1–2 exhibits a better response than others.

TABLE 5. CS optimized FOPI-TIDDN values of the thermal-RS systems considering various solar insolation.

Case (a)	K_P1 = 0.6585	K_I1 = 0.1245	λ₁ = 0.9978	K_T1 = 0.5945	n₁ = 5.1205
	K_I1 = 0.8140	K_DD1 = 0.7015	N₁ = 85.1240	K_P2 = 0.8852	K_I2 = 0.4578
	λ₁ = 0.9978	K_T2 = 0.5012	n₂ = 3.2451	K_I2 = 0.4385	K_DD2 = 0.3104
	N₂ = 60.4503
Case (b)	K_P1 = 0.6645	K_I1 = 0.4512	λ₁ = 0.8879	K_T1 = 0.5680	n₁ = 5.4102
	K_I1 = 0.2478	K_DD1 = 0.7820	N₁ = 64.0528	K_P2 = 0.7845	K_I2 = 0.4532
	λ₂ = 0.8952	K_T1 = 0.4780	n₂ = 2.5478	K_I2 = 0.4196	K_DD2 = 0.4578
	N₂ = 22.4587
Case (c)	K_P2 = 0.6598	K_I2 = 0.4561	λ₂ = 0.4532	K_T1 = 0.2300	n₁ = 1.2450
	K_I1 = 0.8174	K_DD1 = 0.8174	N₁ = 25.4710	K_P2 = 0.4578	K_I2 = 0.3212
	λ₂ = 0.9978	K_T2 = 0.3201	n₂ = 4.1250	K_I1 = 0.5410	K_DD2 = 0.1208
	N₂ = 34.7809
Case (d)	K_P2 = 0.7832	K_I2 = 0.5821	λ₂ = 0.9965	K_T1 = 0.6478	n₁ = 5.1240
	K_I1 = 0.1820	K_DD1 = 0.1047	N₁ = 88.4510	K_P2 = 0.6585	K_I2 = 0.4856
	λ₂ = 0.9899	K_T2 = 0.1780	n₂ = 4.1205	K_I1 = 0.4580	K_DD2 = 0.3019
	N₂ = 18.2045

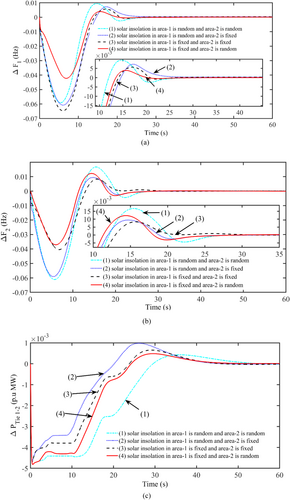
5.7 Impact of Renewables

The effect of RES, such as a PTSTP and RDSTS in area-1, 2, on the system dynamics is examined. The finest solar insolation combinations (fixed and random) are delivered to the RS units. The thermal-RS system with an FOPI-TIDDN controller and the CS technique optimizes its gain parameters. The attained values with CS are noted in case (d) and its dynamics are shown in Figure 11.

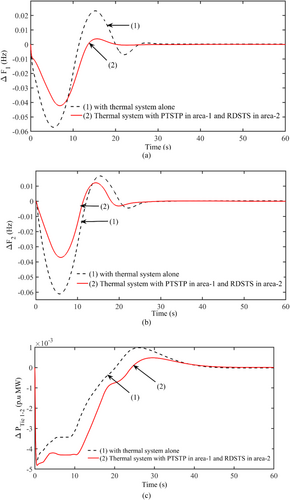
The effect of RES, like PTSTP and RDSTS integration, is highly noticeable when contrasted in a thermal system. Figure 11 shows that integrating the system with RES indicates a significant oscillation reduction.

5.8 Sensitivity Analysis

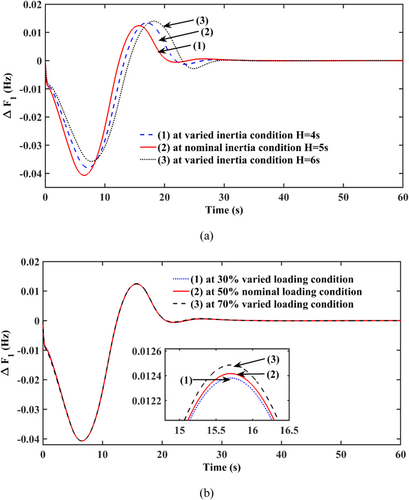
The thermal-RES system with FOPI-TIDDN with CS optimization is considered. Investigations are performed at ± 20% varied inertia and loading conditions and plotted in Figure 12. It is pragmatic that the FOPI-TIDDN controller exhibits almost the same responses.

5.9 Stability Analysis

The thermal-RES-HVDC system with FOPI-TIDDN controller in Figure 1b is investigated for stability analysis by considering eigenvalue analysis. The input and output of each significant block in Figure 1b are under consideration and represented as state variables. Investigations are performed by considering “linmod” function in MATLAB. The obtained eigenvalues are noted in Table 6. It is apparent that eigenvalues are located on the left half of the s-plane. Also, the proposed system is supported by the negative values of the imaginary and real eigenvalues.

TABLE 6. Eigen values of thermal-RES-HVDC system with proposed FOPI-TIDDN controller.

−0.00137 + 0.000i	−1.5100 + 0.000i	−50.000 + 0.000i	−46.100 − 2.2700i
−0.00169 + 0.000i	−2.5700 + 0.000i	−56.400 + 0.000i	−47.700 + 4.060i
−0.00481 + 0.000i	−3.3300 + 0.000i	−100.00 + 0.000i	−47.700 − 4.060i
−0.00500 + 0.000i	−3.8800 + 0.000i	−111.00 + 0.000i	−50.100 + 4.880i
−0.00593 + 0.000i	−9.0100 + 0.000i	−390.00 + 0.000i	−50.100 − 4.880i
−0.3330 + 0.000i	−12.500 + 0.000i	−1000.0 + 0.000i	−52.800 + 4.350i
−0.5560 + 0.000i	−28.000 + 0.000i	−0.2080 + 0.0001i	−52.800 − 4.350i
−0.7310 + 0.000i	−31.600 + 0.000i	−0.2080 + 0.0001i	−55.100 + 2.400i
−1.0000 + 0.000i	−45.500 + 0.000i	−46.100 + 2.2700i	−55.100 − 2.400i

6 Conclusion

A novel method has been obtained using the grouping of fixed-random insolation in a thermal-renewable system. The cascade FOPI-TIDDN controller is used for the first time, and its gain RDSTS parameters are optimized using a novel CS algorithm. System dynamics with the FOPI-TIDDN controller outperform FOPI, PIDN, TIDN, and TIDDN in performance indices. CS optimizes controller gains with a better convergence rate over cuckoo search and particle swarm techniques. Also, studies reveal that the FOPI-TIDDN controller with ISE shows better dynamics over other performance indices. Investigations reveal that insolations of fixed random in area-1 and 2 are the best over other combinations for renewable systems. Moreover, the effect of renewable in combination with AC-HVDC has been evaluated and assessed for two-area thermal systems. Sensitivity analysis suggests that the proposed FOPI-TIDDN controller is robust. Further, stability analysis suggests that the considered system is stable. Furthermore, this work can be extended to realistic scenarios.

Nomenclature

AGC: automatic generation control
CS: crow search
FF: firefly
FOPI-TIDDN: Fractional-Order Proportional-Integral With Tilt Integral Double Derivative and Filter
GRC: generation rate constraints
GW: gray wolf
HVDC: high voltage direct current
PS: power systems
PTSTP: parabolic trough solar thermal plants
RDSTS: realistic dish-stirling solar thermal systems
RES: renewable energy sources

Author Contributions

Naladi Ram Babu: conceptualization, methodology, writing – review and editing. Pamarthi Sunitha: investigation, validation, writing – original draft. Ganesh Pardhu B. S. S.: investigation, validation, formal analysis. Sanjeev Kumar Bhagat: methodology, visualization, formal analysis. Adireddy Ramesh: validation, data curation, resources. Arindita Saha: visualization, formal analysis, resources. Wulfran Fendzi Mbasso: writing – review and editing, project administration, supervision. Pradeep Jangir: supervision, validation, visualization. Ahmed Hossam-Eldin: writing – review and editing, project administration, supervision.

Conflicts of Interest

The authors declare no conflicts of interest.

Appendix A: System Nominal Parameters

System Model: F = 60 Hz; Kpj = 120 Hz/pu MW; loading = 50%, Tjk, AC = 0.086 pu MW/rad; Dj = 8.33 × 10-3 pu MW/Hz; Hj = 5 s; Rj = 2.4 pu MW/Hz; Bi = βj = 0.425 pu MW/Hz; Tpj = 20 s; apf11 = apf21 = apf31 = 0.45; apf12 = apf22 = apf32 = 0.55; SLP = 1%; a12 = −Pr1/Pr2 = −1000/4000 = −1/4; a23 = −Pr2/Pr3 = 4000/8000 = −1/4; a31 = −Pr3/Pr1 = 8000/1000 = −8/1.

Thermal System: Tgj = 0.08 s; Ttj = 0.3 s; Trj = 10s; Krj = 0.5 s.

Parabolic Trough Collector Base Solar Thermal Plant: Ks = 1.8; Ts = 1.8 s; Tgsj = 1.0 s; Ttsj = 3.0 s.

High-Voltage Direct Current: KDC = 0.5; TDC = 0.03 s.

Crow Search Technique: Flight length = 0.2, Awareness Probability = 0.1, flock size = 50, iteration size = 100.

Open Research

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

1O. I. Elgerd, Electric Energy Systems Theory: An Introduction (Tata McGraw-Hill, 2007).
Google Scholar
2P. Kundur, Power System Stability and Control (Tata Mc Graw Hill, 1993).
Google Scholar
3P. I. Kumar and D. P. Kothari, “Recent Philosophies of Automatic Generation Control Strategies in Power Systems,” IEEE Transactions on Power Systems 20, no. 1 (2005): 346–357.
10.1109/TPWRS.2004.840438
Web of Science® Google Scholar
4J. Nanda, S. Mishra, and L. C. Saikia, “Maiden Application of Bacterial Foraging Based Optimization Technique in Multi Area Automatic Generation Control,” IEEE Transactions on Power Systems 24, no. 2 (2009): 602–609.
10.1109/TPWRS.2009.2016588
Web of Science® Google Scholar
5H. Golpira, H. Bevrani, and H. Golpira, “Application of GA Optimization for Automatic Generation Control Design in an Interconnected Power System,” Energy Conversion and Management 52, no. 5 (2011): 2247–2255.
10.1016/j.enconman.2011.01.010
Web of Science® Google Scholar
6K. P. S. Parmar, S. Majhi, and D. P. Kothari, “Load Frequency Control of a Realistic Power System With Multi-Source Power Generation,” International Journal of Electrical Power & Energy Systems 42, no. 1 (2012): 426–433.
10.1016/j.ijepes.2012.04.040
Web of Science® Google Scholar
7H. Bevrani, A. Ghosh, and G. Ledwich, “Renewable Energy Sources and Frequency Regulation: Survey and New Perspectives,” IET Renewable Power Generation 4, no. 5 (2010): 438–457.
10.1049/iet-rpg.2009.0049
Web of Science® Google Scholar
8N. R. Babu, S. K. Bhagat, L. C. Saikia, T. Chiranjeevi, R. Devarapalli, and F. P. García Márquez, “A Comprehensive Review of Recent Strategies on Automatic Generation Control/Load Frequency Control in Power Systems,” Archives of Computational Methods in Engineering 30, no. 1 (2023): 543–572, https://doi.org/10.1007/s11831-022-09810-y.
10.1007/s11831-022-09810-y
Web of Science® Google Scholar
9S. K. Bhagat, N. R. Babu, L. C. Saikia, T. Chiranjeevi, R. Devarapalli, and F. P. G. Márquez, “A Review on Various Secondary Controllers and Optimization Techniques in Automatic Generation Control,” Archives of Computational Methods in Engineering 30, no. 5 (2023): 3081–3111, https://doi.org/10.1007/s11831-023-09895-z.
10.1007/s11831-023-09895-z
Web of Science® Google Scholar
10Y. Sharma and L. C. Saikia, “Automatic Generation Control of a Multiarea ST—Thermal Power System Using Grey Wolf Optimizer Algorithm Based Classical Controllers,” Electrical Power and Energy Systems 73 (2015): 853–862.
10.1016/j.ijepes.2015.06.005
Google Scholar
11A. Rahman, L. C. Saikia, and N. Sinha, “AGC of Dish-Stirling Solar Thermal Integrated Thermal System With Biogeography Based Optimised Three Degree of Freedom PID Controller,” IET Renewable Power Generation 10, no. 8 (2016): 1161–1170.
10.1049/iet-rpg.2015.0474
Web of Science® Google Scholar
12Y. Li, S. S. Choi, and D. M. Vilathgamuwa, “Primary Frequency Control Scheme for a Fixed-Speed Dish-Stirling Solar–Thermal Power Plant,” IEEE Transactions on Power Systems 33, no. 2 (2018): 2184–2194.
10.1109/TPWRS.2017.2724557
Web of Science® Google Scholar
13Y. Li, S. S. Choi, and C. Yang, “Dish-Stirling Solar Power Plants: Modeling, Analysis, and Control of Receiver Temperature,” IEEE Transactions on Sustainable Energy 5, no. 2 (2014): 398–407.
10.1109/TSTE.2013.2291572
Web of Science® Google Scholar
14Y. Li, S. S. Choi, C. Yang, and F. Wei, “Design of Variable-Speed Dish-Stirling Solar–Thermal Power Plant for Maximum Energy Harness,” IEEE Transactions on Energy Conversion 30, no. 1 (2015): 394–403.
10.1109/TEC.2014.2354346
CAS Web of Science® Google Scholar
15N. R. Babu, T. Chiranjeevi, A. Saha, and S. K. Bhagat, “Comparative Analysis of Various Energy Storage Systems in a Conventional LFC System Considering RDSTS, PWTS and AHVDC Models,” Journal of Engineering Research 11, no. 4 (2023): 425–436.
10.1016/j.jer.2023.100123
Google Scholar
16E. Rakhshani and P. Rodriguez, “Inertia Emulation in AC/DC Interconnected Power Systems Using Derivative Technique Considering Frequency Measurement Effects,” IEEE Transactions on Power Systems 32, no. 5 (2017): 3338–3351.
10.1109/TPWRS.2016.2644698
Web of Science® Google Scholar
17N. Pathak, A. Verma, T. S. Bhatti, and I. Nasiruddin, “Modeling of HVDC Tie Links and Their Utilization in AGC/LFC Operations of Multiarea Power Systems,” IEEE Transactions on Industrial Electronics 66, no. 3 (2019): 2185–2197.
10.1109/TIE.2018.2835387
Web of Science® Google Scholar
18O. Singh and I. Nasiruddin, “Optimal AGC Regulator for Multiarea Interconnected Power Systems With Parallel AC/DC Links,” Cogent Engineering 3, no. 1 (2016): 1–17.
10.1080/23311916.2016.1209272
CAS Google Scholar
19K. Jagatheesan, B. Anand, S. Samanta, N. Dey, A. S. Ashour, and V. E. Balas, “Design of a Proportional-Integral-Derivative Controller for an Automatic Generation Control of Multiarea Power Thermal Systems Using Firefly Algorithm,” IEEE/CAA Journal of Automatica Sinica 6, no. 2 (2019): 503–515.
10.1109/JAS.2017.7510436
Google Scholar
20I. Pan and S. Das, “Fractional Order for Distributed Energy Resources Using Robust Optimization,” IEEE Transactions on Smart Grid 7, no. 5 (2016): 2175–2186.
10.1109/TSG.2015.2459766
Google Scholar
21Z. A. Ansari and G. L. Raja, “Enhanced Cascaded Frequency Controller Optimized by Flow Direction Algorithm for Seaport Hybrid Microgrid Powered by Renewable Energies,” Applied Energy 74 (2024): 123996.
10.1016/j.apenergy.2024.123996
Google Scholar
22Z. A. Ansari and G. L. Raja, “Flow Direction Optimizer Tuned Robust FOPID-(1+ TD) Cascade Controller for Oscillation Mitigation in Multi-Area Renewable Integrated Hybrid Power System With Hybrid Electrical Energy Storage,” Journal of Energy Storage 83 (2024): 110616, https://doi.org/10.1016/j.est.2024.110616.
10.1016/j.est.2024.110616
Google Scholar
23L. C. Saikia, N. Sinha, and J. Nanda, “Maiden Application of Bacterial Foraging Based Fuzzy IDD Controller in AGC of a Multiarea Hydrothermal System,” International Journal of Electrical Power & Energy Systems 45, no. 1 (2013): 98–106.
10.1016/j.ijepes.2012.08.052
Web of Science® Google Scholar
24P. K. Mohanty, B. K. Sahu, T. K. Pati, S. Panda, and S. K. Kar, “Design and Analysis of Fuzzy PID Controller With Derivative Filter for AGC in Multiarea Interconnected Power System,” IET Generation Transmission and Distribution 10, no. 15 (2016): 3764–3776, https://doi.org/10.1049/iet-gtd.2016.0106.
10.1049/iet-gtd.2016.0106
Web of Science® Google Scholar
25D. Khamari, R. K. Sahu, T. S. Gorripotu, and S. Panda, “Automatic Generation Control of Power System in Deregulated Environment Using Hybrid TLBO and Pattern Search Technique,” Ain Shams Engineering Journal 11, no. 3 (2020): 553–573.
10.1016/j.asej.2019.10.012
Web of Science® Google Scholar
26A. K. Mohapatra, S. Mohapatra, and A. Pattnaik, “Design and Modelling of an AI Governed Type-2 Fuzzy Tilt Control Strategy for AGC of a Multi-Source Power Grid in Constraint to Optimal Dispatch,” e-Prime—Advances in Electrical Engineering, Electronics and Energy 7 (2024): 100487.
10.1016/j.prime.2024.100487
Google Scholar
27G. Sharma, N. Ibraheem, K. Niazi, and R. C. Bansal, “Adaptive Fuzzy Critic Based Control Design for AGC of Power System Connected via AC/DC Tie-Lines,” IET Generation Transmission and Distribution 11, no. 2 (2016): 560–569.
10.1049/iet-gtd.2016.1164
Web of Science® Google Scholar
28H. H. Coban, A. Rehman, and M. Mousa, “Load Frequency Control of Microgrid System by Battery and Pumped-Hydro Energy Storage,” Water 14 (2022): 1818.
10.3390/w14111818
Web of Science® Google Scholar
29P. Dash, L. C. Saikia, and N. Sinha, “Comparison of Performances of Several FACTS Devices Using Cuckoo Search Algorithm Optimized 2DOF Controllers in Multiarea AGC,” Electrical Power and Energy Systems 65 (2015): 316–324.
10.1016/j.ijepes.2014.10.015
Web of Science® Google Scholar
30B. Begum, N. K. Jena, B. K. Sahu, et al., “Application of an Intelligent Fuzzy Logic Based Sliding Mode Controller for Frequency Stability Analysis in a Deregulated Power System Using OPAL-RT Platform,” Energy Reports 11 (2024): 510–534.
10.1016/j.egyr.2023.12.023
Web of Science® Google Scholar
31W. Tasnin and L. C. Saikia, “Performance Comparison of Several Energy Storage Devices in Deregulated AGC of a Multiarea System Incorporating Geothermal Power Plant,” IET Renewable Power Generation 12, no. 7 (2018): 761–772.
10.1049/iet-rpg.2017.0582
Web of Science® Google Scholar
32P. Dash, L. C. Saikia, and N. Sinha, “Comparison of Performances of Several FACTS Devices using Cuckoo Search Algorithm Optimized 2DOF Controllers in Multi-area AGC,” International Journal of Electrical Power & Energy Systems 65 (2015): 316–324.
10.1016/j.ijepes.2014.10.015
Web of Science® Google Scholar
33A. Dutta and S. Debbarma, “Frequency Regulation in Deregulated Market Using Vehicle-to-Grid Services in Residential Distribution Network,” IEEE Systems Journal 12, no. 3 (2018): 2812–2820.
10.1109/JSYST.2017.2743779
Web of Science® Google Scholar
34K. Peddakapu, P. Srinivasarao, M. R. Mohamed, Y. Arya, and D. J. K. Kishore, “Stabilization of Frequency in Multi-Microgrid System Using Barnacle Mating Optimizer-Based Cascade Controllers,” Sustainable Energy Technologies and Assessments 54 (2022): 102823.
10.1016/j.seta.2022.102823
Web of Science® Google Scholar
35K. Singh and Y. Arya, “Tidal Turbine Support in Microgrid Frequency Regulation Through Novel Cascade Fuzzy-FOPID Droop in de-Loaded Region,” ISA Transactions 133 (2023): 218–232.
10.1016/j.isatra.2022.07.010
PubMed Web of Science® Google Scholar
36R. Choudhary, J. N. Rai, and Y. Arya, “FOPTID+ 1 Controller With Capacitive Energy Storage for AGC Performance Enrichment of Multi-Source Electric Power Systems,” Electric Power Systems Research 221 (2023): 109450.
10.1016/j.epsr.2023.109450
Web of Science® Google Scholar
37E. Çelik, “Exponential PID Controller for Effective Load Frequency Regulation of Electric Power Systems,” ISA Transactions 153 (2024): 364–383.
10.1016/j.isatra.2024.07.038
PubMed Web of Science® Google Scholar
38H. Shayeghi, A. Rahnama, N. Bizon, and A. Szumny, “Interconnected Microgrids Load-Frequency Control Using Stage-By-Stage Optimized TIDA+ 1 Error Signal Regulator,” Engineering Reports 7, no. 1 (2025): e13095.
10.1002/eng2.13095
Web of Science® Google Scholar
39E. Çelik, N. Öztürk, and E. H. Houssein, “Improved Load Frequency Control of Interconnected Power Systems Using Energy Storage Devices and a New Cost Function,” Neural Computing and Applications 35, no. 1 (2023): 681–697.
10.1007/s00521-022-07813-1
Web of Science® Google Scholar
40E. Çelik and N. Öztürk, “Novel Fuzzy 1PD-TI Controller for AGC of Interconnected Electric Power Systems With Renewable Power Generation and Energy Storage Devices,” Engineering Science and Technology, an International Journal 35 (2022): 101166.
10.1016/j.jestch.2022.101166
Web of Science® Google Scholar
41E. Çelik, “Improved Stochastic Fractal Search Algorithm and Modified Cost Function for Automatic Generation Control of Interconnected Electric Power Systems,” Engineering Applications of Artificial Intelligence 88 (2020): 103407.
10.1016/j.engappai.2019.103407
Web of Science® Google Scholar
42A. M. El-Rifaie, S. Abid, A. R. Ginidi, and A. M. Shaheen, “Fractional Order PID Controller Based-Neural Network Algorithm for LFC in Multi-Area Power Systems,” Engineering Reports 7, no. 2 (2025): e70028.
10.1002/eng2.70028
Web of Science® Google Scholar
43E. Çelik, “Design of New Fractional Order PI–Fractional Order PD Cascade Controller Through Dragonfly Search Algorithm for Advanced Load Frequency Control of Power Systems,” Soft Computing 25 (2021): 1193–1217, https://doi.org/10.1007/s00500-020-05215-w.
10.1007/s00500-020-05215-w
Web of Science® Google Scholar
44C. B. A. Raju, S. Debbarma, and R. S. Rao, “Smart Transformer-Assisted Frequency Control Mechanism for RES Penetrated Power Systems Considering Metaheuristic-Based Secondary Controller,” Energies 19961073 17, no. 23 (2024): 5883, https://doi.org/10.3390/en17235883.
10.3390/en17235883
Web of Science® Google Scholar
45A. Askarzadeh, “A Novel Metaheuristic Method for Solving Constrained Engineering Optimization Problems: Crow Search Algorithm,” Journal of Computers & Structures 169 (2016): 1–12, https://doi.org/10.1016/j.compstruc.2016.03.001.
10.1016/j.compstruc.2016.03.001
Web of Science® Google Scholar

Volume7, Issue5

May 2025

e70185

Enhanced Automatic Generation Control in Multiarea Power Systems: Crow Search Optimized Cascade FOPI-TIDDN Controller With Integrated Renewable Solar Thermal Models and HVDC Lines

ABSTRACT