Engineering Reports
Volume 7, Issue 3 e70039
RESEARCH ARTICLE
Open Access

State Identification of Charging Module Based on SN-EMD-SSEE and DBO-HKELM

Bingyu Li, 

Corresponding Author

Bingyu Li

State Grid Hebei Energy Technology Service Co. Ltd, Shijiazhuang, China

Correspondence: Bingyu Li ([email protected])

Contribution: Conceptualization, ​Investigation, Visualization, Validation, Methodology, Formal analysis, Writing - original draft, Writing - review & editing, Data curation

Search for more papers by this author
Xianhai Pang, 

Xianhai Pang

State Grid Hebei Energy Technology Service Co. Ltd, Shijiazhuang, China

Contribution: ​Investigation, Validation, Formal analysis, Writing - original draft

Search for more papers by this author
Xuhao Du, 

Xuhao Du

State Grid Hebei Energy Technology Service Co. Ltd, Shijiazhuang, China

Contribution: ​Investigation, Validation, Visualization, Writing - original draft, Formal analysis

Search for more papers by this author
Ziwen Cai, 

Ziwen Cai

State Grid Hebei Energy Technology Service Co. Ltd, Shijiazhuang, China

Contribution: ​Investigation, Validation, Writing - review & editing, Formal analysis

Search for more papers by this author
First published: 03 March 2025
https://doi.org/10.1002/eng2.70039

Funding: This work was supported by Science and technology projects of State Grid Corporation of China, TSS2022-08.

ABSTRACT

Lithium-ion batteries are widely used in emergency back-up power supply with its superior performance, and they are usually used with a charging module. The charging module is usually composed of power electronic devices, but failures may occur in power electronic devicesdue to device aging and mechanical vibration in the complex environment; it will result in huge economic losses. However, the protection function of the charging module covers short fault, over-voltage fault, and over-current at system level rather than the open-circuit fault of MOSFETs and diodes at component level, which leads to hidden fire danger or accident risks. To address this issue, this paper improved a new state identification method of charging module based on signal normalization (SN) which is specially designed, empirical mode decomposition (EMD), sequence signal entropy extraction (SSEE), hybrid kernel extreme learning machine (HKELM), and dung beetle optimization (DBO). In basic work, 10 measurable variables and 23 fault states are determined by simulating open-circuit faults at MOSFETs and diodes. In data pre-processing, SN-EMD-SSEE is developed to extract state characteristics values for high adaptability to full working condition and high significance for easy identification. In modeling, DBO-HKELM identification model is constructed by improving ELM (Extreme Learning Machine) and optimizing parameters based on DBO 60 state characteristics values and 24 states including normal state, which are, respectively, used as the input and output of the identification model. In verification, the proposed state identification method based on SN-EMD-SSEE and DBO-HKELM is embedded into the control chip of charging module to obtain fault state code in real time. The experimental results show that the proposed state identification method is robust, and its identification accuracy is up to 94.7%.

1 Introduction

With the rapid development of power systems incorporating new energy sources in recent years, lithium-ion batteries have become increasingly popular as emergency backup power supplies for power stations. However, due to the crucial importance of charging safety, the charging module must possess a reliable stable control strategy [1]. Consequently, there is a pressing need to identify fault types and locations in a timely and accurate manner [1, 2]. The output characteristic of the converter is controlled by changing the duty cycle. Varying duty cycles cause small voltage and current fluctuations or a significant change, which results in reduced system stability and its equivalent parameter degradation, even the occurrence of open-circuit and short-circuit faults [2-5]. The fault-induced surge current can cause serious damage to other components. Power electronic switch devices are the weakest link in the reliability of charging modules, and the early diagnosis of their abnormal or fault can assist fault-tolerant operation or fault protection, which is crucial for the safety of battery charging [6-8]. The method of fault diagnosis mainly adopts an analytical model, data-driven technology, and a signal-processing method [9].

Using the method based on the analytical models, circuit operation states are simulated, and voltage or current is predicted, which are compared with their reference value [6, 10]. Then we can find out the abnormal state of the circuit operation. It usually uses the residual values of the phase currents obtained [7] to realize the diagnosis. Although the method can achieve faster fault diagnosis and accurate fault localization, the fault evolution mechanism requires the model with high accuracy, which leads to difficulty in modeling. Data-based modeling methods are usually built on the modeling framework under offline conditions. It usually uses expert systems [8, 9], support vector machines [11], neural networks [3], and other artificial intelligence algorithms to analyze and classify the fault signals that exhibit fault characteristics. Then it constructs the corresponding network model to carry out training and achieves scientific and accurate diagnosis. Signal processing decomposes and transforms the data according to the signal analysis strategy and extracts feature information from it [12-14]. Diagnostic methods can be divided into spectrum analysis method1 and wavelet transform method [15, 16]. Fault diagnosis and identification can be realized by comparing the change rule of feature information before and after the fault, and the diagnosis time is short, but for the complex system fault, the accuracy of this method will decrease.

For charging modules, both short-circuit faults and phase loss faults are protected, but MOSFET and diode degradation and open circuits are not protected. To address this issue, this paper simulates device failures at different locations of the charging module and proposes three risk levels. The main contributions of this paper are as follows:
  1. Based on the simulation and experiment environment, a fault simulation system of the charging module is established to study the change of input and output characteristics before and after a kind of fault occurs.
  2. To accurately identify charging module fault types and fault locations, charging module faults are meticulously categorized and encoded, with a total of 23 fault modes.
  3. According to the different characteristics of different faults, the fault feature vector is extracted from the input and output, the state feature extraction method SN-EMD-SSEE is proposed to improve adaptability and signification, and a generalized state identification model DBO-HKELM is developed, which greatly improves the accuracy and speed of fault diagnosis.
  4. The state identification method based on SN-EMD-SSEE and DBO-HKELM model has been proven to be accurate and robust through numerous fault simulation experiments.

2 Related Basic Work

2.1 Main Circuit and Its Measured Variables

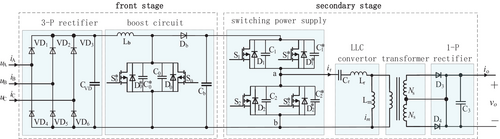
Figure 1 shows the main circuit of charging module, including the front-stage circuit for rectifying and boosting and the secondary circuit for electrical isolation and current modulation. The front-stage circuit consists of six diode VDi (i = 1, 2, 3, 4, 5, 6) with a filter capacitor CVD in 3-Ph, two MOSFETs (S0 and S 0 * $$ {S}_0^{\ast } $$ ) with anti-parallel diodes (D0 and D 0 * $$ {D}_0^{\ast } $$ ) and coupling capacitors (C0 and C 0 * $$ {C}_0^{\ast } $$ ), a filter capacitor Cb, a diode Db, and an inductor Lb for continuous current in boost circuit. The secondary circuit consists of four MOSFETs (S1 and S 1 * $$ {S}_1^{\ast } $$ , S2 and S 2 * $$ {S}_2^{\ast } $$ ) with anti-parallel diodes (D1 and D 1 * $$ {D}_1^{\ast } $$ , D2 and D 2 * $$ {D}_2^{\ast } $$ ) and coupling capacitors (C1 and C 1 * $$ {C}_1^{\ast } $$ , C2 and C 2 * $$ {C}_2^{\ast } $$ ) in switching power supply, a resonant capacitance Cr, a resonant inductor Lr and an excitation inductor Lm in LLC converter, ideal transformer and two diodes (D3 and D4), and a filter capacitor C3 for 1-p full wave rectifier at its output side. uA, uB, and uC are input voltages. iA, iB, and iC are input currents. io is the operating current at the output side of module. vo is the output voltage, equal to the value of battery voltage. In addition, the operating temperature (T0 and T 0 * $$ {T}_0^{\ast } $$ , T1 and T 1 * $$ {T}_1^{\ast } $$ , T2 and T 2 * $$ {T}_2^{\ast } $$ ) of every MOSFET is monitored.

Details are in the caption following the image
FIGURE 1
Open in figure viewerPowerPoint
Main circuit of the charging module.

2.2 Simulation Model and Experimental Platform

To prove the validity and feasibility of the fault identification method proposed in this paper, both the simulation system and experimental platform of the charging module are built, as shown in Figure 2. The main device types used in the platform are as follows: Boost-PFC (Power Factor Correction) circuit inductor model th6-9021.3, size 940 MF, Diode Model C4D15120D, IGBT model IKW40N120H3, Negative Temperature Coefficient (NTC) thermistor CWF4B 103j3950. The simulation of the open circuit fault of diodes and switches at different positions is carried out. The input and output current and working temperature of the charging module are monitored by an oscilloscope.

Details are in the caption following the image
FIGURE 2
Open in figure viewerPowerPoint
Experimental prototype of the charging module.

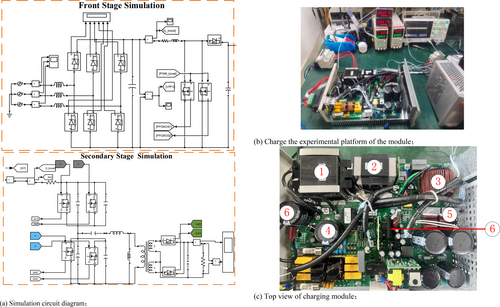
Figure 2c shows the top view of (b), where 1 to 6 are the transformer, resonant inductor, inductor of the pre-stage boost circuit, output filter capacitor, resonant capacitor, output filter capacitor, and main control chip.

To improve the robustness of the diagnostic method, the input voltage is set at intervals within ±15% (i.e., 187V˜264V) of its rated value (i.e., 220VAC), and the output voltage is set at intervals within ±10% (i.e., 198V˜286V) of its rated value (i.e., 220VDC), the simulation of the full operating condition is realized.

2.3 Fault Simulation

We consider the most common failures, which are open-circuit faults, short-circuit faults, and abnormal operating temperatures of MOSFETs or diodes in operation. For charging modules, short-circuit, over-current, and over-voltage faults are protected, but the deterioration and open-circuit faults of MOSFET or rectifier diodes are not in the full scope of protection functions. The simulation results of unprotected faults are shown in Figure 3.

Details are in the caption following the image
FIGURE 3
Open in figure viewerPowerPoint
The simulation results of unprotected faults.

In order to study the characteristics of the electrical changes that occur when the fault occurs, the simulation software is used to simulate the electrical characteristics of the input current output current when the fault occurs at 0.2 s as shown in Figure 3. (a) The input and output currents of the electrical waveforms for the front-stage rectifier circuit diode when the open-circuit fault, occurs. We can see that a single open-circuit only corresponds to the phase missing half of the input, two open-circuit loss of all the input of the phase, the output in a short period of time with almost no change. (b) The figure shows the electrical waveforms and temperature simulation waveforms of the input and output currents when an open-circuit fault occurs in the diode or MOSFET of the preamplifier circuit. It can be seen that the input current slowly increases and the output current slowly decreases when an open-circuit fault occurs in the diode Db of the former circuit. When an open-circuit fault occurs in the power tube S0, there is no change in the input and output for a short period of time because the circuit uses two tubes running in parallel, but the temperature graph shows that the temperature of S 0 * $$ {S}_0^{\ast } $$ decreases and the parallel operation of the non-faulty tube S0 rises and stabilizes with a temperature change of about 10 s. (c) The figure shows the waveforms of the electrical and thermal characteristics of the back-stage circuit LLC during an open-circuit failure of the parallel MOSFET tubes in the bridge arms. When an open-circuit fault occurs in the parallel dual power tubes in either bridge arm, it can be seen that the input drops rapidly to 0 and the output drops rapidly to near the 0 value. When an open-circuit fault occurs in a single power tube S1 in any bridge arm, there is no effect on the input as well as the output for a short period of time because each bridge arm is running dual tubes in parallel, but the temperature graph shows that the temperature of S1 decreases and the parallel operation of the non-faulty tube S 1 * $$ {S}_1^{\ast } $$ rises and stabilizes with a temperature change of about 10 s. (d) The figure shows the electrical waveforms of the input and output currents of the rear output rectifier diode when an open-circuit and a short-circuit fault occurs. The electrical waveform of the input and output currents when D3 is open circuit, the peak value of the input current decreases slightly when D3 is open circuit and the output current decreases from 4 to 3, when D3 and D4 are open circuit at the same time, the input current attenuates to 0 within 0.05 s and the output current attenuates to 0 within 0.052 s, and the output current begins to gradually attenuate when D3 is short-circuited and the output current instantly becomes a sinusoidal waveform with a peak value of 2 from 4A to 2 when D3 and D4 are short-circuited. D3 and D4 short-circuit when the input current begins to gradually decay output current from DC 4A into the peak value from 4 to start decaying sine wave; (e) Figure for the part of the device occurs when the short-circuit failure of the input and output currents of the electrical waveforms, when the VD1, Db, or any of the MSOFET short-circuit, the input current suddenly increased for the original thousands of times and the output current output also shows a different degree of downward trend.

From Figure 3, it can be seen that we can extract fault characteristic parameters from the measured variables, iA, iB, iC, io, Ti, and T i * $$ {T}_i^{\ast } $$ .

3 Method Design

We proposed a new charging module state identification method based on SN, EMD, SSEE, ELM, and DBO, shown in Figure 4. Firstly, the data pre-processing link, SN-EMD-SSEE, is designed to reconstruct state characteristic values from measured current and temperature under all working condition with fault occurrence at given time point. Among them, SN is special made for 3-p input current, output current, and working temperature. Secondly, the state identification model DBO-HKELM is developed by using state characteristic values SN-EMD-SSEE as its input. It involves data set division, model selection and parameter optimization, model training, and model validation. Among them, we improved DBO and HKELM for high precision, and both RMSE and MARE are used for precision assessment. Finally, the state identification based on SN-EMD-SSEE and DBO-HKELM with the optimal parameters is embedded into the charging module for real-time real-time state monitoring.

Details are in the caption following the image
FIGURE 4
Open in figure viewerPowerPoint
Charging module state identification method based on EMD-DBO-HKELM.

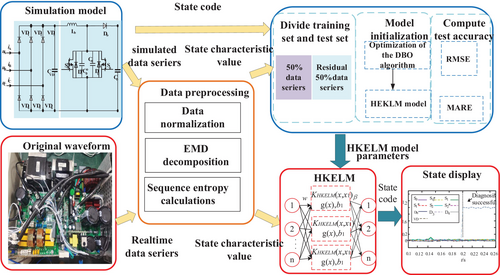
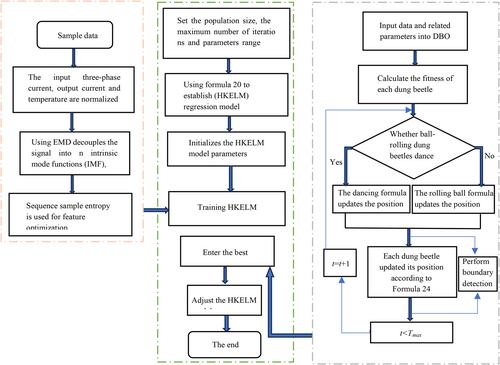
Firstly, the signal is normalized, and then the non-stationary data are smoothed by the EMD (empirical mode decomposition), so that the complex signal is decomposed into a finite IMF (intrinsic mode function) based on the given battery charge and discharge experimental data, the training set and test set are divided, and the input data of the original training set and test set are unified, that is, the input quantity is processed based on the maximum and minimum homogenization principle, and then the features were extracted by Sequence Sample Entropy Extraction. Secondly, introducing the DBO algorithm to optimize the HKELM model parameters, the DBO algorithm divides all mantises in the population into four distinct subpopulations, simulating the five behaviors of rolling ball, dancing, breeding, foraging, and stealing. The positions of the five mantis subpopulations are updated according to the formula iteratively until the number of iterations t reaches the maximum number of iterations Tmax and output the optimal solution of each parameter of the HKELM model to be optimized. So the regularization coefficient C, the mixed kernel parameters σ, m, n, and d, and the weight coefficient λ of the HKELM model were optimized by using dung beetle optimizer (DBO). Finally, the initial values of the optimal network parameters were obtained by the DBO algorithm, and the HKELM model was trained to obtain the global optimum. The feature signal is input into HKELM, and the overall optimization of the model performance is realized. The specific algorithm flowchart is shown in Figure 5.

Details are in the caption following the image
FIGURE 5
Open in figure viewerPowerPoint
Algorithm flowchart.

3.1 Signal Normalization

There are a lot of varying components in the transient current under different conditions, which leads to the reduction of the state identification accuracy. In this paper, signal normalization is separately proposed for the input three-phase current ik, output current io, and temperature Ti are normalized.
  1. The normalized input current i k → $$ \overrightarrow{i_k} $$ is defined as follows:
i k → = i k × 3 U k U o I o $$ \overrightarrow{i_k}={i}_k\times \frac{3{U}_k}{U_o{I}_o} $$ (1)
where ik is the transient value of input current, k = A, B, C; Uk, Uo, and Io are separately the valid value of phase voltage at input side, DC component of output voltage Uo, and output current Io.
  1. The normalized output current i o → $$ \overrightarrow{i_o} $$ is defined as follows:
i o → = I o I oref $$ \overrightarrow{i_o}=\frac{I_o}{I_{\mathrm{oref}}} $$ (2)
where Io is the DC component of output current and I oref $$ {I}_{\mathrm{oref}} $$ is the expectation of output current.
  1. The normalized working T i → $$ \overrightarrow{T_i} $$ is defined as follows:
T i → = T i T ‾ $$ \overrightarrow{T_i}=\frac{T_i}{\overline{T}} $$ (3)
where Ti is the real-time temperature and T ‾ $$ \overline{T} $$ is the average temperature of MOSFETs with temperature coupling.

3.2 Empirical Mode Decomposition

Empirical mode decomposition (EMD) [17, 18] is an adaptive time-frequency processing method for nonlinear non-smooth signals x(t). The non-smooth signals are decomposed into a series of Intrinsic Mode Functions (IMF) with different eigen-scales, and a trend component, described as:
x ( t ) = ∑ i = 1 n c i ( t ) + r n ( t ) $$ x(t)=\sum \limits_{i=1}^n{c}_i(t)+{r}_n(t) $$ (4)

In Equation (4), x(t) is the original signal, ci(t) is the i-th IMF component, which contains the components of the original signal in different frequency bands and different time scales, and rn (t) is the trend component, which represents the average trend information of the original signal.

The IMF component should satisfy the following: (1) the sum of the extreme points should be equal to the number of points over zero or at most one difference; (2) the upper and lower envelopes are locally symmetric on the time axis.

The procedure for the general EMD decomposition of a non-smooth signal x(t) is as follows:
  1. Determine all local extreme points of x(t) and connect the local value points with a cubic spline to form the upper envelope v1(t) and the lower envelope v2(t). The v1(t) and v2(t) are the upper and lower envelopes formed by connecting the local extreme points to the cubic spline, and compute the mean value m(t):
m ( t ) = v 1 ( t ) + v 2 ( t ) 2 $$ m(t)=\frac{v_1(t)+{v}_2(t)}{2} $$ (5)
  1. Calculate h10(t):
h 10 ( t ) = x ( t ) − m ( t ) $$ {h}_{10}(t)=x(t)-m(t) $$ (6)
If h10(t) is an IMF, then it is the first IMF component of x(t), IMF1; if h10(t) is not an IMF, then it is used as the original signal repeating steps (1) and (2) to compute h1k(t), (k = 1, 2 …) until the IMF condition is satisfied, and IMF1 is obtained;
  1. Calculate rn(t):
r n ( t ) = x ( t ) − ∑ i = 1 n IMF i $$ {r}_n(t)=x(t)-\sum \limits_{i=1}^n{\mathrm{IMF}}_i $$ (7)
Taking rn(t) as the original signal, repeat steps (1˜2) until rn(t) becomes a monotone function, whose criterion is that the sd of two continuous IMF is less than the given value and sd is calculated by the following formula:
s d = ∑ t = 0 T h 1 ( k − 1 ) ( t ) − h 1 k ( t ) 2 h 1 k ( t ) 2 $$ {s}_d=\sum \limits_{t=0}^T\frac{{\left|{h}_{1\left(k-1\right)}(t)-{h}_{1k(t)}\right|}^2}{h_{1k(t)}^2} $$ (8)
where T is the time span of the signal, and h1(k−1)(t) and h1k(t) are two consecutive IMFs in the decomposition process.

3.3 Sequence Sample Entropy Extraction

Sequence sample entropy [19] EnSample is a good tool for feature detection of nonlinear time series XN(1) = x(1), x(2), …, x(N). The calculation is as follows:
  1. N − m + 1 vector sequence with dimension m is extracted by ordinal number Xm(i), (i = 1, 2, …,N − m + 1). Calculate the distance between Xm(i) and Xm(j):
d X m ( i ) , X m ( j ) = max [ | x ( i + k ) − x ( j + k ) | ] $$ d\left[{X}_m(i),{X}_m(j)\right]=\max \left[|x\left(i+k\right)-x\left(j+k\right)|\right] $$ (9)
  1. Given r(r > 0), count the number d [ X m ( i ) , X m ( j ) < r ] $$ \left\{d\Big[{X}_m(i),{X}_m(j)<r\Big]\right\} $$ of d [Xm(i), Xm(j)] less than r for each I, calculate its ratio to the total number of distances N-m, marked as B i m ( r ) $$ {B}_i^m(r) $$ :
B i m ( r ) = d [ X m ( i ) , X m ( j ) < r ] N − m , i = 1 , 2 , … , N − m + 1 , i ≠ j $$ {B}_i^m(r)=\frac{\left\{d\Big[{X}_m(i),{X}_m(j)<r\Big]\right\}}{N-m},i=1,2,\dots, N-m+1,i\ne j $$ (10)
Calculate the mean B m ( r ) $$ {B}^m(r) $$ of N-m + 1 ratios B i m ( r ) $$ {B}_i^m(r) $$ :
B m ( r ) = ∑ i = 1 N − m + 1 B i m ( r ) N − m + 1 $$ {B}^m(r)=\frac{\sum \limits_{i=1}^{N-m+1}{B}_i^m(r)}{N-m+1} $$ (11)
  1. N − m vector sequences with m + 1 dimension Xm+1(i) are extracted by ordinal number, (i = 1,2, …, N − m). There are:
B i m + 1 ( r ) = d [ X m + 1 ( i ) , X m + 1 ( j ) < r ] N − m − 1 , i = 1 , 2 , … , N − m , i ≠ j B m + 1 ( r ) = 1 N − m ∑ i = 1 N − m B i m + 1 ( r ) $$ {\displaystyle \begin{array}{c}{B}_i^{m+1}(r)=\frac{\left\{d\Big[{X}_{m+1}(i),{X}_{m+1}(j)<r\Big]\right\}}{N-m-1},\kern0.33em i=1,2,\dots, N-m,i\ne j\\ {}{B}^{m+1}(r)=\frac{1}{N-m}\sum \limits_{i=1}^{N-m}{B}_i^{m+1}(r)\end{array}} $$ (12)
  1. The entropy of sequence sample EnSample(m,r) is calculated as:
En Sample ( m , r ) = lim N → ∞ − ln B m + 1 ( r ) B m ( r ) $$ {En}_{\mathrm{Sample}}\left(m,r\right)=\underset{N\to \infty }{\lim}\left\{-\ln \left[\frac{B^{m+1}(r)}{B^m(r)}\right]\right\} $$ (13)

The sample entropy is closely related to the sequence dimension M and the threshold R. Some studies suggest that m is usually set at 1 or 2, and R is usually set at 0.1–0.25 STD (the standard deviation from the original data). In this paper, m takes the value 2 and R takes 0.1 STD.

3.4 Hybrid Kernel Extreme Learning Machine

The ELM [20-22] is a feed-forward neural network learning algorithm consisting of an input layer, a hidden layer and an output layer, a hidden layer, and an output layer. The core idea of the algorithm is to randomly generate the hidden layer neurons with invariant weights and thresholds in the training process. The ELM regression model is
f ( x ) = H β $$ f(x)= H\beta $$ (14)
where x is the input data vector {xn, n = 1,2, …, N}, f(x) is the output of the network, H is the mapping matrix h(x) of the hidden layer, and β is the weight matrix between the hidden layer and the output layer. The mapping matrix h(x) of ELM model with N input variables and hidden layers is
H = h ( x ) = g ω 1 , b 1 , x 1 ⋯ g ω K , b K , x 1 ⋮ ⋮ ⋮ g ω 1 , b 1 , x N ⋯ g ω K , b K , x N N × K $$ H=h(x)={\left[\begin{array}{lll}g\left({\omega}_1,{b}_{1,}{x}_1\right)& \cdots & g\left({\omega}_K,{b}_{K,}{x}_1\right)\\ {}\vdots & \vdots & \vdots \\ {}g\left({\omega}_1,{b}_{1,}{x}_N\right)& \cdots & g\left({\omega}_K,{b}_{K,}{x}_N\right)\end{array}\right]}_{N\times K} $$ (15)
where g (ωk, bk, xn) is the randomly generated activation function, and ωk and bk are, respectively, the weight and the threshold of node k in the hidden layer. According to the principle of generalized inverse matrix, β can be calculated by
β = H T HH T + I 0 C − 1 y $$ \beta ={H}^T{\left({HH}^T+\frac{I_0}{C}\right)}^{-1}y $$ (16)
The ELM regression model is
f ( x ) = HH T HH T + I 0 C − 1 y $$ f(x)={HH}^T{\left({HH}^T+\frac{I_0}{C}\right)}^{-1}y $$ (17)
where y is the output data vector {ym, i = 1,2, …, M}, C is the penalty coefficient, I0 is unit diagonal matrix, and HHT is calculated from the matrix of random activation function H.
In order to solve the problem that the optimal number of hidden layer nodes cannot be determined, Huang et al. [23] constructed a Machine Learning model named Kernel Extreme Learning Machine (KELM) [24, 25] by using the given kernel function KKELM(xi, xj) instead of the random HHT. Generally speaking, the kernel function is Gaussian function or Polynomial function. Huang et al. improved KELM again, which combines Gaussian and Polynomial to develop a mixed kernel function KHKELM (xi, xj)
K HKELM x i , x j = λ exp − x i − x j 2 2 σ 2 + ( 1 − λ ) m x i ⋅ x j + n d , σ > 0 , d ∈ N $$ {\displaystyle \begin{array}{ll}{K}_{\mathrm{HKELM}}\left({x}_i,{x}_j\right)& =\lambda \exp \left(-\frac{{\left\Vert {x}_i-{x}_j\right\Vert}^2}{2{\sigma}^2}\right)\\ {}& \kern1em +\left(1-\lambda \right){\left(m\left({x}_i\cdot {x}_j\right)+n\right)}^d,\sigma >0,d\in N\end{array}} $$ (18)
where σ, m, n, and d are the mixed kernel parameters, λ is the weight coefficient to be optimized, and λ∈ (0,1). The random matrix HHT in ELM is replaced by a hybrid kernel function matrix KHKELM
K HKELM = K HKELM x i , x j N × N $$ {K}_{\mathrm{HKELM}}={\left[{K}_{\mathrm{HKELM}}\left({x}_i,{x}_j\right)\right]}_{N\times N} $$ (19)
The proposed Hybrid Kernel Extreme Learning Machine (HKELM) regression model is
f ( x ) = K HKELM K HKELM + I 0 C − 1 y $$ f(x)={K}_{\mathrm{HKELM}}{\left({K}_{\mathrm{HKELM}}+\frac{I_0}{C}\right)}^{-1}y $$ (20)

Considering the limitations of global and local cores, the traditional single-core function KLEM model is difficult to accommodate the nonlinear time-varying characteristics of the data samples such as voltage, current, and temperature in the battery dataset during random use. In order to further improve the prediction accuracy of KELM model, this paper combines the advantages of both global and local cores. The complex mixed core function is constructed by using RBF and Poly core functions, and the HKELM model is constructed by using the mixed core function to enhance the non-linear modeling ability. The xi represents the i th input sample. The yj represents the actual output of the ELM. The ωn and βm represent the random input weight between the ith hidden level node of the network and the input node and the output weight with the output node, respectively, bi represents the ith hidden layer offset, and g(x) is the activation function of the hidden layer. This method combines the advantages of ELM and multiple kernel functions, with a strong learning ability and generalization ability. The structure of HKELM neural network is shown in Figure 6.

Details are in the caption following the image
FIGURE 6
Open in figure viewerPowerPoint
The structure of HKELM neural network.

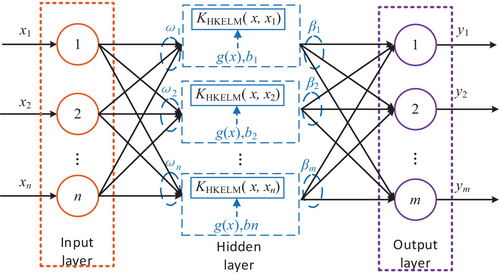
HKELM combines the advantages of kernel method and the ELM to achieve more efficient and accurate regression and classification tasks. HKELM not only inherits the fast training speed and generalization ability of ELM, but also improves the processing ability of the model to the complex data, thus realizing the overall optimization of the model performance.

3.5 Dung Beetle Optimizer

Dung Beetle Optimizer (DBO) [26, 27] is an optimization algorithm that simulates the behavior of Dung beetles in nature and is used to solve global optimization problems. In this paper, the DBO algorithm is introduced to optimize the regularization coefficient C, the mixed kernel parameter σ, m, n, and d, and the weight coefficient λ of the HKELM model with the root mean square error as the fitness function.

Combining Equation (5) determine the objective function of the HKELM model optimization based on the DBO algorithm as
fitness = 1 m ∑ j = 1 m f j − y j 2 $$ \mathrm{fitness}=\sqrt{\frac{1}{m}\sum \limits_{j=1}^m{\left({f}_j-{y}_j\right)}^2} $$ (21)
where m is the number of training set samples, and fj and yj are the actual output and expected output of training set samples, respectively.

The DBO algorithm divides all dung beetles in the population into four different sub-populations and simulates five behaviors, namely, ball-rolling, dancing, reproduction, foraging, and stealing [15].

The θ stands for ball-rolling dung beetle, which can initially look for the direction of its foraging, taking into account the beetle's position, rolling direction, environmental changes, and so on. The location is updated to
x θ ( t + 1 ) = x θ ( t ) + α × k × x θ ( t − 1 ) + b × ∣ x θ ( t ) − x θ w ∣ $$ {x}_{\theta}\left(t+1\right)={x}_{\theta }(t)+\alpha \times k\times {x}_{\theta}\left(t-1\right)+b\times \mid {x}_{\theta }(t)-{x_{\theta}}^w\mid $$ (22)
where xθ is the position of the ball-rolling dung beetle. xθw is the worst individual position in the current population; t is the number of iterations. α is the natural coefficient, which is −1 when the dung beetle moves away from its initial direction, otherwise 1. k is the deflection coefficient and b is the coefficient of environmental change.
When a ball-rolling dung beetle encounters an obstacle blocking its rolling path, it needs to reposition itself by dancing to find a new path. The position of the ball-rolling dung is updated according to formula (10)
x θ ( t + 1 ) = x θ ( t ) + tan ( ϕ ) × x θ ( t ) − x θ ( t − 1 ) $$ {x}_{\theta}\left(t+1\right)={x}_{\theta }(t)+\tan \left(\phi \right)\times \left({x}_{\theta }(t)-{x}_{\theta}\left(t-1\right)\right) $$ (23)
where φ is the deflection angle, φ ∈[0, π].
The ŋ represents breeding, and the algorithm incorporates a boundary selection strategy that allows dung beetles to select a suitable spawning site. The μ represents the foraging dung beetle, and the algorithm introduces the strategy of updating the boundary and position of the optimal foraging area, which helps the young dung beetle to find the source of food during the foraging process. The λ meanwhile, stands for larceny, and the algorithm updates the strategy by introducing the location of the larceny, allowing some species to steal other species' food or resources. The positions of the three species were updated as
x η ( t + 1 ) = x η best + b 1 × x η ( t ) − L η + b 2 × x η ( t ) − U η x μ ( t + 1 ) = x μ ( t ) + c 1 × x μ ( t ) − L μ + c 2 × x μ ( t ) − U μ x λ ( t + 1 ) = x μ best + p ×   | x λ ( t ) − x γ best | + | x λ ( t ) − x μ best | $$ \left\{\begin{array}{l}{x}_{\eta}\left(t+1\right)={x_{\eta}}^{\mathrm{best}}+{b}_1\times \left({x}_{\eta }(t)-{L}_{\eta}\right)+{b}_2\times \left({x}_{\eta }(t)-{U}_{\eta}\right)\\ {}{x}_{\mu}\left(t+1\right)={x}_{\mu }(t)+{c}_1\times \left({x}_{\mu }(t)-{L}_{\mu}\right)+{c}_2\times \left({x}_{\mu }(t)-{U}_{\mu}\right)\\ {}{x}_{\lambda}\left(t+1\right)={x_{\mu}}^{\mathrm{best}}+p\times \left(\mid {x}_{\lambda }(t)-{x_{\gamma}}^{\mathrm{best}}\mid +\mid {x}_{\lambda }(t)-x{\mu}^{\mathrm{best}}\mid \right)\end{array}\right. $$ (24)
where xŋ, xμ, and xλ are the positions of the population of dung ŋ, μ, and λ respectively, and best on the upper corner represents the current best position of the population. b1 and b2 are the uncorrelated random vectors of the dimension of the optimization problem. L and U represent the upper and lower bounds of each population constraint range, respectively. c1∼N(0, 1), c2 are the random numbers between (0, 1), and P is the random vector of normal distribution.

Finally, according to the Equations (8-11), by having different types of mantises perform their corresponding operations, the position and fitness of the subpopulation of dung beetle were updated continuously until the number of iterations t reached the maximum number of iterations Tmax, and the optimal solution of the parameters of the HKELM model to be optimized was the output.

4 The Results of the Experiment

4.1 State Encoding and Risk Description

According to the time-domain characteristics of these variables, we designed three kinds of risk levels G, Y, and R, whichcorrespond to no risk level, low risk level, and high risk level. The risk level R corresponds to the out-of-bounds failure; some variable exceeds its range, which is determined by the protection values or the limit value of the overload state. The risk level G is for no or slight deterioration of components and electrical contacts, corresponding to normal operating conditions; every variable changes in a certain range which is generally determined by rating value and coefficient of use of reduction. The Y level is between G and R, which is usually caused by progressive deterioration and is not to be ignored. We set the risk level threshold of state characteristic, shown in Table 1.

TABLE 1. The risk level threshold of state characteristics.
Variable symbol State characteristics Threshold of risk level G Threshold of risk level R
iK k = A, B, C EnSampleIk k = A, B, C ENIGY, the maximum of EnSampleIk from i k → $$ \overrightarrow{i_k} $$ under 110% rating input current in normal state ENIYR, the minimum of EnSample of from i k → $$ \overrightarrow{i_k} $$ under 90% steady input current in unprotected fault state
io EnSampleo ENOGY, the maximum of EnSampleo from i o → $$ \overrightarrow{i_o} $$ under 110% expected output current under initial state ENOYR, the minimum of EnSampleo from i o → $$ \overrightarrow{i_o} $$ under 90% output current in unprotected fault state

Ti or T i * $$ {T}_i^{\ast } $$

k = 0, 1, 2

 EnSampleTi or EnSampleTi* ENTGY, the maximum of EnSampleo from T → i $$ {\overrightarrow{T}}_i $$ under 10% unprotected operating temperature ENTYR, the minimum of EnSampleo from T → i $$ {\overrightarrow{T}}_i $$ under 90% unprotected operating temperature

According to the risk level thresholds in Table 1, we can encode the fault modes corresponding to the state characteristics and location of the MOSFET or diode through the actual needs of the project, as shown in Table 2. The first column in the table is the fault number, the second column is the device type of the fault, the third column is the location of the fault, the fourth column is the description of the fault set by the simulated waveform, the fifth column is whether it is protected or not, and the sixth column is the risk level assigned according to the actual situation.

TABLE 2. State coding and feature description for fault mode of charging module.
Fault code Fault mode Fault location Feature exception Protection (yes or no) Risk level
0 Normal Nop All EnSample no more than the threshold of risk level G No G
1 Open-circuit fault at single MOSFET S0 EnSampleT0* increase and EnSampleT0 decrease No R
2 Open-circuit fault at single MOSFET S 0 * $$ {S}_0^{\ast } $$ EnSampleT0* decrease and EnSampleT0 increase No R
3 Open-circuit fault at single MOSFET S1 EnSampleT1* increase and EnSampleT1 decrease No R
4 Open-circuit fault at single MOSFET S 1 * $$ {S}_1^{\ast } $$ EnSampleT1* decrease and EnSampleT1 increase No R
5 Open-circuit fault at single MOSFET S2 EnSampleT2* increase and EnSampleT2 decrease No R
6 Open-circuit fault at single MOSFET S 2 * $$ {S}_2^{\ast } $$ EnSampleT2* decrease and EnSampleT2 increase No R
7 Open-circuit fault at two mosfets S0 and S 0 * $$ {S}_0^{\ast } $$ EnSampleIk = 0 and EnSampleT0 and EnSampleT0* No R
8 Open-circuit fault at two mosfets S1 and S 1 * $$ {S}_1^{\ast } $$ EnSampleo decrease and EnSampleT1 and EnSampleT1* No R
9 Open-circuit fault at two mosfets S2 and S 2 * $$ {S}_2^{\ast } $$ EnSampleo decrease and EnSampleT2 and EnSampleT2* No R
10 Open-circuit fault at two mosfets S1 and S 2 * $$ {S}_2^{\ast } $$

EnSampleT1*and EnSampleT2 increase

EnSampleT2*and EnSampleT1 decrease

 No R
11 Open-circuit fault at two mosfets S1 and S2

EnSampleT1*and EnSampleT2* increase

EnSampleT2and EnSampleT1 decrease

 No R
12 Open-circuit fault at two mosfets S2 and S 1 * $$ {S}_1^{\ast } $$

EnSampleT2*and EnSampleT1 increase

EnSampleT2and EnSampleT1* decrease

 No R
13 Open-circuit fault at two mosfets S2 and S1

EnSampleT1*and EnSampleT2* increase

EnSampleT2and EnSampleT1 decrease

 No R
14 Open-circuit fault at single diode Db EnSampleIk increase and EnSampleo decrease No Y
15 Open-circuit fault at single diode D3 or D4 EnSampleIk and EnSampleo decrease in lower speed No R
16 Open-circuit fault at two diodes D3 and D4 EnSampleIk and EnSampleo decrease in certain speed No R
17 Short-circuit fault at single diode D3 or D4 EnSampleIk decrease and EnSampleo jump down firstly and then decrease with oscillation No R
18 Short-circuit fault at two diodes D3 and D4 EnSampleIk decrease and EnSampleo decrease with oscillation No R
19 Open-circuit fault at two diodes VD1 or VD4 A phase missing only IA → 0 Yes R
20 Open-circuit fault at two diodes VD2 or VD5 B phase missing only IB → 0 Yes R
21 Open-circuit fault at two diodes VD3 or VD6 C phase missing only IC → 0 Yes R
22 Short-circuit fault at single diode VDi, Db, Si or S i * $$ {S}_i^{\ast } $$ A sudden increase in the input current EnSampleIk > 5ENIYR Yes R
23 Parameter degeneration Module ENGY < any EnSample < ENYR No Y

Based on risk level thresholds in the table, we can encode the fault modes corresponding to the state features and the position of MOSFET or diode, listed in Table 2.

4.2 State Characteristics Extraction

We take the SSE of IMFi (i = 1,2, …, 6) of 10 normalized state variables within 20 ms after fault occurrence as state characteristics values for all faults of concern. In the case of fault 16, the range of 60 state eigenvalues is shown in Table 3.

TABLE 3. Range of change of state characteristics values during fault 16.
State characteristics values range after fault occurrence within 20 ms
Variable IMF1 IMF2 IMF3 IMF4 IMF5 IMF6
iA 0.503343 → 0.278251 0.406562 → 0.429045 0.585029 → 0.579311 0.513439 → 0.525709 0.318318 → 0.169359 0.048013 → 0.052107
iB 0.548936 → 0.600039 0.576956 → 0.449973 0.559490 → 0.616845 0.405833 → 0.547249 0.056448 → 0.236907 0.022263 → 0.064352
iC 0.548893 → 0.594078 0.529115 → 0.576637 0.572790 → 0.629547 0.409059 → 0.552813 0.090641 → 0.202375 0.087626 → 0.087626
io 0.1000 → 0.0000 0.1000 → 0.0876 0.1000 → 0.0300 0.1000 → 0.0151 0.1000 → 0.0037 0.1000 → 0.0001
T0 0.498761 → 0.496604 0.539895 → 0.54196 0.569124 → 0.569241 0.527450 → 0.527419 0.377150 → 0.377139 0.218492 → 0.219498
T 0 * $$ {T}_0^{\ast } $$ 0.490144 → 0.490428 0.552130 → 0.551272 0.56542 → 0.56232 0.533825 → 0.538277 0.172541 → 0.171158 0.034832 → 0.034734
T1 0.468917 → 0.468916 0.606350 → 0.606349 0.569871 → 0.57889 0.416450 → 0.416417 0.260504 → 0.260506 0.02336 → 0.023355
T 1 * $$ {T}_1^{\ast } $$ 0.490125 → 0.490428 0.551278 → 0.551272 0.56312 → 0.56232 0.538276 → 0.538277 0.171157 → 0.171158 0.034751 → 0.034734
T2 0.515486 → 0.515486 0.608657 → 0.608656 0.503246 → 0.502345 0.398549 → 0.399573 0.108143 → 0.108142 0.033089 → 0.033089
T 2 * $$ {T}_2^{\ast } $$ 0.403019 → 0.403045 0.318797 → 0.328797 0.462913 → 0.462911 0.349429 → 0.349436 0.129684 → 0.129684 0.023672 → 0.023670

From Table 3, we can see that when a fault occurs after the EMD algorithm run processing results from the normal value in front of the arrow to the value behind the arrow, which can be used as a basis for determining whether the fault occurs and its location.

4.3 Identification Results

Some unprotected faults are simulated and identified using the identification method proposed in this paper under full working conditions on the experimental platform. Partial fault identification results are shown in Figure 7 and the fault statistics, the statistical results of identification accuracy are shown in Figure 8.

Details are in the caption following the image
FIGURE 7
Open in figure viewerPowerPoint
Diagnosis results of the charging module.
Details are in the caption following the image
FIGURE 8
Open in figure viewerPowerPoint
Some test set results are compared with the actual values.

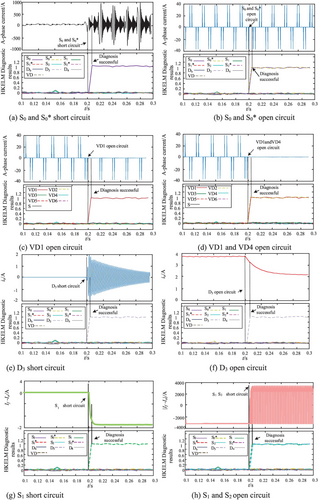
As shown in Figure 7a, the upper part of the figure is the decomposition waveform with obvious characteristics after data preprocessing and EMD decomposition, and the lower part is all the fault curves recognized by the model. When the fault occurs in 0.2 s, the upper part of the waveform undergoes a serious aberration after the model diagnosis of the fault recognition outputs the corresponding fault curves of the lower half. At this time, the corresponding fault curves rise rapidly from the vicinity of the value of 0 to the value of 1 neighborhood, representing the success of fault recognition. In Figure 7b, when the fault occurs, the upper part of the processing waveform cannot be connected and reversed, and the corresponding fault curve rises rapidly from near 0 to 1 neighborhood and represents the success of the fault identification; in Figure 7c, when a fault occurs, part of the upper half of the processing waveform is lost, the corresponding lower part of the fault curve of the diagnostic output of the fault identification model rises rapidly from the vicinity of 0 to the neighborhood of 1, representing the success of fault identification; in graph (d), when a fault occurs, in the upper part of the processing waveform, all the waveforms are lost, and the corresponding lower part of the fault curve rises rapidly from 0 to 1 neighborhood, which represents the success of fault identification; in Figure 7e, when the fault occurs, the upper part of the processing waveform part of the phenomenon of violent oscillation with positive and negative, the corresponding lower part of the fault curve of the diagnostic output of the fault identification model rises rapidly from the vicinity of 0 to the neighborhood of 1, representing the success of fault identification; in graph (f), when a fault occurs, the upper part of the processing waveform part slowly decays away from the normal value, and the fault identification model diagnosis output corresponding to the lower part of the fault curve rises rapidly from near 0 to 1 neighborhood, represents the success of the fault identification; in Figure 7g, when the fault occurs, the upper part of the processing waveform part appears to decline rapidly, the corresponding lower part of the fault curve of the diagnostic output of the fault identification model rises rapidly from the vicinity of 0 to the neighborhood of 1, representing the success of fault identification; in Figure 7h, when a fault occurs, in the upper part of the processing waveform, the amplitude on the side that deviates from the time axis rises rapidly and a severe oscillation occurs, the corresponding lower part of the fault curve rises rapidly from 0 to 1 neighborhood, which represents the success of fault identification.

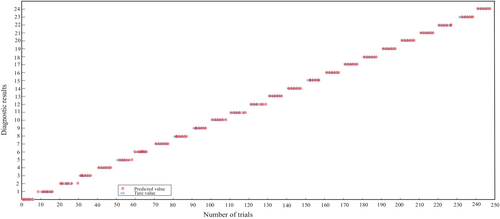
Figure 8 shows the accuracy of using the DBO-HKELM fault diagnosis model, with the samples of faults used on the horizontal axis and the corresponding fault codes on the vertical axis, one fault code for each fault type and 10 samples for each fault type. The test was conducted 10 times for each fault type and the number of results was recorded as shown in Figure 8, so that the fault code corresponding to each fault type could be accurately diagnosed. Finally, based on SN-EMD-SSEE and DBO-HKELM, different faults can be accurately identified and localized with an accuracy of 97.6% and good robustness.

From Figures 7 and 8, it can be seen that the proposed state identification based on SN-EMD-SSEE and DBO-HKELM can provide accurate judgment and location of different faults with good robustness. Fault identification accuracy for MOSFETs or diodes is about 97.6% when additionally considering communication faults, sensor faults, and others.

4.4 Comparison of Fault Identification Methods

To prove the accuracy and validity of the proposed SN-EMD-SSEE and DBO-HKELM model, we select two fault feature extraction methods and four fault identification methods for comparison.

The diagnosis results of fault feature extraction using the original wavelet packet algorithm and Sequence Sample Entropy Extraction are shown in Table 4. It can be seen from the Table 4 that the fault feature extracted by the improved wavelet packet algorithm is more representative and the diagnosis result is better. Table 5 shows diagnostic results with other superior methods, namely ELM, GWO-ELM, DBO-KELM, and DBO-HKELM. It can be seen from Table 5 that the training accuracy and test accuracy of the proposed method are higher than those of the other three methods.

TABLE 4. Comparison results of two feature extraction methods.
Feature extraction Training accuracy (%) Test accuracy (%)
Original wavelet packet 91.16 89.52
Sequence Sample Entropy Extraction 97.78 98.36
TABLE 5. Comparison results of four fault identification methods.
Method Training accuracy (%) Test accuracy (%)
ELM 96.20 92.30
GWO-ELM 97.06 97.20
DBO-KELM 97.50 97.05
DBO-HKELM 98.21 97.6

5 Conclusion

In order to meet the requirements of real-time monitoring of lithium-ion battery charging in case of open-circuit failure of charging modules MOSFET and diode, a state recognition method based on SN-EMD-SSEE and DBO-HKELM is proposed in this paper.

Three-phase AC input current, DC output current, and MOSFET operating temperature of the charging module are measured, and the normalization methods are designed, respectively. Furthermore, a data pre-processing method based on SN-EMD-SSEE is proposed to obtain the state characteristic parameters needed for identification. And the adaptability of the identification method to module power supply and load is improved.

DBO-HKELM model with good robustness and strong generalization ability is constructed based on ELM. Sixty state characteristic parameters with important fault information are extracted as input of the DBO-HKELM model. Twenty-five fault states are determined by fault simulation under full operating conditions and used as the output of DBO-HKELM model. Based on the training and testing of a large number of fault simulation data, the optimal parameters of the DBO-HKELM model are determined. The experimental results show that the identification method has good adaptability, robustness, and high accuracy of source load.

However, it is unable to locate the faults accurately and quickly by 100%, and it cannot be completely intelligent. It is expected that further improvement on the model can speed up the diagnosis time and diagnosis accuracy. Due to the large amount of data classification and summarization, the algorithm program does not run quickly, so in the future, we can further find more convenient and more representative forms of failure to speed up the overall running time.

Nomenclature

  • C1 and C 1 * $$ {C}_1^{\ast } $$ , C2 and C 2 * $$ {C}_2^{\ast } $$
  • coupling capacitors for four MOSFETs in the secondary circuit
  • Cr
  • resonant capacitance in LLC converter
  • CVD
  • a filter capacitor for front-stage circuits
  • D1 and D 1 * $$ {D}_1^{\ast } $$ , D2 and D 2 * $$ {D}_2^{\ast } $$
  • anti-parallel diodes for four MOSFETs in the secondary circuit
  • D3 and D4
  • 1-Ph full-wave rectifier diode at output
  • Db
  • diodes for PFC circuits with front-stage LLCs
  • DBO
  • Dung Beetle optimization
  • ELM
  • extreme learning machine
  • EMD
  • empirical mode decomposition
  • HKELM
  • hybrid kernel extreme learning machine
  • Lr
  • resonant inductor in LLC converter
  • Lm
  • excitation inductor in LLC converter
  • LLC
  • LLC converter
  • io
  • output currents of llc converter
  • iA, iB, and iC
  • input currents of llc converter
  • NTC
  • temperature coefficient thermistor
  • PFC
  • power factor correction circuit
  • S0, S 0 * $$ {S}_0^{\ast } $$
  • two MOSFETs for front-stage circuits
  • S1 and S 1 * $$ {S}_1^{\ast } $$ , S2 and S 2 * $$ {S}_2^{\ast } $$
  • four MOSFETs for secondary-stage circuits
  • SN
  • signal normalization
  • SSEE
  • sequence signal entropy extraction
  • vo
  • output voltage of LLC converter
  • VDi
  • rectifier diode voltage for front-stage circuits
  • T0 and T 0 * $$ {T}_0^{\ast } $$ , T1 and T 1 * $$ {T}_1^{\ast } $$ , T2 and T 2 * $$ {T}_2^{\ast } $$
  • the operating temperature of every MOSFET

    • Author Contributions

    Bingyu Li: conceptualization, investigation, visualization, validation, methodology, formal analysis, writing – original draft, writing – review and editing, data curation. Xianhai Pang: investigation, validation, formal analysis, writing – original draft. Xuhao Du: investigation, validation, visualization, writing – original draft, formal analysis. Ziwen Cai: investigation, validation, writing – review and editing, formal analysis.

    Conflicts of Interest

    The authors declare no conflicts of interest.

    Data Availability Statement

    Data sharing not applicable to this article as no datasets were generated or analysed during the current study.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.