Seismic analysis and test facilities of deep-water bridges considering water–structure interaction: A state-of-the-art review

2.1 Earthquake-induced hydrodynamic forces

There is a complicated interaction between the bridge and surrounding water when an earthquake occurs.¹³ The motion of the bridge under earthquake excitation changes the pressure and flow distribution of surrounding water, and hydrodynamic forces caused by water affect the bridge responses consequently, which is a typical fluid–structure coupling vibration problem. Many studies have been conducted on the hydrodynamic forces acting on different substructures of bridges under earthquakes, such as the single pier, pile group, and pile-pier structure. Among these studies, the Morison equation, radiation wave theory, and numerical simulation are three main methods for the calculation of earthquake-induced hydrodynamic forces.

2.1.1 Morison equation

The Morison equation⁷ was first proposed to calculate the wave force of cylinders with small sizes. It assumed that the cylinder had no influence on the wave. Penzien and Kaul⁸ calculated the hydrodynamic forces under earthquakes using the Morison equation with linearized nonlinear drag term in the equation by the method of Krylov and Bogoliubov.¹⁷ Some studies^{13, 18-20} investigated the effect of drag force in whole hydrodynamic force. Goto and Toki¹⁸ analyzed the influence of drag force on dynamic performance of submerged bridge piers. Results indicated that drag force was ignorable when compared with inertial force. Yang et al.²⁰ compared the drag force and inertial force of hydrodynamic force under typical earthquakes through solving the hydrodynamic equations of the pier. The results indicated that the inertial force could be 10 times larger than the drag force, and the earthquake-induced hydrodynamic forces could be approximately replaced by inertial force.

Except for simplification of the Morison equation, many studies were conducted on the application of the Morison equation to piers of different cross-sections. Lai²¹ summarized the value of inertia and drag coefficients of piers with different cross-sections under wave excitation and presented a conversion formula for the calculation of hydrodynamic forces of square and rectangular piers under earthquakes. Yang and Li²² developed the Morison equation to estimate hydrodynamic forces caused by water inside and outside of a hollow pier, where the hydrodynamic force caused by inside water was described as the inertial force of inside water added mass.

The vibrating structure drives surrounding water to move, which has a different flow field from that of ocean wave excitations. Ocean waves have lower frequencies and bigger amplitudes than that of bridge movements under earthquakes.²⁰ With the thorough research on the Morison equation, there is a doubt on its reliability to calculate the earthquake-induced hydrodynamic forces.^{13, 16, 23-25}

Guo et al.^{16, 24, 25} adopted three simplified methods to calculate hydrodynamic forces of the pier under earthquakes. Three simplified methods, the rigid-structure method,²⁶ the method based on approximation of fundamental frequency,^27-29 and the Morison equation method^{22, 30} were adopted for 15,400 cases including 154 piers under 100 ground motions. Results showed that the added mass obtained with the Morison equation was much bigger compared with that obtained with the other two methods, and the difference increased with the relative size of the cross-section. The mean values of errors of the Morison equation for displacement, shearing force, and bending moment could be up to 28.8%, which was several times bigger than that of the other two methods. The research suggested considering the applicable scope of the Morison equation.

Li et al.^{13, 23} conducted underwater shaking table tests to examine the total hydrodynamic added mass and distribution of hydrodynamic pressure with different specimens, water depths, excitation frequencies, and excitation amplitudes. Figure 1 shows the test system. The test results showed a different rule from the Morison equation that the added mass was not proportional to the square of pier diameter and water depth. The added mass varied significantly with excitation frequencies, which differed from the Morison equation. In addition, there was a huge error of up to 185% between the test result and the value calculated by the Morison equation for hydrodynamic pressure on pier.

Due to its simple expression, many scholars applied the Morison equation to calculate earthquake-induced hydrodynamic. However, it may cause an improper conclusion when directly applying the Morison equation derived from wave excitation to the calculation of earthquake excitation, while the two excitations have different characteristics. Therefore, it is a direction for scholars to investigate the application range of the Morison equation for earthquake-induced hydrodynamic force and modify the Morison equation by conducting experiments.

2.1.2 Radiation wave theory

To calculate the earthquake-induced hydrodynamic forces on piers of big size, the radiation wave theory is proposed, where the influence of pier on the water flow field should be considered. It takes water velocity potential or hydrodynamic pressure as the basic variable and combines free surface boundary, bottom reflection boundary, water–structure boundary, and infinite distance radiation boundary to establish the hydrodynamic pressure solution. The key point is to choose the appropriate method for the separation of variables to obtain the velocity potential.

Westergaard³¹ first proposed a theoretical solution to calculate the hydrodynamic force on a straight dam with a vertical upstream face. Liaw and Chopra²⁶ calculated the hydrodynamic pressure of a cylindrical cantilever structure under harmonic excitation through theoretical deduction, which took water compressibility and surface wave effects into account. It was observed that the water compressibility effect had little influence on the hydrodynamic pressure of slender cylinders, while it significantly affects the hydrodynamic pressure of squatty cylinders oscillated at high frequency, such as a dam with a large amount of water constrained on the boundary. The effect of the surface wave was important when the structure vibrated at low frequency.

Following Liaw and Chopra,²⁶ many studies were conducted on the earthquake-induced hydrodynamic force on cylinders. However, the solution for a hydrodynamic force that is derived from the radiation wave theory is complicated while it contains similar terms, integrals, and special functions. Generally, custom-made programs are developed by scholars using specific mathematical software, which may be difficult in practical applications due to massive calculations. Therefore, it is necessary to present methods to simplify the calculation for the hydrodynamic forces on the deep-water pier.

The simplification of surface wave and water compressibility effects was studied. Without water compressibility, hydrodynamic force is expressed as an inertial force. Hydrodynamic forces on piers can be conveniently described as a product of acceleration of structure and added mass. Tanaka and Hudspeth³² extended the solution of hydrodynamic pressure on a vertical circular cylinder under earthquakes in a compressible fluid. The expression only consisted of a single summation over the eigenfunctions and removed the double summation of the eigenfunctions. The results illustrated that the water compressibility had little influence on the hydrodynamic force of slender cylinders, while it obviously affected the hydrodynamic force of squatty cylinders. Using radiation wave theory, Huang and Li^{33, 34} built the solution for hydrodynamic force on the pier under earthquake, where the surface wave, water compressibility, and flexible reflecting boundary at bottom of water were considered. The analysis revealed that the three effects could be neglected when calculating the seismic response of large bridges, and the simplified formulas were given without the three effects. In addition, studies^35-38 showed that water compressibility and surface wave could be neglected as studying seismic responses of slender structures in water.

Another way for simplification is to figure out the relation between the hydrodynamic force caused by the elastic deformation and rigid deformation of the structure, which can significantly improve the computational efficiency. Li and Yang³⁶ calculated the hydrodynamic force on the circular pier under an earthquake. Added mass resulted from elastic motion and rigid motion were compared. Results indicated that the added mass resulting from elastic motion equaled that of rigid motion. Jiang et al.³⁹ investigated the added mass of six groups of piers based on radiation wave theory. The added mass derived from elastic motion and rigid motion were calculated, respectively. The results showed that added mass curves derived from elastic motion were similar to those of rigid motion over the water depth. In addition, Han and Xu²⁷ and Wang et al.^{40, 41} calculated the added mass derived from rigid vibration with assumption of rigid structures and the added mass derived from elastic vibration by the fundamental frequency reduction rate. The conclusion was obtained that added mass for rigid vibration was much bigger than that for rigid vibration.

The hydrodynamic force solutions of piers of various cross-sections using radiation wave theory were studied.^{36, 42-53} Li and Yang³⁶ and presented the theoretical solutions to calculate earthquake-induced hydrodynamic pressure on a circular hollow pier in Figure 2A, and Du et al.¹¹ proposed solutions for the solid pier. Studies^46-49 explored hydrodynamic force of axisymmetric pier under earthquake. For elliptical hollow cylinders shown in Figure 2B, Wang et al.⁵⁰ established the analytical formula and simplified solution for hydrodynamic pressure under earthquake resulting from outer and inner water. Isaacson and Mathai⁵¹ calculated the hydrodynamic force and damping coefficients of a vertical cylinder with arbitrary cross-section under harmonic oscillations. Yang et al. analyzed hydrodynamic force of twin-column piers⁵² and pile group⁵³ according to the solution for single pier.

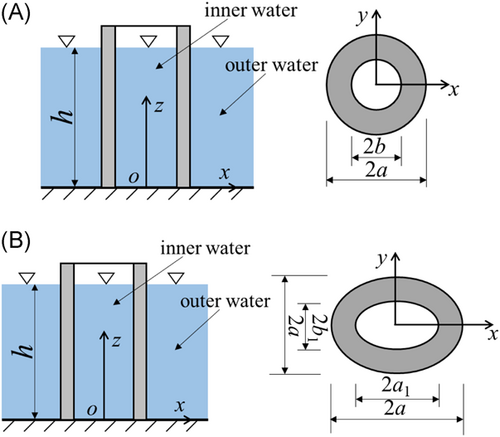
To date, many studies have been conducted to investigate hydrodynamic forces of structures with radiation wave theory. The solutions of hydrodynamic force for various types of structures under earthquake, for example, cylinder, twin-column pier, pile group, and different cross-sections, for example, circle, rectangle, and hollow, are obtained. Among these, simplification of the solutions is always the objective so that it can be readily used by scholars and engineers.

2.2 Wave induced hydrodynamic forces

There are three main effects of wave on the fixed offshore structures: the viscous effect caused by water viscosity, the added mass effect caused by the variation in the flow field due to inertia of fluid and the existence of structure, and the diffraction effect caused by the structures exerting on the incident wave. The role of the three effects in total wave forces depends on the conditions of waves and structures. Generally, the problem is divided into two types according to the size of the upstream face of structure W, and wave height H. When W/L ≥ 0.2, the water viscous effect is negligible, and added mass effect and diffraction effect dominate the wave force. When W/L < 0.2, added mass effect and water viscous effect dominate the wave force as diffraction effect is insignificant. The Morison equation, diffraction wave theory, and numerical simulation are frequently used to obtain the wave-induced hydrodynamic forces on structures.

2.2.1 Morison equation

Morison et al.⁷ first presented the Morison equation to solve the horizontal wave force on a rigid cylinder of a small diameter. It neglected the effect of structures on the wave field. The hydrodynamic forces consisted of drag force related to the water velocity that was calculated based on experience and inertial force related to the water acceleration that was calculated by potential flow theory.

Determining suitable drag coefficient and the inertial coefficient is the key step to calculate wave forces with Morison Equation. Three major factors that affected the value of drag and inertial coefficients were the Keulegan–Carpenter number (KC number), relative roughness of structural surfaces, and the Reynolds number.⁵⁹ Bearman et al.⁶⁰ analyzed the inertial and drag coefficients of cylinders of a square, circular, and diamond section, and flat plate by regular wave tests. It is discovered that the influence of KC number on inertial coefficient changed with cross-section. Cotter and Chakrabarti⁶¹ investigated the inertial and drag coefficients of inclined cylinders through a wave tank test. The local forces of the cylinder were measured to compute the hydrodynamic coefficients. The test results revealed that the two coefficients were functions of KC number. Ikeda et al.⁶² conducted tests on cylinders of the square, circular, and diamond sections, and flat plate excited by regular waves with low KC numbers. The conclusion was obtained that the drag coefficient and inertial coefficient of flat plate under regular wave were smaller than those under oscillatory flow that was calculated in Tanaka et al.⁶³

The inertial and drag coefficients for truncated structures and irregular waves were examined. Vengatesan et al.⁶⁴ conducted test to investigate the two coefficients of a truncated rectangular cylinder loaded by random and regular waves. It was observed that the hydrodynamic coefficients increased with KC number and the aspect ratios of the cylinder had a significant influence on the value of the coefficients. Yuan and Huang⁶⁵ expressed the inertia and drag coefficients with a function of KC number by conducting experiments on vertical truncated circular cylinders excited by regular waves. Konstantinidis and Bouris⁶⁶ carried out simulations on a circular cylinder to calculate the two coefficients, where the waves were of low-amplitude oscillatory and steady flows. Raed and Soares⁶⁷ used four different calibration approaches to study the two coefficients to predict the wave-induced hydrodynamic forces of fixed vertical cylinders in irregular waves as shown in Figure 3.

In addition, the design codes of different countries give the values of inertial and drag coefficients of circular cylinders for engineering applications. Table 1 lists the values of the two coefficients and the wave theory used to calculate the wave force in the Code of Hydrology for Sea Harbour of China (CHSH),⁶⁸ the code of the American Petroleum Institute (API),⁶⁹ and the code of Det Norske Veritas (DNV).⁷⁰ It can be observed from Table 1 that the values in the CHSH code are more conservative than the other two codes. More research on wave force evaluation are needed to accurately estimate the inertial and drag coefficients in the code.

Table 1. Values of inertial and drag coefficients in national codes

Items	National codes
	CHSH	API code	DNV code
Wave theory	Linear wave theory	Stokes' fifth order gravity wave theory	Stokes' fifth order gravity wave theory
Value of inertial coefficient	1.2	0.6–1.0	0.5–1.2
Value of drag coefficient	2.0	1.5–2.0	2.0

• Abbreviations: API, American Petroleum Institute; CHSH, Code of Hydrology for Sea Harbour of China; DNV, Det Norske Veritas.

3.1 Seismic analysis under earthquake excitation

Strong earthquakes have a great impact on bridges during the service period. Transportation of lifeline supplies is prevented and access of the rescuers is denied due to the destruction or damages of the bridges in the earthquake regions.⁴ The earthquake field investigations indicate that the earthquakes mainly destroy the foundation, pier, bearing, and deck of bridges, where the typical forms are foundation sinking, pier cracking and crushing, bearing damage, and deck falling or impacting.^{98, 99} Through review on the damage of various types of bridges with specific strengthening measures, many theories and practices are validated to be useful to enhance dynamic performance of a bridge, for instance, the performance-based seismic design method, seismic energy dissipation, and isolation technology, application of dampers.^{100, 101} In addition, compared with general earthquakes, the near-fault earthquake, soil–structure interaction (SSI), and spatial variability effect of ground motions will further affect the seismic performances of bridges.

Near-fault ground motions possess features of fling slip, forward directivity, hanging wall, and large vertical ground motion component, which can influence the dynamic response of bridges significantly.^102-106 Xie et al.¹⁰² explored the dynamic responses of a cable-stayed bridge under the condition of near-fault ground motion. The research concluded that the displacement and acceleration of girder and tower of cable-stayed bridges were significantly increased under near-fault ground motion. Ada et al.¹⁰³ investigated different influences of the responses of suspension bridges under far-fault ground motions and near-fault ground motions. The results indicated that near-fault ground motions could result in larger internal forces, like axial forces, bending moment, and shearing forces, than that of far-fault ground motions. Yi et al.¹⁰⁴ proceeded with a shaking table test for a single-tower cable-stayed bridge with the 1/20 length scale. Compared with far-fault ground motion, the dynamic responses of bridges were increased under near-fault ground motion. Guan et al.^{105, 106} conducted a shaking table test of a cable-stayed bridge to study the effect of near-fault ground motions. It was observed that near-fault ground motions with short pulse periods increased the internal forces more than displacements for towers, while near-fault ground motions with long pulse periods increased displacements more than internal forces for towers.

For large-span bridges, the ground motion spatial variability effect should be considered. Dynamic responses of those bridges under multisupport excitation will have greater uncertainty than that under uniform earthquake excitation.^107-112 Zong et al.¹⁰⁷ carried out shaking table tests on a three-tower cable-stayed bridge under multisupport excitations. The dynamic responses of displacement and acceleration of the tower and deck were measured. It was observed that the responses of internal forces at the middle tower were much larger than those at side piers bottom. Pieces of Advice were given that the stiffness of the middle tower and deck of multitower cable-stayed bridges need to be intensified to improve the seismic performance. Xie et al.¹⁰⁸ established shaking table tests and numerical simulations of a cable-stayed bridge under longitudinal multisupport excitation to analyze the impact of wave passage effect on dynamic responses. The results declared that vertical acceleration frequency spectra of the girder and the modal participation factor would be considerably impacted by the wave passage effect. With the decrease of wave propagation velocity, the mode shapes with symmetric vertical bending of the deck prominently affected the seismic responses. Raheem et al.¹⁰⁹ investigated the effect of spatial variability of ground motions on dynamic performances of cable-stayed bridges using different control strategies. Due to the differences in ground motion among different foundations induced by the effect of wave passage, the assumption of uniform earthquake excitation could be unpractical for large-span bridges, which might produce differences in dynamic responses of the bridges compared with those under multisupport excitation. Zanardo et al.¹¹⁰ established research of the multispan bridges considering the pounding phenomenon associated with the dynamic responses. It could be observed that the pounding forces could be threee–four times larger than those under uniform excitation or multisupport excitation considering wave passage effect.

The influence of SSI on the dynamic performances of bridges must be considered for large-span bridges. Many scholars^{102, 113-115} have conducted research on seismic responses analysis of large-span bridges considering SSI. It is known that the impact of SSI on the seismic performance of large-span bridges is complex, and the structural seismic responses are related to features of input ground motions, foundation soil, and the structural form of the bridges. Yan et al.¹¹³ carried out a shaking table test to explore the influence of SSI on the seismic response of the bridges on soft soil foundations. The results indicated that the effect of SSI increased the pier deformation, the stress at the pier bottom, the horizontal acceleration at the pier top, and the horizontal acceleration of the deck under earthquake excitation. The sensitivity of SSI on the responses of acceleration, displacement, and strain response was different, where the acceleration response was the most sensitive response to SSI. Li et al.¹¹⁴ built numerical models of a sea-crossing cable-stayed bridges under multisupport excitations to investigate SSI. It was concluded that the system fragilities and responses of the bridge considering SSI were much higher than those without SSI. Chouw and Hao¹¹⁵ proposed the effect of SSI on the responses of two bridges. The results stated that the pounding damage potentials would not be reduced by the high wave apparent propagation velocity when considering SSI.

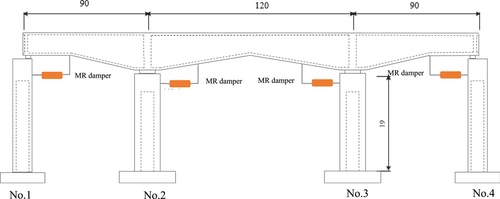
Adding dampers in bridges is an effective way to reduce dynamic responses and damages of bridges under earthquakes. Meanwhile, the development of new dampers for bridges will have significant effects on their seismic design. Han et al.¹¹⁶ studied the design method of cable-stayed bridges and proposed a direct displacement-based seismic design (DDBD) procedure for cable-stayed bridges under seismic ground motions. The research demonstrated that the proposed DDBD procedure was practical and accurate sufficiently for the design of cable-stayed bridges. Shen et al.¹¹⁷ analyzed the influence of the seismic devices on transverse performances of piers in Sutong Bridge. The result was founded that transverse yielding metallic dampers and viscous fluid dampers were much effective for the piers to reduce the transverse forces. Camara¹¹⁸ explored transverse seismic responses of the cable-stayed bridges, which used yielding metallic dampers to concatenate supports with the deck. The results revealed that destructive damage would be prevented by plastic deformation energy dissipation of dampers in the towers under extreme earthquake excitations. Niu et al.¹¹⁹ developed a novel oil damper with variable stiffness (ODVS). The performances of the triangular-plate added damping and stiffness were compared with that of the ODVS under earthquake excitations on finite element simulations of cable-stayed bridges. The results declared that the ODVS had a better effect to reduce the transverse displacements at the deck end. Zhou et al.¹²⁰ and Shen et al.¹²¹ established a transverse steel damper (TSD) and the corresponding TSD seismic system (TSDSS), where the TSDs were installed at the connections of deck-bent and/or deck-tower of the cable-stayed bridges. The curvature demands and transverse displacement along bent/tower columns could be reduced by the TSDSS. Meanwhile, the displacements of connections at deck-bent or deck-tower were in a receivable level in the engineering practice. Li et al.¹²² studied the seismic damage control using magneto-rheological (MR) dampers for the reinforced concrete (RC) bridges under strong earthquakes. Derived from damages of bridge components using the MR dampers, a new real-time semiactive control algorithm was proposed (Figure 4). The results showed that the pier and bearing were more effectively protected by the proposed method than passive controls.

To date, much research has been conducted on the seismic dynamic responses of bridges under earthquake excitations. Strong earthquakes may generate destructive damage to bridges, especially for the excitation of near-fault ground motions. Moreover, the effect of spatial variability of ground motions and SSI need to be taken into account in the study of seismic response of bridges. Dampers can effectively consume earthquake energy, decrease seismic response and reduce seismic damage of bridges, and they have been widely used in bridges.

3.2 Seismic analysis considering water–structure interaction

The studies on the risks of multiple disasters on the bridges have been conducted extensively by many scholars.¹²³ The influence of water–structure interaction is a significant aspect to be considered in its design scheme for deep-water bridges. Commonly, the water–structure interaction may result from earthquake, wave, and current excitation.

To investigate the effect of water–structure interaction on bridge, the added mass method as discussed in Section 2 is adopted in many studies. Li and colleagues^124-126 analyzed the dynamic responses of bridge considering the hydrodynamic force by the added mass method. The results indicated that added mass method was an effective method for nonlinear and linear dynamic analysis of bridges considering water–structure interaction. The impact of water–structure interaction would change the vibration features of the deep-water bridges. Goyal et al.¹²⁷ demonstrated that the vibration frequency of structure would be reduced by considering the hydrodynamic forces. Liu et al.¹²⁸ studied the acceleration response and vibration frequency of a deep-water bridge pier (Figure 7). The results revealed that the first-order vibration frequency was decreased by 10.0% while the second-order vibration frequency was decreased by 6.5% when considering the water–structure interaction.

The analysis methods of dynamic responses of deep-water bridges considering water–structure interaction include numerical simulation and shaking table test.^127-137 Goyal et al.¹²⁷ analyzed the dynamic responses of intake towers considering the hydrodynamic forces, and concluded that the hydrodynamic forces increased the dynamic responses of structure. Gao et al.¹³⁵ built a finite element model of a sea-crossing cable-stayed bridge and analyzed the seismic responses of the bridge with water–structure interaction. The research declared that the maximum internal force of piles might increase by 10%–20% when considering the hydrodynamic effect. Etemad et al.¹³⁶ examined the seismic responses of offshore engineering structures considering different directions of earthquake and wave. The results indicated that the maximum displacement under earthquake and wave combined excitation was 19.0% larger than that under earthquake. Li et al.¹³⁷ used a water flume to simulate the marine environment and carried out a 1/50 scaled high-pile cap shaking table test. It was founded that the shearing force and bending moment at the pier bottom increased up to 31.0% and 50.0%, respectively with the increase of water depth.

Generally, the earthquakes dominate the dynamic response of bridge, while the influence of current and wave excitation could not be ignored.^{138, 139} Wu et al.¹⁴⁰ examined the seismic performances of deep-water piers under earthquake, wave, and current combined excitation. The results stated that the influence factor of wave and current excitation on seismic response was −31.6% to 63.5%. The wave and current would affect both the amplitude of seismic response and the time when the amplitude appeared. Ding et al.¹² analyzed the impact of wave and current excitation on the dynamic response of bridge piers (Figure 5). It was obtained that the wave and current excitation generally increased the hydrodynamic force of bridge piers. The earthquake, current, and wave combined excitation on the bridges should be considered in the design of bridges. Liu et al.¹⁴¹ conducted a shaking table test for single tower of a cable-stayed bridge under earthquake, wave, and current combined excitation. The results showed that maximum increased ratio of acceleration under earthquake and wave combined excitation was 13.2% when compared with that under earthquake excitation.

The influence of water–structure interaction on the bridge performance depends on the characteristics of the earthquake, wave, and current excitations. In the structural design, it is necessary to study the characteristics of seismic responses under different conditions. The research of Li et al.¹²⁴ showed that the peak displacement of piers considering hydrodynamic forces increased by 15.4% and 11.9% under El-Centro and Tianjin ground motions, respectively, when compared with that of piers in air. Jia et al.¹⁴² demonstrated that the response amplitude of deep-water pier was relevant to the features of the ground motion when considering the water–structure interaction. Huang et al.¹⁴³ concluded that the influence of hydrodynamic forces varied with the input ground motions of different frequency characteristics. The amplitude of relative displacement at top of piers in water increased by 40.8%, 47.6%, and 10.9% under Taft, El-Centro, and Tianjin ground motions, respectively, when compared with that of piers in air. Bai et al.¹⁴⁴ conducted the research on seismic responses of a large bridge pier considering wave and current excitation. The results declared that the influence of wave and current excitation on relative displacement at top of piers was less than 14.8% under El-Centro ground motion, while it was 10.0% and 32.8% under Loma Prieta and Kobe ground motions, respectively.

In summary, the added mass is an effective method for nonlinear and linear seismic analysis of bridges considering water–structure interaction. The hydrodynamic forces increase the seismic response and decrease the natural vibration frequency of deep-water bridges. The increase of the seismic responses of bridges resulting from water–structure interaction can be more than 60%, and the influence depends on the characteristics of the earthquake, wave, and current excitations. The existing research are mostly carried out within the elastic range of deep-water bridges, and the study on dynamic response and failure mechanism of bridges is lack considering water–structure interaction in plastic stage. Research considering earthquake, wave, and current combined excitation primarily focused on numerical simulation and single underwater shaking table test of deep-water bridges, and the full-bridge underwater shaking table array test is limited.

4.1 Shaking tables

There are many test techniques to obtain the responses of structure to examine their dynamic performance, one method of which is the application of the shaking table. Shaking table is widely used nowadays in the area of seismic studies, as it provides a useful way to excite structures located in the earthquake region. With the development of more sophisticated testing platforms and techniques, the shaking table system is now able to test the seismic behavior of the deep-water bridges under complex earthquake, wave, and current excitations.

The development of shaking tables dates back about 130 years ago for the first attempt at laboratory to study the effects of earthquakes on structural models at Japan. The strong needs in the seismic research caused by the great threat from every strong earthquake have promoted the development of shaking tables. Severn comprehensively reviewed the history of the shaking tables.¹⁴⁵ To date, most of the shaking table systems installed in universities, industries, and research institutes have only a single table. Japan has built few large size shaking tables since 1970, for example,¹⁴⁶ the unidirectional shaking table constructed by NIED (payload: 500 tons, size: 15.0 × 14.5 m) and the bidirectional shaking table constructed by Nuclear Power Engineering Cooperation at Tadotsu (payload: 1000 tons, size: 15 × 15 m). Motivated by the 1995 Kobe earthquake, Japan has developed the world's current largest shaking table E-Defense. The size of the table is 20 × 15 m and it is able to vibrate payloads of 1200 tons with the maximum horizontal and vertical acceleration of 0.9g and 1.5g, respectively.¹⁴⁶ The single table systems have been used to test bridge components or bridge models with a broad range of input ground motions, involving reproductions of real recorded earthquakes ground motions.^147-149

However, even for the large shaking table, the table size is limited and it is difficult for large bridge testing. The shaking table array system with few tables provides a solution. In 2003, the first set of two-subarray shaking table systems was built in the State University of New York. Meanwhile, the three-subarray system including three movable bidirectional shaking tables was built in the University of Nevada-Reno, with the size of 4.3 m × 4.5 m each, and an acceleration of 1g with 50 tons payload. The three tables could be used individually with the independent ground motions, and they could be subjected to operate together as one single large shaking table. Tongji University in China built one of the largest shaking table array systems in the world. The array system contains four shaking tables and two trenches.¹⁵⁰ The sizes of the tables are 6 m × 4 m, and two of them are with a payload of 30 tons, and the other two with a payload of 70 tons. The shaking tables can move in the two trenches with the length of 70 and 30 m. The shaking table array system enables researchers to explore the seismic behavior of the bridges through model testing under multiple-support excitation.

4.2 Underwater shaking tables

For deep-water bridges, the seismic behavior can be significantly affected by the water. Many researchers^151-154 have developed simplified testing platforms to consider the water effect to the bridge by adopting a temporarily built water tank on the shaking table. For example, Wei et al.¹⁵¹ built a rigid brick basin without a shaking table to investigate the experimental responses on submerged foundations of the bridge pile in water using an impact steel hammer. The maximal depth of the flume was 2.65 m, and the plan view size was 3.48 × 3.48 m. Ai et al.¹⁵³ installed a water tank with dimensions of 3.76 × 3.76 × 1.51 m on a shaking table in the key Laboratory of High-Speed Railway Engineering at the Southwest Jiaotong University, China. Generally, the size of the water tank is constrained by the shaking table size, and the specimens (normally the bridge piers) are with a small size to consider the boundary influence of the flume. In addition, the water tank can only provide hydrodynamic forces to the specimens and it is difficult to include other functions, such as wave generating.

The underwater shaking table system is a more sophisticated testing platform to consider the water effect and seismic excitations. The shaking table is typically installed at the base of a permanent water pool. To protect the shaking table equipment, such as the actuators and motors, the shaking table is normally connected to its surrounding base by a waterproof seal to keep the water out of the equipment room. The Port and Airport Research Institute (PARI), Japan, built a three-directional underwater shaking table system in 1997 after the Great Hanshin-Awaji earthquake. The table is with a diameter of 6 m and a payload of 40 tons, and the water pool is with a size of 13.0 × 13.0 m and the depth of the water reach to 2 m. Hohai University built an underwater shaking table in 2018 with a diameter of 5.75 m and a payload of 20 tons.¹⁵⁵ The size of the pool is much larger as 30 × 20 m. Dalian University of Technology upgraded the original underwater shaking table system in 2011 to simulate wave and current (Figure 6), which include the current and wave force to the structures under seismic input.¹⁵⁶ The dimension of the pool is 21.6 × 5.0 × 1.0 m. The ellipse shape shaking table is constructed in the middle of the flume. The sizes of minor and major axis of this shaking table are 3.0 and 4.0 m, respectively. The maximum vertical and horizontal displacement capacities are 50 and 75 mm, respectively. Its maximum vertical and horizontal acceleration capacities are 0. 7g and 1.0g, respectively. The payload capacity is 10 tons. For the generating system of the wave, the maximum height of wave generated by the wave maker is 0.33 m, and the period range of the wave is 0.5–4.0 s. For the generating system of the current, the maximal flow quantity is 1.0 m³/s, and the maximal velocity of the current is 0.5 m/s with 0.4 m water depth.

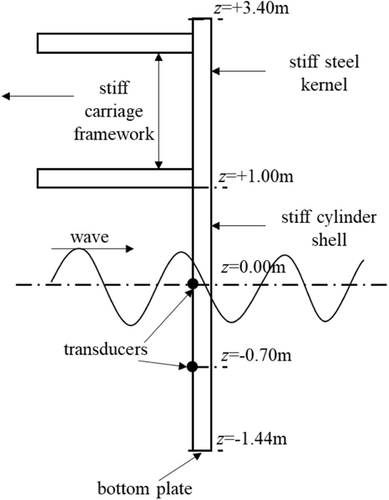
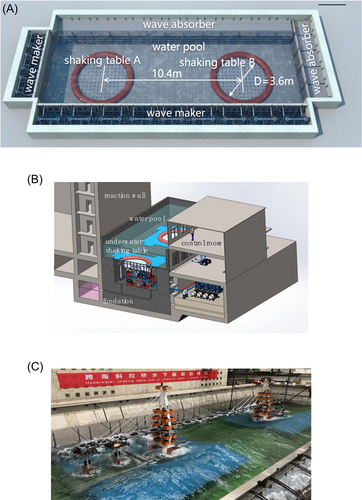
Although the underwater shaking table system can provide means to investigate the seismic behavior of the bridge component such as piers, hydrodynamics, under earthquakes, current, and wave load, however, a single table system cannot provide enough space to install a long bridge model. In addition, the multiple-support excitation which is important for long bridges cannot be realized by the previously constructed tables either. In view of this, Tianjin University started to build a new multifunctional dual underwater shaking table system from 2015, and the system is open since July 2021.¹³

Figure 7 shows the configuration of the underwater shaking table array system. The two identical tables are with a diameter of 3.6 m, and is constructed at the bottom of a water pool with the size of 28.5 × 12.0 m. The distance between the two tables is 10.4 m. Each table has two actuators in horizontal direction and four actuators in vertical direction. There are a group of L-shaped wavemakers located at the front and left side of the pool to produce the wave load. A reaction wall is built at the back side of the pool to allow for hybrid testing.

A novel feature of the Tianjin University underwater shaking table system is that the waterproof seal is air inflated. The whole equipment room under the water pool is infilled with air and the pressure is adjusted according to the water depth in the pool. The waterproof seal does not drop under the weight of the water during the test thanks to the pressure of the air, and this reduces the stress of the seal and undesired disturbance from the water movement to the specimen. Also, the air pressure helps supporting both the weight of the table and the water, so that the actuators can contribute more forces to vibrate the table.

Each table is able to produce a 1.5g horizontal acceleration and 1.7g vertical acceleration with a payload of 26 tons with/without water. The maximum velocity and displacement capacities are 1.1 m/s and 300 mm in the horizontal direction, and 0.9 m/s and 200 mm in the vertical direction. The shaking table is capable to work with the range of 0.1–100 Hz, which satisfies the testing demand of relatively stiff models scaled from large size prototype structures. The maximum water depth in the pool is 2.0 m. For the wave makers, the maximum wave height is 0.52 m, and the loading period range of the waves is 0.5–2.5 s.

4.3 Similarity design of water–structure interaction

Normally, the specimen in shaking table test is scaled from real structures and the scaling process needs to follow similitude criterions. As the models are located in the same gravity field with the real structures, a specific material with large density, and small elastic modulus is needed to model the material of real structures to meet similitude criteria. However, the material is difficult to obtain as it should be similar to the material of real structures in the constitutive relation. Additional mass is commonly attached to the specimen to increase its effective material density. When underwater shaking table is conducted, the force caused by the hydrodynamics, wave and current also needs to be scaled. However, the density of water used in the tests can hardly be changed, which causes trouble in pursuing a balanced scale of the forces caused by seismic vibration and water environment.

To solve the problem, Li et al.¹⁵⁶ proposed a model design method, named coordinative similitude law, to guide the design of models in underwater shaking table tests. Based on radiation wave theory and diffraction wave theory, the wave-induced hydrodynamic force on specimen was increased by increase the wave height and the earthquake induced hydrodynamic force was increased by increase the length of the upstream face of the specimen. To ensure the accuracy of test results, the similarity ratios of hydrodynamic forces and other forces were supposed to be the same. Finite element simulation and underwater shaking table test were conducted to verify presented model design method, where the ordinary specimen designed by traditional artificial mass simulation was used to compare with the coordinative specimen designed by the model design method. The conclusion was observed that the responses of coordinative specimen are of smaller error than conventional specimen. Details of model design of underwater shaking table test can be referred to Li et al.¹⁵⁶