Pulse-like ground motions significantly influence structural responses, indicating that more consideration should be given to the seismic design of structures in the near-site region. However, less effort focuses on the seismic response of a cable-stayed bridge under near-field pulse-like excitations, and the difference in structural responses caused by near-field pulse-like and far-field ground motions is not fully captured. This paper, therefore, aims to investigate the effect of pulse-like ground motions on a cable-stayed bridge, and it presents a comparison of far-field earthquakes. Considering the finite number of recorded ground motions, artificial pulse-like ground motions are adopted in this study. Furthermore, two classical intensity measures (peak ground velocity [PGV] and peak ground acceleration) were used to establish the probabilistic seismic demand model for cable-stayed bridges. Then, fragility curves associated with the pylon of the bridge were compared under the action of different types of excitations, and the damage state of the whole pylon is presented through the median point of the slight damage of the curvature of each pylon section. The results indicate that the bottom section of the pylon is damaged first under different seismic excitations, with the PGV as the index. Moreover, far-fault ground motions have a greater impact on the curvature response of the longitudinal bridge section of the pylon than the near-fault ground motions, so the damage is more serious.

1 INTRODUCTION

At present, there are three main formulations for near seismicity, namely, near-field earthquakes, near-fault earthquakes, and near-source earthquakes, which represent those from the distance from the site to the epicenter, fault, and hypocenter, respectively. Anil K. Chopra, Alavi, et al. suggested that near-field earthquakes have a distance from the site of less than 10 km.¹ Campbell² considered that when the magnitude is less than 6, the near-field earthquake should be within 50 km. In recent years, researchers have found that earthquakes are mostly triggered by fault fracture, and the fault distance is generally used as the basis for the discrimination of near-fault ground motions. Such motions have a vertical distance from the field point to the seismic fault that is less than a certain range. Stewart et al.³ believed that the fault distance between near-fault pulses and far-fault ground motions is within the range of 20–60 km. The differences in vibrations between the near and far surface motions are mainly as follows:

(1)
The propagation direction of a fault is the main influencing factor of near-site vibrations, but the soil condition has little influence. For far-field records, the soil condition is the most important for wave propagation and site conditions.
(2)
In the near-field region, there is an obvious low-frequency jump in the earthquake's acceleration time-history curves and a continuous jump in the time history of velocity and displacement, and the duration of ground motions is very short. The time history of acceleration, velocity, and displacement displayed by far-field records have cyclic motions and last for a long time.
(3)
The near-field ground motion speed is very large. In the Beijing and Kobe earthquakes, the ground peak velocity was relatively large, that is, 150–200 cm/s, while in the far-field region, the velocity did not exceed 30–40 cm/s. Therefore, in the near-field design concept, velocity is the most important, replacing the most important acceleration in the far field.
(4)
Due to the consistency between the ground vertical motion frequency and structure vertical frequency, an important vertical plane amplification effect may occur. At the same time, considering that the probability of plastic deformation and attenuation in the vertical displacement direction decreases, the behavior in the vertical direction may be the most important to the structure in the near-field region.
(5)
For the jumping characteristics of ground motions and high speed, the demand for structure ductility may be very high. Moreover, the short period of ground motions is a very favorable factor in the near-field region. Hence, the balance among the ductile demand, jumping behavior, and short duration must be reasonably analyzed.

Compared with far-fault earthquakes, near-fault earthquakes have three main features of ground motions: directional effect, velocity pulse-like effect, and vertical acceleration effect.^{4, 5} In some earthquakes, the rupture velocity of faults is close to the shear speed of the soil layer, resulting in the superposition of waves caused by the fault fracture and earthquake propagation in the soil layer, forming pulse-like earthquakes. The superposition of a fault rupture wave and earthquake energy in seismic causes an energy surge, which leads to the emergence of a velocity pulse. Sucuoǧlu and Nurtuǧ⁶ quantified the velocity pulse effect by utilizing the ratio of the peak ground acceleration (PGA) to peak ground velocity (PGV). The amplitude of the vertical component of ground motions recorded in some near-field areas is also large, even close to the amplitude of the horizontal component, and contains a large number of high-frequency components. This phenomenon is called the vertical acceleration effect. This effect has a serious impact on flexible structures, such as bridges, long-span structures, and long cantilever structures.

At present, there are few studies on the analysis and comparison of the response law and fragility of cable-stayed bridges under near-field and far-field earthquakes in China. In probabilistic seismic hazard analysis, traditional seismic models do not consider the pulse effect of ground motions on bridge structures, which would underestimate the hazard of bridges near faults. Using a cable-stayed bridge as an example, Zhong et al.⁷ propose a reliable risk assessment tool for large-span bridges with spatially varying ground motions. Yang et al.⁸ chose Taiwan(China)'s lumped near-fault ground motion records as the ground motion input and systematically investigated the influence of near-fault ground motions' directional effect, velocity pulse-like effect, and vertical acceleration effect on the earthquake's response to bilinear single-degree-of-freedom system, long-period isolated buildings, and cable-stayed bridges. Fu⁹ studied the seismic performance of a curved continuous beam bridge considering collisions under near-field and far-field seismic and found that the damage and failure of curved bridges will be more serious than those of far-field earthquakes. Zhang et al.¹⁰ used the Sutong Yangtze Bridge to analyze and study the seismic response of a large cable-stayed bridge under pulse-like ground motions. Their research results can provide a reference for the seismic design of large cable-stayed bridges under pulse-like ground motions. Zhang and Zhang¹¹ studied the response of reinforced concrete rigid frame bridges under the longitudinal excitation of near-field and far-field ground motions using near-field and far-field vibrations recorded by four stations and put forward some suggestions on the seismic design of large rigid frame bridges located in some near-field areas.

Although the seismic performance of building structures located in near-field earthquakes has been widely studied for many years, there is little research on the response law and fragility of each section of the pylons of large cable-stayed bridges under pulse-like and far-fault earthquakes. Accordingly, the purpose of this paper is to select an optimal intensity measure (IM) and draw the probabilistic seismic demand model (PSDM) and fragility curve of the pylon columns of bridges under the action of near-field pulse-like and far-field earthquakes. Finally, the PGA and PGV are selected as the strength indices to analyze and compare the curvature response law (along the bridge direction) and fragility of each section of the main pylon of a huge cable-stayed bridge under the action of near-field and far-field earthquakes. These results will provide a reference for the seismic demand estimation of cable-stayed bridges under near-field and far-field earthquakes.

2 GROUND MOTIONS

2.1 Artificial pulse-like ground motions

Although recorded seismic data are increasing, the records of near-fault motions, especially pulse ground motions, are still pretty scarce. The extensive destruction of engineering structures has prompted seismic engineers and seismologists to seek a deeper understanding of near-fault pulse ground motions. At the same time, the availability and convenience of near-fault ground motions data facilitate the study of such ground motions and their impact on structures.

Accordingly, the methodology of generating artificial pulse-like ground motion is used in this study. Ground motions are rotated and classified as pulse or nonpulse.

The formula of the velocity pulse is

()

In the above formula, the start time of the pulse is

, and the end time is

. The pulse amplitude is V_p, the pulse period is T_p, the phasic angle is ν, γ represents the number of oscillations in the pulse, and t_max,q represents the peak time of the velocity pulse. The pulse is defined by the five parameters, as proposed by Mavroeidis and Papageorgiou.

The residuals of pulse-like near-field ground motions are generally broadband time series, which are simulated as a modulated, white-noise filtering process. The formula is described by

()

represents the white-noise process, the unit impulse response curve of the linear wave filter with time-dependent parameters is expressed by

(

), the standard deviation in the integral definition is

, and

is a temporal modulation function, which is used to express the equal root of the acceleration procedure.

()

The rejector frequency representing the main periodicity of earthquakes could be expressed as

()

In the above formula, the rejector frequency in the middle of the earthquake ground is represented by

, the frequency change ratio over time is

, and the wave rejector antihunting is viewed as a constant factor

, which represents the bandwidth of the accelerating procedure.

()

when an artificial wave is fitted, and

()

Dating from

, the peak time of the modulation curve is

, and the amplitude conditioning function is controlled by a multinomial accumulation stage α (reach to

), followed by an exponential decay rate β and argument c in the form of an attenuation stage. Following Rezaeian and Der Kiureghian,¹² the four parameters (c, α, β, and

) could be expressed by D_5–95 (validity range from 5% to 95% of the Arias earthquake strength, I_a), D_0–5 (time from

to 5% of I_a) and D_0–30 (time from

to 30% of I_a).

In this way, seven physical-related arguments (I_a, D_5–95, D_0–5, D_0–30, , , and ) are used to perfectly define the course of showing the broadband near-field ground motion acceleration.

The goal is to produce artificial synthetic seismicity motions for the specified seismic-resistant design scheme. Therefore, manufacturing projection equations according to the seismic and field characteristics should be available for design engineers. The regression equation of parameters similar to the pulse model for each transformation has the following form:

()

where F is the site category (F = 0 represents the slump fault, F = 1 represents the thrust and thrust-diagonal fault), M is the magnitude of the moment, Z_TOR is the distance to the fracture plane's top, R_RUP is the nearest distance from the field to the fault rupture, V_s30 is the transverse wave velocity (30 m soil layer above the site), s_ord is the directional rating, and

are the transformed pulse-like model parameters, presented in detail in Table 1.

()

where

are the interpretative jargons and

are the relative regression factors. The details of

and regression error can be found in Dabaghi and Kiureghian.¹³

Table 1. Concrete parameters of the artificial pulse sample motion

Pulse parameters	V_p (cm/s)	T_p (s)	γ	ν/π (rad)	t_max,p (s)
Residual parameters	I_a,res (cm/s)	D_5–95,res (s)	D_0–5,res (s)	D_0–30,res (s)	f_mid,res (Hz)		ζ_f,res
Orthogonal parameters	I_a,PO (cm/s)	D_5–95,PO (s)	D_0–5,PO (s)	D_0–30,PO (s)	f_mid,PO (Hz)	f_PO (Hz/s)	ζ_f,PO

2.2 Selection of far-fault ground motions

This study selected far-fault records used in Jiang et al.¹⁴ Records 1–80 were selected from the Pacific Earth Engineering Research Center (PEER), and records 80–100 were selected from the database of the SAC project. The magnitude ranges from 5.8 to 6.9, and the epicentral distance ranges from 10 to 60 km. The PGA, magnitude, and epicentral distance of the records are shown in Appendix Table A1. The 20 ground motions selected from the SAC have exceedance probabilities of 2% and 10% in 50 years. The corresponding acceleration spectrum is given in Figure 1B.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Distribution of (A) near-fault ground motions and (B) far-fault ground motions.

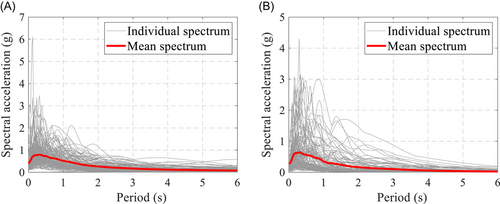
2.3 Input ground motions

To obtain the desired seismic effects, 100 far-field records and 121 artificial pulse-like ground motions were inputted along the longitudinal bridge section, transversal bridge section, and vertical bridge section, and the critical elements of the cable-stayed bridge were analyzed through dynamic time-history analysis.

3 CASE STUDY

3.1 Modeling of the bridge

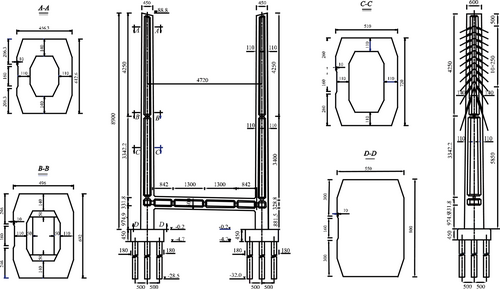
A single-tower, double-cable-plane cable-stayed bridge was taken as the study object. Its span combination is 150 + 150 m. The general size layout of the bridge is presented in Figure 2. The detailed geometric shapes of the cable-stayed bridge's pylons are shown in Figure 3.

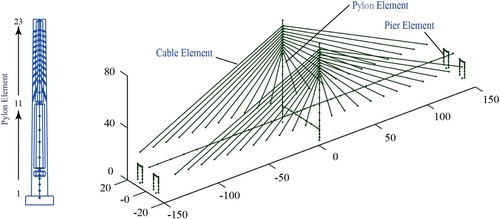
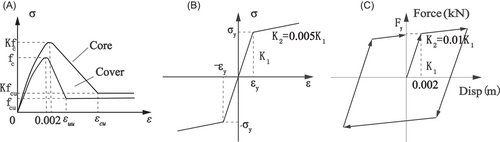
The finite element analysis software OpenSees was used to establish an accurate nonlinear 3D model. The main girder of the upper structure was linear, and the linear elastic beam elements were used for the simulation, as shown in Figure 2. The response of the cable was simulated using a nonlinear tension-only element. It was modeled as a large-displacement truss element using the Ernst method or modified elastic modulus method as a result of the easy usage and capability to include the sag effect.¹⁵ Meanwhile, the distributed plastic fiber element was used to model the section of the tower and auxiliary pier to account for the axial force–moment interaction and material nonlinearity. The fiber section must be modeled using a reasonable stress-strain correlation. Figure 4A shows the closed concrete and unconfined concrete, and Figure 4B shows the longitudinal rebar. The transverse of the bearing was completely fixed, but the response to the longitudinal part of this bearing is based on a nonlinear bilinear constitutive model (Figure 4C). The foundation model consisting of six linear lumped springs was used to simulate the stiffness of the pile foundation.

3.2 Selection of the damage index

For the study of piers and towers of cable-stayed bridges, curvature ductility^{15, 17} is widely selected as the engineering demand parameter (EDP) to measure the damage to piers and towers. The limit states for the pylons follow the guidelines of Zhong et al.^{18, 19} and are listed in Tables 2 and 3. Therefore, this study analyzed the fragility of recording the curvature of pylons (μ_ϕ) under far-fault ground motions and near-fault pulse-like ground motions.

Table 2. Critical parameters of the bridge pylon under far-field records (with the slight damage)

EDPs	a	b	β_D/IM	β_C	R²
μ_φ-1x	5.94	1.87	0.88	0.35	0.92
μ_φ-2x	1.38	1.33	0.56	0.35	0.93
μ_φ-3x	0.86	1.21	0.50	0.35	0.93
μ_φ-4x	1.08	1.35	0.55	0.35	0.93
μ_φ-5x	1.90	1.52	0.76	0.35	0.91
μ_φ-6x	1.00	1.25	0.51	0.35	0.94
μ_φ-7x	0.68	1.08	0.43	0.35	0.94
μ_φ-8x	0.61	0.99	0.38	0.35	0.94
μ_φ-9x	0.61	0.93	0.38	0.35	0.94
μ_φ-10x	0.62	0.90	0.43	0.35	0.92
μ_φ-11x	0.58	0.87	0.48	0.35	0.89
μ_φ-12x	0.44	0.84	0.51	0.35	0.87
μ_φ-13x	0.42	0.83	0.53	0.35	0.86
μ_φ-14x	0.41	0.85	0.56	0.35	0.86
μ_φ-15x	0.41	0.88	0.58	0.35	0.86
μ_φ-16x	0.40	0.91	0.60	0.35	0.86
μ_φ-17x	0.38	0.93	0.62	0.35	0.85
μ_φ-18x	0.35	0.95	0.64	0.35	0.85
μ_φ-19x	0.31	0.97	0.66	0.35	0.85
μ_φ-20x	0.27	0.98	0.69	0.35	0.84
μ_φ-21x	0.22	1.01	0.72	0.35	0.83
μ_φ-22x	0.19	1.04	0.77	0.35	0.83
μ_φ-23x	0.18	0.94	0.72	0.35	0.82

Table 3. Critical parameters of the bridge pylon under near-field ground motions (with the slight damage)

EDPs	a	b	β_D/IM	β_C	R²
μ_φ-1x	2.4	2.24	1.65	0.35	0.53
μ_φ-2x	0.96	1.29	0.89	0.35	0.55
μ_φ-3x	0.65	0.97	0.71	0.35	0.53
μ_φ-4x	0.54	0.89	0.67	0.35	0.50
μ_φ-5x	0.56	1.08	0.68	0.35	0.59
μ_φ-6x	0.49	0.90	0.63	0.35	0.55
μ_φ-7x	0.42	0.80	0.59	0.35	0.53
μ_φ-8x	0.37	0.73	0.53	0.35	0.53
μ_φ-9x	0.32	0.67	0.48	0.35	0.53
μ_φ-10x	0.27	0.64	0.46	0.35	0.54
μ_φ-11x	0.20	0.64	0.47	0.35	0.53
μ_φ-12x	0.14	0.71	0.48	0.35	0.56
μ_φ-13x	0.13	0.86	0.52	0.35	0.60
μ_φ-14x	0.13	0.94	0.56	0.35	0.61
μ_φ-15x	0.12	1.02	0.59	0.35	0.62
μ_φ-16x	0.12	1.09	0.62	0.35	0.63
μ_φ-17x	0.12	1.15	0.64	0.35	0.64
μ_φ-18x	0.11	1.19	0.65	0.35	0.64
μ_φ-19x	0.09	1.19	0.67	0.35	0.64
μ_φ-20x	0.08	1.19	0.68	0.35	0.63
μ_φ-21x	0.06	1.18	0.70	0.35	0.61
μ_φ-22x	0.06	1.16	0.71	0.35	0.60
μ_φ-23x	0.06	0.88	0.59	0.35	0.56

4 PSDM

Earthquake risk probabilistic evaluation methods have gradually developed into the core of structural and infrastructure system risk mitigation decisions.^20-23 Plotting the fragility curve of the structure allows intuitively observing this risk probability. The fragility curve could be established as a conditional probability table in which the structural requirement exceeds its capability under a given ground motion intensity (IM).^{4, 5, 24} The calculation formula is as follows:

()

where the accumulative normal curve of the distribution function is expressed as Φ [•]; S_C and S_D are the medians of the structural capacity and seismic demand, respectively; and β_C and β_D/IM are the logarithmic standard deviations of the structural capacity and seismic demand, respectively.

The PSDM describes the relationship between elements' earthquake demand and surface motion. Thus, the demand model (S_D) is typically set as

()

A and B are the coefficients of the regression by counted. The log-standard deviation β_D/IM of the seismic demand could be set as

()

where C_i and n are the ith implementation and the number of simulations of the requirement, respectively.

By making use of the corresponding requirements and IMs for all sections of the tower response (EDPs), the PSDM was established, which is a regression model of demand–IM pairs in the logarithmic transformation space. For illustration, in Figures 5 and 6, the PSDM of the ductility curvature demand μ_φ-1x at the roof, middle (at beam), and foundation sections of the pylon under the far-field and near-field pulse-like ground motions is drawn under the ground motion intensity indices of the PGA and PGV, respectively.

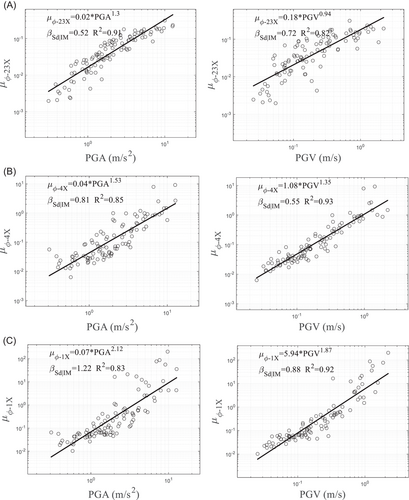
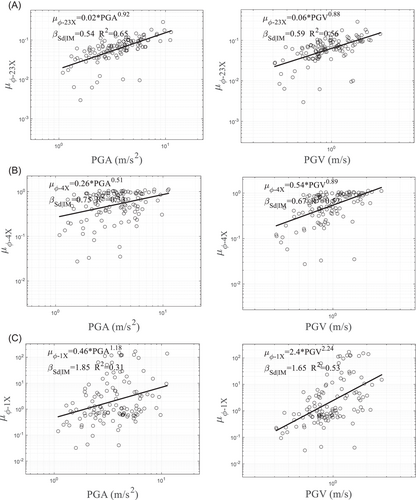
In addition, Zhong et al.^{4, 21, 25-27} show that the PGA is highly suitable for the IM selection of a short-period structural system, whereas the PGV can be selected as the IM for a medium–long-period structural system (e.g., a cable-stayed bridge). As shown in Figures 5 and 6, the PGV can meet the requirements of efficiency and adequacy.^{4, 28}

5 RESEARCH ON THE FRAGILITY CURVE ANALYSIS

The key components and their corresponding EDPs are shown in Tables 2 and 3, which summarize the parameters (a, b, β_D/IM, and β_C) required to draw the fragility curve and the EDP representing the ductility requirements of the component. EDP represents the ductility requirement of the pylon curvature (μ_φ-ix, i = 1, 2, …) (subscript x is the vertical bridge direction, and the numbers after the subscript φ represent the number of units). During the dynamic analysis, the deformation of the supports of the auxiliary piers and pylon and the displacement at the top of the tower column along the downstream bridge direction (δ_pylon) were also recorded.

By convoluting the PSDM with the limit state, the fragility curve can be easily constructed. Because it is assumed in advance that the demand (EDPS) and limit state have a lognormal distribution, the damage probability still obeys the lognormal distribution function. Equation (9) can be used to calculate the seismic fragility curve of each section of the pylon. For ease of illustration, the fragility curves of the tip, middle (beam), and underside sections of the bridge pylon under the action of far-field and near-field earthquakes are drawn in Figures 7 and 8, respectively, and the ground motion intensity index is the PGV.

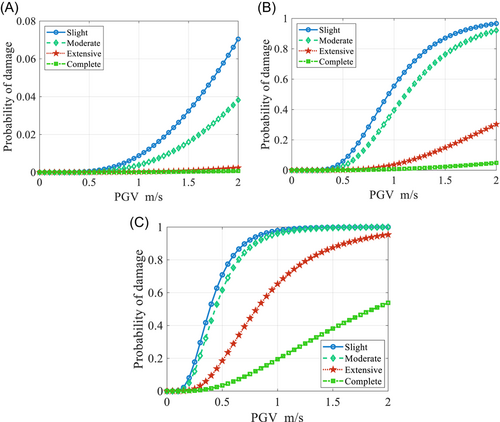
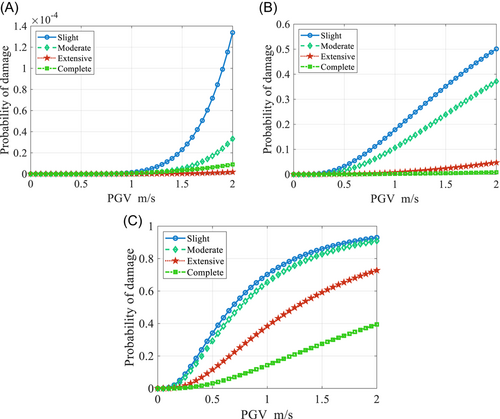
When the PGV was used as the strength index, although the PGV (peak value) of near-field pulse-like earthquakes was larger than that of far-fault earthquakes, far-fault ground motions possessed much higher seismic energy than pulse-like ground motions for a specific PGV value (as shown in Figures 7 and 8). Finally, the energy input to the structure is large, so the damage probability of the cable-stayed bridge pylon under the far-field ground motion is large.

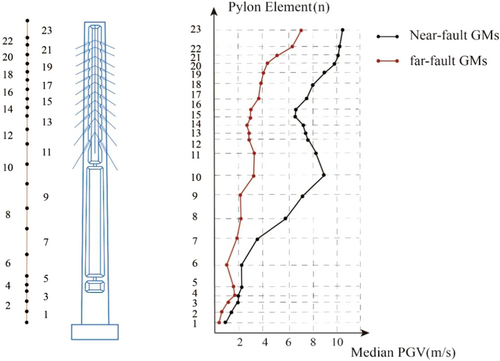
In addition, to observe the damaged state of the whole section of the pylon intuitively, the fragility midpoint of each section of the pylon is depicted in Figure 9. As shown in the figure, the damage probability of the bridge tower under far-field vibrations is large.

6 CONCLUSIONS

(1)
The OpenSees analysis software was used to establish the finite element model of the Qianhai bridge, and the seismic analysis of the model was conducted with 100 far-field records and 121 pulse-like ground motions. The results show that the pylon components of the cable-stayed bridge can be damaged more easily than other components under the action of earthquakes. With the PGV as the index, far-fault ground motions possessed much higher seismic energy than pulse-like ground motions for a specific PGV value. Thus, the far-fault records have a greater impact on the curvature of the pylon section (along the bridge direction seismic response) than the near-fault pulse-like ground motions. Hence, the damage is more serious.
(2)
The PSDM and fragility analysis curve (PGV as the analysis index) were established for each section of the pylon. The damage degree of each section of the pylon was also very different. The bottom section of the pylon was destroyed first, and the section gradually close to the top of the pylon was safe and can be easily damaged under far-fault vibrations.

ACKNOWLEDGMENT

This research was supported by the National Natural Science Foundation of China (52178135). The supports are gratefully acknowledged.

CONFLICTS OF INTEREST

The author declares no conflicts of interest.

APPENDIX A

See Table A1

Table A1. Characteristics of the far-fault sample surface motions in the PEER NGA

	Records	Earthquake name	Year	M	R (km)	Site	x	y	z
	Records	Earthquake name	Year	M	R (km)	Site	PGA (g)
1	AGW	Loma Prieta	1989	6.9	28.2	Agnews State Hospital	0.159	0.172	0.093
2	CAP	Loma Prieta	1989	6.9	14.5	Capitola	0.443	0.529	0.541
3	G03	Loma Prieta	1989	6.9	14.4	Gilroy Array #3	0.367	0.555	0.338
4	G04	Loma Prieta	1989	6.9	16.1	Gilroy Array #4	0.212	0.417	0.159
5	GMR	Loma Prieta	1989	6.9	24.2	Gilroy Array #7	0.323	0.226	0.115
6	HCH	Loma Prieta	1989	6.9	28.2	Hollister City Hall	0.215	0.247	0.216
7	HDA	Loma Prieta	1989	6.9	25.8	Hollister Differential Array	0.279	0.269	0.154
8	SVL	Loma Prieta	1989	6.9	28.8	Sunnyvale—Colton Ave.	0.209	0.207	0.104
9	CNP	Northridge	1994	6.7	15.8	Canoga Park—Topanga Can.	0.42	0.356	0.489
10	FAR	Northridge	1994	6.7	23.9	LA—N Faring Rd.	0.242	0.273	0.191
11	FLE	Northridge	1994	6.7	29.5	LA—Fletcher Dr.	0.24	0.162	0.109
12	GLP	Northridge	1994	6.7	25.4	Glendale—Las Palmas	0.206	0.357	0.127
13	HOL	Northridge	1994	6.7	25.5	LA—Hollywood Stor FF	0.358	0.231	0.139
14	NYA	Northridge	1994	6.7	22.3	La Crescenta—New York	0.159	0.178	0.106
15	LOS	Northridge	1994	6.7	13	Canyon Country—W Lost Cany	0.482	0.41	0.318
16	RO3	Northridge	1994	6.7	12.3	Sun Valley—Roscoe Blvd	0.443	0.303	0.306
17	PEL	San Fernando	1971	6.6	21.2	LA—Hollywood Stor Lot	0.174	0.21	0.136
18	B-ICC	Superstition Hills	1987	6.7	13.9	El Centro Imp. Co. Cent	0.258	0.358	0.128
19	B-IVW	Superstition Hills	1987	6.7	24.4	Wildlife Liquef. Array	0.207	0.181	0.408
20	B-WSM	Superstition Hills	1987	6.7	13.3	Westmorland Fire Station	0.211	0.172	0.249
21	A-ELC	Borrego Mountain	1968	6.8	46	El Centro Array #9	0.057	0.13	0.03
22	A2E	Loma Prieta	1989	6.9	57.4	APEEL 2E Hayward Muir Sch.	0.139	0.171	0.095
23	FMS	Loma Prieta	1989	6.9	43.4	Fremont—Emerson Court	0.141	0.192	0.067
24	HVR	Loma Prieta	1989	6.9	31.6	Halls Valley	0.103	0.134	0.056
25	SJW	Loma Prieta	1989	6.9	32.6	Salinas—John & Work	0.112	0.091	0.101
26	SLC	Loma Prieta	1989	6.9	36.3	Palo Alto—SLAC Lab.	0.278	0.194	0.09
27	BAD	Northridge	1994	6.7	56.1	Covina—W. Badillo	0.079	0.1	0.043
28	CAS	Northridge	1994	6.7	49.6	Compton—Castlegate St.	0.136	0.088	0.046
29	CEN	Northridge	1994	6.7	30.9	LA—Centinela St.	0.322	0.465	0.109
30	DEL	Northridge	1994	6.7	59.3	Lakewood—Del Amo Blvd.	0.123	0.137	0.058
31	DWN	Northridge	1994	6.7	47.6	Downey—Co. Maint. Bldg.	0.23	0.158	0.146
32	JAB	Northridge	1994	6.7	46.6	Bell Gardens—Jaboneria	0.068	0.098	0.049
33	LH1	Northridge	1994	6.7	36.3	Lake Hughes #1	0.077	0.087	0.099
34	LOA	Northridge	1994	6.7	42.4	Lawndale—Osage Ave.	0.152	0.084	0.053
35	LV2	Northridge	1994	6.7	37.7	Leona Valley #2	0.063	0.091	0.058
36	PHP	Northridge	1994	6.7	43.6	Palmdale—Hwy 14 & Palmdale	0.067	0.061	0.04
37	PIC	Northridge	1994	6.7	32.7	LA—Pico & Sentous	0.186	0.103	0.065
38	SOR	Northridge	1994	6.7	54.1	West Covina—S. Orange Ave.	0.067	0.063	0.049
39	SSE	Northridge	1994	6.7	60	Terminal Island—S. Seaside	0.194	0.133	0.048
40	VER	Northridge	1994	6.7	39.3	LA—E Vernon Ave.	0.153	0.12	0.063
41	H-CA	Imperial Valley	1979	6.5	23.8	Calipatria Fire Station	0.078	0.128	0.055
42	H-CHI	Imperial Valley	1979	6.5	28.7	Chihuahua	0.254	0.27	0.218
43	H-E01	Imperial Valley	1979	6.5	15.5	El Centro Array #1	0.134	0.139	0.056
44	H-E12	Imperial Valley	1979	6.5	18.2	El Centro Array #12	0.116	0.143	0.066
45	H-E13	Imperial Valley	1979	6.5	21.9	El Centro Array #13	0.139	0.117	0.046
46	H-WSM	Imperial Valley	1979	6.5	15.1	Westmorland Fire Station	0.11	0.074	0.082
47	A-SRM	Livermore	1980	5.8	21.7	San Ramon Fire Station	0.04	0.058	0.016
48	A-KOD	Livermore	1980	5.8	17.6	San Ramon—Eastman Kodak	0.076	0.154	0.042
49	M-AGW	Morgan Hill	1984	6.2	29.4	Agnews State Hospital	0.032	0.032	0.016
50	M-G02	Morgan Hill	1984	6.2	15.1	Gilroy Array #2	0.212	0.162	0.578
51	M-G03	Morgan Hill	1984	6.2	14.6	Gilroy Array #3	0.2	0.194	0.395
52	M-GMR	Morgan Hill	1984	6.2	14	Gilroy Array #7	0.113	0.19	0.428
53	PHN	Point Mugu	1973	5.8	25	Port Hueneme	0.083	0.112	0.047
54	BRA	Westmorland	1981	5.8	22	5060 Brawley Airport	0.171	0.169	0.101
55	NIL	Westmorland	1981	5.8	19.4	724 Niland Fire Station	0.176	0.105	0.126
56	A-CAS	Whittier Narrows	1987	6	16.9	Compton—Castlegate St.	0.333	0.332	0.167
57	A-CAT	Whittier Narrows	1987	6	28.1	Carson—Catskill Ave.	0.059	0.042	0.037
58	A-DWN	Whittier Narrows	1987	6	18.3	14368 Downey—Co Maint Bldg.	0.141	0.221	0.177
59	A-W70	Whittier Narrows	1987	6	16.3	LA—W 70th St.	0.151	0.198	0.077
60	A-WAT	Whittier Narrows	1987	6	24.5	Carson—Water St.	0.133	0.104	0.046
61	B-ELC	Borrego	1942	6.5	49	El Centro Array #9	0.044	0.068	0.033
62	H-C05	Coalinga	1983	6.4	47.3	Parkfield—Cholame 5 W	0.131	0.147	0.034
63	H-C08	Coalinga	1983	6.4	50.7	Parkfield—Cholame 8 W	0.1	0.098	0.024
64	H-CC4	Imperial Valley	1979	6.5	49.3	Coachella Canal #4	0.128	0.115	0.038
65	H-CMP	Imperial Valley	1979	6.5	32.6	Compuertas	0.147	0.186	0.075
66	H-DLT	Imperial Valley	1979	6.5	43.6	Delta	0.351	0.238	0.145
67	H-NIL	Imperial Valley	1979	6.5	35.9	Niland Fire Station	0.069	0.109	0.034
68	H-PLS	Imperial Valley	1979	6.5	31.7	Plaster City	0.057	0.042	0.026
69	H-VCT	Imperial Valley	1979	6.5	54.1	Victoria	0.167	0.122	0.059
70	A-STP	Livermore	1980	5.8	37.3	Tracy—Sewage Treatment Plant	0.073	0.05	0.021
71	M-CAP	Morgan Hill	1984	6.2	38.1	Capitola	0.142	0.099	0.045
72	M-HCH	Morgan Hill	1984	6.2	32.5	Hollister City Hall	0.071	0.071	0.118
73	M-SJB	Morgan Hill	1984	6.2	30.3	San Juan Bautista	0.036	0.044	0.052
74	H06	N. Palm Springs	1986	6	39.6	San Jacinto Valley Cemetery	0.063	0.069	0.053
75	INO	N. Palm Springs	1986	6	39.6	Indio	0.117	0.064	0.087
76	A-BIR	Whittier Narrows	1987	6	56.8	Downey—Birchdale	0.299	0.243	0.23
77	A-CTS	Whittier Narrows	1987	6	31.3	LA—Century City CC South	0.063	0.051	0.021
78	A-HAR	Whittier Narrows	1987	6	34.2	LB—Harbor Admin FF	0.071	0.058	0.028
79	A-SSE	Whittier Narrows	1987	6	35.7	Terminal Island—S. Seaside	0.041	0.042	0.021
80	A-STC	Whittier Narrows	1987	6	39.8	Northridge—Saticoy St.	0.118	0.161	0.084

REFERENCES

1Alvai B, Krawinker H. Consideration of near-fault motion effect motion effects in seismic design. Proceedings of 12th World Conference on Earthquake Engineering, New Zealand; 2000.
Google Scholar
2Campbell KW, Eguchi RT, Duke CM. The use of reliability in lifeline earthquake engineering. Probabilistic Mechanics and Structural Reliability (1979). ASCE; 2014.
Google Scholar
3Stewart JP, Chious SJ, Bray JD, et al. Ground Motion Evaluation Procedure for Performance-Based Design. Pacific Earthquake Engineering Research Centre; 2001. Report No. 01-09: 63-67.
Google Scholar
4Zhong J, Jeon JS, Shao YH, Chen L. Optimal intensity measures in probabilistic seismic demand models of cable-stayed bridges subjected to pulse-like ground motions. J Bridge Eng. 2019; 24(2).
Google Scholar
5Shao Y, Wei Y, Yang T, Ni M, Zhong J. Empirical models of bridge seismic fragility surface considering the vertical effect of near-fault ground motions. Structures. 2021; 34: 2962-2973.
10.1016/j.istruc.2021.09.021
Web of Science® Google Scholar
6Sucuoǧlu H, Nurtuǧ A. Earthquake ground motion characteristics and seismic energy dissipation. Earthq Eng Struct D. 1995; 24(9): 1195-1213.
10.1002/eqe.4290240903
Web of Science® Google Scholar
7Zhong J, Jeon JS, Ren W. Risk assessment for a long-span cable-stayed bridge subjected to multiple support excitations. Eng Struct. 2018; 176: 220-230.
10.1016/j.engstruct.2018.08.107
Web of Science® Google Scholar
8Yang DX, Zhao Y, Li G. Influence analysis of motion characteristics of near-fault ground motions on seismic responses of long-period structures. J Disaster Prev Reduct Eng. 2007; 2: 133-140.
Google Scholar
9Fu JS. Seismic analysis of continuous girder curved bridge considering impact behavior under near-or-far field earthquake ground motions. Chongqing University; 2017.
Google Scholar
10Zhang F, Li S, Yan XW, Wang JQ. Effects of near-fault pulse-type ground motions on the seismic responses of a long-span cable-stayed bridge. Vib Impact. 2017; 36(21): 163-172+184.
Google Scholar
11Zhang LC, Zhang AL. Comparison of near and far ground motion responses of a rigid frame bridge under longitudinal excitation. Low Temp Build Technol. 2010; 32(6): 78-79.
CAS Google Scholar
12Rezaeian S. Stochastic modeling and simulation of ground motions for performance-based earthquake engineering. University of California, Berkeley; 2010.
Google Scholar
13Dabaghi M, Der Kiureghian A. Stochastic modeling and simulation of near-fault ground motions for performance-based earthquake engineering. University of California; 2014.
Google Scholar
14Jiang L, Zhong J, Yuan W. The pulse effect on the isolation device optimization of simply supported bridges in near-fault regions. Structures. 2020; 27: 853-867.
10.1016/j.istruc.2020.06.034
Web of Science® Google Scholar
15Zhong J, Wan H-P, Yuan W, He M, Ren W-X. Risk-informed sensitivity analysis and optimization of seismic mitigation strategy using Gaussian process surrogate model. Soil Dyn Earthquake Eng. 2020; 138:106284.
10.1016/j.soildyn.2020.106284
Web of Science® Google Scholar
16Shahi SK. A probabilistic framework to include the effects of near-fault directivity in seismic hazard assessment. Stanford University; 2011.
Google Scholar
17Tothong P, Cornell CA. Structural performance assessment under near-source pulse-like ground motions using advanced ground motion intensity measures. Earthq Eng Struct D. 2008; 37(7): 1013-1037.
10.1002/eqe.792
Web of Science® Google Scholar
18Zhong J, Ni M, Hu H, Yuan W, Yuan H, Pang Y. Uncoupled multivariate power models for estimation performance-based seismic damage states of column curvature ductility. Structures. 2022; 36: 752-764.
10.1016/j.istruc.2021.12.041
Web of Science® Google Scholar
19Zhong J, Yang T, Pang Y, Yuan W. A novel structure-pulse coupled model for quantifying the column ductility demand under pulse-like GMs. J Earthquake Eng. 2021: 1-19.
Google Scholar
20Baker JW. Quantitative classification of near-fault ground motions using wavelet analysis. B Seismol Soc Am. 2007; 97(5): 1486-1501.
10.1785/0120060255
Web of Science® Google Scholar
21Baker JW, Cornell CA. A vector-valued ground motion intensity measure consisting of spectral acceleration and epsilon. Earthq Eng Struct D. 2005; 34(10): 1193-1217.
10.1002/eqe.474
Web of Science® Google Scholar
22Zhong J, Jiang L, Pang Y, Yuan W. Near-fault seismic risk assessment of simply supported bridges. Earthq Spectra. 2020; 36(4): 1645-1669.
10.1177/8755293020935145
Web of Science® Google Scholar
23Zhong J, Pang Y, Jeon JS, Desroches R, Yuan W. Seismic fragility assessment of long-span cable-stayed bridges in China. Adv Struct Eng. 2016; 19(11): 1797-1812.
10.1177/1369433216649380
Web of Science® Google Scholar
24Padgett JE, DesRoches R. Methodology for the development of analytical fragility curves for retrofitted bridges. Earthq Eng Struct D. 2008; 37(8): 1157-1174.
10.1002/eqe.801
Web of Science® Google Scholar
25Padgett JE, Nielson BG, DesRoches R. Selection of optimal intensity measures in probabilistic seismic demand models of highway bridge portfolios. Earthq Eng Struct D. 2008; 37(5): 711-725.
10.1002/eqe.782
Web of Science® Google Scholar
26Yang D, Pan J, Li G. Non-structure-specific intensity measure parameters and characteristic period of near-fault ground motions. Earthq Eng Struct Dyn. 2009; 38(11): 1257-1280.
10.1002/eqe.889
Web of Science® Google Scholar
27Yang D, Zhou J. A stochastic model and synthesis for near-fault impulsive ground motions. Earthq Eng Struct D. 2015; 44(2): 243-264.
10.1002/eqe.2468
Web of Science® Google Scholar
28Luco N, Cornell CA. Structure-specific scalar intensity measures for near-source and ordinary earthquake ground motions. Earthq Spectra. 2007; 23(2): 357-392.
10.1193/1.2723158
Web of Science® Google Scholar

Citing Literature

Volume1, Issue2

June 2022

Pages 225-240

This article also appears in:

Resilience of Cities and Infrastructures

Probabilistic seismic performance of pylons of a cable-stayed bridge under near-fault and far-fault ground motions

Abstract

1 INTRODUCTION