Infrastructure systems play a crucial role in ensuring the safety of cities and the well-being of residents after earthquakes. Meanwhile, infrastructure systems are vulnerable to earthquakes and may fail to provide necessary services, highlighting the significant need to improve seismic emergency performance. Nevertheless, the seismic emergency performance of infrastructure systems still lacks effective enhancement strategies and optimization models, which makes it challenging to devise and benchmark appropriate emergency enhancement actions. This study proposes an emergency performance optimization model for infrastructure systems against earthquakes. The model aims at maximizing the effects of resistance actions and short-term recovery actions on infrastructure systems with consideration of residents' expectations of infrastructure performance after earthquakes. The efficacy of the proposed model is tested by a case study in China. Experiments and results illustrate advantages of the seismic emergency performance optimization and prioritize resistance and short-term recovery activities within constraints set by available resources.

1 INTRODUCTION

Earthquakes have caused serious problems in urban systems due to their unpredictable and destructive characteristics.^{1, 2} According to the Centre for Research on the Epidemiology of Disasters, the global deaths caused by earthquakes reached 721,318 from 2000 to 2019, accounting for 58% of the total deaths from natural disasters.³ Under earthquakes, the safety of infrastructure systems is essential to the well-being of the affected cities and people.⁴ For example, the 2008 Sichuan Earthquake caused 11,117 deaths and 36.6 billion dollars of direct losses to infrastructure systems, including transportation, power, and communications systems in Mianzhu City, Sichuan Province.⁵

During a seismic emergency, essential infrastructure systems are required to be more than structurally safe. They must maintain performance and continue to provide services for residents.^6-8 The concept of seismic resilience provides a new perspective for infrastructure systems to explore emergency management.^{1, 9} Seismic resilience emphasizes the comprehensive capacity to resist, absorb and recover quickly from the disruption of earthquakes.^{10, 11} Emergency measures help absorb seismic energy, reduce economic losses when an earthquake occurs, and recover quickly to meet residents' needs provided by infrastructure systems.⁶ Therefore, improving emergency performance capabilities is the basis for improving the resilience of infrastructure systems.^{11, 12} Optimizing emergency performance is essential and fundamental to improving emergency capabilities, which aims to reduce the decline in system performance after earthquakes and quickly restore necessary services without the help of external resources.^{11, 13} Two corresponding preparedness measures are required: one for resistance actions and the other for short-term recovery actions, which work together for the infrastructure system to improve emergency performance. To be specific, resistance actions ensure the safety of residents' lives, such as engineering reinforcement measures to prevent houses from collapsing.^{14, 15} Short-term recovery actions maintain the well-being of residents, such as providing redundant medical supplies, food, and water shortly after the earthquake.¹⁶ This study uses this framework to optimize the effectiveness of resilience measures in infrastructure systems to improve emergency performance under earthquake strikes.

Performance optimization models for infrastructure systems have been developed to formulate the optimal combination of performance enhancement measures to improve the emergency ability of infrastructure systems.^{17, 18} Several performance indicators have been proposed to study the problem of optimizing infrastructure system performance under extreme events. Faturechi and Miller-Hooks¹⁹ maximized the system performance of transportation networks by travel time. Ouyang²⁰ studied the functionality of different stages of a nine-node power system, quantifying infrastructure performance by accumulating system functions in stages. Zhang et al.²¹ proposed a bilevel optimization model for the configuration of logistics service centers, quantifying the system performance by cumulative travel time. These studies particularly focus on the performance of infrastructure systems from the engineering perspective. However, residents' needs for the expected performance of infrastructure systems remain a gap in these studies. Postdisaster residents' demand for services provided by infrastructure systems typically changes, leading to a severe imbalance of supply and demand.^{22, 23} For example, the hospital system performance dropped significantly during the 2008 Sichuan Earthquake.²⁴ If the performance of the infrastructure system was simply restored to the pre-disaster levels, the services provided by the hospital system would not be able to meet the growing medical needs of residents. Therefore, optimization baselines need to be set for residents' expected system performance to make the optimization results meaningful. Statistical experiments show that the service demands of infrastructure systems can be estimated and simulated through experiments.^{25, 26} The needs for a certain type of disaster can be summed up from the analogous historical disaster cases, and statistical methods are used to derive the models and rules.^27-29

Although the mathematical model of system performance optimization has been studied in different fields, there still lacks universal agreement on how to connect the infrastructure system performance with postdisaster demand changes. This study proposes a novel emergency performance optimization model considering residents' demand for the infrastructure system. The developed optimization model incorporates the effects of the resistance actions and the short-term recovery actions. Furthermore, a series of experiments are performed in a real hospital system as a case study to illustrate the emergency performance optimization model.

The contributions of this study are as follows. A comprehensive optimization model is formulated to maximize the effect function of resistance actions and short-term recovery actions of the seismic emergency performance, with the consideration of demand differences and different types of infrastructure systems. In addition, the expected performance of the residents is proposed to set the baseline for the target of the emergency performance optimization model, which provides practical significance for the optimization results. Moreover, this study illustrates the circumstances under which resilience enhancement actions may fail and that external assistance is necessary. The rest of this paper is organized as follows: Section 2 describes the research method and the proposed model formulation; Section 3 introduces the emergency performance optimization model and the algorithms for the solution; Section 4 demonstrates a case study and numerical analysis to illustrate the proposed model; Section 5 presents the concluding remarks and possible future research directions.

2 PROBLEM DESCRIPTION

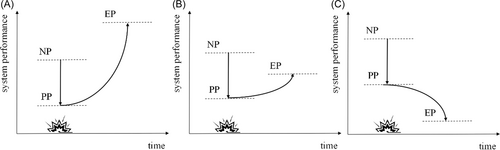
This section presents a detailed description of the emergency performance optimization problem studied herein. The model aims at maximizing the effects of emergency enhancement measures to meet the expected performance of the residents with constraints set by available resources. Through the process of the change of the system performance, three functionality variables are designed in the stage of emergency. Denote NP as the normal performance of the infrastructure system. NP represents the system performance under normal daily conditions at a certain seismic intensity, which can be quantified by the daily number of inpatients in the hospital system, and the water supply of the water supply system before the disaster. Denote PP as the postdisaster performance. PP represents the lowest seismic system performance, which takes into account the effects of cascading failures. Denote EP as the expected postdisaster performance. EP represents the residents' expectation of the system performance and stands for the baseline that the system performance needs to achieve. Three patterns of possible changes in infrastructure system performance are illustrated in Figure 1. For example, when earthquakes occur, the system performance drops from NP to PP in a short period due to the fragility of the infrastructure system. The rebound from PP to EP is the response of the infrastructure system to changes in the demand of residents. In the emergency recovery stage, the rebound process from PP to EP is the response of the infrastructure system. The more resilient an infrastructure system is, the faster it achieves the desired performance, and the more effective its ability to respond to residents' demands.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Patterns of the infrastructure system performance in the stage of emergency.

This study proposed three types of infrastructure systems after taking into account the three patterns of changes in system performance shown in Figure 1: (a) Type I infrastructure system (EP > NP > PP); (b) Type II infrastructure system (NP > EP > PP); (c) Type III infrastructure system (NP > PP > EP).

Type 1 infrastructure systems (EP > NP > PP)

The services provided by a Type 1 infrastructure system are vital to the lives of urban residents. Infrastructure systems of PP drop significantly while EP increases significantly. Take the hospital system as an example. The gap between NP to PP is obvious after the 2008 Sichuan Earthquake, but the need for medical services surged. Even if the infrastructure system recovers to the full capacity of the NP level, it cannot adapt to the surge of postearthquake residents' demands.
Type 2 infrastructure systems (NP > EP > PP)

Moreover, when the residents' demands have not increased but the PP drops significantly, causing the services to fail to meet the EP. This type of infrastructure system should be assigned to a Type II infrastructure system. For example, some lifeline infrastructure systems belong to this type, such as power systems, transportation systems, water supply systems, and communication systems.³⁰ The main reason that this type of infrastructure cannot reach a satisfactory state is poor vulnerability.³¹
Type 3 infrastructure systems (NP > PP > EP)

Lastly, other types can be assigned to a Type III infrastructure system. The services provided by this type are not urgent, such as the high-level needs of human beings.³² Even if the PP decreases, the infrastructure system can still fully meet the needs of the residents' EP due to the low level of the expected performance, such as the cultural system and entertainment systems.²²

3 MATHEMATICAL MODEL DEVELOPMENT

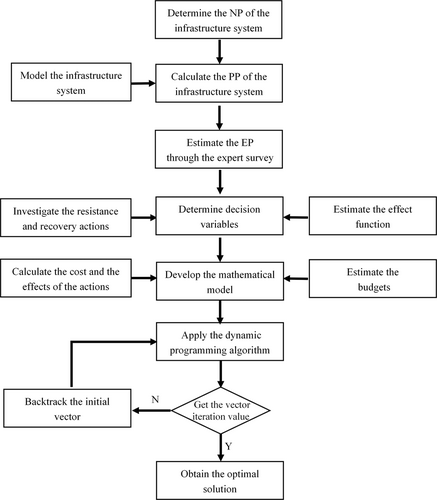
The emergency performance optimization problem addressed in this study is formulated as a group knapsack problem. The notations employed for the mathematical model are described in Table 1, and the computational flowchart is shown in Figure 2.

Table 1. Key components of the emergency performance optimization model

Model type	Nomenclature	Description
Sets	S = {s₁, …, s_n}	Set of resistance actions
	T = {t₁, …, t_n}	Set of short-recovery actions
	P_a	Set of upstream infrastructure systems
Decision variables	X_s: s ∈ S	=1 if resistance action s is taken and 0 otherwise
Decision variables	X_t: t ∈ T	=1 if short-recovery action t is taken and 0 otherwise
Parameters	V_s, s ∈ S	The function of effects of resistance actions
	L_s, s ∈ S	Level of resistance action (e.g., number, scale, utility time of action)
	N_s, s ∈ S	Number of resistance action
	V_t, t ∈ T	The function of effects of short-recovery action
	L_t, t ∈ T	Level of short-recovery action (e.g., number, scale, utility time of action)
	N_t, t ∈ T	Number of short-recovery action
	ε	The Gaussian noise
	σ	The standard deviation
	q	The seismic intensity
	p, p ∈ P_a	Single upstream infrastructure system
	K_p, p ∈ P_a	The system performance of the infrastructure system
	C_s, s ∈ S	Given the cost of implementing resistance enhancement actions
	C_t, t ∈ T	Given the cost of implementing short-recovery enhancement actions
	C, s ∈ S t ∈ T	Given the cost of implementing resilience enhancement actions

3.1 Model formulation

()

The decision variables X_s and X_t are binary variables indicating whether resistance actions and short-term recovery actions are taken. The objective function (1) maximizes the comprehensive effects of resistance actions and short-term recovery actions. The effects are achieved by taking resistance actions and short-term recovery actions , respectively. Constraint (2) is the budget constraint, in which the given cost under seismic funds does not exceed budget C. The different types of optimized infrastructure systems can allocate budgets according to the importance of nodes. Constraint (3) restricts the system performance by taking into account the functional degradation caused by upstream-related infrastructure. K_p indicates the maximum performance that the infrastructure system can provide, and p represents one upstream infrastructure system. For example, the number of people treated by the hospital system depends on the performance of the upstream system such as the power system and water supply system. Constraints (4) and (5) specify that at most one set of resistance actions and short-term recovery actions can be taken. Constraints (6) and (7) are binary variable constraints.

The effect functions of performance enhancement measurements include effect function and . The effect function of resistance actions reflects the fragility of the infrastructure system, which coordinates engineering and nonengineering resistance measures, such as reinforcement of structures, and maintenance of important instruments.^{14, 15} The performance of infrastructure systems usually declines under a certain intensity of earthquake disasters. For the resistance actions, NP drops to PP when the resistance optimization measures are not carried out, which is counted as the initial state and . As resistance actions move up to the maximum unit , PP gradually increases to NP. With the increase of the resistance action levels, the improvement effects gradually decrease. When approaching the limit state of NP, the boosting effect per unit measure level approaches zero. Therefore, the effect function can be represented by a convex polynomial form passing through the origin. However, the effect function of short-term recovery actions reflect the ability of infrastructure systems to respond to residents' demand changes. Short-term recovery actions show the characteristics of an emergency, such as the storage of important materials, and the set of backup instruments. Each additional unit of short-term recovery action level brings an additional unit of effect. The effect function can be represented by a linear function form.³³

The EP sets the baseline for the emergency performance optimization model. Different baselines need to be set for the optimization results of different types of infrastructure systems. However, the Type III infrastructure system does not need to be optimized as the needs of the higher tiers of residents are not affected in the emergency stage. Due to the surge in residents' demand for the services provided by the Type I infrastructure system after the disaster, the optimized goal of system performance needs to exceed the NP of the predisaster. It is necessary to improve the system performance from NP to EP to adapt to the surging needs. Therefore, the mathematical model can be reformulated as follows.

()

Constraint sets (2)–(8), as well as the following constraints:

()

Constraint (12) sets the goal of optimization effect from PP to EP. Constraint (13) sets the goal for recovery actions from NP to EP. V_s is the resistance action effect function, L_s is the level of resistance actions such as the number, scale, and utility time of action s. When no measures are taken, L_s is regarded as 0, the effect function reaches the level of PP. When all effective measures are taken, the effect function reaches the level of NP. V_t is the short-term recovery action effect function, L_t is the level of short-term recovery action such as the number, scale, and utility time of action t. When no measures are taken, L_t is regarded as 0, When all effective measures are taken, the effect function reaches the level of EP.

As for the Type II infrastructure system mathematical model, the residents' EP for services provided by the Type II infrastructure system has not increased but the PP drops significantly, causing services to fail to meet the needs of residents. As is shown in constraint (17), the optimization goal of resistance actions aims to reduce the decline from NP to PP. Constraint (18) aims to improve the system performance from PP to EP after the disaster. The mathematical model can be reformulated as follows:

()

Constraint sets (2)–(8), as well as the following constraints:

()

3.2 Solution algorithm

This study applies the dynamic programming algorithm to solve this group knapsack problem.³⁴ The emergency performance optimization problem aims at maximizing the value of the item within the size of the package, considering only one option can be selected for the same group. This emergency performance optimization aims at maximizing the effect of resilience action level under a series of constraints, with only one option can be selected for the same action.

To be specific, a series of items in the group knapsack problem corresponds to the resilience enhancement action level l_s and l_t in the optimization model. The items in the knapsack problem are divided into groups according to categories, and different actions of resilience enhancement measures are divided into resistance action s and short-term recovery action t in the optimization model. it should be noted that the items in each group in the knapsack problem conflict with each other, that is, only one item can be selected in the group. Corresponding to this, only one action level can be selected for each enhancement measure in the optimization model. For example, the action x_i for reserve materials has three different resilience action level: reserving half of the current materials, reserving the current level of materials, and reserving twice the current materials. Each item in the knapsack problem has a certain size and value, which corresponds to the constraint and effect of the resilience enhancement measures action level in the optimization model.

The knapsack problem is a classic nondeterministic polynomial problem. The polynomial-time algorithm of the knapsack problem obtains an approximate solution under a certain accuracy. This study uses an approximate algorithm to adjust the accuracy of the approximate solution according to the accuracy parameter set by the infrastructure management department, that is, given the accuracy parameter , the algorithm can get an approximate solution in the range of .

In the optimization of the infrastructure system resilience, the manager manually adjusts this accuracy parameter

to control the time consumption and accuracy of the algorithm. The approximation algorithm consists of two steps. The first is to calculate the modified accuracy parameter m and the optimal effect according to Equation (19) and Equation (20). The second is to calculate the optimization model by a dynamic programming algorithm. The optimal solution to the group knapsack problem is obtained by backtracking the initial vector to get the vector iteration value.

()

where is the accuracy parameter set for the optimized infrastructure system, is the optimal effect of all the resilience enhancement actions, action level l is the number of all resilience actions , represents the value related to the precision parameter, is the effect of a resilience action level, and is the result of rounding down the value of each item.

4 CASE STUDY

To demonstrate the optimization model of the infrastructure system and to assess its applicability, the model is implemented in a hospital system located in Mianzhu City in China, as shown in Table 2. The hospital system in this case refers to a comprehensive infrastructure system with four hospitals in Mianzhu City. For this case, the optimization model is employed to simulate the impacts caused by the extreme earthquakes during the 2008 Sichuan Earthquake, and the results are used to test emergency performance enhancement strategies of the hospital system and derive the optimal actions. An expert interview was conducted in Mianzhu City in March 2018, and a total of 15 experts were invited to evaluate the hospital resilience enhancement measures and their effects. Experts who participated in the survey were the medical staff and managers of four hospitals in Mianzhu City, 14 were involved in the disaster emergency rescue, as shown in Table 3.

Table 2. Information of the four hospitals of Mianzhu City

Item	No. of hospitals
Item	A	B	C	D
Initial capacity (beds)	500	180	171	72
Maximum capacity (beds)	695	300	206	100
Number of staff	1040	280	66	54
Building	3	2	1	1
Reconstructed after the 2008 Sichuan Earthquake or not.	Not reconstructed	Reconstructed	Reconstructed	Reconstructed

Table 3. Respondent information for expert interviews

Item	Position	Experienced the Wenchuan earthquake or not	Participated in emergency rescue or not
1	Director of Emergency Office	Yes	Yes
2	Director of emergency department	Yes	Yes
3	Director of Medical Department	Yes	Yes
4	Emergency department nurse	No	No
5	Emergency doctor	No	Yes
6	Director of emergency department	No	Yes
7	Associate dean	Yes	Yes
8	Director of emergency department	Yes	Yes
9	Director of Emergency Office	Yes	Yes
10	Director of Nursing	Yes	Yes
11	Director of Medical Department	Yes	Yes
12	Associate dean	Yes	Yes
13	Associate dean	Yes	Yes
14	Office manager	Yes	Yes
15	Dean	Yes	Yes

The functionality variables (EP, NP, PP) are quantified to conduct numerical experiments on the hospital system. The hospital system belongs to the Type I infrastructure system (EP > NP > PP) as aforementioned. The system performance can be quantified as the number of patients treated or cured. For instance, normal performance is quantified as the number of patients received daily.

HAZUS system analyzes the trend of system performance conforming to the vulnerability function of the hospital system after earthquakes.^{31, 35} When the earthquake intensity is at the level of low earthquakes, the impact of small earthquakes on the infrastructure system performance is not obvious. When the earthquake intensity is strengthened to the level of moderate earthquakes, each unit of disaster intensity causes a serious decline in the system performance. When the seismic intensity reaches a high level of earthquakes, the system performance of infrastructure drop to zero.³⁵ This study analyzes the system performance of the hospital system after the 2008 Wenchuan earthquake based on the earthquake function assessment method of HAZUS. This study adopts the Modified Mercalli Intensity scale to distinguish earthquake vibration intensity.³⁶ According to the system performance function of the hospital system of Mitrani-Reiser et al.³⁷ and Jacques et al.,³⁸ combined with the investigation of the postdisaster data of the 2008 Wenchuan earthquake, the PP function is as follows:

()

q represents the seismic intensity of an earthquake disaster, corresponding to the Modified Mercalli Intensity scale. For example, when the seismic intensity reaches 10 and above, the intensity scale reaches extremes of earth vibrations, which is represented by a q value of 10.

Peek-Asa et al.³⁹ studied the function of seismic intensity and the medical needs of residents after the earthquake. This study applied this method of goal setting and set the EP of residents in Mianzhu City after the earthquake. The function of EP is as follows, which means that the hospital system can receive at least

times the number of patients compared with NP.

()

Note that and represent the emergency performance enhancement actions. For example, each action is mapped to the activities at different action levels , respectively corresponding to the current level, the halved level, and the doubled level through the way of expanding alternative measures. The levels of resistance actions and short-term recovery actions are listed in Table 4.

Table 4. Summary of resistance actions and short-term recovery actions

Activity	Action	Action level
Resistance actions	Prepare the frequency of large-scale maintenance of equipment
	Improve the layout of departments and repair the structure
	Improve equipment record and status registration system
	Replace old significant equipment such as ECG machine
	Replace shock-absorbing pads
Short-term recovery actions	Restore emergency supplies and damaged infrastructure
Short-term recovery actions	Emergency rescue training and drills for personnel

The parameters in each scenario are set up based on investigations in Mianzhu City. Effect function on resistance actions and short-term recovery actions are as Equations (23) and (24). The case comprehensively considered the results of field investigations in four hospital systems in Mianzhu City, combined with the statistical results of historical events, to estimate the function parameters. The Gaussian noise

is added to reflect the effect uncertainty of the same performance enhancement action in different scenarios, which obeys the Gaussian distribution with a mean value and a standard deviation of

()

where

are function parameters of each resilience enhancement action, and

indicate the action level of resistance actions and short-term recovery actions. For example, when the large equipment is routinely repaired every 4 months and 100 people are treated per day under this condition, the current action is regarded as

. When the equipment is routinely repaired every 2 months and the 500 people are treated per day,

. Substituting Equation (23) and Equation (25), the study got Equation (28). When the material reserving maintains the current level and 200 patients can be treated, it is regarded as

. When the reserving is doubled and the number of people treated is doubled, it is regarded as

. Substituting Equation (24) and Equation (26), the study got Equation (29).

()

The cost of emergency performance enhancement action can be quantified by linear functions, including the fixed cost b and the variable cost a.⁴⁰ In addition, this study considers that the variable cost a is related to the action level l. C represents the given cost of implementing emergency performance enhancement actions, l represents the level of resistance action. The cost is as follows:

()

5 RESULTS AND ANALYSIS

A series of experiments are carried out with different Gaussian noise under the different budget C and seismic intensity q. Three scenarios are designed to illustrate the emergency performance optimization model. In each scenario, an independent optimization model is established and the optimal solution obtained is the combination of a series of emergency performance enhancement actions [. In three scenarios, the experiment analyzes the impact of budget C and seismic intensity q on the optimization of hospital system performance.

Scenario 1: Evaluating effects on performance optimization at different seismic intensity levels.

Scenario 1 simulates the optimization value of the hospital system performance at different resilient intensity levels within a sufficient budget. The available budget is assumed to be 3 million RMB for optimization actions of each hospital system. A total of 100 trials are conducted under each intensity under the Modified Mercalli Intensity scale. The seismic intensity increases from 1 to 10. The results in Scenario 1 are shown in Figure 3. The abscissa represents seismic intensity q, and the ordinate is the average optimal objective value of the emergency performance optimization model in 100 random trials. This shows that the effect of optimal resilience enhancement actions gradually decreases when the seismic intensity q increases. In addition, the magnitude of the reduction becomes flat with the increase of the seismic intensity q, which indicates that the seismic intensity q makes less impact on the optimization effect when it increases to a higher level. However, when the seismic intensity reaches q = 6, the optimal target value of hospital A drops rapidly from 3200 to 0. This is due to the high floor of buildings and the lack of seismic design.

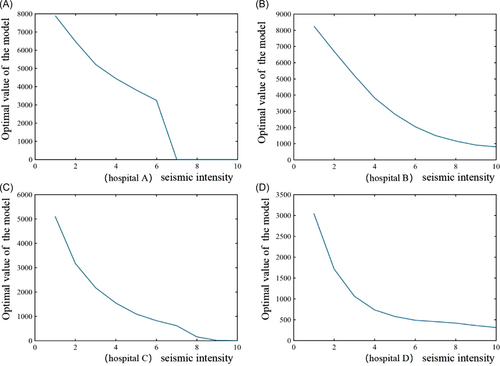
EP sets the baseline for optimization results. In Figure 3, when the optimal objective function value reaches 0, it shows that there is no solution to the optimization problem under the current disaster intensity. In other words, even the optimal resilience enhancement action cannot make up the gap between PP and EP. For example, when the intensity reaches q = 7, no matter what measures hospital A takes, it cannot meet the EP after the earthquake.

Scenario 2: Evaluating effects on performance optimization at different budget.

Scenario 2 simulates the optimization value of the hospital system performance at different budgets. The budget increases from 0 to 3 million RMB and 100 trials are conducted under each level of budget. The results in Scenario 2 are shown in Figure 4. The abscissa represents the different budgets, and the ordinate is the average optimal value of the emergency performance optimization model in the trials. When the budget increases, the effect of the optimal resilience measures under the intensity increases monotonously. The results indicate that the stage where the effect improves rapidly is the initial investment of the budget. In this stage, the optimization work shows more significant effects than in other stages. For example, when the budget of hospital C reaches 1.5 million RMB, the unit budget effect decreases after this inflection point of the first derivative is exceeded.

EP sets a baseline for optimization results. In Figure 4, when the optimal objective function value reaches 0, it shows that there is no solution to the optimization problem when not enough budget is invested. For example, when the budget investment is less than 2 million RMB, no matter what measures hospital A and hospital B takes, they cannot meet the expected number of treatments after the earthquake. This brings enlightenment to government managers. If there is no adequate budget for the corresponding intensity planning, the hospital system cannot achieve the EP of the residents.

Scenario 3: Evaluating priority of emergency performance enhancement action.

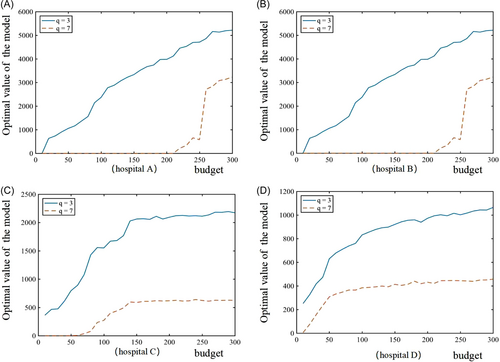
Scenario 3 simulates the priority of two types of emergency performance enhancement actions. This experiment set a sufficient budget to ensure that all alternative measures have a chance to be selected as the optimal solution. We assumed that each hospital has a budget of 3 million RMB. The priority of the emergency performance enhancement measures varies with different levels of seismic intensity, as is shown in Figure 5. The proportion of effects of resistant actions accounts for more than 50% in a series of optimal solutions such as hospital A and hospital C of , hospital B of and hospital D of . When seismic intensity increases than the value above, the proportion of effects of short-term recovery enhancement actions is dominant. The results show that different maximum points are in seismic intensity q = 3, seismic intensity q = 2, seismic intensity q = 2, and seismic intensity q = 1. It could be noticed that the resistance activities would be taking the leading role early under a relatively low seismic intensity. Thus, the hospital systems are supposed to take measures to increase the resistance actions first, and then increase the level of short-term recovery actions after the resistance effects reach a certain level.

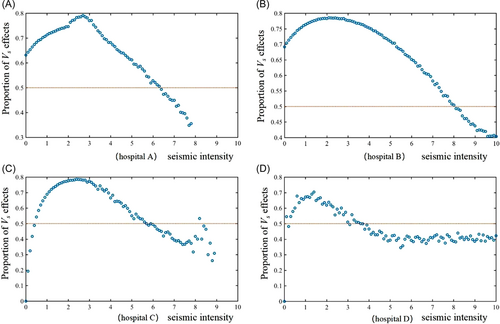
EP sets the baseline for optimization results. Under a relatively low seismic intensity, the number of people treated by the hospital system reaches a satisfactory state, mainly due to the improvement of the instantaneous decline in the emergency stage. Under a relatively high seismic intensity, meeting EP is mainly due to the improvement of the recovery actions. When seismic intensity reaches the higher-level q = 8 for hospital B or q = 9 for hospital C, no measures can make them reach a satisfactory state.

6 CONCLUSIONS AND FUTURE RESEARCH

This study proposed a seismic emergency performance optimization model for infrastructure systems under demand differences. Specifically, the model considered different seismic intensities, aiming at maximizing the effects of resilience enhancement measures to meet the expected performance of residents within the resource constraints. In addition, the model set the baseline for the optimization results by means of three functionality variables in earthquake scenarios. The group knapsack problem and the dynamic programming algorithm were applied to the solution of the mathematical formulation. Moreover, a case study was developed based on the realistic data of the hospital system in Mianzhu City during the 2008 Sichuan Earthquake. Three scenarios were designed to examine the impact of the seismic intensity, budget, and priority on the optimization results through experimental simulations. The results indicated that adequate budget allocation and the priority of appropriate resilience enhancement actions can serve as a tool for decision-makers to improve the emergency performance of infrastructure systems.

The study suggested that government decision-makers should consider the concept of resilience in the emergency management of infrastructure systems, including the system performance enhancement actions for self-resistance and recovery strategies. Government should pay attention to improving self-aid ability before the assistance of external resources. Furthermore, constructing the baseline for the optimization results was suggested to cope with the needs of residents under earthquake conditions. After establishing the emergency performance optimization model, decision-makers were supposed to determine the baseline for the optimization results to maximize the optimal allocation of resources.

The proposed approach bears several limitations that should be acknowledged. Future research should implement the developed emergency optimization model for other types of natural or man-made hazards, such as floods, and public health events, which may require more interdisciplinary knowledge in resilience and management. In addition, there can be additional cases for other types of infrastructure systems to explore seismic emergency optimization, such as the emergency performance improvement of the urban lifeline system. For a practical optimization model, consideration of the uncertainties of the external environment is suggested, such as changes in residents' needs and expected performance. Lastly, while the EP baseline of the optimization model has been demonstrated, how to develop a set of criteria that quantify the expected performance, requires more attention in future research.

We acknowledge the potential limitations of the proposed approach and opportunities for future work. First, some parameters in the proposed optimization model are set based on assumptions, and the appropriate value range under different earthquake intensities has not been explored. In addition, due to the very nature of different types of infrastructures, the specific characteristics of infrastructure have not yet been fully considered. This represents an opportunity to explore models in greater depth through future research. Future research should implement the developed emergency optimization model for other types of natural or man-made hazards, such as floods, and public health events, which may require more interdisciplinary knowledge in resilience and management. In addition, there can be additional cases for other types of infrastructure systems to explore seismic emergency optimization, such as the emergency performance improvement of the urban lifeline system. For a practical optimization model, consideration of the uncertainties of the external environment is suggested, such as changes in residents' needs and expected performance. Lastly, while the baseline of the optimization model has been demonstrated, how to develop a set of criteria to quantify the expected performance requires more attention in future research.

ACKNOWLEDGMENT

This material is based on work supported by the National Natural Science Foundation of China (NSFC) under Grant Nos. U1709212 and 71974106, the National Key Research and Development Program of China under Grant No. 2018YFC0809900, and the Beijing Natural Science Foundation (BJNSF) under Grant No. 8202027. Any opinions, findings, conclusions, or recommendations expressed in this paper are those of the authors and do not necessarily reflect the views of the funding agencies. The authors are thankful to the experts in Mianzhu for providing valuable advice on this study.

CONFLICTS OF INTEREST

The authors declare no conflicts of interest.

REFERENCES

1Feofilovs M, Romagnoli F. Dynamic assessment of urban resilience to natural hazards. Int J Disast Risk Reduct. 2021; 62:102328.
10.1016/j.ijdrr.2021.102328
Web of Science® Google Scholar
2Liao TY, Hu TY, Ko YN. A resilience optimization model for transportation networks under disasters. Nat Hazards. 2018; 93(1): 469-489.
10.1007/s11069-018-3310-3
Web of Science® Google Scholar
3 CRED. (2020). Human Cost of Disasters. An Overview of the Last 20 Years 2000–2019. Centre for Research on the Epidemiology of Disasters. https://cred.be/sites/default/files/CRED-Disaster-Report-Human-Cost2000-2019.pdf
Google Scholar
4Ouyang M. Review on modeling and simulation of interdependent critical infrastructure systems. Reliab Eng Syst Saf. 2014; 121: 43-60.
10.1016/j.ress.2013.06.040
Web of Science® Google Scholar
5 The People's Government of Mianzhu City. Mianzhu Statistical Yearbook 2007. Mianzhu, Sichuan Province. 2008. Mianzhu Statistics Bureau Publishing.
Google Scholar
6Francis R, Bekera B. A metric and frameworks for resilience analysis of engineered and infrastructure systems. Reliab Eng Syst Saf. 2014; 121: 90-103.
10.1016/j.ress.2013.07.004
Web of Science® Google Scholar
7Liu W, Song Z. Review of studies on the resilience of urban critical infrastructure networks. Reliab Eng Syst Saf. 2020; 193:106617.
10.1016/j.ress.2019.106617
Web of Science® Google Scholar
8Peng C, Yuan M, Gu C, Peng Z, Ming T. A review of the theory and practice of regional resilience. Sustain Cities Soc. 2017; 29: 86-96.
10.1016/j.scs.2016.12.003
Web of Science® Google Scholar
9Bruneau M, Chang SE, Eguchi RT, et al. A framework to quantitatively assess and enhance the seismic resilience of communities. Earthq Spectra. 2003; 19(4): 733-752.
10.1193/1.1623497
Web of Science® Google Scholar
10Kammouh O, Cimellaro GP, Mahin SA. Downtime estimation and analysis of lifelines after an earthquake. Eng Struct. 2018; 173: 393-403.
10.1016/j.engstruct.2018.06.093
Web of Science® Google Scholar
11Kammouh O, Dervishaj G, Cimellaro GP. Quantitative framework to assess resilience and risk at the country level. ASCE-ASME J Risk Uncertain Eng Syst A: Civil Eng. 2018; 4(1):04017033.
10.1061/AJRUA6.0000940
Web of Science® Google Scholar
12Cutter SL, Burton CG, Emrich CT. Disaster resilience indicators for benchmarking baseline conditions. J Homel Secur Emerg Manage. 2010; 7(1): 1-24.
10.2202/1547-7355.1732
Web of Science® Google Scholar
13Panteli M, Mancarella P, Trakas DN, Kyriakides E, Hatziargyriou ND. Metrics and quantification of operational and infrastructure resilience in power systems. IEEE Trans Power Syst. 2017; 32(6): 4732-4742.
10.1109/TPWRS.2017.2664141
Web of Science® Google Scholar
14Rogers CDF, Bouch CJ, Williams S, et al. Resistance and resilience—paradigms for critical local infrastructure. Proc Instit Civil Eng Municipal Eng. 2012; 165(2): 73-83.
Google Scholar
15Zhong S, Clark M, Hou X-Y, Zang Y, FitzGerald G. Validation of a framework for measuring hospital disaster resilience using factor analysis. Int J Environ Res Public Health. 2014; 11(6): 6335-6353.
10.3390/ijerph110606335
PubMed Web of Science® Google Scholar
16Zhang X, Miller-Hooks E. Scheduling short-term recovery activities to maximize transportation network resilience. J Comput Civil Eng. 2015; 29(6):04014087.
10.1061/(ASCE)CP.1943-5487.0000417
Web of Science® Google Scholar
17Alisan O, Tuydes-Yaman H, Kocatepe A, Ozguven EE. Developing performance measures to evaluate impact of cross-county collaboration for populations with access and functional needs. Int J Disast Risk Reduct. 2018; 31: 873-885.
10.1016/j.ijdrr.2018.08.007
Web of Science® Google Scholar
18Dulebenets MA, Pasha J, Abioye OF, et al. Exact and heuristic solution algorithms for efficient emergency evacuation in areas with vulnerable populations. Int Journal of Disast Risk Reduct. 2019; 39:101114.
10.1016/j.ijdrr.2019.101114
Web of Science® Google Scholar
19Faturechi R, Miller-Hooks E. Travel time resilience of roadway networks under disaster. Transport Res B: Methodol. 2014; 70: 47-64.
10.1016/j.trb.2014.08.007
Web of Science® Google Scholar
20Ouyang M. A mathematical framework to optimize resilience of interdependent critical infrastructure systems under spatially localized attacks. Eur J Operat Res. 2017; 262(3): 1072-1084.
10.1016/j.ejor.2017.04.022
Web of Science® Google Scholar
21Zhang X, Hu Z, Mahadevan S. Bilevel optimization model for resilient configuration of logistics service centers. IEEE Trans Reliab. 2020; 71(1): 469-483.
10.1109/TR.2020.2996025
Web of Science® Google Scholar
22 National Institute of Standards and Technology (NIST). Community resilience planning guide for buildings and infrastructure systems, volume II. NIST Special Publication 1190; 2015.
Google Scholar
23Sanusi F, Choi J, Ulak MB, Ozguven EE, Abichou T. Metadata-based analysis of physical–social–civic systems to develop the knowledge base for hurricane shelter planning. J Manage Eng. 2020; 36(5):04020041.
10.1061/(ASCE)ME.1943-5479.0000802
Web of Science® Google Scholar
24Li Z, Li N, Cimellaro GP, Fang D. System dynamics modeling-based approach for assessing seismic resilience of hospitals: methodology and a case in China. J Manage Eng. 2020; 36(5):04020050.
10.1061/(ASCE)ME.1943-5479.0000814
Web of Science® Google Scholar
25Holguín-Veras J, Jaller M. Immediate resource requirements after hurricane katrina. Nat Hazards Rev. 2012; 13(2): 117-131.
10.1061/(ASCE)NH.1527-6996.0000068
Web of Science® Google Scholar
26Kappes MS, Keiler M, von Elverfeldt K, Glade T. Challenges of analyzing multi-hazard risk: a review. Nat Hazards. 2012; 64(2): 1925-1958.
10.1007/s11069-012-0294-2
Web of Science® Google Scholar
27Kamenetzky RD, Shuman LJ, Wolfe H. Estimating need and demand for prehospital care. Operat Res. 1982; 30(6): 1148-1167.
10.1287/opre.30.6.1148
CAS Web of Science® Google Scholar
28Paul BK, Acharya B, Ghimire K. Effectiveness of earthquakes relief efforts in Nepal: opinions of the survivors. Nat Hazards. 2017; 85(2): 1169-1188.
10.1007/s11069-016-2627-z
Web of Science® Google Scholar
29Vile JL, Gillard JW, Harper PR, Knight VA. Predicting ambulance demand using singular spectrum analysis. J Operat Res Soc. 2012; 63(11): 1556-1565.
10.1057/jors.2011.160
Web of Science® Google Scholar
30Oh EH, Deshmukh A, Hastak M. Criticality assessment of lifeline infrastructure for enhancing disaster response. Nat Hazards Rev. 2013; 14(2): 98-107.
10.1061/(ASCE)NH.1527-6996.0000084
Web of Science® Google Scholar
31Cimellaro GP, Reinhorn AM, Bruneau M. Framework for analytical quantification of disaster resilience. Eng Struct. 2010; 32(11): 3639-3649.
10.1016/j.engstruct.2010.08.008
Web of Science® Google Scholar
32Maslow AH. A theory of human motivation. Psychol Rev. 1943; 50(4): 370-396.
10.1037/h0054346
Web of Science® Google Scholar
33Todini E. Looped water distribution networks design using a resilience index based heuristic approach. Urban Water. 2000; 2(2): 115-122.
10.1016/S1462-0758(00)00049-2
Google Scholar
34Zhu N. A relation between the knapsack and group knapsack problems. Discrete Applied Mathematics. 1998; 87(1-3): 255-268.
10.1016/S0166-218X(98)00061-4
Web of Science® Google Scholar
35HAZUS MH. Multi-hazard loss estimation methodology: earthquake model. Federal Emergency Management Agency: Washington, D.C. Technical manual, Hazus-MH MR5, Department of Homeland Security; 2003.
Google Scholar
36Kircher CA, Whitman RV, Holmes WT. HAZUS earthquake loss estimation methods. Nat Hazard Rev. 2006; 7(2): 45-59.
10.1061/(ASCE)1527-6988(2006)7:2(45)
Google Scholar
37Mitrani-Reiser J, Mahoney M, Holmes WT, de la Llera JC, Bissell R, Kirsch T. A functional loss assessment of a hospital system in the Bío-Bío province. Earthq Spectra. 2012; 28(1_suppl 1): 473-502.
10.1193/1.4000044
Web of Science® Google Scholar
38Jacques CC, McIntosh J, Giovinazzi S, Kirsch TD, Wilson T, Mitrani-Reiser J. Resilience of the canterbury hospital system to the 2011 Christchurch earthquake. Earthq Spectra. 2014; 30(1): 533-554.
10.1193/032013EQS074M
Web of Science® Google Scholar
39Peek-Asa C, Kraus JF, Bourque LB, Vimalachandra D, Yu J, Abrams J. Fatal and hospitalized injuries resulting from the 1994 Northridge earthquake. Int J Epidemiol. 1998; 27(3): 459-465.
10.1093/ije/27.3.459
CAS PubMed Web of Science® Google Scholar
40Henry D, Emmanuel Ramirez-Marquez J. Generic metrics and quantitative approaches for system resilience as a function of time. Reliab Eng Syst Saf. 2012; 99: 114-122.
10.1016/j.ress.2011.09.002
Web of Science® Google Scholar

Citing Literature

Volume1, Issue2

June 2022

Pages 196-210

This article also appears in:

Resilience of Cities and Infrastructures

A seismic emergency performance optimization model for infrastructure systems under demand differences: A case study in China

Abstract

1 INTRODUCTION

2 PROBLEM DESCRIPTION

3 MATHEMATICAL MODEL DEVELOPMENT

3.1 Model formulation

3.2 Solution algorithm

4 CASE STUDY

5 RESULTS AND ANALYSIS

6 CONCLUSIONS AND FUTURE RESEARCH

ACKNOWLEDGMENT

CONFLICTS OF INTEREST

REFERENCES

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

A seismic emergency performance optimization model for infrastructure systems under demand differences: A case study in China

Abstract

1 INTRODUCTION

2 PROBLEM DESCRIPTION

3 MATHEMATICAL MODEL DEVELOPMENT

3.1 Model formulation

3.2 Solution algorithm

4 CASE STUDY

5 RESULTS AND ANALYSIS

6 CONCLUSIONS AND FUTURE RESEARCH

ACKNOWLEDGMENT

CONFLICTS OF INTEREST

REFERENCES

Citing Literature

Figures

References

Related

Information