Fuzzy constrained optimization of eco-friendly reservoir operation using self-adaptive genetic algorithm: a case study of a cascade reservoir system in the Yalong River, China
ABSTRACT
With the increasing demands for hydropower development in China, it is particularly important to implement eco-friendly reservoir operation in consideration of the vulnerability of downstream aquatic environment. In this paper, a fuzzy constrained nonlinear programming model is presented. Fuzzy programming is used to deal with the inherent imprecision and vagueness in constraints, and a self-adaptive genetic algorithm with simulated binary crossover is proposed for searching for the optimal reservoir operating rules. First, the fuzzy reservoir operation model is transformed into two deterministic sub-models. Self-adaptive genetic algorithm is then used to generate optimal solutions by applying penalty functions to integrate constraints into the objective function to form the fitness function. To achieve a final compromise between the fuzzy objective and the constraints, a ‘max-min’ decision principle is incorporated into the optimization process to obtain satisfactory operating schemes. The methodology is demonstrated through a cascade system of reservoirs in the Yalong River, southwest China. A monthly reservoir operation model, which considered downstream ecological flow requirements as fuzzy constraints, is developed to optimize eco-friendly reservoir operation with the objective of maximizing total hydropower generation. Monthly operating rules are generated for two cascade reservoirs, and the optimal hydropower generation is also obtained. Results indicate that the proposed approach can effectively improve the operation of the cascade reservoir system and fulfill the flow requirements of the downstream ecosystem that are expressed as fuzzy sets. It is a useful tool for generating optimal strategy to achieve an eco-friendly reservoir operation under uncertainty. Copyright © 2011 John Wiley & Sons, Ltd.
INTRODUCTION
Reservoir operation for both water supply and hydroelectric generation is not always rational to satisfy the full current demand because of insufficient insight into the changing inflows and fuzzy water requirements. With currently less development and utilization of hydropower resources in comparison with developed countries, China is prioritizing hydropower in the national new energy agenda. Furthermore, hydropower is clean. It provides a cheap source of electricity with few carbon emissions (Yoo, 2009). Therefore, the potential for development of Chinese hydropower resources is enormous in a long period. On the other hand, however, well-known detrimental effects arise, such as impoundment of free-flowing river habitat, blockage of fish migration, and reduced water quality in reservoirs and downstream river reaches (Postel and Richter, 2003; Wohl, 2004; Graf, 2006; Richter and Thomas, 2007; Jager and Smith, 2008). It is no longer possible to exploit water resources without taking into consideration the ecological needs.
Dam construction on rivers remains the main form of hydropower resources exploitation. Hydroelectricity is generated by implementing reservoir operation and running turbine generators. Generally, reservoir operation influences temporal flow patterns, which have profound impact on the health of the downstream ecosystem (Arthington et al., 2006; Jager and Smith, 2008). Consequently, water release from a reservoir is increasingly required to guarantee necessary ecological flows at downstream locations, and ‘ecological flows’ refers to water considered sufficient for sustaining the structure and function of an ecosystem and its dependent species. There have been many studies on reservoir release optimization that consider the ecological flow requirements in the objective or constraints of ecological demands (Gibbins et al., 2001; Arthington et al., 2006; Suen and Eheart, 2006; McCartney, 2007; Bauer and Olsson, 2008; Jager and Smith, 2008). However, the ecological target was often set as a single value of minimum instream flow requirements that eliminated the flow variability sustaining healthy and diverse aquatic communities. Also, there has been a great deal of efforts for evaluating the ecological flows and to identify the needs of maintaining downstream ecosystem integrity to protect biodiversity (Poff et al., 2003; Lytle and Poff, 2004). They demonstrated the importance of mimicking the components of natural flow regime. However, it is difficult to simulate the natural flow process in reservoir operation due to the larger number of variables. Moreover, translating general hydrologic-ecological principles and knowledge into specific operating rules remains a daunting challenge (Harman and Stewardson, 2005; Chang et al., 2010; Jing and Chen, 2011). Hydrologic methods for estimating the ecological flows require less understanding of the ecosystem processes and goals, and they are less data-intensive than hydraulic and habitat methods. Tennant (1976) suggested that 10% of the average flow provided minimum protection and 30% of average flow was satisfactory.
Uncertainties often exist in human knowledge and ecological studies (Zhang et al., 2011). A large inherent uncertainty of ecological information results from the presence of random variables, incomplete or inaccurate data, and approximate estimations instead of measurements (Salski, 2003; Ahmadi-Nedushan et al., 2006). One way of handling the uncertainty is to use fuzzy-based approaches. According to Tennant's (1976) principle, the ecological flow requirements are uncertain, and it is difficult to directly incorporate the rule into the operation programming. Fortunately, the ecological flow as Tennant suggested can be quantified by fuzzy membership function. As a result, it is viable that the ecological flow requirements be presented as fuzzy constraints when optimizing the reservoir operations (Huang and Chang, 2003; Li, 2003). Fuzzy programming considers random parameters as fuzzy numbers and constraints as fuzzy sets. Constraint violation is allowed to a degree that it is defined as the membership function of the constraint (Huang et al., 1993; Yin et al., 1999; Sahinidis, 2004; Li et al., 2007; Lv et al., 2010; Sun and Huang, 2010). Furthermore, decision makers may establish an aspiration level and a tolerable interval for the objective that they desire to achieve, and each constraint can be modeled as a fuzzy set. A fuzzy programming problem can be transformed into deterministic problems for improving the communication between the fuzzy objective and constraints and thus generating satisfactory solutions to support decision making (Maqsood et al., 2005; Nie et al., 2007).
Application of optimization techniques to reservoir operation problems has been a major focus of water resources planning and management (Chen, 2003; Ahmed and Sarma, 2005; Mousavi et al., 2005; Ngo et al., 2007; Cheng et al., 2008; Hakimi-Asiabar et al., 2010). The previous studies indicated various complexities in water resources management. Labadie (2004) reviewed various optimization methods of reservoir system operation. For maximizing hydropower generation, the objective function may be highly nonlinear. Evolutionary algorithms are capable of generating globally optimal solution for problems where traditional algorithm methods would fail to converge or be trapped in local optima and have more advantages of robust ability to solve highly nonlinear, non-convex reservoir operation problems (Labadie, 2004). In recent decades, evolutionary computation techniques, such as genetic algorithm (GA), have become popular in global optimization of water resource management with their potential in optimization techniques for complex systems (Cai et al., 2001; Huang et al., 2002; Kerachian and Karamouz, 2007; Chaves and Chang, 2008). Oliveira and Loucks (1997) used GA to evaluate operation rules for multi-reservoir systems and demonstrated that GA could be used to identify effective operating policies. Subsequently, more and more Genetic Algorithms (GAs) are applied to the optimization of reservoir operations (Cheng et al., 2002; Chang et al., 2003; Cheng et al., 2006).
It has been shown that real-coded GAs are more suitable for large dimensional search spaces than binary-coded GAs, since they are more consistent and precise and they lead to faster convergence (Baskar et al., 2003). Moreover, a binary GA requires the knowledge of bounds on parameter values bracketing the true optimal solution. A real-parameter GA does not demand this knowledge and can be used in problems where such information is not available. Nonetheless, relative computational complexity, genetic drift, inaccuracy in local search intensification, and slow rate convergence remain to be solved in GA. In order to enhance the efficiency of GA, self-adaptation feature is incorporated in the real-coded GA using special crossover operators, such as simulated binary crossover (SBX), which create offspring statistically located in proportion to the difference of the parents in the search space (Deb and Beyer, 1999; Su and Chiang, 2004; Subbaraj et al., 2011). The population diversity is introduced by making use of distribution index in the SBX operator to create a better offspring. This leads to a high diversity in population, which can increase the probability toward the global optimum and prevent premature convergence (Subbaraj et al., 2011). However, in the SBX operator, the variance of children distribution depends on the distance between the two parents. It is important to use a distribution that assigns more probability for creating near-parent solutions than solutions away from the parents (Deb and Beyer, 2001).
Therefore, one approach to potentially address the uncertainties in ecological flow requirements and the complexities in nonlinear problems is to integrate self-adaptive GA with SBX to fuzzy programming framework. Such an approach would directly incorporate the uncertainties of ecological flows expressed as fuzzy membership functions. Moreover, it possesses the excellent attributes of self-adaptive evolutionary algorithms for solving complex problems. This leads to a fuzzy constrained self-adaptive GA for implementing eco-friendly reservoir operation. It could bridge the gap between simple minimum ecological flows and the great complexity of the natural flow regime, and help decision-makers evaluate alternative operating rules. Furthermore, it will be expected to effectively achieve the optimization of an eco-friendly reservoir operation. In this paper, the methodology is successfully applied to the cascade system of Jingping reservoirs in southwest of China. The results demonstrate how the methodology performs to obtain hydropower generation and to provide ecological releases for the downstream river. It is also shown that the proposed methodology is useful for developing monthly operating rules for reservoirs and implementing eco-friendly reservoir operation. A monthly reservoir operation model for cascade reservoirs is established, aiming to obtain optimal operating schemes for maximizing hydropower generation while providing satisfactory ecological releases at downstream river reach of the cascade system of reservoirs.
METHODOLOGY
Framework
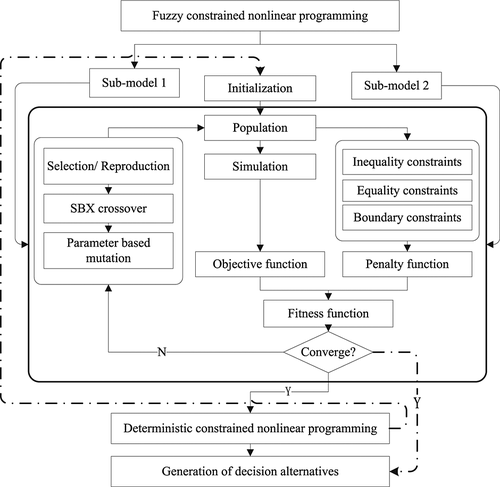
Figure 1 presents the framework of the proposed methodology. As it can be seen in the figure, a fuzzy programming model is first transformed into two deterministic sub-models to obtain the most desirable and least desirable objective values (Huang et al., 1993; Cai et al., 2001). In order to solve constrained nonlinear programming problem, the self-adaptive GA with SBX is used to search for the optimal solutions. To tackle uncertain information in the model, membership function is introduced to combine the objective function and fuzzy constraints into an integrated deterministic constrained nonlinear programming problem, and the proposed GA with SBX method is then iterated to search for the maximal membership degree. Thus, it is supposed that the optimal objective with adequate satisfaction of fuzzy constraints is achieved.
Fuzzy programming
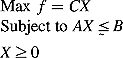 (1)
(1) ’ denotes that the relationship between AX and B is fuzzy, and in order to obtain a deterministic solution, B is always considered as an interval parameter [B−, B+], with B− and B+ representing the lower and upper bounds of fuzzy set B, respectively.
’ denotes that the relationship between AX and B is fuzzy, and in order to obtain a deterministic solution, B is always considered as an interval parameter [B−, B+], with B− and B+ representing the lower and upper bounds of fuzzy set B, respectively.Solution scheme
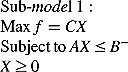 (2)
(2)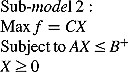 (3)
(3)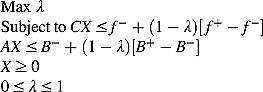 (4)
(4)Constrained genetic algorithm
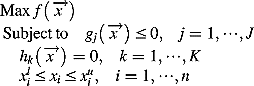 (5)
(5)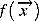 is the objective function,
is the objective function,  is the jth inequality constraints, and
is the jth inequality constraints, and 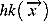 is the kth equality constraints. The ith variable varies in the range [
is the kth equality constraints. The ith variable varies in the range [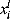 ,
,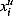 ]. A solution
]. A solution  that satisfies all the above equality and inequality constraints and the above variable bounds is called a feasible solution. The others are called infeasible solutions.
that satisfies all the above equality and inequality constraints and the above variable bounds is called a feasible solution. The others are called infeasible solutions.Generation of initial population
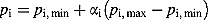 (6)
(6)The vector (p1, p2, p3,…, pn) is identified as an individual, and M individuals are combined to form the initial population. The fitness of each individual is then evaluated. The fitness is defined as a value that quantifies the optimality of a solution in such a way that any individual in the population can be compared and ranked against all the other individuals.
Tournament selection
The tournament selection method has several advantages (Goldberg and Deb, 1991). It is faster than the roulette wheel selection method (RWS) as a result of the computation of the average fitness required in the RWS. Moreover, the RWS is always noisy and suffers from scaling problem. In the case of tournament selection, sets (of fixed size called tournament size) of individuals are randomly chosen from the population, and the fitness of individuals from each set is compared with one another, and the individual with better fitness is taken to the mating pool. Consequently, tournament selection is easy to parallelize, and the scaling problem is eliminated by making the individuals compete with each other to gain entry to the mating pool. According to Blickle and Thiele (1995), the loss of diversity of the population increases with the increase in the tournament size. Hence, in order to keep the diversity loss to the minimum, the tournament size is chosen as two in this paper. This selection process is repeated once again in order to make the number of individuals in the mating pool equal to the population size. As a result, two copies of the best parents from the population will be present in the mating pool, whereas the worst parents will be eliminated (Subbaraj et al., 2011).
Generation of children solutions by simulated binary crossover
The SBX operator works with two parent solutions and creates two children solutions based on the single-point crossover operation of binary strings (Deb and Beyer, 2001). During this operation, common interval schemata between the parents are preserved in the children. The procedure of computing the children c1 and c2 from the parents x1 and x2 is described as follows.
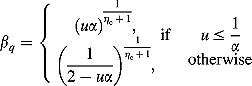 (7)
(7)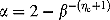 , and β is calculated using Equation (8):
, and β is calculated using Equation (8):
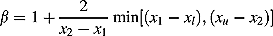 (8)
(8)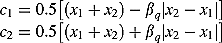 (9)
(9)It is assumed here that x1 < x2. A simple modification to the above equation can be performed for x1 > x2. For handling multiple variables, each variable is chosen with a probability 0.5 and the above SBX operator is applied variable by variable. In all simulation results here, we have used ηc = 1.
Parameter-based mutation
A polynomial probability distribution is used to create a solution c in the vicinity of a parent solution x under the mutation operator. The following procedure is used for a parameter x ∈ [xl, xu].
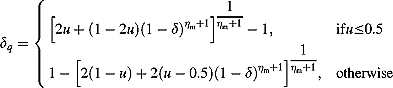 (10)
(10)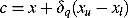 (11)
(11)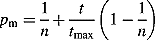 (12)
(12)Criteria of stop
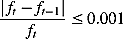 (13)
(13)Penalty constraint handling strategy
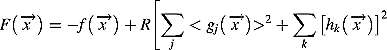 (14)
(14)CASE STUDY
The study area
The Yalong River is located in the Sichuan province, southwest China. The mainstream of Yalong River is 1571 km before joining the Yangtze River and drains an area of 136000 km2. The mainstream has a natural drop of 3830 m, and gives an annual runoff of 60.20 billion cubic meters. The river has a theoretically hydropower reserve of 33.40 GW and a technically development capacity of 29.188 GW. This would be equal to an annual power generation of 151.636 TW∙h, accounting for roughly 5% of the total generation of the whole country.
A development scheme of 21 cascade reservoirs (or dams) has been planned along the mainstream, which have a total capacity of 29.17 GW and put the river in the fourth place in terms of installed capacity among China's 13 major hydropower bases. As illustrated in Figure 2, the Jinping-Ι and Jinping-П cascade projects are located in the midstream of the Yalong River. Their construction is expected to be completed in 2014. The Jinping-Ι reservoir is of yearly regulation, with the normal pool level and the dead level as 1880 and 1800 m, respectively. The Jinping-П is designed to cut the 150-km river bend by a group of power tunnels to use the natural drop created by the bend, and its dam is 7.5 km downstream of Jinping-Ι. The Jinping-П reservoir itself only has a capacity of daily regulation with the normal pool level and the dead level as 1646 and 1640 m, respectively, but when jointly operated with Jinping-Ι, it also has the capacity of yearly regulation.
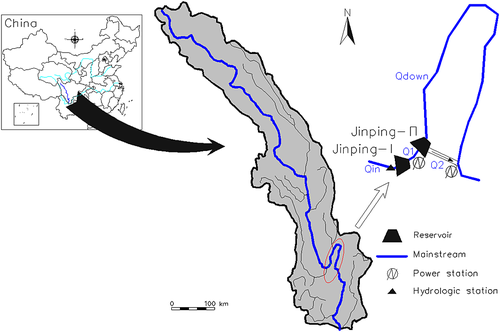
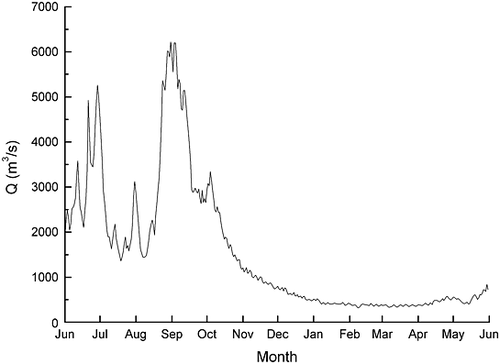
When the Jinping-П reservoir operates, most of the storage water will be diverted by tunnels for generating hydropower. As a result, less water is maintained in the river bend, although there is a tributary Jiulong He with a mean annual runoff of 106.5 m3/s, which is located 36 km downstream of the Jinping-П dam. According to the investigation, the Jinping river bend provides habitats and spawning/incubation grounds for many important fish species of the subfamily Schizothoracinae, which are among the unique species found upstream of the Yangtze River. Hence, it is necessary to take into consideration the downstream ecological flow requirements when planning reservoir operations. Figure 3 shows the natural inflows at the Santan hydrological monitoring station located upstream of the Jinping-Ι reservoir during the hydrologic year from June of 2001 to May of 2002.
Ecological demands
The minimum flow designates a minimum range of water flow that provides a certain level of protection for the downstream aquatic environment. However, the minimum flow only provides a basic requirement; it lacks deep insight into ecological integrity, and as a result, the ecological flow is always uncertain and site specific. Quantitative methods for the ecological flow are generally divided into three major categories: (1) historic flow regime, (2) hydraulic, and (3) habitat (Jowett, 1997). An ecological flow policy requires clear and measurable goals, ideally defining the goal, the extent to which this is to be achieved, and the criteria for evaluating the achievement. Considering the variations in natural flows during 1 year and the uncertain downstream ecological demands, the ecological flow demands are supposed to be variational, and the ecological flow with fuzzy sets representation may be more suitable and effective when accounting for downstream ecological demands. For example, fishes at different life stages or at different seasons have different demands for flows. To better communicate the uncertain demands, Tennant's (1976) method is employed to quantify the fuzzy requirements of downstream ecosystem. Based on the criteria, 10% and 30% of average monthly flow rates of multi-years (1965–2000) at the Jinping-П dam site are considered as the lower and upper bounds of the ecological flow requirements. Thus, a fuzzy constrained programming model of reservoirs' operation was developed, which considered the ecological flow needs as fuzzy constraints.
RESERVOIR OPERATION FORMULATION
Objective function
 (15)
(15)Constraints
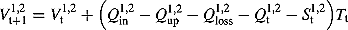 (16)
(16)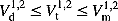 (17)
(17)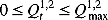 (18)
(18)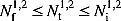 (19)
(19) (20)
(20)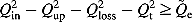 (21)
(21)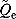 is the fuzzy ecological flow of downstream with the upper and lower limits of Qemax and Qemin, and the superscripts 1 and 2 represent the Jingping-Ι and Jinping-П reservoirs, respectively. Equation (16) is related to the water balance equation, and Equations (17)–(19) are related to the upper and lower bounds on release and storage, the release through the turbines, and the hydropower output, respectively. Equation (20) defines the relationship between hydropower outputs and discharges with net heads of hydroelectric power stations. The downstream ecological flow was assured by Equation (21).
is the fuzzy ecological flow of downstream with the upper and lower limits of Qemax and Qemin, and the superscripts 1 and 2 represent the Jingping-Ι and Jinping-П reservoirs, respectively. Equation (16) is related to the water balance equation, and Equations (17)–(19) are related to the upper and lower bounds on release and storage, the release through the turbines, and the hydropower output, respectively. Equation (20) defines the relationship between hydropower outputs and discharges with net heads of hydroelectric power stations. The downstream ecological flow was assured by Equation (21).The parameters of genetic algorithm with simulated binary crossover
The constrained GA with SBX is applied to searching for the optimal water levels of two cascade storage reservoirs within 1 year according to the designed objective and constraints. The inflow records of the hydrologic year 2001 are utilized with the highest and lowest values of 4105.9 and 364.7 m3/s, respectively. Hydrological data of the Jinping-П dam site for the period of 1965 to 2000 are processed to create the fuzzy downstream ecological flows. A month period is used as a time step; hence, every year has 12 time steps. Consequently, in each year, there are 24 water storages (variables) that need to be identified, and the corresponding water releases can then be obtained, as well as the generated, abandoned, and downstream water flows. The initial water level at the beginning of each year is set at the same value as that of water storage level at the end of the year, with 1800 m for the Jinping-Ι reservoir and 1646 m for the Jinping-П reservoir. The maximum iteration number of GA is set at 1000, and the crossover and mutation rates are designated as 0.9 and 0.1, respectively.
RESULTS AND DISCUSSION
The fuzzy constrained reservoir operation model of the two cascade reservoirs was computed using the water flow data of the hydrologic year 2001 as inputs following the proposed method, as discussed in the above sections. First, the operation model was converted into two sub-models by letting  be Qemax and Qemin. Note that both Qemax and Qemin have 12 variables, which means 12 ecological flow constraints of each reservoir in the operation model. Then, a population with 100 individuals, each of which was composed of 24 variables of water levels, was evolved to search for the optimal population and the best individual. Finally, the optimized total hydropower generation of two reservoirs and optimal downstream releases could be obtained. When the ecological flow is based on the minimum requirements, the optimized hydropower generation E1 is 4.146 × 1010 kW∙h. Whereas the ecological flow reaches the most desirable value in Equation (21), the optimized total generation E2 reaches 4.519 × 1010 kW∙h. Consequently, the final hydropower generation of reservoir operation would be in the range of 4.146 × 1010 to 4.519 × 1010 kW∙h under the ecological flow requirements. To achieve a compromise between generation and ecological flow, it needs to maximize the membership degree λ for the objective and constraints at the same time. After implementing the integrated deterministic reservoir operation model, the optimal hydropower generation Eopt is 4.379 × 1010 with an optimal membership degree of 0.62492. Thus, feasible discharges from the Jinping-П dam are released to maintain the downstream aquatic ecosystem with allowable loss of hydropower generation.
be Qemax and Qemin. Note that both Qemax and Qemin have 12 variables, which means 12 ecological flow constraints of each reservoir in the operation model. Then, a population with 100 individuals, each of which was composed of 24 variables of water levels, was evolved to search for the optimal population and the best individual. Finally, the optimized total hydropower generation of two reservoirs and optimal downstream releases could be obtained. When the ecological flow is based on the minimum requirements, the optimized hydropower generation E1 is 4.146 × 1010 kW∙h. Whereas the ecological flow reaches the most desirable value in Equation (21), the optimized total generation E2 reaches 4.519 × 1010 kW∙h. Consequently, the final hydropower generation of reservoir operation would be in the range of 4.146 × 1010 to 4.519 × 1010 kW∙h under the ecological flow requirements. To achieve a compromise between generation and ecological flow, it needs to maximize the membership degree λ for the objective and constraints at the same time. After implementing the integrated deterministic reservoir operation model, the optimal hydropower generation Eopt is 4.379 × 1010 with an optimal membership degree of 0.62492. Thus, feasible discharges from the Jinping-П dam are released to maintain the downstream aquatic ecosystem with allowable loss of hydropower generation.
The computation processes of GA with the lower and upper bounds of the ecological flow requirements were further examined. As shown in Figure 4, the fitness values decrease dramatically during the evolutional processes of solutions. It is suggested that the computation method featured fast convergence, and the optimal solutions converged at the generation of less than 310. The convergence rate under the ecological flow constraints of Qemin is faster than that under the ecological flow constraints of Qemax, while the optimal solutions under the ecological flow constraints of Qemin are reached until the iteration number reaches 305. In comparison with Qemin, higher ecological demands downsized the solutions search space under the ecological flow constraints of Qemax. However, there is still difficulty in searching for the optimal solutions in the local region. Generally, the entire evolution process is mainly dominated by the SBX operator. However, the function of mutation operator for preventing premature convergence is so significant that the optimal solutions must be achieved.
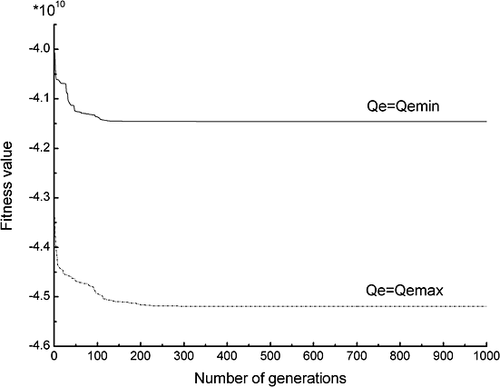
Water levels
Figure 5 represents the water levels of the Jinping-Ι and Jinping-П reservoirs over the hydrologic year. In order to achieve good utilization of hydropower on the condition that sufficient releases can be satisfied, the Jinping-Ι reservoir has 6 months to be implemented at the normal storage water level. While the Jinping-П reservoir mostly holds the dead water level during the year, the Jinping-П reservoir only has a capacity of daily regulation; consequently, the water level should be considered as the water level at the end of each month, and the daily changes of the water levels could be determined through short-term operation planning. Nonetheless, when operated jointly with the Jinping-Ι reservoir, the Jinping-П reservoir also has the capacity of yearly regulation. In the flood season, the Jinping-Ι reservoir stores water to elevate the water level, and in order to regulate the flood, abandoned water is directly released to the Jinping-П reservoir over the period from June to October. Especially, the abandoned water is as high as 4.67 × 109 m3 in September with an average inflow rate of 4105.89 m3/s. In the dry season, the Jinping-Ι reservoir operates at the normal water level with decreasing hydropower generation because of low inflows from November to February. Then, the water level of the Jinping-Ι reservoir gradually decreases to ensure adequate water releases until the dead water level to guarantee the firm output of the Jinping-П generation station and to meet the necessary requirements of the downstream aquatic ecosystem of the Jinping-П reservoir.
Discharge
As presented in Table 1, the optimal releases of two reservoirs through the turbines for generating hydroelectricity are calculated. The Q1 releases of the Jinping-Ι reservoir change with the change of the inflows. The generation turbines of the Jinping-Ι hydropower station run at the upper release limit to obtain great hydropower in June and July, while the water release for generation is reduced because of the upper hydropower output limit and the increasing water level. Abandoned water is released from the reservoir as a result of the installed capacity of the generator. When winter comes, the low inflows cannot provide adequate water for the cascade reservoir system to simultaneously generate hydropower and sustain the downstream ecosystem. Releases through turbines are less than 1000 m3/s from December until March in the following year, but the reservoir operates at high water levels to guarantee the minimum hydropower output. In the case of the Jinping-П reservoir, it holds high releases until November in order to generate hydropower. During the dry season from December to March, the reservoir combined with the Jinping-Ι reservoir operates to guarantee downstream releases from the Jinping-П reservoir for meeting the requirements of the ecological flow. In order to counteract the flooding in the coming season, the Jinping-Ι reservoir increases the release during March, April, and May to vacate the storage volume and operates at dead water level by the end of May.
| Jun | Jul | Aug | Sep | Oct | Nov | Dec | Jan | Feb | Mar | Apr | May | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Q1 | 2024 | 2024 | 1909.2 | 1764.7 | 1764.7 | 967 | 481.5 | 426.89 | 376.45 | 707.2 | 1096.8 | 1460.8 |
| Q2 | 1753.8 | 1860 | 1860 | 1860 | 1720.8 | 784.55 | 371.08 | 345.83 | 303.52 | 632.91 | 953.22 | 1303.3 |
| Qin | 3141.51 | 2152.47 | 3138.10 | 4105.89 | 2084.37 | 967.00 | 481.49 | 426.89 | 376.45 | 364.73 | 453.85 | 547.40 |
Ecological flows
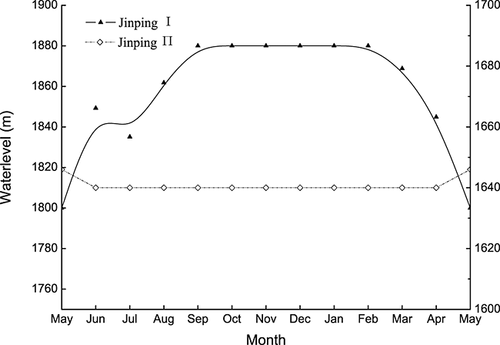
The downstream releases from the Jinping-П reservoir, Qdown, should be equal to or greater than the ecological flow demands as required by Equation (21). Figure 6 depicts the changes of Qdown during the year, and we can find that the downstream releases are mostly between the bounds of Qemax and Qemin, and the minimum ecological flow is satisfied over the year. In September, the inflow rate is so high (4105.89 m3/s) that the two hydroelectric power stations are run at their maximum hydropower outputs. To regulate the flood, the downstream release from the Jinping-П reservoir is greater than the most desirable ecological flow requirement in September. We also compared the downstream releases with the ecological flows proposed by the habitat method (Li et al., 2010) as shown in Figure 6. The optimal releases mostly guarantee the requirements of downstream habitat, although there is a lack of water release in March, April, and May as a result of special requirements of the target fish species chosen by the habitat method; it also demonstrates the feasibility and applicability of the proposed method in this study.
Ecological demands for water flows vary during the year. One the one hand, the organisms living in the stream and inhabiting the river bank have adapted to the hydrologic regime, and a specific or solid life pattern for each organism has been shaped. In this study, simulated downstream releases accord well with the pattern of the natural hydrologic regime. Hence, it can be supposed that the organisms' perception for hydrological change is not disturbed, and as a result, such damages as habitat loss would not happen although there may be influences on the adaption of specific fish or animals. On the other hand, special hydrological conditions, e.g. peak flow, may be ecologically significant for specific species. The extreme discharge as shown in Figure 6, which corresponds to the peak flow in the natural runoff in September, plays an important part in meeting special requirements of organisms, such as the spawning/incubation requirements of many fish species. Thereafter, the proposed downstream releases satisfy the necessary ecological flow and are beneficial to the protection of downstream ecological integrity.
Tradeoff between hydropower generation and ecological flows
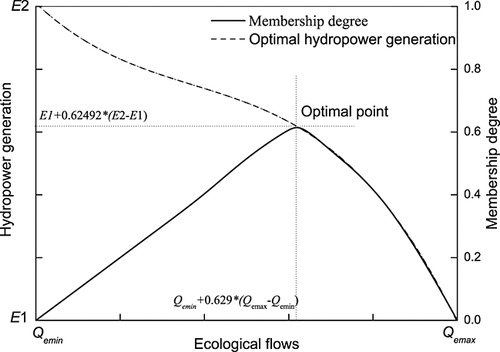
In order to achieve a satisfactory scheme accepted by both the project decision makers and the environmentalists, the tradeoff between the objective of hydropower generation and the constraints of the ecological flow would be further discussed. Figure 7 demonstrates the optimal hydropower generation under different ecological flow demands. The dashed line in the figure denotes the changes of optimal hydropower generation with the increasing membership degree of ecological flow, and the solid line, which represents the membership degree of the operation system benefit, has an extreme point. According to the ‘max–min’ principle in decision theory, the vertex is the optimal point, and thus, a compromise is reached between optimal hydropower generation and fuzzy ecological flow constraints. At the vertex, a best system performance is achieved and the optimal operating rules are obtained. To maintain the downstream ecological flows, the hydropower generation is reduced in order to guarantee adequate water release, whereas the ecological flow requirements are uncertain, as well as the hydropower generation objective. The concept of membership function is utilized to maximize the hydropower generation and ecological flows at the same time. In terms of decision theory, the conflict between the hydropower generation objective and the ecological flow demands is then resolved, and thus, we can make the most satisfactory decisions.
CONCLUSION
A fuzzy constrained nonlinear programming model has been developed for implementing reservoir operation under uncertainty. The model incorporates fuzzy ecological flows as constraints and improves the computation efficiency by using self-adaptive real-coded GA with SBX. In its solution process, the fuzzy constrained operation model is transformed into two deterministic sub-models, which correspond to the lower and upper bounds of the desired objective. This transformation is based on an interactive algorithm. To solve the complex nonlinear programming problem, adaptive GA is employed in search of optimal solutions with advantages of fast iteration and stable convergence. Thus, the proposed methodology not only provides a framework for implementing eco-friendly reservoir operation but also considers uncertain information, which is very important in ecological studies. As a result, we obtain the optimal result and operating rules to assist the reservoir management. The proposed model and solution framework could be very effective by considering fuzzy parameters or similar uncertainty information in the real world, and can suitably reach a compromise between the objective function and fuzzy constraints.
The applied case study showed that the optimal solutions for an eco-friendly reservoir operation could be obtained through self-adaptive GA with SBX, where an optimal output was achieved and the ecological flow demands were met. The adaptive GA was enhanced in its global searching ability and provided an adequate, effective, and robust way for searching reasonable reservoir operating hydrographs in an eco-friendly manner. In addition, uncertain ecological flow demands were expressed and optimized during the year, and the downstream water releases changed with the natural flow regime and were supposed to provide good performance in protecting downstream ecosystem. The developed model also proposed a framework for implementing an eco-friendly reservoir operation that was useful and easy to realize.
However, there are still limits when using the proposed method to solve fuzzy constrained nonlinear programming problems because we assumed that the objective value changes monotonously with the change of fuzzy parameters in constraints. Moreover, it will be also more difficult to obtain the optimal solutions when there are two or more uncertain parameters in the model. Consequently, we need more complex uncertainty analysis methods or techniques to deal with fuzzy parameters or uncertainty variables in the real world in future studies.
ACKNOWLEDGEMENTS
This study was financially supported by the Major Science and Technology Program for Water Pollution and Treatment of China (2009ZX07104-004). The authors are grateful to the editor and reviewers for their valuable comments and suggestions.




