Photons can convey information via their energy (or color), polarization, coherence, and timing. Energetics of molecules is dealt with spectroscopy, and the absorption and emission spectra act as fingerprints of molecules, which reflect changes in structure and environment with high sensitivity, being the spectra continuous in general. In conventional flow cytometry detection of fluorescence color has been mainly restricted to the detecting just a few discrete wavelength ranges (bands) often separated by gaps like “missing teeth.” The enhanced information content meant by continuity of spectra has been first exploited in imaging when the output of a scanning microscope has been fed into a spectrograph and the whole emission spectrum has been recorded with a point detector at each pixel of the image [1, 2]. Recording emission spectra can also be parallelized by dispersing and projecting the light by a prism onto a pixel array of a CCD camera, onto an array of photomultipliers (PMTs), alternatively onto a multicathode PMT, through micro lenses [3, 4]. This latter method has also been applied in flow cytometry, where serially dispersive methods are not feasible due to the short dwell time of cells in the illuminating light beam. The finesse of the spectra on the wavelength scale is determined by the quality of the dispersive element and the number of detectors, or number of pixels in a CCD array. The fact that whole spectra are now recorded per cell in a flow cytometer, in dozens of channels instead of only a few, however, has drastically changed the attitude towards data analysis [5-7]. Classically fluorescence light is detected via just a few discrete channels from some fluorophores. However, due to the substantial width of emission spectra of the fluorophores, the contents of the different channels are not uniquely characterizing the individual fluorophores, but they are often characteristic mixtures of the individual emissions. Cleaning of signals of the different channels has been accomplished in hardware as well as software levels. At the hardware-, or “before acquisition” level, it covers the often not so easily done procedure, termed “compensation.” At the software, or “after acquisition” level, it covers signal cleaning via extra calculations with the so called “spillage factors,” applied, for example, in the ratiometric “Förster resonance energy transfer (FRET)” method, in the version “dual laser flow cytometric FRET” called FCET. Determination of compensation or spillage factors necessitates extra measurements on the pure spectral components. With a huge number of channels, as in spectral cytometry, however, such a correction is impossible.

If the number of spectral components, fluorophores, is known in advance, with well-determined and time-constant spectra as their “fingerprints,” and the components are not interacting, then the net spectrum is considered as a linear superposition of the component spectra (Figure 1) [5]. Alternatively, the net spectrum is considered as a vector, which can be expanded according to the component spectra as basis vectors, with the individual coefficients as the “coordinates,” which are relative amounts, or concentrations in nature. Interaction between the components, for example, FRET, can be taken into account by appropriate extra relationships, “constraints” between the expansion coefficients.

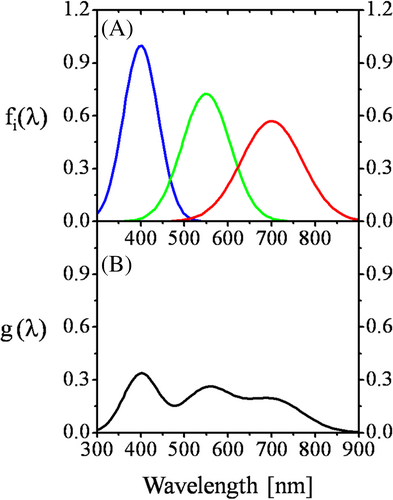
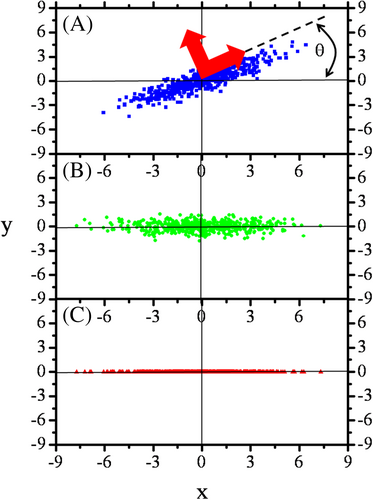
When the number of spectral components is large and unknown, another approach called principle components analysis (PCA) can be applied (Figure 2) [6, 7]. If a phenomenon is described by a few variables then they can be dependent on each other, the degree of which is quantified by the pair wise covariances. Their partial dependencies imply that their information content is overlapping, that is, information content of a variable can be influenced also by other variable. However, it is possible to find independent variables whose variances successively decrease. Independence here means that the directions in which the variables change the most are perpendicular to each other. Due to independence, information content can be directly assigned to the new variables in the form of their variances. Mathematically this procedure corresponds to finding the main directions of the covariance matrix called also “eigenvalue problem,” or “main axis (canonical) transformation.” In classical mechanics an analogous problem is finding the main directions of inertia of a rigid body via finding the eigenvalues of the inertia tensor. After establishing the order of the variables according to their information content, it is possible to reduce the data set, by leaving out those data having information below a given threshold. Utilizing the above principles, spectral flow cytometry became a routine approach of the today laboratory for solving “many variable problems” such as immune phenotyping [8, 9], detecting 3D gradients of cAMP [10], and analyzing solid tissue suspensions [11]. However, the application of spectral flow cytometry to FRET has remained a challenge.

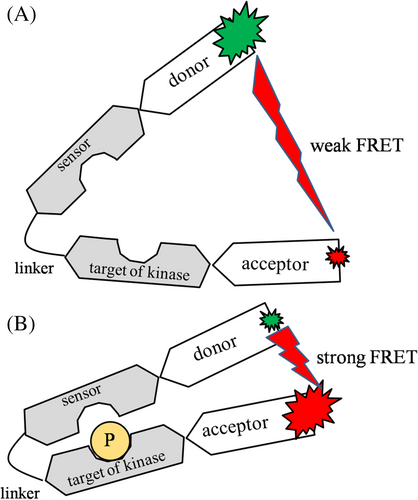
In their recent work, Henderson et al. [12] critically compare the detectibility of FRET in the same biological samples, with conventional and spectral flow cytometries. As to the biological nature of the investigated FRET samples, they belong to the “kinase assay by a FRET reporter” category. The structural building blocks of such an assay are depicted on Figure 3, Panel A. It is composed of a kinase target domain, which can be phosphorylated, a domain (sensor) recognizing the phosphorylated target, a hinge region connecting the target and sensor domains, and the donor (a cyan fluorescent protein, Cerulene3, briefly C3) and acceptor (a yellow fluorescent protein, cpVenus[E172], briefly cpV) fused to the ends of the sensor and target domains. Function is based on that the sensor domain binds the phosphorylated target, thereby reducing donor-acceptor distance, and enhancing FRET (Figure 3, Panel B). For monitoring AKT kinases, Lyn-AktAR2-EV is the “live” reporter, for probing the equilibria between the kinases and phosphatases (e.g., PTEN). Lyn-AktAR2-EV-D is the “dead” (or inactive) reporter possessing target moiety, which can not be phosphorylated, to determine baseline FRET. In these constructs, AktAR2 containing C3 and cpV as the FRET donor and acceptor, is the “core reporter” of AKT kinase activity in the cell cytoplasm. It has been extended with the Lyn and EV moieties for targeting the sensor from the cytosol into the cell membrane and spatially extending the dynamic range for FRET, respectively. For assaying PKA kinase activity the corresponding “live” (or active) sensor is LPAR-AKAR-WT, with LRRATLVD target domain, which can be phosphorylated, and FHA1 the recognizing, phosphate-sensing domain. The inactive assay here is LPAR-AKAR-mt, which contains a mutation in the target domain. According to the authors, these assays are applicable to monitor signaling pathways involving kinases (AKT, PKA) and phosphatases downstream to the B-cell receptor (BcR), and thereby for monitoring effects of drugs and gene knockouts, with an exceptionally good efficiency if combined with spectral flow cytometry. Basically the same principles of sensing have been utilized earlier for detecting cAMP levels via the H188 probe (Turquoise-Epac-Venus) [10].

Regarding the technique of flow cytometric spectral FRET, the authors find spectral FRET more versatile (or robust) and applicable than the conventional approach of ratiometric (or “3-cube”) FRET. While conventional FRET can be computed only “offline,” that is, after data collection, because of the need for spectral spillage factors and the calibrating G (or α) factor, spectral FRET determination can be carried out also in real time, for example, during data collection and cell sorting. The only prerequisite is the presence of a library of standard spectra (“end members”) for the spectral unmixing.

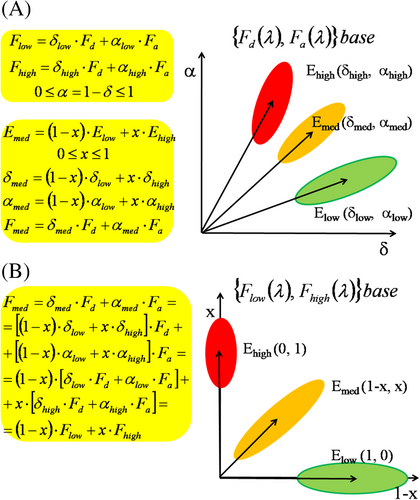
As to the analysis of spectral FRET data, the conventional approach is when the measured FRET spectra are decomposed into the linear combination of the spectra of the donor, acceptor and cell background, as “end members” (Figure 4, Panel A) [5, 13]. However, these authors noticed that FRET can be followed more sensitively, if the spectrum of the FRET sample is expanded according to the spectra of two special FRET samples—called “low” and “high” FRET spectra—differing in the FRET efficiency, but belonging to the same donor and acceptor fluorophores (Figure 4, Panel B). The dynamic range and sensitivity of the FRET measurement is determined by the difference in the two FRET efficiencies. Large difference favors for larger dynamic range and higher sensitivity. This approach has also the advantage that all factors mutually present in the “low” and “high” FRET samples and the interested “medium” FRET sample, drop out. This way spectral effects of cell background, and different markers for cell phenotyping—inasmuch as they are “spectrally inactive,” non-interacting—can be eliminated. But for this, their spectra should be placed in advance in the library of spectra (of endmembers) used for spectral decomposition.

Flow cytometry is a technique inherently applicable for multiplexing. Multiplexing in turn implies information transmission at a much higher rate, manifesting itself in an increased contrast between the subpopulations, called biochemical resolution [14-16]. Esposito et al. [15] gave a theoretical foundation of this notion by establishing a common framework for spatial and biochemical resolution based on Fisher information. According to this theory, degree of multiplexing can be quantitated. Increased multiplexing implies a finer degree of classification of fluorescence photons according to its properties, leading to an increase in Fisher information as well as to an increased degree in distinguishability in spatial and biochemical environments (Figure 5).

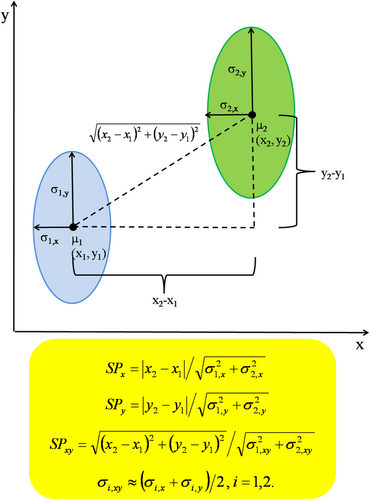
Approaching the end of this short discussion, as a resume, we can say that significant step-forward already happened in the subject of spectral FRET in flow cytometry. Yet, there remained some open questions pertaining to the accurate theoretical treatment of spectral FRET, and ways of recovery, if it is feasible at all, of wavelength dependence of FRET. As to the mathematical analysis, the emerging utilization of phasor plots—introduced in the field of fluorescence lifetime—in spectral analysis and for describing fluorescence polarization might be expected to bring significant leap forward also in the field of spectral FRET [16, 18]. As to the photon properties amenable for information transmission, measurement of fluorescence polarization in flow cytometry has already been realized [19]. Time (pulsed) and frequency domain measurement of excited state (fluorescence) lifetime has also been recently demonstrated [20]. Unifying these facilities in a joint spectral platform would culminate in a hyper dimensional flow cytometry, as it has already been proven in microscopy [16].

AUTHOR CONTRIBUTIONS

László Bene: Conceptualization (equal); methodology (equal); writing – original draft (equal); writing – review and editing (equal). Laszlo Damjanovich: Conceptualization (equal); investigation (equal); methodology (equal); supervision (equal); writing – original draft (equal); writing – review and editing (equal).

CONFLICT OF INTEREST

The authors have no conflict of interest of any kind in the publication of this commentary.