Many problems of modern laser physics are governed by equations or sets of equations in an unbounded domain. For solving these problems using the computer simulation, it is necessary to introduce the bounded domain, which size should be extended significantly to avoid the spurious wave reflection from the domain boundaries. Alternatively, the artificial (non-reflective or transparent) boundary conditions should be stated. This approach is also effective for enhancing computation performance at the numerical solution of the nonlinear partial differential equations (PDEs). In the current paper, we investigate the laser pulse propagation in a semiconductor, governed by the Schrödinger equation, under the appearance of spatio-temporal contrast structures of semiconductor characteristics. Their evolution is described by a set of PDEs. The optical pulse is partly reflected from the boundaries of these structures. Consequently, even a little reflection of the optical pulse from the artificial boundaries can essentially distort the numerical solution. Thus, these artificial boundary conditions must possess a high quality to minimize their reflection coefficients. With this aim, we propose the method for constructing adaptive artificial boundary conditions and discuss their advantages.

1 INTRODUCTION

Many problems of laser physics and nonlinear optics are governed by sets of nonlinear time-dependent PDEs. In particular, the pulse interaction with a semiconductor is governed by such sets of the PDEs. At certain parameters, the interaction can be accompanied by an optical bistability. This phenomenon is a base for the development of all-optical data processing devices and attracts the interest of many authors.^1-6 Recently,⁷ it was shown that the laser beam longitudinal diffraction plays a fundamental role at the laser pulse interaction with a semiconductor under the appearance of the laser-induced high absorption domain because this leads to the reflection of laser energy from the domain boundaries. This phenomenon can essentially change the process of this interaction. To describe the laser pulse reflection from the high absorption domain, it is necessary to involve in the set of equations the nonlinear Schrödinger equation with the second-order derivative on the coordinate along which the optical pulse propagates. As a consequence of this, to increase the computer simulation efficiency, one needs to apply the artificial boundary conditions (ABCs) for the nonlinear Schrödinger equation.

It should be stressed that during the last decades, many authors pay attention to solving the wave equation and the Schrödinger equation in an unbounded domain (see, e.g., References 8-40). Applying computer modeling techniques for such problems requires also introducing artificial boundaries. In turn, this may lead to the occurrence of a spurious wave reflection from the boundaries. To avoid this reflection, one could solve this problem by shifting the artificial boundaries afar the domain in which the computation occurs. Obviously, this way is impractical from a computational point of view and leads to a significant increasing computational expense, which could become a crucial problem in solving multidimensional problems.

Another way to avoid a spurious wave that appeared due to a laser beam reflection from the artificial boundaries is the introducing transparent (non-reflecting) ABCs. Previously, various authors have proposed methods for transparent ABCs constructing. So, for the 1D linear Schrödinger equation, exact transparent ABCs were also developed. However, their implementation requires information about the solution on all previous time layers, which is unacceptable for the numerical solution due to the computational restrictions. Approximate ABCs could be constructed without all that information, but they lead to a reflected wave's appearance. At linear propagation of the laser beam, the presence of a reflected wave, which amplitude is about 3%–5% of the incident wave amplitude, may be acceptable. But at the optical wave propagation in a nonlinear medium described by the corresponding nonlinear Schrödinger equation, a reflected wave with such amplitude leads to significant distortion of the numerical solution. Therefore, the construction of effective ABCs, which could be easily applying in computer modeling, is an urgent problem.

In our opinion, using the information about the solution in the vicinity of the artificial boundary is one of the promising ways for adaptive ABCs construction.^{25, 36-39} In Reference 38, it was proposed to compute an effective wavenumber using the Fourier-Gabor transform. This approach is also effective for multidimensional problems because it is possible to write a chain of the corresponding 1D problems. However, such an approach has at least two disadvantages. Firstly, it is not always possible to compute analytically the required integral. Secondly, and this seems more important, in the case of the optical radiation nonlinear propagation, the problem exact solution is usually absent. Let us note that in Reference 39 the nonlinear multidimensional problem was reduced to a chain of 1D problems using the splitting method, and, therefore, the constructed finite-difference scheme was non-conservative according to certain invariants of the problem.

In the current paper, we develop the adaptive ABCs based on computing the time-dependent local wavenumber (or local group velocity) of the laser beam (or pulse) near the artificial boundary. An algorithm of local wavenumbers computing is based on the problem invariants parts. At their computation, we pay careful attention to the correctness of the spurious wave accounting. For clarifying the proposed method's efficiency, we compare the computer simulation results obtained by using non-adaptive ABCs or adaptive ones with the corresponding solution of the Schrödinger equation computed in large enough. Their effectiveness is also demonstrated at solving the 2D problem of the laser pulse propagation in a semiconductor. The necessity of introducing the adaptive ABCs for the Schrödinger equation is illustrated by considering the laser beam propagation under its strong diffraction.

The paper is organized as follows. Section 2 is devoted to the statement of the 2D problem of the laser-induced electron-ionized-donor plasma generation in a semiconductor. We discuss a mathematical model for the problem under consideration, including two ways for standing initial problem for the Schrödinger equation. Presented results of the computer modeling demonstrate the fundamental role of the laser beam longitudinal diffraction under investigation. In Section 3, we develop non-adaptive and adaptive ABCs for the 1D Schrödinger equation and propose the numerical method for their computation. On the base of the provided simulations, we proved the efficiency of the second approach. In Section 4, we briefly conclude the main results.

2 THE 2D PROBLEM OF LASER-INDUCED ELECTRON-IONIZED-DONOR PLASMA GENERATION IN A SEMICONDUCTOR

2.1 Mathematical model of 2D problem

We consider the laser pulse interaction with a semiconductor, which has a rectangular form and could be placed in the external electric field. The mathematical model for the problem consists of a set 2D dimensionless PDEs, which involves the Poisson equation concerning laser-induced electric field potential φ(x, z, t), two nonlinear equations describing the evolution of free-electron concentration n(x, z, t) and concentration of ionized donors N(x, z, t), and the nonlinear Schrödinger equation describing laser pulse propagation in a semiconductor. We emphasize that to obtain an adequate description of the laser pulse interaction with a semiconductor, it is necessary to take into account longitudinal and transverse diffraction of the beam because of an appearance of the free-charge concentration contrast structures, and they are caused by optical bistability occurrence. In the general case, the Schrödinger equation is written with respect to a complex amplitude A(x, z, t), which is slowly varying in time and on the spatial coordinate, directed transversely to the pulse propagation direction. However, the amplitude is a fast-varying function in the direction of the pulse propagation. In this case we take into account the laser beam reflection from the laser-induced spatio-temporal structures. Thus, the laser-induced plasma evolution in a semiconductor is governed by the following set of the dimensionless equations:

\frac{\partial N}{\partial t} = G (n, N, {| A |}^{2}) - R (n, N), 0 < x < L_{x}, L_{z_{l}} < z < L_{z_{r}}, 0 < t \leq L_{t},

()

\frac{\partial n}{\partial t} = D_{n_{x}} \frac{\partial}{\partial x} (\frac{\partial n}{\partial x} - μ_{x} n \frac{\partial φ}{\partial x}) + D_{n_{z}} \frac{\partial}{\partial z} (\frac{\partial n}{\partial z} - μ_{z} n \frac{\partial φ}{\partial z}) + G (n, N, {| A |}^{2}) - R (n, N),

()

\frac{\partial^{2} φ}{\partial x^{2}} + \frac{\partial^{2} φ}{\partial z^{2}} = γ (n - N),

()

ϵ \frac{\partial A}{\partial t} + {iD}_{A_{z}} \frac{\partial^{2} A}{\partial z^{2}} + {iD}_{A_{x}} \frac{\partial^{2} A}{\partial x^{2}} + \frac{δ_{0}}{2} δ (n, N) A = 0,

()

ϵ \frac{\partial A}{\partial t} + ν_{z} \frac{\partial A}{\partial z} + {iD}_{A_{z}} \frac{\partial^{2} A}{\partial z^{2}} + {iD}_{A_{x}} \frac{\partial^{2} A}{\partial x^{2}} + \frac{δ_{0}}{2} δ (n, N) A = 0, 0 < x < L_{x}, L_{z_{l}} < z < L_{z_{r}}, 0 < t \leq L_{t} .

()

First of all, let us stress that both Schrödinger equations with the corresponding choice of their diffraction coefficients and the initial conditions are equivalent. We demonstrate this below.

Above the dimensionless spatial coordinates x, z belongs to the ranges [0,L_x], [ $L_{z_{l}}$ , $L_{z_{r}}$ ], respectively. The laser pulse propagates along z-coordinate. The parameter ν_z characterizes the laser pulse group velocity and denotes the dimensionless velocity of the laser pulse propagation. Coordinate x is perpendicular to z-coordinate, and it is named as transverse coordinate. Dimensionless time is notated by variable t. L_t characterizes a dimensionless time interval during which the laser pulse interaction with a semiconductor is analyzed. The electron diffusion coefficients $D_{n_{x}}$ , $D_{n_{z}}$ , and the diffraction coefficients $D_{A_{x}}, D_{A_{z}}$ , and the electron mobility coefficients μ_x, μ_z are non-negative parameters. ϵ is a dielectric permittivity of a medium. Parameter γ depends, in particular, on the maximal concentration of free charged particles. Parameter δ₀ denotes the laser energy maximal absorption. According to the physical sense of the problem, the concentrations n(x, z, t), N(x, z, t) and the absorption coefficient δ(n, N) must be non-negative. Because of the chosen normalization of the parameters, the ionized donor concentration N(x, z, t) must not exceed unity.

Function G is the generation of charged particles, and function R is their recombination:

G (n, N, {| A |}^{2}) = \{\begin{cases} q_{0} {| A |}^{2} δ (n, N), 0 \leq x \leq L_{x}, 0 \leq z \leq L_{z_{r}}, 0 \leq t \leq L_{t}, \\ 0, 0 \leq x \leq L_{x}, L_{z_{l}} \leq z \leq 0, 0 \leq t \leq L_{t}, \end{cases}

()

R (n, N) = \{\begin{cases} \frac{nN - n_{0}^{2}}{τ_{R}}, 0 \leq x \leq L_{x}, 0 \leq z \leq L_{z_{r}}, \\ 0, 0 \leq x \leq L_{x}, L_{z_{l}} \leq z \leq 0 . \end{cases}

()

Above q₀ is the dimensionless laser pulse maximal intensity. Parameter n₀ is the equilibrium value of the free electron concentration and ionized donor concentration in a semiconductor before the laser pulse action, τ_R characterizes a recombination time of the free charged particles. The absorption coefficient δ(n, N) is governed by the nonlinear function:

δ (n, N) = (1 - N) e^{- ψ (1 - ξ n)},

()

where ξ, ψ are non-negative constants. This absorption coefficient corresponds to an occurrence of so-called concentration absorption optical bistability.

The homogenous BCs concerning the free-electron flow correspond to the electric current absence through a semiconductor surface:

{(\frac{\partial n}{\partial x} - μ_{x} n \frac{\partial φ}{\partial x})|}_{x = 0, L_{x}} = 0, {(\frac{\partial n}{\partial z} - μ_{z} n \frac{\partial φ}{\partial z})|}_{z = 0, L_{z_{r}}} = 0 .

()

If the external electric field is absent, then the zero-value Neumann conditions for the electric field potential are stated as follows:

{\frac{\partial φ}{\partial x}|}_{x = 0, L_{x}} = 0, {\frac{\partial φ}{\partial z}|}_{z = 0, L_{z}} = 0 .

()

Initial distributions of the electric field potential and the free-charged particles concentrations are defined as:

{φ |}_{t = 0} = 0, {n |}_{t = 0} = {N |}_{t = 0} = n_{0},

()

where n₀ is an equilibrium value of free-electron concentration and ionized donor one. Because we consider the bounded time interval and finite initial distribution of the complex amplitude, then one can state the zero-value BCs for this function:

{A |}_{x = 0} = {A |}_{x = L_{x}} = 0, {A |}_{z = L_{z_{l}}} = {A |}_{z = L_{z_{r}}} = 0 .

()

However, for unbounded domain on a spatial coordinate, as a rule, it supposes that the function A and its n-th derivatives decrease exponentially at tending of the corresponding coordinate to plus or minus infinity.

It should be stressed that the size of the spatial domain in z-direction is determined by the requirement of optical pulse non-reflection from the domain boundaries at providing computations. Depending on different characteristics of the laser pulse interaction with a semiconductor, the values $L_{z_{l}}, L_{z_{r}}$ are chosen, and they could be rather big and have to be increased with growing of time interval. Obviously, using this extended domain increases essentially the computational cost of the problem solving.

At writing the initial distribution for the complex amplitude, it should be stressed that its spatial distribution along a longitudinal coordinate coincides with its time distribution because a laser pulse propagates in a linear medium before its interaction with a semiconductor. We choose the incident laser beam complex amplitude distribution in the form of Gaussian profile along x-coordinate and hyper-Gaussian one along z-coordinate in the form:

{A |}_{t = 0} = e^{- {(\frac{x - L_{c_{x}}}{a_{x}})}^{2} - {(\frac{z - L_{c_{z}}}{a_{z}})}^{10} - 2 i π χ (z - L_{c_{z}})},

()

if we solve Equation (4′) or

{A |}_{t = 0} = e^{- {(\frac{x - L_{c_{x}}}{a_{x}})}^{2} - {(\frac{z - L_{c_{z}}}{a_{z}})}^{10}},

()

if we solve Equation (4″). Here

L_{c_{x}}, L_{c_{z}}

are the coordinates of the incident laser beam center position, and a_x, a_z are the beam radiuses on x- and z-coordinates, respectively. Parameter χ is a dimensionless wavenumber of the laser beam on z-coordinate.

Let us stress that if we use Equation (4′) with initial distribution (12′) for computation of the complex amplitude, then the diffraction coefficient

D_{A_{z}}

is defined by the parameter χ as follows:

D_{A_{z}} = \frac{1}{4 π χ},

()

that corresponds to the laser pulse propagation with the unit group velocity. In turn, at solving Equation (4″) with the initial distribution of the complex amplitude (12″), the diffraction coefficient

D_{A_{z}}

does not depend on the laser pulse propagation velocity ν_z. If the dimensionless group velocity of the pulse is defined as unity (ν_z = 1), then it will coincide with those for the problem (4′), (12′).

Let us demonstrate that both problem statements for describing the laser pulse propagation are equivalent to each other. With this aim we transform Equation (4′) using substitution

A = \overline{A} e^{- i β z}

. Taking into account the following equalities:

\frac{\partial \overline{A} e^{- i β z}}{\partial z} = \frac{\partial \overline{A}}{\partial z} e^{- i β z} - i β \overline{A} e^{- i β z},

\frac{\partial^{2} \overline{A} e^{- i β z}}{\partial z^{2}} = \frac{\partial}{\partial z} (\frac{\partial \overline{A}}{\partial z} e^{- i β z} - i β \overline{A} e^{- i β z}) = (\frac{\partial^{2} \overline{A}}{\partial z^{2}} - 2 i β \frac{\partial \overline{A}}{\partial z} - β^{2} \overline{A}) e^{- i β z},

it is easy to see that Equation (4′) transformed to the form:

ϵ \frac{\partial \overline{A}}{\partial t} + 2 D_{A_{z}} β \frac{\partial \overline{A}}{\partial z} + {iD}_{A_{z}} \frac{\partial^{2} \overline{A}}{\partial z^{2}} + {iD}_{A_{x}} \frac{\partial^{2} \overline{A}}{\partial x^{2}} + \frac{δ_{0}}{2} δ (n, N) \overline{A} - {iD}_{z} β^{2} \overline{A} = 0 .

()

Choosing parameter β as follows: β = 2πχ and taking into account the expression (13), we see that Equation (14) coincides with Equation (4″) except the last term corresponding to a homogeneous shift of the beam phase with time. But this shift does not influence both the laser beam profile and shape and the pulse interaction with a semiconductor. Nevertheless, using these equations ((4′) and (4″)) at computer simulation may lead to different requirement on a choice of the difference grid steps.

2.2 Computer modeling of the 2D problem

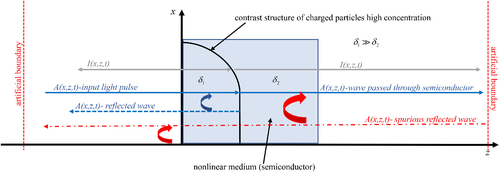
In Reference 7, we demonstrated that the optical pulse reflects partly from the boundaries of the contrast structures of the high electron concentration induced in a semiconductor by laser radiation. This occurs due to the longitudinal diffraction, which plays the main role in the laser radiation reflection. The process is shown schematically in Figure 1.

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

The scheme of laser pulse interaction with the boundaries of the contrast laser-induced structures and artificial boundaries

Let us emphasize that such problems belong to a new field of nonlinear optics: gradient nonlinear optics. If the longitudinal diffraction of a beam does not take into account (in this case, the laser pulse is depicted in Figure 1 by the beam intensity I(x, z, t) = |A|²), then the laser pulse propagates only in the positive direction of the z-axis. To prove this proposition, we compare below the computer simulation results obtained with (

D_{A_{z}} \neq 0

) and without (

D_{A_{z}} = 0

) diffraction term in Equations (4′) or (4″). The computer simulation is provided for the problem parameters:

\begin{array}{l} ϵ = 1, L_{t} = 10, L_{x} = 1, L_{z_{l}} = - 30, L_{z_{r}} = 30, γ = 1000, D_{n_{x}} = D_{n_{z}} = 10^{- 5}, μ_{x} = μ_{z} = 1, ψ = 2.553, ξ = 3, \\ n_{0} = 0.01, q_{0} = 4, D_{A_{x}} = 10^{- 5}, δ_{0} = 3.927, a_{z} = 0.1, L_{c_{x}} = 0.5 \cdot L_{x}, L_{c_{z}} = - 2, \end{array}

and

D_{A_{z}} = 0.016

, χ = 5 if Equation (4′) with initial condition (12′) is solved, and

D_{A_{z}} = 0

, ν_z = 1 at solving Equation (4″) with initial condition (12″). For the numerical solution of the problem, we use the two-stage iterative process, which is written on the base of the conservative finite-difference scheme, and it is discussed in detail in Reference 41.

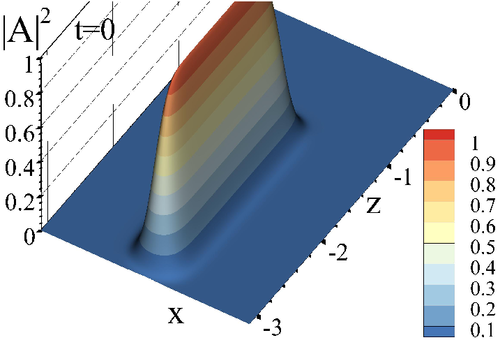
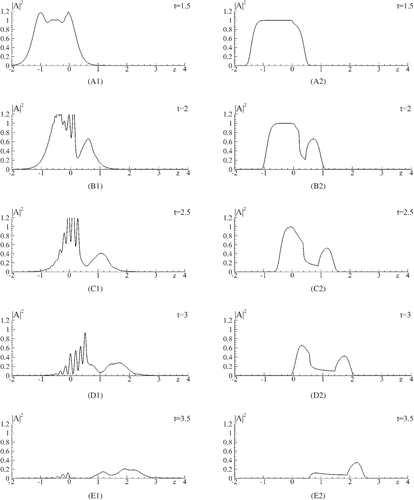
In Figure 2, the incident laser pulse distribution is depicted. Figure 3 demonstrates a formation and evolution of the free electron high concentration domain at the laser pulse interaction with a semiconductor, while the laser pulse profile is depicted in Figure 4. The high absorption domain appears with a certain delay with respect to the pulse front propagation. As a result, a part of the pulse firstly penetrates a semiconductor, and then a reflection of another part of the beam occurs from the domain boundary. We see that at a moment t = 1.5 (Figure 3(A1),(A2)) the laser pulse penetrates a semiconductor, and the free-electron high concentration domain starts to grow. At the time moment t = 2 (Figure 3(B1),(B2), Figure 4(B1)) this domain appears near the semiconductor face, and the traveling part of the optical beam reflects from the domain boundary. The reflected part of the beam propagates in the opposite direction to the incident laser pulse propagation direction. This leads to the interference between these beams and causes the intensity oscillation.

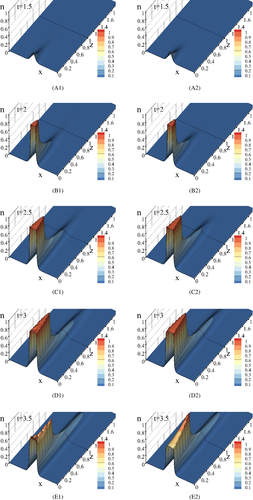
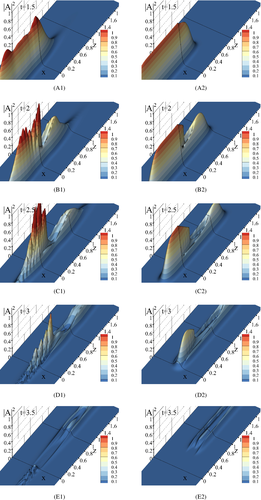
We can see the fundamental differences between the intensity distribution computed at taking into account or not the longitudinal diffraction for the description of the laser pulse propagation: if the longitudinal diffraction is under consideration, then the optical radiation reflected from the boundary of the contrast structure results in both the intensity oscillation (Figure 4(B1)–(D1)) and re-shaping of the free-electron high concentration domain (Figure 3(C1)–(D1)). If the computation of the laser pulse interaction with a semiconductor is provided without considering longitudinal diffraction, then there is not this optical radiation reflection and the domain profile differs from the previous case (Figure 3(B2)–(D2) and Figure 4(B2)–(D2)). In Figure 3(E1),(E2) and Figure 4(E1),(E2), a final stage of the process is depicted.

One more manifestation of the influence of the longitudinal diffraction on the laser pulse interaction with a semiconductor is demonstrated in Figure 5. We see a very pronounced difference between the profiles of the beams propagating with or without taking into account the longitudinal diffraction. The appearance of the reflected beam is the most interesting for us in the current paper. This part of the beam propagates in the direction opposite to the incident beam propagation direction. After three dimensionless units on time, the reflected beam passes distance, which is greater than one dimensionless spatial unit. As a rule, a computation is provided during about one thousand dimensionless units on time, we need to increase a domain size on z-coordinate by a few hundred times for a solution only a linear Schrödinger equation. This leads to enhancing many times a computation cost. That is why it is necessary to develop the ABCs for the problem under consideration. Let us stress that this problem is a typical one for nonlinear optics. Therefore, in the next paragraphs we discuss developing the adaptive ABCs for the 1D Schrödinger equation.

3 DEVELOPING ABC FOR 1D SCHRÖDINGER EQUATION

3.1 Statement of 1D problem and finite-difference scheme construction

The artificial boundaries in the spatial domain allow us to decrease the computational time. However, it could lead to the appearance of the spurious waves, reflected from the artificial boundary (red point-dash line in Figure 1), which can crucially change the computer simulation results. We believe that the adaptive ABCs can minimize the reflection wave and to avoid its influence on the problem solution.

At first, we propose below and discuss one of the types of such a non-adaptive ABCs. For illustrative clarity, we consider the 1D case (A = A(z, t)) of the laser pulse propagation in a linear medium, which is governed by the 1D linear Schrödinger equation:

ϵ \frac{\partial A}{\partial t} + ν_{z} \frac{\partial A}{\partial z} + {iD}_{A_{z}} \frac{\partial^{2} A}{\partial z^{2}} = 0, L_{z_{l}} < z < L_{z_{r}}, 0 < t \leq L_{t}

()

with uniform ABCs:

{(ϵ \frac{\partial A}{\partial t} - ν_{z_{l}} \frac{\partial A}{\partial z})|}_{z = L_{z_{l}}} = 0, {(ϵ \frac{\partial A}{\partial t} + ν_{z_{r}} \frac{\partial A}{\partial z})|}_{z = L_{z_{r}}} = 0

()

and the corresponding initial condition:

A (z, t = 0) = e^{- {(\frac{z - L_{c_{z}}}{a_{z}})}^{2}} .

()

Alternatively, we can use another form of the problem description:

ϵ \frac{\partial A}{\partial t} + {iD}_{A_{z}} \frac{\partial^{2} A}{\partial z^{2}} = 0, L_{z_{l}} < z < L_{z_{r}}, 0 < t \leq L_{t},

()

{(ϵ \frac{\partial A}{\partial t} - 2 D_{A_{z}} k_{z_{l}} \frac{\partial A}{\partial z} + {iD}_{z} k_{z_{l}}^{2} A)|}_{z = L_{z_{l}}} = 0, {(ϵ \frac{\partial A}{\partial t} + 2 D_{A_{z}} k_{z_{r}} \frac{\partial A}{\partial z} + {iD}_{z} k_{z_{r}}^{2} A)|}_{z = L_{z_{r}}} = 0,

()

{A |}_{t = 0} = e^{- {(\frac{z - L_{c_{z}}}{a_{z}})}^{2} - 2 i π χ (z - L_{c_{z}})} .

()

Above $ν_{z_{l}}$ , $ν_{z_{r}}$ and $k_{z_{l}}$ , $k_{z_{r}}$ are the local group velocities and local wavenumbers, respectively, near the corresponding boundaries. Their values are chosen as constant at using non-adaptive ABCs, and they should be computed at using adaptive (time-dependent) ABCs.⁴⁰ The sign of the group velocity ν_z in (15′) defines the beam propagation direction: it is moving in left direction if ν_z < 0, and in right direction if ν_z > 0. The question is what values of the local wavenumbers (local group velocities) are should be chosen to achieve the most effectiveness of the ABCs.

For solving the problem (15′-17′) or (15″-17″) numerically we construct the finite-difference schemes. For this purpose, in the domain

Γ = {L_{z_{l}} \leq z \leq L_{z_{r}}} \times {0 \leq t \leq L_{t}}

we introduce a uniform difference grid Ω = ω_z × ω_t,

ω_{z} = \{z_{j} = {jh}_{z}, j = \overline{0, P_{z}}, h_{z} = \frac{L_{z}}{P_{z}}\}, ω_{t} = \{t_{m} = m τ, m = \overline{0, P_{t}}, τ = \frac{L_{t}}{P_{t}}\} .

Using the following notations:

A = A_{j}^{m} = A (z_{j}, τ_{m}), \hat{A} = A_{j}^{m + 1} = A (z_{j}, τ_{m + 1}), A_{z} = \frac{A_{j + 1}^{m} - A_{j}^{m}}{h_{z}}, A_{\overline{z}} = \frac{A_{j}^{m} - A_{j - 1}^{m}}{h_{z}}, A_{\dot{z}} = \frac{A_{j + 1}^{m} - A_{j - 1}^{m}}{2 h_{z}}, A_{\overline{z} z} = \frac{A_{j + 1}^{m} - 2 A_{j}^{m} + A_{j - 1}^{m}}{h_{z}^{2}},

{\hat{A}}_{z} = \frac{{\hat{A}}_{j + 1}^{m} - {\hat{A}}_{j}^{m}}{h_{z}}, {\hat{A}}_{\overline{z}} = \frac{{\hat{A}}_{j}^{m} - {\hat{A}}_{j - 1}^{m}}{h_{z}}, A_{\overline{z} z} = \frac{{\hat{A}}_{j + 1}^{m} - 2 {\hat{A}}_{j}^{m} + {\hat{A}}_{j - 1}^{m}}{h_{z}^{2}},

\overset{0.5}{A_{\overline{z} z}} = 0.5 ({\hat{A}}_{\overline{z} z} + A_{\overline{z} z}), {\overset{0.5}{A}}_{z} = 0.5 ({\hat{A}}_{z} + A_{z}), {\overset{0.5}{A}}_{\overline{z}} = 0.5 ({\hat{A}}_{\overline{z}} + A_{\overline{z}}), {\overset{0.5}{A}}_{\dot{z}} = 0.5 ({\hat{A}}_{\dot{z}} + A_{\dot{z}}),

we write the Crank-Nicolson finite-difference scheme for the problem (15′-17′):

ϵ \frac{\hat{A} - A}{τ} + ν_{z} {\overset{0.5}{A}}_{\dot{z}} + {iD}_{z} {\overset{0.5}{A}}_{\overline{z} z} = 0, j = 1, {\overline{P}}_{z} - 1, m = 0, {\overline{P}}_{t} .

()

The following equations are written in the boundary nodes of the mesh ω_z

\begin{array}{l} ϵ \frac{{\hat{A}}_{0} - A_{0}}{τ} - ν_{z_{l}} {\overset{0.5}{A}}_{z, 0} = 0, \\ ϵ \frac{{\hat{A}}_{P_{z}} - A_{P_{z}}}{τ} + ν_{z_{r}} {\overset{0.5}{A}}_{\overline{z}, P_{z}} = 0, \end{array}

()

and initial condition is stated as:

A (z_{j}, 0) = e^{- {(\frac{z_{j} - L_{c_{z}}}{a_{z}})}^{2}}, j = \overline{0, P_{z}} .

()

The problem (15″-17″) is approximated by the following finite-difference scheme:

ϵ \frac{\hat{A} - A}{τ} + {iD}_{z} {\overset{0.5}{A}}_{\overline{z} z} = 0, j = 1, {\overline{P}}_{z} - 1, m = 0, {\overline{P}}_{t}

()

\begin{array}{l} ϵ \frac{{\hat{A}}_{0} - A_{0}}{τ} - 2 D_{A_{z}} k_{z_{l}} {\overset{0.5}{A}}_{z, 0} + {iD}_{z} k_{z_{l}}^{2} A = 0, \\ ϵ \frac{{\hat{A}}_{P_{z}} - A_{P_{z}}}{τ} + 2 D_{A_{z}} k_{z_{r}} {\overset{0.5}{A}}_{\overline{z}, P_{z}} + {iD}_{z} k_{zr}^{2} A = 0, \end{array}

()

A (z_{j}, 0) = e^{- {(\frac{z_{j} - L_{c_{z}}}{a_{z}})}^{2} - 2 i π χ (z_{j} - L_{c_{z}})}, j = \overline{0, P_{z}} .

()

The Thomas algorithm is used for solving the stated above initial-boundary difference problems.

3.2 Computer simulation results at using non-adaptive ABCs

We provide series of computations to demonstrate the inefficiency of the non-adaptive ABCs application under certain conditions. Below we present the computer simulation results obtained for parameters:

ν_{z} = - 1, ν_{zl} = ν_{zr} = 1, a_{z} = 0.5, L_{c_{z}} = 5, ϵ = 1,

and mesh steps h_z = 0.001, τ = 0.001 for the spatial domain $[L_{z_{l}} = 0, L_{z_{r}} = 10]$ at the solution of the problem (15′-17′). The incident laser pulse is located symmetrically with respect to the center of the spatial domain at the initial time moment. For definiteness, we should stress that the computations are provided using C++ realization of the finite-difference scheme (18′-20′) or (18″-20″) on multi-processors work-station Dell Precision T7910 2 x.

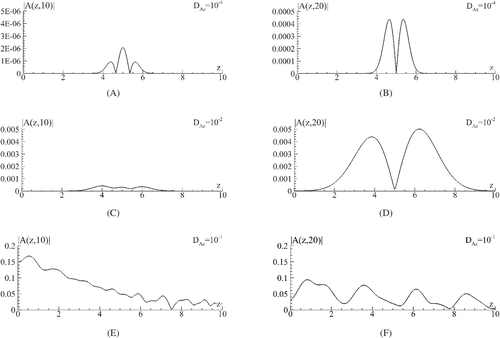
According to the set parameters, the beam propagates in the negative direction along z-axis. When the beam reaches the left artificial boundary, its certain part reflected, and it propagates in the positive direction of z-axis (Figure 6(A), (C), (E)). After reaching by this reflected (spurious) wave the right artificial boundary, then it also reflects. However, the reflected part of the beam may have a rather small amplitude compared with the maximal incident intensity (Figure 6(B),(D),(F)) if the diffraction of the beam is small enough (Figure 6(A),(B)), and these results are in agreement with the computational accuracy. The situation changes if the diffraction coefficient increases (Figure 6(C),(D)). In this case, the beam spreads due to diffraction action, and the beam local group velocity near the boundary differs from the wave packet velocity. As a result, a substantial part of the beam is reflected (Figure 6(E),(F)). Thus, the amplitude of the reflected wave depends strongly on the diffraction coefficient, and the non-adaptive ABCs are not effective enough under large diffraction.

To estimate the efficiency of the developed non-adaptive ABCs, one can compare the computer simulation results obtained using this method with the solution obtained for the extended spatial domain

[L_{z_{l}} = - 50, L_{z_{r}} = 50]

. In this case, the domain boundaries influence is absence, and we name this solution as reference one. Below in figures we use the following notations: A_ABC = A_ABC(z = 0,t) is an amplitude of the reflected wave computed using ABCs, and A_REF = A_REF(z = 0,t) is an amplitude of the reference wave computed on the extended domain. Functions:

E_{ABC} = \int_{0}^{L_{z_{r}}} {| A_{ABC} |}^{2} dz, E_{REF} = \int_{0}^{L_{z_{r}}} {| A_{REF} |}^{2} dz

are the energy of the reflected part of the beam computed using ABCs and the energy of the beam propagating in the extended domain, respectively. We also follow the energies difference ΔE = E_ABC − E_REF. Another introduced characteristic is a modulus of the relative difference between the modulus of the laser beam amplitudes A_ABC and A_REF in the section z = 0:

Δ A = \frac{| | A_{ABC} | - | A_{REF} | |}{| A_{REF} |},

and if the condition |A_REF| > 10⁻⁶ is valid, we avoid a division by zero. In Figure 7 both these time-dependent characteristics are depicted: the difference ΔA is shown in the left plane, and the dynamics of ΔE are depicted in the right plane. As seen in Figure 7, the increasing of the diffraction coefficient leads to the growth of the difference between the reference solution and the solution obtained using the ABCs. The energies difference is positive or negative, depending on a moment of time. The positive difference means that the energy of the beam computed using the ABCs is greater than the reference beam's energy. In turn, it means that the real group velocity of the reference pulse is greater than those values for the beam computed using the ABCs. For negative difference there is an opposite relation between the group velocities for both cases of computation. This statement is valid if we consider a time interval corresponding to those during which the beam passes through the artificial boundary.

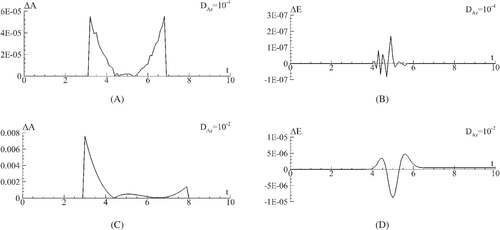
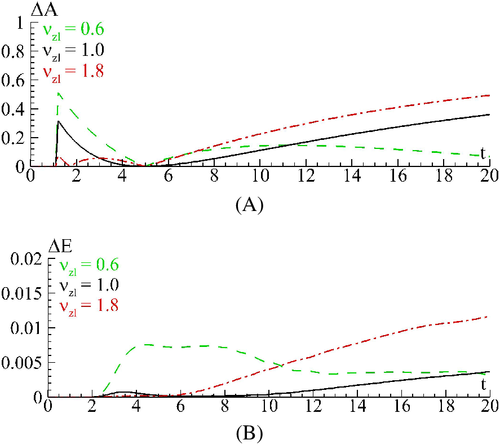
Another illustration of the necessity of using adaptive ABCs at large diffraction of the beam is presented in Figure 8 by comparison of computational results obtained at the different (constant) local group velocities. We see that at the local group velocity $ν_{z_{l}} = 0.6$ (the green dashed line) the high efficiency of left ABC is observed in the vicinity of time point t = 5, but then its efficiency becomes worse (deviation from the reference solution increases). The same trend is observed for other values of the local group velocity (black solid and red dashed-point lines).

It should be mentioned that for the beam small diffraction, the ABCs with a constant value of the local group velocity may be applicable. This confirms by the computer experiments and follows from the obtained analytical expressions for the linear Schrödinger equation (we will discuss this below). Thus, based on the presented results, we can conclude that it is necessary to use the adaptive ABCs for decreasing the amplitude of the beam reflected from the artificial boundary. In this case, the local group velocities (local wavenumbers) must depend on both time and spatial coordinates.

3.3 Developing of the adaptive ABCs and computer simulation results

We illustrate the advantages of the adaptive ABCs by solving the problem (15″-17″). As it is well-known, the local wavenumber of the beam is defined as:

k_{z} = \frac{\partial S}{\partial z},

()

where S is a beam phase and it relates with the complex amplitude by the well-known expression:

A = A_{0} e^{iS},

()

where A₀ and S are the real functions. Therefore, we can write the equality:

A^{*} \frac{\partial A}{\partial z} = {iA}_{0}^{2} \frac{\partial S}{\partial z} + A_{0} \frac{\partial A_{0}}{\partial z} .

()

Basing on this formula, we propose to compute the local wavenumber numerically as a ratio of integrals taken in the vicinity of the artificial boundary⁴⁰ (for brevity, we write a formula only for the right artificial boundary):

k_{z_{num}} = \frac{Im \int_{z_{0}}^{z_{1}} (A^{*} (z, t) \frac{\partial A (z, t)}{\partial z}) dz}{\int_{z_{0}}^{z_{1}} {| A (z, t) |}^{2} dz},

()

where z₀, z₁ are coordinates, which are close to the right artificial boundary. They are used to avoid the influence of the reflected beam on the local wavenumber of the beam, which is falling on the artificial boundary. To illustrate the correctness of such an approach for the computation of the local wavenumber, we compare the wavenumber computed using (24) with its value obtained from the well-known analytical solution of the initial-boundary problem (15″-17″) for incident Gaussian beam:

A = \frac{1}{\sqrt{f}} \exp \{- {(\frac{z - L_{c_{z}} - t}{f})}^{2} + i ψ (t, z) + iφ (t)\},

ψ (t, z) = - \frac{{(z - L_{c_{z}} - t)}^{2}}{4 D_{A_{z}}} \frac{1}{f} (\frac{df}{dt}) - \frac{2 (z - L_{c_{z}} - t)}{4 D_{A_{z}}} \frac{1}{f} (t \frac{df}{dt} + \frac{1}{f}),

φ (t) = - \frac{2 t}{4 D_{A_{z}} f} (t \frac{df}{dt} + \frac{1}{f}) + \frac{1}{2} arctg (4 D_{A_{z}} t), f^{2} = 1 + {(4 D_{A_{z}} t)}^{2} .

Using it, we can write the expression for the local wavenumber (for brevity, we presented only formula for right local wavenumber):

k_{{an}_{r}} = \frac{\partial S}{\partial z} = \frac{8 D_{A_{z}} t (z - L_{c_{z}} - t)}{1 + {(4 D_{A_{z}} t)}^{2}} + \frac{1}{2 D_{A_{z}}} .

()

In our notation the local group velocity is defined from the equality: $ν_{{an}_{r}} = 2 D_{A_{z}} k_{{an}_{r}}$ .

Let us mention that from formula (25) it is also seen that if $D_{A_{z}}$ is rather small, then a time coordinate does not influence the local wavenumber during computation in a long time interval, and ABCs with constant local wavenumbers (or local group velocity) provide the high computation accuracy. If $D_{A_{z}}$ has a big value, the local wavenumber varies essentially in time, and non-adaptive ABCs' efficiency decreases.

For numerical computation of the adaptive local wavenumber

k_{z_{num}}

, we use formula (24) and a representation of the complex amplitude in the form

A_{j} = A_{j}^{R} + {iA}_{j}^{I}

. The expression (24) is approximated by difference formula:

k_{z_{num}} = \frac{\sum_{j = P - s}^{P} (A_{j}^{R} A_{j - 1}^{I} - A_{j}^{I} A_{j - 1}^{R})}{\sum_{j = P - s}^{P} {| A_{j} |}^{2} h_{z}},

()

where P is a node number of the mesh ω_z and is situated near the right boundary. Parameter s designates a number of the mesh nodes used for integral computation. In our numerical simulation we compute (26) using three mesh nodes (s = 3). The mesh node P is chosen according to the requirement:

| A_{P} | > ρ, ρ = const > 0,

()

where ρ is a minimal admissible value of the complex amplitude modulus, which is used for computation of the local wavenumber, and it is defined by the approximation order of the finite-difference scheme. Thus, we prevent division by zero or too small value in the denominator of the expression (26). The value of P is equal to P_z or less than it. In the last case we chose P as a maximal number of the mesh node satisfying the condition (27).

In Figures 9 and 10, the computer simulation results are presented at solving of the numerical problem (18″-20″) with the following parameters χ = 1, $D_{A_{z}} = 0.0795775$ , a_z = 1, L_z = 10, $L_{c_{z}} = 5,$ L_t = 10, h_z = 10⁻³, τ = 10⁻³. First of all, in Figure 9(A),(B) we depict and compare time-dependent $k_{z_{r}}$ computed using formula (26) for $k_{z_{num}}$ with P = P_z and analytical formula (25) for $k_{{an}_{r}}$ . It is clearly seen that both values of the local wavenumbers are in good agreement except a certain time interval, where $k_{z_{r}}$ values differ essentially regardless of whether we use ρ = 10⁻⁶ or ρ = 10⁻⁴. This computational inaccuracy appears because of the influence of the reflected beam on computation of the local wavenumbers. To decrease this impact, we propose to compute the integrals, involving in (24), not exact in the boundary node but at a certain distance from it, for example, in the point P ≤ P_z − 100. For P definition we use the criterion (27), but its maximal value is bounded by P_z − 100. The obtained results are shown in Figure 9(C),(D), and we see clearly, that they have an excellent correlation.

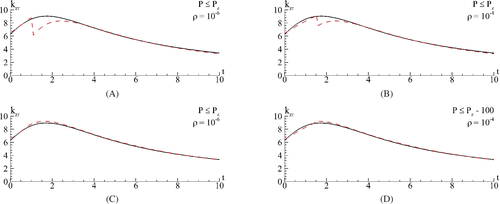
Thus, it could be inferred that the using integral ratio (24) for computation of the local wavenumber leads to the high accurate approximation of the real local wavenumber.

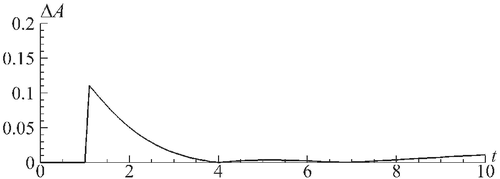
Furthermore, to estimate the correctness and accuracy of the proposed method for the adaptive ABCs computation, we also compare the reference solution with the solution computed at using the adaptive ABCs. As shown in Figure 10, the relative difference between the amplitude of the reflected part of the beam, which appears at using adaptive ABCs, and the reference solution's amplitude is about two times smaller than the best result obtained with non-adaptive ABCs (Figure 8(A)). Moreover, in this case ΔA does not grow in time as it is occurring at using non-adaptive ABCs.

3.4 Remark concerning the computational accuracy for different problem statements

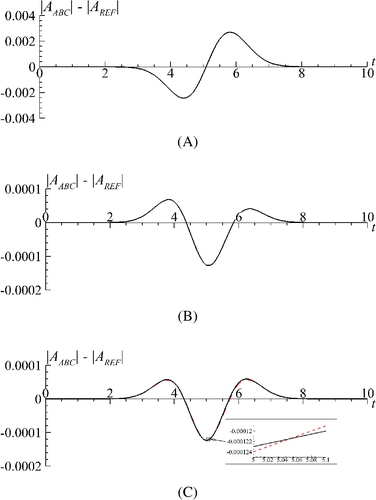
The statements of the 1D problem (15′-17′) and (15″-17″) are equivalent from a mathematical point of view. On the contrary, there are some peculiarities at the numerical solution of the problem. Analyzing Figure 11, we can see that at computing problem (15″-17″) the step of spatial mesh has a significant effect on obtained results: a difference between the amplitude of the reflected part of the laser pulse and amplitude of the reference solution computed on an extended domain decreases on order with decreasing h_z from 10⁻³ to 10⁻⁴ (Figure 11(A),(B)). As it follows from Figure 11(C) at computing problem (15′-17′) obtained results do not depend critically on h_z. It should be stressed that at solving the problem in the statement (15″-17″) with h_z = 10⁻³ we obtained results with the same accuracy order as at solving (15′-17′) with h_z = 10⁻⁴. This is an important feature of the problem under consideration and should be taken into account, especially at solving multidimensional problems.

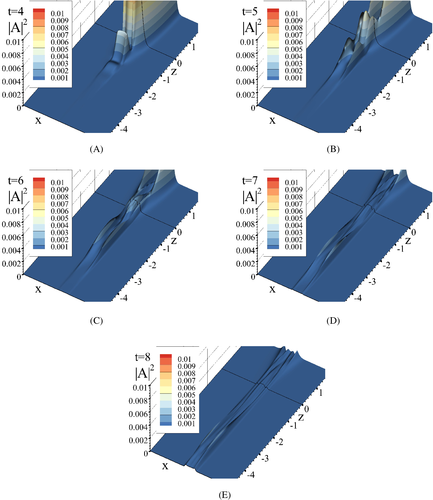
3.5 Computer simulation results for 2D problem at using adaptive ABCs

Now we consider the 2D problem (1)–(3), (4′) with corresponding boundary and initial conditions and apply the developed adaptive ABCs:

k {(x, t)}_{z_{num}} = \frac{Im \int_{z_{0}}^{z_{1}} (A^{*} (x, z, t) \frac{\partial A (x, z, t)}{\partial z}) dz}{\int_{z_{0}}^{z_{1}} {| A (x, z, t) |}^{2} dz},

()

at its numerical solution. Let us discuss the process of the pulse intensity evolution shown in Figure 12. According to the scheme depicted in Figure 1, the laser pulse propagates in the positive direction along z-coordinate. Its part is reflected from the laser-induced contrast structure's boundaries and propagates in the negative direction. In Figures 3 and 4 the same process is depicted, but those computations are done on an extremely extended domain

[L_{z_{l}} = - 30, L_{z_{r}} = 30]

. Computation with the adaptive ABCs is provided on the significantly decreased domain

[L_{z_{l}} = - 5, L_{z_{r}} = 20]

with the parameters similar to those in Figure 4. As shown in Figure 12, there is no spurious beam reflected from the left artificial boundary and computational time decreases essentially in comparison with those for the extended domain. Thus, we can state that developed adaptive ABCs are an effective tool for solving nonlinear problems stated in an unbounded domain.

4 CONCLUSIONS

We demonstrated that the longitudinal diffraction of a laser beam plays a fundamental role at the laser pulse propagation in a semiconductor under the occurrence of contrast structures of its characteristics. Its accounting leads to the appearance of the beam reflected from the boundaries of the laser-induced high absorption domain. We proved this statement by comparing the computer simulation results obtained for two mathematical models of the problem under consideration. Let us emphasize that the solving problem refers to the new field of nonlinear optics: nonlinear gradient optics.

The appearance of the beam reflected from the contrast structure boundaries requires the extension of a spatial domain size that is governed by the time interval. It results in a decrease in computational efficiency. Therefore, it is necessary to use ABCs. We demonstrated that ABCs with constant parameters are not effective if the beam undergoes strong diffraction. To overcome these disadvantages of ABCs for the Schrödinger equation, the adaptive those were proposed. Their efficiency is demonstrated both on the solution of the 1D linear Schrödinger equation and the 2D problem of the laser pulse propagation in a semiconductor.

The developed method has wide applications for solution of various laser physics problems which are governed by a set of equations containing Schrödinger one.

ACKNOWLEDGMENT

Maria Loginova and Vladimir Egorenkov are thankful for the financial support to the Russian Science Foundation (Grant No. 19-11-00113).

Biographies

Vyacheslav Trofimov is a Professor at the South China University of Technology, Guangzhou, China. He received his PhD in Physics and Mathematics (with specialization in laser physics) in 1983 and Dr. Sc. in Physics and Mathematics (with specialization in Applied Mathematics) in 1995 from Lomonosov Moscow State University. Prof. Trofimov's research areas are mathematical models in physics, numerical methods, conservative finite-difference schemes, nonlinear optics and photonics, optical switching, terahertz spectroscopy and 3D printing. He has published over 600 research articles, most of them in high-rank international journals. Prof. Trofimov participated in more than 250 Russian and international conferences and was a member of scientific committees of 20 international conferences.
Maria Loginova received PhD in Physics and Mathematics (with specialization in mathematical modeling) in 2005 from Lomonosov Moscow State University. She is currently a scientific researcher in the faculty of Computational Mathematics and Cybernetics at Lomonosov Moscow State University. Her research interests are mathematical modeling of semiconductor plasma generation, optical bistability, and numerical methods for solving nonlinear PDEs. Dr. Loginova has more than 60 scientific publications including articles in high-rank international journals. She regularly participates in international conferences as a speaker.
Vladimir Egorenkov received a mathematics specialist degree from Lomonosov Moscow State University in 2014. He is currently working towards his PhD degree in Physics and Mathematics and is a predoctoral researcher in the faculty of Computational Mathematics and Cybernetics at Lomonosov Moscow State University. His research interest is the development of conservative finite-difference schemes for computer modeling of laser pulse interaction with the nonlinear medium. He has more the 30 scientific publications, among them 13 journal articles.

REFERENCES

1Gibbs HM. Optical Bistability: Controlling Light with Light. New York, NY: Academic Press; 1985.
Google Scholar
2Rosanov NN. Optical Bistability and Hysteresis in Distributed Nonlinear Systems. Moscow, Russia: Nauka; 1997.
Google Scholar
3 H Haug, ed. Optical Nonlinearities and Instabilities in Semiconductors. San Diego, CA: Academic Press; 2012.
Google Scholar
4Schmidt HE, Haug H, Koch SW. Theoretical explanation of the absorptive optical bistability in semiconductors due to band-gap shrinkage. Appl Phys Lett. 1984; 44(8): 787-789.
10.1063/1.94886
CAS Web of Science® Google Scholar
5Hurtado A, Nami M, Henning ID, Adams MG, Lester LF. Bistability patterns and nonlinear switching with very high contrast ratio in a 1550 nm quantum dash semiconductor laser. Appl Phys Lett. 2012; 101(16): 161117.
10.1063/1.4761473
Web of Science® Google Scholar
6Trofimov VA, Loginova MM, Egorenkov VA. Switching waves dynamics in optical bistable cavity-free system at femtosecond laser pulse propagation in semiconductor under light diffraction. Proc SPIE. 2018; 10522: 105221M.
Google Scholar
7Trofimov VA, Loginova MM, Egorenkov VA. Fast and slow light observation at laser pulse interaction with contrast structures induced in semiconductor due to its nonlinear absorption and optical beam diffraction. Proc SPIE. 2018; 10755: 107550A. https://doi.org/10.1117/12.2322534.
Google Scholar
8Dubach E. Artificial boundary conditions for diffusion equations: numerical study. J Comput Appl Math. 1996; 70(1): 127-144. https://doi.org/10.1016/0377-0427(95)00140-9.
10.1016/0377-0427(95)00140-9
Web of Science® Google Scholar
9Sanz-Serna JM, Verwer JG. Conservative and non-conservative schemes for the solution of the nonlinear Schrödinger equation. IMA J Numer Anal. 1986; 6(1): 25-42.
10.1093/imanum/6.1.25
Web of Science® Google Scholar
10Halpern L. Artificial boundary-conditions for the linear advection diffusion equation. Math Comput. 1986; 46(174): 425-438. https://doi.org/10.2307/2007985.
10.1090/S0025-5718-1986-0829617-8
Web of Science® Google Scholar
11Du Q, Wu XN. Numerical solution of the three-dimensional Ginzburg-Landau models using artificial boundary. SIAM J Numer Anal. 1999; 36(5): 1482-1506. https://doi.org/10.1137/s0036142997330317.
10.1137/S0036142997330317
Web of Science® Google Scholar
12Gustafsson B, Kreiss HO. Boundary-conditions for time-dependent problems with an artificial boundary. J Comput Phys. 1979; 30(3): 333-351. https://doi.org/10.1016/0021-9991(79)90119-0.
10.1016/0021-9991(79)90119-0
Web of Science® Google Scholar
13Lill G. Exact and approximate boundary conditions at artificial boundaries. Math Methods Appl Sci. 1993; 16(10): 691-705. https://doi.org/10.1002/mma.1670161003.
10.1002/mma.1670161003
Web of Science® Google Scholar
14Antoine X, Arnold A, Besse C, Ehrhardt M, Schadle A. A review of transparent and artificial boundary conditions techniques for linear and nonlinear Schrodinger equations. Commun Comput Phys. 2008; 4(4): 729-796.
Web of Science® Google Scholar
15Antoine X, Besse C, Mouysset V. Numerical schemes for the simulation of the two–dimensional Schrödinger equation using non–reflecting boundary conditions. Math Comput. 2004; 73(248): 1779-1799.
10.1090/S0025-5718-04-01631-X
Web of Science® Google Scholar
16Ciegis R, Laukaityte I, Radziunas M. Numerical algorithms for Schrodinger equation with artificial boundary conditions. Numer Funct Anal Optim. 2009; 30(9-10): 903-923. https://doi.org/10.1080/01630560903393097.
10.1080/01630560903393097
Web of Science® Google Scholar
17Ehrhardt M, Zheng CX. Exact artificial boundary conditions for problems with periodic structures. J Comput Phys. 2008; 227(14): 6877-6894. https://doi.org/10.1016/j.jcp.2008.03.042.
10.1016/j.jcp.2008.03.042
CAS Web of Science® Google Scholar
18Gao GH, Sun ZZ, Zhang YN. A finite difference scheme for fractional sub-diffusion equations on an unbounded domain using artificial boundary conditions. J Comput Phys. 2012; 231(7): 2865-2879. https://doi.org/10.1016/j.jcp.2011.12.028.
10.1016/j.jcp.2011.12.028
Web of Science® Google Scholar
19Hsiao GC, Weinacht RJ. Transparent boundary conditions for the wave equation-a Kirchhoff point of view. Math Methods Appl Sci. 2013; 36(15): 2011-2017. https://doi.org/10.1002/mma.1524.
10.1002/mma.1524
Web of Science® Google Scholar
20Givoli D. Non-reflecting boundary conditions. J Comput Phys. 1991; 94(1): 1-29.
10.1016/0021-9991(91)90135-8
Web of Science® Google Scholar
21Liu TY, Xu QJ. Discrete artificial boundary conditions for transient scalar wave propagation in a 2D unbounded layered media. Comput Methods Appl Mech Eng. 2002; 191(27-28): 3055-3071. https://doi.org/10.1016/s0045-7825(02)00237-2.
10.1016/S0045-7825(02)00237-2
Web of Science® Google Scholar
22Mauser NJ, Zhang Y. Exact artificial boundary condition for the poisson equation in the simulation of the 2D Schrodinger-Poisson system. Commun Comput Phys. 2014; 16(3): 764-780. https://doi.org/10.4208/cicp.110813.140314a.
10.4208/cicp.110813.140314a
Web of Science® Google Scholar
23Ryaben'kii VS, Tsynkov SV, Turchaninov VI. Global discrete artificial boundary conditions for time-dependent wave propagation. J Comput Phys. 2001; 174(2): 712-758. https://doi.org/10.1006/jcph.2001.6936.
10.1006/jcph.2001.6936
Web of Science® Google Scholar
24Song EX, Luo S. A local artificial boundary for transient seepage problems with unsteady boundary conditions in unbounded domains. Int J Numer Anal Methods Geomech. 2017; 41(8): 1108-1124. https://doi.org/10.1002/nag.2667.
10.1002/nag.2667
CAS Web of Science® Google Scholar
25Trofimov VA, Denisov AD. Adaptive artificial boundary conditions for Schrodinger equation taking into account the first order dispersion of laser pulse and diffraction of laser beam. Paper presented at: Proceedings of the IEEE East-West Design & Test Symposium (EWDsTS 2014)Click here to enter text, Kiev, Ukraine: 2014; IEEE.
Google Scholar
26Wang B, Liang D. The finite difference scheme for nonlinear Schrodinger equations on unbounded domain by artificial boundary conditions. Appl Numer Math. 2018; 128: 183-204. https://doi.org/10.1016/j.apnum.2018.02.005.
10.1016/j.apnum.2018.02.005
Web of Science® Google Scholar
27Zhao M, Du XL, Liu JB, Liu H. Explicit finite element artificial boundary scheme for transient scalar waves in two-dimensional unbounded waveguide. Int J Numer Methods Eng. 2011; 87(11): 1074-1104. https://doi.org/10.1002/nme.3147.
10.1002/nme.3147
Web of Science® Google Scholar
28Alpert B, Greengard L, Hagstram J. Nonreflecting boundary conditions for the time-dependent wave equation. J Comput Phys. 2002; 180(1): 270-296.
10.1006/jcph.2002.7093
CAS Web of Science® Google Scholar
29Han H, Yin D, Huang Z. Numerical solutions of Schrödinger equations in R3. Numer Methods Part Differ Equat. 2007; 23(3): 511-533.
10.1002/num.20193
Web of Science® Google Scholar
30Jiang S, Greengard L. Efficient representation of nonreflecting boundary conditions for the time-dependent Schrödinger equation in two dimensions. Commun Pure Appl Math. 2008; 61(2): 261-288.
10.1002/cpa.20200
Web of Science® Google Scholar
31Schadle A. Non–reflecting boundary conditions for the two-dimensional Schrödinger equation. Wave Motion. 2002; 35(2): 181-188.
10.1016/S0165-2125(01)00098-1
Web of Science® Google Scholar
32Soffer A, Stucchio C. Open boundaries for the nonlinear Schrödinger equation. J Comput Phys. 2007; 225(2): 1218-1232.
10.1016/j.jcp.2007.01.020
Web of Science® Google Scholar
33Sun Z, Wu X. The stability and convergence of a difference scheme for the Schrödinger equation on an infinite domain by using artificial boundary conditions. J Comput Phys. 2006; 214(1): 209-223.
10.1016/j.jcp.2005.09.011
Web of Science® Google Scholar
34Szeftel J. Absorbing boundary conditions for one-dimensional nonlinear Schrödinger equations. Numer Math. 2006; 104(1): 103-127.
10.1007/s00211-006-0012-7
Web of Science® Google Scholar
35Ji SS, Yang YB, Pang G, Antoine X. Accurate artificial boundary conditions for the semi-discretized linear Schrodinger and heat equations on rectangular domains. Comput Phys Commun. 2018; 222: 84-93. https://doi.org/10.1016/j.cpc.2017.09.019.
10.1016/j.cpc.2017.09.019
CAS Web of Science® Google Scholar
36Luchini P, Tognaccini R. Direction-adaptive nonreflecting boundary conditions. J Comput Phys. 1996; 128(1): 121-133.
10.1006/jcph.1996.0199
Web of Science® Google Scholar
37Trofimov VA, Dogadushkin PV. Boundary conditions for the problem of femtosecond pulse propagation in absorption layered structure. Paper presented at: Proceedings of 4th International Conference on Finite Difference Methods: Theory and Applications, Lozenetz, Bulgaria: 2007; 307-313.
Google Scholar
38Xu Z, Han H, Wu X. Adaptive absorbing boundary conditions for Schrödinger-type equations: application to nonlinear and multi-dimensional problems. J Comput Phys. 2007; 225(2): 1577-1589.
10.1016/j.jcp.2007.02.004
Web of Science® Google Scholar
39Xu Z, Han H. Absorbing boundary conditions for nonlinear Schrödinger equations. Phys Rev E. 2006; 74(3):037704.
10.1103/PhysRevE.74.037704
Web of Science® Google Scholar
40Trofimov VA, Trykin EM. Construction of adaptive artificial boundary conditions using the invariant rations for Schrödinger equation. Paper presented at: Proceedings of the IEEE East-West Design & Test Symposium (EWDTS 2014), Kiev, Ukraine; 2014; IEEE. https://doi.org/10.1109/EWDTS.2014.7027098.
Google Scholar
41 Trofimov VA, Loginova MM, Egorenkov VA. Conservative finite-difference scheme for the 2D problem of femtosecond laser pulse interaction with kink structure of high absorption in semiconductor. Int J Comput Maths. 2020; 97(1-2): 207-244. https://doi.org/10.1080/00207160.2018.1492117.
10.1080/00207160.2018.1492117
Web of Science® Google Scholar

Citing Literature

All articles

Efficiency of using adaptive artificial boundary conditions at computer simulation of contrast spatio-temporal laser-induced structures in a semiconductor

Abstract

1 INTRODUCTION

2 THE 2D PROBLEM OF LASER-INDUCED ELECTRON-IONIZED-DONOR PLASMA GENERATION IN A SEMICONDUCTOR

2.1 Mathematical model of 2D problem

2.2 Computer modeling of the 2D problem

3 DEVELOPING ABC FOR 1D SCHRÖDINGER EQUATION

3.1 Statement of 1D problem and finite-difference scheme construction

3.2 Computer simulation results at using non-adaptive ABCs

3.3 Developing of the adaptive ABCs and computer simulation results

3.4 Remark concerning the computational accuracy for different problem statements

3.5 Computer simulation results for 2D problem at using adaptive ABCs

4 CONCLUSIONS

ACKNOWLEDGMENT

Biographies

REFERENCES

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Efficiency of using adaptive artificial boundary conditions at computer simulation of contrast spatio-temporal laser-induced structures in a semiconductor

Abstract

1 INTRODUCTION

2 THE 2D PROBLEM OF LASER-INDUCED ELECTRON-IONIZED-DONOR PLASMA GENERATION IN A SEMICONDUCTOR

2.1 Mathematical model of 2D problem

2.2 Computer modeling of the 2D problem

3 DEVELOPING ABC FOR 1D SCHRÖDINGER EQUATION

3.1 Statement of 1D problem and finite-difference scheme construction

3.2 Computer simulation results at using non-adaptive ABCs

3.3 Developing of the adaptive ABCs and computer simulation results

3.4 Remark concerning the computational accuracy for different problem statements

3.5 Computer simulation results for 2D problem at using adaptive ABCs

4 CONCLUSIONS

ACKNOWLEDGMENT

Biographies

REFERENCES

Citing Literature

Figures

References

Related

Information