Object classification in analytical chemistry via data-driven discovery of partial differential equations

1 INTRODUCTION

The biological significance of glycans is evident from the numerous studies demonstrating their roles in living systems. These molecules alone, as well as in conjunction with other biomolecules, participate in important biological functions. For example, glycosylation is one of the major post-translational modifications^{1, 2} and is known to mediate a broad range of biological processes such as cell recognition,³ cell signaling,^{3, 4} immune response,⁵ and protein stability.⁶ Furthermore, aberrations in glycosylation patterns are found to be related to various diseases, including cancers.^{3, 7-11}

Glycans display high structural complexity owing to the presence of diverse monosaccharide composition, different linkages, and various branching options.¹² Tandem mass spectrometry (MS) has emerged as an effective technique for glycan structural studies.¹ This technique in conjunction with liquid chromatography (LC) provides a powerful tool for studying molecular structures.^{1, 13-16} Additionally, various derivatization techniques are employed to pursue sensitive and efficient investigation of the glycans. Some of the derivatization reagents include 2-aminobenzamide, procainamide, aminoxyTMT, RapiFluor-MS (RFMS) labeling, and iodomethane permethylation.¹⁷ Our particular method of choice for the current study is permethylation as it delivers several advantages over other derivatization techniques.^13-16 In this technique, methyl groups replace the existing hydrogens, oxygen, and nitrogen atoms in a glycan structure. Permethylated glycans have increased hydrophobicity, which makes them ideal for reverse phase separation. It also prevents fucose (sugar) migration^{18, 19} and sialic acid loss.²⁰ Also, due to increased positive ion efficiency of glycans, ionization efficiency is improved, thereby enhancing the sensitivity.²¹

Despite the availability of sensitive structural investigation techniques, inter-instrument, as well as inter-laboratory variations, in the data acquisition complicates the identification and characterization of glycans. This motivates the need for the development of universally applicable instrument, as well as laboratory, independent classification techniques. The glucose unit index (GUI) is one such method, as it relies only on the relative retention time of sample molecules with respect to the glucose units. Ashwood et al. recently reported the retention time normalization of native glycans based on GUI as well as m/z values.²²

In this study, we develop a method which only utilizes GUI for characterizing permethylated glycans, independent of m/z values of the permethylated glycan structures. Dextrin, which is utilized as a reference frame in this study, consists of a mixture of oligosaccharides of D-glucose units which form linear chains consisting of either $\alpha$-(1 → 4) or $\alpha$-(1 → 6) glycosidic bonds. The retention times of these glucose units are used to calculate the normalized retention times of the reduced and permethylated N-glycans derived from samples. The use of Dextrin as an internal standard allows for the elimination of inter-injection variations and improves the accuracy of the measurements. This approach then allows for the development of a mathematical model employing the LC-MS/MS-based data for efficient identification of permethylated N-glycans.

In particular, we employ a so-called data-driven methodology for constructing an associated partial differential equation (PDE) which allows for a straightforward classification procedure. The use of data-driven PDEs and other data-driven methodologies have recently garnered much attention in the literature due to their ability to efficiently learn in relation to dynamical systems and physical processes (see, for instance, References 23-37 and the references therein). The coupling of such approaches with deep learning methods has allowed for the efficient and accurate handling of situations involving quite large data sets. Herein, we consider a modified approach which avoids standard regression methods in favor of a more mathematically informed process for determining the coefficients necessary for object classification. By modifying an approach employed by Einstein (e.g., Reference 38) we are able to deduce more clearly the form of the undetermined PDE—making our approach closer to a supervised learning method (with some distinct differences). Moreover, we demonstrate that performing a single learning procedure on a particular data set will allow for highly accurate classification of unknown data sets of a particular type. This, of course, motivates a wide array of novel questions related to learning procedures in both mathematics and the physical sciences.

This article is organized as follows. Section 2 provides a heuristic description of the algorithm in order to provide the reader clarity regarding our goal and general methodologies. In Section 3, we use a modification of the original Einstein argument for the classical development of standard Brownian motions (see Reference 38, for example) to derive the primary equation of interest. This section also includes a more generalized procedure for the derivation which reduces the necessary assumptions on the system of interest. Section 4 builds on the material in Section 3, allowing for the construction of a closed-form solution to our theoretical model—thus, bypassing the need for numerical approximations and complicated learning procedures. We then use this model in Section 5 to classify unknown samples via our proposed algorithm. This section also clearly outlines the parameters for the physical experiments carried out to produce the data set for classification. Finally, Section 6 provides some concluding remarks and also alludes to possible future endeavors related to the current work.

2 OUTLINE OF PROPOSED ALGORITHM

We briefly outline the ideas behind the newly proposed algorithm, below. Note that the algorithm will be more completely and rigorously described in Main Algorithm (see Section 5). For clarity, we allude to specific aspects of the experiment of interest, whose specific protocol is outlined in Section 5.2.

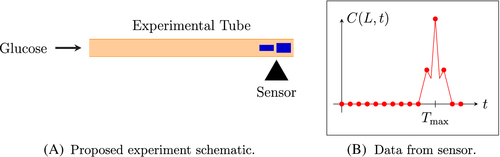
The generic description provided by (i)–(vii) in Proposed Algorithm are meant to provide a rough blueprint of the method we employ, herein. However, there are numerous mathematical details needed before we can rigorously formulate the final algorithm. A schematic depiction of Proposed Algorithm (and Main Algorithm) is provided in Figure 1, below.

As noted in (iv) of Proposed Algorithm, our method is based on the important assumption that for all i, j ∈ N∗, such that i ≠ j, the molecules M_i and M_j are not mixing throughout the experiment. This is formalized in the following assumption.

Assumption 1 is a vital assumption in our proposed method. However, it is worth noting that Assumption 1 may not be valid in all physical experiments of interest. For our particular situation, empirical evidence (obtained from experiments employing the guidelines outlined in Section 5.2) suggests that Assumption 1 does in fact hold. The process of molecular mixing requires further generalizations of Einstein's paradigm for Brownian motion and will be a focus of forthcoming research. More details on this process are provided in Section 3.

3 EINSTEIN'S PARADIGM FOR MOLECULAR TRANSPORT IN A TUBE

In this section we will reformulate Einstein's model for Brownian motion to the case where glucose molecules are being transported in the tube filled with porous material. Einstein derived his seminal mathematical framework based upon his visual observations of the random jumps of pollen grains of the plant Clarkia pulchella suspended in water (see References 38 and 39). He then provided a mathematical framework to describe the observed phenomena, which resulted in his model of classical Brownian motion. A less understood fact is that Einstein's approach can also be applied to many generic processes arising in physics, chemistry, and engineering. This is the key observation employed to derive our novel classification algorithm.

3.2 Derivation of associated equation with drift and absorption

For the development of our PDE model, we employ the notation used in the original work of Einstein.³⁸ Denote by $n\in \mathbb{N}$ the total number of particles of a molecule M, presented in a unit volume, and let $\mathrm{\Delta }\in ℳ(\tau )$ (cf. Assumption 3). Let $dn\in \mathbb{N}$ denote the number of particles located in an arbitrary interval of length $d\mathrm{\Delta }$ experiencing a displacement of magnitude $\mathrm{\Delta }$ in the time interval $\tau$ (cf. Assumption 2). This value can be expressed via the following equation

$$dn=n\phi (\mathrm{\Delta })d\mathrm{\Delta },$$ ()

where $\phi :ℝ\to [0,1]$ is the frequency (or probability density) of free jumps with length $\mathrm{\Delta }.$ Note that in his original work, Einstein assumed that φ was an even function which differs from zero only for very small values of $\mathrm{\Delta }$ (e.g., [38, Page 13]).

Remark 2.It is worth noting that Einstein's assumptions on φ are natural assumptions in the particular case involving Brownian motion. However, it is important to observe that this assumption may not be reasonable for all physical phenomena.

Based on Remark 2, it should be clear that our intentions are to consider a more general case than that of Einstein's original work. Therefore, we must clearly indicate what assumptions we will employ (as an arbitrary probability density will be too general to allow for any meaningful data-driven learning). To this end, we assume that there exists $\sigma \in [0,\infty )$ such that the function φ satisfies

$${\int }_{-\infty }^{\infty }\phi (\mathrm{\Delta })d\mathrm{\Delta }=1,$$ ()

which we refer to as the whole universe axiom,

$${\int }_{-\infty }^{\infty }\mathrm{\Delta }\phi (\mathrm{\Delta })d\mathrm{\Delta }={\mathrm{\Delta }}_e$$ ()

(cf. Remark 1), which we refer to as the expected length of the free jumps, and

$${\int }_{-\infty }^{\infty }{(\mathrm{\Delta }-{\mathrm{\Delta }}_e)}^2\phi (\mathrm{\Delta })d\mathrm{\Delta }={\sigma }^2$$ ()

(cf. Remark 1), which we refer to as the standard variance of the free jump lengths.

Next, let $f:ℝ\times [0,\infty )\to [0,\infty )$ be the function which represent the number of particles per unit volume present at position $x\in ℝ$ at time t ∈ [0, ∞). With this Equations (3)–(5), we may now formulate a crucial axiomatic conservation law.

Axiom 1.There exists a continuous function $F:ℝ\to ℝ$ such that the number of particles found at time $t+\tau$ (cf. Assumption 2) between two planes perpendicular to the x-axis with abscissas x and $x+\delta$ (where $\delta \in ℝ$) is given by

$${\int }_x^{x+\delta }f(y,t+\tau )dy={\int }_x^{x+\delta }{\int }_{-\infty }^{\infty }f(y+\mathrm{\Delta },t)\phi (\mathrm{\Delta })d\mathrm{\Delta }dy+{\int }_x^{x+\delta }{\int }_t^{t+\tau }F(f(y,s))dsdy.$$ ()

The second term in the right-hand-side of Equation (6) is a result of possible bonding and/or absorption with other molecules in the sample or with the porous media within the tube. In general, for Equation (6) to be well-defined, all one needs is that F is finite and measurable on the codomain of the function f. However, throughout this article, we will assume that there exists $\omega \in ℝ$ such that for all $x\in ℝ$, t ∈ [0, ∞) this term is well-approximated by the linear function $\omega ·f(x,t)$. The conservation law given by Equation (6) is depicted schematically in Figure 2, below.

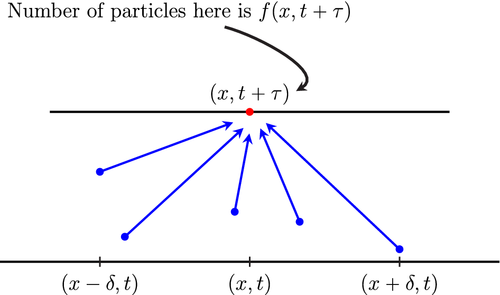
Remark 3.In Equation (7), we assume that φ has compact support. This assumption is physical in nature, as the ensuing theoretical work follows in a similar fashion if φ does not have compact support.

Note that for all $x\in ℝ$ it holds that

$${\int }_{-\infty }^{\infty }f(x+\mathrm{\Delta },t)\phi (\mathrm{\Delta })d\mathrm{\Delta }={\int }_{-\infty }^{\infty }[f(x+\mathrm{\Delta },t)-f(x+{\mathrm{\Delta }}_e,t)+f(x+{\mathrm{\Delta }}_e,t)]\phi (\mathrm{\Delta })d\mathrm{\Delta }$$ ()

(cf. Remark 1). Next, observe that the multi-dimensional Carathéodory Theorem (e.g., Bartle et al. [40, Theorem 6.1.5]) ensures that there exist measurable functions ${\psi }^x,{\psi }^t:ℝ\times [0,\infty )\to ℝ$ such that for all $x\in ℝ$, t ∈ [0, ∞) it holds that

$$f(x,t+\tau )-f(x+{\mathrm{\Delta }}_e,t)=\tau [{\psi }^t(x,t+\tau )]+{\mathrm{\Delta }}_e[{\psi }^x(x+{\mathrm{\Delta }}_e,t)],$$ ()

where for all $x\in ℝ$, t ∈ [0, ∞) it holds that

$${\psi }^t(x,t+\tau )\approx \frac{\partial f(x,t)}{\partial t}\text{and}{\psi }^x(x+{\mathrm{\Delta }}_e,t)\approx \frac{\partial f(x,t)}{\partial x}.$$ ()

Furthermore, applying Taylor's theorem to $f(x+\mathrm{\Delta },t)$, with respect to x, centered at the point $x+{\mathrm{\Delta }}_e$, yields (under appropriate smoothness assumptions) that for all $x\in ℝ$, t ∈ [0, ∞) it holds that

$$\begin{array}{ll}f(x+\mathrm{\Delta },t)& =f(x+{\mathrm{\Delta }}_e,t)+{\displaystyle \sum _{k=1}^{\infty }}\frac{{(\mathrm{\Delta }-{\mathrm{\Delta }}_e)}^k}{k!}\frac{{\partial }^{k}f}{\partial x^k}(x+{\mathrm{\Delta }}_e,t)\\ & =f(x+{\mathrm{\Delta }}_e,t)+(\mathrm{\Delta }-{\mathrm{\Delta }}_e)\frac{\partial f}{\partial x}(x+{\mathrm{\Delta }}_e,t)+\frac{{(\mathrm{\Delta }-{\mathrm{\Delta }}_e)}^2}{2!}\frac{{\partial }^{2}f}{\partial x^2}(x+{\mathrm{\Delta }}_e,t)\\ & +\frac{{(\mathrm{\Delta }-{\mathrm{\Delta }}_e)}^3}{3!}\frac{{\partial }^{3}f}{\partial x^3}(x+{\mathrm{\Delta }}_e,t)+𝒪(|\mathrm{\Delta }-{\mathrm{\Delta }}_e{|}^4).\end{array}$$ ()

Next, we assume that $|\mathrm{\Delta }-{\mathrm{\Delta }}_e|\ll 1$ and that for all $k\in \mathbb{N}$ it holds that

$$f(x+{\mathrm{\Delta }}_e,t)\approx f(x,t)\text{and}\frac{{\partial }^{k}f}{\partial x^k}(x+{\mathrm{\Delta }}_e,t)\approx \frac{{\partial }^{k}f}{\partial x^k}(x,t).$$ ()

Combining this with Equations (3)–(5), (7), and (10) (after disregarding the higher-order terms in Equation (10)—justified by the assumption that $|\mathrm{\Delta }-{\mathrm{\Delta }}_e|\ll 1$), and straightforward calculus demonstrates that for all $x\in ℝ$, t ∈ [0, ∞) it holds that the function f satisfies

$$\tau \frac{\partial f}{\partial t}(x,t)+{\mathrm{\Delta }}_e\frac{\partial f}{\partial x}(x,t)=\frac{{\sigma }^2}{2}\frac{{\partial }^{2}f}{\partial x^2}(x,t)+\tau \omega f(x,t).$$ ()

For convenience, we will rewrite Equation (12) in the form:

$$\frac{\partial f}{\partial t}(x,t)-D\frac{{\partial }^{2}f}{\partial x^2}(x,t)+\gamma \frac{\partial f}{\partial x}(x,t)-\omega f(x,t)=0,$$ ()

where for all $x\in ℝ$, t ∈ [0, ∞), $\tau \in ℳ(\tau )$ (cf. Assumption 2) the diffusion, drift (convection), and absorption terms are given by

$$\frac{{\sigma }^2}{2\tau }=D,\frac{{\mathrm{\Delta }}_e}{\tau }=\gamma ,\text{and}\frac{1}{\tau }{\int }_t^{t+\tau }F(f(x,s))ds\approx \omega f(x,t),$$ ()

respectively. The differential equation given in Equation (13) is the well-known convection-diffusion-absorption equation which arises in the study of numerous physically relevant phenomena. It is worth noting that Equation (13) immediately follows from Einstein's original equation for Brownian motion (e.g., [38, Equation (10)]) if we set ${\mathrm{\Delta }}_e=0$ (no drift) and $\omega =0$ (no absorption).

We conclude this subsection with some final remarks. In the arguments above, we have assumed sufficient smoothness conditions in order to allow for all claims to hold globally (i.e., for all t ∈ [0, ∞)). However, this can easily be circumvented by constructing Equation (13) locally (e.g., for some c ∈ (0, ∞) with t ∈ [0, c)) and then “gluing” the results together. This approach is avoided, herein, for simplicity and ease of exposition. Furthermore, the assumption that $|\mathrm{\Delta }-{\mathrm{\Delta }}_e|\ll 1$ is not an inherently restrictive assumption. This assumption loosely can be thought of as removing the possibility of so-called long-range interactions within the experiment. One can allow for such interactions, but the resulting PDE may involve non-local operators such as the fractional Laplacian (see, for instance, References 41-44 and the references therein). Finally, we note that the assumptions in Equation (11) are purely for convenience, as we can obtain a result similar to Equation (13) through a simple re-scaling of the function f.

Remark 4.For the remainder of our study, we will assume that $\mathrm{\Delta }$ , φ, and $\tau$ (cf. Assumption 2) are independent of the function f. In general, these parameters can upon both the spatial and temporal variables, x and t, respectively, as well as the underlying porous media. Moreover, in more general situations, these parameters can further depend on the dependent variables' derivatives.

Remark 5.Herein, we assume that $\tau$ (cf. Assumption 2) is the same for each of the types of molecules of interest. That is, for each M_i, i ∈ {1, 2, … , n}, we assume that the associated ${\tau }_i=\tau$. One can always find such a $\tau$ by simply choosing the minimum of the set of associated ${\tau }_i$, i ∈ {1, 2, … , n}.

4 CLOSED-FORM SOLUTIONS TO THE EINSTEIN EQUATION IN APPLICATION TO GUI CLASSIFICATION VIA RETRIEVAL TIME

As should be clear from Section 3, we intend to use the Einstein model of random jumps to interpret the results of experimental observations. This approach should present a stark contrast to the traditional approach of employing Fick's law, flux conservation laws, and the thermodynamical law that density is proportional to the mass concentration function (see, for example, the classical work by Reference 45). The arguments in this section motivate the novel approach with the particular case of GUI classification via retrieval time in mind.

4.2 Employing closed-form solutions to the Einstein equation to classify GUI via retrieval time

Recall that we have experimental data from trials employing pure samples of each GUI. Thus, we will use this data to determine explicitly the D_i, i ∈ {1, 2, … , n}, coefficients for all components of the N-glycans and the GUIs. In order to find the extreme values at the point of observation, we differentiate Equation (25) to obtain for each i ∈ {1, 2, … , n}, t ∈ (0, ∞) that

$$\frac{\frac{\partial C_i}{\partial t}(L,t)}{C_i(L,t)}={\omega }_i-\frac{{\gamma }_i^2}{4D_i}+\frac{L^2}{4D_i{t}^2}-\frac{1}{2t}\text{and}\frac{\frac{{\partial }^2{C}_i}{\partial t^2}(L,t)}{C_i(L,t)}=-\frac{L^2}{2D_i{t}^3}+\frac{1}{2t^2}.$$ ()

Combining this with the assumption that ${\mathrm{\Delta }}_e\approx 0$ (no drift—cf. Remark 1) and the assumption that for all i ∈ {1, 2, … , n} it holds that ${\omega }_i=0$ (no absorption) yields that for all i ∈ {1, 2, … , n} it holds that

$$D_i=\frac{1}{2}\left(\frac{L^2}{t_{\max }^i}\right),$$ ()

where for each i ∈ {1, 2, … , n} it holds that $t_{\max }^i\in (0,\infty )$ is the maximal critical point from Equation (26). Combining Equation (27) with experimental data will allow for the determination of the D_i, i ∈ {1, 2, … , n}, by letting the retrieval time for each pure sample correspond to the $t_{\max }^i$, i ∈ {1, 2, … , n}.

Note that Figure 3 presents a graph of the actual spectrometer signals, with associated peaks, which correspond to the molecules of GUI passing through the receiver of the mass spectrometer (obtained via the methods outlined in Section 5.2). As we can see, there are eight distinct GUIs and they each have different retrieval times. Figure 4(A) presents the calculated diffusion coefficients D_i, i ∈ {1, 2, … , n}, for each retention time. Figure 4(A,B) together demonstrate the expected inverse proportional relationship between retention time and diffusivity.

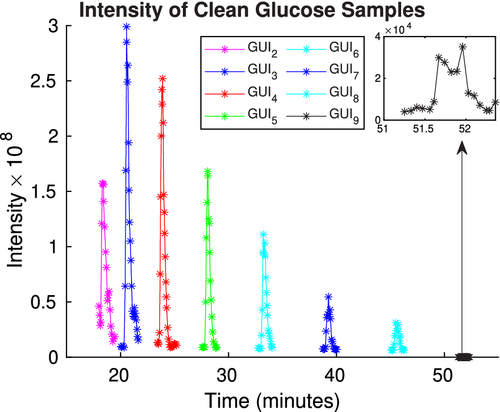
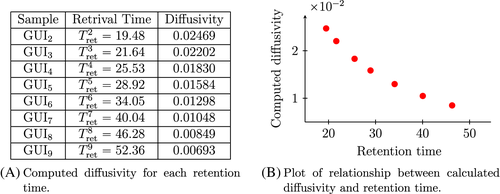
The intuition provided by the Einstein paradigm tells us that the molecule's retrieval time should depend on the molecule's time of free travel and that the value should increase proportionally with the molecules mass. This observation is clearly supported by our data (see Figure 4), as we have the mass of the GUI molecules increases with their index value. Furthermore, our post-processing—which can be performed using our analytical formula for pure samples—confirms this intuitive observation and Einstein's theory that the diffusion coefficients are inversely proportional to $\tau$ (cf. Assumption 2).

Indeed, consider two GUIs, say, GUI₁ and GUI₂. These two GUIs correspond to the molecules M₁ and M₂, respectively. Since these are distinct types of glucose molecules, it is well-known that the molecules will not develop novel chemical bonds throughout the experiment. Therefore, their “free jump” lengths are mutually independent. These “free jumps” of molecule M₁ corresponds to ${\tau }_1$ and the “free jumps” of molecule M₂ corresponds to ${\tau }_2$ (cf. Assumption 2). If we let C₁(x, t) and C₂(x, t) denote the concentrations at position x and time t of the molecules M₁ and M₂, respectively, then both of these functions will satisfy Equation (13) (each with their appropriate associated parameters). This intuition combined with Einstein's paradigm and the assumptions outlined above then implies for all i ∈ {1, 2, … , n} it holds that

$$D_i=\frac{1}{2{\tau }_i}{\int }_{-\infty }^{\infty }{(\mathrm{\Delta }-{\mathrm{\Delta }}_e)}^2\phi (\mathrm{\Delta })d\mathrm{\Delta }\text{and}{\gamma }_i=\frac{1}{{\tau }_i}{\int }_{-\infty }^{\infty }\mathrm{\Delta }\phi (\mathrm{\Delta })d\mathrm{\Delta },$$ ()

where $\phi (\mathrm{\Delta })$ is frequency at which free jumps of the length $\mathrm{\Delta }$ occur. Note that in this formulation we have assumed that the C_i, i ∈ {1, 2, … , n}, are associated to each molecule M_i, i ∈ {1, 2, … , n}, and no novel molecular bonds are formed. Therefore, the ${\mathrm{\Delta }}_i$, i ∈ {1, 2, … , n}, are the lengths of the associated “free jumps” of the entire compound of molecules of type M_i, i ∈ {1, 2, … , n}. We also assumed that the expected length of free jumps were the same for all i ∈ {1, 2, … , n}; that is, we assumed that ${\mathrm{\Delta }}_{i,e}={\mathrm{\Delta }}_e$, i ∈ {1, 2, … , n} (cf. Remark 1). Moreover, the molecules are arranged by their molecular weight as their lengths are proportional to i ∈ {1, 2, … , n}. Clearly, a higher molecular mass is associated to smaller “free jump” lengths. Mathematically, this means for all i, j ∈ {1, 2, … , n} with i < j it holds that ${\tau }_i<{\tau }_j$.

Note that the experimental observations presented in Figure 4 support precisely this claim. Further observe that the velocity of the filtration (drift) is so small that diffusion is the dominant transport property. Indeed, if drift had a larger influence than diffusion, then the decrease of the retrial time with respect to the GUI mass would be linear. Since Figure 4(B) clearly indicates an inversely propositional relationship, we conclude that diffusion is dominant. This is an important observation as drift mainly depends upon the boundary conditions of a problem whereas diffusion depends only on object versus tube structure properties. This crucial observation is what allows for the proposed classification method to work so well. Finally, we mention that in this preliminary result we have also ignored the associated absorption rates. However, classification methods for complex serum samples will consider these effects.

Remark 6.From the Einstein paradigm it follows that the calculated diffusion coefficients are inversely proportional to $\tau$ (the “free jump times”—cf. Equation 2) of each molecule. Equation (27) provides an explicit relationship between retrieval time and the “free jumps” for molecule M_i, i ∈ {1, 2, … , n}: smaller retrieval times correspond to larger $\tau$.

Note that further refinement of the classification criteria may come from information which is hidden in the dynamics of the intensity of the signal prior to the retrieval time. In our future research, we intend to generalize our procedure by further incorporating the area under the graph of the signal, prior to retrieval time, for each molecule. Such considerations result in a need for better understanding the following functional

$$I(t)=\frac{d}{dt}\ln \left({\int }_0^{t}C(L,\tau )d\tau \right)=\frac{C(L,t)}{{\int }_0^{t}C(L,\tau )d\tau }.$$ ()

From this it is clear that if T_ret is the retrieval time, then Equation (29) evaluates to (T_ret)⁻¹, if we employ a (very) rough numerical approximation of the integral which employs one rectangle of height H = T_ret. This of course agrees with Equation (27). In this regard, one can see that Equation (29) is a true generalization of Equation (27).

5 SERUM CLASSIFICATION USING GUIS AS MARKERS

We will use the general ideas of Remark 6 as a basis for the development of our classification algorithm using GUIs as markers. The basic idea of the algorithm (which was outlined in the Proposed Algorithm) consists of determining the diffusivity coefficients of “marker” molecules in a base sample of interest (cf. Equation 13). The remaining molecules are classified by grouping them based on diffusivity coefficient ranges and computing the associated absorption coefficients, which serve as a correction term of sorts (cf. Equation 13). We assume throughout that drift coefficients are negligible (cf. Equation 13). This assumption is justified due to the intended use of post-processing in the actual physical experiment.

5.3 Data classification of an actual experiment using the proposed algorithm

We now demonstrate Main Algorithm and its efficacy through an experimental example. We will use data obtained via the methods and procedures outlined in Section 5.2. To obtain the data in Figures 5-7 below we implemented our algorithm for a particular set of experiments (obtained via the methods outlined in Section 5.2). In the first table (left table) in Figure 5, the GUIs were known (green rows). Then this data is then used according to Main Algorithm to identify the eight GUI markers in five other (unknown) experiments via the same instrumentation. We then later used precise verification methods to determine that Main Algorithm can distinguish GUIs with an error of no more than two percent.

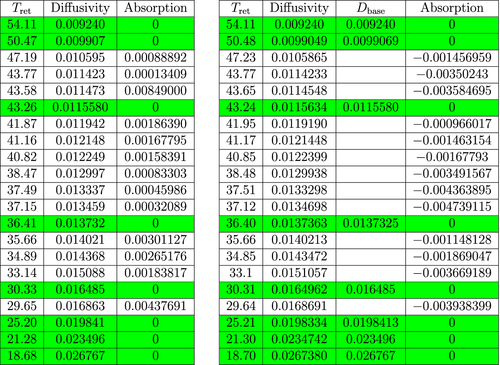
As noted above, the left table in Figure 5 consists of the data obtained from mass spectrometer readings for the sample A₀ (cf. Main Algorithm) and the calculated absorption coefficients for that sample. The first column of the table contains the retention time data. The second column contains the corresponding calculated diffusion coefficients. The last column contains the calculated absorption coefficients. The green rows in each table represent the data corresponding to the injected GUI molecules. As mentioned above, for the sample A₀, manual intervention to the mass spectrometer data is mandatory for finding the GUI retention times. See Section 5.2 for more details.

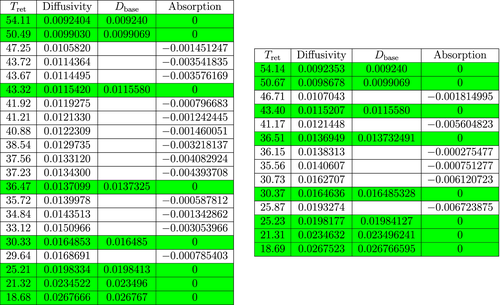
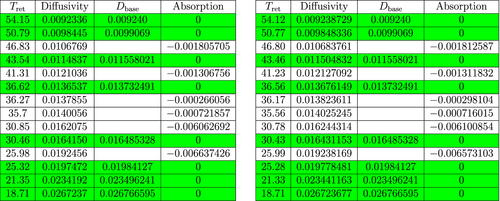
The second table in Figure 5 contains the data that was obtained from the mass spectrometer after the experiment for sample A₁ (cf. Main Algorithm) and implementation of Main Algorithm for that sample. The first column of the table contains the retention times for the sample. The second column contains the corresponding calculated diffusion coefficients. The third column contains the coefficients of the GUI molecules from sample A₀ (used for classification). The last column contains the calculated absorption coefficients. The tables in Figures 6 and 7 may be interpreted in a similar manner as the second table of Figure 5.

Remark 8.As is well understood, manual classification of molecular structures via the mass spectrometer is a time consuming and difficult task. However, Main Algorithm is demonstrated to be able to successfully identify GUI molecules in all experimental samples and also classify the remaining molecular structures using only retention times (after the initial classification of the “marker” molecules.

6 CONCLUSIONS AND FUTURE ENDEAVORS

In this article, we developed a novel mathematical method which allows for an efficient classification of experimental samples using a GUI as the reference frame. These interpretations were associated directly to the experimental spectrometer data in particular examples. In order to develop the novel method, we presented a data-driven partial differential equation model based on modified Einstein paradigm arguments. This extends Einstein's original study of Brownian motion to the situation of a more general conservation law. Once this data-driven model is obtained, we develop a closed-form solution of the model in order to avoid numerical approximations. A simple learning procedure is performed in order to determine the solutions coefficients on an initial sample. These coefficients are then used in additional learning procedures for computing the coefficients associated with unknown samples.

In order to further justify our method, we provide physical interpretations of the model coefficients. These coefficients are shown to be related to the experimental retrieval times, as well. This serves as the basis for the novel algorithm used for data classification (cf. Main Algorithm). Moreover, the proposed algorithm is successfully implemented and its efficacy is demonstrated via examples. Through the consideration of six independent samples we demonstrate that our method successfully classifies the unknown samples with errors which do not exceed two percent. Moreover, our novel method can be shown to be ten percent more accurate than the traditional method of using retrieval time only for classification.

It is important to mention that the retrieval time and shape of the peak in the spectrometer data depend on three main parameters: drift (velocity), variance (diffusion), and absorption. In this article we demonstrated that if the drift is fixed, due to reprocessing of the data, then the diffusion and absorption coefficients can accurately classify molecules in an unknown sample. Our future endeavors will focus on including all three characteristics for the N-glycan classification. This inclusion will make use of iterative deep learning algorithms of Kolmogorov-type (see, for instance, References 46-48).