Volume 3, Issue 6 e1151

SPECIAL ISSUE PAPER

Full Access

A high-order numerical method for sediment transport problems simulation and its comparison with laboratory experiments

María Teresa Capilla Romá,

Corresponding Author

María Teresa Capilla Romá

[email protected]

orcid.org/0000-0002-8764-5754

Departamento de Matemática Aplicada, Universitat Politècnica de València, Valencia, Spain

Correspondence María Teresa Capilla Romá, Departamento de Matemática Aplicada, Universidad Politècnica de Valencia, Camino de Vera, s/n. 46022 Valencia, Spain.

Email: [email protected]

Search for more papers by this author

Angel Balaguer-Beser,

Angel Balaguer-Beser

Grupo de Cartografía Geoambiental y Teledetección, Universitat Politècnica de València, Valencia, Spain

Search for more papers by this author

Beatriz Nácher-Rodríguez,

Beatriz Nácher-Rodríguez

Instituto Universitario de Investigación de Ingeniería del Agua y Medio Ambiente, Universitat Politècnica de València, Valencia, Spain

Search for more papers by this author

Francisco J. Vallés-Morán,

Francisco J. Vallés-Morán

Instituto Universitario de Investigación de Ingeniería del Agua y Medio Ambiente, Universitat Politècnica de València, Valencia, Spain

Search for more papers by this author

María Teresa Capilla Romá,

Corresponding Author

María Teresa Capilla Romá

[email protected]

orcid.org/0000-0002-8764-5754

Departamento de Matemática Aplicada, Universitat Politècnica de València, Valencia, Spain

Correspondence María Teresa Capilla Romá, Departamento de Matemática Aplicada, Universidad Politècnica de Valencia, Camino de Vera, s/n. 46022 Valencia, Spain.

Email: [email protected]

Search for more papers by this author

Angel Balaguer-Beser,

Angel Balaguer-Beser

Grupo de Cartografía Geoambiental y Teledetección, Universitat Politècnica de València, Valencia, Spain

Search for more papers by this author

Beatriz Nácher-Rodríguez,

Beatriz Nácher-Rodríguez

Instituto Universitario de Investigación de Ingeniería del Agua y Medio Ambiente, Universitat Politècnica de València, Valencia, Spain

Search for more papers by this author

Francisco J. Vallés-Morán,

Francisco J. Vallés-Morán

Instituto Universitario de Investigación de Ingeniería del Agua y Medio Ambiente, Universitat Politècnica de València, Valencia, Spain

Search for more papers by this author

First published: 07 February 2021

https://doi.org/10.1002/cmm4.1151

Citations: 1

Funding information: Generalitat Valenciana, AICO/2019/039

Share a link

Email
Wechat
Bluesky

Abstract

This article describes a high-order well-balanced central finite volume scheme for solving the coupled Exner−shallow water equations in one dimensional channels with rectangular section and variable width. Such numerical method may solve the proposed bedload sediment transport problem without the need to diagonalize the Jacobian matrix of flow. The numerical scheme uses a Runge–Kutta method with a fourth-order continuous natural extension for time discretization. The source term approximation is designed to verify the exact conservation property. Comparison of the numerical results for two accuracy tests have proved the stability and accuracy of the scheme. The results of the laboratory tests have also been used to calibrate different expressions of the solid transport discharge in the computer code. Two experimental tests have been carried out to study the erosive phenomenon and the consequent sediment transport: one test consisting of a triangular dune, and other caused by the effect of channel contraction.

1 Introduction

In this work, a well-balanced central finite volume scheme is presented, which is fourth order accurate in time and space, for solving the coupled shallow water equations (SWEs)-Exner equation system in one-dimensional channels with rectangular section and variable width. Sediment transport processes are caused by gravity effects and by friction effects with the air or the fluid containing the sediment. In this article, we focus the study on bedload sediment transport, defined as the type of transport where sediment grains roll or slide along the bed. To model the bedload sediment transport phenomenon caused by the movement of a fluid in contact with the bed sediment, we consider a coupled model constituted by a hydrodynamical component and a morphodynamical component. The hydrodynamical component is given by the SWEs,¹ used to study fluid movement in rivers, channels, and so on. A sediment transport equation, depending on the bedload transport rate, is considered to model the morphodynamical component. It is necessary to develop efficient numerical methods to solve this problem accurately.

The need for high accuracy computational schemes has driven the development of numerical schemes for higher-order spatial accuracy. There have been fourth-order accurate numerical methods for certain fluid flows and the convergence analysis has been establish for the incompressible Boussinesq equations.² Numerical methods for higher-order spatial accuracy also include weighted essentially non-oscillatory (WENO) schemes, discontinuous Galerkin (DG) schemes and P_NP_M schemes (see for instance a recent review in Reference 3). On the other hand, the most popular numerical methods for higher-order temporal accuracy are the the Runge–Kutta methods and the ADER (Arbitrary DERivative in space and time) methods.⁴ The Runge–Kutta discretization of a time-dependent ordinary differential equations splits the time evolution into a sequence of stages, each of which is only first order in time. The implementation of these methods is simple because each stage is practically identical to the previous stage. ADER schemes are computationally less expensive because the reconstruction is done only once.

Caleffi et al.⁵ presented a well-balanced central WENO scheme, fourth-order accurate in space and in time, for numerical integration of 1D SWEs over movable bed. That method combines a great versatility, due to the use of the central approach, with the main advantages of the WENO schemes to achieve fourth-order formal accuracy in smooth regions while maintaining stable, to keep non-oscillatory property near strong discontinuity.⁶ Even though a high order WENO schemes may use more CPU time than a second order scheme, it may still be advantageous for many application problems because of its high accuracy.⁷ Balaguer and Conde⁸ described a new fourth-order nonoscillatory reconstruction procedure for central schemes that satisfies shape preserving and number of extrema decreasing properties. That scheme can be an interesting computational alternative to fourth-order WENO schemes in terms of efficiency and stability. In this article, we will use central schemes with this type of spatial reconstruction.

This article uses a central scheme to solve the proposed sediment transport problem without the need to diagonalize the Jacobian matrix of flow. This property has facilitated its application in problems by incorporating new physical parameters to the model. The numerical scheme uses a Runge–Kutta method with a fourth-order continuous natural extension for time discretization. A Gaussian quadrature rule with two integration nodes is used to evaluate the time integrals. The reconstruction operator, which calculates point values from average values, is based on a third degree polynomial that avoids increasing the number of extreme points of the solution inside each cell. Such polynomial also guarantees that the total number of local maxima and minima does not exceed the initial number of extremes and therefore prevents the development of spurious numerical oscillations. The source term approximation has been designed to verify the exact conservation property. This numerical scheme has been applied in previous works by the authors^{9, 10} to solve accurately other kind of problems. This article presents its extension to solve bedload sediment transport problems in channels with a rectangular section and variable width, adding new terms of friction.

Some experimental tests in the laboratory of the Institute of Water and Environmental Engineering of the Polytechnic University of Valencia have been carried out in this article to study the erosive phenomenon, and the consequent sediment transport. The first test case consists of a triangular dune, and the second is selected to analyze the effects of flow contraction and expansion, due to the existence of inserted structures such as bridges. Comparison of the numerical results for some accuracy tests have demonstrated the stability and accuracy of the numerical scheme and the results of the laboratory tests have been used to calibrate different expressions of the solid transport discharge in the computer code, computing the best threshold value. The numerical results showed a good agreement with the measured experimental data.

2 The sediment transport system

The system of equations that models sediment transport in one dimensional channels with rectangular section and variable width, including the friction term, can be expressed as coupled system with the SWEs¹¹ and the Exner equation,¹² given by

\{\begin{cases} h_{t} + {(q)}_{x} = - q \frac{B^{'} (x)}{B (x)} \\ {(q)}_{t} + {(\frac{q^{2}}{h} + \frac{1}{2} g h^{2})}_{x} = - g h {(Z_{b})}_{x} - \frac{q^{2}}{h} \frac{B^{'} (x)}{B (x)} - g n^{2} q |\frac{q}{h}| R_{h}^{- 4 / 3} \\ {(Z_{b})}_{t} + ξ {(q_{b})}_{x} = - ξ q_{b} \frac{B^{'} (x)}{B (x)} \end{cases}

()

where h(x, t) is the water depth, q(x, t) is the specific discharge (flow rate per unit-width), which is related to the average horizontal velocity v(x, t) by the expression q(x, t) = h(x, t)v(x, t); Z_b(x, t) is the bed elevation, g = 9.8 m/s² is the acceleration of gravity, B(x) is the channel width at each point, n is Manning's roughness coefficient, and R_h(x, t) represents the hydraulic radius, which is given by:

R_{h} (x, t) = \frac{h (x, t) B (x)}{B (x) + 2 h (x, t)}

()

The first two equations in (1), the hydrodynamical component of the system, simulate the movement of a fluid in areas such as rivers, channels, coastal areas, and so on. The third equation of the system (1) is the Exner equation and it represents the sediment transport phenomenon, defined by the solid bed flux (volume rate of transport per unit length of surface) q_b(h, q), applied on the moving bed Z_b(x, t). The parameter

ξ

is defined by:

ξ = \frac{1}{1 - ρ_{0}}

()

where

ρ_{0}

is the porosity of the riverbed. For the resolution of the system (1), a transport equation is necessary to evaluate q_b from the results (h, q) of the hydrodynamic module of the system. Subsequently, Z_b(x, t) is obtained from the third equation of (1).

2.1 Formulation for the bedload sediment transport rate

Bed load sediment transport can be expressed by the simple power law: q_b(h, q) = A(q/h)³ as in Reference 9, where A is a constant. However, in the comparative between numerical results and laboratory experiments to evaluate q_b(h, q) in this article, transport models were proposed for granular non-cohesive sediments.^{13, 14} We used well-known transport formulas based on the bed shear stress. These models, which apply for the sand size used in the experimental campaign, are the classical Meyer-Peter and Müller formulation (MPM)¹⁵ or with Wong and Parker (W-P) correction,¹⁶ the Einstein-Brown (E-B),^{17, 18} Van Rijn formulation (VR),¹⁹ and Nielsen (Niel)²⁰ equation. These formulations are usually expressed as a relation between three nondimensional parameters, which are the dimensionless bed-load flux q^∗, the Shields stress

τ^{*}

and the dimensionless particle diameter d^∗, given by

q^{*} = \frac{q_{b}}{\sqrt{(G - 1) g d_{s}^{3}}}, τ^{*} = \frac{τ_{b}}{ρ (G - 1) g d_{s}}, d^{*} = d_{s} {(\frac{(G - 1) g}{ν^{2}})}^{\frac{1}{3}},

()

where d_s is the diameter of the sediment,

G = ρ_{s} / ρ

is the relative density of sediment in water, and

ν

is the water kinematic viscosity.

Using these dimensionless parameters, sediment transport formulas used in this article are given by

\begin{align} MPM : & q^{*} = 8 {(τ^{*} - τ_{c}^{*})}^{3 / 2}, \end{align}

()

\begin{align} W-P : & q^{*} = 3.97 {(τ^{*} - τ_{c}^{*})}^{3 / 2}, \end{align}

()

\begin{align} VR : & q^{*} = \frac{0.053}{{d^{*}}^{0.3}} {(\frac{τ^{*}}{τ_{c}^{*}} - 1)}^{2.1}, \end{align}

()

\begin{align} Niel : & q^{*} = 12 (τ^{*} - τ_{c}^{*}) \sqrt{τ^{*}} . \end{align}

()

These equations assume that the movement of the granular sediment begins when the shear stress is bigger than a certain critical shear stress (

τ^{*} > τ_{c}^{*}

). This parameter can be quantified using the Shields diagram for incipient motion. The original paper of MPM¹⁵ assumed

τ_{c}^{*} = 0.047

while W-P suggested

τ_{c}^{*} = 0.0495

. On the other hand, Van Rijn's formulation¹⁹ uses the following definition for

τ_{c}^{*}

\begin{align} τ_{c}^{*} = \{\begin{cases} 0.24 {(d^{*})}^{- 1} & if d^{*} \leq 4 \\ 0.14 {(d^{*})}^{- 0.64} & if 4 < d^{*} \leq 10 \\ 0.04 {(d^{*})}^{- 0.1} & if 10 < d^{*} \leq 20 \\ 0.013 {(d^{*})}^{0.29} & if 20 < d^{*} \leq 150 \\ 0.056 & if d^{*} > 150 \end{cases} \end{align}

()

Instead, Einstein-Brown formulation modifies the expression of q^∗ depending on whether the

τ^{*}

value is less or greater than 0.182, as we see in the following definition:

\begin{align} E-B : q^{*} = \{\begin{cases} \frac{K \exp (\frac{- 0.391}{τ^{*}})}{0.465} & if τ^{*} < 0.182 \\ 40 K {(τ^{*})}^{3} & if τ^{*} \geq 0.182 \end{cases} \end{align}

()

being:

\begin{align} K = \sqrt{\frac{2}{3} + \frac{36}{{(d^{*})}^{3}}} - \sqrt{\frac{36}{{(d^{*})}^{3}}} . \end{align}

()

These formulas have a range of application in function of grain size and the slope of the bottom. In this work, shear stress has been obtained using Manning's coefficient given by Strickler's formula:

τ^{*} = \frac{n^{2} v^{2}}{(G - 1) d_{s} R_{h}^{1 / 3}},

where v = v(x, t) is the average horizontal velocity defined below equation (1). To determine

τ_{c}^{*}

many experiments have been performed. For example, Shields proposed the well known Shields diagram. Meyer-Peter and Müller (MPM) is one of the most used models and it is applied to rivers and channels with slope lower than 2%, but the rest of the methods were subsequently introduced with the aim of trying to adjust the formulation to experimental results. In Section 4, we have used these models in order to compare numerical results with experimental data.

2.2 Algebraic manipulation of the sediment transport system

The system of equations (1) can be rewritten using the total surface elevation,

η (x, t) = h (x, t) + Z_{b} (x, t)

, instead of the water depth h(x, t), as suggested by Caleffi et al.,²¹ resulting in this matrix form system:

{(\begin{array}{c} η \\ q \\ Z_{b} \end{array})}_{t} + {(\begin{array}{c} q + ξ q_{b} \\ \frac{q^{2}}{η - Z_{b}} + \frac{1}{2} g {(η - Z_{b})}^{2} \\ ξ q_{b} \end{array})}_{x} = (\begin{array}{c} - (q + ξ q_{b}) \frac{B^{'} (x)}{B (x)} \\ - g (η - Z_{b}) {(Z_{b})}_{x} - \frac{q^{2}}{η - Z_{b}} \frac{B^{'} (x)}{B (x)} - g S_{f} \\ - ξ q_{b} \frac{B^{'} (x)}{B (x)} \end{array}),

()

where S_f models the friction term by means of the Manning's law:

S_{f} = n^{2} q |\frac{q}{η - Z_{b}}| {(R_{h})}^{- 4 / 3} .

The matrix system (12) can be expressed as u_t + f(u)_x = s(x, u) = s₁(x, u) + s₂(x, u) + s₃(x, u), where u = u(x, t) is the vector of variables

u = {[η, q, Z_{b}]}^{T}

, f(u(x, t)) is the flux vector, s₁(x, u) is the source term related to the bed slope, s₂(x, u) depends on the channel width, and s₃(x, u) is the friction term:

\begin{align} s_{1} = (\begin{array}{c} 0 \\ - g (η - Z_{b}) {(Z_{b})}_{x} \\ 0 \end{array}), s_{2} = (\begin{array}{c} - (q + ξ q_{b}) \frac{B^{'} (x)}{B (x)} \\ - \frac{q^{2}}{η - Z_{b}} \frac{B^{'} (x)}{B (x)} \\ - ξ q_{b} \frac{B^{'} (x)}{B (x)} \end{array}), s_{3} = (\begin{array}{c} 0 \\ - g S_{f} \\ 0 \end{array}) . \end{align}

()

In the next sections, we extend the methodology presented by Capilla and Balaguer in Reference 9 to develop a high-order well-balanced numerical scheme that solves the system (12). This extension incorporates to the numerical model the new source term, s(x, u(x, t)), that includes the width of the channel and the friction term.

3 Numerical Scheme

The computational domain [0, L] is divided into N equally spaced nodes x_j, then the spatial step $Δ x = L / N$ is defined. We consider five additional nodes on the left of x = 0, and also on the right of x = L, to avoid loss of accuracy in the domain boundaries and therefore we have the points $x_{j + \frac{1}{2}} = - 5 Δ x + j Δ x, j = 0, 1, \dots, (N + 10)$ . Then the nodes $x_{j} = \frac{1}{2} (x_{j - \frac{1}{2}} + x_{j + \frac{1}{2}}), j = 1, \dots (N + 10)$ are considered.

The time interval is discretized into the values

t^{0} = 0, t^{n} = t^{n - 1} + Δ t^{n}, n \geq 1

. The time step

Δ t^{n}

is computed taking into account the following Courant-Friedrichs-Lewy or CFL condition that is a necessary condition for the stability of numerical methods:

\begin{align} Δ t^{n} = CFL \frac{Δ x}{\max_{j} (\sqrt{g ĥ_{j}^{n}} + | {\hat{v}}_{j}^{n} |)}, CFL \leq 0.35 \end{align}

()

where

ĥ_{j}^{n}

and

{\hat{v}}_{j}^{n}

are the point-values at time tⁿ of the water depth h and the water velocity v, respectively, considering x = x_j when n is even and

x = x_{j + \frac{1}{2}}

when n is odd. The use of a CFL equal to 0.45 is recommended in central schemes, when the scheme used is second order in accuracy. In river hydrodynamic models, a value between 0.30 and 0.45 is usually used to correctly represent the flow operation, without reaching prohibitive calculation times. In our case, the value of 0.35 has been a good compromise solution, thus achieving a stable model, sufficiently accurate and with acceptable computation times. This choice is related to the numerical stability of the Runge–Kutta scheme used in the time integration and the capability of this method to achieve the desired fourth order of accuracy, as can be seen in previous works with central schemes.²² Large values of CFL number >0.35 may lead to an instable solutions.

The central scheme integrates Equation (12) in the control volume [x_j, x_j + 1] × [tⁿ, t^n + 1] when n is odd, obtaining

\begin{align} {\overline{u}}_{j + \frac{1}{2}}^{n + 1} = {\overline{u}}_{j + \frac{1}{2}}^{n} - \frac{1}{Δ x} (\int_{t^{n}}^{t^{n + 1}} f_{j + 1} (τ) d τ - \int_{t^{n}}^{t^{n + 1}} f_{j} (τ) d τ) + \int_{t^{n}}^{t^{n + 1}} {\overline{s}}_{j + \frac{1}{2}} (τ) d τ, \end{align}

()

being:

\begin{align} {\overline{u}}_{j + \frac{1}{2}}^{n} = \frac{1}{▵ x} \int_{x_{j}}^{x_{j + 1}} u (x, t^{n}) d x, f_{j} (t) = f (u (x_{j}, t)), {\overline{s}}_{j + \frac{1}{2}} (t) = \frac{1}{▵ x} \int_{x_{j}}^{x_{j + 1}} \sum_{k = 1}^{3} s_{k} (x, u (x, t)) d x . \end{align}

()

At the next time step, the solution is computed on the non-staggered grid, from the calculated cell averages

{\overline{u}}_{j + \frac{1}{2}}^{n + 1}

and using a similar procedure:

\begin{align} {\overline{u}}_{j}^{n + 2} = {\overline{u}}_{j}^{n + 1} - \frac{1}{Δ x} [\int_{t^{n + 1}}^{t^{n + 2}} f_{j + \frac{1}{2}} (τ) d τ - \int_{t^{n + 1}}^{t^{n + 2}} f_{j - \frac{1}{2}} (τ) d τ] + \int_{t^{n + 1}}^{t^{n + 2}} {\overline{s}}_{j} (τ) d τ . \end{align}

()

The ideas described in previous works^{9, 23} are extended for developing the numerical scheme of this article, considering the source term s, which also includes the channel width s₂, and the friction term s₃. As we will describe, the numerical algorithm takes into account the reconstruction, at time tⁿ, of averages ${\overline{u}}_{j + \frac{1}{2}}^{n}$ and point-values $û_{j}^{n}$ , and the reconstruction of Runge–Kutta fluxes, $k_{j}^{(i)}$ . Time integration will be developed by means of a Runge–Kutta scheme coupled with a natural continuous extension (NCE).²¹

In the next subsections, we describe the steps of the numerical algorithm, needed to obtain the solution (15) in a single time step.

3.1 Reconstruction, at time tⁿ, of point-values and averaged values

We start the reconstruction at time t = tⁿ, with a given approximation of fourth order of the cell averages:

{\overline{u}}_{j}^{n} = \frac{1}{Δ x} \int_{x_{j - \frac{1}{2}}}^{x_{j + \frac{1}{2}}} u (φ, t^{n}) d φ .

We analyzed⁹ the definition of the reconstruction three-degree polynomial

R_{j} (x; {\overline{u}}^{n})

, which approximates the pointwise values starting from the cell averages

{\overline{u}}_{i}^{n}, i \in \{j - 2, j - 1, j, j + 1, j + 2\}

, so:

\begin{align} R_{j} (x; {\overline{u}}^{n}) = u (x, t^{n}) + O ({(Δ x)}^{4}), \forall x \in [x_{j - \frac{1}{2}}, x_{j + \frac{1}{2}}] . \end{align}

()

We use these polynomials to approximate the point-values of the solution on the non-staggered grid at time tⁿ:

\begin{align} û_{j}^{n} \equiv {\overline{u}}_{j}^{n} - \frac{θ_{j}^{n}}{24} ({\overline{u}}_{j - 1}^{n} - 2 {\overline{u}}_{j}^{n} + {\overline{u}}_{j + 1}^{n}), \end{align}

()

that will be used in the numerical approximation of source term and fluxes. Also, the cell-averaged values on the staggered grid at time tⁿ are approximated:

\begin{align} {\overline{u}}_{j + \frac{1}{2}}^{n} \equiv \frac{1}{Δ x} (\int_{x_{j}}^{x_{j + \frac{1}{2}}} R_{j} (x; {\overline{u}}^{n}) d x + \int_{x_{j + \frac{1}{2}}}^{x_{j + 1}} R_{j + 1} (x; {\overline{u}}^{n}) d x) . \end{align}

()

The polynomial

R_{j} (x, {\overline{u}}^{n})

has been designed in order to have the same shape as the cell-averages,

{{\overline{u}}_{j - 1}^{n}, {\overline{u}}_{j}^{n}, {\overline{u}}_{j + 1}^{n}}

in the domain

I_{j} = [x_{j - \frac{1}{2}}, x_{j + \frac{1}{2}}]

so that:

$R_{j} (x; {\overline{u}}^{n})$ is monotonically increasing in I_j if ${\overline{u}}_{j - 1}^{n} \leq {\overline{u}}_{j}^{n} \leq {\overline{u}}_{j + 1}^{n}$ .
$R_{j} (x; {\overline{u}}^{n})$ is monotonically decreasing in I_j if ${\overline{u}}_{j - 1}^{n} \geq {\overline{u}}_{j}^{n} \geq {\overline{u}}_{j + 1}^{n}$ .
$R_{j} (x; {\overline{u}}^{n})$ has a maximum in I_j if and only if ${\overline{u}}_{j - 1}^{n} < {\overline{u}}_{j}^{n} > {\overline{u}}_{j + 1}^{n}$ .
$R_{j} (x; {\overline{u}}^{n})$ has a minimum in I_j if and only if ${\overline{u}}_{j - 1}^{n} > {\overline{u}}_{j}^{n} < {\overline{u}}_{j + 1}^{n}$ .

Moreover, the parameter $θ_{j}^{(n)}$ in (19) has been defined to preserve the stability and the non-oscillatory behavior of the numerical scheme. In this way, our central approximation give rise to monotone scheme that it avoids spurious oscillations in the solution using a fixed-central stencil. For more details, see References 8 and 9. To maintain the positivity of the numerical scheme, we should add additional requirements to the $θ_{j}^{(n)}$ definition, similar to those described by Liu and Osher²⁴ to satisfy the local maximum principle. This would allow a better treatment of wet/dry fronts.

In Reference 9, a test with a dry bed generation was solved in a fixed bed suggesting that the water depth may be negative if that local maximum principle condition has not been taken into account. We could also change the definition of $θ_{j}^{(n)}$ using the positivity-preserving limiter introduced by Xing et al.²⁵ or Xing and Shu.²⁶ In fact, there have been many scientific computing articles that have theoretically addressed the positivity property for certain physical variables, such as local Lax-Friedrichs type positivity-preserving flux for compressible Navier-Stokes equations,²⁷ positivity-preserving schemes of density and pressure in ideal magnetohydrodynamics and positivity and bound-preserving limiters for the compressible Euler equations.²⁸

3.2 Time integration: Runge–Kutta scheme

The time flux integrals in Equation (15) are evaluated by means of a Gaussian quadrature rule with two integration nodes:

\begin{align} \frac{1}{Δ x} \int_{t^{n}}^{t^{n + 1}} f_{j} (τ) d τ \equiv \frac{Δ t}{2 Δ x} (f (û_{j}^{n + β_{0}}) + f (û_{j}^{n + β_{1}})), \end{align}

()

where

β_{0} = 1 / 2 (1 - 1 / \sqrt{3})

and

β_{1} = 1 / 2 (1 + 1 / \sqrt{3})

. Then, we have to compute the point-values of the solution,

u (x_{j}, t^{n} + β_{k} Δ t)

, at two intermediate time steps,

t^{n + β_{k}}

for k = 0, 1. For this purpose, we apply a Runge–Kutta scheme coupled with the following NCE:²⁹

\begin{align} û_{j}^{n + β_{k}} \equiv u (x_{j}, t^{n} + β_{k} Δ t) = û_{j}^{n} + ▵ t \sum_{i = 1}^{4} b_{i} (β_{k}) k_{j}^{(i)}, \end{align}

()

where the constants

b_{i} (β_{k})

can be seen in Reference 9 and

k_{j}^{(i)}, 1 \leq i \leq 4

are the Runge–Kutta fluxes, which coincide with a numerical evaluation of (− f_x + s₁ + s₂ + s₃) in Eq. (12) and are computed considering the point-values of

û_{k}^{(i)}

, k ∈ {j − 2, j − 1, j, j + 1, j + 2}, being:

\begin{align} û_{j}^{(1)} = û_{j}^{n}, û_{j}^{(2)} = û_{j}^{n} + \frac{▵ t}{2} k_{j}^{(1)}, û_{j}^{(3)} = û_{j}^{n} + \frac{▵ t}{2} k_{j}^{(2)}, û_{j}^{(4)} = û_{j}^{n} + ▵ t k_{j}^{(3)} . \end{align}

()

3.2.1 Reconstruction of the Runge–Kutta fluxes

We calculate the Runge–Kutta fluxes

k_{j}^{(i)}, 1 \leq i \leq 4

in Equation (22), starting from the approximation described in Reference 9. Then we define a function given by:

\begin{align} K_{j} (x_{k}; û^{(i)}) = - [f (û_{k}^{(i)}) - f (û_{j}^{(i)})] + \int_{x_{j}}^{x_{k}} (s_{1} (x, û^{(i)}) + s_{2} (x, û^{(i)}) + s_{3} (x, û^{(i)})) d x, \end{align}

()

where the contribution of the channel width and friction term has been incorporated into the source term of the system of equations. From the definition (24) of the function

k_{j}^{(i)}

, it holds that

\begin{align} {\frac{\partial K_{j}^{(i)}}{\partial x}|}_{x = x_{j}} = k_{j}^{(i)} = {(- f_{x} + s_{1} + s_{2} + s_{3})}_{j}^{(i)} . \end{align}

()

Considering the point-values of

û_{k}^{(i)}

, k ∈ {j − 2, j − 1, j, j + 1, j + 2}, we calculate the function

K_{j} (x_{k}; û^{(i)})

. The integrals

\int_{x_{j}}^{x_{k}} s (x, û^{(i)}) d x, x_{j} \leq x_{k}

can be calculated adding integrals of the type (26), changing the sign when x_j > x_k.

\begin{align} \int_{x_{j}}^{x_{j + 1}} s (x, û^{(i)}) d x = \int_{x_{j}}^{x_{j + \frac{1}{2}}} P_{j} (x; û^{(i)}) d x + \int_{x_{j + \frac{1}{2}}}^{x_{j + 1}} P_{j + 1} (x; û^{(i)}) d x . \end{align}

()

Using the interpolating polynomial $P_{j} (x; {\hat{K}}_{j}^{(i)})$ of degree three defined in Reference 9, the evaluation of the Runge–Kutta fluxes $k_{j}^{(i)}$ is performed. Furthermore, in the case of a flow at rest, with q = 0 and $η = cte$ , then $K_{j} (x_{k}; û^{(i)}) = 0$ and this ensures that the scheme is well balanced.

3.3 Source term integration

The time source term integrals in Equation (15) are also evaluated using a Gaussian quadrature rule with two integration nodes:

\begin{align} \int_{t^{n}}^{t^{n + 1}} {\overline{s}}_{j + \frac{1}{2}} (τ) d τ = \frac{Δ t}{2} ({\overline{s}}_{j + \frac{1}{2}}^{n + β_{0}} + {\overline{s}}_{j + \frac{1}{2}}^{n + β_{1}}), with {\overline{s}}_{j + \frac{1}{2}}^{n + β_{k}} = \frac{1}{▵ x} \int_{x_{j}}^{x_{j + 1}} \sum_{i = 1}^{3} s_{i} (x, u (x, t^{n} + β_{k} ▵ t)) d x, \end{align}

()

where

t^{n + β_{k}} = t^{n} + β_{k} Δ t

(k = 0, 1), and

{\{s_{i}\}}_{i = 1}^{3}

were defined in (13). The integration of the source term

s_{1} (u (x, t^{n + β_{k}}))

in (27) is calculated using the procedure described in Reference 9. The first step to perform this integration consists of an integration by parts, in order to involve the spatial derivative of the free surface elevation

η = h + Z_{b}

instead of the water depth h:

\begin{align} {\overline{s}}_{1, j + \frac{1}{2}}^{[2]} & = - \frac{1}{▵ x} \int_{x_{j}}^{x_{j + 1}} g (η - Z_{b}) \frac{\partial Z_{b}}{\partial x} d x \\ = \frac{g}{2 ▵ x} [{\hat{Z}}_{b, j + 1}^{2} - {\hat{Z}}_{b, j}^{2} - 2 {\hat{η}}_{j + 1} {\hat{Z}}_{b, j + 1} + 2 {\hat{η}}_{j} {\hat{Z}}_{b, j}] + \frac{1}{▵ x} \int_{x_{j}}^{x_{j + 1}} ψ (x) d x, \end{align}

()

where

ψ (x) = g Z_{b} \frac{\partial η (x)}{\partial x}

. This formulation depends on the spatial derivative of the free surface level (

η

), which is preferable to prevent numerical errors in the solutions. In order to compute

\frac{1}{▵ x} \int_{x_{j}}^{x_{j + 1}} ψ (x) d x

in Equation (28), we follow this numerical treatment:

Starting from the point-values ${\hat{η}}_{j}$ , we compute the interpolating polynomials $P_{j} (x; \hat{η})$ , that approximate the point-values ${\hat{ψ}}_{j}$ starting from point-values.⁹
We compute the polynomials $P_{j} (x; \hat{ψ})$ starting from the point-values ${\hat{ψ}}_{j}$ and with these polynomials, we evaluate the integration of the function $ψ (x)$ in (28).

The integrals of the source terms relative to the width channel, $s_{2} (u (x, t^{n + β_{k}}))$ , and the friction source term $s_{3} (u (x, t^{n + β_{k}}))$ are evaluated using the procedure shown in (26).

4 Applications

In this section, the numerical method described previously is calibrated by means of different test cases. First, in order to prove the global order of accuracy of our method, we present in Section 4.1 two accuracy tests. In Sections 4.2 and 4.3, we describe laboratory scale experiments where we simulate sediment evolution and the numerical solution is compared with the experimental data obtained by the Institute of Water and Environmental Engineering of the Polytechnic University of Valencia. These experiments were carried out in a sand bed open channel, and they will be described in the following paragraphs.

Numerical results for these test experiments were obtained with transport equations described in Section 2.1. Different values for critical shear stress are also considered in the simulations.

These are the values considered in the comparison with laboratory experiments for the Manning coefficient n, the relative density of sediment in water G, the diameter of the sediment d_s, the porosity of the riverbed

ρ_{0}

and the water kinematic viscosity

ν

n = 0.0136, G = \frac{ρ_{s}}{ρ} = 2.65, d_{s} = 0.000515 m, ρ_{0} = 0.4, ν = 1.09 \cdot 1 0^{- 6} m^{2} / s .

4.1 Test 1: Accuracy tests

We tested the order accuracy of our scheme using the tests cases proposed in References 30 and 5. Initial conditions were given by the following expressions:

h (x, 0) = 5 + e^{\cos (2 π x)}, q (x, 0) = \sin (\cos (2 π x)), Z_{b} (x, 0) = \sin^{2} (π x), x \in [0, 1]

()

and periodic boundary conditions are considered. The width of the channel was not modified at any point so B′(x) = 0, ∀x ∈ [0, 1] and for simplicity we assumed a null Manning's roughness coefficient so the friction term S_f = 0. The analytical solution is not known for this problem, and therefore we used our scheme with NX = 128, 00 cells to compute a reference solution. We took this reference solution as the exact solution in computing the numerical errors.

First, in the Exner equation, we considered that q_b(h, q) = 0 and $ξ = 0$ . It can be seen that despite the absence of sediment transport, our scheme interpolates bed elevation values on a staggered grid. Table 1 shows errors in the L¹ and L^∞ norms together with the numerical orders of accuracy, computed considering different number of cells. Final time of computation was equal to T = 0.1 s, when the solution is still smooth because shocks developed later in time for this problem. We can see that fourth order accuracy is achieved for this example for the free surface elevation and the specific discharge. Figure 1 shows L¹ errors given in Table 1 versus CPU times, in a log-log scale. The points of this figure fit a straight line.

TABLE 1. Errors at T = 0.1 sin L¹ and L^∞ norms and the numerical orders of accuracy considering (29) as initial conditions, periodic boundary conditions, q_b(h, q) = 0,

ξ = 0

, B^′(x) = 0, ∀x ∈ [0, 1] and a null Manning's roughness coefficient

Cells	L¹	Order	L^∞	Order	L¹	Order	L^∞	Order
	$η$ , free surface elevation				q, specific discharge
100	8.99E-04		1.14E-02		7.64E-03		9.11E-02
200	7.33E-05	3.62	1.23E-03	3.20	6.15E-04	3.63	1.02E-02	3.16
400	3.95E-06	4.21	9.22E-05	3.74	3.22E-05	4.26	7.82E-04	3.71
800	1.77E-07	4.47	5.93E-06	3.96	1.35E-06	4.58	5.15E-05	3.93
1600	8.74E-09	4.34	2.62E-07	4.50	6.97E-08	4.27	2.22E-06	4.54

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

L¹ errors given in Table 1 as function of the CPU time (in seconds), in logarithmic scale

Second, we considered the bed load transport problem assuming that $q_{b} (h, q) = 0.2 {(\frac{q}{h})}^{3}$ and $ξ = \frac{1}{8}$ as in.⁵ Errors in the L¹ and L^∞ norms and the numerical orders of accuracy are presented in Table 2. Shape-preserving conditions imposed to define $R_{j} (x, {\overline{u}}^{n})$ may cause that the numerical scheme is not of order O(▵ x)⁴ in a small number of cells, so the experimental order of accuracy may be about 3 as we can see in Table 2.

TABLE 2. Errors in L¹ and L^∞ norms and the numerical orders of accuracy considering (29) as initial conditions, periodic boundary conditions, bed load transport with

q_{b} (h, q) = 0.2 {(\frac{q}{h})}^{3}

ξ = \frac{1}{8}

, B^′(x) = 0, ∀x ∈ [0, 1] and a null Manning's roughness coefficient

Cells	L¹	Order	L^∞	Order	L¹	Order	L^∞	Order
	$η$ , free surface elevation				q, specific discharge
200	2.96E-04		8.21E-03		2.49E-03		6.91E-02
400	2.65E-05	3.48	1.15E-03	2.84	2.22E-04	3.49	9.69E-03	2.83
800	1.40E-06	4.25	9.53E-05	3.59	1.19E-05	4.23	8.08E-04	3.58
1600	5.94E-08	4.56	6.41E-06	3.89	5.17E-07	4.52	5.44E-05	3.89

4.2 Test 2: Triangular dune

In the first case, we apply the numerical model presented to an experiment that consists of a triangular dune. The experimental test was developed introducing a sand layer in the laboratory channel, as it is shown in the sketch of the experiment with dimensions in Figure 2. The dune is 0.15 m long and 0.02 m high, and it starts at x = 0.10 m and ends at x = 0.25 m. The peak is located at x = 0.215 m. The width of the channel is not modified at any point, being 0.064 m in the entire section. For the numerical computations, we consider the one-dimensional domain of 0.6 m length discretized in 360 mesh points.

As the width of the channel B(x) is constant, the system of equations (12), applied to this particular test, takes this form:

{(\begin{array}{c} η \\ q \\ Z_{b} \end{array})}_{t} + {(\begin{array}{c} q + ξ q_{b} \\ \frac{q^{2}}{η - Z_{b}} + \frac{1}{2} g {(η - Z_{b})}^{2} \\ ξ q_{b} \end{array})}_{x} = (\begin{array}{c} 0 \\ - g (η - Z_{b}) {(Z_{b})}_{x} - g S_{f} \\ 0 \end{array}) .

()

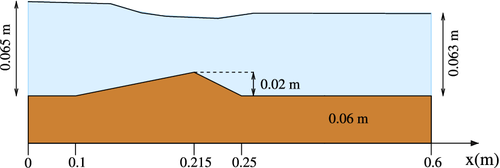
Boundary conditions for this problem are: q(0, t) = (8.75 · 10⁻⁴/0.064) m²/s for the water discharge and h(0.6, t) = 0.063 m for the fixed downstream water depth. The following initial conditions are also considered: h(x, 0) = 0.063 m ∀x ∈ [0, 0.6] and q(x, 0) = (8.75 · 10⁻⁴/0.064) m²/s ∀x ∈ [0, 0.6]. Remember that B(x) = 0.064 m ∀x. The experimental value, h(0, t) upstream, has been around 0.065 m although it will only be used for comparison.

4.2.1 Numerical-experimental comparative for Test 2

4.2.1.1 Water surface profile

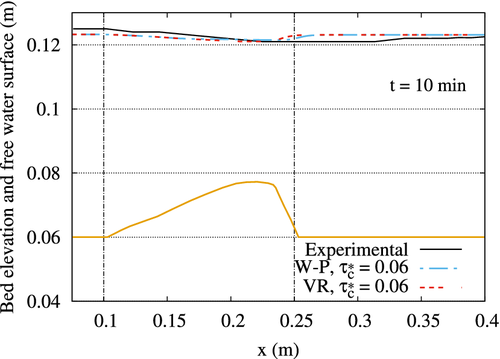
Figure 3 shows numerical and experimental results for the free water surface at t = 10 min in the range 0.07 m ≤ x ≤ 0.4 m. Numerical solutions were obtained with Wong and Parker and Van Rijn models (see Equations (6) and (7)) considering $τ_{c}^{*} = 0.06$ ; this value for $τ_{c}^{*}$ has been chosen since the bed elevation obtained with it is closer to the experimental results as will be analyzed later in Figures 4 and 5. The value of the critical shear stress using formula (9) is equal to 0.0311. Figure 3 also shows the experimental result for the sand bed profile at this time step in the same range. The vertical dashed lines represent where the dune starts and ends at the initial time t = 0 s. Numerical water surfaces represented in Figure 3 show that the model is able to simulate the drop in the water level that occurs when the bed level rises, under subcritical flow conditions. This same drop is observed in the experimental results, although it occurs slightly downstream.

4.2.1.2 Sand bed profile

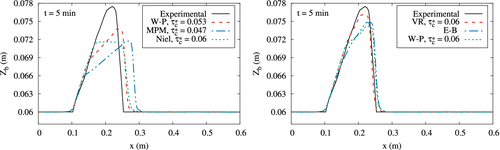
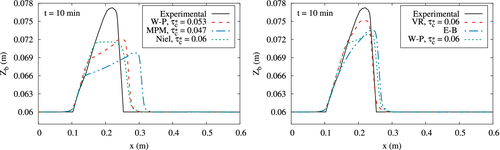
Figures 4 and 5 show the computed profile of the dune at two time steps, t = 5 min and t = 10 min, together with the experimental data for this test. These figures show numerical results obtained with the different formulations described in Section 2.1 for the bedload sediment transport rate. Classical Meyer-Peter and Müller formulation (MPM, Equation (5)) with $τ_{c}^{*} = 0.047$ produces excessive erosion. The same occurs with Wong and Parker (W-P) method with $τ_{c}^{*} = 0.053$ , which is the value of the dimensionless shear stress according to Shields diagram for the hydraulic conditions of the test. The results improve with this same method by increasing $τ_{c}^{*}$ to $τ_{c}^{*} = 0.06$ , which is the maximum value that is usually recommended. The Einstein-Brown (E-B, Equation (10)) solution is similar to that of Wong and Parker (W-P) with $τ_{c}^{*} = 0.06$ . Finally, Van Rijn's formulation (VR) using $τ_{c}^{*} = 0.06$ produces results closer to the experimental results. This value for $τ_{c}^{*}$ is much higher than that defined using formula (9), which would give a value equal to 0.0311.

4.3 Test 3: Channel with variable width

This case is selected from a set of experiments presented by Nácher-Rodríguez et al. in Reference 23, to be simulated with the numerical model. Cross section of the channel is rectangular, with a variable width. The sand used to represent the river bed has a very uniform grain size distribution. The sketch and parameters for this experiment can be seen in Figure 6. Channel length is 0.9 m with abutment plates of width 0.013 m located in the center.

Simulations were carried out by establishing a constant flow rate and a fixed downstream depth as boundary conditions:

\begin{align} h (0.9, t) = 0.066 m; q (0, t) = (8.8333 \cdot 1 0^{- 4} / 0.064) m^{2} / s . \end{align}

()

Initial conditions are the following:

\begin{align} h (x, 0) = 0.066 m; q (x, 0) = (8.8333 \cdot 1 0^{- 4} / 0.064) m^{2} / s; Z_{b} (x, 0) = 0.072 m . \end{align}

()

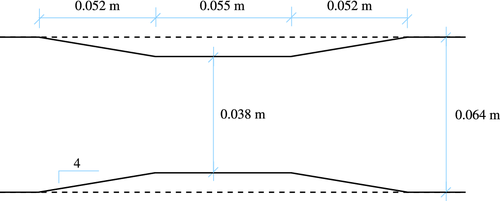
For the numerical computations, we consider the one-dimensional domain of 0.9 m length discretized in 540 mesh points. During the test experiment, a set of photographs were made in order to analyze the profile. To extract data from pictures, two moving vertical scales were located against channel walls. Experimental results from this test comprise water surface and sand bed profiles at different time steps.

The test was carried out for a longer period of time, but after 90 min (1.5 h), we observed that the erosive part of the bed profile did not change significantly. Two different values for critical shear stress are considered in this simulation, these values are $τ_{c}^{*} = 0.053$ and $τ_{c}^{*} = 0.06$ . As in Test 2, first value corresponds to dimensionless shear stress according to Shields diagram for the hydraulic conditions of the test. Second value was fixed in order to achieve a better agreement between numerical and experimental results.

4.3.1 Numerical-experimental comparative for Test 3

4.3.1.1 Water surface profile

Figure 7 shows computed versus experimental free water surface at t = 90 min with W-P and VR models, considering $τ_{c}^{*} = 0.053$ . With the rest of the formulations presented in Section 2.1, the changes in the free water surface are minimal and therefore, as an example, this figure presents results with the two methods that are subsequently deeply analyzed. Figure 7 also shows the experimental sand bed profile at t = 90 min along the maximum depth location; it can be seen that maximum erosion takes place close to the abutments. Vertical dashed lines represent where abutments start and where they end, and also the transitions.

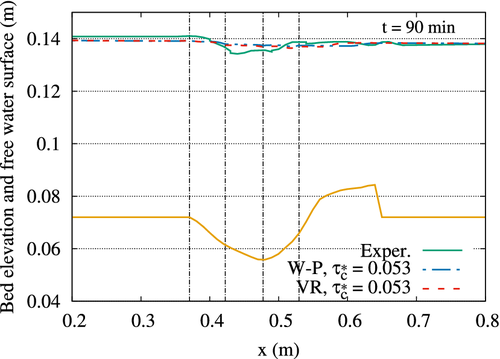
We observe from that figure that there is reasonable agreement between numerical and experimental water surfaces, despite the minor oscillations located between the abutments. These fluctuations in experimental profile located in the contracted flow area are not obtained with the numerical model.

4.3.1.2 Sand bed profiles

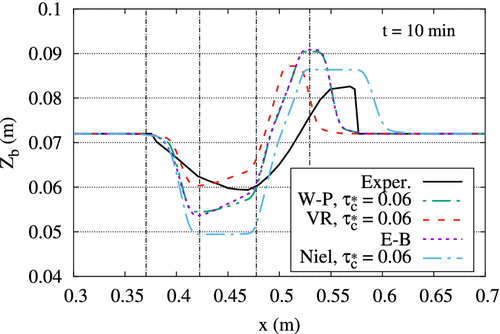
Figure 8 shows the sand bed results at time t = 10 min; in this figure different transport methods are compared with each other and with the experimental data. The transport methods used in this figure are Wong and Parker, Van Rijn, Einstein-Brown and Nielsen, with $τ_{c}^{*} = 0.06$ . We have observed that the results of this same comparison at time t = 30 min are very similar. In this Test, W-P and E-B methods give very similar results; in the erosion zone the W-P method is closer to the experimental result, since the maximum depth is less and therefore more similar to the experiment. From the results obtained for this Test case with the different transport models, we have selected the W-P and VR methods to carry out a more in-depth analysis, as will be shown in the following.

In Figure 9, a comparison between numerical and experimental sand bed profiles is shown for several time steps (10, 30, 60, and 90 min). Left column in the figure shows results obtained with the W-P transport equation, and right column corresponds to VR transport equation. Results of both transport models are presented for two different values for critical shear stress ( $τ_{c}^{*} = 0.053$ and $τ_{c}^{*} = 0.06$ ). It can be seen that both transport models give an erosion/deposition profile qualitatively similar to the experimental profile. Erosion is located between the abutments, and deposition starts at downstream transition. Wong and Parker formula tends to overestimate maximum scour depth, whereas Van Rijn's equation provides smaller values, more consistent with those from the experiment.

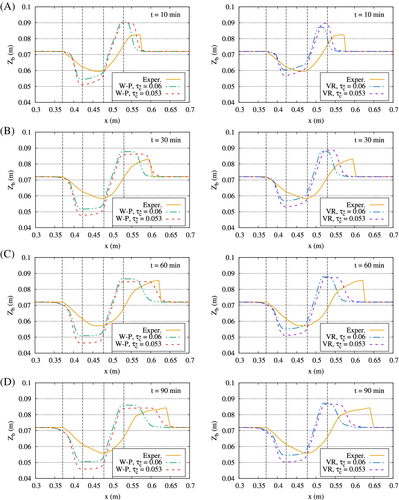
The deposition starts before in the numerical model than in the lab test. At early time steps, both numerical models overestimate maximum height of deposition, but numerical and experimental tend to reach the same value after approximately 60 min. The numerical model described in this research is 1D, and it gives good results when compared to the experiment, where the flow has one main direction, which is the longitudinal one. However, the laboratory flume has a certain width (which is small, in comparison to its length) and the erosive process that takes place is intrinsically 3D, as downward and lateral flows appear as the erosion hole starts to develop. In this case, erosion is mainly caused by the increase in the longitudinal velocity of the flow due to a local narrowing of the channel, and that is why a 1D model is able to simulate the location of the scour hole and its maximum depth. However, there are other processes taking place due to the actual 3D nature of the flow, and while they are not so relevant, they play a role in the final configuration of the sand bed profile. The numerical model cannot represent that effect. Therefore, differences between the experimental and computed bed profile are to be expected.

Table 3 displays the values of the maximum scour depth and its location at different time steps; the table compares the data of the experiment with the numerical results obtained with Wong and Parker and Van Rijn's models and considering two different values for critical shear stress. The relative errors for the values obtained for maximum depth and its location, with respect to the experimental data, are tabulated in Table 4. We can see from these tables that solutions using Van Rijn's model with the higher Shields parameter $τ_{c}^{*} = 0.06$ , differ from experimental result by a 10%, which is acceptable taking into account the model limitations.

TABLE 3. Values of maximum scour depth and its location

		t = 10 min		t = 30 min		t = 60 min		t = 90 min
		Scour depth	X	Scour depth	X	Scour depth	X	Scour depth	X
Experimental		0.0126	0.469	0.0137	0.474	0.0149	0.475	0.0162	0.479
Numerical	$τ_{c}^{*}$
W-P	0.053	0.0208	0.421	0.0241	0.419	0.0257	0.431	0.0261	0.441
W-P	0.06	0.0175	0.421	0.0202	0.416	0.0211	0.444	0.0215	0.438
VR	0.053	0.0150	0.418	0.0188	0.428	0.0208	0.431	0.0216	0.436
VR	0.06	0.0116	0.418	0.0149	0.423	0.0167	0.433	0.0174	0.434

Note: Length units are in meters.

TABLE 4. Relative errors in erosive profile (scour depth and location) between numerical and experimental results

Model	$τ_{c}^{*}$	Scour depth	X	Scour depth	X	Scour depth	X	Scour depth	X
		t = 10 min		t = 30 min		t = 60 min		t = 90 min
W-P	0.053	65.1	−10.3	75.9	−11.5	72.5	−9.2	61.1	−8.1
	0.06	38.9	−10.3	47.4	−12.1	41.6	−6.4	32.7	−8.7
VR	0.053	19.0	−11.0	37.2	−9.6	39.6	−9.2	33.3	−9.1
	0.06	−7.9	−11.0	8.8	−10.8	12.1	−8.8	7.4	−9.5

5 Conclusions and Future Work

5.1 Conclusions

After analyzing the experimental results and the numerical comparison, we establish the conclusions of this work. We have presented a fourth order accurate central scheme that solves the 1D coupled SW–Exner Equation system in a rectangular channel with variable width. The treatment for the source term spatial integration preserves the time and space accuracy and has been designed to obtain a well-balanced finite volume scheme. This central numerical scheme has been tested in previous works by the authors with other kind of problems, and now the method is extended to the incorporation of the variable width and the friction term. The method is capable of achieving great accuracy without using a very fine mesh. Its non-oscillatory behavior prevents the presence of new outliers in the computed solutions. Also, the method allows to work with different models for the sediment transport rate and to incorporate new physical parameters in the model.

A comparative between experimental results and numerical model has been analyzed: an acceptable agreement under certain conditions was found. Figures 4, 5, 8, and 9 show significant differences between computed sand bed profiles with different critical shear stress values. The model is highly sensitive to this parameter, and therefore special attention is required to determine its value. Model calibration is crucial in sediment transport problems, and when experimental data is not available, sensitivity analysis should always be performed to assess the model's uncertainty.

In the two laboratory tests used in this work, it was necessary to choose a higher Shields parameter $τ_{c}^{*}$ than that used in previous references in order to obtain results closer to the experimental ones, avoiding excessive erosion. In the second laboratory test, maximum scour locating was properly computed, and the model is able to simulate both erosion and deposition, but overestimates scour depths. Then, additional modifications have to be implemented, in order to accurately compute maximum scour depths with more representative parameters.

5.2 Future work

Transition from one to two-dimensional tests is necessary and it will provide a better representation of experimental tests. Also the incorporation in the model of a non-erodible fixed bed and the existence of bedforms, that may be the key to obtain smaller computed scour depths. Other factors have to be taken into account; for example, different bed materials and more complex structures or different angles of approach of the flow to the structure, which are factors that normally influence erosive processes.

ACKNOWLEDGEMENT

This work was supported by the Generalitat Valenciana under Project AICO/2019/039. The authors thank the anonymous reviewers for their comments and suggestions.

Biographies

María Teresa Capilla Romá completed her PhD in 2000 at the Faculty of Physics of the Universitat de València, Spain. She is currently an Assoc. Professor at the Department of Applied Mathematics of the Universitat Politècnica de València (UPV). She teaches multivariable calculus in engineering degrees. Her research interests include numerical methods for systems of differential equations, techniques of approximation, and techniques of numerical analysis.
Angel Balaguer-Beser completed his PhD in Mathematics sciences in 1996. He is currently an Assoc. Professor at the Department of Applied Mathematics and a member of the Geo-Environmental Cartography and Remote Sensing Group (http://cgat.webs.upv.es/) at the Universitat Politècnica de València in Spain. He teaches Mathematical Methods, Geostatistics and Multivariate Analysis in Geomatic. His research focuses on modeling of beach and fluvial systems using high-order interpolation methods.
Beatriz Nácher-Rodríguez completed her Civil Engineering Degree in 2011, and MSc Degree in Hydraulics Engineering and Environment in 2012. She has been collaborating as a researcher in the Hydraulic Engineering Laboratory at the Universitat Politècnica de València since 2010. Her research area is mainly focused in river engineering, sediment processes and river morphodynamics, but also in flood analysis and urban hydraulics.
Francisco J. Vallés Morán Assoc. Professor at the Hydraulic Engineering and Environment Department at UPV. MSc Civil Engineer and PhD in Hydraulic Engineering and Environment from UPV. He is a researcher in the Hydraulics and Hydrology area at the Research Institute of Water and Environmental Engineering (IIAMA) in the UPV and head of the Hydraulic Engineering Laboratory in the same university. He is also the head of the Group IIAMA-UPV in the Spanish Hydraulics Laboratory Network (RLHE). He is a specialist in hydraulic design and modeling—both mathematical and physical reduced.

References

1Toro EF. Shock-Capturing Methods for Free Surface Shallow Flows. Boca Raton, FL: John Wiley & Sons; 2001.
Google Scholar
2Wang C, Liu JG, Johnston H. Analysis of a fourth order finite difference method for the incompressible Boussinesq equations. Numer Math. 2004; 97(3): 555-594. https://doi.org/10.1007/s00211-003-0508-3.
10.1007/s00211-003-0508-3
Web of Science® Google Scholar
3 Busto S, Chiocchetti S, Dumbser M, Gaburro E, Peshkov I. High order ADER schemes for continuum mechanics. Front Phys. 2020; 8. https://doi.org/10.3389/fphy.2020.00032.
10.3389/fphy.2020.00032
Web of Science® Google Scholar
4Titarev VA, Toro EF. ADER: arbitrary high order Godunov approach. J Sci Comput. 2002; 17: 609-618. https://doi.org/10.1023/A:1015126814947.
10.1023/A:1015126814947
Web of Science® Google Scholar
5Caleffi V, Valiani A, Bernini A. High-order balanced CWENO scheme for movable bed shallow water equations. Adv Water Resour. 2007; 30(4): 730-741.
10.1016/j.advwatres.2006.06.003
Web of Science® Google Scholar
6Wang X, Li G, Qian S, Li J, Wang Z. High order well-balanced finite difference WENO schemes for shallow water flows along channels with irregular geometry. Appl Math Comput. 2019; 363:124587.
Web of Science® Google Scholar
7Shu CW. High order weighted essentially nonoscillatory schemes for convection dominated problems. SIAM Rev. 2009; 51(1): 82-126.
10.1137/070679065
Web of Science® Google Scholar
8Balaguer A, Conde C. Fourth-order nonoscillatory upwind and central schemes for hyperbolic conservation laws. SIAM J Numer Anal. 2005; 43(2): 455-473.
10.1137/S0036142903437106
Web of Science® Google Scholar
9Capilla MT, Balaguer-Beser A. A well-balanced high-resolution shape-preserving central scheme to solve one-dimensional sediment transport equations. Adv Eng Softw. 2012; 50: 19-28.
10.1016/j.advengsoft.2012.04.003
Web of Science® Google Scholar
10Balaguer-Beser A, Capilla MT, Nacher-Rodriguez B, Valles-Moran FJ, Andres-Domenech I. A high-order well-balanced central scheme for the shallow water equations in channels with irregular geometry. In: F Casas, V Martinez, eds. Advances in Differential Equations and Applications. SEMA SIMAI Springer Series. Vol 4. New York, NY: Springer; 2014: 229-237. https://doi.org/10.1007/978-3-319-06953-1.
10.1007/978-3-319-06953-1_22
Google Scholar
11Vázquez-Cendón ME. Improved treatment of source terms in upwind schemes for the shallow water equations in channels with irregular geometry. J Comp Phys. 1999; 148: 497-526.
10.1006/jcph.1998.6127
Web of Science® Google Scholar
12Exner F. Uber die wechselwirkung zwischen wasser und geschiebe in flüssen. Akad Wiss Wien Math Naturwiss Klasse. 1925; 134(2a): 165-204.
Google Scholar
13Berthon C, Cordier S, Delestre O, Le MH. An analytical solution of the shallow water system coupled to the Exner equation. C R Acad Sci Paris Ser I. 2012; 350: 183-186.
10.1016/j.crma.2012.01.007
Web of Science® Google Scholar
14Castro MJ, Fernández-Nieto ED, Ferreiro AM. Sediment transport models in shallow water equations and numerical approach by high order finite volume methods. Comput Fluids. 2008; 37(3): 299-316.
10.1016/j.compfluid.2007.07.017
Web of Science® Google Scholar
15Meyer-Peter E, Müller R. Formulae for bedload transport. Paper presented at: Proceedings of 3rd Congress, International Association of Hydraulic Research; 1948:39-64; Sweden.
Google Scholar
16Wong M, Parker G. Reanalysis and correction of bed-load relation of Meyer-Peter and Müller using their own database. J Hydraul Eng. 2006; 132(11): 1159-1168.
10.1061/(ASCE)0733-9429(2006)132:11(1159)
Web of Science® Google Scholar
17Einstein HA. Formulae for transportation of bed-load. Trans ASCE. 1942; 107: 561-577.
Google Scholar
18Brown CB. Sediment transport. In: H Rouse, ed. Engineering Hydraulics. Vol 12. New York, NY: Wiley; 1950.
Web of Science® Google Scholar
19Van Rijn LC. Sediment transport, Part I: bed load transport. J Hydraul Eng. 1984; 110(10): 1431-1456.
10.1061/(ASCE)0733-9429(1984)110:10(1431)
Web of Science® Google Scholar
20 Nielsen P. Coastal Bottom Boundary Layers and Sediment Transport. Singapore: World Scientific; 1992.
10.1142/1269
Google Scholar
21Caleffi V, Valiani A, Bernini A. Fourth-order balanced source term treatment in central WENO schemes for shallow water equations. J Comput Phys. 2006; 218: 228-245.
10.1016/j.jcp.2006.02.001
Web of Science® Google Scholar
22Xu Z, Chen XY, Liu Y. A new Runge-Kutta discontinuous Galerkin method with conservation constraint to improve CFL condition for solving conservation laws. J Comput Phys. 2014; 278: 348-377.
10.1016/j.jcp.2014.08.042
PubMed Web of Science® Google Scholar
23Nácher-Rodríguez B, Vallés-Morán FJ, Balaguer-Beser A, Capilla MT. Numerical-experimental modelling of local scouring downstream of protected bridges in alluvial river beds. Paper presented at: E-proceedings of the 36th IAHR World Congress; 2015; The Hague, Netherlands.
Google Scholar
24Liu XD, Osher S. Nonoscillatory high order accurate self-similar maximum principle satisfying shock capturing schemes I. SIAM J Numer Anal. 1996; 33: 760-779.
10.1137/0733038
Web of Science® Google Scholar
25Xing Y, Zhang X, Shu CW. Positivity-preserving high order well-balanced discontinuous Galerkin methods for the shallow water equations. Adv Water Resour. 2010; 33(12): 1476-1493.
10.1016/j.advwatres.2010.08.005
Web of Science® Google Scholar
26Xing Y, Shu CW. High-order finite volume WENO schemes for the shallow water equations with dry states. Adv Water Resour. 2011; 34(8): 1026-1038.
10.1016/j.advwatres.2011.05.008
Web of Science® Google Scholar
27Zhang X. On positivity-preserving high order discontinuous Galerkin schemes for compressible Navier-Stokes equations. J Comput Phys. 2017; 328: 301-343.
10.1016/j.jcp.2016.10.002
CAS Web of Science® Google Scholar
28Li P, Don WS, Wang C, Gao Z. High order positivity-and bound-preserving hybrid compact-weno finite difference scheme for the compressible Euler equations. J Sci Comput. 2018; 74(2): 640-666.
10.1007/s10915-017-0452-5
Web of Science® Google Scholar
29Bianco F, Puppo G, Russo G. High-order central schemes for hyperbolic systems of conservation laws. SIAM J Sci Comput. 1999; 21(1): 294-322.
10.1137/S1064827597324998
Web of Science® Google Scholar
30Xing Y, Shu CW. High order finite difference WENO schemes with the exact conservation property for the shallow water equations. J Comput Phys. 2005; 208: 206-227.
10.1016/j.jcp.2005.02.006
Web of Science® Google Scholar

Citing Literature

All articles

A high-order numerical method for sediment transport problems simulation and its comparison with laboratory experiments

Abstract

1 Introduction

2 The sediment transport system

2.1 Formulation for the bedload sediment transport rate

2.2 Algebraic manipulation of the sediment transport system

3 Numerical Scheme