Volume 3, Issue 6 e1145

SPECIAL ISSUE PAPER

Full Access

Parallel framework for dynamic domain decomposition of data assimilation problems: a case study on Kalman Filter algorithm

Luisa D'Amore,

Corresponding Author

Luisa D'Amore

[email protected]

orcid.org/0000-0002-3379-0569

Department of Mathematics and Applications, University of Naples Federico II, Naples, Italy

Correspondence Luisa D'Amore, Department of Mathematics and Applications, University of Naples Federico II, Complesso Monte Sant'Angelo, Via Cintia, Naples, Italy.

Email: [email protected]

Search for more papers by this author

Rosalba Cacciapuoti,

Rosalba Cacciapuoti

Department of Mathematics and Applications, University of Naples Federico II, Naples, Italy

Search for more papers by this author

Luisa D'Amore,

Corresponding Author

Luisa D'Amore

[email protected]

orcid.org/0000-0002-3379-0569

Department of Mathematics and Applications, University of Naples Federico II, Naples, Italy

Correspondence Luisa D'Amore, Department of Mathematics and Applications, University of Naples Federico II, Complesso Monte Sant'Angelo, Via Cintia, Naples, Italy.

Email: [email protected]

Search for more papers by this author

Rosalba Cacciapuoti,

Rosalba Cacciapuoti

Department of Mathematics and Applications, University of Naples Federico II, Naples, Italy

Search for more papers by this author

First published: 02 January 2021

https://doi.org/10.1002/cmm4.1145

Share a link

Email
Wechat
Bluesky

Abstract

We focus on Partial Differential Equation (PDE)-based Data Assimilation problems (DA) solved by means of variational approaches and Kalman filter algorithm. Recently, we presented a Domain Decomposition framework (we call it DD-DA, for short) performing a decomposition of the whole physical domain along space and time directions, and joining the idea of Schwarz's methods and parallel in time approaches. For effective parallelization of DD-DA algorithms, the computational load assigned to subdomains must be equally distributed. Usually computational cost is proportional to the amount of data entities assigned to partitions. Good quality partitioning also requires the volume of communication during calculation to be kept at its minimum. In order to deal with DD-DA problems where the observations are nonuniformly distributed and general sparse, in the present work we employ a parallel load balancing algorithm based on adaptive and dynamic defining of boundaries of DD—which is aimed to balance workload according to data location. We call it DyDD. As the numerical model underlying DA problems arising from the so-called discretize-then-optimize approach is the constrained least square model (CLS), we will use CLS as a reference state estimation problem and we validate DyDD on different scenarios.

1 INTRODUCTION

Data assimilation (DA, for short) encompasses the entire sequence of operations that, starting from observations/measurements of physical quantities and from additional information—such as a mathematical model governing the evolution of these quantities—improve their estimate minimizing inherent uncertainties. DA problems are usually formulated as an optimization problem where the objective function measures the mismatch between the model predictions and the observed system states, weighted by the inverse of the error covariance matrices.^{1, 2} In operational DA the amount of observations is insufficient to fully describe the system and one cannot strongly rely on a data driven approach: the model is paramount. It is the model that fills the spatial and temporal gaps in the observational network: it propagates information from observed to unobserved areas. Thus, DA methods are designed to achieve the best possible use of a never sufficient (albeit constantly growing) amount of data, and to attain an efficient data model fusion, in a short period of time. This poses a formidable computational challenge, and makes DA an example of big data inverse problems.^3-6 There is a lot of DA algorithms. Two main approaches gained acceptance as powerful methods: variational approach (namely, 3DVAR and 4DVAR) and Kalman filter (KF).^7-9 Variational approaches are based on the minimization of the objective function estimating the discrepancy between numerical results and observations. These approaches assume that the two sources of information, forecast and observations, have errors that are adequately described by stationary error covariances. In contrast to variational methods, KF (and its variants) is a recursive filter solving the Euler-Lagrange equations. It uses a dynamic error covariance estimate evolving over a given time interval. The process is sequential, meaning that observations are assimilated in chronological order, and KF alternates a forecast step, when the covariance is evolved, with an analysis step in which covariance of the filtering conditional is updated. In both kind of methods the model is integrated forward in time and the result is used to reinitialize the model before the integration continues. For any details interested readers are referred to References 10-12.

Main operators of any DA algorithm are dynamic model and observation mapping. These are two main components of any variational approach and state estimation prolem, too. In the following, we start considering CLS model, seen as a prototype of any DA model.¹³ CLS is obtained combining two overdetermined linear systems, representing the state and the observation mapping, respectively. In this regards, in Reference 14 we presented a feasibility analysis on constrained least square (CLS) models of an innovative domain decomposition framework for using CLS in large-scale applications. DD-DA framework, based on Schwarz approach, properly combines localization and partial differential equation (PDE)-based model reduction inheriting the advantages of both techniques for effectively solving any kind of large-scale and/or real-time KF application. It involves decomposition of the physical domain, partitioning of the solution, filter localization and model reduction, both in space and in time. There is a quite different rationale behind the framework and the so-called model order reduction methods (MOR),¹⁵ even though they are closely related each other. The primary motivation of Schwarz methods was the inherent parallelism arising from a flexible, adaptive and independent decomposition of the given problem into several subproblems, though they can also reduce the complexity of sequential solvers. Schwarz methods and theoretical frameworks are, to date, the most mature for this class of problems.^{13, 16-18} MOR techniques are based on projection of the full-order model onto a lower dimensional space spanned by a reduced-order basis. These methods has been used extensively in a variety of fields for efficient simulations of highly intensive computational problems. But all numerical issues concerning the quality of approximation still are of paramount importance.¹⁹ As mentioned previously DD-DA framework makes it natural to switch from a full scale solver to a model order reduction solver for solution of subproblems for which no relevant low-dimensional reduced space should be constructed. In the same way, DD-DA framework allows to employ a model reduction in space and time which is coherent with the filter localization. In conclusion, main advantage of the DD-DA framework is to combine in the same theoretical framework model reduction, along the space and time directions, with filter localization, while providing a flexible, adaptive, reliable and robust decomposition. That said, any interest reader who wants to apply DD-DA framework in a real-world application, that is, with a (PDE-based) model state and an observation mapping, once the dynamic (PDE-based) model has been discretized, he should rewrite the state estimation problem under consideration as a CLS model problem (cfr Section 3.1) and then apply DD-DA algorithm. In other words, she/he should follow the discretize-then-optimize approach, common to most DD-DA problems and state estimation problems, before employing the DD-DA framework. Summarizing, main topics of DD-DA framework can be listed as follows.

DD step: we begin by partitioning along space and time the domain into subdomains and then extending each subdomain to overlap its neighbors by an amount. Partitioning can be adapted according to the availability of measurements and data.
Filter Localization and MOR: on each subdomain we formulate a local DA problem analogous to the original one, combining filter localization and MOR approaches.
Regularization constraints: in order to enforce the matching of local solutions on the overlapping regions, local DA problems are slightly modified by adding a correction term. Such a correction term balances localization errors and computational efforts, acting as a regularization constraint on local solutions. This is a typical approach for solving ill posed inverse problems (see, for instance, 33).
Parallel in time: as the dynamic model is coupled with DA operator, at each integration step we employ, as initial and boundary values of all reduced models, estimates provided by the DA model itself, as soon as these are available.
Conditioning: localization excludes remote observations from each analyzed location, thereby improving the conditioning of the error covariance matrices.

To the best of our knowledge, such ab initio space and time decomposition of DA models has never been investigated before. A spatially distributed KF into sensor based reduced-order models, implemented on a sensor network where multiple sensors are mounted on a robot platform for target tracking, is presented in References 20-22.

1.1 Contribution of the present work

The introduction of a dynamic redefining of the DD (we call it DyDD), aimed to efficiently deal with DA problems where observations are nonuniformly distributed and general sparse is the main focus of the present work. Indeed, in such cases a static and/or a priori DD strategy could not ensure a well-balanced workload, while a way to repartition the domain so that subdomains maintain a nearly equal number of observations plays an essential role in the success of any effective DD approach. We present a revision of DD-DA framework such that a dynamic load balancing algorithm allows for a minimal data movement restricted to the neighboring processors. This is achieved by considering a connected graph induced by the domain partitioning whose vertices represent a subdomain associated with a scalar representing the number of observations on that subdomain. Once the domain has been partitioned, a load balancing schedule (scheduling step) should make the load on each subdomain equals to the average load providing the amount of load to be sent to adjacent subdomains (migrations step). The most intensive kernel is the scheduling step which defines a schedule for computing the load imbalance (which we quantify in terms of number of observations) among neighboring subdomains. Such quantity is then used to update the shifting of the boundaries of adjacent subdomains (Migration step) which are finally re mapped to achieve a balanced decomposition. We are assuming that load balancing is restricted to the neighboring domains so that we reduce the overhead processing time. Finally, following Reference 23 we use a diffusion type scheduling algorithm minimizing the Euclidean norm of data movement. The resulting constrained optimization problem leads to normal equations whose matrix is associated to the decomposition graph. The disadvantage is that the overhead time, due to the final balance among subdomains, strongly depends on the degree of the vertices of processors graph, gien by the number of neighboring subdomains of each subdomain. Such overhead represents the surface-to-volume ratio whose impact on the overall performance of the parallel algorithm decreases as the problem size increases.

1.2 Related works

There has been widespread interests in load balancing since the introduction of large-scale multiprocessors.²⁴ Applications requiring dynamic load balancing mainly include parallel solution of a PDE by finite elements on an unstructured grids²⁵ or parallelized particle simulations.²⁶ Load balancing is one of the central problems which have to be solved in designing parallel algorithms. Moreover, problems whose workload changes during the computation or it depends on data layout which may be unknown a priori, will necessitate the redistribution of the data in order to retain efficiency. Such a strategy is known as dynamic load balancing. Algorithms for dynamic load balancing, as in References 27-30, are based on transferring an amount of work among processors to neighbors; the process is iterated until the load difference between any two processors is smaller than a specified value, consequently it will not provide a balanced solution immediately. A multilevel diffusion method for dynamic load balancing,³¹ is based on bisection of processor graph. The disadvantage is that, to ensure the connectivity of subgraphs, movement of data between nonneighboring processors can occur. The mentioned algorithms do not take into account one important factor, namely that the data movement resulting from the load balancing schedule should be kept to minimum.

1.2.1 Organization of the work

The present work is organized as follows. As we apply the proposed framework to CLS model which can be seen as prototype of variational DA models, in order to improve the readability of the article, in Section 2 we give a brief overview of DA methods, that is, both KF and Variational DA, the variational formulation of KF and finally we give a brief description of CLS model. In Section 3, we describe main features of DD-DA framework and its application to CLS model. DyDD is presented in Section 4, through a graphical description and the numerical algorithm. Validation and performance results are presented in Section 5 and, finally, in Section 6 we give conclusions and future works.

2 THE BACKGROUND

In order to improve the readability of the article, in this section we give a brief overview of DA methods, that is, both KF and Variational DA, then we review CLS model as prototype of DA models. To this end, we also review the variational formulation of KF, that is, the so-called VAR–KF formulation, obtained minimizing the sum of the weighted Euclidean norm of the model error and the weighted Euclidean norm of the observation error.

2.1 Kalman filter

Given

x_{0} \in ℝ^{n}

, let

x (t) \in ℝ^{n}

, ∀t ∈ [0, T], denote the state of a dynamic system governed by the mathematical model

ℳ_{t, t + Δ t} [x (t)]

Δ t > 0

\{\begin{cases} x (t + Δ t) = ℳ_{t, t + Δ t} (x (t)), & \forall t, t + Δ t \in [0, T] \\ x (0) = x_{0} \end{cases},

()

and let:

y (t + Δ t) = ℋ_{t + Δ t} [x (t + Δ t)],

()

denote the observations where

ℋ_{t + Δ t}

is the observations mapping. Chosen

r \in ℕ

, we consider r + 2 points in [0, T] and

Δ t = \frac{T}{r + 1}

Let {t_k}_{k = 0, 1, … , r + 1} be a discretization of [0, T], where

t_{k} = k Δ t

, and let

{\hat{x}}_{k}

be the state estimate at time t_k, for k = 1, … , r + 1; we will use the following operators:⁹, for k = 0, 1, … , r,

M_{k, k + 1} \in ℝ^{n \times n}

, denoting the discretization of a linear approximation of

ℳ_{t_{k}, t_{k + 1}}

and for k = 0, 1, … , r + 1,

H_{k} \in ℝ^{m \times n}

which is the discretization of a linear approximation of

ℋ_{t}

with m > n. Moreover, we let

w_{k} \in ℝ^{n}

and

v_{k} \in ℝ^{m}

be model and observation errors with normal distribution and zero mean such that

E [w_{k} v_{i}^{T}] = 0

, for i, k = 0, 1, … , r + 1, where E[·] denotes the expected value;

Q_{k} \in ℝ^{n \times n}

and

R_{k} \in ℝ^{m \times m}

, are covariance matrices of the errors on the model and on the observations, respectively, that is,

Q_{k} : = E [w_{k} w_{k}^{T}] R_{k} : = E [v_{k} v_{k}^{T}] \forall k = 0, 1, \dots, r + 1 .

These matrices are symmetric and positive definite.

KF method: KF method consists in calculating the estimate

{\hat{x}}_{k + 1}

, at time t_k + 1, of the state

x_{k + 1} \in ℝ^{n}

x_{k + 1} = M_{k, k + 1} x_{k} + w_{k}, \forall k = 0, 1, \dots, r

()

such that

y_{k + 1} = H_{k + 1} x_{k + 1} + v_{k + 1}, \forall k = 0, 1, \dots, r .

()

KF algorithm: Given

{\hat{x}}_{0} \in ℝ^{n}

and

P_{0} = O \in ℝ^{n \times n}

a null matrix, for each k = 0, 1, … , r KF algorithm is made by two main operations: the Predicted phase, consisting of the computation of the predicted state estimate:

x_{k + 1} = M_{k, k + 1} {\hat{x}}_{k};

()

and of the predicted error covariance matrix:

P_{k + 1} = M_{k, k + 1} P_{k} M_{k, k + 1}^{T} + Q_{k};

()

and the Corrector phase, consisting of the computation of Kalman gain:

K_{k + 1} = P_{k + 1} H_{k + 1}^{T} {(H_{k + 1} P_{k + 1} H_{k + 1}^{T} + R_{k + 1})}^{- 1},

()

of Kalman covariance matrix:

P_{k + 1} = (I - K_{k + 1} H_{k + 1}) P_{k + 1},

and of Kalman state estimate:

{\hat{x}}_{k + 1} = x_{k + 1} + K_{k + 1} (y_{k + 1} - H_{k + 1} x_{k + 1}) .

()

Finally, we introduce the VAR-KF model. For k = 0, 1, … , r:

\begin{align} {\hat{x}}_{k + 1} & = {argmin}_{x_{k + 1} \in ℝ^{n}} J_{k + 1} (x_{k + 1}) \\ = {argmin}_{x_{k + 1} \in ℝ^{n}} \{| | x_{k + 1} - M_{k, k + 1} {\hat{x}}_{k} | |_{Q_{k}}^{2} + | | y_{k + 1} - H_{k + 1} x_{k + 1} | |_{R_{k + 1}}^{2}\} . \end{align}

3 VAR DA MODEL SET UP

Ω \subset ℝ^{n}

n \in ℕ

, is a spatial domain with a Lipschitz boundary, let:

\{\begin{cases} u (t + h, x) = ℳ_{t, t + h} [u (t, x)] & \forall x \in Ω, t, t + h \in [0, T], (h > 0) \\ u (t_{0}, x) = u_{0} (x) & t_{0} \equiv 0, x \in Ω \\ u (t, x) = f (x) & x \in \partial Ω, \forall t \in [0, T] \end{cases},

()

be a symbolic description of the 4D–DA model of interest where

u : (t, x) \in [0, T] \times Ω \mapsto u (t, x) = [u [1] (t, x), u [2] (t, x), \dots, u [p v] (t, x)],

is the state function of

ℳ

with

p v \in ℕ

the number of physical variables, f is a known function defined on the boundary

\partial Ω

, and let

v : (t, x) \in [0, T] \times Ω \mapsto v (t, x),

be the observations function, and

ℋ : u (t, x) \mapsto v (t, x), \forall (t, x) \in [0, T] \times Ω,

denote the nonlinear observations mapping. To simplify future treatments we assume pv ≡ 1. We consider N_p points of

Ω \subset ℝ^{n}

{x_{j}}_{j = 1, \dots, N_{p}} \subset Ω

; n_obs points of

Ω

, where n_obs ≪ N_p, :

{y_{j}}_{j = 1, \dots, n_{obs}}

; N points of [0,T] : D([0, T]) = {t_l}_{l = 0, 1, … , N − 1} with t_l = t₀ + l(hT); the vector

u_{0} = {u_{0, j}}_{j = 1, \dots, N_{p}} \equiv {u_{0} (x_{j})}_{j = 1, \dots, N_{p}} \in ℝ^{N_{p}},

which is the state at time t₀; the operator

M_{l - 1, l} \in ℝ^{N_{p} \times N_{p}}, l = 1, \dots, N,

representing a discretization of a linear approximation of

ℳ_{t_{l - 1}, t_{l}}

from t_l − 1 to t_l; the vector

b \in ℝ^{N_{p}}

accounting boundary conditions; the vector

u^{b} : = {u_{l, j}^{b}}_{l = 1, \dots, N - 1; j = 1, \dots, N_{p}} \equiv {u^{b} (t_{l}, x_{j})}_{l = 1, \dots, N - 1; j = 1, \dots, N_{p}} \in ℝ^{N_{p} \cdot (N - 1)},

representing solution of M_{l − 1, l} at t_l for l = 1, … , N, that is, the background; the vector

v_{l} \equiv {v (t_{l}, y_{j})}_{j = 1, \dots, n_{obs}} \in ℝ^{l \cdot n_{obs}},

consisting of observations at t_l, for l = 0, … , N − 1; the linear operator

H_{l} \in ℝ^{n_{obs} \times N_{p}}, l = 0, \dots, N - 1,

representing a linear approximation of

ℋ

; matrix

G \equiv G_{N - 1} \in ℝ^{(N \cdot n_{obs}) \times N_{p}}

such that

G_{l} = \{\begin{cases} [\begin{array}{l} H_{0} \\ H_{1} \\ ⋮ \\ H_{l - 1} \end{array}] & l > 1 \\ H_{0} & l = 1 \end{cases},

and R = diag(R₀, R₁, … , R_N − 1) and Q=VV^T, covariance matrices of the errors on observations and background, respectively. We now define the 4D–DA inverse problem.³²

Definition 1.(The 4D–DA inverse problem).³³ Given the vectors $v = {v_{l}}_{l = 0, \dots, N - 1} \in ℝ^{N \cdot n_{obs}}, u_{0} \in ℝ^{N_{p}},$ and the block matrix $G \in ℝ^{(N \cdot n_{obs}) \times N_{p}},$ a 4D–DA problem concerns the computation of

u^{DA} \in ℝ^{N_{p}},

such that

v = G \cdot u^{DA},

()

subject to the constraint that

u_{0}^{DA} = u_{0} .

We also introduce the regularized 4D–DA inverse problem, that is, the 4D–VAR DA problem.

Definition 2.(The 4D–VAR DA problem). The 4D–VAR DA problem concerns the computation of:

u^{DA} = {argmin}_{u \in ℝ^{N_{p}}} J (u),

()

with

J (u) = α | | u - u^{b} | |_{Q^{- 1}}^{2} + | | G u - v | |_{R^{- 1}}^{2},

()

where

α

is the regularization parameter.

Remark: It is worth noting that here we are considering a linear approximation of the observation operator, hence a linear operator G, although this is not at all required, at least in the formulation of the 4D–VAR problem. A more general approach for numerically linearize and solve 4D–VAR DA problem consists in defining a sequence of local approximations of J where each member of the sequence is minimized by employing Newton's method or one its variants.^{34, 35} More precisely, two approaches could be employed:

(a)
by truncating Taylor's series expansion of J at the second order, giving a quadratic approximation of J, let us say J^QN. Newton'methods (including LBFGS and Levenberg–Marquardt) use J^QD. The minimum is computed solving the linear system involving the Hessian matrix ∇²J, and the negative gradient − ∇ J.
(b)
by truncating Taylor's series expansion of J at the first order which gives a linear approximation of J, let us say let us say J^TL. Gauss–Newton's methods (including Truncated or Approximated Gauss–Newton uses J^TL). The minimum is computed solving the normal equations arising from the local Linear Least Squares problem.

Both approaches will employ the tangent linear model and the adjoint operator of the observation mapping and of the model of interest.³⁶

Remark: Computational kernel of variational approaches (namely, 3D-VAR and 4D-VAR) is a linear system, generally solved by means of iterative methods; the iteration matrix is related to matrix Q, which usually has a Gaussian correlation structure.⁶ Matrix Q can be written in the form Q=VV^T, where V is the square root of Q, namely, it is a Gaussian matrix. As a consequence, products of V and a vector z are Gaussian convolutions which can be efficiently computed by applying Gaussian recursive filters as in Reference 37.

In our case study we carry out on CLS model, we apply KF and DD-KF to CLS model, then in this case it results that matrix Q is the null matrix while matrix R is diagonal.¹⁴

3.1 CLS problem

Let

H_{0} x_{0} = y_{0}, H_{0} \in ℝ^{m_{0} \times n}, y_{0} \in ℝ^{m_{0}}, x_{0} \in ℝ^{n}

()

be the overdetermined linear system (the state), where rank(H₀) = n > 0, m₀ > n.

Given

H_{1} \in ℝ^{m_{1} \times n}

y_{1} \in ℝ^{m_{1}}

x_{1} \in ℝ^{n}

x \in ℝ^{n}

(observations), we consider the system

S : A x = b

()

where

A = [\begin{array}{llll} H_{0} \\ H_{1} \end{array}] \in ℝ^{(m_{0} + m_{1}) \times n}, b = [\begin{array}{llll} y_{0} \\ y_{1} \end{array}] \in ℝ^{m_{0} + m_{1}},

()

and m₁ > 0. Let

R_{0} \in ℝ^{m_{0} \times m_{0}}

R_{1} \in ℝ^{m_{1} \times m_{1}}

be weight matrices and

R = diag (R_{0}, R_{1}) \in ℝ^{(m_{0} + m_{1}) \times (m_{0} + m_{1})}

CLS problem consists in the computation of

\hat{x}

such that:

CLS : \hat{x} = {argmin}_{x \in ℝ^{n}} J (x)

()

with

\begin{array}{ll} J (x) = | | A x - b | |_{R}^{2} = | | H_{0} x - y_{0} | |_{R_{0}}^{2} + | | H_{1} x - y_{1} | |_{R_{1}}^{2}, \end{array}

()

where

\hat{x}

is given by

(A^{T} R A) \hat{x} = A^{T} R b \Rightarrow \hat{x} = {(A^{T} R A)}^{- 1} A^{T} R b

()

or,

\hat{x} = {(H_{0}^{T} R_{0} H_{0} + H_{1}^{T} R_{1} H_{1})}^{- 1} (H_{0}^{T} R_{0} y_{0} + H_{1}^{T} R_{1} y_{1}) .

()

We refer to $\hat{x}$ as solution in least squares sense of system in (14).

Remark: Besides covariance matrices of errors, main components of KF algorithm are dynamic model and observation mapping. These are two main components of any variational DA operator and state estimation problem, too. In this regard, in the following, as proof of concept of DD-DA framework, we start considering CLS model as a prototype of a variational DA model, at a given time. CLS is obtained combining two overdetermined linear systems, representing the state and the observation mapping, respectively. Then, we introduce VAR-KF method as reference data sampling method solving CLS model problem. VAR-KF will be decomposed by using the proposed framework. That said, any interest reader who wants to apply DD-DA framework in a real-world application, that is, with a (PDE-based) model state and an observation mapping, once the dynamic (PDE-based) model has been discretized, he should rewrite the state estimation problem under consideration as a CLS model problem (cfr Section 3.1) and then to apply CLS algorithm. In other words, she/he should follow the discretize-then-optimize approach, common to most DA problems and state estimation problems, before employing DD-DA and DyDD framework.³⁸

4 DD-FRAMEWORK

As DyDD is the refinement of initial DD-DA, in the following we first give mathematical settings useful to define the domain decomposition framework. Then, the following section we focus on DyDD.

4.1 DD set up

Definition 3. (Matrix Reduction)Let $B = [B^{1} B^{2} \dots B^{n}] \in ℝ^{m \times n}$ be a matrix with m, n ≥ 1 and B^j the jth column of B and I_j = {1, … , j} and I_i, j = {i, … , j} for i = 1, … , n − 1; j = 2, … , n, and i < j for every (i, j). Reduction of B to I_j is:

|_{I_{j}} : B \in ℝ^{m \times n} \to B |_{I_{j}} = [B^{1} B^{2} \dots B^{j}] \in ℝ^{m \times j}, j = 2, \dots, n,

and to I_i, j

|_{I_{i, j}} : B \in ℝ^{m \times n} \to B |_{I_{i, j}} = [B^{i} B^{i + 1} \dots B^{j}] \in ℝ^{m \times j - i}, i = 1, \dots, n - 1, j > i,

where

B |_{I_{j}}

and

B |_{I_{i, j}}

denote reduction of B to I_j and I_i, j, respectively.

Definition 4. (Vector Reduction)Let $w = {[w_{t} w_{t + 1} \dots w_{n}]}^{T} \in ℝ^{s}$ be a vector with t ≥ 1, n > 0, s = n − t and I_1, r = {1, … , r}, r > n and n > t. The extension of w to I_r is:

{EO}_{I_{r}} : w \in ℝ^{s} \to {EO}_{I_{r}} (w) = {[{\overline{w}}_{1} {\overline{w}}_{2} \dots {\overline{w}}_{r}]}^{T} \in ℝ^{r},

where i = 1, … , r

{\overline{w}}_{i} = \{\begin{cases} w_{i} & i f t \leq i \leq n \\ 0 & i f i > n a n d i < t \end{cases} .

We introduce reduction of J, as given in (17).

Definition 5. (Model Reduction)Let us consider $A \in ℝ^{(m_{0} + m_{1}) \times n}$ , $b \in ℝ^{m_{0} + m_{1}}$ , the matrix and the vector defined in (15), I₁ = {1, … , n₁}, I₂ = {1, … , n₂} with n₁, n₂ > 0 and the vectors $x \in ℝ^{n}$ . Let

J |_{(I_{i}, I_{j})} : (x |_{I_{i}}, x |_{I_{j}}) \mapsto J |_{(I_{i}, I_{j})} (x |_{I_{i}}, x |_{I_{j}}) \forall i, j = 1, 2

denote the reduction of J defined in (17). It is defined as

J |_{(I_{i}, I_{j})} (x |_{I_{i}}, x |_{I_{j}}) = | | H_{0} |_{I_{i}} x |_{I_{i}} - (y_{0} + H_{0} |_{I_{j}} x |_{I_{j}}) | |_{R_{0}}^{2} + | | H_{1} |_{I_{i}} x |_{I_{i}} - (y_{1} + H_{1} |_{I_{j}} x |_{I_{j}}) | |_{R_{1}}^{2},

()

for i, j = 1, 2.

For simplicity of notations we let $J_{i, j} \equiv J |_{(I_{i}, I_{j})}$ .

4.2 DD-CLS problems: DD of CLS model

We apply DD approach for solving system S in (14). Here, for simplicity of notations, we consider two subdomains.

Definition 6. (DD-CLS model[¹²])Let S be the overdetermined linear system in (14) and $A \in ℝ^{(m_{0} + m_{1}) \times n}$ , $b \in ℝ^{m_{0} + m_{1}}$ the matrix and the vector defined in (15) and $R_{0} \in ℝ^{m_{0} \times m_{0}}$ , $R_{1} \in ℝ^{m_{1} \times m_{1}}$ , $R = diag (R_{0}, R_{1}) \in ℝ^{(m_{0} + m_{1}) \times (m_{0} + m_{1})}$ be the weight matrices with m₀ > n and m₁ > 0. Let us consider the index set of columns of A, I = {1, … , n}. DD-CLS model consists of:

DD step. It consists of DD of I:
$I_{1} = {1, \dots, n_{1}}, I_{2} = {n_{1} - s + 1, \dots, n},$ ()
where s ≥ 0 is the number of indexes in common, |I₁| = n₁ > 0, |I₂| = n₂ > 0, and the overlap sets
$I_{1, 2} = {n_{1} - s + 1, \dots, n_{1}},$ ()
If s = 0, then I is decomposed without using the overlap, that is, I₁ ∩ I₂ = ∅ and I_1, 2 ≠ ∅, instead if s > 0, that is, I is decomposed using overlap, that is, I₁ ∩ I₂ ≠ ∅ and I_1, 2 = ∅; restrictions of A to I₁ and I₂ defined in (21)
$A_{1} = A |_{I_{1}} \in ℝ^{(m_{0} + m_{1}) \times n_{1}}, A_{2} = A |_{I_{2}} \in ℝ^{(m_{0} + m_{1}) \times n_{2}},$ ()
DD-CLS step: given $x_{2}^{0} \in ℝ^{n_{2}}$ , according to the alternating Schwarz method in Reference 11, DD-CLS approach consists in solving for n = 0, 1, 2, … the following overdetermined linear systems:
$S_{1}^{n + 1} : A_{1} x_{1}^{n + 1} = b - A_{2} x_{2}^{n}; S_{2}^{n + 1} : A_{2} x_{2}^{n + 1} = b - A_{1} x_{1}^{n + 1},$ ()
by employing a regularized VAR-KF model. It means that DD-CLS consists of a sequence of two subproblems:
$\begin{align} P_{1}^{n + 1} : {\hat{x}}_{1}^{n + 1} & = {argmin}_{x_{1}^{n + 1} \in ℝ^{n_{1}}} J_{1} (x_{1}^{n + 1}, x_{2}^{n}) \\ = {argmin}_{x_{1}^{n + 1} \in ℝ^{n_{1}}} [J |_{(I_{1}, I_{2})} (x_{1}^{n + 1}, x_{2}^{n}) + μ \cdot 𝒪_{1, 2} (x_{1}^{n + 1}, x_{2}^{n})] \end{align}$ ()

$\begin{align} P_{2}^{n + 1} : {\hat{x}}_{2}^{n + 1} & = {argmin}_{x_{2}^{n + 1} \in ℝ^{n_{2}}} J_{2} (x_{2}^{n + 1}, x_{1}^{n + 1}) \\ = {argmin}_{x_{2}^{n + 1} \in ℝ^{n_{2}}} [J |_{(I_{2}, I_{1})} (x_{2}^{n + 1}, x_{1}^{n + 1}) + μ \cdot 𝒪_{1, 2} (x_{2}^{n + 1}, x_{1}^{n + 1})] \end{align}$ ()
where I_i is defined in (21) and $J |_{I_{i}, I_{j}}$ is defined in (20), $𝒪_{1, 2}$ is the overlapping operator and $μ > 0$ is the regularization parameter.

Remark 1.If I is decomposed without using overlap (i.e., s = 0), then ${\hat{x}}_{1}^{n + 1} \in ℝ^{n_{1}}$ and ${\hat{x}}_{2}^{n + 1} \in ℝ^{n_{2}}$ can be written in terms of normal equations as follows

\begin{align} {\tilde{S}}_{1}^{n + 1} : (A_{1}^{T} {RA}_{1}) {\hat{x}}_{1}^{n + 1} = A_{1}^{T} R (b - A_{2} x_{2}^{n}) & \Rightarrow {\hat{x}}_{1}^{n + 1} = {(A_{1}^{T} {RA}_{1})}^{- 1} A_{1}^{T} R b_{1}^{n} \\ {\tilde{S}}_{2}^{n + 1} : (A_{2}^{T} {RA}_{2}) {\hat{x}}_{2}^{n + 1} = A_{2}^{T} R (b - A_{1} x_{1}^{n + 1}) & \Rightarrow {\hat{x}}_{2}^{n + 1} = {(A_{2}^{T} {RA}_{2})}^{- 1} A_{2}^{T} R b_{2}^{n + 1}, \end{align}

()

where

b_{1}^{n} = b - A_{2} x_{2}^{n}

and

b_{2}^{n + 1} = b - A_{1} x_{1}^{n + 1}

Remark 2.Regarding the operator $𝒪_{1, 2}$ , we consider $x_{1} \in ℝ^{n_{1}}$ and $x_{2} \in ℝ^{n_{2}}$ , and we pose

𝒪_{1, 2} (x_{i}, x_{j}) = | | {EO}_{I_{i}} (x_{i} |_{I_{1, 2}}) - {EO}_{I_{i}} (x_{j} |_{I_{1, 2}}) | |, i, j = 1, 2

with

{EO}_{I_{i}} (x_{1} |_{I_{1, 2}})

{EO}_{I_{i}} (x_{2} |_{I_{1, 2}})

be the extension to I_i, of restriction to I_1, 2 in (22) of

x_{1} \in ℝ^{n_{1}}

and

x_{2} \in ℝ^{n_{2}}

, respectively. Operator

𝒪_{1, 2}

represents the exchange of data on the overlap I_1, 2 in (22).

Remark 3.DD-CLS gives to sequences ${x^{n + 1}}_{n \in ℕ_{0}}$ :

x^{n + 1} = \{\begin{cases} {\hat{x}}_{1}^{n + 1} |_{I_{1} ∖ I_{1, 2}} & o n I_{1} ∖ I_{1, 2} \\ \frac{μ}{2} ({\hat{x}}_{2}^{n + 1} |_{I_{1, 2}} + {\hat{x}}_{1}^{n + 1} |_{I_{1, 2}}) & o n I_{1, 2} \\ {\hat{x}}_{2}^{n + 1} |_{I_{2} ∖ I_{1, 2}} & o n I_{2} ∖ I_{1, 2} \end{cases},

()

where I₁, I₂ are defined in (21) and I_1, 2 in (22).

Remark 4.For DD-CLS model we considered, DD of $I = {1, \dots, n} \subset ℕ$ , that is, the index set of columns of m A, similarly we can apply DD approach to 2D domain $I \times J \subset ℕ \times ℕ$ , where J = {1, … , (m₀ + m₁)} is the rows index set of A. Subdomains obtained are I₁ × J₁ = {1, … , n₁} × {1, … , m¹} and I₂ × J₂ = {n₁ − s_I + 1, … , n} × {m¹ − s_J + 1, … , (m₀ + m₁)}, where s_I, s_J ≥ 0 are the number of indexes in common between I₁ and I₂, J₁ and J₂, respectively. Restrictions of A to I₁ × J₁ and I₂ × J₂ are $A_{1} : = A |_{I_{1} \times J_{1}}$ and $A_{2} : = A |_{I_{2} \times J_{2}}$ .

Remark 5.The cardinality of J, that is, the index set of rows of matrix A, represents the number of observations available at time of the analysis, so that DD of I × J allows us to define DD-CLS model after dynamic load balancing of observations by appropriately restricting matrix A.

5 DyDD: DYNAMIC DD-DA FRAMEWORK

For effective parallelization of DD-DA, domain partitioning into subdomains must satisfy certain conditions. First the computational load assigned to subdomains must be equally distributed. Usually, computational cost is proportional to the amount of data entities assigned to partitions. Good quality partitioning also requires the volume of communication during calculation to be kept at its minimum.³⁹ We employ a dynamic load balancing scheme based on adaptive and dynamic redefining of initial DD-DA aimed to balance workload between processors. Redefining of initial partitioning is performed by shifting the boundaries of neighboring domains (this step is referred to as Migration step).

DyDD algorithm we implement is described by procedure DyDD shown in Table 13. To the aim of giving a clear and immediate view of DyDD algorithm, in the following figures (Figures 1-4) we outline algorithm workout on a reference initial DD configuration made of eight subdomains. We assume that at each point of the mesh we have the value of numerical simulation result (the so-called background) while the circles denote observations. DyDD framework consists in four steps:

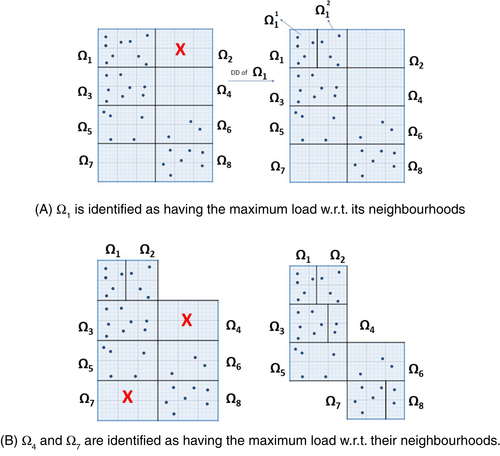
DD step: starting from the initial partition of $Ω$ provided by DD-DA framework, DyDD performs a check of the initial partitioning. If a subdomain is empty, it decomposes subdomain adjacent to that domain which has maximum load (decomposition is performed in two subdomains). See Figure 1.
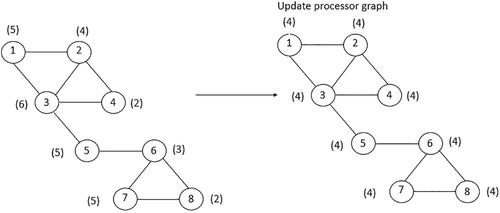
Scheduling step: DyDD computes the amount of observations needed for achieving the average load in each subdomain; this is performed by introducing a diffusion type algorithm (by using the connected graph G associated to the DD) derived by minimizing the Euclidean norm of the cost transfer. Solution of the Laplacian system associated to the graph G gives the amount of data to migrate. See Figure 2.
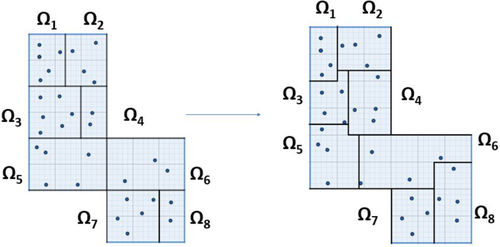
Migration step: DyDD shifts the boundaries of adjacent subdomains to achieve a balanced workload. See Figure 3.
Update step: DyDD redefines subdomains such that each one contains the number of observations computed during the scheduling step and it redistributes subdomains among processors grids. See Figure 4.

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

DyDD framework—Step 1. Check of the initial partitioning, identification of subdomains which do not have data or they suffer of any load imbalance and redefinition of subdomains. We observe that the workload of each subdomain after this repartitioning is now l_r(1) = 5, l_r(2) = 4, l_r(3) = 6, l_r(4) = 2, l_r(5) = 5, l_r(6) = 3, l_r(7) = 5, and l_r(8) = 2. The average load is then $\overline{l} = 4$

Scheduling step is the computational kernel of DyDD algorithm. In particular, it requires definition of Laplacian matrix and load imbalance associated to initial DD-DA and its solution. Let us give a brief overview of this computation. Generic element L_ij of Laplacian matrix is defined as follows:¹⁹

L_{i j} = \{\begin{cases} - 1 & i \neq j and edge (i, j) \in G \\ \deg (i) & i = j, \\ 0 & otherwise \end{cases}

()

and the load imbalance

b = (l (i) - \overline{l})

, where

d (i)

is the degree of vertex i,

l (i)

and

\overline{l}

are the number of observations and the average workload, respectively. Hence, as more edges are in G (as the number of subdomains which are adjacent to each other increases) as more nonzero elements are in L.

Laplacian system

L λ = b

, related to the example described below, is the following:

L = [\begin{array}{ccccccccc} 2 & - 1 & - 1 & 0 & 0 & 0 & 0 & 0 \\ - 1 & 3 & - 1 & - 1 & 0 & 0 & 0 & 0 \\ - 1 & - 1 & 4 & - 1 & - 1 & 0 & 0 & 0 \\ 0 & - 1 & - 1 & 2 & 0 & 0 & 0 & 0 \\ 0 & 0 & - 1 & 0 & 2 & - 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & - 1 & 3 & - 1 & - 1 \\ 0 & 0 & 0 & 0 & 0 & - 1 & 2 & - 1 \\ 0 & 0 & 0 & 0 & 0 & - 1 & - 1 & 2 \end{array}]

()

while the right-hand side is the vector whose ith component is given by the load imbalance, computed with respect to the average load. In this example, solution of the Laplacian system gives

λ = (0.36, 0.25, 0 ., 1.12, - 1 ., - 5 ., - 6.33, - 6.67)

so that the amount of load (rounded to the nearest integer) which should be migrated from

Ω_{i}

Ω_{j}

\begin{array}{c} δ_{1, 2} = 1; δ_{1, 3} = 0; δ_{3, 2} = 0; δ_{3, 4} = 1; δ_{3, 5} = 1; δ_{5, 6} = 2; δ_{6, 7} = 0; δ_{6, 8} = 1; δ_{7, 8} = 1 . \end{array}

that is,

δ_{i, j}

is the nearest integer of

(λ_{i} - λ_{j})

6 VALIDATION RESULTS

Simulations were aimed to validate the proposed approach by measuring performance of DyDD algorithm as shown in Table 13. Performance evaluation was carried out using Parallel Computing Toolbox of MATLABR2013a on the high-performance hybrid computing (HPC) architecture of the Sistema Cooperativo Per Elaborazioni scientifiche multidiscipliari data center, located at University of Naples Federico II. More precisely, the HPC architecture is made of 8 nodes, consisting of distributed memory DELL M600 blades connected by a 10 Gigabit Ethernet technology. Each blade consists of 2 Intel [email protected] GHz quadcore processors sharing 16 GB RAM memory for a total of 8 cores/blade and of 64 cores, in total. In this case for testing the algorithm we consider up to n_sub = 64 subdomains equally distributed among the cores. This is an intranode configuration implementing a coarse-grained parallelization strategy on multiprocessor systems with many-core CPUs.

DyDD set up. We will refer to the following quantities: $Ω \subset ℝ^{2}$ : spatial domain; n = 2048: mesh size; m: number of observations; p: number of subdomains and processing units; i: identification number of processing unit, which is the same of the associated subdomain; for i = 1, … , p, deg(i): degree of i, that is, number of subdomains adjacent to $Ω_{i}$ ; $i_{ad} (i) \in ℕ$ : identification of subdomains adjacent to $Ω_{i}$ ; $l_{in} (i) \in ℕ$ : number of observations in $Ω_{i}$ before the dynamic load balancing; $l_{r} (i) \in ℕ$ : number of observations in $Ω_{i}$ after DD step of DyDD procedure; $l_{f i} (i) \in ℕ$ : number of observations in $Ω_{i}$ after the dynamic load balancing; $T_{DyDD}^{p} (m)$ : time (in seconds) needed to perform DyDD on p processing units; T_r(m): time (in seconds) needed to perform repartitioning of $Ω$ ; $O h_{DyDD} (m) = \frac{T_{r} (m)}{T_{DyDD}^{p} (m)}$ overhead time to the dynamic load balancing.

As measure of the load balance introduced by DyDD algorithm, we use:

ℰ = \frac{\min_{i} (l_{f i} (i))}{\max_{i} (l_{f i} (i))}

that is, we compute the ratio of the minimum to the maximum of the number of observations of subdomains

Ω_{1}, \dots, Ω_{p}

after DyDD, respectively. As a consequence,

ℰ

= 1 indicates a perfectly balanced system.

Regarding DD-DA, we let $n_{loc} : = \frac{n}{p}$ be local problem size and we consider as performance metrics, the following quantities: $T^{1} (m, n)$ denoting sequential time (in seconds) to perform KF solving CLS problem; $T_{DD-DA}^{p} (m, n_{loc})$ denoting time (in seconds) needed to perform in parallel DD-KF solving CLS problem after DyDD; $T_{o h}^{p} (m, n_{loc})$ being the overhead time (measured in seconds) due to synchronization, memory accesses, and communication time among p cores; ${\hat{x}}_{KF} \in ℝ^{n}$ denoting KF estimate obtained by applying the KF procedure on CLS problem after DyDD; ${\hat{x}}_{DD-DA} \in ℝ^{n}$ denoting estimate obtained by applying DD-KF on CLS problem after DyDD; ${error}_{DD-DA} : = ‖ {\hat{x}}_{KF} - {\hat{x}}_{DD-DA} ‖$ denoting the error introduced by the DD-DA framework; $S^{p} (m, n_{loc}) : = \frac{T^{1} (m, n)}{T_{DD-DA}^{p} (m, n_{loc})}$ , which refers to the speed-up of DD-DA parallel algorithm; $E^{p} (m, n_{loc}) : = \frac{S^{p} (m, n_{loc})}{p}$ which denotes the efficiency of DD-DA parallel algorithm.

In the following tables we report results obtained by employing three scenarios, which are defined such that each one is gradually more articulated than the previous one. It means that the number of subdomains which are adjacent to each subdomain increases, or the number of observations and the number of subdomains increase. In this way the workload re distribution increases.

Example 1.First configuration: p = 2 subdomains and m = 1500 observations. In Case1, both $Ω_{1}$ and $Ω_{2}$ have data, that is, observations, but they are unbalanced. In Case2, $Ω_{1}$ has observations and $Ω_{2}$ is empty. In Tables 1 and 2, respectively, we report values of the parameters after applying DyDD algorithm. This is the simplest configuration we consider just to validate DyDD framework. In both cases, l_fi(1) and l_fi(2), that is, number of observations of $Ω_{1}$ and $Ω_{2}$ , are equal to the average load $\overline{l} = 750$ and $ℰ$ = 1. As the workload re distribution of Case 1 and Case 2 is the same, DD-DA performance results of Case 1 and Case 2 are the same, and they are reported in Table 9, for p = 2 only. In Table 3, we report performance results of DyDD algorithm.

TABLE 1. Example 1. DyDD parameters in Case 1

p	i	deg(i)	l_in	l_fin	i_ad
2	1	1	1000	750	2
	2	1	500	750	1

Note: Both subdomains have data but they are unbalanced. We report values of p, which is the number of subdomains, i the identification number of processing unit, deg(i) degree of i, that is, number of subdomains adjacent to $Ω_{i}$ , l_in(i) which is number of observations in $Ω_{i}$ before dynamic load balancing, l_fi(i) number of observations in $Ω_{i}$ after dynamic load balancing, i_ad identification of subdomains adjacent to $Ω_{i}$ .

TABLE 2. Example 1. DyDD parameters in Case 2

p	i	deg(i)	l_in	l_r	l_fin	i_ad
2	1	1	1500	1000	750	2
	2	1	0	500	750	1

Note: $Ω_{2}$ is empty. We report values of p, that is, number of subdomains, i identification number of processing unit, deg(i) degree of i, that is, number of subdomains adjacent to $Ω_{i}$ , l_in(i) which is number of observations in $Ω_{i}$ before dynamic load balancing, l_r(i) number of observations in $Ω_{i}$ after DD step of DyDD procedure, l_fi(i) number of observations in $Ω_{i}$ after dynamic load balancing, i_ad which is identification of subdomains which are adjacent to $Ω_{i}$ .

TABLE 3. Example 1. Execution times: We report values of

T_{DyDD}^{p} (m)

, time (in seconds) needed to perform DyDD on p processing units, T_r(m), time (in seconds) needed to perform repartitioning of

Ω

, Oh_DyDD(m) overhead time due to dynamic load balancing and

ℰ

measuring load balance

Case	$T_{DyDD}^{p} (m)$	T_r(m)	Oh_DyDD(m)	$ℰ$
1	4.11 × 10⁻²	0	0	1
2	3.49 × 10⁻²	4.00 × 10⁻⁶	1.15 × 10⁻⁴	1

Example 2.Second configuration. In this experiment we consider p = 4 subdomains and m = 1500 observations, and four cases which are such that the number of subdomains not having observations, increases from 0 up to 3. In particular, in Case 1, all subdomains have observations. See Table 4. In Case 2, only one subdomain is empty, namely, $Ω_{2}$ . See Table 5. In Case 3, two subdomains are empty, namely, $Ω_{1}$ and $Ω_{2}$ are empty. See Table 6. In Case 4, three subdomains are empty, namely, $Ω_{j}$ , for j = 1, 2, 3, is empty. See Table 7. In all cases, $ℰ$ reaches the ideal value 1 and $l_{fin} (i) = \overline{l} = 375$ , i = 1, 2, 3, 4. Then, DD-DA performance results of all cases are the same and they are reported in Table 9 for p = 4. In Table 8, we report performance results of the four cases.

TABLE 4. Example 2. DyDD parameters in Case 1

p	i	deg(i)	l_in	l_fin	i_ad
4	1	2	150	375	[ 2 4 ]
	2	2	300	375	[ 3 1 ]
	3	2	450	375	[ 4 2 ]
	4	2	600	375	[ 3 1 ]

Note: All subdomains have data. We report values of p, which is the number of subdomains, i identification number of processing unit, deg(i) degree of i, that is, number of subdomains adjacent to $Ω_{i}$ , l_in(i) the number of observations in $Ω_{i}$ before dynamic load balancing, l_fi(i) the number of observations in $Ω_{i}$ after dynamic load balancing, i_ad identification of subdomains which are adjacent to $Ω_{i}$ .

TABLE 5. Example 2. DyDD parameters in Case 2

p	i	deg(i)	l_in	l_r	l_fin	i_ad
4	1	2	450	450	375	[ 2 4 ]
	2	2	0	225	375	[ 3 1 ]
	3	2	450	225	375	[ 4 2 ]
	4	2	600	600	375	[ 3 1 ]

Note: $Ω_{2}$ is empty. We report values of p, which is number of subdomains, i, that is, identification number of processing unit, deg(i), that is, degree of i, that is, number of subdomains which are adjacent to $Ω_{i}$ , l_in(i), that is, number of observations in $Ω_{i}$ before dynamic load balancing, l_fi(i) number of observations in $Ω_{i}$ after dynamic load balancing, i_ad identification of subdomains adjacent to $Ω_{i}$ .

TABLE 6. Example 2. DyDD parameters in Case 3

p	i	deg(i)	l_in	l_r	l_fin	i_ad
4	1	2	0	300	375	[ 2 4 ]
	2	2	0	450	375	[ 3 1 ]
	3	2	900	450	375	[ 4 2 ]
	4	2	300	600	375	[ 3 1 ]

Note: $Ω_{1}$ and $Ω_{2}$ are empty. We report values of p, which is the number of subdomains, i identification number of processing unit, deg(i), that is, degree of i, that is, number of subdomains adjacent to $Ω_{i}$ , l_in(i) number of observations in $Ω_{i}$ before dynamic load balancing, l_fi(i) number of observations in $Ω_{i}$ after dynamic load balancing, i_ad identification of subdomains which are adjacent to $Ω_{i}$ .

TABLE 7. Example 2. DyDD parameters in Case 4

p	i	deg(i)	l_in	l_r	l_fin	i_ad
4	1	2	0	500	375	[ 2 4 ]
	2	2	0	250	375	[ 3 1 ]
	3	2	0	250	375	[ 4 2 ]
	4	2	1500	500	375	[ 3 1 ]

Note: $Ω_{1}$ , $Ω_{2}$ , and $Ω_{3}$ are empty. We report values of p, that is, number of subdomains, i identification number of processing unit, deg(i) degree of i, that is, number of subdomains which are adjacent to $Ω_{i}$ , l_in(i) the number of observations in $Ω_{i}$ before dynamic load balancing, l_fi(i) number of observations in $Ω_{i}$ after dynamic load balancing and i_ad identification of subdomains which are adjacent to $Ω_{i}$ .

TABLE 8. Example 2. Execution times: We report values of

T_{DyDD}^{p} (m)

, that is, time (in seconds) needed to perform DyDD algorithm on p processing units, T_r(m) time (in seconds) needed to perform repartitioning of

Ω

, Oh_DyDD(m) overhead time to the dynamic load balancing and

ℰ

parameter of load balance

Case	$T_{DyDD}^{p} (m)$	T_r(m)	Oh_DyDD(m)	$ℰ$
1	5.40 × 10⁻²	0	0	1
2	5.84 × 10⁻²	2.35 × 10⁻⁴	0.4 · 10⁻²	1
3	4.98 × 10⁻²	3.92 × 10⁻⁴	0.8 · 10⁻²	1
4	4.63 × 10⁻²	5.78 × 10⁻⁴	0.1 · 10⁻¹	1

TABLE 9. Example 1–2: DD-DA performance results in Examples 1 and 2

p = 1	n = 2048	m = 1500		T¹(m, n) = 5.67 × 10⁰
p	n_loc	$T_{DD-DA}^{p} (m, n_{loc})$	$S^{p} (m, n_{loc})$	$E^{p} (m, n_{loc})$
2	1024	4.95 × 10⁰	1.15 × 10⁰	5.73 × 10⁻¹
4	512	2.48 × 10⁰	2.29 × 10⁰	5.72 × 10⁻¹

Note: We report values of p, which is the number of subdomains, n mesh size, n_loc, that is, local problem size, m number of observations, $T^{1} (m, n)$ sequential time (in seconds) to perform KF solving CLS problem, $T_{DD-DA}^{p} (m, n_{loc})$ time (in seconds) needed to perform in parallel DD-DA solving CLS problem with DyDD, $S^{p} (m, n_{loc})$ and $E^{p} (m, n_{loc})$ the speed-up and efficiency of DD-DA parallel algorithm, respectively. We applied DyDD to all cases of Example 1 and Example 2 and obtained the perfect load balance, as reported in Tables 3 and 8, respectively. As the workload distribution is the same, DD-DA performance results are the same in all cases of Example 1, then we show results for p = 2, only. In the same way, for all cases of Example 2, we show results for p = 4, only.

Example 3.We consider m = 1032 observations and a number of subdomains p equals to p = 2, 4, 8, 16, 32. We assume that all subdomains $Ω_{i}$ has observations, that is, for i = 1, … , p, l_in(i) ≠ 0; $Ω_{1}$ has p − 1 adjacent subdomains, that is, n_ad := deg(1) = p − 1; $Ω_{i}$ has 1 adjacent subdomain, that is, for i = 2, … , p, deg(i) = 1; finally i = 1, … , p, we let the maximum and the minimum number of observations in $Ω_{i}$ be such that l_max = max_i(l_fin(i)) and l_min = min_i(l_fin(i)). Table 10 shows performance results and Figure 5 reports the error of DD-DA with respect to KF.

TABLE 10. Example 3. Execution times: We report values of p, that is, the number of subdomains, n_ad, the number of adjacent subdomains to

Ω_{1}

T_{DyDD}^{p} (m)

, time (in seconds) needed to perform DyDD on p processing units,

ℰ

which measures load balance, l_max and l_min, that is, maximum and minimum number of observations between subdomains after DyDD, respectively

p	n_ad	$T_{DyDD}^{p} (m)$	l_max	l_min	$ℰ$
2	1	6.20 × 10⁻³	516	515	9.98 × 10⁻¹
4	3	2.60 × 10⁻²	258	257	9.96 × 10⁻¹
8	7	9.29 × 10⁻²	129	128	9.92 × 10⁻¹
16	15	1.11 × 10⁻¹	71	64	8.88 × 10⁻¹
32	31	1.36 × 10⁻¹	39	32	8.21 × 10⁻¹

Note: $ℰ$ depends on n_ad(≡ deg(1)), that is, as n_ad(≡ deg(1)) increases (consequently p increases), then $ℰ$ decreases. For i = 1, … , p, subdomain $Ω_{i}$ has observations, that is, l_in(i) ≠ 0, consequently we do not need to perform repartitioning of $Ω$ , then T_r(m) ≡ 0.

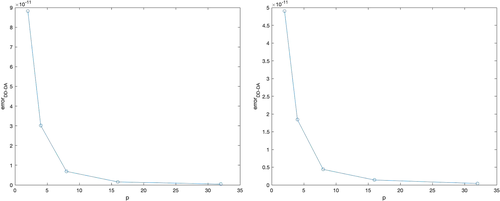
Example 4.We consider m = 2000 observations and p = 2, 4, 8, 16, 32 we assume that $Ω_{i}$ has observations, that is, for i = 1, … , p, l_in(i) ≠ 0; $Ω_{1}$ and $Ω_{p}$ have 1 adjacent subdomain, that is, deg(1) = deg(p) = 1; $Ω_{i}$ and $Ω_{p}$ have 2 adjacent subdomains, that is, for i = 2, … , p − 1, deg(i) = 2. In Table 12, we report performance results and in Figure 5 the error of DD-DA with respect to KF is shown.

Finally, regarding the accuracy of the DD-DA framework with respect to computed solution, in Table 11 (Examples 1-2) and in Figure 5 (Examples 3-4), we get values of error_DD-DA. We observe that the order of magnitude is about 10⁻¹¹ consequently, we may say that the accuracy of local solutions of DD-DA and hence of local KF estimates, are not impaired by DD approach.

TABLE 11. Examples 1–2. We report values of error_DD-DA, that is, the error introduced by the DyDD framework, in Example 1 (with p = 2) and Example 2 (with p = 4)

p	error_DD-DA
2	8.16 × 10⁻¹¹
4	8.82 × 10⁻¹¹

From these experiments, we observe that as the number of adjacent subdomains increases, data communications required by the workload repartitioning among subdomains increases too. Accordingly, the overhead due to the load balancing increases (for instance, see Table 8). As expected, the impact of such overhead on the performance of the whole algorithm strongly depends on the problem size and the number of available computing elements. Indeed, in Case 1 of Example 1 and of Example 2, when p is small in relation to n_loc (see Table 9) this aspect is quite evident. In Example 4, instead, as p increases up to 32, and n_loc decreases the overhead does not affect performance results (see Table 12). In conclusion, we recognize a sort of trade-off between the overhead due to the workload repartitioning and the subsequent parallel computation (Table 13).

TABLE 12. Example 4. Performance results of DyDD framework: We report values of p, which is the number of subdomains, n, that is, the mesh size, n_loc, that is, the local problem size, m the number of observations,

T^{1} (m, n)

, that is, sequential time (in seconds) needed to perform KF,

T_{DyDD}^{p} (m)

, that is, time (in seconds) needed to perform DyDD on p processing units,

T_{DD-DA}^{p} (m, n_{loc})

, that is, time (in seconds) needed to perform in parallel DD-DA with DyDD,

S^{p} (m, n_{loc})

and

E^{p} (m, n_{loc})

, that is, speed-up and efficiency of DD-DA parallel algorithm, respectively

p	n = 2048	m = 2000	T¹(m, n) = 4.88 × 10⁰
p	n_loc	$T_{DyDD}^{p} (m)$	$T_{DD-DA}^{p} (m, n_{loc})$	$S^{p} (m, n_{loc})$	$E^{p} (m, n_{loc})$
2	1024	4.10 × 10⁻³	4.71 × 10⁰	1.04 × 10⁰	5.18 × 10⁻¹
4	512	4.29 × 10⁻²	2.61 × 10⁰	1.87 × 10⁰	4.67 × 10⁻¹
8	256	1.07 × 10⁻¹	8.43 × 10⁻¹	5.79 × 10⁰	6.72 × 10⁻¹
16	128	1.42 × 10⁻¹	3.46 × 10⁻¹	1.41 × 10¹	8.81 × 10⁻¹
32	64	3.49 × 10⁻¹	1.66 × 10⁻¹	2.94 × 10¹	9.19 × 10⁻¹

TABLE 13. Procedure DyDD

Procedure DyDD-Dynamic Load Balancing(in: p,

Ω

, out: l₁,…,l_p)

%Procedure DyDD allows to balance observations between adjacent subdomains

% Domain

Ω

is decomposed in p subdomains and some of them may be empty.

% DBL procedure is composed by: DD step, Scheduling step and Migration Step.

% DD step partitions

Ω

in subdomains and if some subdomains have not any observations, partitions adjacent subdomains with maximum load

%in two subdomains and redefines the subdomains.

% Scheduling step computes the amount of observations needed for shifting boundaries of neighboring subdomains

%Migration step decides which subdomains should be reconfigured to achieve a balanced load.

% Finally, the Update step redefines the DD.

DD step

% DD step partitions

Ω

(Ω_{1}, Ω_{2}, \dots, Ω_{p})

Define n_i, the number of adjacent subdomains of

Ω_{i}

Define l_i: the amount of observations in

Ω_{i}

repeat

% identification of

Ω_{m}

, the adjacent subdomain of

Ω_{i}

with the maximum load

Compute

l_{m} = \max_{j = 1, \dots, n_{i}} (l_{j})

: the maximum amount of observations

Decompose

Ω_{m}

in two subdomains:

Ω_{m} \leftarrow (Ω_{m}^{1}, Ω_{m}^{2})

until (l_i ≠ 0)

end of DD Step

Begin Scheduling step

Define G: the graph associated with initial partition: vertex i corresponds to

Ω_{i}

Distribute the amount of observations l_i on

Ω_{i}

Define deg(i) = n_i, the degree of node i of G:

repeat

Compute the average load:

\overline{l} = \frac{\sum_{i = 1}^{p} l_{i}}{p}

Compute load imbalance:

b = {(l_{i} - \overline{l})}_{i = 1, \dots, p}

Compute L, Laplacian matrix of G

Call solve(in:L, b, out:

λ_{i}

) % algorithm solving the linear system

L λ_{i} = b

Compute

δ_{i, j}

, the load increment between the adjacent subdomains

Ω_{i}

and

Ω_{j}

δ_{i, j}

is the nearest integer of

(λ_{i} - λ_{j})

Define

n_{s_{i}}, n_{r_{i}}

, number of those subdomains whose configuration has to be updated

Update graph G

Update amount of observations of

Ω_{i}

l_{i} = l_{i} - \sum_{j = 1}^{n_{s_{i}}} δ_{i, j} + \sum_{j = 1}^{n_{r_{i}}} δ_{j, i}

until

(\max ‖ l_{i} - \overline{l} ‖ = = \frac{\deg (i)}{2})

%, that is, maximum load-difference is deg(i)/2

end Scheduling step

Begin Migration Step

Shift boundaries of two adjacent subdomains in order to achieve a balanced load.

end Migration Step

Update DD of

Ω

end Procedure DyDD

7 CONCLUSIONS

For effective DD-DA parallelization, partitioning into subdomains must satisfy certain conditions. First the computational load assigned to subdomains must be equally distributed. Usually the computational cost is proportional to the amount of data entities assigned to partitions. Good quality partitioning also requires the volume of communication during calculation to be kept at its minimum. In the present work we employed a dynamic load balancing scheme based on an adaptive and dynamic redefining of initial DD-DA aimed to balance load between processors according to data location. We call it DyDD. A mechanism for dynamically balancing the loads encountered in particular DD configurations has been included in the parallel framework we implement for solving large-scale DA models. In particular, we focused on the introduction of a dynamic redefining of initial DD-DA in order to deal with problems where the observations are nonuniformly distributed and general sparse. This is a quite common issue in DA. We presented first results obtained by applying DyDD in space of CLS problems using different scenarios of the initial DD-DA. Performance results confirm the effectiveness of the algorithm. We observed that the impact of data communications required by the workload repartitioning among subdomains affects the performance of the whole algorithm depending on the problem size and the number of available computing elements. As expected, we recognized a sort of trade-off between the overhead due to the workload repartitioning and the subsequent parallel computation. As in the assimilation window the number and the distribution of observations change, the difficulty to overcome is to implement a load balancing algorithm, which should have to dynamically allow each subdomain to move independently with time, that is, to balance observations with neighboring subdomains, at each instant time. We are working on extending DyDD framework to such configurations.

ACKNOWLEDGEMENTS

The authors thank the reviewers for their valuable comments.

Biographies

Luisa D'Amore Luisa D'Amore has the degree in Mathematics, and the Ph.D. in Applied Mathematics and Computer Science. She is professor of Numerical Analysis at University of Naples Federico II. She is member of the Academic Board of the Ph.D. in Mathematics and Applications, at University of Naples Federico II where she teaches courses of Numerical Analysis, Scientific Computing and Parallel Computing. Research activity is placed in the context of Scientific Computing. Her main interest is devoted to designing effective numerical algorithms solving ill-posed inverse problems arising in the applications, such as image analysis, medical imaging, astronomy, digital restoration of films and data assimilation. The need of computing the numerical solution within a suitable time, requires the use of advanced computing architectures. This involves designing and development of parallel algorithms and software capable of exploiting the high performance of emerging computing infrastructures. Research produces a total of about 200 publications in refereed journals and conference proceedings.
Rosalba Cacciapuoti Rosalba Cacciapuoti received the degree in Mathematics at University of Naples Federico II. She is a student of the PhD course in Mathematics and Applications at the University of Naples, Federico II. Her research activity is focused on designing of parallel algorithms for solving data assimilation problems.

REFERENCES

1Cohn SE. An introduction to estimation theory. J Meteor Soc Japan. 1997; 75(1B): 257-288.
10.2151/jmsj1965.75.1B_257
Web of Science® Google Scholar
2Nichols NK. Mathematical concepts of data assimilation. In: W Lahoz, B Khattatov, R Menard, eds. Data Assimilation: Making Sense of Observations. New York, NY: Springer; 2010: 13-40.
10.1007/978-3-540-74703-1_2
Google Scholar
3Arcucci R, D'Amore L, Carracciuolo L, Scotti G, Laccetti G. A decomposition of the Tikhonov regularization functional oriented to exploit hybrid multilevel parallelism. Int J Parallel Program. 2017; 45: 1214-1235. https://doi.org/10.1007/s10766-016-0460-3.
10.1007/s10766-016-0460-3
Web of Science® Google Scholar
4Arcucci R, D'Amore L, Carracciuolo L. On the problem-decomposition of scalable 4D-var data assimilation model. Proceedings of the 2015 International Conference on High Performance Computing and Simulation, HPCS 2015 2 September 2015, Pages 589-594, 13th International Conference on High Performance Computing and Simulation, HPCS; 20 July 2015 through 24 July 20152015; Amsterdam; Netherlands.
Google Scholar
5Arcucci R, D'Amore L, Celestino S, Laccetti G, Murli A. A scalable numerical algorithm for solving tikhonov regularization problems. Parallel Processing and Applied Mathematics. Lecture Notes in Computer Science. Vol 9574. Heidelberg, Germany: Springer; 2016: 45-54. https://doi.org/10.1007/978-3-319-32152-3-5.
10.1007/978-3-319-32152-3_5
Google Scholar
6D'Amore L, Cacciapuoti R. Model reduction in space and time for decomposing AB initio 4D variational data assimilation problems. Appl Numer Math. 2021; 160: 242-264. https://doi.org/10.1016/j.apnum.2020.10.003.
10.1016/j.apnum.2020.10.003
Web of Science® Google Scholar
7Evensen G. The ensemble Kalman filter: theoretical formulation and practical implementation. Ocean Dyn. 2003; 53: 343-367.
10.1007/s10236-003-0036-9
Web of Science® Google Scholar
8 Kalman RE. A new approach to linear filtering and prediction problems. Trans ASME J Basic Eng. 1960; 82: 35-45.
10.1115/1.3662552
Google Scholar
9Sorenson HW. Least square estimation: from gauss to Kalman. IEEE Spectr. 1970; 7: 63-68.
10.1109/MSPEC.1970.5213471
Web of Science® Google Scholar
10Kalnay E. Atmospheric Modeling, Data Assimilation and Predictability. Cambridge, MA: Cambridge University Press; 2003.
Google Scholar
11 Arcucci R, D'Amore L, Pistoia J, Toumi R, Murli A. On the variational data assimilation problem solving and sensitivity analysis. J Comput Phys. 2017; 335: 311-326.
10.1016/j.jcp.2017.01.034
Web of Science® Google Scholar
12 D'Amore L, Arcucci R, Carracciuolo L, Murli A. A scalable approach for variational data assimilation. J Sci Comput. 2014; 61: 239-257. https://doi.org/10.1007/s10915-014-9824-2.
10.1007/s10915-014-9824-2
Web of Science® Google Scholar
13Gander MJ. Schwarz methods over the course of time. ETNA. 2008; 31: 228-255.
Google Scholar
14D'Amore L, Cacciapuoti R, Mele V - Ab initio domain decomposition approaches for large scale kalman filter methods: a case study to constrained least square problems. Paper presented at: Proceedings of the 13th International Conference, PPAM 2019, LNCS Vol. 12044, Bialystok, Poland, September 8-11, 2019; Springer, Cham. https://doi.org/10.1007/978-3-030-43222-5.
Google Scholar
15Rozier D, Birol F, Cosme E, Brasseur P, Brankart JM, Verron J. A reduced-order Kalman filter for data assimilation in physical oceanography. SIAM Rev. 2007; 49(3): 449-465.
10.1137/050635717
Web of Science® Google Scholar
16 D'Amore L, Cacciapuoti R. A note on domain decomposition approaches for solving 3D variational data assimilation models. Ricerche mat. 2019; 68: 679-691. https://doi.org/10.1007/s11587-019-00432-4.
10.1007/s11587-019-00432-4
Web of Science® Google Scholar
17Schwarz HA. Ueber einige Abbildungsaufgaben. J fur die reine und angewandte Mathematik. 1869; 70: 105-120.
10.1515/crll.1869.70.105
PubMed Web of Science® Google Scholar
18 Chan TF, Mathew TP. Domain decomposition algorithms. Acta Numerica. 1994; 1993: 61-143.
10.1017/S0962492900002427
Google Scholar
19Homescu C, Petzold LR, Seban R. Error estimation for REduced order models of dynamical systems, UCRL-TR-2011494; December 2003.
Google Scholar
20Battistelli G, Chisci L. Stability of consensus extended Kalman filter for distributed state. Automatica. 2016; 68: 169-178.
10.1016/j.automatica.2016.01.071
Web of Science® Google Scholar
21 Khan UA. Distributing the Kalman filter for large-scale systems. IEEE Trans Signal Process. 2008; 56(10): 4919-4935.
10.1109/TSP.2008.927480
Web of Science® Google Scholar
22 Fujimoto M, Kawahara M. Domain decomposition for Kalman filter method and its application to tidal flow at Onjuku coast. In: T Chan, T Kako, H Kawarada, O Pironneau, eds. Paper presented at: Proceedings of 12th International Conference on Domain Decomposition Methods; 2001.
Google Scholar
23Hu YF, Blake RJ, Emerson DR. An optimal migration algorithm for dynamic load balancing. Concurr Pract Exper. 1998; 10(6): 467-483.
10.1002/(SICI)1096-9128(199805)10:6<467::AID-CPE325>3.0.CO;2-A
Web of Science® Google Scholar
24 Murli A, D'Amore L, Laccetti G, Gregoretti F, Oliva G. A multi-grained distributed implementation of the parallel block conjugate gradient algorithm. Concurr Comput Pract Exper. 2010; 22(15): 2053-2072.
10.1002/cpe.1548
Web of Science® Google Scholar
25Diniz P, Plimpton S, Hendrickson B, Leland R. Parallel algorithms for dynamically partitioning unstructured grids. Paper presented at: Proceedings of the 7th SIAM Conference Parallel Processing for Scientific Computing. San Francisco, CA: SIAM; 1995:615-620.
Google Scholar
26Kohring GA. Dynamic load balancing for parallelized particle simulations on MIMD computers. Parallel Comput. 1998; 21: 683-693.
10.1016/0167-8191(94)00112-N
Web of Science® Google Scholar
27Cybenco G. Dynamic load balancing for distributed memory multiprocessors. J Parallel Distrib Comput. 1989; 7: 279-301.
10.1016/0743-7315(89)90021-X
Web of Science® Google Scholar
28Boillat JE. Load balancing and Poisson equation in a graph. Concurr Pract Exper. 1990; 2: 289-313.
10.1002/cpe.4330020403
Google Scholar
29Xu CZ, Lau FCM. Analysis of the generalizes dimension exchange method for dynamic load balancing. J Parallel Distrib Comput. 1992; 16: 385-393.
10.1016/0743-7315(92)90021-E
Web of Science® Google Scholar
30Xu CZ, Lau FCM. The generalized dimension exchange method for load balancing in K-ary ncubes and variants. J Parallel Distrib Comput. 1995; 24: 72-85.
10.1006/jpdc.1995.1007
Web of Science® Google Scholar
31Horton G. A multi-level diffusion method for dynamic load balancing. Parallel Comput. 1993; 9: 209-218.
10.1016/0167-8191(93)90050-U
Web of Science® Google Scholar
32Murli A, D'Amore L. Regularization of a Fourier series method for the Laplace transform inversion with real data. Inverse Probl. 2002; 18(4): 1185.
10.1088/0266-5611/18/4/315
Web of Science® Google Scholar
33 Antonelli L, Carracciuolo L, Ceccarelli M, D'Amore L. A. murli - total variation regularization for edge preserving 3D SPECT imaging in high performance computing environments. In: PMA Sloot, AG Hoekstra, CJK Tan, JJ Dongarra, eds. Computational Science, ICCS 2002. Lecture Notes in Computer Science. Vol 2330. Berlin/Heidelberg, Germany: Springer; 2002.
10.1007/3-540-46080-2_18
Google Scholar
34 D'Amore L, Laccetti G, Romano D, Scotti G, Murli A. Towards a parallel component in a GPU-CUDA environment: a case study with the L-BFGS Harwell routine. Int J Comput Math. 2015; 92(1): 59-76. https://doi.org/10.1080/00207160.2014.899589.
10.1080/00207160.2014.899589
Web of Science® Google Scholar
35 Nocedal J, Wright SJ. Numerical Optimization. New York, NY: Springer-Verlag; 1999.
10.1007/b98874
Web of Science® Google Scholar
36Cacuci DG. Sensitivity and Uncertanty Analysis. New York, NY: Chapman&Hall/CRC Press; 2003.
Google Scholar
37Cuomo S, Severino G, Sommella A, D'Urso G. Numerical effects of the gaussian recursive filters in solving linear systems in the 3Dvar case study. Water Resour Res. 2017; 53(10): 8614-8625. https://doi.org/10.1002/2017WR020904.
Google Scholar
38 Gander W. Least squares with a quadratic constraint. Numer Math. 1980; 36: 291-307.
10.1007/BF01396656
Web of Science® Google Scholar
39 D'Amore L, Mele V, Romano D, Laccetti G, Romano D. A multilevel algebraic approach for performance analysis of parallel algorithms. Comput Inform. 2019; 38(4): 817-850. https://doi.org/10.31577/cai_2019_4_817.
10.31577/cai_2019_4_817
Web of Science® Google Scholar

All articles

Parallel framework for dynamic domain decomposition of data assimilation problems: a case study on Kalman Filter algorithm

Abstract

1 INTRODUCTION

1.1 Contribution of the present work

1.2 Related works

1.2.1 Organization of the work

2 THE BACKGROUND

2.1 Kalman filter

3 VAR DA MODEL SET UP

3.1 CLS problem

4 DD-FRAMEWORK

4.1 DD set up

4.2 DD-CLS problems: DD of CLS model

5 DyDD: DYNAMIC DD-DA FRAMEWORK

6 VALIDATION RESULTS

7 CONCLUSIONS

ACKNOWLEDGEMENTS

Biographies

REFERENCES

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley