A stabilized semi-Lagrangian finite element method for natural convection in Darcy flows

1 Introduction

When a saturated aquifer is subject to an internal motion due only to gravity, heat and mass transfer can take place between different regions as a result of temperature and concentration differences. This type of transfer is well known in the literature by natural convection. Physically speaking, the concept refers to the process of moving energy from or to a material by means of an adjacent fluid in motion in the presence of a gravitational field. This fluid movement is generated exclusively by differences in the density as a result of temperature and concentration gradients within the fluid itself but not by any external source such as a pump, extractor or fan. Natural convection is an important topic that has received growing attention in theoretical and applied researches over recent decades because of its presence in nature and many industrial processes. For example, in the process of mixing ocean waters and storms. In industry, the use of natural convection for heat dissipation is a determining factor for some electronic equipments. The effect of natural convection on the fluid flow was first studied experimentally in concentric spheres and horizontal tubes of various dimensions in References 1-3. It has been shown that this natural convection depends on the variation in some dimensionless control parameters such as Reynolds, Prandtl, Grashof, and Nusselt numbers. In other geometric configurations considered later in References 4, 5, it was shown that this complex process involves also the Frank–Kamenetskii parameter along with the Rayleigh number and the stationary and oscillating regimes on the thermal transfer behavior can occur. Authors showed how complex regimes appeared through successive bifurcations leading from a stable stationary temperature distribution without convection to a stationary symmetric and asymmetric convective solutions and later to a periodic and aperiodic oscillations. In Reference 6, the impact of the critical value of the thickness of the porous layers on the characteristics of natural convection in an open-ended squared cavity was discussed numerically. In Reference 7, the existence of an adiabatic obstacle in a horizontal enclosure of fluid was taken into account, and numerical simulations were developed for different Rayleigh numbers at which the dynamic behavior is evolved from a steady-state to a chaotic pattern. In Reference 8, the case of natural convective flow was studied within an inclined rectangular enclosure by using the linear stability analysis. It was found that, the natural convection generates more stable inclined propagating fronts than those obtained without inclination. In all these works, natural convection is considered in a gaseous or liquid medium with their motion described either by the Navier–Stokes equations or by the Darcy equation in a quasi-stationary form under the Boussinesq approximation. In underground applications, one key issue is how injection of water or other solutes into aquifers affects the natural convection along with the flowing groundwater in the presence of underground services such as pipes or piles, and how they can contribute to wearing down these services. The answer may help to troubleshoot many concerns such as the use of suitable materials for underground services, the detection of parameters and factors affecting performance, the selection of the optimum installation location, and thus to prevent from wrong decisions that can give rise to undesired and nonreversible effects in terms of underground materials lifetime.

The purpose of this article is to present a stabilized semi-Lagrangian finite element method for the numerical study of natural convection effects on groundwater flows and solute transport. Consider for example an unconfined aquifer which is recharged primarily from surface water deposits such as snow melt and precipitation, that flow through underground pipes and drain gradually toward a discharge area such as a river, sea, or lake. This study is intended to be useful not only to simulate the solute transport and groundwater flow but also to show its variation in case of the introduction of solutes other than water or contaminants within the recharge area, that can cause aquifer contamination and then lead to important changes of critical hydrological and medium properties. Examples of groundwater flow models with natural convection that have been studied in similar ways can be found in References 9-14 among others. The governing equations consist of a coupled Darcy problem for the flow and a convection–diffusion equation for the concentration. This includes a wide variety of difficulties which typically arise in the numerical approximation of partial differential equations which describe and consequently determine their dynamics. Current trends in incompressible viscous flows are to combine these equations with complex components to simulate various problems in many applications such as fluid mechanics, ocean circulation, turbulence and multiphase flow models. All these applications require a very efficient and robust numerical solvers for the coupled systems computing the numerical solutions is very often not easy due to the nonlinear form and the presence of the convective terms. For many viscous hydrodynamics problems, the convective term is distinctly more important than the diffusive term, particularly when the Reynolds numbers reach high values, as it becomes a source of computational difficulties and oscillations. Furthermore, It is well known that the solutions of these equations present steep fronts, which need to be resolved accurately in applications and often cause severe numerical difficulties. Hence, semi-Lagrangian methods as known in meteorological community make use of the transport nature of the governing equations by combining the fixed Eulerian grids with a particle tracking along the characteristic curves of the problem under study, see for instance References 15-19. The main idea in these approaches is to rewrite the governing equations in terms of Lagrangian coordinates as defined by the particle trajectories (or characteristic curves) associated with the problem under consideration. The time derivative and the convection terms are combined as a directional derivative along the characteristics leading to a characteristic time-stepping procedure. The Lagrangian treatment in these methods significantly reduces the time truncation errors in the Eulerian methods. Moreover, the semi-Lagrangian method offers the possibility of using time steps that exceed those permitted by the Courant–Friedrichs–Lewy (CFL) stability condition in the Eulerian methods for convection-dominated flows. A class of semi-Lagrangian methods has been investigated in References 16, 20-23 among others. The authors in Reference 24 have studied a semi-Lagrangian method for the incompressible Navier–Stokes equations in the finite element framework. In this reference, the solutions at characteristic feet are approximated by interpolation from finite element basis functions. A first-order semi-Lagrangian approach combined with finite element method has been analyzed for the Navier–Stokes equations in Reference 22. It has been shown that the method is unconditionally stable provided the characteristics are transported by a divergence-free field that is deduced from the flow velocity. The case where the characteristics are transported by a discrete velocity field which is not divergence-free has been studied in Reference 23. Analysis of a semi-Lagrangian method using finite difference discretization has been presented in Reference 20 for convection–diffusion equations.

In most numerical methods using finite element discretizations, mixed formulations in which two finite element spaces are used to approximate the velocity and pressure variables have been well established. However, in the current study, the proposed finite element method consists of using the same approximation spaces for all the variables including the pressure, velocity and concentration. We also the L²-projection to stabilize the finite element method for the coupled system. A similar unified finite element method has been developed and analyzed in Reference 25 for several Darcy flow problems. It is based on regularization of the mixed variational form of the Darcy equations by using the same low-order finite element spaces to approximate both velocity and pressure variables. The method is an extension of the proposed polynomial pressure projection stabilization of the Stokes equations presented in References 26, 27. The results have shown that the method is stable and its accuracy is competitive with that of other mixed finite element formulations since the matrix condition numbers are better and it is less sensitive to the choice of the stabilization parameter used in the stabilized finite element discretizations. This article is organized as follows. The description of the mathematical model is presented in Section 2. Section 3 is devoted to the formulation of the unified semi-Lagrangian finite element method. This section includes the finite element solution of Darcy problem, calculation of departure points, and the formulation of semi-Lagrangian method for solving the convection–diffusion equation. The numerical results for a groundwater benchmark problem are presented in Section 4. Section 5 contains some conclusions and perspectives.

2 Mathematical model

In the present study, we consider natural convection by Darcy flows in two-dimensional domains. An illustration of the physical model considered is shown in Figure 1. Here, a groundwater flow problem in an unconfined aquifer with a well is recharged by a solute with an inlet concentration and subject to a thermal variation $(c_{\infty }^{\prime }-c_0^{\prime })$, where $c_{\infty }^{\prime }$ is the concentration at saturation and $c_0^{\prime }$ is the reference concentration. Let $\mathrm{\Omega }\subset {\mathbf{R}}^2$ be an open bounded domain with piecewise smooth boundaries $\mathrm{\Gamma }$ as shown in Figure 1. The mathematical formulation consists of coupling Darcy problem for velocity and pressure to a convection–diffusion equation for the change in the concentration. To close the coupled system, a state equation is used to update the density distribution. These equations involve various thermophysical parameters namely the velocity u′, pressure p′, concentration of the solute c′, and the mass density ${\rho }^{\prime }$ which depend continuously on the location ${\mathbf{\text{x}}}^{\prime }=(x,z^{\prime })\in \mathrm{\Omega }$ and the time t′. The fluid is taken to be Darcian and variations in its properties other than density are ignored. Under the Boussinesq approximation, it is assumed that the density variation has no influence on the flow field except that it gives rise to buoyancy forces. With these constitutive assumptions, the governing equations in a two-dimensional domain are:

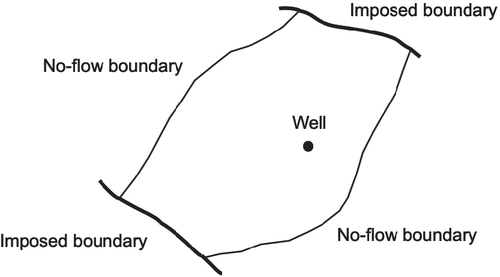
The areas of recharge and discharge along with the other areas are considered as boundary conditions. These can be specified as Neumann or Dirichlet conditions depending on the case to be studied. In the Darcy equation (1), u′ = (u′, v′)^⊤ is the velocity field, p′ the pressure, $\rho$ the density, $ϵ$ the porosity, $\mu$ the dynamic viscosity of the fluid, ${\mathrm{\Phi }}^{\prime }$ the volumetric flow rate source or sink terms, ${K_p}^{\prime }$ the permeability, g the gravitational force, and g_c is a conversion constant that can be changed so as to increase or decrease the influence of gravity in the system References 28, 29. In the transport equation (2), c′ is the concentration, Q′ the source term, ${\gamma }^{\prime }$ the rate of concentration distribution, and ${\kappa }^{\prime }$ the diffusion coefficient which may depend on the molecule size and other properties of the diffusing substance as well as on concentration and pressure. The state equation (3) describes the relationship between density and concentration by neglecting any changes in the temperature. Here, $c_0^{\prime }$ and ${\rho }_0^{\prime }$ are, respectively, the initial or reference concentration and density of the solute, and ${\beta }_c$ is the solutal expansion coefficient which depends on the solute type dissolved in the groundwater.

Note that the system (4)–(5) has to be solved in the bounded spatial domain $\mathrm{\Omega }$ with given boundary conditions on $\mathrm{\Gamma }$ and given initial conditions. Initially, the concentration is set to zero and a source of the solute is assumed to generate a propagating plume inside the domain. In this study, we propose a numerical technique combining the semi-Lagrangian method and finite element discretization for solving the coupled problem (4)-(5). We also consider a fractional step procedure where the convective part in (5) is decoupled from the generalized system of equations in the time integration process. First, the velocity and pressure are obtained by solving the Darcy problem (4) at each time step then, the concentration is updated at each time step by solving the convection equation (5).

3 A stabilized semi-Lagrangian finite element method

The symbol ∘ denotes the Hadamard product that produces vectors through element-by-element multiplication of the original two vectors. The functions ${𝒰}_j^n$, ${𝒞}_j^n$, and ${𝒫}_j^n$ are respectively, the corresponding nodal values of the velocity ${\mathbf{\text{u}}}_h^n(\mathbf{\text{x}})$, concentration $c_h^n(\mathbf{\text{x}})$ and pressure $p_h^n(\mathbf{\text{x}})$ defined as ${𝒰}_j^n=u_h^n({\mathbf{\text{x}}}_j)$, ${𝒞}_j^n=c_h^n({\mathbf{\text{x}}}_j)$ and ${𝒫}_j^n=p_h^n({\mathbf{\text{x}}}_j)$, where ${\{{\mathbf{\text{x}}}_j\}}_{j=1}^M$ is the set of mesh points in the partition ${\mathrm{\Omega }}_h$. In (7),${\{{\phi }_j\}}_{j=1}^M={\{({\varphi }_j,{\varphi }_j)\}}_{j=1}^M$ and ${\{{\varphi }_j\}}_{j=1}^M$ are the basis vectors and functions of V_h and V_h respectively given by the Kronecker delta symbol.

3.3 Time integration procedure

For simplicity in the presentation, the time integration of the coupled system is carried out using a first-order implicit Euler scheme. The method consists of the following two steps:

•  

  Step 1. Solve the Darcy problem at the next time step for ${\mathbf{\text{u}}}_h^{n+1}$ and $p_h^{n+1}$:

  $$\begin{array}{ll}{\mathbf{\text{u}}}_h^{n+1}+K_p\mathrm{\nabla }{p}_h^{n+1}& ={\mathbf{\text{f}}}_h^n,\\ \mathrm{\nabla }·{\mathbf{\text{u}}}_h^{n+1}& =\mathrm{\Phi },\end{array}$$ ()
  where ${\mathbf{\text{f}}}_h^n=K_p{R}_p(c_h^n+c_0){\mathbf{\text{e}}}_z$.

•  

  Step 2. Solve the convection–diffusion problem for $c_h^{n+1}$:

  $$\begin{array}{ll}\frac{c_h^{n+1}-{\widehat{c}}_h^n}{\mathrm{\Delta }t}-{\mathrm{\nabla }}^2{c}_h^{n+1}+\gamma c_h^{n+1}& =Q-\gamma c_{\infty }.\end{array}$$ ()

Based on the above variational formulation along with the local L²-projection stabilization technique used, Equations (21)–(22) can be written as a system of linear equations that may be represented in a matrix form as

$$\begin{array}{ll}A{\mathbf{\text{U}}}_h^{n+1}+B{P}_h^{n+1}& =F_h^n,\\ C{\mathbf{\text{U}}}_h^{n+1}+\beta D{P}_h^{n+1}& =\mathbf{\Phi },\\ ([\mathbf{\text{M}}]+\mathrm{\Delta }t[\mathbf{\text{S}}]+\mathrm{\Delta }t\gamma [\mathbf{\text{M}}]){\mathbf{\text{C}}}_h^{n+1}& =[\mathbf{\text{M}}]{\widehat{\mathbf{\text{C}}}}_h^n+\mathrm{\Delta }t(\mathbf{\text{Q}}+{\mathbf{\text{C}}}_{\infty }),\end{array}$$ ()

where ${\mathbf{\text{U}}}_h^{n+1}={({𝒰}_1^{n+1},\dots ,{𝒰}_M^{n+1})}^{\top }$, $P_h^{n+1}={({𝒫}_1^{n+1},\dots ,{𝒫}_M^{n+1})}^{\top }$, ${\mathbf{\text{C}}}_h^{n+1}={({𝒞}_1^{n+1},\dots ,{𝒞}_M^{n+1})}^{\top }$, and ${\widehat{\mathbf{\text{C}}}}_h^n={({\widehat{𝒞}}_1^n,\dots ,{\widehat{𝒞}}_M^n)}^{\top }$ according to (7). Here, A, B, C, and D are matrices whose elements are given respectively by

$$\begin{array}{ll}{a}_{ij}={\int }_{\mathrm{\Omega }}{\phi }_j\circ {\phi }_{i}d\mathrm{\Omega },b_{ij}={\int }_{\mathrm{\Omega }}{K}_p{\varphi }_j\mathrm{\nabla }{\phi }_{i}d\mathrm{\Omega },c_{ij}={\int }_{\mathrm{\Omega }}(\mathrm{\nabla }·{\phi }_j){\varphi }_{i}d\mathrm{\Omega },d_{ij}={\int }_{\mathrm{\Omega }}{\varphi }_j{\varphi }_{i}d\mathrm{\Omega },i,j=1,\dots ,M.& \end{array}$$

The right-hand sides $F_{0_h}^n$ and $\mathbf{\Phi }$ are vectors whose components are given by

$$\begin{array}{ll}{F}_h^n={\left({\int }_{\mathrm{\Omega }}{f}_h^n\circ {\phi }_{1}d\mathrm{\Omega },\dots ,{\int }_{\mathrm{\Omega }}{f}_h^n\circ {\phi }_{M}d\mathrm{\Omega }\right)}^{\top },\mathbf{\Phi }={\left({\int }_{\mathrm{\Omega }}\mathrm{\Phi }{\varphi }_{1}d\mathrm{\Omega },\dots ,{\int }_{\mathrm{\Omega }}\mathrm{\Phi }{\varphi }_{M}d\mathrm{\Omega }\right)}^{\top }.& \end{array}$$

In (23), $[\mathbf{\text{M}}]$ and $[\mathbf{\text{S}}]$ are respectively the mass and stiffness matrices whose elements are

$$\begin{array}{ll}{m}_{ij}={\int }_{\mathrm{\Omega }}{\varphi }_j{\varphi }_{i}d\mathrm{\Omega }\text{and}{s}_{ij}={\int }_{\mathrm{\Omega }}\mathrm{\nabla }{\varphi }_j\mathrm{\nabla }{\varphi }_{i}d\mathrm{\Omega },i,j=1,\dots ,M.& \end{array}$$

The terms Q and C_∞ on the right-hand side are given by

$$\begin{array}{ll}\mathbf{\text{Q}}={\left({\int }_{\mathrm{\Omega }}Q{\varphi }_{1}d\mathrm{\Omega },\dots ,{\int }_{\mathrm{\Omega }}Q{\varphi }_{M}d\mathrm{\Omega }\right)}^{\top }\text{and}{\mathbf{\text{C}}}_{\infty }={\left({\int }_{\mathrm{\Omega }}\gamma c_{\infty }{\varphi }_{1}d\mathrm{\Omega },\dots ,{\int }_{\mathrm{\Omega }}\gamma c_{\infty }{\varphi }_{M}d\mathrm{\Omega }\right)}^{\top }.& \end{array}$$

Note that in the current study, the same finite elements are used for solving both the Darcy problem and the convection–diffusion–reaction equations without requiring mixed formulations widely used in the literature. This results in a simple and efficient implementation of the method without need for mixed finite element techniques. In our simulation, linear systems of algebraic equations are solved using the conjugate gradient solver with incomplete Cholesky decomposition, and all stopping criteria for iterative solvers are set to 10⁻⁷ which is small enough to guarantee that the algorithm truncation error dominates the total numerical error.

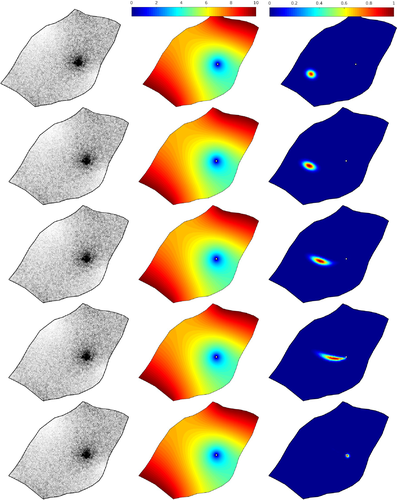
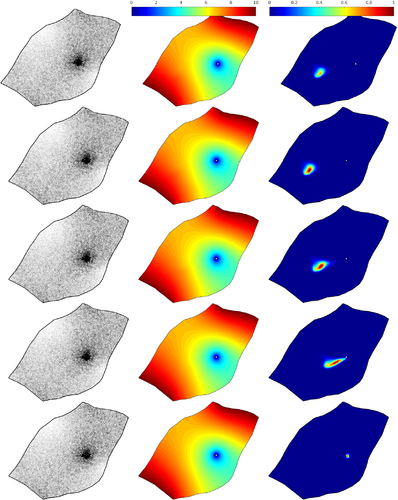
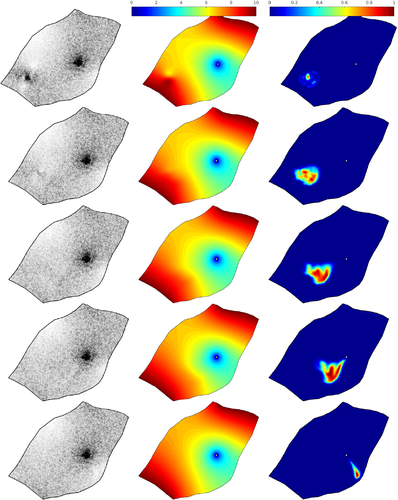
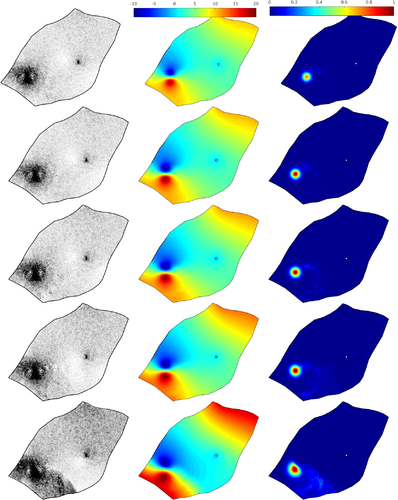
4 Numerical Results

In Figures 3-6 we depict velocity fields and snapshots of the pressure and concentration obtained at five different instants using R_p = 0, R_p = 1, R_p = 10, and R_p = 100, respectively. It should be stressed that the selection of these values for the Rayleigh number R_p is adopted here to check the performance of the proposed stabilized semi-Lagrangian finite element method for diffusion-dominated flows at R_p = 0 and convection-dominated flows at R_p = 100. In both cases, the results presented in Figures 3-6 demonstrate that the proposed method is able to simulate solute transport in groundwater at different flow regimes without requiring complicated mixed finite elements and stabilization techniques. In all considered cases, the concentration plume is transported toward the well and both velocity fields and pressure structures are altered by the solute concentration. At low Rayleigh numbers, the distribution of the solute concentration is characterized by high momentum diffusion and low momentum convection with a high local pressure around the solute. At higher Rayleigh numbers, convective term dominates and as a consequence, the solute concentration is mainly transported by the natural convection rather than the diffusion and the local pressure becomes less important. Notice that the main physical structures expected for this type of problems have been accurately captured by our stabilized semi-Lagrangian finite element method. In addition, the performance of our method is very attractive since the computed solutions remain stable without nonphysical oscillations appearing in the vicinity of sharp gradients in the solute concentration and pressure distributions. These features are resolved without requiring small time steps or solvers for nonlinear systems of algebraic equations.

5 Conclusions

In this article, a stabilized semi-Lagrangian finite element method is developed to numerically study natural convection in porous medium using coupled Darcy flow problem and a convection–diffusion equation. This can be useful in several instances such as: to accurately simulate the dispersion of solutes or pollutants released in groundwater aquifers in order to assess and predict their deplorable impact on the quality of water, to efficiently help understanding the effect of these solutes in the presence of underground services, and to assist in decision-making for optimizing the choice of underground materials. The numerical results obtained for the groundwater flow problem in an aquifer with a well are very encouraging, since they demonstrate the capability of the method to provide insight into the groundwater flow behavior in the presence of solutes or pollutants. As future works, we intend to extend the numerical method to more generalized groundwater flow problems. We will focus on studying the equations governing the hydrodynamic dispersion of a solute in heterogeneous and anisotropic porous media. In this case, the dispersion term is treated as a tensor that is characterized by the principal direction that coincides with that of the groundwater flow. Then, a spatially varying velocity field leading to an eventual change of the anisotropy direction, is expected to appear due to heterogeneity in the porous medium. This results in a system subject to a wide variety of computational difficulties which generally arise in the numerical approximation of the associated partial differential equations that should capture the effects of these spatial changes.