Funding information: COST Action: FA 1405 - ``Food and Agriculture: Using three-way interactions between plants, microbes and arthropods to enhance crop protection and production'', ---; TUBITAK (The Scientific and Technological Research Council of Turkey), TOVAG-110O160, TOVAG-110O160

About

Sections

PDF

Tools

Share a link

Email
Wechat
Bluesky

Abstract

A mathematical model is proposed for simulating and understanding the relationship between the potato plant and its most significant pest, the Colorado potato beetle, when mediated by mycorrhiza, a symbiotic plant-fungus association. From its analysis it is seen that, quite counterintuitively, an overabundant use of mycorrhiza for enhancing productivity is rather detrimental, in that it triggers persistent oscillations in the foliage and the population of the beetle, giving an instance of the paradox of enrichment. Some indications for biological pest control arise from the investigation of the bifurcations that occur in the model ecosystem.

1 INTRODUCTION

The Colorado potato beetle (CPB) originated from the south-west of North America, where it fed on plants of the genus Solanum in the family Solanaceae. It has now spread through most of North America, Europe, and Asia (especially Russia and China), feeding on the potato, Solanum tuberosum. The potato plant is native to the central Andes in South America, but is now an important and widely cultivated food crop. CPB is one of its most destructive and devastating insect pests. Chemical control has proven not to provide a long-term solution to the problems created by CPB, as the beetle has become resistant to a wide variety of chemicals. Biological control may represent a viable alternative. In this context, the use of mycorrhiza, a symbiotic association between the root of the plant and a fungus, has been advocated, as it shows interesting features. Mycorrhiza is indeed known to affect mineral composition of plants.¹ Mycorrhiza symbiosis influences several aspects of plant physiology: mineral nutrition uptake, plant growth, and plant resistance.^2-4 Among these we mention improved rooting and plant establishment, enhanced uptake of low mobile ions, improved nutrient cycling, enhanced plant tolerance to biotic and abiotic stress factors, enhanced quality of soil structure, improved plant community diversity.

The beneficial effects of mycorrhiza on plants decrease if mycorrhizal dependency levels are reduced due to various factors such as root exudates, in particular carbon, physical texture of soil, and competition with other soil-borne beneficial and disease-causing microorganisms. The development of mycorrhiza in the rhizosphere depends on root exudates, especially carbon allocated to roots and all the other factors mentioned above.

In this article we propose a model for the interactions of the three agents described above, the potato plant, the CPB, and mycorrhiza. The article is structured as follows. Section 2 contains the biological background, the following one describes the mathematical model for the mutual interactions, whose analysis for equilibria feasibility and their local stability is performed in Section 4. This section contains also the study of global stability for some of these equilibria, and of the bifurcations that relate them to each other. A final section consisting of interpretation and discussion of the model concludes the paper.

2 BIOLOGICAL BACKGROUND

The view that the likelihood of pest outbreaks is reduced with organic farming practices, including the establishment and maintenance of “healthy soil,” has long been promoted by proponents of alternative agricultural methods.^{5, 6} On the other hand, organic farmers still need to employ natural pest controls, for example, biological control, enhancing plant growth and resistance, plant varieties with pest control properties.⁷ In organic farming, a variety of practices were used to enhance soil fertility that contribute to plant resistance of insects and diseases through creating optimal physical, chemical, and, perhaps most importantly, biological properties of soil.⁸ It was reported that plants grown on organic farms were less favorable to herbivorous insects than those grown in soils treated with synthetic fertilizers^9-11 and that pest densities in organic farms are lower.^9-13

The Colorado potato beetle, Leptinotarsa decemlineata, is one of the most destructive and devastating insect pests of potato. Uncontrolled CPB populations can completely defoliate potato plants and can cause a complete loss of tuber production.¹⁴ In Reference 15 it is claimed that the control techniques against this pest developed in the past provided only limited protection of potato crops. High fecundity, flexible life history, and development of pesticide resistance are the main tasks in the control of the CPB.¹⁶ Chemical control has not yet provided long-term solutions to the problems created by CPB, so searching for alternative approaches is inevitable. If soil management could decrease beetle damage, this might provide a valuable addition to the CPB chemical control.¹⁷ In Reference 17 it was discovered that CPB populations were almost universally lower in plots receiving manure soil amendments in combination with reduced amounts of synthetic fertilizers compared with plots receiving full rates of synthetic fertilizers, but no manure. Unlike beetle abundance, plant height and canopy cover were comparable between plots receiving manure and synthetic fertilizer. Furthermore, tuber yields were higher in manure-amended plots. Thus, the difference in beetle density was unlikely to be explained simply by poor plant vigor in the absence of synthetic fertilizers. Subsequent field-cage and laboratory experiments¹⁸ confirmed that potato plants grown in manure-amended soil were indeed inferior CPB hosts compared with plants grown in synthetically fertilized soil. The observed negative effects were broad in scope. Female fecundity was lower in field cages set up on manure-amended plots early in the season, although it later became comparable between the treatments. Fewer larvae survived past the first instar, and development of immature stages was slowed down on manure-amended plots.¹⁸ Plant susceptibility to phytophagous insects is determined by behavioral responses (host finding and acceptance), developmental responses (efficiency of food utilization, developmental rate, and survivorship), or by their combination.¹⁰ Mineral composition has been shown to affect both behavioral and developmental responses of pests.^{10, 11, 18-21} Effects of soil fertility management on pest resistance can be mediated through changes in nutritional content of crops.⁸ Soil microorganisms are an important factor in the soil fertility and the health of plants. Symbiotic arbuscular mycorrhizal fungi (AMF) form a key component of the microbial populations influencing plant growth and uptake of nutrient.²² The function of AMF depends on the ability of the fungal symbiont in the absorption of nutrients available in inorganic and/or organic forms in soil. In most mycorrhizal types, organic carbon derived by photosynthesis is also transferred from the plant to the fungus followed by translocation to the growing margins of the extra radical mycelium and to the developing spores and fruit bodies.¹ The fungus, in fact, becomes an integral part of the root system. The symbiosis is considered the most metabolically active component of the absorbing organs of the autotrophic host plant, which, in addition to furnishing the heterotrophic fungal associate with organic nutrients, is an ecologically protected habitat for the fungus.^{3, 4} The physiology of the plant is highly affected by the presence of the fungal symbionts.¹ The key effects of AMF symbiosis can be summarized as follows: (1) improved rooting and plant establishment; (2) enhanced uptake of low mobile ions; (3) improved nutrient cycling; (4) enhanced plant tolerance to biotic and abiotic stress factors; (5) enhanced quality of soil structure; (6) improved plant community diversity.^2-4 Thus, AMF symbiosis influences a variety of aspects of plant physiology, such as mineral nutrition uptake, plant growth, and plant resistance. The natural roles of the organisms in the mycorrhizosphere (the zone influenced by both the root and the mycorrhizal fungus) may have been marginalized in intensive agriculture, since microbial communities in conventional farming systems have been modified due to tillage, and high inputs of inorganic fertilizers, herbicides, and pesticides.²³ Microbial diversity in these systems has been reduced.²⁴ As a consequence, AMF fungi seem to be only of minor importance under conventional agricultural conditions, whereas the AMF symbiosis is regarded as a key component of sustainable agriculture.

We formulate the following hypothesis: soil amendment using arbuscular mycorrhiza may be helpful to achieve an optimal nutrient condition that results in both good plant health and resistance to herbivory in ecologically sound crop management systems. However, the effect of soil amendment on the ecology of pests needs to be closely monitored and studied for a sustainable organic farming system.

The overall objective of research in this domain is to determine the effect of soil amendment using AMF on potato tolerance to CPB. In order to accomplish the whole objective, the following specific objectives have been established and need to be answered from the biological prospective:

To determine the impacts of AMF on the development, survival, and fecundity, that is, the population parameters of the Colorado potato beetle.
To determine the impacts of AMF on feeding capacity (or the consumption rate and the damage potential) of the Colorado potato beetle.

While these objectives pertain to field and laboratory experiments, their outputs will be needed for the simulations of the mathematical model describing the interactions of the three populations.

3 THE MODEL

We consider the following time-dependent populations: B represents the Colorado potato beetle population, L denotes the potato leaf area, and M is the symbiotic association of fungus with the potato plant, that is, the mycorrhiza.

The equations that describe the model are the following ones:

\begin{align} B^{'} & = e a (M) B \frac{L}{1 + h L} - n B - b B^{2}, \\ L^{'} & = s L - m L - c L^{2} + p L g (M) - a (M) B \frac{L}{1 + h L}, \\ M^{'} & = r M - d M - f M^{2} + (1 - p) g (M) L . \end{align}

()

In the equation for the plant leaf area L, the first term assumes that the potato plant has enough resources so that it can grow, that is, the leaves can extend their surface at rate s. Furthermore, they are subject to losses, modeled in the next two terms. They may experience natural mortality at rate m and also competition for resources, at rate c. This occurs primarily for light, when the lower leaves are somewhat overshadowed by the uppermost ones. In addition, we consider the interactions that are described in what follows. There is a direct beneficial influence that the leaves receive from the mycorrhiza, modeled by the function g(M), which occurs only if leaves are present and disappears if L = 0, as is given by the fourth term in the second equation. Note also that we assume that only a fraction p of the mycorrhiza is used for this task. Moreover, there is a loss of leaves due to the predation exerted by the grazing beetles, modeled in the last term. The function L(1 + hL)⁻¹ expresses the beetles' feeding saturation. This harvest function is mitigated by the influence of the mycorrhiza, via the function a(M). Note that the function a(M) is taken to be a decreasing function of M, so that the larger M is, the more effective the reduction by the mycorrhiza of the damage incurred.

The beetle population, modeled in the first equation, is assumed to grow as long as leaves are available, with a feeding saturation feature, modeled via a Holling type II functional response of the resource L, where the maximal intake of food per unit of time is h⁻¹ and with conversion coefficient e. Furthermore, as remarked above, its growth rate is also hindered by the presence of the mycorrhiza and is expressed by the decreasing function a(M). In addition, beetles have a natural mortality rate n, second term, and compete with each other for grazing on the leaves, at intraspecific competition rate b, third term.

The last equation models the mycorrhiza dynamics. It grows at rate r, has natural mortality d, intraspecific competition rate f, facts expressed respectively by the first three terms in the third equation of (1). Furthermore, this population can benefit itself, the feature being modeled by the last term in the equation. In this last process, we assume that only the portion 1 − p of mycorrhiza that does not contribute to the enhancement of the leaves growth rate can be used by the mycorrhiza itself for its own benefit. In this preliminary model we shall take p = 1 and b = 0, assuming thereby that all the mycorrhiza is used to hinder the herbivores and the latter have enough available food and do not compete for it. Again, assuming that mycorrhiza contributes to a reduction in the beetle reproduction rate, the specific form for the function modeling the mycorrhiza effects is:

\begin{align} a (M) = a_{0} - \frac{(a_{0} - a_{1}) M}{a_{2} + M} > 0, a_{1} < a_{0}, a_{2} > 0 . \end{align}

()

Note that a is decreasing with a(0) = a₀, a(M) → a₁ as M → ∞. Strictly speaking, a(M) is defined for M ≥ 0 only, but in order to analyze the bifurcation structure of the system we can and shall extend it to M < 0 as long as M > −a₂. Two possible alternatives for the direct effect of M on the leaves growth rate can be considered:

g (M) = g_{1} M, g (M) = \frac{g_{1} M}{g_{2} + M} .

Here for simplicity we consider only g(M) = g₁M, but there are no major differences in the analysis with the alternative form for g. Finally, for notational simplicity only, we shall henceforth define h(L) = 1/(1 + hL).

Table 1 lists all the model parameters with their meaning.

TABLE 1. The model parameters

Parameter	Interpretation
n	Mortality rate of B
m	Mortality rate of L
d	Decreased growth rate of M
b	Intraspecific competition rate among B
c	Intraspecific competition rate among L
f	Intraspecific competition rate among M
e	Conversion factor
a(M)	Direct mycorrhiza-induced inhibition on beetle growth rate
a₀	Basic (maximal) beetles harvesting rate
a₁	Minimal beetles harvesting rate due to mycorrhiza presence
h⁻¹	Beetle feeding saturation level
g(M)	Direct enhancement of M on the growth rate of L
g₁	Mycorrhiza enhancement rate on leaves growth
p	Portion of mycorrhiza used for leaves growth enhancement
1 − p	Portion of mycorrhiza used for mycorrhiza's own benefit
s	Growth rate of L
r	Growth rate of M

The system, after the previous assumptions, becomes

\begin{align} B^{'} & = e a (M) B L h (L) - n B, \\ L^{'} & = s L - m L - c L^{2} + g_{1} M L - a (M) B L h (L), \\ M^{'} & = r M - d M - f M^{2}, \end{align}

()

with Jacobian:

J = (\begin{matrix} e a (M) L h (L) - n & e a (M) B {(h (L))}^{2} & e a^{'} (M) B L h (L) \\ - a (M) L h (L) & J_{2, 2} & g_{1} L - a^{'} (M) B L h (L) \\ 0 & 0 & r - d - 2 f M \end{matrix}),

()

where

J_{2, 2} = s - m - 2 c L + g_{1} M - a (M) B {(h (L))}^{2} .

()

We shall often be concerned with the eigenvalues of the two-by-two minor M⁽²⁾ given by

M^{(2)} = (\begin{matrix} e a (M) L h (L) - n & e a (M) B {(h (L))}^{2} \\ - a (M) L h (L) & s - m - 2 c L + g_{1} M - a (M) B {(h (L))}^{2} \end{matrix}) .

()

M is uncoupled in the system (3), and M(t) → 0, if r < d or if r > d, M tends to

M_{2} = (r - d) / f .

The first two equations with M = 0 or with M = M₂ are versions of the Rosenzweig-MacArthur²⁵ predator-prey model, whose behavior is well known. The matrix M⁽²⁾ with M = 0 or with M = M₂ are the Jacobian matrices for these two versions.

4 ANALYSIS

4.1 Boundedness

First note that the system (3) is in Kolmogorov form, so that the positive octant is invariant. Next observe that the third equation of (3) is uncoupled from the first two. If r < d, clearly M tends monotonically to zero, so that it is bounded by the initial condition M(0). Otherwise, the equation is logistic, so that for large T_M, for all t ≥ T_M, we have the bound

M (t) < M_{2} + η

, M₂ = (r − d)f⁻¹. Thus finally, for all t > 0,

\begin{align} M (t) \leq \hat{M} = \max {M (0), M_{2} + η} . \end{align}

()

(Alternatively, and more simply, it follows from the fact that M decreases whenever it is greater than M₂ that

M (t) \leq \hat{M} = \max {M (0), M_{2}}

for all t > 0.) Let us define the nonnegative quantity P = B + eL. Summing the first two equations in (3) we obtain

\begin{align} P^{'} = e (s L - m L - c L^{2} + g_{1} M L) - n B . \end{align}

Hence P′ = 0 when

\begin{align} n B = e (s L - m L - c L^{2} + g_{1} M L) \leq e (s L - m L - c L^{2} + g_{1}) \hat{M} L = Q (L), \end{align}

say, where nB = Q(L) is a concave parabola in the (L, B) plane with Q(0) = 0. If

s - m + g_{1} \hat{M} < 0

then Q(L) < 0 for L > 0, and P decreases everywhere in the positive quadrant of the (L, B) plane. Alternatively

s - m + g_{1} \hat{M} > 0

, Q increases and then decreases past zero for L > 0, and P decreases everywhere above nB = Q(L). In the first case P(t) → 0 as t → ∞, so both B(t) and L(t) do. In the second case we can construct nested positively invariant sets D_K in (B, L, M) space defined by

\begin{align} D_{K} = {(B, L, M) | L \geq 0, B \geq 0, P \leq K, 0 \leq M \leq \hat{M}} . \end{align}

Any initial conditions are in D_K for K sufficiently large, and the trajectory from these initial conditions remains in D_K for all t ≥ 0, so all trajectories are bounded.

4.2 Equilibria and their feasibility

The following equilibria are easily established. The origin, E₁, then the points E_k = (B_k, L_k, M_k), which specifically are:

\begin{align} E_{2} & = (0, 0, M_{2}) = (0, 0, \frac{r - d}{f}), E_{3} = (0, L_{3}, 0) = (0, \frac{s - m}{c}, 0), \\ E_{4} & = (0, L_{4}, M_{4}), L_{4} = \frac{s - m}{c} + \frac{g_{1}}{c} \frac{r - d}{f}, M_{4} = \frac{r - d}{f} . \end{align}

Respectively, they are feasible for

(E_{2}) : r \geq d, (E_{3}) : s \geq m, (E_{4}) : r \geq d and f (s - m) + g_{1} (r - d) \geq 0 .

()

Next, we find E₅ = (B₅,L₅,0), with, explicitly,

B_{5} = \frac{1}{a_{0}} (s - m - c L_{5}) (1 + h L_{5}), L_{5} = \frac{n}{e a_{0} - n h},

and with feasibility conditions:

e a_{0} > n h, s - m \geq c L_{5} = \frac{c n}{e a_{0} - n h} .

()

Finally we have coexistence E₆ = (B₆, L₆, M₆) with population values

\begin{align} B_{6} = \frac{1 + h L_{6}}{f a (M_{6})} [g_{1} (r - d) + f (s - m) - f c L_{6}], L_{6} = \frac{n}{e a (M_{6}) - n h}, M_{6} = \frac{r - d}{f}, \end{align}

which is feasible for

r \geq d, e a (M_{6}) > n h, g_{1} (r - d) + f (s - m) \geq f c L_{6} = \frac{f c n}{e a (M_{6}) - n h} .

()

Note that M₂ = M₄ = M₆, since the M equation is uncoupled from the system.

4.3 Stability of equilibria

For the local stability of the equilibria, we find the following results.

At the origin E₁, the Jacobian eigenvalues are −n, s − m, and r − d, which give the local stability conditions

r < d, s < m .

()

At E₂ we instead find eigenvalues −n, s − m + g₁M₂, r − d − 2fM₂, giving with M₂ = (r − d)/f the local stability conditions:

r > d, g_{1} (r - d) + f (s - m) < 0,

()

the first always satisfied if E₂ is feasible with M₂ > 0.

For E₃ the eigenvalues are

e a_{0} L_{3} h (L_{3}) - n, - (s - m), r - d,

therefore E₃ is stable if

r < d, s > m, (e a_{0} - n h) L_{3} < n .

()

The second condition is always satisfied if E₃ is feasible with L₃ = (s − m)/c > 0. The third condition is satisfied (with L₃ = (s − m)/c > 0) if either (a) ea₀ < nh (or equivalently L₅ < 0) or (b) ea₀ > nh (or equivalently L₅ > 0) and s − m < nc/(ea₀ − nh) (or equivalently s − m < cL₅ or B₅ < 0). In other words, the third condition is satisfied if E₅ is not feasible.

At E₄ we have

\begin{align} e a (M_{4}) L_{4} h (L_{4}) - n, s - m - 2 c L_{4} - g_{1} M_{4}, - (r - d) . \end{align}

The stability conditions in this case, with L₄ = (g₁(r − d) + f(s − m))/(fc) and M₄ = (r − d)/f, are

r > d, g_{1} (r - d) + f (s - m) > 0, (e a (M_{4}) - n h) (g_{1} (r - d) + f (s - m)) < n c f .

()

If L₄ > 0 and M₄ > 0 the first two conditions are automatically satisfied. Noting that M₄ = M₆, the third is satisfied if either (a) ea(M₆) < nh (or equivalently L₆ < 0) or (b) ea(M₆) > nh (or equivalently L₆ > 0) and g₁(r − d) + f(s − m) < ncf/(ea(M₆) − nh) (or equivalently s − m + g₁M₆ < cL₆ or B₆ < 0). In other words, the third condition is satisfied if E₆ is not feasible.

For E₅ one eigenvalue factorizes, r − d, to give

r < d .

()

The remaining eigenvalues arise from the two-by-two minor defined in (6), given at this point by

M_{5}^{(2)} = M^{(2)} (E_{5}) = (\begin{matrix} 0 & e a_{0} B_{5} {(h (L_{5}))}^{2} \\ - a_{0} L_{5} h (L_{5}) & - c L_{5} + a_{0} B_{5} h (L_{5}) (1 - h (L_{5})) \end{matrix}),

()

where we have used the equilibrium equations to simplify the diagonal components. The Routh-Hurwitz conditions for stability are tr(M₅) < 0 and

\det M_{5} > 0

. Clearly the determinant condition is satisfied whenever E₅ is feasible, so we only need to satisfy the trace condition, given by

tr (M_{5}) = - c L_{5} + a_{0} B_{5} h (L_{5}) (1 - h (L_{5})) < 0 .

()

But a₀B₅h(L₅) = s − m − cL₅, and 1 − h(L₅) = hL₅/(1 + hL₅), so if L₅ > 0 this simplifies to

s - m < 2 c L_{5} + \frac{c}{h} = \frac{2 n c}{e a_{0} - n h} + \frac{c}{h} .

()

At coexistence E₆ one eigenvalue factorizes again, d − r, and provides the first stability condition

r > d,

()

always true if E₆ is feasible so that M₆ = (r − d)/f > 0. Here the remaining minor is given by

M_{6}^{(2)} = M^{(2)} (E_{6}) = (\begin{matrix} 0 & e a (M_{6}) B_{6} {(h (L_{6}))}^{2} \\ - a (M_{6}) L_{6} h (L_{6}) & - c L_{6} + a (M_{6}) B_{6} h (L_{6}) (1 - h (L_{6})) \end{matrix}),

()

again simplifying using the equilibrium equations. The Routh-Hurwitz determinant condition is once more always satisfied if E₆ is feasible, and we only need to satisfy the trace condition,

tr (M_{6}) = - c L_{6} + a (M_{6}) B_{6} h (L_{6}) (1 - h (L_{6})) < 0 .

()

But M₆ = (r − d)/f, a(M₆)B₆h(L₆) = s − m − cL₆ + g₁M₆, and 1 − h(L₆) = hL₆/(1 + hL₆), so if L₆ > 0 this simplifies to

f (s - m) + g_{1} (r - d) < 2 f c L_{6} + \frac{f c}{h} = \frac{2 f n c}{e a (M_{6}) - n h} + \frac{f c}{h} .

()

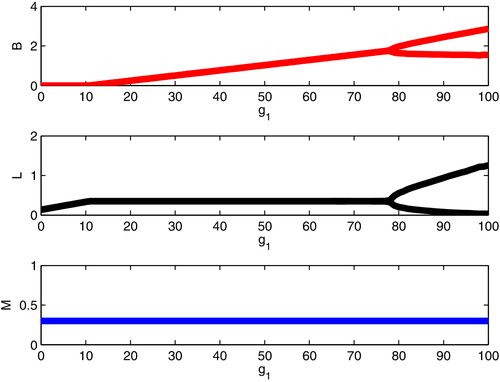
Remark. Note that, whenever the trace vanishes, a Hopf bifurcation arises, in view of the fact that the determinant is positive. A discussion of this occurrence can be found below, and an illustration through a simulation is reported in Figure 2.

In Table 2 we summarize the possible equilibria of system (3) and in Table 3 their salient features.

TABLE 2. The equilibria of system (3)

Point	Population values
E₁ = (0, 0, 0)	(0, 0, 0)
E₂ = (0, 0, M₂)	$(0, 0, \frac{r - d}{f})$
E₃ = (0, L₃, 0)	$(0, \frac{s - m}{c}, 0)$
E₄ = (0, L₄, M₄)	$(0, \frac{s - m}{c} + \frac{g_{1}}{c} \frac{r - d}{f}, \frac{r - d}{f})$
E₅ = (B₅, L₅, 0)	$(\frac{(s - m - c L_{5}) (1 + h L_{5})}{a_{0}}, \frac{n}{e a_{0} - n h}, 0)$
E₆ = (B₆, L₆, M₆)	$(\frac{(s - m - c L_{6} + g_{1} M_{6}) (1 + h L_{6})}{a (M_{6})}, \frac{n}{e a (M_{6}) - n h}, \frac{r - d}{f})$

TABLE 3. The feasibility and stability conditions for the equilibria of system (3)

	Feasibility	Stability (if feasible)
E₁	Always feasible	r < d, s < m
E₂	r ≥ d	g₁(r − d) + f(s − m) < 0
E₃	s ≥ m	r < d, (ea₀ − nh)(s − m) < nc
E₄	r ≥ d, g₁(r − d) + f(s − m) ≥ 0	(ea(M₆) − nh)(g₁(r − d) + f(s − m)) < ncf
E₅	ea₀ > nh, s − m ≥ cL₅	r < d, s − m < 2cL₅ + c/h
E₆	r ≥ d, ea(M₆) > nh,	f(s − m) + g₁(r − d) < 2fcL₆ + fc/h
	g₁(r − d) + f(s − m) ≥ fcL₆

Note: The stability conditions are given assuming the feasibility conditions hold with strict inequality.

4.4 Global stability issues

In this section we consider some of the equilibria and formally show, for mathematical sake, their global stability. For the remaining more complicated ones, we discuss here briefly some of their features.

Note that E₂, E₃, and E₄ are not globally stable when they are stable, because trajectories starting at the origin do not tend to them, but they are globally stable for initial conditions in the interior of the positive octant.

For the remaining nontrivial equilibria E₅ and E₆ note that for r < d, all trajectories tend to the plane M = 0, as seen above in Subsection 4.1. Bounded trajectories in the plane M = 0 can only tend to either an equilibrium or a periodic solution surrounding an equilibrium. If E₅ is not feasible there is no equilibrium to surround, so the trajectory tends to an equilibrium in that plane, that is, E₃. A similar situation occurs for r > d if E₆ is not feasible, with the plane M = M₆, in this case with possible omega points E₂ or E₄.

4.4.1 E₁

On the assumption that the origin E₁ is stable, namely (11) hold, we show that the ecosystem collapse follows.

In the above assumptions, considering the mycorrhiza equation and an arbitrary

η > 0

, for a suitable T_M0 that depends on

η

, for all t > T_M0, it follows for some k > 0

M^{'} = r M - d M - f M^{2} + (1 - p) g (M) L < - k M .

Hence

M (t) < η

whenever t > T_M0. Thus from the second equation we obtain, for t > T_M0 and imposing

η - (m - s) g_{1}^{- 1} = - θ < 0

L^{'} < (g_{1} η + s - c L - m) L < - θ L

from which L → 0. Thus for t > T_L0 > T_M0,

L (t) < ξ

. From the first equation using M(a₂ + M)⁻¹ < 1 it follows then for

ε = n - e a_{1} ξ > 0

B^{'} = [\frac{e a_{1} L}{1 + h L} - n] B < (e a_{1} ξ - n) B < - ε B,

so that also B → 0. This result is independent of the initial conditions, which means that starting from any arbitrary point in the phase space, the trajectories ultimately approach the origin, if conditions (11) hold.

4.4.2 E₂

We now consider equilibrium E₂. Again assuming its local stability, namely that (8) and (12) hold, from the mycorrhiza equation we find the logistic behavior, that is, M → M₂. Thus for an arbitrary

η > 0

, for all t > T_M2,

| M (t) - M_{2} | < η

. The second equation in (3) then yields:

\begin{align} L^{'} < [g_{1} (M_{2} + η) + s - c L - m] L . \end{align}

Observe that from (12) it follows that g₁M₂ < m − s, so that if we restrict

η < (m - s - g_{1} M_{2}) g_{1}^{- 1}

and let

θ = m - s - g_{1} (M_{2} + η) > 0

, the differential inequality is further bounded from above by

L^{'} < - θ L

. Hence, for any arbitrary 0 < ε < n[ea(M₂)]⁻¹ and for all t > T_L2 > T_M2, we have the estimate L(t) < ε. Finally from the Colorado potato beetle equation, we obtain the following inequalities

\begin{align} B^{'} \leq [e a (M_{2}) \frac{L}{1 + h L} - n] B < [e a (M_{2}) ε - n] B < - ζ B \end{align}

for an arbitrary

ζ < n - e a (M_{2}) ε

. Thus for all t > T_B2 > T_L2, we find that B → 0. This result is once more independent of the initial conditions provided they are taken in the interior of the positive octant, showing thus in this region the global stability of E₂ having assumed that (12) holds.

4.4.3 E₃

As in the first above case, from the third equation we can deduce that for all t > T_M3 the mycorrhiza population satisfies

M (t) < η

for an arbitrary

0 < η < m g_{1}^{- 1}

. The second equation can again be estimated from above by

\begin{align} L^{'} < [g_{1} η + s - c L - m] L \end{align}

and by (13) now this population tends to its carrying capacity L₃, so that for an arbitrary

ξ

, for all t > T_L3 we find

| L - L_{3} | < ξ

. From the last stability condition (13), we can take

0 < κ < n (1 + h L_{3}) - e a_{0} L_{3} - (e a_{0} L_{3} + n h) ξ

. The first equation in (3) can be estimated then as follows, recalling (2):

\begin{align} B^{'} & < [e a_{0} \frac{L}{1 + h L} - n] B < [\frac{e a_{0} (L_{3} + ξ)}{1 + h (L_{3} - ξ)} - n] B \\ < [e a_{0} L_{3} - n (1 + h L_{3}) + (e a_{0} L_{3} + n h) ξ] B < - κ B, \end{align}

from which once again b → 0 follows from any initial condition in the interior of the positive octant. Thus global stability, in the interior of the positive octant, is proved also in this case.

4.4.4 E₄

Once again here from the third equation we find that it has a logistic behavior from the first stability condition (14). For a sufficiently small

η > 0

, such that

a_{2} + M_{4} > η

, we then ultimately obtain that

| M - M_{4} | < η

. From the first equation of the model (3), we have

\begin{align} B^{'} & \leq [e \frac{a_{0} a_{2} + a_{1} M_{4}}{a_{2} + M_{4} - η} \frac{L}{1 + h L} - n - η e \frac{a_{0} - a_{1} + a_{0}}{a_{2} + M_{4} - η} \frac{L}{1 + h L}] B \\ = \frac{1}{a_{2} + M_{4} - η} [\frac{e (a_{0} a_{2} + a_{1} M_{4}) L}{1 + h L} - n (a_{2} + M_{4}) + n η - \frac{η e (2 a_{0} - a_{1}) L}{1 + h L}] B \\ \leq \frac{a_{2} + M_{4}}{a_{2} + M_{4} - η} [e \frac{a_{0} a_{2} + a_{1} M_{4}}{a_{2} + M_{4}} - n + \frac{η}{a_{2} + M_{4}} (n - e \frac{(2 a_{0} - a_{1}) L}{1 + h L})] B \\ \leq \frac{a_{2} + M_{4}}{a_{2} + M_{4} - η} [- ξ + \frac{η n}{a_{2} + M_{4}}] B, \end{align}

where the last inequality follows in view of the assumption (2) on the coefficients of a(M), and by using the stability condition (14), setting:

- ξ = e \frac{a_{0} a_{2} + a_{1} M_{4}}{a_{2} + M_{4}} - n < 0 .

Finally, by choosing

- θ = η [ξ + n (a_{2} + M_{4}) - ξ (a_{2} + M_{4})] < 0

for large t we find

B^{'} \leq - θ \frac{a_{2} + M_{4}}{a_{2} + M_{4} - η} B,

from which B → 0, as required, from any initial condition. From the second equation of the model (3), since a(M) > 0 for all M, we then find the estimate

\begin{align} L^{'} \leq [g_{1} (M_{4} + η) + s - c L - m] L . \end{align}

Thus for t > T_L4 the following bound holds for any arbitrary

ζ > 0

|L_{4} + \frac{g_{1} η}{c} - L| < ζ,

which corresponds to

| L_{4} - L | < κ

in view of

- ζ - η \frac{g_{1}}{c} < L_{4} - L < ζ - η \frac{g_{1}}{c}, κ = ζ + η \frac{g_{1}}{c} .

Hence, L → L₄ as desired, from any initial condition in the interior of the positive octant.

4.5 Bifurcations

The bifurcations that occur in the system are shown in Figure 1. The bifurcation curves (or lines) are marked with the bifurcation that occurs as they are crossed. Curves marked with two numbers XY represent a transcritical bifurcation between E_X and E_Y. For example, the negative s − m axis in panel (i) is a bifurcation curve marked 12, and E₂ passes through E₁ and becomes stable through a transcritical bifurcation as r increases through d and the curve is crossed from left to right. Dashed curves are also bifurcation curves marked in the same way, but there is no interchange of stability. The curves marked H5 and H6 represent Hopf bifurcations, so, for example, E₆ loses stability through a Hopf bifurcation leading to a periodic solution (which we call H(E₆)) as H6 is crossed from below to above in the right-hand half plane. Again, there is no transfer of stability on the dashed parts of these curves. Finally, the curve H56 represents a bifurcation between H(E₅) and H(E₆), with H(E₆) passing through H(E₅) and becoming stable as the curve is crossed from left to right. Note that H(E₅) is a periodic solution in the M = M₅ = 0 plane, while H(E₆) is a periodic solution in the M = M₆ = (r − d)/f plane, and they coincide when M₆ = 0, that is, when r = d.

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

The figure represents bifurcation curves (or lines) in two-dimensional parameter space, with bifurcation parameters r − d and s − m. It indicates the bifurcations that occur as we cross the curves and the asymptotic behavior of the system in the regions of parameter space bounded by the curves. Bifurcation curves with the same asymptotic behavior on either side are shown as dashed lines. Panel (i) is for the case ea₁ < ea₀ < nh, (ii) for ea₁ < nh < ea₀, and (iii) for nh < ea₁ < ea₀

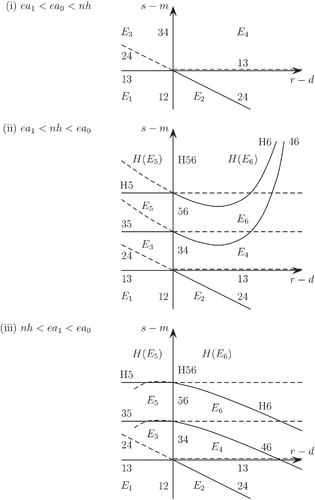
There is no bistability in the system, so that its asymptotic behavior may be marked unambiguously in each region bounded by the bifurcation curves. There is no change in asymptotic behavior on crossing a dashed curve.

The s − m axis is unusual in that (because M₂ = M₄ = M₆ = 0) several bifurcations occur simultaneously as it is crossed, namely 12 and 34, and 56 and H56 when the parameters are such that E₅ and E₆ exist. The one that we have marked on each part of the axis in the figure is the one where an interchange of stability occurs. For example, E₂ passes through E₁ with an interchange of stability on crossing 12; E₄ also passes through E₃ but does not become feasible or stable, since L₃ = L₄ < 0 here.

4.5.1 Case (i): ea₁ < ea₀ < nh

This case is the simplest, since both L₅ and L₆ are negative (whatever the value of M₆ = (r − d)/f), so neither E₅ nor E₆ can be a feasible equilibrium. The only bifurcation curves are 12, 34, 13, and 24. The equilibrium E₁ is stable between 12 and 13, E₂ between 12 and 24, E₃ between 13 and 34, and E₄ between 24 and 34, as shown, always disregarding the dashed lines when seeking a change of asymptotic behavior.

4.5.2 Case (ii): ea₁ < nh < ea₀

In this case L₅ > 0, so E₅ is a feasible equilibrium as long as B₅ > 0. L₆ > 0 if ea(M₆) > nh, or M₆ = (r − d)/f < M_crit = a⁻¹(nh/e). Both L₆ > 0 and M₆ > 0 if (r − d) is sufficiently small and positive, and then E₆ is feasible if B₆ > 0. Three additional transcritical bifurcation curves appear in the figure: line 35, where s − m = cL₅, or B₅ = 0; line 46, where s − m + g₁M₆ = cL₆, or B₆ = 0; and line 56, where M₆ = 0. Two Hopf bifurcation curves also appear: H5, where s − m = 2cL₅ + c/h, or $tr (M_{5}^{(2)}) = 0$ ; and H6, where s − m + g₁M₆ = 2cL₆ + c/h, or $tr (M_{6}^{(2)}) = 0$ . Finally H56 appears, the bifurcation with an interchange of stability between the two periodic Hopf solutions H(E₅) and H(E₆). The s − m axis is divided into 12, 34, 56, and H56, as shown.

4.5.3 Case (iii): nh < ea₁ < ea₀

In this case, both L₅ and L₆ are positive wherever we are in the (r − d, s − m) plane, but there are still conditions for B₅ > 0 and B₆ > 0. The lines 46 and H6 look rather different (because their vertical asymptotes are now in the left half plane), but the bifurcations we see are essentially the same as in case (ii).

4.5.4 Bifurcation parameters g₁ and a₁

We have discussed bifurcations with the parameters r − d and s − m, and sketched the bifurcation curves in (r − d, s − m) space.

Armed with that information, it is possible to deduce the bifurcations that occur with other parameters. Biologically important parameters are g₁, a measure of the direct benefit of the mycorrhiza on the plant, and (a₀ − a₁), the maximum mycorrhizal inhibition of herbivory.

So let us fix r > d (otherwise the mycorrhiza cannot survive) and s > m (otherwise the plant cannot survive in the absence of mycorrhiza) and decrease a₁ from a₀, or increase the mycorrhizal inhibition of herbivory from zero. If ea₀ < nh there is essentially no effect, as herbivory is too small even without mycorrhiza to allow the beetle to survive. But if ea₀ > nh then we move from case (iii) to case (ii), as the lines 46 and H6 acquire a vertical asymptote (at a value of r − d defined by ea((r − d)/f) = nh). It is easy to show that the lines 46 and H6 move upward as a₁ decreases, so that the sequence of bifurcations is H(E₆) to E₆ to E₄, at least for r − d and s − m sufficiently large. The beetle is driven to extinction, and we are left with the plant and the symbiotic mycorrhiza.

Now consider the effect of increasing g₁, with nh < ea₁ < ea₀. The lines f(s − m) + g₁(r − d) = 0, f(s − m) + g₁(r − d) = fcL₆, and f(s − m) + g₁(r − d) = 2fcL₆ + fc/h become steeper, and a typical progression is from E₄ to E₆ to H(E₆). This destabilization of the system, allowing the beetle to invade, is detrimental to the plant. It is an example of the paradox of enrichment,²⁶ where an increase in the resources available to a prey species leads to destabilization of a prey-predator system.

A numerical simulation to this effect relates this behavior, see Figure 2.

5 INTERPRETATION AND DISCUSSION

The model introduced here contains a combination of predator-prey and symbiotic mechanisms. CPB harvests the plants leaves, but the latter receive benefit from and provide benefit to mycorrhizal fungi. In this three populations interactions, CPB still negatively affects the plant, but with some mitigation provided by mycorrhiza, which also directly enhances plant growth.

The model indicates that for increasing values of the benefit that the fungus exerts on the leaves, expressed by the parameter g₁ on the horizontal axis of Figure 2, at first the beetles are absent, see the top frame, for low values of the mycorrhiza enhancement rate on the growth of the leaves. Then past the value g₁ = 10, CPBs invade the plant attaining larger and larger numbers, the higher g₁ becomes. Correspondingly, in the middle frame the leaves have an initial benefit in the absence of the beetles, and grow linearly with g₁. When the beetles are present, the leaves are kept at a constant level, without being able to increase even by increasing the mycorrhiza enhancement rate, g₁. Then at a value near 80 the beetle and leaves populations start to persistently oscillate. In so doing, the leaves drop to alarmingly low levels, which most likely indicates the plant death. Furthermore, this destabilization of the system through higher mycorrhizal input rates induces persistent oscillations that favor beetle invasion, which in turn hinders plant thriving. The phenomenon is known as the paradox of enrichment.²⁶ Although we might have expected that increasing g₁ and decreasing a₁ would both be beneficial to the plant, in fact the paradox of enrichment implies that increasing g₁ beyond a certain threshold is instead detrimental, while decreasing a₁ is indeed beneficial.

Looking at the possible ecosystems outcomes, see Table 2, the equilibrium that should absolutely be avoided is E₂. To achieve this goal, it should be rendered either unfeasible or unstable. The feasibility issue entails that mycorrhiza mortality should exceed its reproduction rate. This is quite unexpected, but it is linked to the above remarks on the paradox of enrichment. Alternatively, the stability condition could be violated. Note that if feasible, for stability to hold, the requirement s < m is necessary, which means that the plant dies off, as is implied by the population values of the equilibrium itself. But to reverse the inequality and obtain fs > fm − g₁(r − d), a condition that ensures instability, is probably biologically not possible. How indeed to enhance the growth rate of a plant under attack by its predators in practice?

Also possibly to be avoided is E₅, because there mycorrhiza vanishes. There are four conditions among feasibility and stability. The occurrence of this equilibrium could be prevented by ensuring that the mycorrhiza net growth rate s − m is kept at low values, lower than cL₅. Maybe a way of doing it is by pruning the leaves.

Coexistence, E₆, implies that the CPB persists in the environment. In such case, perhaps external interventions could be aimed at keeping low the beetle population, while enhancing the foliage L₆. This can be obtained by reducing r − d, thereby externally incrementing the mycorrhiza death rate d to levels close to its reproduction rate r, or by incrementing its intraspecific competition rate f. Again, this is counterintuitive, but related to the paradox of enrichment. To increase the foliage instead entails increasing the CPB mortality rate n, possibly, again with external measures, or reducing the gap between ea(M₆) and nh, which could be obtained by reducing h, which means increasing the beetles' feeding saturation level. This may not be a viable biological measure, however.

The CPB-free equilibria are E₁, E₃, E₄, but the first one is not acceptable as the ecosystem collapses. To attain the latter two beneficial equilibria, the necessary feasibility conditions require s > m and r < d, while for E₄, r > d. Moreover, additional more complicated inequalities are needed. For E₃ one must impose either ea₀ < nh or an upper bound on s − m. At E₄, s − m could also be negative, provided that g₁(r − d) + f(s − m) is positive. But in addition, it should either be bounded above, or ea(M₆) < nh, to achieve stability. Also, in view of the transcritical bifurcation between them, the two system's outcomes E₃ and E₄ cannot occur simultaneously.

Alternative control measures as mentioned could consider both the feasibility and stability conditions of the above relevant equilibria. However, more is needed as in such case, the transcritical bifurcation analysis of Subsection 4.5 proves to be instrumental, in that the possible measures taken should have in mind their outcomes, so as not to destabilize a configuration and then ending up in a worse one. For instance, in case the system is settling toward E₅, where mycorrhiza disappears, the beetles and plant thriving together, we are in case (ii) or (iii) of Figure 2, as ea₀ > nh at this point. From the bifurcation diagrams, an increase in the net mycorrhiza reproduction rate r − d to make it positive would push the system toward coexistence, which does not help if the goal is beetles eradication. Only a further increase of r − d to higher positive values could make the system attain the best possible beetle-free equilibrium E₄. Instead, an increase of s − m past the value 2cL₅ + c/h triggers oscillations, without altering the presence of the populations thriving already at E₅. One should strive instead to reduce s − m so as to achieve the desirable but mycorrhiza-free equilibrium E₃. From it, moving toward positive values of r − d would yield the optimal ecosystem outcome, E₄. Whether biological means of achieving these transitions are not only available, but also implementable in practice is still debatable.

The proposed system is a first attempt to model these three populations interactions. It still has some drawbacks, but nevertheless its analysis sheds some light on its possible outcomes. Among the shortcomings of this model, we observe that the mycorrhizal equation is almost essentially uncoupled from the rest of the system. There is indeed no direct influence of leaves on mycorrhiza. Perhaps a better formulation should account for the whole plant as a dependent variable, in place of just the leaves. We shall leave this for a subsequent investigation.

Biographies

Remzi Atlihan received Bachelor's degree (1990): Yuzuncu Yil University, Faculty of Agriculture, Department of Plant Protection. PhD degree (1997): Çukurova University, Institute of Science, Department of Entomology, Adana, Turkey. Postdoctoral: 2004: Visiting scientist at the University of Maine, Orono, USA via NATO Science Fellowship (NATO B2). 2011: Visiting scientist at University of Newcastle (UK) via Scholarship by The Council of Higher Education, Turkey. Research interests: Insect ecology, pest management, interactions between plants, microbes, and arthropods.
Nicholas F. Britton was for many years director of the Centre for Mathematical Biology at the University of Bath, UK, where he is now Professor Emeritus. His research interests are in mathematical biology, mainly in ecology and epidemiology.
Semra Demir received Bachelor's degree (1991): Yuzuncu Yil University, Faculty of Agriculture, Department of Plant Protection. PhD degree (1999): Ege University, Institute of Science, Department of Phytopathology, İzmir, Turkey. Postdoctoral (2003): Visiting Scientist at the University of Bari, Italy via project of The Scientific and Technological Research Council of Turkey (Turkey-Italy Cooperation). Research interests: Mycology, arbuscular mycorhizae plant pathology, physiology of plant diseases, biological control of plant diseases.
Annalisa Papasidero is currently finishing her Master degree in Mathematics.
Mehmet Ramazan Risvanli received Bachelor's degree (2012): Kahramanmaraş Sütçü İmam University, Faculty of Agriculture, Department of Plant Protection, Kahramanmaraş, Turkey. MSc degree (2015): Kahramanmaraş Sütçü İmam University, Institute of Science, Department of Entomology, Kahramanmaraş, Turkey. Current status: research assistant, PhD student. Research interests: Insect ecology, interactions between plants, microbes, and arthropods
Manuela Seminara is currently finishing her Master degree in Mathematics.
Ezio Venturino received his PhD degree in Applied Mathematics from SUNY at Stony Brook in 1984. He is currently Professor of Mathematics at the Dipartimento di Matematica, University of Torino, Italy. He has visited several international institutions worldwide and has a wide scientific collaboration network. His research earlier focused on numerical analysis, mainly methods for integral equations, and currently on nonlinear models for biological and ecological applications.

REFERENCES

1Smith SE, Read DJ. Mycorrhizal Symbiosis. Cambridge, UK: Academic Press; 2008.
Google Scholar
2Linderman RG. Role of VAM fungi in biocontrol. In: FL Pfleger, RG Linderman, eds. 344 p Mycorrhizae and Plant Health. Minnesota: APS Press, St Paul; 1994: 1-17.
Web of Science® Google Scholar
3Azcón C, Barea JM. Interactions of arbuscular mycorrhiza with rhizosphere microorganisms. Mycorrhiza. Biological Soil Resource. Bogota, Colombia: FEN; 1996: 47-68.
Google Scholar
4Azcón-Aguilar C, Barea JM. Arbuscular mycorrhizas and biological control of soil-borne plant pathogens – an overview of the mechanisms involved. Mycorrhiza. 1997; 6: 457-464.
10.1007/s005720050147
Web of Science® Google Scholar
5Merrill MC. Eco-agriculture: a review of its history and philosophy. Biol Agric Hortic. 1983; 1(3): 181-210.
10.1080/01448765.1983.9754395
Google Scholar
6Oelhaf R. Economic and Ecological Comparisons with Conventional Methods. New York, NY: John Wiley and Sons; 1978.
Google Scholar
7Miller SC, Brown SJ, Tomoyasu Y. Larval RNAi in Drosophila? Dev Genes Evol. 2008; 218(9): 505-510.
10.1007/s00427-008-0238-8
CAS PubMed Web of Science® Google Scholar
8Altieri MA, Nicholls CI. Soil fertility management and insect pests: harmonizing soil and plant health in agroecosystems. Soil Tillage Res. 2003; 72(2): 203-211.
10.1016/S0167-1987(03)00089-8
Web of Science® Google Scholar
9Eigenbrode SD, Pimentel D. Effects of manure and chemical fertilizers on insect pest populations on collards. Agric Ecosyst Environ. 1988; 20(2): 109-125.
10.1016/0167-8809(88)90151-X
Web of Science® Google Scholar
10Phelan P, Mason J, Stinner B. Soil-fertility management and host preference by European corn borer, Ostrinia nubilalis (Hübner), on Zea mays L: a comparison of organic and conventional chemical farming. Agric Ecosyst Environ. 1995; 56(1): 1-8.
10.1016/0167-8809(95)00640-0
Web of Science® Google Scholar
11Phelan P, Norris K, Mason J. Soil-management history and host preference by Ostrinia nubilalis: evidence for plant mineral balance mediating insect-plant interactions. Environ Entomol. 1996; 25(6): 1329-1336.
10.1093/ee/25.6.1329
Web of Science® Google Scholar
12Culliney TW, Pimentel D. Ecological effects of organic agricultural practices on insect populations. Agric Ecosyst Environ. 1986; 15(4): 253-266.
10.1016/0167-8809(86)90124-6
Web of Science® Google Scholar
13Arancon N, Edwards C, Bierman P, Welch C, Metzger J. Influences of vermicomposts on field strawberries: 1. effects on growth and yields. Bioresour Technol. 2004; 93(2): 145-153.
10.1016/j.biortech.2003.10.014
CAS PubMed Web of Science® Google Scholar
14Hare JD. Ecology and management of the Colorado potato beetle. Ann Rev Entomol. 1990; 35(1): 81-100.
10.1146/annurev.en.35.010190.000501
Web of Science® Google Scholar
15Casagrande R. The Colorado potato beetle: 125 years of mismanagement. Bull ESA. 2014; 33(3): 142-150.
Google Scholar
16Weber DC, Ferro DN. Movement of overwintered Colorado potato beetles in the field. J Agric Entomol. 1994; 11(1): 17-27.
Google Scholar
17Alyokhin A, Porter G, Groden E, Drummond F. Colorado potato beetle response to soil amendments: a case in support of the mineral balance hypothesis? Agric Ecosyst Environ. 2005; 109(3-4): 234-244.
10.1016/j.agee.2005.03.005
Web of Science® Google Scholar
18Alyokhin A, Atlihan R. Reduced fitness of the Colorado potato beetle (Coleoptera: Chrysomelidae) on potato plants grown in manure-amended soil. Environ Entomol. 2005; 34(4): 963-968.
10.1603/0046-225X-34.4.963
Web of Science® Google Scholar
19Clancy KM. Response of western spruce budworm (Lepidoptera: Tortricidae) to increased nitrogen in artificial diets. Environ Entomol. 1992; 21(2): 331-344.
10.1093/ee/21.2.331
Web of Science® Google Scholar
20Busch JW, Phelan PL. Mixture models of soybean growth and herbivore performance in response to nitrogen-sulphur-phosphorous nutrient interactions. Ecolog Entomol. 1999; 24(2): 132-145.
10.1046/j.1365-2311.1999.00185.x
Web of Science® Google Scholar
21Beanland L, Phelan PL, Salminen S. Micronutrient interactions on soybean growth and the developmental performance of three insect herbivores. Environ Entomol. 2003; 32(3): 641-651.
10.1603/0046-225X-32.3.641
CAS Web of Science® Google Scholar
22Gianinazzi S, Schüepp H. Impact of Arbuscular Mycorrhizas on Substainable Agriculture and Natural Ecosystems. Berlin, Germany: Springer Science & Business Media; 1994.
10.1007/978-3-0348-8504-1
Google Scholar
23McGonigle TP, Miller MH. Development of fungi below ground in association with plants growing in disturbed and undisturbed soils. Soil Biol Biochem. 1996; 28(3): 263-269.
10.1016/0038-0717(95)00129-8
CAS Web of Science® Google Scholar
24Johansson JF, Paul LR, Finlay RD. Microbial interactions in the mycorrhizosphere and their significance for sustainable agriculture. FEMS Microbiol Ecol. 2004; 48(1): 1-13.
10.1016/j.femsec.2003.11.012
CAS PubMed Web of Science® Google Scholar
25Rosenzweig M, MacArthur R. Graphical representation and stability conditions of predator-prey interaction. Am Nat. 1963; 97: 209-223.
10.1086/282272
Web of Science® Google Scholar
26Rosenzweig M. The paradox of enrichment. Science. 1971; 171: 385-387.
10.1126/science.171.3969.385
CAS PubMed Web of Science® Google Scholar

Citing Literature

All articles

Can symbiotic fungi protect plants from insect pests? A simple mathematical model

Abstract

1 INTRODUCTION

2 BIOLOGICAL BACKGROUND

3 THE MODEL

4 ANALYSIS

4.1 Boundedness

4.2 Equilibria and their feasibility

4.3 Stability of equilibria

4.4 Global stability issues

4.4.1 E₁

4.4.2 E₂

4.4.3 E₃

4.4.4 E₄

4.5 Bifurcations

4.5.1 Case (i): ea₁ < ea₀ < nh

4.5.2 Case (ii): ea₁ < nh < ea₀

4.5.3 Case (iii): nh < ea₁ < ea₀

4.5.4 Bifurcation parameters g₁ and a₁

5 INTERPRETATION AND DISCUSSION

Biographies

REFERENCES

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Can symbiotic fungi protect plants from insect pests? A simple mathematical model

Abstract

1 INTRODUCTION

2 BIOLOGICAL BACKGROUND

3 THE MODEL

4 ANALYSIS

4.1 Boundedness

4.2 Equilibria and their feasibility

4.3 Stability of equilibria

4.4 Global stability issues

4.4.1 E1

4.4.2 E2

4.4.3 E3

4.4.4 E4

4.5 Bifurcations

4.5.1 Case (i): ea1 < ea0 < nh

4.5.2 Case (ii): ea1 < nh < ea0

4.5.3 Case (iii): nh < ea1 < ea0

4.5.4 Bifurcation parameters g1 and a1

5 INTERPRETATION AND DISCUSSION

Biographies

REFERENCES

Citing Literature

Figures

References

Related

Information

4.4.1 E₁

4.4.2 E₂

4.4.3 E₃

4.4.4 E₄

4.5.1 Case (i): ea₁ < ea₀ < nh

4.5.2 Case (ii): ea₁ < nh < ea₀

4.5.3 Case (iii): nh < ea₁ < ea₀

4.5.4 Bifurcation parameters g₁ and a₁