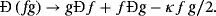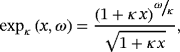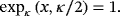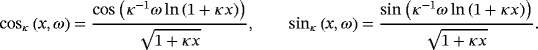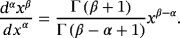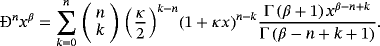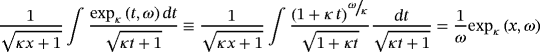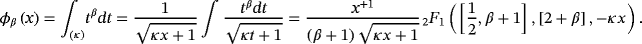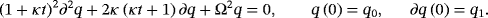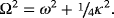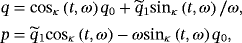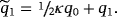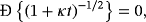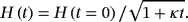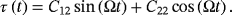Non-Leibniz Hamiltonian and Lagrangian formalisms for certain class of dissipative systems
List of Symbols: Ð, Anti–self-adjoint generalized derivation operator; κ, scaling parameter dimension of an inverse time or inverse length; expκ(x, ω), κ-exponential function of argument x and eigenvalue ω; cosκ(x, ω), sinκ(x, ω), κ-trigonometric functions of argument x and eigenvalue ω; , κ-indefinite integral (κ-antiderivative); ϕβ(x), indefinite integral (κ-antiderivative) of the function f = xβ; pi, κ-canonical momenta; qi, generalized coordinates; L, dissipative Lagrange function; L0, conservative Lagrange function.
Abstract
The non-Leibniz Hamiltonian and Lagrangian formalism for the certain class of dissipative systems is introduced in this article. The formalism is based on the generalized differentiation operator (κ-operator) with a nonzero Leibniz defect. The Leibniz defect of the introduced operator linearly depends on one scaling parameter. In a special case, if the Leibniz defect vanishes, the generalized differentiation operator reduces to the common differentiation operator. The κ-operator allows the formulation of the variational principles and corresponding equations of Lagrange and Hamiltonian types for dissipative systems. The solutions of some generalized dynamical equations are provided closed form.
1 INTRODUCTION
It is well known that there is no variational principle without complementary equations that yields to a linear dissipative set of differential equations with constant coefficients.1 By adding an exact differential to the integrand of a variational problem, it is possible to formulate the variational principles for the certain dissipative systems.2 In these cases, a set of solutions of the additional equations can be expressed in terms of the solutions of the original equations. Using these relations, the Lagrangian function expresses through of the dependent variables in the original set of equations.
To define the metriplectic systems, the structures of Hamiltonian and metric systems were combined.3 The phase space for metriplectic systems is equipped with a bracket operator. The bracket operator possesses an antisymmetric Poisson bracket part and a symmetric dissipative part. The combination of the Casimir invariants of the Poisson bracket represents the entropy.
Consider an ensemble of states that occupies a particular volume of phase space in the initial moment. The evolution of the volume of phase space is governed by Hamilton's equations. The flow of phase space may deform the shape of the ensemble, but it does not change its volume. The conservation of the phase space volume is known as the Liouville's theorem. On the other hand, it is well known that, for dissipative systems, the phase space volume is not conserved.4 This means the evolution of the system could not be described by Hamilton's equations in their ordinary formulation. The multiplication of the undamped Lagrangian by an increasing exponent of time leads to a formally correct Hamilton's equation5. Conversely, the modified Hamiltonian is not a sum of potential and kinetic energy of the system. Bloch et al6 showed that the system on Lie algebras cannot have linear dissipative terms of a Rayleigh dissipation type.
For Lagrangian treatment of the dissipative systems, Kaufman7 introduced “dissipative bracket.” For a dissipative bracket, a certain set of observables was associated, for which the dissipative bracket vanishes with any observable. The dissipative invariants, such as energy and momentum, were pointed. Furthermore, this idea was reformulated in the Lorentz-covariant form.8 The evolution of the system was associated with two scalar functionals. One functional was the Lagrangian action, and the second was the global entropy. The introduction of the bracket established the local covariant laws of entropy production and of energy momentum conservation.
Mshelia9 evaluated the probability amplitude for the transfer of collective excitation energy in coupled dissipative systems. The normalization and orthogonalization of eigenvectors corresponding to degenerate eigenvalues were carefully considered.
The Lagrangian with derivatives of fractional order was also proposed.10, 11 The Euler–Lagrange equation of motion for nonconservative forces was obtained in previous studies using the variation of the fractional Lagrangian. Using methods of classical mechanics with fractional and higher-order derivatives, the conjugate moments were defined. The method was applied to the frictional force proportional to velocity. However, the dissipation matrix appears in an unusual, skew-symmetric form. Extending this approach12 implemented the Riemann-Liouville fractional derivative of curves evolving on real space. With the fractional derivative, a restricted variational principle for Lagrangian systems yielding the so-called restricted fractional Euler–Lagrange equations (both in the continuous and discrete settings) was developed. The application of a variational principle and summation of the variations yields the restricted fractional Euler–Lagrange equation, which admits invariant linear change of variables.
The dissipation effects in quantum systems were studied by Tarasov.13 For the construction of quantum theory, the mathematical concepts that are general for Hamiltonian and non-Hamiltonian systems were implemented. Quantum dynamics was described by the one-parameter semigroups and the differential equations on operator spaces and algebras using the Lie–Jordan algebraic structure, Liouville space, and superoperators. This method consistently formulates the evolution of quantum systems and permits the investigation of the dynamics for open, non-Hamiltonian, dissipative, and nonlinear quantum systems.
The conditions for a Lagrangian formulation of dissipative dynamical systems were summarized by Musielak.14 In the previous study, the nonstandard Lagrangians and the corresponding equations of motions were derived.
In the current article, an alternative way is examined. Instead of modifying the Hamilton's function, we look at the alteration of the derivatives. The formalism is based on the generalized differentiation operator with a nonzero Leibniz defect. The Leibniz defect of the generalized differentiation operator linearly depends on one scaling parameter.15 In a special case, if the scaling parameter turns to one, the Leibniz defect vanishes, and a generalized differentiation operator reduces to the common differentiation operator. The generalized differentiation operator allows the formulation of the variational principles and corresponding Lagrange and Hamiltonian equations. In the present article, the alternative definition of the derivatives and the mechanical consequences of this alterative definition are investigated.
The structure of the article is as follows. The first section introduces the generalized differentiation operator with a nonzero Leibniz defect. The relation between common and generalized differentiation operators is established. The expression of the generalized differentiation operator in terms of a common differential operator facilitates the solution of the generalized differentiation equations and the investigation of special functions. The next addressed question is the uniqueness of the derivative definition. All solution operators of the classical Leibniz product rule were determined by König and Milman.16 Their method is extended to the operators with the Leibniz defect, and the uniqueness is confirmed.
In the second section, the solutions of the generalized differential equations of the first and second orders are found. The solutions of the linear equations present the κ-exponential function and κ-trigonometric functions.
In the third section, the κ-derivatives of higher and fractional order are introduced. The integer higher κ-derivative is based on the common binomial formula. Using the fractional binomial formula, the definition of the fractional derivatives follows from the expression of the integer higher κ-derivative.
The κ-antiderivative is defined in the fourth section. This definition is necessary for the integration procedure and is required in the succeeding sections.
The κ-Lagrange function of the systems with a single and multiple degrees of freedom could now be defined. The corresponding procedure is studied in the fifth section. The κ-canonical moments are used instead of common canonical moments, which are defined by the ordinary partial derivatives of Lagrangian.
The κ-Lagrange oscillating systems with a single degree and multiple degrees of freedom are studied later in the sixth section. The closed-form solutions are found for the dynamic equations.
The Poisson bracket and conservation laws in the non-Leibniz mechanics are investigated in the seventh section. The investigation is based on the formal replacement of the common derivative thought its generalized analog.
The eighth section establishes the solutions of the homogeneous linear dissipative wave equation in spaces of different dimensions. The most impressive result is the following. For the nonvanishing defect, the frequency and wavelength depend on the distance from the source. The character hangs on the sign of the defect constant. The frequency fades with the travel distance if κ > 0. Accordingly, the wavelength increases with the distance, giving rise for the “red shift” of the linear κ-wave. Oppositely, if κ < 0, the frequency increases with the travel distance. The wavelength reduces with the distance, and the ultimate radius of the wave propagation is |κ|.
2 GENERALIZED DIFFERENTIATION OPERATOR
2.1 Definition of generalized differentiation operator
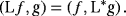
Here f and g are arbitrary vectors in the Hilbert space equipped with the corresponding inner product. The role of the inner product in mechanics plays the integration.
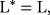
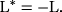
For example, the common derivative ∂ is anti–self-adjoint if the end terms in the Lagrangian vanish. This property is used to derive Euler–Lagrange equations.
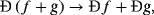 (1)
(1)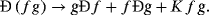 (2)
(2)From 1 to 2, it immediately follows that the operator Ð is linear.
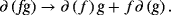
The common Leibniz ∂ differentiation operator is anti–self-adjoint ∂ = −∂*. Namely, the integration by parts could be expressed by the anti–self-adjoint of the common Leibniz derivative. The derivation of the Euler equation in the variational calculus is based on the integration by parts. The anti–self-adjointness of the common Leibniz ∂ differentiation is essential for Hamiltonian and Lagrangian mechanics.
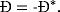 (3)
(3)2.2 Relation between common and generalized differentiation operators
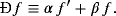 (4)
(4)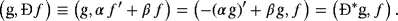
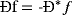
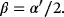
The substitution of the expression 3 in Equation 2 delivers an equation α′ = 2K.
Each appropriate choice for the pair of the coefficients α = α(x) and β = β(x) leads to a certain operator algebra. The initial conditions for the differential equations specify the functions uniquely. The motivation for the choice α(x = 0) = 1 is the following. With this condition, expression 4 reads Ðx ≡ α ∂x+β x. Both operators Ðx and ∂x match in the point x = 0, if α(x = 0) = 1. In this case, Ðx ≡ α ∂x = ∂x.
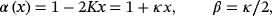
 (5)
(5)2.3 Uniqueness of the derivative definition
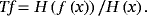 (6)
(6)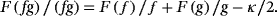 (7)
(7)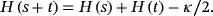 (8)
(8)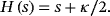 (9)
(9)The considerations of König and Milman16 are repeated with some minor alterations for the product rule with a similar entropy function that contains the nonvanishing Leibniz defect κ. Thus, all solution operators of the product rule with the Leibniz defect are determined.
3 GENERALIZED DIFFERENTIAL EQUATIONS OF THE FIRST AND SECOND ORDER
3.1 κ-Exponential function
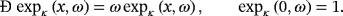 (10)
(10)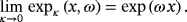 (13)
(13)3.2 κ-trigonometric functions
 (14)
(14) (15)
(15) (17)
(17)4 κ-DERIVATIVES OF HIGHER AND FRACTIONAL ORDER
4.1 κ-derivatives of higher integer order
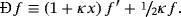
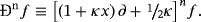
The above expression could be transformed to a sum of the common derivatives dn − kf/dxn − k of the function by the use of the binomial formula.19
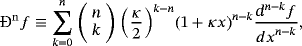 (18)
(18)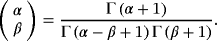
4.2 Fractional κ-derivatives
Using the expressions for the higher integer order κ-derivatives, the fractional κ-derivative will be straightforward defined. For this purpose, the representation of κ-derivative in the form 18 is applied.
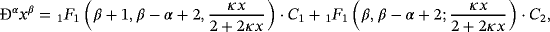 (21)
(21)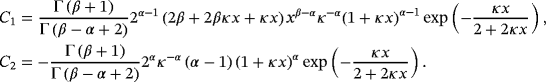
The expression 21 allows the calculation of the derivatives of any rational order.
The solutions of the fractional κ-differential equations could be studied using the expression 21 in closed form, but the corresponding solutions are dispensable for the principal tasks of the current article.
5 INTEGRATION
5.1 κ-antiderivative
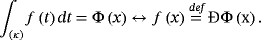 (22)
(22)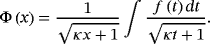 (23)
(23)5.2 Integral of κ-exponential function
5.3 Integral of power function
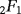 is the hypergeometric function.21 In the limit case, the κ-indefinite integral 25 turns into the common indefinite integral:
is the hypergeometric function.21 In the limit case, the κ-indefinite integral 25 turns into the common indefinite integral:
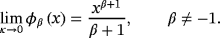 (26)
(26)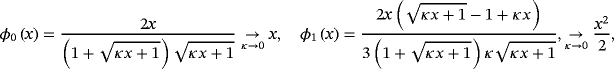 (27)
(27)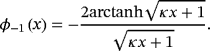
Since the κ-integration is a linear operation, integrals of polynomials and Taylor series can also be integrated using the rule 25.
6 LAGRANGIAN AND HAMILTONIAN
6.1 κ-Lagrange function
In mechanics, the time t plays frequently the role of the independent variable x and marks the evolution of the system. The basic method in the Lagrange mechanics consists in treating the generalized coordinates qi, i = 1,…, n, as independent variables. The lover Latin indices are used for generalized coordinates. The time dependence of these variables is determined by the Lagrange equations of the second order. The generalized velocities Ðqi are all dependent, derived quantities. The initial values for qi and Ðqi are determined from the 2n integration constants.
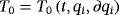

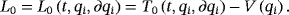 (28)
(28)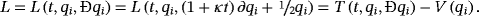 (29)
(29)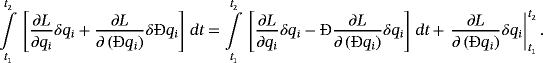
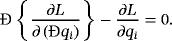 (30)
(30)6.2 Canonical moments
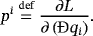 (31)
(31)The canonical moments pi(t) are used instead of the common canonical moments, which are defined by the ordinary partial (functional) derivatives of the ordinary Lagrangian.4
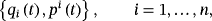
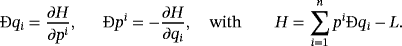 (32)
(32)In the following, we imply the convention for a summation about repeated indexes. The variable q or p without an index designates the whole sequence.
7 LINEAR HARMONIC OSCILLATOR
7.1 Linear system with one degree of freedom
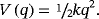
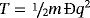
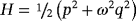
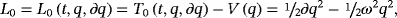 (33)
(33)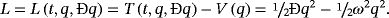 (34)
(34) (34)
(34)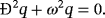 (35)
(35)7.2 Linear system with several degrees of freedom
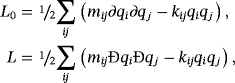
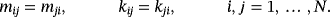
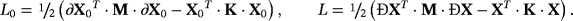 (37)
(37)Here, M is the mass matrix, K is the stiffness matrix, and X = (q1, …, qN).
 (38)
(38)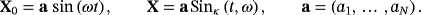 (39)
(39)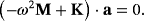 (40)
(40)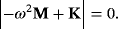 (41)
(41)The characteristic of Equation 41 defines the fundamental frequencies ωi, i = 1,…,N of both systems 38. By transformation to normal coordinates, the quadratic forms for the kinetic and potential energies in Equation 37 can be reduced simultaneously to sums of squares in these coordinates and their derivatives, hence making the coupled oscillator problem separable into independent motions, each with a particular normal frequency. One can prove that the fundamental frequencies of both systems 38 are positive if the potential energy is a positively defined bilinear form, as it is the case for the energy minimum.
8 POISSON BRACKET AND CONSERVATION LAWS IN THE NON-LEIBNIZ MECHANICS
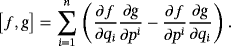 (42)
(42)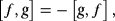 (43)
(43)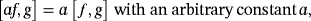 (44)
(44)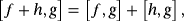 (45)
(45)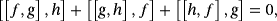 (46)
(46)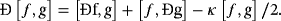 (47)
(47)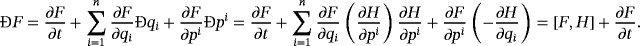 (48)
(48) (49)
(49)Equations 49 are referred to as equations of motion 32 in Poisson bracket form.
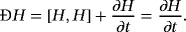 (50)
(50)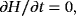
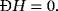 (51)
(51)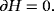
9 THREE-DIMENSIONAL HOMOGENEOUS LINEAR DISSIPATIVE WAVE EQUATION
9.1 Three-dimensional waves
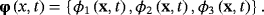
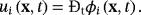
 (52)
(52)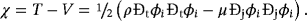 (53)
(53)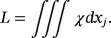 (54)
(54)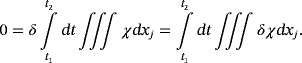
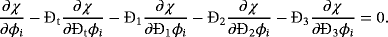 (55)
(55)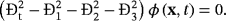 (56)
(56)The solution of the homogeneous wave Equations 56 in the case N = 1 with the initial conditions ϕ|t = 0 = ϕ1(x), ∂ϕ/∂t|t = 0 = ϕ2(x) can be found by means of characteristics method.23
9.2 Radial green functions
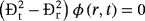
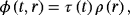
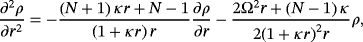 (57)
(57)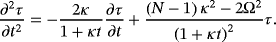 (58)
(58)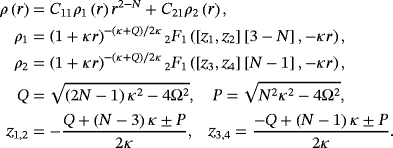 (59)
(59)Here, 2F1 are the hypergeometric functions.21
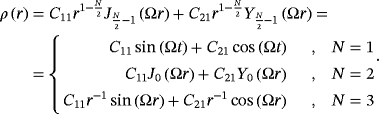 (61)
(61)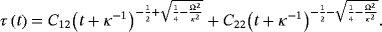 (62)
(62)The frequency of the linear wave depends 60 on the distance from the source. For positive κ, the frequency fades with the travel distance. Consequently, the wavelength grows with the distance to the source, resulting in the “red shift” of the linear κ-wave. Contrarily, for negative κ, the frequency grows with the travel distance. It turns to infinity at the point r = |κ|. The wavelength declines with the distance to the source, resulting in the “blue shift” of the κ-wave. The distance r = |κ| could be considered the confinement radius of the wave.
10 CONCLUSIONS
The method for the study of dynamical systems is based on the introduction of a derivative with the Leibniz defect. The differential algebra of this generalized derivative is briefly established. The simple non-Leibniz differential equations and their solutions are solved in closed form in terms of special functions. The introduction of the derivative allows the formulating of the dissipative equations with Lagrange and Hamilton structures. The analytical solution of the equations of dissipative oscillator is found. The most notable result is the frequency distance reliance of the linear dissipative wave. The frequency depends on the distance from the source. For positive κ, the frequency declines with the travel distance. Consequently, the wavelength grows with the distance to the source, resulting in the “red shift” of the linear κ-wave.
For negative κ, the frequency increases with the travel distance and turns to infinity at the distance |κ|. The wavelength reduces with the distance to the source, resulting in the “blue shift” of the κ-wave.
ACKNOWLEDGEMENT
This paper was supported in part by Alexander von Humboldt Foundation, Bonn, Germany.
CONFLICT OF INTERESTS
The authors have no conflict of interests.
Biography

Vladimir Kobelev, PhD, Dr rer nat habil, received the Dipl Physics and PhD degrees from the Department of Aerophysics and Space Research, Moscow Institute of Physics and Technology, Dolgoprudny, Russia. Since 2000, he has been an APL Professor with the Department of Mechanical Engineering, Universität Siegen, Siegen, Germany. He is the author of two books, Durability of Springs and Design and Analysis of Composite Structures for Automotive Applications.