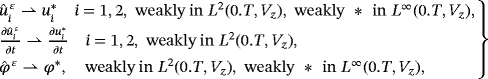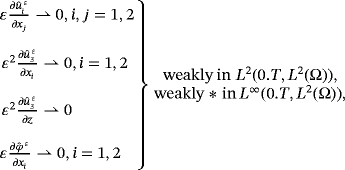Asymptotic analysis of quasistatic electro-viscoelastic problem with Tresca's friction Law
Abstract
This paper is devoted to the study of the asymptotic analysis of a mathematical model involving a frictionless contact between an quasistatic electro-viscoelastic and a conductive foundation in a three-dimensional thin domain Ωε. The contact is modeled with Tresca friction law. We derive a variational formulation of the problem and prove its unique weak solution. Then, we study the asymptotic analysis when the small parameter of the domain tends to zero. Finally, the specific Reynolds limit equation and the limit of Tresca free boundary conditions are obtained.
1 INTRODUCTION AND STATEMENT OF THE PROBLEM
Scientific research in mechanics are articulated around two main components: one devoted to the laws of behavior and the other on boundary conditions imposed on the body. For the constitutive law, we consider an quasistatic electro-viscoelastic body with Tresca free boundary friction conditions in the dynamic regime occupying a bounded homogeneous domain of 3D. The piezoelectric is characterized by the coupling between the mechanical and the electrical properties of the material: it was observed that the appearance of electric charges on some crystals was due to the action of body forces and surface tractions and, conversely, the action of the electric field generated strain or stress in the body (see the work of Batra and Yang1 and the references therein). This coupling leads to the appearance of electric potential when mechanical stress is present and, conversely, mechanical stress is generated when electric potential is applied. Piezoelectric materials for which the mechanical properties are elastic are called electro-elastic materials and those for which the mechanical properties are viscoelastic are called electro-viscoelastic materials. Antiplane shear deformations are one of the simplest examples of deformations that solids can undergo. In the work of Sofonea and Dalah,2 the authors studied antiplane frictional contact problem of electro-viscoelastic cylinders. Chougui and Drabla3 studied a frictional contact problem with adhesion between an elastic piezoelectric body and a deformable obstacle. Contact problems for electro-viscoelastic materials were considered in the works of Sofonea et al.4, 5 In most cases, the authors are interested in studying the weak formulation of the solution, then prove the existence and uniqueness of the solution.
Here, we continue this line of research and study the asymptotic analysis of the electro-viscoelastic quasistatic problem with friction modeled by the law of Tresca, in a thin domain
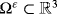 , where 0 < ε < 1 is a small parameter that will tend to zero. The boundary of Ω ε will be noted
, where 0 < ε < 1 is a small parameter that will tend to zero. The boundary of Ω ε will be noted
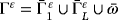 , such that
, such that
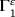 is the upper boundary of equation x3 = εh(x1,x2),
is the upper boundary of equation x3 = εh(x1,x2),
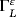 is the lateral boundary and ω is a fixed bounded domain of
is the lateral boundary and ω is a fixed bounded domain of
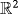 of equation x3 = 0, which is bottom of the domain Ω ε.
of equation x3 = 0, which is bottom of the domain Ω ε.
In mathematical literature, there are many research papers regarding the asymptotic analysis of the problems that arise in a thin domain of which we mention; Benseridi and Dilmi6 studied the asymptotic analysis of a dynamical problem of isothermal elasticity with nonlinear friction of Tresca type. The asymptotic behavior of a dynamical problem of nonisothermal elasticity with nonlinear friction of Tresca type was studied in the work of Saadallah.7 Bayada and Lhalouani8 investigated the asymptotic and numerical analysis for a unilateral contact problem with Coulomb's friction between an elastic body and a thin elastic soft layer. Benseghir et al9 studied the theoretical analysis of a frictionless contact between two general elastic bodies in a stationary regime in a three-dimensional thin domain with Tresca friction law. The asymptotic analysis of some problem in mechanics of the fluids in a thin domain in the stationary case is found in the works of Bayada and Boukrouche10 and Dilmi et al.11
Our work is structured as follows. In Section 1, we present the model of the electro-viscoelastic, and we give some notation on the data of the problem. In Section 2, we derive the variational formulation for the problem and state our result of existence and uniqueness of the solution. In Section 3, we employ the change of variable z = x3/ε to transform the initial problem posed in the domain Ω ε at a new problem posed on a fixed domain Ω independent of parameter ε. We establish some estimates independent of parameter ε, for the displacement
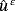 and the electric potential
and the electric potential
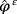 . Finally, we give the convergence results, the limit problem, and its uniqueness in Section 4.
. Finally, we give the convergence results, the limit problem, and its uniqueness in Section 4.
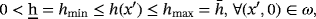
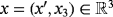 ,
,
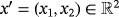 . The domain Ω ε is given by
. The domain Ω ε is given by
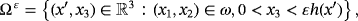
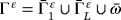 as its boundary.
as its boundary.Let uε(x,t) be the displacement field and φε(x,t) be the electric potential in Ω ε.
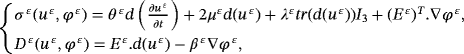
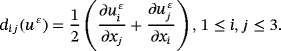
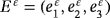 is the piezoelectric tensor, where
is the piezoelectric tensor, where
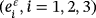 is the piezoelectric coefficient, (E ε)T is the transposed of the tensor E ε, μ ε, λε are the coefficients of Lamé, I3 is the identity, θε is the viscosity term, and βε is the electric coefficient of permitting.
is the piezoelectric coefficient, (E ε)T is the transposed of the tensor E ε, μ ε, λε are the coefficients of Lamé, I3 is the identity, θε is the viscosity term, and βε is the electric coefficient of permitting.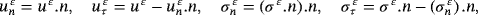
The classical model for quasistatic electro-viscoelastic problem is as follows.
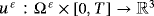 , and the electric potential
, and the electric potential
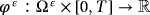 such that
such that
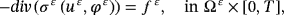 ()
()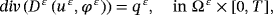 ()
()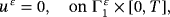 ()
()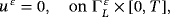 ()
()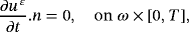 ()
()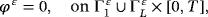 ()
()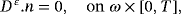 ()
() ()
()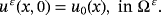 ()
()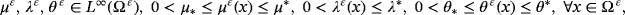
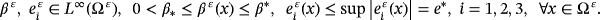
2 WEAK FORMULATION
 , H1(Ω ε)3 is the space of Sobolev, which is given by
, H1(Ω ε)3 is the space of Sobolev, which is given by
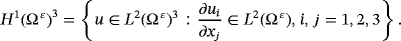
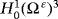 is the closing of D(Ω ε)3 in H1(Ω ε)3, and H−1(Ω ε)3 is the dual space of
is the closing of D(Ω ε)3 in H1(Ω ε)3, and H−1(Ω ε)3 is the dual space of
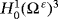 .
.We suppose that the problem of electro-viscoelastic (PE.V) admits a solution (uε,φε) regular, and let (v,ψ)∈(H1(Ω ε)3,H1(Ω ε)). We multiply Equation 1 by the element
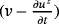 , in the same way for Equation 2 by the element ψ ∈ H1(Ω ε), then we integrate on Ω ε and, using the Green's formula, we obtain the following variational problem.
, in the same way for Equation 2 by the element ψ ∈ H1(Ω ε), then we integrate on Ω ε and, using the Green's formula, we obtain the following variational problem.
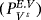 . Find the displacement field
. Find the displacement field
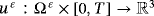 , and the electric potential
, and the electric potential
 such that
such that
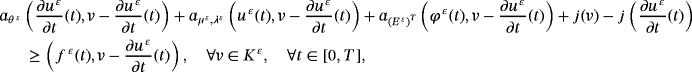 ()
()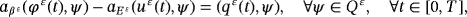 ()
()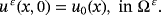 ()
()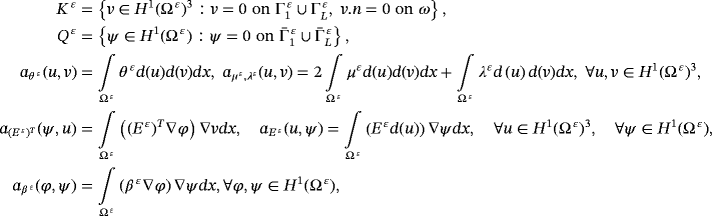
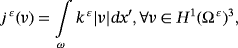 ()
()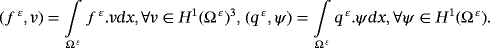 ()
()
Theorem 1.Under the assumptions
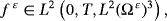 ()
()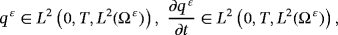 ()
()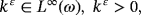 ()
() ()
()The problem 10-12 admits a unique solution (uε,φε) ∈ K ε × Q ε, such that
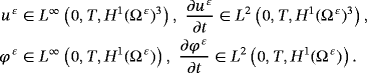 ()
()
Proof.The proof is based on the regularization method, which is based on an approximation of nondifferentaible term j ε(.) by a family of differentaible onse
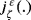 , where
, where
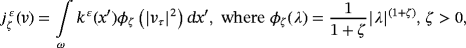
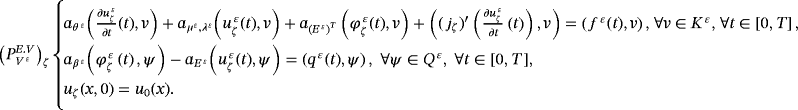
 of this last approximate problem (see the works of Duvaut and Lions12, 13). Then, the limit of
of this last approximate problem (see the works of Duvaut and Lions12, 13). Then, the limit of
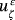 when ζ tends to zero is a solution of 10-12.
when ζ tends to zero is a solution of 10-12.
3 CHANGE OF THE DOMAIN AND A PRIORI ESTIMATES
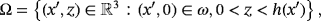
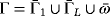 , its boundary. We define now on Ω the following functions:
, its boundary. We define now on Ω the following functions:
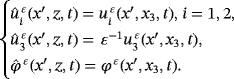
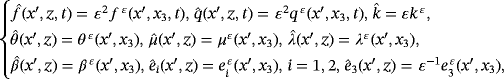
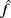 ,
,
 ,
,
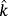 ,
,
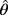 ,
,
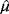 ,
,
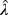 ,
,
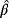 , and
, and
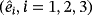 do not depend on ε.
do not depend on ε.Now, we define the function spaces on Ω.
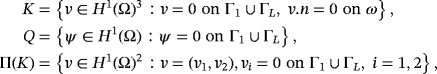
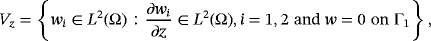
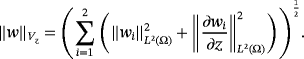
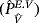 . Find the displacement field
. Find the displacement field
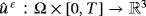 , and the electric potential
, and the electric potential
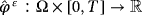 such that
such that
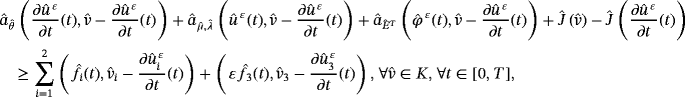 ()
()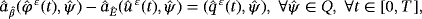 ()
()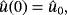
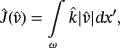
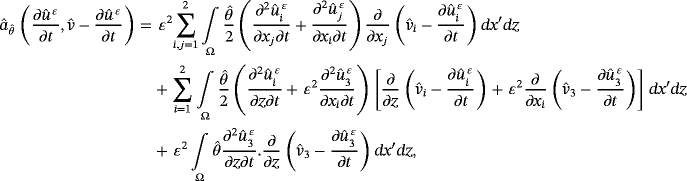
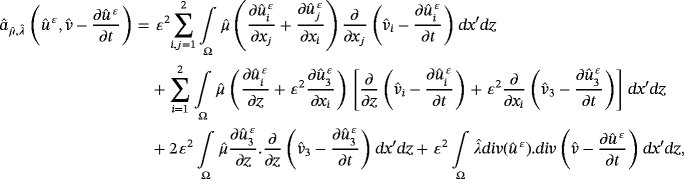
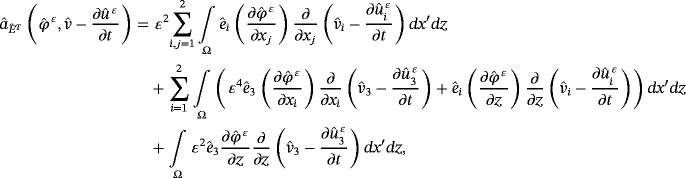
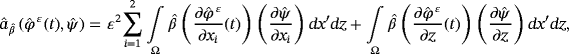
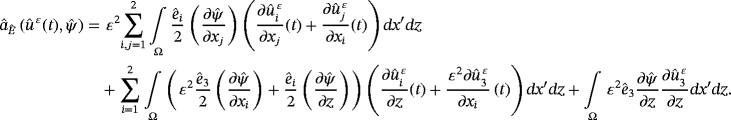
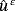 and the electric potential
and the electric potential
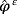 .
.
Theorem 2.Under the same assumptions as in Theorem 1, there exists a constant c independent of ε such that
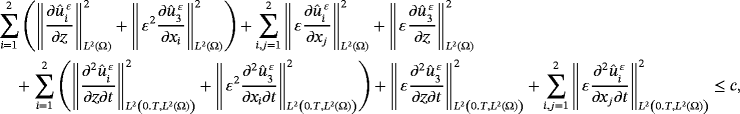 ()
()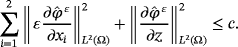 ()
()
Proof.Let (uε,φε) the solution of the problem 10-12, then we have
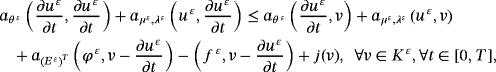 ()
()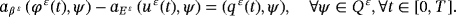 ()
()We derive 25 for t, then choose ψ = φε and we use Korn's inequality
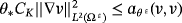 , we find
, we find
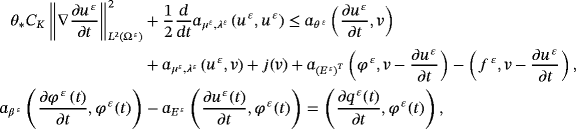
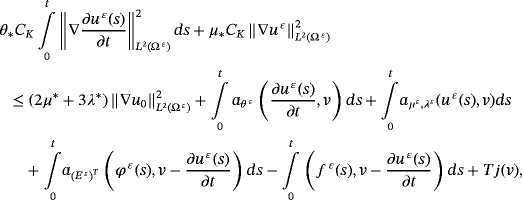
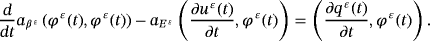 ()
()By integration of 26, we have
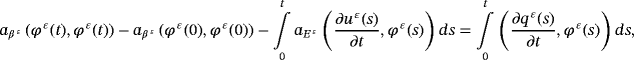
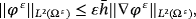
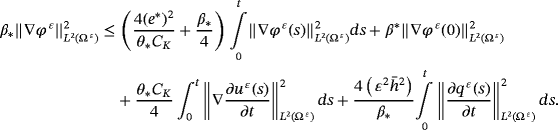 ()
()By applying the Hölder and Young inequalities, we find
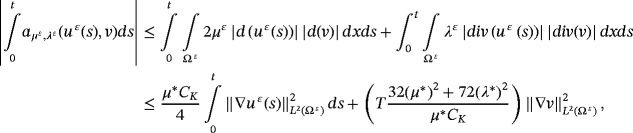 ()
()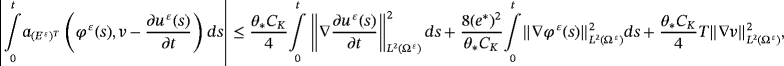 ()
()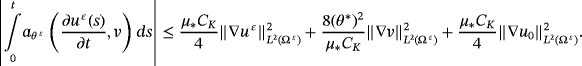 ()
()By Poincaré's inequality
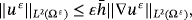
 ()
()From 27-31, we find
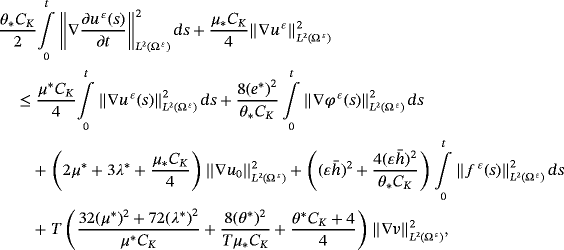 ()
()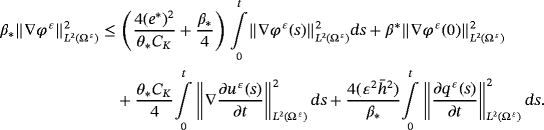 ()
()It is necessary to estimate ∇φε(0). From 11, we deduce that
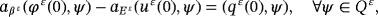
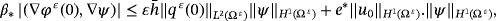
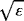 , we obtain
, we obtain
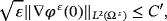
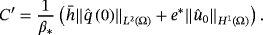
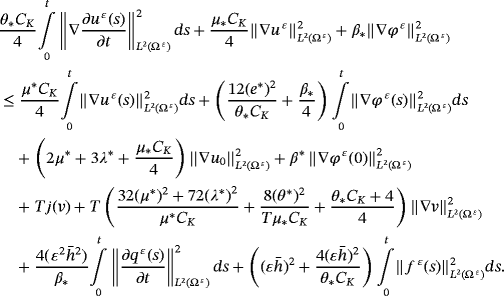 ()
()As
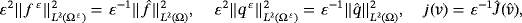
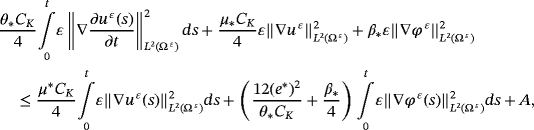 ()
()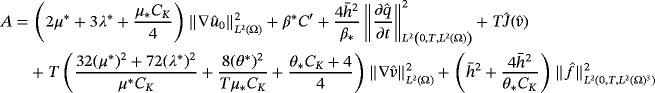
Using Gronwall's lemma in inequality 35, we get
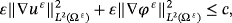
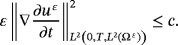
4 CONVERGENCE RESULTS AND LIMIT PROBLEM
Proof.According to Theorem 2, there is constant c independent of ε such that
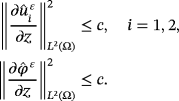
Theorem 4.With the same assumptions of Theorem 3, (u∗,φ∗) satisfies the following relations:
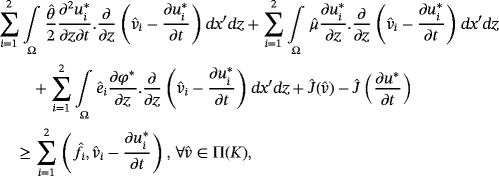 ()
()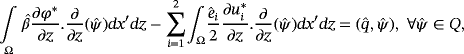 ()
()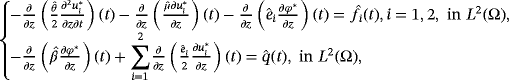 ()
()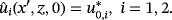
Proof.As J(.) is convex and lower semicontinuous
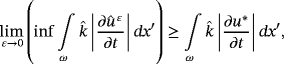
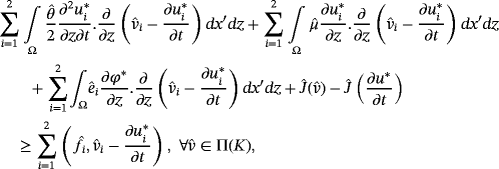 ()
()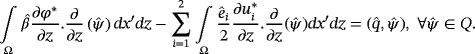 ()
()We choose now in the variational equation 42
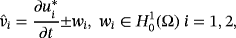
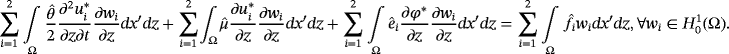
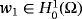 , then w1 = 0, and
, then w1 = 0, and
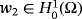 , we obtain
, we obtain
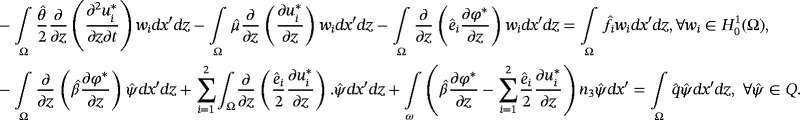
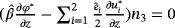 , thus we get
, thus we get
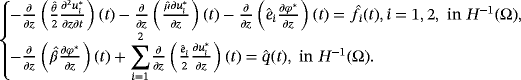 ()
()As
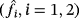 ,
,
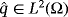 , then 44 is valid in L2(Ω).
, then 44 is valid in L2(Ω).
Theorem 5.Let
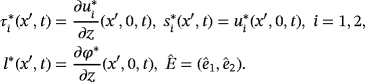
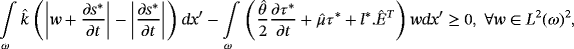 ()
()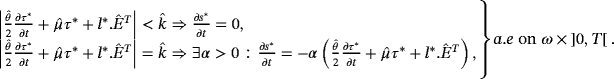 ()
()Moreover, (u∗,φ∗) satisfies the following weak form of the Reynolds equation:
 ()
()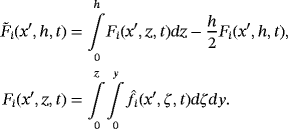
Proof.For 45 and 46, it is enough to follow the same techniques in the work of Bayada and Boukrouche.10 To prove 47, we integrate 41 between 0 and z, it is seen that
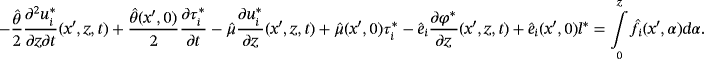
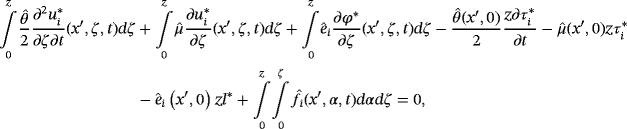 ()
()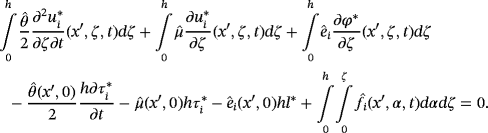 ()
()By integrating 48 from 0 to h(x ′), we get
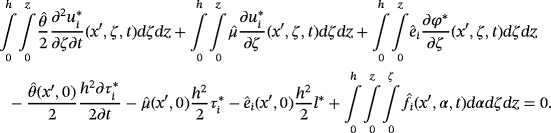 ()
()
Theorem 6.The solution (u∗,φ∗) of limit problem 41 is unique in L∞(0,T,Vz) × L∞(0,T,Vz).
Proof.Let us suppose that there are two solution (u∗1,φ∗1) and (u∗2,φ∗2) of variational equations 39 and 40, we have
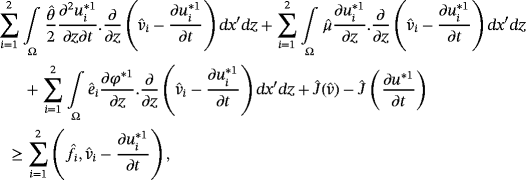 ()
()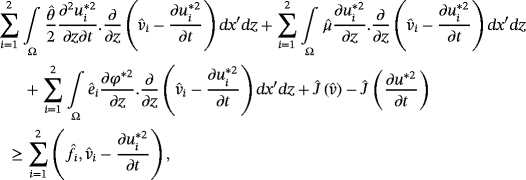 ()
()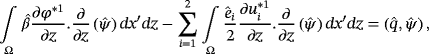 ()
()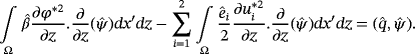 ()
()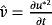 in 51 and
in 51 and
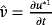 in 52 (respectively), and
in 52 (respectively), and
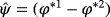 in 53 and
in 53 and
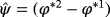 in 54 (respectively). By summing the two inequalities and two equations, we obtain
in 54 (respectively). By summing the two inequalities and two equations, we obtain
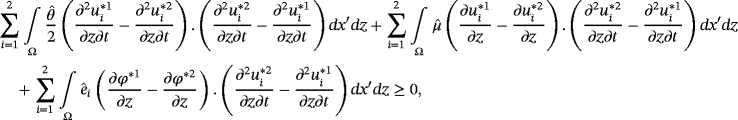 ()
()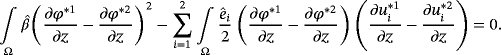 ()
()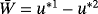 and
and
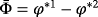 , according to 55 and 56, we find
, according to 55 and 56, we find
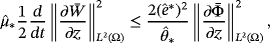 ()
()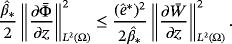 ()
()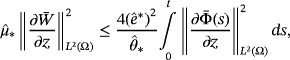 ()
()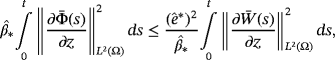 ()
()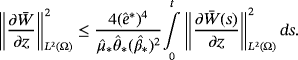
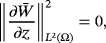
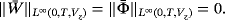
Biographies

Mohamed Dilmi is a PhD in applied mathematics from the University of M'sila. His research area includes the asymptotic analysis of some boundary value problems in a thin film.

Mourad Dilmi is a full professor in the Department of Mathematics at the Sétif 1 University (Algeria). He holds degrees in Magister (2001) and a PhD in Applied Mathematics (2009). He is the author of more than thirty research papers in topics such as existence and uniqueness results for boundary value problems, singularity of the solutions, transmission problem, and asymptotic analysis in a thin domain.

Hamid Benseridi is currently a professor in the Department of Mathematics, Faculty of Science, University of Sétif 1. His research area includes applied mathematics (modeling in continuous porous media) and asymptotic analysis in a thin domain.



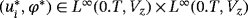 , i = 1,2 such that
, i = 1,2 such that