A class of four parametric with- and without-memory root finding methods
Abstract
In this paper, we have constructed a derivative-free weighted eighth-order iterative method with and without memory for solving nonlinear equations. This method is an optimal method as it satisfies the Kung-Traub conjecture. We have used four accelerating parameters, a univariate and a multivariate weight function at the second and third step of the method, respectively. This method is converted into with-memory method by approximating the parameters using Newton's interpolating polynomials of appropriate degree to increase the order of convergence to 15.51560 and the efficiency index is nearly two. Numerical comparison of our methods is done with the recent methods of respective domain.
1 INTRODUCTION
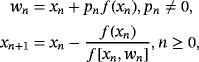
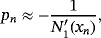
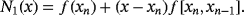
In this paper, we construct a new four-parametric three-step with and without-memory family of methods with high efficiency index. The scheme is constructed by modifying optimal fourth-order two-step King's method6 to an optimal eighth-order three-step derivative-free method by the insertion of a new substep using four parameters and two weight functions of one and two variables. Some special cases from the new scheme are compared with the methods of respective domain using standard nonlinear test functions.
2 DERIVATIVE-FREE THREE-STEP OPTIMAL EIGHTH-ORDER CLASS INVOLVING WEIGHT FUNCTIONS OF ONE AND TWO VARIABLES
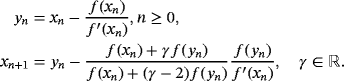
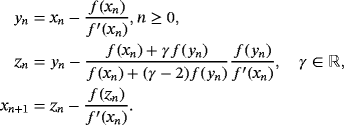
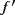 (xn) involved in the iterative expression are approximated by
(xn) involved in the iterative expression are approximated by
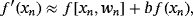
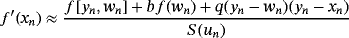
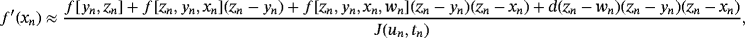
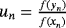 ,
,
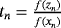 and
and
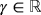 . In addition, a,b,d, and q are real free parameters, S (un) and J(un,tn) are weight functions.
. In addition, a,b,d, and q are real free parameters, S (un) and J(un,tn) are weight functions. (1)
(1)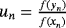 ,
,
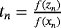 ,
,
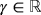 , Pn = f [ yn,zn] + f [zn,yn,xn](zn − yn) + f [zn,yn,xn,wn](zn − yn)(zn − xn) + d(zn − wn)(zn − yn)(zn − xn), a, b, q, and d are real free parameters and weight functions S(un) and J(un,tn) are chosen in such a way that the members of the class are of optimal order eight. To show the order of convergence of class 1, the following result is proven.
, Pn = f [ yn,zn] + f [zn,yn,xn](zn − yn) + f [zn,yn,xn,wn](zn − yn)(zn − xn) + d(zn − wn)(zn − yn)(zn − xn), a, b, q, and d are real free parameters and weight functions S(un) and J(un,tn) are chosen in such a way that the members of the class are of optimal order eight. To show the order of convergence of class 1, the following result is proven.
Theorem 1.Let us suppose that
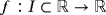 is a real-valued nonlinear sufficiently differentiable function and σ is a real simple zero of the function in the open interval I. If the initial guess x0 is close enough to σ, then all the members of the class of iterative methods 1 have optimal order eight, if weight functions S(un) and J(un,tn) satisfy conditions
is a real-valued nonlinear sufficiently differentiable function and σ is a real simple zero of the function in the open interval I. If the initial guess x0 is close enough to σ, then all the members of the class of iterative methods 1 have optimal order eight, if weight functions S(un) and J(un,tn) satisfy conditions
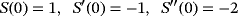
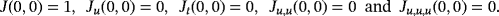
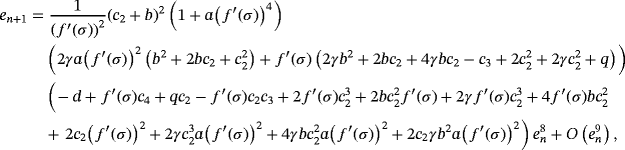 (2)
(2)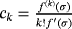 , k ≥ 2.
, k ≥ 2.
Proof.Let us define the error at the nth step as en = xn − σ. By using Taylor series, we expand f (x) about the real root σ as
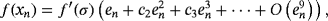 (3)
(3)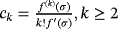 . By using Taylor series, the error term en,w = wn − σ = en + af (xn) is
. By using Taylor series, the error term en,w = wn − σ = en + af (xn) is
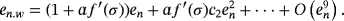
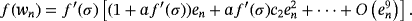
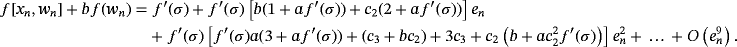 (4)
(4)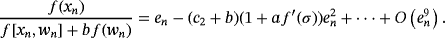
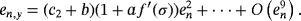
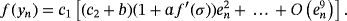
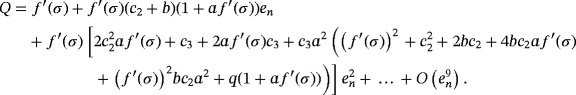
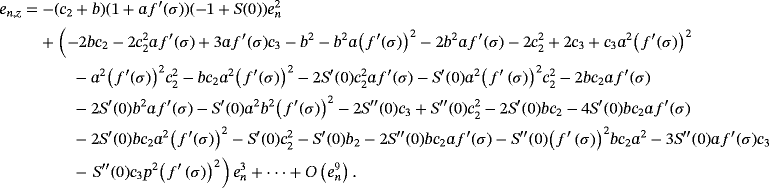
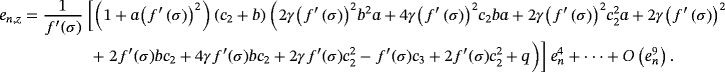
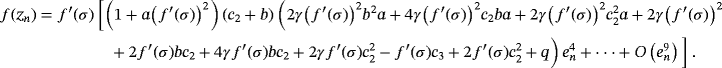
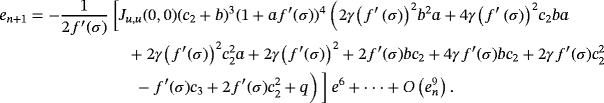
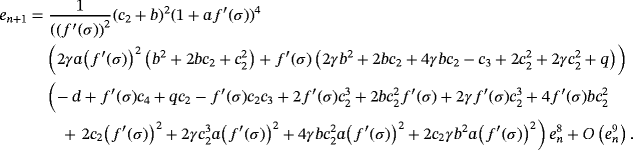
Let us remark that, as the error equation has (c2 + b)2 and (1 + a f ′(σ))4 as factors, it can be seen that this method is extendable to with memory.
3 CONSTRUCTION OF THE FOUR-PARAMETRIC WITH-MEMORY ITERATIVE CLASS
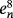 in the error equation 2 disappears if
in the error equation 2 disappears if
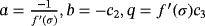 and d = f ′(σ)c4, being
and d = f ′(σ)c4, being
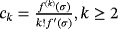 . For construction of methods with memory, free parameters a,b,q, and d are calculated by formulas
. For construction of methods with memory, free parameters a,b,q, and d are calculated by formulas
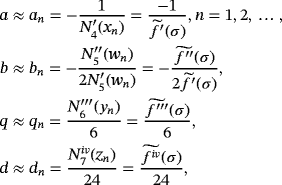 (5)
(5)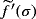 ,
,
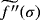 ,
,
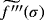 and
and
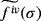 are approximations to
are approximations to
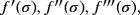 and
and
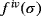 , respectively. These estimations are made by using N4(xn),N5(wn),N6(yn) and N7(zn), Newton's interpolating polynomials of degree four, five, six and seven respectively defined by:
, respectively. These estimations are made by using N4(xn),N5(wn),N6(yn) and N7(zn), Newton's interpolating polynomials of degree four, five, six and seven respectively defined by:
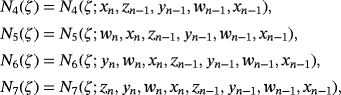
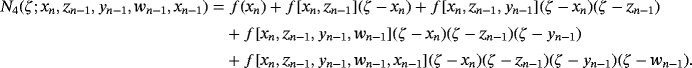 (6)
(6)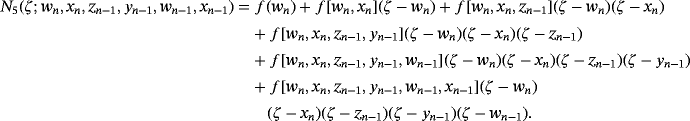 (7)
(7)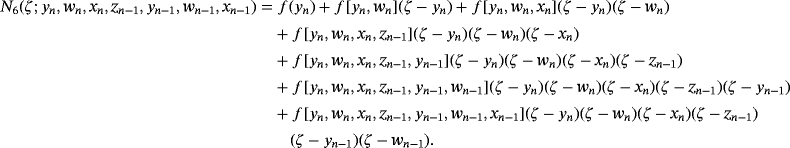 (8)
(8)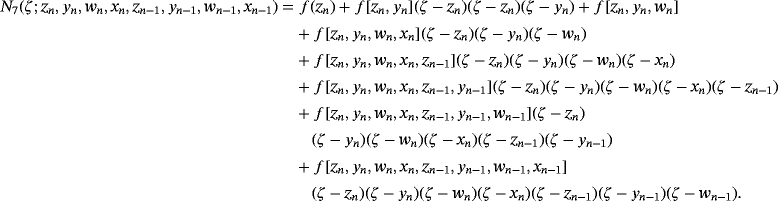 (9)
(9)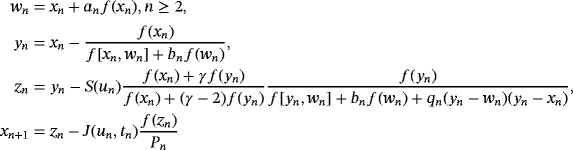 (10)
(10)
Theorem 2.Let us suppose that
 is a real-valued nonlinear sufficiently differentiable function and σ is a real simple zero of the function in the open interval I. Let us also suppose that x0 and x1 are the initial guesses satisfactorily close to the zero σ of f (x). If self-accelerating parameters an,bn,dn and qn are calculated from 5, then the R-order of convergence of 10 is at least 15.51560 with efficiency index
is a real-valued nonlinear sufficiently differentiable function and σ is a real simple zero of the function in the open interval I. Let us also suppose that x0 and x1 are the initial guesses satisfactorily close to the zero σ of f (x). If self-accelerating parameters an,bn,dn and qn are calculated from 5, then the R-order of convergence of 10 is at least 15.51560 with efficiency index
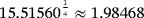 .
.
Proof.We will determine the R-order of convergence of the class of iterative methods with memory 10 by means of Herzberger's matrix method.7 Spectral radius of a matrix B (p) = (tij), 1 ≤ i,j ≤ p, associated with one step p -point method with memory xm = Ψ(xm − 1,xm − 2,…,xm − p) is the lower bound of its convergence order. Associated matrix has following elements:

The spectral radius of B1·B2·⋯·Bp is the lower bound of order of a p-step method Ψ = Ψ1∘Ψ2∘…∘Ψp, where matrices Br corresponds to the iteration step Ψr,1 ≤ r ≤ p. From 5 and 10, the construction of matrices is made following the iterative expression of each step, starting from the last one. For
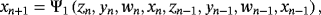



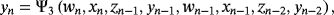

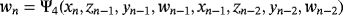


Let us remark that, from Theorem 2, the R-order of convergence of presented class with memory 10 is 15.51560, with the highest efficiency index
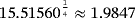 .
.
4 SOME SPECIAL CASES
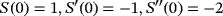
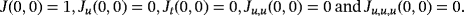
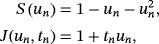
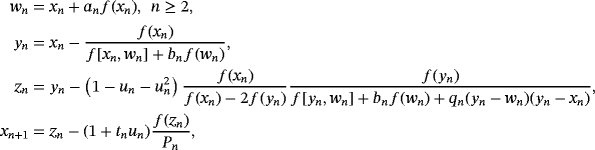
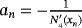 ,
,
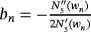 ,
,
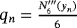 ,
,
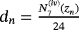 ,
,
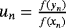 ,
,
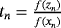 and Pn = f [ yn,zn] + f [zn,yn,xn](zn − yn) + f [zn,yn,xn,wn](zn − yn)(zn − xn) + dn(zn − wn)(zn − yn)(zn − xn).
and Pn = f [ yn,zn] + f [zn,yn,xn](zn − yn) + f [zn,yn,xn,wn](zn − yn)(zn − xn) + dn(zn − wn)(zn − yn)(zn − xn).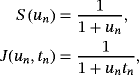
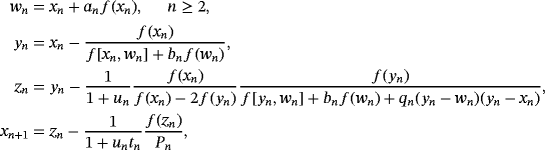
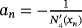 ,
,
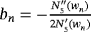 ,
,
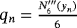 ,
,
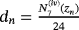 ,
,
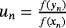 ,
,
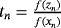 and Pn = f [yn,zn] + f [zn,yn,xn](zn − yn) + f [zn,yn,xn,wn](zn − yn)(zn − xn) + dn(zn − wn)(zn − yn)(zn − xn).
and Pn = f [yn,zn] + f [zn,yn,xn](zn − yn) + f [zn,yn,xn,wn](zn − yn)(zn − xn) + dn(zn − wn)(zn − yn)(zn − xn).5 NUMERICAL RESULTS
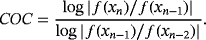
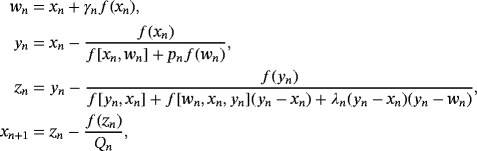
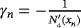 ,
,
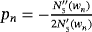 ,
,
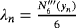 ,
,
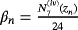 and Qn = f [xn,zn] + ( f [wn,xn,yn] − f [wn,xn,zn] − f [ yn,xn,zn])(xn − zn) + βn(zn − xn)(zn − wn)(zn − yn). With these accelerating parameters, the scheme LA reaches order of convergence 15.51560.
and Qn = f [xn,zn] + ( f [wn,xn,yn] − f [wn,xn,zn] − f [ yn,xn,zn])(xn − zn) + βn(zn − xn)(zn − wn)(zn − yn). With these accelerating parameters, the scheme LA reaches order of convergence 15.51560.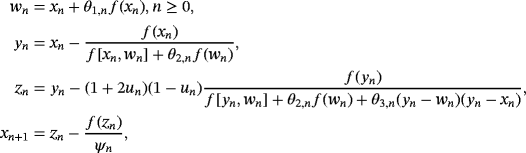
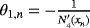 ,
,
 ,
,
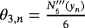 , and
, and
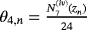 . Moreover,
. Moreover,
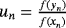 and ψn = f [ yn,zn] + f [ zn,yn,xn](zn − yn) + f [ zn,yn,xn,wn](zn − yn)(zn − xn) + θ4,n(zn − wn)(zn − yn)(zn − xn).
and ψn = f [ yn,zn] + f [ zn,yn,xn](zn − yn) + f [ zn,yn,xn,wn](zn − yn)(zn − xn) + θ4,n(zn − wn)(zn − yn)(zn − xn).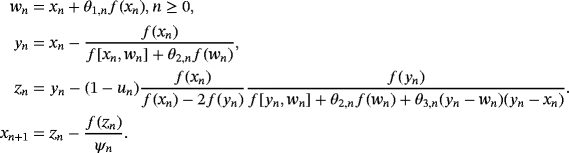
Examples 1.Function
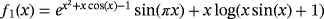 has two real roots at σ = 0 and −1.2829, we seek to approximate the null solution with x0 = 0.6 as initial estimation. When numerical tests are made on f1(x) by using iterative schemes without memory (see Table 1), the best results in terms of precision are obtained by schemes ZR18 and M28. In Table 2, the errors obtained by their with-memory schemes ZR1 and ZR2 are showing the smallest error. In all cases, the COC coincides with the theoretical value.
has two real roots at σ = 0 and −1.2829, we seek to approximate the null solution with x0 = 0.6 as initial estimation. When numerical tests are made on f1(x) by using iterative schemes without memory (see Table 1), the best results in terms of precision are obtained by schemes ZR18 and M28. In Table 2, the errors obtained by their with-memory schemes ZR1 and ZR2 are showing the smallest error. In all cases, the COC coincides with the theoretical value.
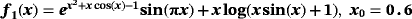 . . |
|||||
|---|---|---|---|---|---|
| LA8 | M18 | M28 | ZR18 | ZR28 | |
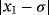 |
6.639 × 10−2 | 8.537 × 10−4 | 1.193 × 10−3 | 7.193 × 10−4 | 1.639 × 10−3 |
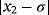 |
4.331 × 10−19 | 7.754 × 10−24 | 9.837 × 10−25 | 1.564 × 10−25 | 1.958 × 10−22 |
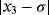 |
1.579 × 10−148 | 3.566 × 10−184 | 2.123 × 10−193 | 7.795 × 10−199 | 7.937 × 10−174 |
| COC | 7.999 | 8.000 | 7.999 | 8.000 | 8.000 |
- Abbreviation: COC, computational order of convergence.
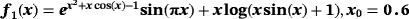 |
|||||
| LA | M1 | M2 | ZR1 | ZR2 | |
|---|---|---|---|---|---|
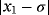 |
6.639 × 10−3 | 8.537 × 10−4 | 1.193 × 10−3 | 7.193 × 10−4 | 1.639 × 10−3 |
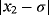 |
1.440 × 10−37 | 2.675 × 10−48 | 4.512 × 10−49 | 6.253 × 10−49 | 2.828 × 10−49 |
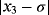 |
4.079 × 10−569 | 5.575 × 10−734 | 1.177 × 10−737 | 1.332 × 10−744 | 2.089 × 10−749 |
| COC | 15.33 | 15.40 | 15.15 | 15.43 | 15.29 |
- Abbreviation: COC, computational order of convergence.
Examples 2.In function
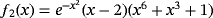 , the only real root is σ = 2, which is efficiently reached by all proposed and known methods; however, the precision reached by iterative schemes with memory is much bigger than the error of their without-memory partners. In Tables 3 and 4, it is shown that the best performance without using memory is obtained by methods ZR1 and M2; when memory is used, the exact error is reduced by a factor of almost 1/5, being the more precise results given by our proposed methods ZR1 and ZR2.
, the only real root is σ = 2, which is efficiently reached by all proposed and known methods; however, the precision reached by iterative schemes with memory is much bigger than the error of their without-memory partners. In Tables 3 and 4, it is shown that the best performance without using memory is obtained by methods ZR1 and M2; when memory is used, the exact error is reduced by a factor of almost 1/5, being the more precise results given by our proposed methods ZR1 and ZR2.
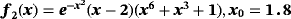 |
|||||
| LA8 | M18 | M28 | ZR18 | ZR28 | |
|---|---|---|---|---|---|
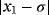 |
1.185 × 10−6 | 1.508 × 10−6 | 5.633 × 10−7 | 2.594 × 10−7 | 7.558 × 10−7 |
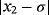 |
2.116 × 10−47 | 1.760 × 10−45 | 3.197 × 10−50 | 1.213 × 10−52 | 9.952 × 10−50 |
 |
2.189 × 10−373 | 6.039 × 10−357 | 3.439 × 10−396 | 2.786 × 10−415 | 8.992 × 10−393 |
| COC | 7.999 | 7.999 | 7.999 | 7.999 | 8.000 |
- Abbreviation: COC, computational order of convergence.
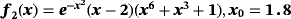 |
|||||
| LA | M1 | M2 | ZR1 | ZR2 | |
|---|---|---|---|---|---|
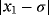 |
1.185 × 10−6 | 1.508 × 10−6 | 5.663 × 10−7 | 2.594 × 10−7 | 7.558 × 10−7 |
 |
7.208 × 10−97 | 9.283 × 10−96 | 6.033 × 10−102 | 7.648 × 10−103 | 1.564 × 10−99 |
 |
3.191 × 10−1498 | 1.335 × 10−1479 | 7.590 × 10−1578 | 1.278 × 10−1592 | 8.037 × 10−1592 |
| COC | 15.53 | 15.51 | 15.54 | 15.59 | 15.52 |
- Abbreviation: COC, computational order of convergence.
Examples 3.Function
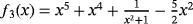 has three real roots, −0.566312746, 1, and 0.620346251, but the desired one in the numerical tests is σ = 1. When the methods without memory are used (see Table 5), the best results (lowest exact error) have been obtained by ZR28 and M28. Regarding the performance of iterative schemes with memory (see Table 6), the lowest errors have been obtained by the proposed methods ZR1 and ZR2, although the reduction of the error had a factor of 1/4, approximately.
has three real roots, −0.566312746, 1, and 0.620346251, but the desired one in the numerical tests is σ = 1. When the methods without memory are used (see Table 5), the best results (lowest exact error) have been obtained by ZR28 and M28. Regarding the performance of iterative schemes with memory (see Table 6), the lowest errors have been obtained by the proposed methods ZR1 and ZR2, although the reduction of the error had a factor of 1/4, approximately.
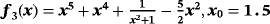 |
|||||
| LA8 | M18 | M28 | ZR18 | ZR28 | |
|---|---|---|---|---|---|
 |
2.831 × 10−2 | 6.761 × 10−2 | 1.974 × 10−2 | 3.346 × 10−2 | 1.038 × 10−2 |
 |
1.900 × 10−9 | 1.497 × 10−5 | 1.326 × 10−10 | 9.698 × 10−9 | 2.064 × 10−13 |
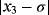 |
1.425 × 10−66 | 1.129 × 10−33 | 8.615 × 10−76 | 2.011 × 10−61 | 1.693 × 10−98 |
| COC | 7.963 | 7.472 | 7.944 | 7.990 | 7.937 |
- Abbreviation: COC, computational order of convergence.
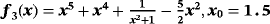 |
|||||
| LA | M1 | M2 | ZR1 | ZR2 | |
|---|---|---|---|---|---|
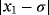 |
2.831 × 10−2 | 6.761 × 10−2 | 3.607 × 10−2 | 3.346 × 10−2 | 1.038 × 10−2 |
 |
3.345 × 10−19 | 6.912 × 10−13 | 5.721 × 10−17 | 1.802 × 10−17 | 1.924 × 10−25 |
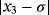 |
5.898 × 10−290 | 3.448 × 10−188 | 1.611 × 10−253 | 1.510 × 10−261 | 3.509 × 10−389 |
| COC | 15.99 | 15.79 | 15.98 | 15.92 | 15.98 |
- Abbreviation: COC, computational order of convergence.
Examples 4. (Continuous stirred tank reactor (CSTR))Let us consider an isothermal continuous stirred tank reactor (CSTR). Components A & R are fed to the reactor at rates of Q and q-Q respectively. The following reaction scheme develops in the reactor:
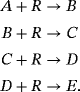
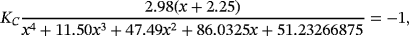
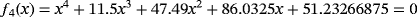 (11)
(11)In case of parametric eighth-order schemes (see Table 7), the best results are provided by ZR28 and M28 methods, holding in all cases a computational order that agrees with the theoretical one. When methods with memory are used, we can see in Table 8 that the most precise solution is obtained by ZR2 scheme, followed in a big distance by the LA method. The process of using memory in the accelerating parameters has decreased the error in a factor of 1/4, approximately. The estimation of the order of convergence again agrees with the theoretical one.
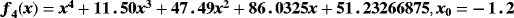 |
|||||
| LA8 | M18 | M28 | ZR18 | ZR28 | |
|---|---|---|---|---|---|
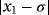 |
5.546 × 10−5 | 7.586 × 10−4 | 5.204 × 10−5 | 1.270 × 10−4 | 3.529 × 10−6 |
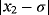 |
2.2504 × 10−33 | 2.372 × 10−22 | 1.643 × 10−33 | 1.643 × 10−30 | 1.213 × 10−42 |
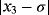 |
1.654 × 10−260 | 2.205 × 10−170 | 1.626 × 10−261 | 1.304 × 10−237 | 2.366 × 10−334 |
| COC | 7.999 | 7.999 | 7.999 | 7.999 | 7.999 |
- Abbreviation: COC, computational order of convergence.
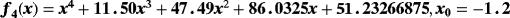 |
|||||
| LA | M1 | M2 | ZR1 | ZR2 | |
|---|---|---|---|---|---|
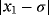 |
5.546 × 10−5 | 7.586 × 10−4 | 5.204 × 10−5 | 1.270 × 10−4 | 3.529 × 10−6 |
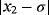 |
3.627 × 10−67 | 2.408 × 10−48 | 5.847 × 10−67 | 9.266 × 10−61 | 1.168 × 10−85 |
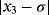 |
4.063 × 10−1062 | 2.591 × 10−760 | 3.771 × 10−1058 | 5.963 × 10−959 | 2.434 × 10−1357 |
| COC | 15.99 | 15.99 | 15.99 | 15.99 | 15.99 |
- Abbreviation: COC, computational order of convergence.
6 CONCLUSIONS
We have proposed new three-step four-parametric family of iterative methods by using two weight functions. We have taken test functions of different types and have applied our newly proposed methods on them. We also have compared our results with recent three-step four-parametric methods. In case of schemes without memory, our methods ZR1 and ZR2 give much better accuracy and COC for test functions f1, f2, f3, and f4 as compared to the methods LA, M1, and M2. In case of extension with memory of our methods, efficiency index is increased from 1.6817 to 1.9847 and we obtain much better results and high COC. As a future extension, we can analyze the stability of the proposed family of methods using complex dynamics similar to the works of Chun and Neta9 and Gdawiec.10
ACKNOWLEDGEMENTS
This research was partially supported by Ministerio de Economía y Competitividad MTM2014-52016-C2-2-P, Generalitat Valenciana PROMETEO/2016/089 and Schlumberger Foundation-Faculty for Future Program.
CONFLICT OF INTEREST
The authors declare no potential conflict of interests.
Biographies

Fiza Zafar completed her bachelor's degree and master's degree in applied mathematics with a gold medal at Bahauddin Zakariya University, Multan, Pakistan. She obtained her PhD in mathematics in 2010 from the Centre for Advanced Studies in Pure and Applied Mathematics, Bahauddin Zakariya University, Multan, Pakistan for the dissertation “Some Generalizations of Ostrowski Inequalities and Their Applications to Numerical Integration and Special Means.” During these years, she has worked in the fields of calculus of variation, numerical solution of nonlinear equations, and numerical integration and has significant number of international impact factor publications in these areas. Recently, she has completed a one-year postdoctoral research fellowship with Professor Juan Ramon Torregrosa and Professor Alicia Cordero in the research area of iterative methods for solving nonlinear equations and the dynamic study of associated rational functions at Institute for Multidisciplinary Mathematics, Universitat Politècnica de València, Spain.
Currently, she is working as a tenured assistant professor at Bahauddin Zakariya University, Multan, Pakistan. She has supervised 21 MS and 2 PhD theses. She has also been listed as a Dynamic Woman Scientist of Pakistan and Productive Young Scientist of Pakistan under 40 by Pakistan Council for Science and Technology. She is a guest editor for a special issue of Algorithms (MDPI), an active reviewer for many renowned scientific publishers like Elsevier, Springer, Taylor & Francis, and Hindawi Publishing Corporation, and has been a speaker at several national and international conferences.

Alicia Cordero Since her PhD dissertation in 2003, “Cadenas de Órbitas Periódicas en la Variedad S2xS1,” supervised by Professors J.A. Martínez (Universitat de València) and P. Vindel (Universitat Jaume I de Castellón UJI), her research career had two branches, which have finally converged: her doctoral thesis, and the subsequent research until 2007, was focused on continuous dynamic systems and decomposition into round handles of the three-dimensional surface S2xS1, with applications to celestial mechanics. From 2005, and simultaneously with the previous one, she started a new line of research in numerical analysis, specifically in iterative techniques for solving equations and nonlinear systems. The design and analysis of the convergence of iterative methods is a field of research that has developed very rapidly in recent years. The first works in this line, which dealt with the extension to nonlinear systems of specific methods for equations, were published in 2006 and 2007 and have been widely cited. During this time, she has coadvised four PhD in numerical analysis, framed in the Doctorate with Mention of Quality “Multidisciplinary Mathematics” of the Department of Applied Mathematics of the Polytechnic University of Valencia (UPV).
The mentioned research has also led to her role as guest editor in several special issues in international journals as Journal of Applied Mathematics and Abstract and Applied Analysis, both published by Hindawi, Journal of Computational and Applied Mathematics (Elsevier), Algorithms (MDPI). Likewise, since 2015, she is an editor of the journal Discrete Dynamics in Nature and Society and the journal Algorithms (MDPI). On the other hand, she is a reviewer of different indexed journals indexed in JCR.
Regarding research grants, she has participated in more than ten research projects of the Spanish Government, regional grants by Generalitat Valenciana, and in international research projects at Dominican Republic, which aims to create a computer center that provides mathematical coverage in numerical modeling and simulation, basic and applied research in the region.

Juan R. Torregrosa is a full professor of mathematics at the Universitat Politècnica de València (UPV). He has researched in functional analysis, specifically in geometrical properties of Banach spaces, in matrix analysis, namely, in the theory of completion of partial matrices and in totally positive matrices. Since 2006, and initially simultaneously with the previous ones, he started a line of research on numerical analysis, in particular, in iterative methods for solving nonlinear equations and systems, topic that has developed very rapidly in recent years. The first works in this area, which deal with the extension to nonlinear systems of specific methods for equations, were published in 2006 and 2007 and have been widely cited. From the point of view of publications, his work has been seen to be reflected in 182 publications in journals indexed in JCR, 15 publications in journals not indexed in JCR, 151 papers in national and international conferences, and collaboration in 7 monographs on different research topics.
During this time, he has advised nine PhD in matrix analysis and numerical analysis, the most of them, framed in the Doctorate with Mention of Quality “Multidisciplinary Mathematics” of the Department of Applied Mathematics of the UPV. He has also led 5 master dissertation and more than 50 final dissertation degree.
The mentioned research has also led to his role as a managing guest editor in several special issue of Journal of Applied Mathematics (Hindawi), Abstract and Applied Analysis (Hindawi), Journal of Computational and Applied Mathematics (Elsevier), Algorithms (MDPI), Discrete Dynamics in Nature and Society (Hindawi), Axioms (MDPI), and Mathematics (MDPI). On the other hand, he has acted as a reviewer of many journals indexed in JCR.
Regarding research grants, he has participated in 2 projects of European Commission, 11 projects of the Spanish Government, 5 of Generalitat Valenciana, and 7 of UPV. Recently, his research group has formed part of two coordinated research projects MTM2011-28636-C02-02 and MTM2014-52016-C2-2-P, as well as a PROMETEO/2016/089 funded by the Generalitat Valenciana, in all of them, he is the main researcher. He is also participating in two research projects of Ministerio de Educación Superior, Ciencia y Tecnología, at Dominican Republic.

Anneqa Rafi completed her bachelor's degree (2014) and master's degree (2016) in computational mathematics by securing second position from the Centre for Advanced Studies in Pure and Applied Mathematics, Bahauddin Zakariya University, Multan, Pakistan. Her MS dissertation titled “Optimal Three Step Four Parametric With- and Without-Memory Iterative Method with Convergence Planes” was supervised by Dr Fiza Zafar. She is currently working as an elementary school educator for science and mathematics at Government Girls Elementary School, Multan, Pakistan.




