Bending of plates with transverse shear deformation: The Robin problem
Abstract
The Robin problem in a finite domain for the system of equations describing the bending of elastic plates with transverse shear deformation is solved by means of a generalized Fourier series method based on the structure of the governing system. The numerical illustration of the results, obtained by three different computational methods, is also provided.
1 INTRODUCTION
Many times, solutions of boundary value problems for a mathematical model cannot be computed explicitly, but they can be approximated within acceptable tolerances by means of expansions in a complete set of functions in a Banach space such as L2. The method acquires additional interest and usefulness when the choice of these functions is based on the structure of the layer potentials associated with the problem. This type of expansion may encounter problems when the set in question is orthonormalized by, for example, the Gram-Schmidt technique. In this paper, we propose an algorithm that bypasses orthonormalization issues and yields highly promising numerical results within a prescribed accuracy. We illustrate this technique by solving an interior Robin problem for the system governing the bending of elastic plates with transverse shear deformation. Problems with the Dirichlet and Neumann boundary conditions have been solved in our previous works.1, 2
-
S: a finite domain in
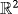 , bounded by a simple, closed, C2-curve ∂S;
, bounded by a simple, closed, C2-curve ∂S; - x, y: generic points in S or on ∂S;
-
h0 = const > 0, h0 ≪ diam S;
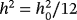 ;
; - λ, μ: the Lamé constants of a homogeneous and isotropic medium filling the three-dimensional region (S∪∂S) × [− h0/2,h0/2].
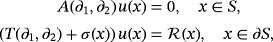 (1)
(1)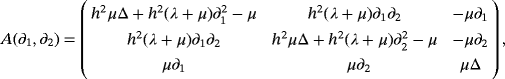
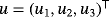 is a vector characterizing the displacements,
is a vector characterizing the displacements,
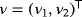 is the unit vector of the outward normal to ∂S, σ ∈ C 0,α(∂S), α ∈ (0,1), is a symmetric, positive definite 3 × 3 matrix function on ∂S, and
is the unit vector of the outward normal to ∂S, σ ∈ C 0,α(∂S), α ∈ (0,1), is a symmetric, positive definite 3 × 3 matrix function on ∂S, and
 is a prescribed 3 × 1 vector function.
is a prescribed 3 × 1 vector function.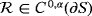 , α ∈ (0,1). The proof of this assertion involves the matrix of fundamental solutions D(x,y) computed in the work of Constanda3 and the associated matrix
, α ∈ (0,1). The proof of this assertion involves the matrix of fundamental solutions D(x,y) computed in the work of Constanda3 and the associated matrix
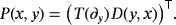
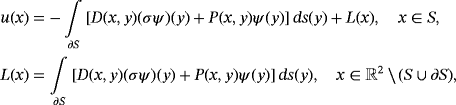 (2)
(2)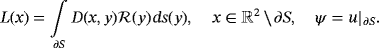 (3)
(3)2 COMPUTATIONAL ALGORITHM
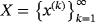
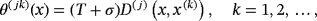 (4)
(4)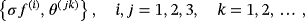
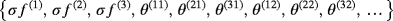
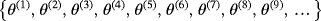
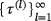 .
.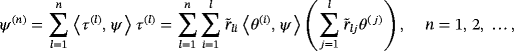 (5)
(5)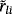 are the orthonormalization coefficients and ⟨· ,·⟩ is the inner product on L2(∂S), we use 2 to construct the approximate solution
are the orthonormalization coefficients and ⟨· ,·⟩ is the inner product on L2(∂S), we use 2 to construct the approximate solution
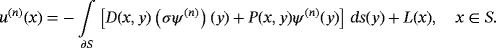 (6)
(6)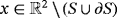 by x(k) in 3 to arrive at
by x(k) in 3 to arrive at
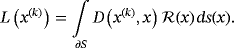 (7)
(7)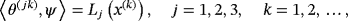
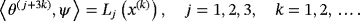 (8)
(8)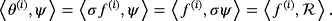 (9)
(9)This computational scheme shows that the approximation u(n) is given by 6, with ψ(n) determined from 5, ⟨θ(i),ψ⟩ from 8 and 9, and Lj(x(k)) from 7. Detailed analysis indicates that the sequence u(n) converges uniformly in the L2-norm on any closed subdomain of S to the solution u of the problem.
3 NUMERICAL ILLUSTRATION
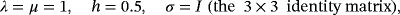
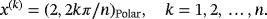
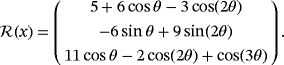
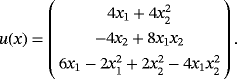
The set
 is orthonormalized by three different procedures: the classical Gram-Schmidt (CGS), the modified Gram-Schmidt (MGS), and the Householder reflections (HR); see the work of Trefethen.4 We also use a fourth technique, which, based on row reduction, makes orthonormalization unnecessary. Below are the graphical results of the computation.
is orthonormalized by three different procedures: the classical Gram-Schmidt (CGS), the modified Gram-Schmidt (MGS), and the Householder reflections (HR); see the work of Trefethen.4 We also use a fourth technique, which, based on row reduction, makes orthonormalization unnecessary. Below are the graphical results of the computation.
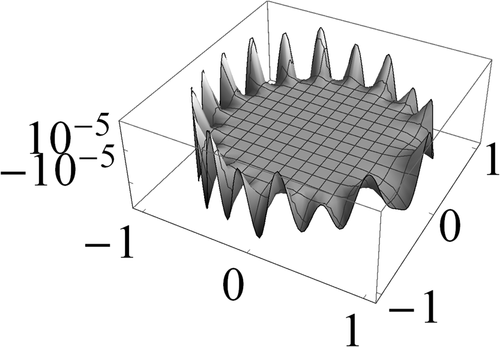
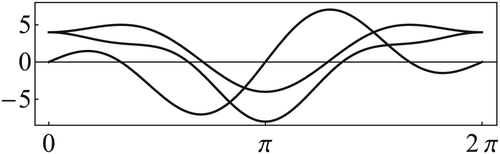
Figures 1 to 3 display the three components of u(63) in S. Figures 4 to 6 show the corresponding computational errors for the approximate boundary values of u(63). The curves in Figure 7 are the graphs (in terms of the polar angle) of the computed traces of the components of u(63) on ∂S. The graph in Figure 8 indicates the computed error in the traces on ∂S of the components of u(63).
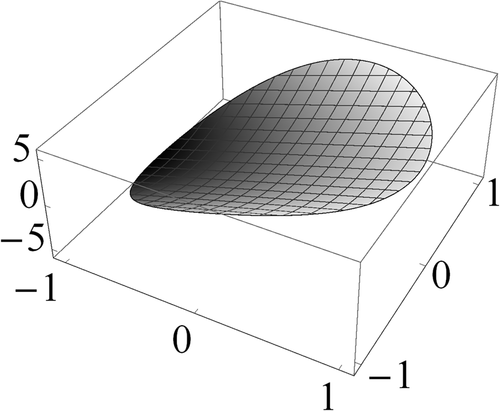
 in S
in S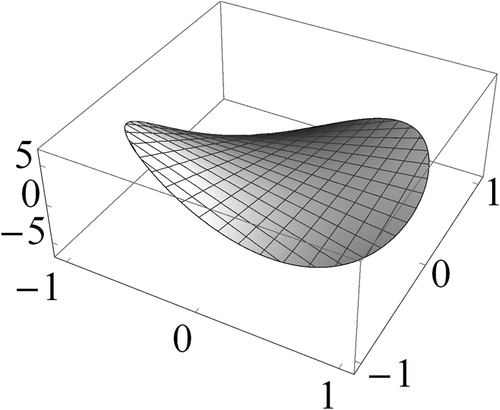
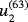 in S
in S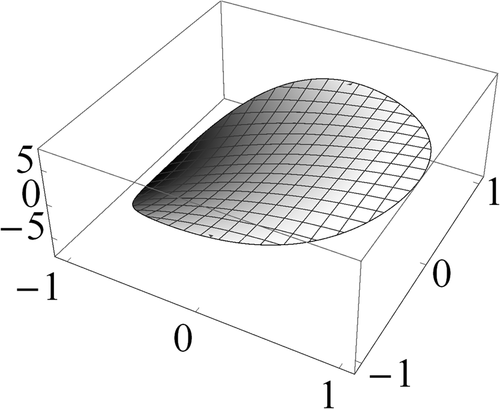
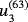 in S
in S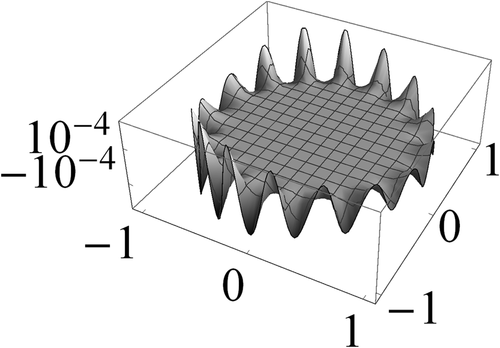
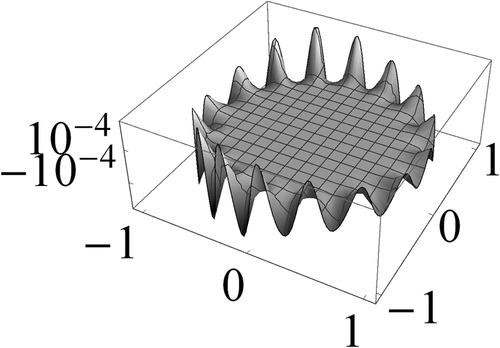
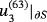
Biographies

Christian Constanda, received the MS degree in mathematics and mechanics from the University of Iaşi, Iaşi, Romania, in 1966; the PhD degree in mathematics from the Romanian Academy of Sciences, Bucharest, Romania, in 1972; and the DSc degree (the rarely awarded British Higher Doctorate) from the University of Strathclyde, Glasgow, UK, in 1997. He was a Research Fellow at the Romanian Academy of Sciences from 1967 and 1975 and a Professor of mathematics at the University of Strathclyde from 1976 to 2002. Since 2002, he has been with the University of Strathclyde, where he is currently an Emeritus Professor, and since 2003, he has been with The University of Tulsa, Tulsa, Oklahoma, where he is currently the Charles W. Oliphant Endowed Chair of Mathematics and the Director of the Center for Boundary Integral Methods. His areas of specialty are applied analysis, boundary integral equations, and mathematical problems in elasticity theory. He is the Chairman of the International Consortium on Integral Methods in Science and Engineering. He is the author of more than 145 published research papers and author, editor, or translator of 32 mathematical books.

Dale Doty, received the PhD degree in mathematics from Michigan State University, East Lansing, Michigan, in 1975. Since 1975, he has been with The University of Tulsa, Tulsa, Oklahoma, where he is currently a Professor of mathematics. His areas of specialty are approximation theory, numerical analysis, boundary integral methods, and petroleum production technology. He was the Associate Director of Tulsa University Artificial Lift Projects, a petroleum industry-supported consortium funding both research and graduate students with an annual budget of $500,000 from 1983 to 2002. He is the author of more than 45 published research papers and several books.




