Drying Rate Prediction for Droplets under Combined Convection and Infrared Radiation Drying
Abstract
Combined drying through convection and radiation allows for process intensification and thus for an increase in the drying rate as well as in the range of applications. Established combined drying models have mainly focused on drying thin layers of wet solids, not liquid droplets. In this work, the drying of pure solvent droplets as well as the drying of a polymer solution were studied. Experiments were performed to determine the influence of convective airflow temperature and radiative power on the mass reduction rate in the first phase of drying. A simplified model was developed for the combined drying of large solvent droplets and transferred to the polymer solution. The developed empirical model allowed for drying rate predictions with an accuracy similar to established convective drying models.
1 Introduction
Drying is an essential unit operation in many industrial processes, such as in the manufacturing of spherical particles via spray drying for food and pharmaceutical applications. In spray drying, the drying process is typically limited by the rate of the energy transfer from the drying medium onto the droplet because the generally used drying media have a high velocity and a low starting concentration of the liquid to be vaporized. In this case, the convective drying of liquid droplets containing a solid component can be subdivided into several phases (Fig. 1). Upon entry into the drying chamber, the droplet is heated up from its initial conditions. Meanwhile, the drying rate, which is defined as the mass loss per time, increases (section 1a) because of the increasing vapor pressure. The droplet temperature and drying rate converge on a constant value as an equilibrium between the energy input by the drying process and the energy consumed by the mass flow of evaporated liquid is reached (section 1b). This equilibrium phase is referred to as the “constant rate period” or the “first drying phase” and is mainly characterized by the liquid characteristics and initial conditions. Once the solubility concentration of the dissolved solid is exceeded at the surface of the droplet, a solid shell is formed. The dried solid acts as a barrier to the solvent diffusion, thus reducing the drying rate while increasing the particle temperature. This phase of decreasing drying rate is referred to as the “second phase” of drying (section 2), and it continues until the particle temperature and moisture are in equilibrium with the convective airflow [1-5].
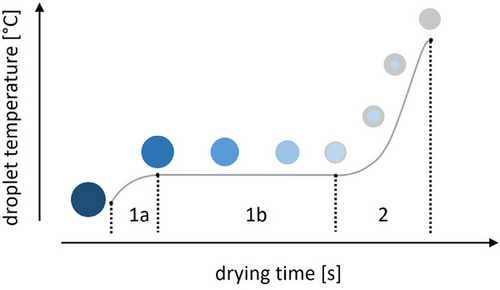
The aim in convective drying processes, such as spray drying, is generally to continue the drying process until this equilibrium is reached. Particle formation in purely convective spray-drying processes has been studied extensively [2-9]. However, traditional spray-drying processes are limited in regard to the droplet size that can be dried: The nature of the spray-drying process restricts feasible residence times [4], whereas the desired structural and chemical integrity of the product limits the range of applicable air temperatures. If the chosen air temperature is too high, chemical degradation of the product could occur. Additionally, the formations of hollow spheres with blowholes or collapsing particles have been observed [3, 8, 10-13].
A possible approach to mitigate these issues is the use of a two-step drying process: a primary drying step in free-fall with a large energy and mass flow rate, in which the product is dried until a solid crust is formed around a wet core (Fig. 1, sections 1a and 1b). This is then followed by a secondary, slower drying process (Fig. 1, section 2). If the outer shell is solid and not sticky, the remaining moisture can be removed in any conventional drying apparatus, such as a fluid-bed dryer, because a contact-free process is no longer required. With this approach, large droplets could be dried without the aforementioned characteristic blowholes associated with high-temperature spray drying while also allowing for the use of heat-sensitive substances.
In order to increase the heat transfer during the first drying step, a radiative heat source was added to the convective drying process, from now on called the combined drying process. This utilizes the rapid and effective energy transfer of the radiative drying while benefitting from the efficient solvent vapor removal seen in convective drying. Such combinations have been intensively studied for food preservation as well as for other industrial applications, where they are frequently employed to dry thin layers of materials, such as rice, onion, fruit leathers, paper, and textiles [4, 14-18]. Because the starting point of these drying processes is generally a solid containing a liquid, the majority of the drying time corresponds to the second phase of drying (Fig. 1, section 2). Therefore, the relevant material surface remains mostly constant, whereas the drying rate depends on the physicochemical characteristics of the solid component and decreases over time [1, 2, 4]. In the aforementioned two-step drying process, however, the combined drying is employed for the first phase of drying (Fig. 1, sections 1a and 1b). In this phase, the drying rate is mainly determined by the liquid properties, and the particle size is subject to change. Thus, a model for the first phase of drying should be developable using pure solvent droplets.
The aim of this investigation was to develop a model for the prediction of the mass reduction rate of liquid droplets in the first drying phase undergoing combined convection and radiation drying. As the focus of the model is the first drying phase, theoretical considerations and experiments can be performed for water droplets and subsequently applied to an aqueous polymer solution. The model should use easily accessible experimental data while simultaneously retaining predictive power and general applicability. In the pursuit of this aim, several assumptions are made to simplify the complexities of radiative energy transfer and thus reduce the need for more computationally intensive calculations. For example, the temperature dependence of emitted wavelengths generally observed and described is neglected, as well as the wavelength dependence of the absorption coefficient of water and the temperature gradients formed within the heated droplet. Furthermore, the semi-transparent nature of liquid droplets, allowing for radiation transmission, scattering, and volume absorption, is not discussed. Rigorous descriptions of radiative energy transfer can be found in literature [19-24].
2 Model Development
2.1 Model Approach
2.2 Convection
The convective heat transfer coefficient can be determined from the Nusselt number , which in turn can be found using the Ranz–Marshall equation [26]. The Ranz–Marshall equation and variations of it are ubiquitously used in literature and have been shown to accurately describe the heat and mass transfer at the surface of a single droplet for Reynolds numbers below 2000 [3, 12]. In a recent review paper concerning droplet dispersion modelling, only 2 of the 10 reviewed studies did not use some variation of the Ranz–Marshall equation to account for the droplet evaporation [27].
The Ranz–Marshall equation defines the Nusselt number in dependence of the Reynolds and Prandtl numbers. As the density (ρG), the thermal conductivity (λ), the viscosity (η), and the specific heat capacity (cp) of the drying gas can be found in literature, only the relative velocity (v) between the droplet and the surrounding air and the droplet diameter (dD) must be measured to access the convective heat transfer coefficient ().
Eq. (5) allows for a description of the convective energy transport using physical properties and process parameters.
2.3 Radiation
The absorptance (μIR) of the droplet depends on droplet size, droplet temperature, and irradiation wavelength. For the purpose of this study, the changes in absorptance of the droplet with varying droplet temperature were assumed to be negligible. [29] Because semi-transparent liquids do not absorb the entire infrared spectrum equally, a detailed description of the transferred radiative energy would require a spectral treatment of the absorptance and absorption mode [20, 21]. When using a non-ideal black body, a set-up with an undetermined view factor, droplets exhibiting volume absorption, or an emitter of unknown spectral composition, the product of the absorptance (μIR) and the view factor (φE,D) could be replaced by an empirical absorption parameter (Φ).
To determine the absorption parameter for a new set-up with an unknown emitter temperature and view factor, an initial preliminary measurement using purely radiative energy transport can be performed. If the droplet temperature is constant, the measured mass reduction rate can be multiplied by the known enthalpy of vaporization to assess , and thus the radiative energy flow.
Eq. (12) allows for the description of the radiative energy transport even for unknown emitter temperatures and view factors when determining the absorption parameter from a singular initial pre-test using purely radiative energy. It should be noted that the absorption parameter determined with this approach cannot be transferred to systems using other droplet sizes, droplet media, or other emitters, as the absorptance of semi-transparent liquids strongly depends on the wavelength of radiation and the droplet size. Furthermore, as the wavelength emitted also depends on the temperature of the emitter, the applicability of a single absorption parameter, either representative or averaged, for different emitter temperatures should be verified prior to model application.
2.4 Combined Convection and Radiation Drying
In this work, the combination of radiative and convective drying is investigated. As previously established in Eq. (2), the energy flow of the combined drying process can be described by the sum of the convective and radiative energy flows.
The droplet temperature (TD) during the first phase of drying is frequently not easily accessible, and, even if it can be measured, is often distorted by the measurement itself [30]. However, because it is dependent on the gas temperature (TG) and the radiative energy transfer, it can be derived from them. Gnielinski et al. determined the surface temperature during first-phase drying based on the mass transfer laws for a semipermeable boundary and corrected for vapor superheating [31].
In these equations, P is the total pressure, pg,∞ is the partial vapor pressure in the gas, and is the saturation pressure at the surface temperature. Furthermore, β represents the mass transfer coefficient, R is used for the gas constant, Mg is the molar mass of the surrounding gas, and [31].
Eq. (16) is a general form of the analogy between heat and mass transfer and can be derived from the ratio of the Stanton numbers for heat and mass transfer [32, 33]. In this equation, Le is the Lewis number and is a set-up parameter, the value of which depends on the flow behavior of the drying medium. For the case of a turbulent flow with a laminar boundary layer, [25], though the precise value of is of secondary importance, as Le ≈ 1 for water–air mixtures [31, 34].
With this set of Eqs. (11), (17), and (18), the drying rate for any set point of constant relative velocity can be determined using only the air temperature, black body temperature, droplet diameter, and solvent characteristics.
For the model application, the droplets were assumed to be spherical, and the droplet diameter was averaged over the observed drying time for all predicted values. Furthermore, it is important to note that the drying process was assumed to be limited by the energy transport rate, resulting in constant droplet temperature values during the first drying phase, and that interactions between the convective and radiative drying were neglected. Additionally, the emitter temperature, emitter spectrum, and droplet absorptance were assumed to be constant. Only the net absorbed energy was considered, omitting a differentiation between transmitted or reflected radiation and volume or surface absorption.
3 Experimental Section
3.1 Experimental Procedures
Experiments were performed to determine the emitted power via IR, the droplet temperature, and the droplet drying rate resulting from the combined as well as the two singular drying processes.
The emitted power via IR was determined using a matte black circular disc with a thickness of 1 mm and the same diameter as the focal point of the IR emitter (black body).
Experiments regarding the droplet temperature and drying rate were performed for pure water droplets. In these experiments, the airflow rate was held constant, whereas the varied parameters were air temperature and IR radiation intensity.
Select experiments were subsequently repeated with a polymer solution to verify applicability for droplets containing solids. For these transfer experiments, an aqueous dispersion containing 17 % (w/w) of a commercial HPMC ready-mix coating (Aquarius Preferred HSP, Ashland, Wilmington, Delaware, USA), was used.
3.2 Experimental Set-Up
The experimental data were gathered using two variations of the set-up shown in Fig. 2: The investigated object (black body, 20 µL water or polymer solution droplet) was suspended in the focal point of two IR spotlights (Xenophot HLX64635, Osram, Munich, Germany). For experiments employing a convective component, a hot air stream with a velocity of 2 m s−1 was added by leading compressed air through a pressure regulator (M10, Fairchild, Winston-Salem, North Carolina, USA) and a pressure gauge (test gauge 312.20, WIKA Alexander Wiegand, Klingenberg, Germany). The airflow was subsequently led through a flowmeter (D10A11, ABB Asea Brown Boveri, Zürich, Switzerland) to ensure consistent airflow rates for all experiments and through a heater (LHS15 System, Leister Technologies Sarnen, Switzerland). The suspension of the measured object either enabled a measurement of the object's temperature or its mass.
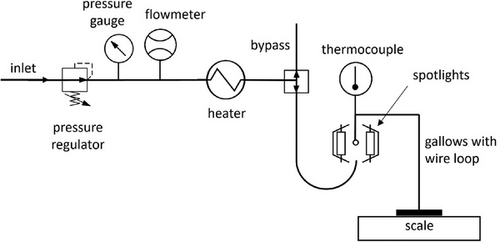
The emitted power was calculated using a variation of the Stefan–Boltzmann equation (Eq. 6) and the temperature achieved in the black body. For the determination of this temperature, the measuring point of the thermocouple was positioned in contact with the side of the black body, thus preventing the thermocouple from shading the black body.
The thermocouple was replaced by a silver wire loop hanging from a gallows mounted on a high-precision scale (Mass Comparator MCM66, Sartorius, Göttingen, Germany) for the drying rate experiments, enabling a precise measurement of the droplet mass over time.
3.3 Experimental Results
In Fig. 3, the relative droplet mass is shown over time. Without IR, the drying times of the droplets range between about 170 and 250 s, depending on the airflow temperature. This time can be reduced down to about 35 s with increased radiative power and high airflow temperatures. As expected, the drying time was shortest for the highest radiative power and highest airflow temperature. In addition, the drying time for pure radiative drying is much longer than the combined drying rates for low values of IR power (about 450 s vs. 100–200 s). However, the drying times with and without airflow converge with increasing IR power.
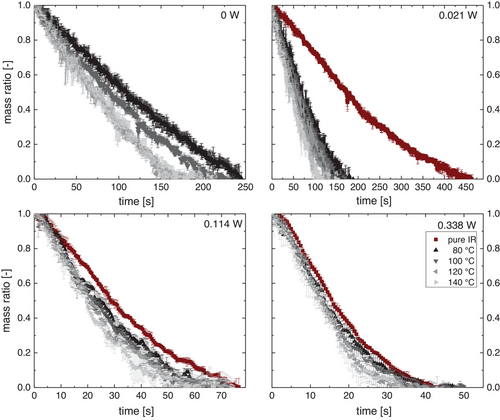
As the IR power increases, at some point it must become the major driving force for evaporation, thus superseding the importance of the airflow.
To gain more insight into the relative contribution of two heat sources, the mass flow rate was evaluated for the first drying phase (1b) marked in Fig. 1. The mass flow rate was evaluated for a droplet mass ratio between 0.6 and 0.2 for all measurements to ensure all data points remained in the first drying phase, thus fulfilling the assumption of a linear mass reduction, as well as fulfilling the assumption of an approximately spherical droplet shape.
The resulting drying rates for the combined drying are shown in Fig. 4 and lend credence to the observation that the IR power influences the drying process more strongly than the airflow temperature. An increase in net IR power from 0.021 to 0.338 W increases the drying rate by a factor of about 5–6, whereas an increase in airflow temperature only increases the drying rate by a factor of about 0.2–0.5.
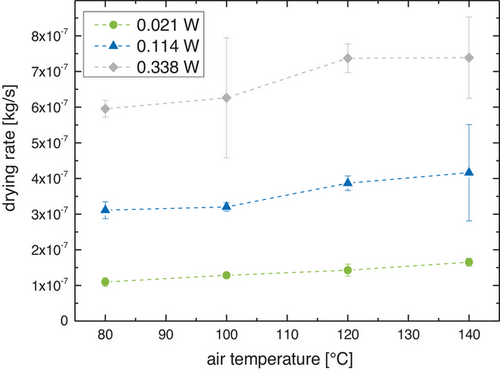
The drying rates for pure IR drying were in the size range of 5 × 10−8 to 6 × 10−7 kg s−1, matching the trend observed for the drying times.
The pure IR drying rates were used to determine the absorption parameter of water as described above using Eq. (11). The average value of the absorption parameter for all net power values was 25.8 and was subsequently used for all power levels in the drying rate prediction. For the transfer of the empirical model to polymer solution droplets, the absorption parameter was determined as 15.7.
4 Model Application
The mass reduction rates predicted by the model are shown in Fig. 5 in comparison to the experimentally determined drying rate values.
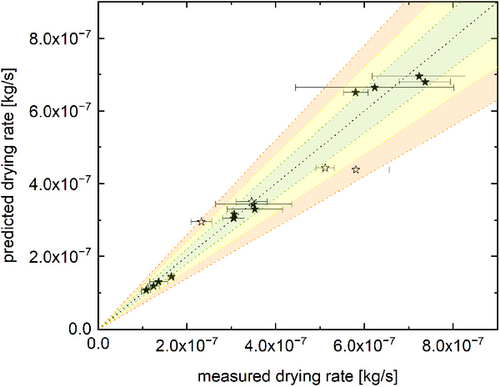
All measured drying rate values were in close agreement with the predicted values, with deviations being below 15 % for the 20 µL water droplets. This is quite remarkable, as variations of the Ranz–Marshall equation described in literature often exhibit comparable or even larger deviations for pure convective drying, even with the use of fit adjustments. For a flow around a single droplet, Whitaker observed deviations of up to 30 % [26, 35], whereas Renksizbulut and Yuen as well as Kuznetsov et al. observed deviations of up to 15 % [26, 36]. Jayawickrama et al. compared a fitted Ranz–Marshall model to simulation data, resulting in a root mean square deviation of 12.6 % over all data points and a maximum value of 73 % [37]. Three further points not used in the determination of the absorption parameter were measured to gauge the transferability of the model to other set points and showed deviations of 30 % or less, which is in line with the aforementioned deviations for pure convective drying models.
The contour plot in Fig. 6 also shows the close agreement between the calculated and the measured values.
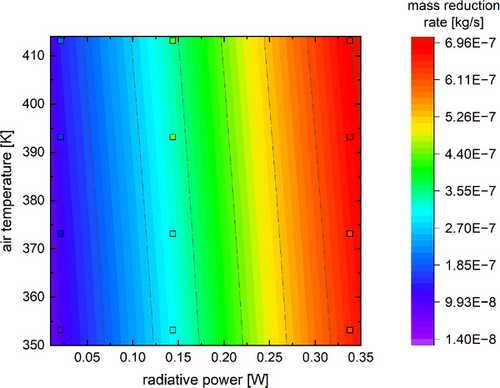
The background contour colors reflect the calculated values, whereas the measurement points are outlined in black and filled based on their corresponding measured mass reduction rate. As both data sets correlate to the same color scale, the close visual alignment between the measured and calculated data also indicates a close alignment regarding their values. Furthermore, the color gradient matches the trend shown in Fig. 4, with the radiative power dominating the resulting drying rate. This can also be correlated with the magnitude of change in the input variables. Although the radiative power increased by a factor of 12 from the lowest to the highest set point, the change in temperature gradient between the drying air and the calculated surface temperature was no higher than a factor of 2. The straight model boundaries are caused by the postulated independence of the radiative energy transfer from the convective heat transfer.
Finally, the drying rate prediction was transferred onto the aforementioned polymer solution droplets. To this end, the absorption parameter was determined at a value of 15.7 from IR drying experiments, whereas the temperature of the polymer droplet was assumed to be equal to that of a water droplet experiencing the same drying conditions. This assumption was verified with a droplet temperature measurement at a net power of 0.021 W and 80 °C, as this is the combined set point with the longest first drying phase. The polymer solution reached a temperature of 44.4 °C, whereas the water droplets were measured at 44.1 ± 2.4 °C. For higher energy inputs, the first drying phase was not clearly recognizable in the temperature curves.
Fig. 7 shows the resulting calculated as well as the measured drying rates for the polymer solution droplets. The mass reduction rate was experimentally observed for a relative mass between 0.85 and 0.5 for all data points.
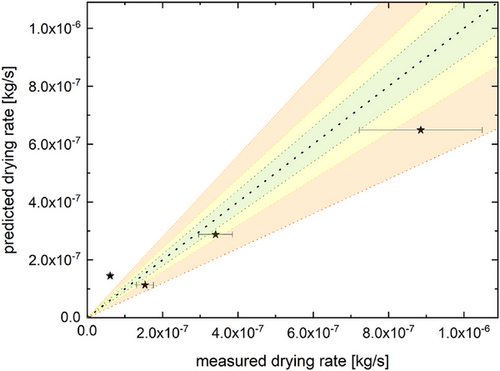
The resulting fit indicates potential applicability, with average deviations in the size range of approximately 30 %. It can also be observed that the data points do not necessarily scatter equally but instead appear to skew toward an underestimation in the predicted drying rate. This might be explained by the reduced surface tension of the droplets. Because the used ready-mix coating polymer contained surfactants, the surface tension of the polymer droplets was reduced to 41.5 ± 1.2 mN m−1 (; av ± s). This is expected to have increased the vapor pressure of the polymer droplets in comparison to the pure water droplets, thus leading to a faster evaporation rate than predicted by the water-based model. Furthermore, the reduced surface tension also increases the risk of droplet deformation, potentially increasing the surface area of the droplet. Nonetheless, the extent of the deviation is in line with the previously mentioned deviations observed in literature for the use of convective drying models [26, 35]. A reduction in model deviation could presumably be achieved by a more detailed description of the absorbed infrared radiation and droplet temperature development as performed by, e.g., Strizhak et al. [38] or Zhang et al. [21]. Alternatively, addressing potential changes in the droplet shape as discussed by Zubkov et al. [39] could also improve the fit of the drying rate predictions. However, this would significantly increase the effort needed for model implementation, counteracting the intent of a model for chemical engineering applications using easily accessible experimental data.
Although the general applicability of the model is still to be shown, it could facilitate the planning and construction of combined convection and radiation dryers for first-phase drying processes. Aside from the substance properties, the main values needed for the application of the model are the set process parameters, dryer geometry, and droplet size. These values are fairly easily accessible, rendering the model itself easy to use for drying rate estimations in chemical engineering contexts.
5 Conclusion
An easily applicable method for the prediction of the drying rate during the first drying phase for combined IR and convective drying was developed and successfully used to predict the drying rates of several temperature and radiative power combinations in water droplets. Subsequently, the empirical model was applied to polymer solution droplets and performed equally well for the investigated system. An absorption parameter was defined using the mass reduction rate of pure infrared radiation, as the radiator temperature and wavelength spectrum were unknown. Thus, with the use of different radiators, the need for the absorption parameter could be eliminated and the absorptance used directly in the case of surface absorption or opaque droplets.
Acknowledgments
The authors would like to thank the German Federal Ministry for Economic Affairs and Climate Action (BMWK) for the funding of this project within the WIPANO framework. The authors would also like to thank Ashland for kindly providing the coating polymer used in the transfer experiments.
Open access funding enabled and organized by Projekt DEAL.
Symbols used
-
- A
-
- [m2]
-
- cp
-
- [J kg−1 K−1]
-
- d
-
- [m]
-
-
- [–]
-
- E
-
- [J]
-
- h
-
- [kJ kg−1]
-
-
- [kg s−1]
-
- M
-
- [g mol−1]
-
- n
-
- [–]
-
- p
-
- [bar]
-
- p*
-
- [bar]
-
- P
-
- [bar]
-
-
- [W]
-
- R
-
- [J mol−1 K−1]
-
- s
-
- [–]
-
- t
-
- [s]
-
- T
-
- [K]
Greek letters
-
- α
-
- [W m2 K−1]
-
- β
-
- [m3 m2 s−1]
-
- Γ
-
- [–]
-
- Δ
-
- [–]
-
- ɛ
-
- [–]
-
- η
-
- [Pas]
-
- λ
-
- [W mK−1]
-
- μ
-
- [–]
-
- Φ
-
- [–]
-
- ρ
-
- [kg m3−1]
-
- σ
-
- [W m2 K4−1]
-
- τ
-
- [–]
-
- φ
-
- [–]
Sub- and Superscripts
-
- B
-
- black body
-
- conv
-
- convection
-
- D
-
- droplet
-
- E
-
- emitter
-
- G
-
- gas
-
- LV
-
- liquid to vapor, evaporation
-
- m
-
- average
-
- rad
-
- radiation
-
- S
-
- surface
Abbreviations
-
- av
-
- Average
-
- Fig.
-
- Figure
-
- IR
-
- Infrared radiation
-
- Le
-
- Lewis number
-
- Nu
-
- Nusselt number
-
- Pr
-
- Prandtl number
-
- Re
-
- Particle Reynolds number
Open Research
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.




