Exposure assessment of mobile phone base station radiation in an outdoor environment using sequential surrogate modeling
Abstract
Human exposure to background radiofrequency electromagnetic fields (RF-EMF) has been increasing with the introduction of new technologies. There is a definite need for the quantification of RF-EMF exposure but a robust exposure assessment is not yet possible, mainly due to the lack of a fast and efficient measurement procedure. In this article, a new procedure is proposed for accurately mapping the exposure to base station radiation in an outdoor environment based on surrogate modeling and sequential design, an entirely new approach in the domain of dosimetry for human RF exposure. We tested our procedure in an urban area of about 0.04 km2 for Global System for Mobile Communications (GSM) technology at 900 MHz (GSM900) using a personal exposimeter. Fifty measurement locations were sufficient to obtain a coarse street exposure map, locating regions of high and low exposure; 70 measurement locations were sufficient to characterize the electric field distribution in the area and build an accurate predictive interpolation model. Hence, accurate GSM900 downlink outdoor exposure maps (for use in, e.g., governmental risk communication and epidemiological studies) are developed by combining the proven efficiency of sequential design with the speed of exposimeter measurements and their ease of handling. Bioelectromagnetics 34:300–311, 2013. © 2012 Wiley Periodicals, Inc.
INTRODUCTION
Nowadays, a person is almost constantly exposed to radiofrequency electromagnetic fields (RF-EMF) emitted by one or more numerous possible sources. The World Health Organization (WHO) recently listed in its RF Research Agenda the need for the quantification of the exposure to widespread (e.g., Global System for Mobile Communications (GSM), Universal Mobile Telecommunications System (UMTS)) as well as emerging (e.g., Long Term Evolution (LTE)) RF sources [WHO, 2010]. This information is valuable for both epidemiological research and governmental risk communication toward the general public.
RF-EMF measurements can be divided in two categories—broadband and spectral measurements. Broadband measurements are performed with a combination of a field meter and a broadband probe and involve measuring over a span of several GHz at once. Spectral measurements, on the other hand, involve band-specific measurements and can be performed using two different types of measurement devices—spectrum analyzers (SAs) and personal exposure meters (exposimeters). Using these three types of devices, previous attempts have been aimed at geostatistical exposure prediction models (theoretical models), relying heavily on base station parameters, using exposimeter [Breckenkamp et al., 2008; Bürgi et al., 2008, 2010; Isselmou et al., 2008; Frei et al., 2009b] or SA measurements [Neitzke et al., 2007; Elliott et al., 2010; Joseph et al., 2012a] for optimization and validation, as well as measurement models interpolating exposimeter [Azpurua and Dos Ramos, 2010] or broadband measurements [Paniagua et al., 2012] at randomly or uniformly chosen locations.
However, a robust measurement-based RF-EMF assessment is not yet possible in a real-world situation, as the necessary time-expensive measurements cannot yet be made under a wide range of typical operating conditions. Therefore, only a limited data set of measured exposure samples is available at a given time. It is of great interest for authorities, for example, if a model of the RF-EMF exposure in a certain outdoor environment could be built that would allow them to obtain an accurate estimation of the human exposure in that specific area, despite the incomplete set of measurements and limited accuracy.
With this purpose in mind, we propose an entirely new modeling approach in the domain of dosimetry for human RF exposure based on surrogate modeling and sequential design. A surrogate model is a compact model that is calculated to provide an analytical mapping between the geographic coordinates and the RF-EMF exposure. In order to build such a model, one only needs data samples at a limited set of key locations in the analyzed area, chosen as optimally as possible using a sequential design approach. Starting from a small initial number of measurement locations, the next locations are iteratively selected using a sequential design algorithm based on variation in the measurement data and overall coverage of the area [Crombecq et al., 2011].
The advantages over the previously mentioned studies are the complete independency on accurate base station operating parameters, and the iterative selection of measurement locations instead of a random or uniform distribution. Performing measurements at uniformly distributed locations is essentially a one-shot approach [Crombecq et al., 2011], meaning that the resulting model is based only on data gathered at points that were fixed all at once. The advantage of using a sequential design approach is that more measurements will be performed in those areas where the RF-EMF fields change more rapidly (because these areas are usually more difficult to approximate with limited samples), using only as many measurements as needed to obtain a desired accuracy (this is preferable to choosing a fixed uniform distribution of measurement locations, for which the resulting accuracy of the model will be unpredictable).
The objective of this article is thus to conceptualize a new methodology to obtain an accurate street environment, RF-EMF exposure assessment as efficiently as possible, enabling one to accurately map the exposure to the RF-EMF without being dependent on accurate base station parameters. This approach can be performed while “in the field,” with new measurement locations being advised based on the obtained results.
MATERIALS AND METHODS
Area
The area under study is shown in Figure 1. It is a small (0.04 km2) urban area in Ghent, Belgium. Using an SA and a conical dipole antenna, we performed a spectral survey to identify the dominant signals in the area. Consistent with the findings of Joseph et al. [2008], the downlink of GSM900 was found to be the dominant signal and it is the only signal considered in this study. There was one GSM900 base station inside the area and many close by.
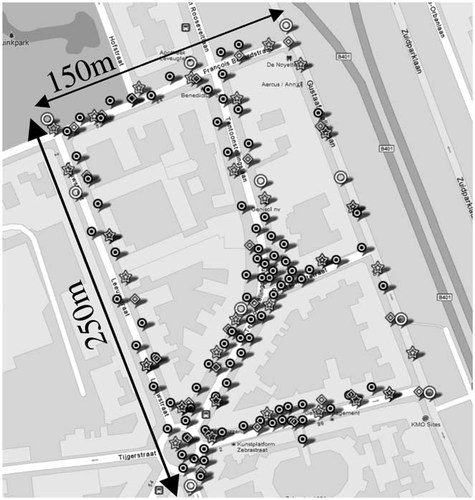
Area under study with dimensions and all 100 measurement locations: 10 from the initial design (open circles), 90 selected with the LOLA-Voronoi algorithm (black-dot circles), 31 SA validation measurements (diamonds), and 30 exposimeter validation measurements (stars).
Measurement Devices and Methods
As we will be focusing on one signal only, we had the choice between exposimeter or SA measurements. Both have their advantages and disadvantages and have been used extensively in RF-EMF exposure assessment studies [Joseph et al., 2008, 2010a, 2012a].
For in situ measurements of the EMF strength related to human exposure in the vicinity of base stations with an SA, a standard has been written by the European Committee for Electrotechnical Standardization (CENELEC) [CENELEC, 2008], and procedures for RF exposure measurements in the vicinity of GSM base stations are available in Joseph et al. [2006], Olivier and Martens [2007], and Kim et al. [2008].
Commercial personal RF exposimeters, on the other hand, have been developed in the past years specifically for epidemiological studies. They are easy to carry and use, and they are able to measure over a long period of time. For current state-of-the-art exposimeters, we refer the reader to Mann [2010] and Röösli et al. [2010]. A vast amount of research on the feasibility of performing epidemiological studies with exposimeters and their limitations has been published [Mann et al., 2005; Radon et al., 2006; Neubauer et al., 2007], and measurement campaigns and their results have been presented [Joseph et al., 2008, 2010b; Röösli et al., 2008; Thomas et al., 2008a, b; Frei et al., 2009a; Viel et al., 2009]. While not as accurate as the SA, we chose to perform all measurements for model building with a DSP120 EME SPY exposimeter (Satimo, Villebon-sur-Yvette, France) because of its measurement speed (the minimum acquisition time is 4 s per sample) and ease of handling. This exposimeter can measure 12 frequency bands (88–108 MHz, 174–223 MHz, 308–400 MHz, 470–830 MHz, 880–915 MHz, 925–960 MHz (GSM900), 1710–1785 MHz, 1805–1880 MHz, 1880–1900 MHz, 1920–1980 MHz, 2110–2170 MHz, 2400–2500 MHz) and identify the contribution of each band to the total electric field. Its lower and upper detection limits are 0.05 and 5 V/m, respectively. Its expanded measurement uncertainty (confidence interval (CI) 95%) for GSM900 is 4.6 dB [Bolte et al., 2011] without taking into account possible influences of the body.
The exposimeter measurement method we propose resembles the sweeping method sometimes applied to SA measurements [Neubauer et al., 2005; Bornkessel et al., 2007]. The exposimeter is placed inside a backpack and the operator walks around randomly in an area of about 10 m2 for 3.5 min. This way, with a minimum acquisition time of 4 s per sample, 50 samples are obtained, which should be sufficient to limit time variations as well as account for small-scale fading in the measurement area. The average electric field strength is then calculated as the root mean square (RMS) of these samples. Note that measuring the average electric field strength in a small area corresponds with a more realistic exposure scenario than a measurement at one specific location. A number of articles have measured the response of an exposimeter to standard input signals in a laboratory and discussed the ability of the exposimeter to accurately measure base station radiation [Mann et al., 2005; Radon et al., 2006; Knafl et al., 2008; Bornkessel et al., 2010; Bolte et al., 2011].
We also performed SA validation measurements, for which the setup consisted of a Precision Conical Dipole (PCD) 8250 antenna (Austrian Research Centers (ARC) Seibersdorf Research, Seibersdorf, Austria), with a dynamic range of 1.1 mV/m–100 V/m and a frequency range of 80 MHz–3 GHz, in combination with an SA with a frequency range of 9 kHz–6 GHz (Model FSL6, Rhode & Schwarz, Zaventem, Belgium). We opted for the RMS mode, with a sweep time (SWT) of 300 ms per trace, and calculated the average of the traces over 0.5 min in W/m2 before converting it to V/m. The expanded measurement uncertainty (CI 95%) for the electric field for the considered setup is ±3 dB [CENELEC, 2008]. The antenna is positioned at 1.5 m above the ground [CENELEC, 2008]. For each frequency band, the three mutually orthogonal components of the electric field are measured during a time (several min) until the signal stabilizes, resulting in a total measurement time of more than 15 min per location (considering only a single signal, i.e., GSM900).
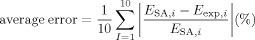 (1)
(1)| Spectrum analyzer | Exposimeter | |
|---|---|---|
| Average E (V/m) | 0.216 | 0.162 |
| Maximum E (V/m) | 0.356 | 0.234 |
| 95th percentile E (V/m) | 0.331 | 0.234 |
| Standard deviation (V/m) | 0.090 | 0.058 |
| Average error (vs. SA) | — | 19.28% (1.53 dB) |
- All measured values satisfy ICNIRP reference levels.
Surrogate Modeling
Surrogate models using a sequential design algorithm as an optimal sample selection strategy offer a key advantage over models created from a random or uniform sample distribution. Sequential sampling methods start from a limited set of measurements and determine the optimal location of additional measurements in an automated way [Crombecq et al., 2011; Stephens et al., 2011]. In this study, the algorithm “learns” the EMF exposure on the fly, based on the knowledge that becomes available from the previous measurements, and sequentially proposes optimal locations that must be performed for future measurements. At any moment in time, the gain of these additional measurements—a quantification of how much information is added to the model—can be assessed, and a well-chosen stopping criterion can be defined to detect convergence of the algorithm. It should be noted that such an approach significantly limits the time to perform measurements [Deschrijver et al., 2011, 2012].
A sequential design always represents a trade-off between exploration and exploitation, with the former selecting data points in unexplored regions and the latter suggesting points in regions previously identified as interesting, that is, peaks and valleys. The robust and efficient hybrid sequential design algorithm developed by Crombecq et al. [2011] employs Voronoi tessellation for exploration and local linear approximation (LOLA) for exploitation. A Voronoi tessellation divides the area into multiple polygonal cells generated by the selected measurements locations. Each cell consists of those points that are closer to one measurement location (i.e., the one that generated the cell) than any other point. The algorithm then distributes more data points in the larger cells, as far as possible from the previously chosen locations. LOLA, on the other hand, distributes the data points such that the density of the points is proportional to the local nonlinearity of the approximation function (in this case, the interpolation model), because dynamic regions are more difficult to approximate than linear regions. This dual strategy (combined using a weight function) results in a more efficient distribution of measurement locations compared to other traditional designs, such as uniform or random distributions used by Azpurua and Dos Ramos [2010], Joseph et al. [2012a], and Paniagua et al. [2012], for example. As an interpolation technique, we use cubic splines, which are smooth interpolating functions piecewise-defined by third degree polynomials
Measurement Procedure
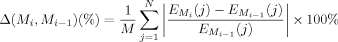 (2)
(2)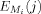 the electric field values of Model Mi at all N grid points (j) of the surface of the considered area (i.e., the streets in the demarcated area), with a resolution of 1 × 1 m2. Step 4: Use the LOLA-Voronoi algorithm in the “surrogate-model toolbox” (SUMO) [Gorissen et al., 2010] to calculate a new batch of sample locations (the number of locations in each batch is set by the user of the procedure). It should be noted that the use of batches is a practical choice, and the number of locations per batch is a trade-off based on the measurement and processing time of a batch. In this study, we performed 100 measurements with each batch consisting of ten locations, resulting in ten consecutive models (M0 to M9). The measurements performed at the 10 locations given by the initial design result in Model M0. Based on these measurements, the next batch of ten locations is calculated in real-time with the LOLA-Voronoi algorithm. Measurements performed at these locations are then used to update the surrogate model, resulting in Model M1 (which is thus constructed from 20 samples) and so on. Repeat Steps 3 and 4 until a certain stopping criterion x is reached, for example, a certain value for Δ. In this study, the stopping criterion was a mean relative deviation Δ(Mi, Mi−1) of 1%. Step 5: Validate the final model. Step 6: The result is an accurate map of the RF exposure in a certain area. This procedure is developed in such a way that it can be applied in situ; that is, one performs measurements, the results are processed using Matlab, new locations are provided by the algorithm and shown in Google Earth, etc., while in the field.
the electric field values of Model Mi at all N grid points (j) of the surface of the considered area (i.e., the streets in the demarcated area), with a resolution of 1 × 1 m2. Step 4: Use the LOLA-Voronoi algorithm in the “surrogate-model toolbox” (SUMO) [Gorissen et al., 2010] to calculate a new batch of sample locations (the number of locations in each batch is set by the user of the procedure). It should be noted that the use of batches is a practical choice, and the number of locations per batch is a trade-off based on the measurement and processing time of a batch. In this study, we performed 100 measurements with each batch consisting of ten locations, resulting in ten consecutive models (M0 to M9). The measurements performed at the 10 locations given by the initial design result in Model M0. Based on these measurements, the next batch of ten locations is calculated in real-time with the LOLA-Voronoi algorithm. Measurements performed at these locations are then used to update the surrogate model, resulting in Model M1 (which is thus constructed from 20 samples) and so on. Repeat Steps 3 and 4 until a certain stopping criterion x is reached, for example, a certain value for Δ. In this study, the stopping criterion was a mean relative deviation Δ(Mi, Mi−1) of 1%. Step 5: Validate the final model. Step 6: The result is an accurate map of the RF exposure in a certain area. This procedure is developed in such a way that it can be applied in situ; that is, one performs measurements, the results are processed using Matlab, new locations are provided by the algorithm and shown in Google Earth, etc., while in the field.Validation
After the construction of ten consecutive models, we validate them with two different sets of measurements—SA and exposimeter measurements. The results of this validation help us quantify the correlation between model and measurements and find an optimal number of samples to accurately characterize an area of this size.
The first validation set consists of 31 accurate narrowband measurements performed at randomly selected locations, different from the 100 measurement locations used to construct Models M0 to M9. A second validation set comprises 30 exposimeter measurements using the method described above, performed at random locations chosen independently from the procedure above. Figure 1 shows the locations of these validation measurements.
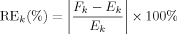 (4)
(4)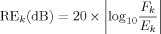 (5)
(5)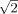 in electric field strength). To quantify the correlation between model and validation sets, we use the following correlation parameters: r, the Pearson correlation coefficient; ρs, Spearman's rank correlation coefficient; κ, Cohen's kappa; sensitivity; and specificity. The sensitivity is the ratio of the number of correctly identified exposed samples to the total number of measured exposed samples. The specificity is the ratio of the number of correctly identified unexposed samples to the total number of measured unexposed samples. A certain sample is classified as “exposed” when it lies above a certain percentile or a fixed field value, while “unexposed” means that the sample lies below a certain percentile. In this article, we used the 80th percentiles as cut-off values. It should be noted that the 90th percentile is often used [Breckenkamp et al., 2008; Frei et al., 2009b] but with validation sets of 30 measurements we would only have three samples above this cut-off, rendering any statistical conclusion useless. Also, Bürgi et al. [2008] used tertiles as cut-offs but a 66th percentile cannot be considered as high exposure.
in electric field strength). To quantify the correlation between model and validation sets, we use the following correlation parameters: r, the Pearson correlation coefficient; ρs, Spearman's rank correlation coefficient; κ, Cohen's kappa; sensitivity; and specificity. The sensitivity is the ratio of the number of correctly identified exposed samples to the total number of measured exposed samples. The specificity is the ratio of the number of correctly identified unexposed samples to the total number of measured unexposed samples. A certain sample is classified as “exposed” when it lies above a certain percentile or a fixed field value, while “unexposed” means that the sample lies below a certain percentile. In this article, we used the 80th percentiles as cut-off values. It should be noted that the 90th percentile is often used [Breckenkamp et al., 2008; Frei et al., 2009b] but with validation sets of 30 measurements we would only have three samples above this cut-off, rendering any statistical conclusion useless. Also, Bürgi et al. [2008] used tertiles as cut-offs but a 66th percentile cannot be considered as high exposure.A model used for epidemiological studies should have a high specificity [Neubauer et al., 2007] since a low specificity value would mean that a large part of the small exposed group is actually unexposed. In the case of a low sensitivity, only a small fraction of the much larger unexposed group is in fact exposed.
Cohen's kappa is a statistical measure of the agreement between two data sets, taking into account the agreement occurring by chance. It represents the fraction of samples that are expected not to be in agreement (as in “fall in the same exposure category”) when only chance agreement would be present, but, in fact, are in agreement. For the calculation of this value, we use the 50th and 80th percentiles of the predicted and measured electric field values as cut-offs. Note that sometimes a weighed kappa is calculated (e.g., in Bürgi et al. [2010]; see also Table 3), whereas classification into adjacent categories (i.e., high–medium and medium–low exposure) counts as 50% agreement. All kappa values in this article are non-weighted, unless stated differently.
RESULTS
Surrogate Modeling
Figure 1 shows all 100 measurement locations used to calculate the GSM900 exposure interpolation Models M0 to M9 (10–100 measurement locations). The contour plots of Models M0 (10 samples), M4 (50 samples), M6 (70 samples), and M9 (100 samples) are shown in Figure 2a–d, respectively. Table 2 summarizes the model parameters (average electric field strength, Eavg, recalculated from the average power density; 95th percentile of the electric field values, E95; range of minimum to maximum electric field strengths, Emin − Emax; and standard deviation (STD) of the power density value, recalculated to electric field values) of M0 to M9, as well as the mean relative deviation (Eq. 2) of each Model Mi compared to the previous Model Mi−1. For example, by measuring at 10 additional locations, our surrogate model changed 15.57% going from Model M2 (30 points) to Model M3 (40 points).
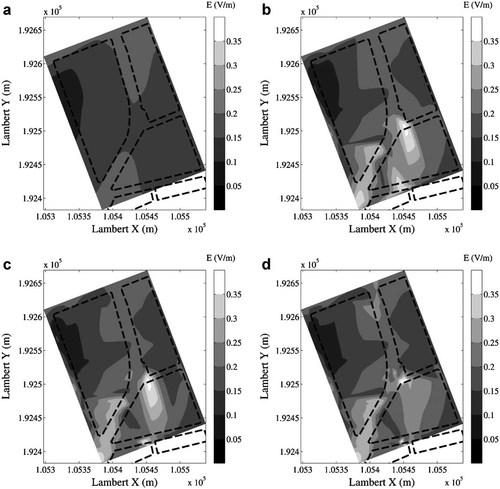
Contour plots of Models (a) M0; (b) M4; (c) M6; and (d) M9. Axes are in Belgian Lambert 1972 coordinates; that is, a projection of geographic coordinates determined using the Hayford 1924 ellipsoid.
| Model | Eavg (V/m) | STD (V/m) | Emin − Emax (V/m) | E95 (V/m) | Δ(Mi,Mi−1) (%) |
|---|---|---|---|---|---|
| M0 | 0.142 | 0.078 | 0.075–0.195 | 0.167 | — |
| M1 | 0.151 | 0.077 | 0.080–0.197 | 0.173 | 8.41 |
| M2 | 0.163 | 0.112 | 0.062–0.268 | 0.231 | 11.88 |
| M3 | 0.182 | 0.147 | 0.071–0.345 | 0.287 | 15.57 |
| M4 | 0.187 | 0.152 | 0.070–0.360 | 0.295 | 5.21 |
| M5 | 0.182 | 0.142 | 0.070–0.359 | 0.271 | 3.20 |
| M6 | 0.180 | 0.142 | 0.069–0.360 | 0.270 | 3.06 |
| M7 | 0.181 | 0.140 | 0.069–0.361 | 0.268 | 2.31 |
| M8 | 0.182 | 0.141 | 0.070–0.386 | 0.268 | 1.56 |
| M9 | 0.182 | 0.141 | 0.070–0.384 | 0.268 | 1.20 |
- Eavg, average electric field strength; STD, standard deviation; Emin and Emax = minimum and maximum electric field strengths, respectively, and E95 = 95th percentile of the electric field strength of a certain model. Δ(Mi,Mi−1) is the mean relative change of the surrogate model according to Equation (1). All measured values satisfy ICNIRP reference levels.
Models M0 and M1 show a relatively constant electric field distribution with only slight variation. In Models M2 to M4, four hotspots are identified (defined as regions with electric field levels above 0.25 V/m in Fig. 2), each significantly changing the model and none are found in subsequent models. Once the main variations in the field are discovered in Model M4, the mean relative model change drops below 5% and the statistical parameters of the electric field in the area under study stay relatively constant; the average electric field strength in the streets is 0.18 V/m, with a standard deviation of 0.14 V/m, min–max interval of 0.07–0.36 V/m and 95th percentile of 0.27 V/m. In the models following Model M4, the exposure map is further refined and after 70 measurements (Model M6), the model change drops below 2.5%.
Validation
The results of the validation with both SA as well as exposimeter measurements can be found in the online version of this article (Tables 4 and 5 contain the error metrics and correlation coefficients, respectively; Online Supplementary Material). Figures 3 (exposimeter validation) and 4 (SA validation) show a comparison between the measurements and the predictions of Models M0, M4, M6, and M9, and the cumulative distribution function (cdf) of the relative error (RE) in dB. It is clear from the scatter plots in Figures 3a and 4a that there are not many large errors (i.e., above 3 dB), not even for the first models, although the electric field distribution in the area under study is not spread wide enough for a definite conclusion. The cdfs of the RE in Figures 3b and 4b show the steady offset to the left of the early models, and from Model M4 on, the cdfs nearly coincide.
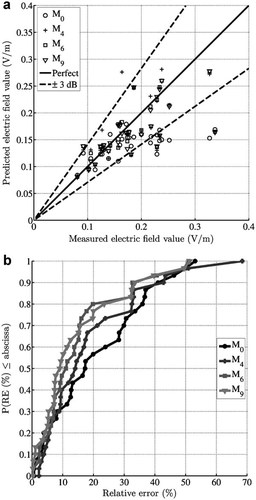
Exposimeter validation of Models M0, M4, M6, and M9. a: Scatter plot for the comparison of predicted (by the four models) and measured (with the SA) electric field values. Full line depicts a perfect prediction and dotted lines define the region with errors below 3 dB. b: Cumulative distribution functions of the relative error of the four models in comparison with the SA data.
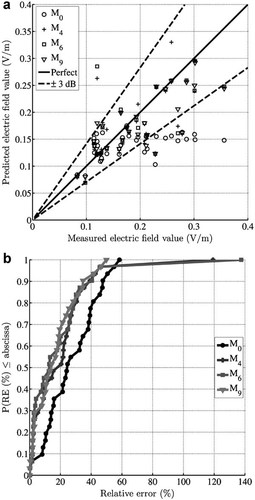
Spectrum analyzer validation of models M0, M4, M6, and M9. a: Scatter plot for the comparison of predicted (by the four models) and measured (with the exposimeter) electric field values. Full line depicts a perfect prediction and dotted lines define the region with errors below 3 dB. b: Cumulative distribution functions of the relative error of the four models in comparison with the exposimeter data.
Compliance of the Electric Field Levels
All exposimeter measurements were above the detection limit of 0.05 V/m and lie between 0.07 and 0.38 V/m, with an average of 0.20 V/m and a standard deviation of 0.16 V/m. All measurements satisfy the guidelines issued by the International Commission on Non-Ionizing Radiation Protection (ICNIRP) [1998]. The maximum measured electric field strength (0.38 V/m) or average power density (0.38 mW/m2) corresponds to 0.01% of the ICNIRP power density reference level for the general public for 900 MHz, according to the European Commission Recommendation 1999/519/EC [EC, 1999].
DISCUSSION
A new method to accurately map the exposure to base station radiation in an outdoor environment based on surrogate modeling and sequential design was proposed and tested for GSM900 in a small urban area. A total of 100 exposimeter measurements were performed in 10 batches of 10. After each batch, the interpolation model was updated with the new measurements based on the next optimal measurement locations determined using the LOLA-Voronoi algorithm.
Based on the results shown in Table 2, we can conclude that 50 measurements (Model M4) are sufficient to discover the main variations in the field and create a crude map of the GSM900 (downlink) electric field distribution in this particular region. Seventy measurements (Model M6), on the other hand, might be sufficient to completely characterize the area and create an accurate exposure map because more measurements do not add much more information to the interpolation model.
We have shown the validity of our model with SA measurements, as the average relative error found (1.5 dB) is well within the measurement accuracy of the SA (3 dB). The final model, M9, built from 100 measurements, shows the best validation results (see Tables 4 and 5 in the Online Supplementary Material) with very small errors (REmax below 50%), very good correlation with exposimeter (r = 0.7, ρ = 0.75) and SA measurements (r = 0.8, ρ = 0.75) and high probabilities of classifying exposed and unexposed samples correctly (specificity = 0.92, sensitivity = 0.67/0.83, for exposimeter/SA validation, respectively). We can conclude that in terms of error metrics, performing even more measurements might not enhance the model much. This was to be expected because both exposimeter and SA measurements inhibit a certain uncertainty. Furthermore, based on error metrics alone, we already obtain excellent results from Model M4 (50 measurements) with 80% of the predicted values within 3 dB (factor √2 in electric field strength) of the measurements. Correlation is also reasonable; for example, r = 0.66/0.62, κ = 0.25/0.23 (which is rather weak) and specificity = 0.88/0.84, but from Model M6 on, correlation is notably better (r = 0.71/0.67, κ = 0.41/0.44 (moderate) and specificity = 0.92/0.88). This high specificity, and in a lesser way the moderate sensitivity (0.67 for M6), strengthens our belief that our procedure can quickly result in a trustworthy exposure prediction model.
Comparison to Existing Exposure Models
As mentioned, there have been previous attempts at exposure prediction models, namely by Bürgi et al. [2008, 2010], Breckenkamp et al. [2008], Isselmou et al. [2008], Frei et al. [2009b], Elliott et al. [2010], Azpurua and Dos Ramos [2010] and Paniagua et al. [2012]. Their results, along with the results of our M6 Model (70 measurements), are summarized in Table 3, except for Azpurua and Dos Ramos [2010] who compared interpolation techniques, Paniagua et al. [2012] who compared the interpolation models of a dense and a scarce set of broadband measurements, and Elliott et al. [2010] who used an empirical model of the power density in which some of the parameters were based on SA measurements. Azpurua and Dos Ramos, and Paniagua et al. only published absolute errors and did not mention relative errors or correlation parameters. Comparing solely the number of measurement locations per unit of study area would also be irrelevant, thus making it very difficult to compare their results with those of our study. Elliott et al. [2010] only mentioned the Spearman correlation coefficient, which is similar to ours (0.66 compared to 0.74/0.66 in the case of exposimeter/SA validation), and R2 values.
| Model | r | ρs | κ | Sensitivity | Specificity | # Points |
|---|---|---|---|---|---|---|
| Total field indoor + outdoor cut-offs 50th and 90th percentiles | ||||||
|
Frei et al. [2009b ] (eval/valid) |
— | 0.51/0.65 | 0.28/0.55 | 0.56/0.67 | 0.95/0.96 | 163/31 |
| Total field indoor cut-off 90th percentiles | ||||||
|
Breckenkamp et al. [2008 ] |
— | — | 0.17/0.34 | 0.25/0.40 | 0.92/0.94 | 1132/343 |
| Total field outdoor cut-offs tertiles | ||||||
|
Bürgi et al. [2010 ] |
0.54 | 0.64 | 0.48a | — | — | 113 |
| GSM900 indoor cut-off 0.137 V/m | ||||||
|
Neitzke et al. [2007 ] |
0.64 | — | 0.50a | 0.56 | 0.93 | 610 |
|
Bürgi et al. [2010 ] |
0.57 | 0.66 | 0.60a | 0.63 | 0.90 | 133 |
| GSM900 outdoor cut-offs tertiles | ||||||
|
Bürgi et al. [2008 ] (urban/rural) |
0.76/0.86 | — | 0.77a/0.75a | — | — | 20/18 |
| GSM900 outdoor cut-offs 50th and 80th percentiles | ||||||
| Model M6 (exp/SA valid) | 0.71/0.67 | 0.74/0.66 | 0.41 (0.51a)/0.44 (0.50a) | 0.67/0.67 | 0.92/0.88 | 30/31 |
- r = Pearson correlation coefficient, ρs = Spearman's rank correlation coefficient, and κ = Cohen's kappa. # Points is the number of measurement locations used for the comparison, eval = evaluation, valid = validation, exp = exposimeter and SA = spectrum analyzer. All parameters are unitless.
- a Weighted kappa, counting classification into adjacent categories as 50% agreement.
All models in Table 3 are simulation models using exposimeter measurements as validation (except in Bürgi et al. [2008] where a broadband probe was used, and Neitzke et al. [2007] who used SA measurements), and need many accurate input parameters (e.g., technical parameters of base station antennas, relative positions, and housing conditions). From three of these models, results have been published about GSM900 measurements. Only one of them has been validated outdoors [Bürgi et al., 2008].
Our correlation coefficients are very good compared to other studies, and our kappa (although moderate), sensitivity and specificity values are also relatively consistent (Table 3). Additionally, in more than 80% of the cases, measurements and Model M6 agree within 3 dB, corresponding to a factor 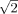 in electric field strength, while Bürgi et al. [2008] mention just 60% agreement within a factor of 2.
in electric field strength, while Bürgi et al. [2008] mention just 60% agreement within a factor of 2.
Strengths and Limitations
Our work makes a valuable contribution to the overall human RF exposure assessment since the outdoor environment and its continuous background radiation emitted by numerous base stations are an important aspect of everyday life. A key strength of our approach is that prior knowledge concerning sources (number of antennas, location, power levels, etc.) and the environment (three-dimensional building coordinates, building materials, etc.) is not required since the exposure assessment is measurement-based in a real-life environment. As such, one can use it to create an outdoor field exposure model in an urban, suburban or rural area of choice, without any a priori knowledge (except two-dimensional geo-coordinates of building blocks), making the proposed method interesting for authorities seeking to assess the RF-EMF exposure in a certain area, for example.
If one is interested in a globally accurate exposure map of an entire city, of course, by definition, a large amount of measurements will have to be performed. Note, however, that the number of measurements needed depends on (a) the amount of variation in the RF-EMF fields, and (b) the desired resolution or accuracy of the map. If exposure maps are to be built for large areas or even entire cities, slight variations in a certain street might be of less importance. Hence, the number of measurements can be reduced by relaxing the desired accuracy constraints.
Our method can be applied to any environment including indoors, although it would need some modifications to take the internal structure of a building into account (such as walls, etc.). In reality, however, it would prove extremely difficult to perform the necessary measurements in every house or building, as one would need permission from a large number of people. To apply the sequential surrogate modeling for houses, we propose to perform outdoor measurements and combine them with the building penetration losses of Plets et al. [2009]. This would be a sound approach and would allow us to create a field exposure map including the houses' ground floors. It should be noted, however, that this would only result in an extended 2D exposure map. A full 3D model incorporating higher floor levels cannot be built without knowledge of the relevant base station parameters (e.g., antenna tilts).
All measurements were performed on weekdays between 10 am and 4 pm while avoiding busy hours (e.g., noon, schools out). However, temporal variations are currently not accounted for. In future research, it will be investigated whether temporal exposure measurements (i.e., during 24 h, 1 week, etc.) at a carefully selected number of measurement locations in the area could enable the derivation of a time-domain exposure map of the area.
In this study, we used an EME SPY120 exposimeter. Lauer et al. [2012] stated that GSM base station exposure might be underestimated because if not all eight time slots in the GSM downlink band are occupied, the EME SPY120 exposimeter would not detect the signal (corresponding to a “measured” sample value of 0.05 V/m). However, as we had only a few non-detects in our sample data for GSM900 exposure, we consider our calculated averages to be sound. This is also our conclusion when comparing SA and exposimeter measurements for GSM900 signals (Table 1). Note that Isselmou et al. [2008] did a comparison between exposimeter and SA measurements for GSM900 signals as well, finding a similar result. Moreover, Neubauer et al. [2010] found an average degree of underestimation by the exposimeter of 0.76 for GSM900 exposure due to the presence of the body, while we found that the exposimeter underestimates the field exposure in comparison with the SA results by an average of 0.75.
The exposimeter and SA validations were performed independently, and although both equipment have very different measurement accuracies, they gave similar results (e.g., for Model M6 the MRE is 1.5–1.7 dB, 83–84% of the errors are below 3 dB, and the correlation coefficient equals 0.7). This shows that our models can handle the larger measurement inaccuracy of the exposimeter, and the proposed procedure is suitable to predict GSM900 downlink exposure.
In order to assess the RF-EMF exposure to (the sum of) more sources, in the future we will make use of a combination of broadband probe, exposimeter, and SA measurements. It is possible to measure all signals of interest at selected locations that are “optimal” for one particular signal (e.g., GSM900) and re-use these results as an initial sample distribution to model the next signal (e.g., UMTS, around 2.1 GHz). The algorithm and its stopping criterion will then decide if/where additional measurements are needed.
Finally, we performed measurements of the average electric field strength in order to provide field exposure maps, not the specific absorption rate. However, actual absorption can be determined from field exposure using the data from Neubauer et al. [2010] and Joseph et al. [2010b, 2012b]. This will also be part of future research.
CONCLUSION
A new, efficient measurement and modeling approach is proposed for the mapping of base station exposure based on surrogate modeling and sequential design. It can be applied in real time and without a priori knowledge. We used a fast and efficient exposimeter measurement method to obtain an accurate surrogate model of the exposure to GSM900 radiation in a small suburban area in Ghent, Belgium, by interpolating measurements at locations selected sequentially in batches of ten using the LOLA-Voronoi algorithm. The models are validated with independent SA and exposimeter measurements and excellent results are obtained.
Up to now, this measurement procedure, measurement method, and modeling technique have not been applied for experimental exposure assessment in real environments. However, our results are only investigated outdoors for GSM900 downlink exposure in a small-sized area (about 0.04 km2). The application of our procedure to other signals as well as to different and larger areas will be the subject of future research. In a case where the exposimeter does not measure another signal correctly or cannot measure it at all (e.g., LTE), one will have to use an SA instead.
Acknowledgements
D. Deschrijver and W. Joseph are Post-Doctoral Fellows of the FWO-V (Research Foundation—Flanders).




