Lineares und gewickeltes Cp*2Si: Reversibler Phasendurchgang eines Schlüsselmoleküls
Abstract
Bislang galt die Struktur des Decamethylsilicocens Cp*2Si mit einem gewinkelten und einem linearen Molekül in derselben Elementarzelle als die Ausnahme unter den ansonsten ausschließlich gewinkelten schweren Homologen Cp*2E mit E=Ge, Sn, Pb. Hier stellen wir des Rätsels Lösung mit einer Tieftemperaturphase vor, in der alle drei symmetrieunabhängigen Moleküle die gewinkelte Konformation einnehmen. Der reversible Phasendurchgang geschieht im Temperaturbereich zwischen 80 und 130 K und bietet eine rationale Erklärung auf der Grundlage der Entropie. Nebelhafte Erklärungsversuche mit Packungseffekten werden damit überflüssig.
Divalente metallorganische Verbindungen der Gruppe-14-Elemente spielten seit jeher eine wichtige Rolle in der Entwicklung von Bindungskonzepten. Eine strukturelle Schlüsselstellung nimmt dabei das stereochemisch aktive und energetisch hochliegende freie Elektronenpaar ein, das zugleich das Reaktivitätszentrum in dieser Verbindungsklasse ist. Der legendäre Cyclopentadienylsubstituent ist dabei ein Grundpfeiler in der Entwicklung hin zu stabilen divalenten metallorganischen Derivaten der Gruppe-14-Elemente. Die π-Wechselwirkung mindert dabei die ansonsten hohe Lewis-Basizität der Zentralatome. Ausgehend von wegweisenden Cp2E Verbindungen wurde in den letzten fünf Dekaden eine unglaublich reichhaltige Chemie der Tetrylene R2E entwickelt. Gegenwärtig werden sie sogar in der Bindungsaktivierung1 und der Katalyse2 eingesetzt.
Gerade aufgrund der stabilisierenden Cp-Liganden sind die relativ robusten Tetrelocene, und im Besonderen dessen leichtester Vertreter, das Silicocen, bedeutsame Lehrbuchverbindungen von fundamentaler Bedeutung.
Überhaupt haben die Cyclopentadienyl-Gruppe-14-Elementverbindungen seit des ersten Berichts über das Bis(cyclopentadienyl)blei im Jahre 1956 durch Fischer and Grubert3 und das Cp2Sn im selben Jahr4 das Interesse der synthetischen Chemiker erweckt. In den Folgejahren wurde das Gebiet durch die Synthese des Cp2Ge maßgeblich weiterentwickelt.5
Während die Struktur des Cp2Ge von Grenz et al. bestimmt wurde,6 haben Atwood und Hunter die Struktur des monomeren Cp2Sn berichtet.7 In derselben Publikation berichten sie ebenfalls über die Synthese und Festkörperstruktur des Decamethylplumbylens. Zuvor war die erfolgreiche Verwendung des Pentamethylcyclopentadienylsubstituenten beim Germanium und Zinn von Jutzi und Mitarbeitern berichtet worden.8 So wurden nicht nur die Strukturen selbst darstellbar, sondern es konnten auch die Pentamethylcyclopentadienylgermanium- und -zinnkationen synthetisiert werden. Ihrem bereits zuvor publizierten Ansatz9 folgend, gelang Jutzi und Mitarbeitern schließlich die erste Synthese und Bestimmung der Festkörperstruktur des Decamethylsilicocenes als dem ersten Derivat mit Silicium in der Oxidationsstufe +2.10 Kurz darauf folgte von derselben Gruppe eine Fülle von detaillierten analytischen und theoretischen Daten über dieselbe Verbindung.11
Die Festkörperstruktur, so wie sie von Jutzi, Krüger, et al. beschrieben wird (s. die analoge Struktur in Abbildung 1, links), enthält die Decamethylsilicocenmoleküle in zwei unterschiedlichen Konformeren.10 Das erste Molekül nimmt eine gewinckelte Konformation ein, die bereits von den Germanium- und Zinnderivaten gut bekannt ist8 und für eine SiII-Verbindung aufgrund des stereochemisch aktiven freien Elektronenpaares am Silicium zu erwarten wäre. Die asymmetrische Einheit enthält vom zweiten Molekül nur eine Hälfte, dessen zweite Hälfte sich durch das Inversionszentrum auf der Position des Siliciumatoms ergibt. Folglich nimmt das Molekül die Konformation eines D5d-symmetrischen Hacke-Spitze-Sandwichkomplexes mit planparallelen Cyclopentadienylringen ein. In der Zelle sind insgesamt zwölf Moleküle vorhanden, von denen vier die lineare und acht die gewinkelte Konformation einnehmen. Die Anordnung der Moleküle im Kristall wird damit erklärt, “daß der Öffnungswinkel von Molekül B (dem gewinkelten Molekül; vom Autor ergänzt) durch schwache intermolekulare Wechselwirkungen verursacht wird und packungsbedingt ist”. Während die Gruppe um Jutzi erfolgreich zeigen konnte, dass das gewinkelte Konformer das stabilere in der Gasphase ist, wurden dennoch in folgenden Publikationen12 nach wie vor Packungseffekte herangezogen, um die Unterschiede zwischen der berechneten gewinkelten Cp2Si und der experimentellen Cp*2Si Struktur zu erklären.13
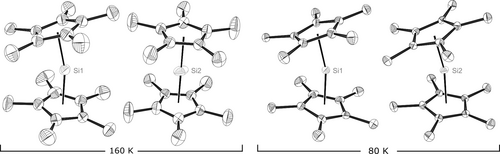
Moleküle in der Kristallstruktur des Decamethylsilicocens bei 80 K und 160 K. Das dritte Molekül der asymmetrischen Einheit bei 80 K ist nicht dargestellt, weil es eine zum linken Molekül im entsprechenden Block sehr ähnliche Struktur hat.
Die Existenz zweier sehr verschiedener Konformere mit einem so unterschiedlichen Charakter des freien Elektronenpaares am SiII initiierte die Messung eines qualitativ hochwertigen Röntgendiffraktionsdatensatzes bei 90 K mit der ursprünglichen Absicht, die experimentelle Elektronendichteverteilung zu bestimmen. Letztlich beschränkte die große Beweglichkeit des Moleküls die Auflösung auf nur 0.60 Å und verhinderte diese Untersuchung. Die analysierte Struktur zeigte jedoch eine neue Phase in einer anderen Raumgruppe. Im Folgenden wollen wir die scheinbare Einzigartigkeit des Decamethylsilicocens auflösen, indem wir einen nicht-destruktiven Phasendurchgang zu ausschließlich gewinkelten Molekülen in der Elementarzelle bei tiefen Temperaturen vorstellen (Abbildung 1, rechts). Wir sammelten weitere Einkristall-Röntgenbeugungsdatensätze im Temperaturbereich zwischen 80 und 160 K, um den Phasendurchgang von der früher beschriebenen C2/c Phase zur Tieftemperaturphase, die am besten in P21/c beschrieben wird, näher zu klären (zu weiteren Details der Untersuchungen in diesem Temperaturbereich siehe Hintergrundinformationen).
Naheliegend ist die Untersuchung der Änderungen der Geometrie, d. h. die Änderung des Winkels α zwischen dem Siliciumatom und dessen jeweiliger Projektion auf die beiden C5-Cyclopentadenylebenen. Dazu verfeinerten wir alle Beugungsdatensätze in der Raumgruppe P21/c. Die sich ergebenden experimentellen Winkel sind im Vergleich zu den berechneten aus plane-wave DFT Methoden in Abbildung 2 dargestellt (siehe unten).
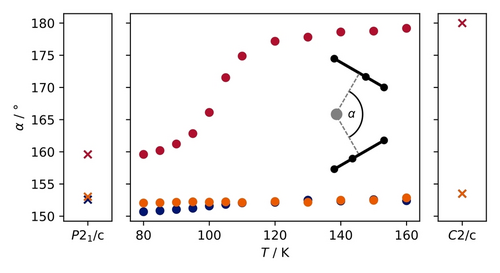
Entwicklung des Anstellwinkels α für die drei unabhängigen Moleküle in der asymmetrischen Einheit in P21/c der Tieftemperaturphase von Cp*2Si bei zunehmender Temperatur (Punkte) und die berechneten Winkel der beiden unterschiedlichen Strukturen in ihren jeweiligen Raumgruppen (Kreuze).
Die plane-wave DFT Berechnungen wurden mit ultra-weichen Pseudopotenzialen mit Quantum Espresso15 und dem PBE16 Funktional durchgeführt, wobei die Begrenzungsenergie für die Wellenfunktion auf 80 Ry und für die Dichte am Γ-Punkt auf 800 Ry gesetzt wurde. Grimmes D3BJ-Korrektur17, 18 für dispersive Wechselwirkungen wurde ebenfalls angewandt. Ausgehend von den experimentellen Geometrien wurden für beide Strukturen die Atompositionen und die Größe der Elementarzelle mit den zugrundeliegenden Symmetriebedingungen der Raumgruppe optimiert. Wie bereits aus dem Vorliegen zweier Phasen vermutet, sind die relativen Energien sehr ähnlich, mit nur leichten Vorteilen für die Tieftemperaturphase. Der berechnete Unterschied für beide vollständigen Zellen ist 0.191 eV, was 1.54 kJ mol−1 für Cp*2Si mit zwölf Molekülen in der Zelle entspricht. Augenfällig unterscheiden sich die beiden gewinkelten Moleküle (verbunden über kristallographische Symmetrie) der Hochtemperaturphase geringfügig in der Tieftemperaturphase. Ausgehend von α=152.60(12)° (ber. 153.50°) verengt sich der erste Winkel beim Kühlen auf 80 K um fast 2° auf 150.69(11)° (ber. 152.57°), während der zweite einen kleineren Unterschied von nur 0.4° auf 152.05(11)° (ber. 153.03°) zeigt. Wie erwartet ist der Effekt beim linearen Molekül am größten. Der Winkel zeigt 180° bei 160 K (180° ber.) und ändert sich auf 159.60(12)° (ber. 159.60°) bei 80 K, erreicht also nicht die Werte, die die beiden anderen gewinkelten Moleküle in der asymmetrischen Einheit zeigen. Die Länge der Zellkanten a und b zeigt ein Plateau zwischen 95 und 110 K, während sich die Steigung des Längenzuwachses für die Zellkante c bei etwa 110 K ändert. Eine detaillierte Darstellung mit den zugrundeliegenden Werten findet sich in Abbildung S3 und Tabelle S2 der Hintergrundinformationen. Der Phasendurchgang kann ebenfalls anhand der systematischen Auslöschungen verfolgt werden (Abbildung 3), da sich die Raumgruppe von C2/c nach P21/c ändert. Die Intensitätszunahme der vorher ausgelöschten Reflexe beim Kühlen kann zwischen 120 K und 90 K klar beobachtet werden. Die Intensität der systematisch ausgelöschten Reflexe bei 90 K in C2/c ist mit einem mittleren I/σ von 20.3 hoch, vergleichbar zu 20.9 für die in beiden Raumgruppen vorhandenen Reflexe. Das ändert sich zu 12.5/19.0 bei 100 K. Bei 120 K ist die mittlere Intensität I/σ nur 0.9. Die systematischen Auslösungen sind erfüllt, während die übrigen Reflexe eine mittlere Intensität von 15.9 zeigen.
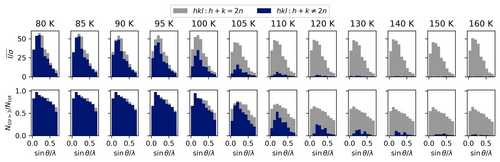
Temperaturabhängigkeit der mittleren Reflexionsintensität geteilt durch die geschätzte Standardabweichung (oben) und der Anteil der Reflexe, die das Signifikanzkriterium erfüllen (unten), in Auflösungsbereichen für die Reflexe, die in beiden Raumgruppen (grau) vorhanden sind, und diejenigen Reflexe, die in der Hochtemperatur-Raumgruppe systematisch fehlen (blau).
Da beide Konformere nebeneinander in der Festkörperstruktur vorliegen stellt sich die Frage, wie groß der Energieunterschied zwischen beiden ist. Mehrere Autoren haben sich bereits mit dieser Problematik auseinandergesetzt. Eine der tiefergehenden Untersuchungen haben Schoeller et al.19 beigesteuert. In CCSD(t)-Berechnungen zeigten sie, dass Cp2Si gewinkelt ist. Darüber hinaus zeigte der Vergleich auf dem B3LYP/6-31G(d)-Niveau, dass die Methylgruppen keinen essentiellen Unterschied machen. Sapunov et al.20 bezogen Cp*2Si in ihre Analyse ein und schlossen, dass “die meisten Unterschiede zwischen s0p0 und s2p0 Metallocenen sekundäre, nicht prinzipielle, Variationen der strukturellen- und Reaktivitätsmuster betreffen” (vom Autor übs.). Sie schrieben die Struktur zu großen Teilen dem Gleichgewicht zwischen van der Waals-Anziehung und -Abstoßung zu. Vor diesem Hintergrund wollten wir Rechnungen beitragen, die Dispersionskorrekturen beinhalten. Wir optimierten Cp*2Si mit dem PBE0 Funktional auf der Basis def2-TZVP22 und mit Grimmes D3BJ Dispersionskorrektur innerhalb des ORCA-Programmpakets.23 Die erste Geometrie wurde mit erzwungener Ci-Symmetrie erhalten, die zweite ohne Symmetrieauflagen. Die gewinkelte C1 Konformation ergab eine um 4.5 kJ mol−1 niedrigere Energie als die aus Ci Symmetrie fixierte Konformation. Etwa 3.5 kJ mol−1 trägt die Dispersion bei. Überhaupt spielen dispersive Wechselwirkungen bei der Begünstigung der gewinkelten Struktur eine wichtige Rolle, wenn auch die Unterschiede gering sind. Es muss gesagt werden, dass die Ci Konformation kein lokales Minimum in der Rechnung ist. Es werden zwei Schwingungsmoden mit imaginären Frequenzen beobachtet, die beide zum Schlupf der Cp*-Ringe um das Siliciumatom gehören. Obgleich es plausibel ist, dass die zusätzliche dispersive Wechselwirkung im gewinkelten Konformer von den beiden Cp* Substituenten stammt, bleibt dies zu verifizieren. Wir setzten NCIPlot ein, um die Wechselwirkungen zu lokalisieren.24 In Abbildung 4 wird deutlich, dass die dispersive Wechselwirkung zwischen beiden Cp* Substituenten lokalisiert ist, welches die Ursache für den Energieunterschied zwischen beiden Konformeren ist und dass sie letztlich das gewinkelten Konformer begünstigt. Zwar gibt es im zentrosymmetrischen Cp*2Si auch dispersive Wechselwirkungen, jedoch reduziert der größere Abstand ihre Stärke. Dies ist verständlich, wenn man berücksichtigt, dass van der Waals Wechselwirkungen mit r−6 vom Abstand abhängen.
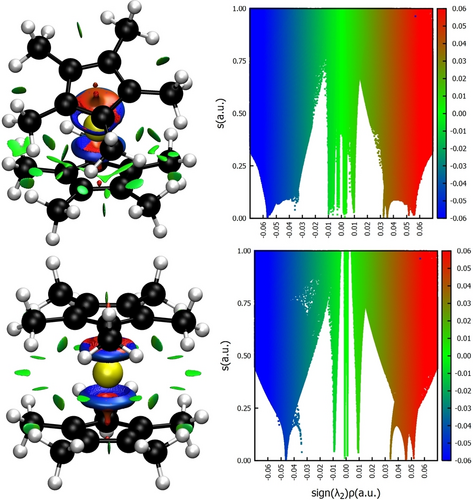
Darstellungen der NCI-Analyse24 für die optimierten Strukturen des gewinkelten (obere Reihe) und des linearen Konformers (untere Reihe). Dargestellt ist der reduzierte Dichtegradient als Isofläche auf dem Niveau 0.3 a.u. Die grüne Farbe (RDG) stellt eine geringe Dichteakkumulation und damit dispersive Wechselwirkungen da. Auf der rechten Seite sind die Werte des RDG gegen das Vorzeichen von λ2 multipliziert mit der Dichte aufgetragen.
Abschließend konnten wir die Ausnahmestellung des Cp*2Si erfolgreich klären, indem wir sowohl das lineare als auch das gewinkelte Konformer im Festkörper als Grundlage für die Diskussion seiner elektronischen Struktur bestimmten. Die lineare Konformation des Moleküls kommt nur in der Hochtemperaturphase vor, während bei tiefen Temperaturen alle Moleküle die gewinkelte Konformation einnehmen. Deshalb ist die Triebkraft zur Hochtemperaturphase mit dem linearen Molekül entropischer Natur und sollte nicht in der Energie gesucht werden. Tatsächlich ist das lineare Molekül kein Minimum in den verwendeten Rechnungen, wohingegen die periodische plane-wave Berechnung eine niedrigere Energie für die Festkörperstruktur mit drei gewinkelten Molekülen ergibt.
Obwohl insgesamt nur gering konnten wir einen Großteil der Stabilisierungsenergie den dispersiven Wechselwirkungen zuschreiben. Es liegen mehr als 35 Jahre zwischen dem ersten Bericht der Struktur und dieser Überarbeitung. Wir konnten vom technologischen und Softwarefortschritt profitieren, besonders im Hinblick auf Röntgenbeugungsmessungen und routinemäßiger Kristallkühlung. Grundsätzlich haben wir gezeigt, dass wir uns im Klaren darüber sein sollten, was wir eigentlich aufnehmen. Gleichgewicht bedeutet nicht, dass wir uns im Minimum der elektronischen Energiehyperfläche befinden, besonders bei höheren Temperaturen nicht, wenn entropische Effekte zunehmend wichtiger werden. Vor diesem Hintergrund sollten -wo immer dies möglich ist- Messungen routinemäßig bei niedrigen Temperaturen durchgeführt werden, insbesondere dann, wenn man aus den erhaltenen Geometrien verallgemeinerbare Aussagen beitragen will. Gleichzeitig sollten wir sehr vorsichtig sein, Unterschiede dem schwammigen Konzept der Packungseffekte zuzuschreiben, die im Allgemeinen einen sehr niedrigen Vorhersage- und gar keinen erklärenden Wert haben. Es könnte sich lohnen, Strukturen zu überprüfen, bei denen Packungseffekte als letzte Zuflucht genutzt wurden, um Raumtemperaturgeometrien zu “klären”.
Danksagung
Diese Arbeit wurde von der Deutschen Forschungsgemeinschaft (DFG, 389479699/GRK2455) gefördert. Computerchemische Ergebnisse wurden vom Göttinger Chemie Computer Cluster erhalten, der ebenfalls von der Deutschen Forschungsgemeinschaft (DFG, 405832858) finanziert wurde. Open Access Veröffentlichung ermöglicht und organisiert durch Projekt DEAL.
Interessenkonflikt
Die Autoren erklären, dass keine Interessenkonflikte vorliegen.
Open Research
Data Availability Statement
Die Daten, die die Ergebnisse dieser Studie unterstützen, sind in den Hintergrundinformationen zu diesem Artikel verfügbar.




