Standard sirens have been the central paradigm in gravitational-wave cosmology so far. From the gravitational wave signature of compact star binaries, it is possible to measure the luminosity distance of the source directly, and if additional information on the source redshift is provided, a measurement of the cosmological expansion can be performed. This review article discusses several methodologies that have been proposed to use gravitational waves for cosmological studies. Methods that use only gravitational-wave signals and methods that use gravitational waves in conjunction with additional observations such as electromagnetic counterparts and galaxy catalogs will be discussed. The review also discusses the most recent results on gravitational-wave cosmology, starting from the binary neutron star merger GW170817 and its electromagnetic counterpart and finishing with the population of binary black holes, observed with the third Gravitational-wave Transient Catalog GWTC–3.

1 Introduction

The observation of gravitational waves (GWs) by interferometric detectors provides a new channel to study the Universe. Among the various scientific results, GWs have shown the existence and properties of a population of binary black holes (BBHs),^[^{1, 2}^] binary neutron stars (BNSs)^[³^] as well as systems with a neutron star and a black hole (NSBH).^[⁴^]

The latest gravitational-wave transient catalog (GWTC–3)^[²^] from the LIGO, Virgo, and KAGRA detectors^[^5-8^] presents almost 100 compact binary sources, thus allowing for a statistical study of the population of these sources in terms of their distances, masses, and spins.^[^9-11^]

From the GW signal alone, it is possible to directly measure the luminosity distance (d_L) of the source. If provided with an estimation of the source redshift, GWs, therefore, offer a new independent mechanism to study the cosmology of our Universe. This is of fundamental importance as the standard cosmological model still suffers some difficulties. On the experimental side, there are discrepancies between different independent measurements of the Hubble constant (H₀)—the expansion rate of the Universe today—which is a fundamental parameter. The most cited tension is a 4.2σ discrepancy between the value of

\begin{equation} H_0 =67.8 \pm 0.9 \ {\rm km} \, {\rm s}^{-1} \, {\rm Mpc}^{-1} \end{equation}

(1)

inferred by the Planck collaboration from cosmic microwave background (CMB)^[¹²^] and the value of

\begin{equation} H_0 =73.0 \pm 1.4 \ {\rm km} \, {\rm s}^{-1} \, {\rm Mpc}^{-1} \end{equation}

(2)

measured from Type Ia Supernovae.^[¹³^] Throughout this paper we report 68.3% confidence intervals. Other measurements of H₀ seem to confirm this discrepancy on smaller and larger scales.^[¹⁴^]

However, the source redshift cannot be inferred from the GW signal. Therefore additional methodologies using additional observations and/or astrophysical assumptions have been proposed and used in current literature. In this article, we provide a review of these methods and their latest results. Although in this review we focus on measures of H₀ using the standard cosmological model, the methods discussed can also be applied to probe general relativity deviations on cosmological scales.^[^15-18^]

In Section 2 we provide an overview of the different methodologies for GW cosmology. We will focus on methods that either use complementary observations such as electromagnetic counterparts and galaxy catalogs or methods that exploit the knowledge about the BBHs and BNSs astrophysical formation channels. In Section 3 we discuss the most recent results on GW cosmology with the last GW transient catalog. Finally in Section 4, we draw our conclusions and future perspectives for GW cosmology.

2 Methods for GW Cosmology

In this section, we discuss various methods that have been proposed and exploited to study cosmology with GWs. However, we do not discuss methods that use strongly lensed GW events^[¹⁹^] and cross-correlation of clustering range of GW-sources and galaxies^[^{20, 21}^] or exploit the GW lensing field.^[²²^]

2.1 Direct Electromagnetic Counterparts

This method is usually referred to as bright siren method. GWs can provide a direct sky localization and d_L measurement of the source. Provided a cosmological model, the GW localization can be used to select possible host galaxies. However, a typical GW localization includes thousands of possible host galaxies,^[²³^] and an unambiguous identification is possible only if an associated electromagnetic counterpart (EM) is detected. At that point, an accurate redshift estimation can be provided from the host galaxy. Based on the current observation technology, we can study the host galaxy from multi-band observations. The expected EM for BNS,^[²⁴^] and possibly some NSBH, consists of a short γ-ray burst(GRB) and kilonova. While for BBHs, we might expect an associated flare if the binary merges in a dense matter environment.^[²⁵^]

Given the source redshift and the d_L measured from the GW, one can use the relation

\begin{equation} d_{\rm L}(z)=\frac{c(1+z)}{H_0} \int _0^z \frac{\text{d}z^{\prime }}{\sqrt {\Omega _{\rm m}(1+z^{\prime })^3+\Omega _\Lambda }} \end{equation}

(3)

to measure the cosmological parameters. In the above equation, c is the speed of light, Ω_m the matter–energy fraction of the Universe, and

\Omega _\Lambda

the dark energy fraction (note that we have assumed a flat Universe and neglected the radiation energy density).

Unfortunately, for GW events, the luminosity distance is expected to be determined with a large uncertainty due to its strong degeneracy with the determination of the orbital inclination angle with respect to the line-of-sight^[²⁶^]. The uncertainty on the d_L estimation can be leveraged by studying the afterglow light curve of the EM counterpart. The light curve contains relevant information about the inclination angle of the orbital plane with respect to the line-of-sight.^[²⁷^]

Despite being a precise method to measure cosmological parameters with GWs (compared with the population methods discussed later), the bottleneck of this method is represented by the rarity of this kind of detection. Therefore, improving the odds of detecting events associated with EM counterparts (e.g., BNS events) and providing a well-localized skymap is foundational to enhancing cosmological inferences from future GW runs. This effort is aided by: improving the sensitivity of current GW detectors, having an international network of GW detectors, and coordinating observations with multi-band observatories.

2.2 Galaxy Catalog Method

Without a viable EM counterpart, one can still use galaxy surveys in combination with GW observations to identify possible host galaxies.^[^28-30^] On the one hand, GWs can provide sky localization and luminosity distance. On the other hand, the galaxy survey, for example, Sloan Digital Sky Survey (SDSS),^[³¹^] can provide a list of galaxies observed in the GW localization area. Using this method, we can obtain a list of potential host galaxies for the GW event. All potential galaxies are taken into account in the statistical inference.

Because of the lack of direct EM counterparts, this method is often referred to as the dark-siren method. One strong point about this method is that the analysis can be done using galaxies reported in different observational bands. This can provide a self-consistency check for the presence of unaccounted selection biases. Moreover, this method can potentially be applied to any dark siren, that is, BBHs, BNSs or NSBHs. However, this method has two weak points. First, galaxy catalogs are incomplete: individual surveys have intrinsic capability limits due to apparent magnitude limits in the different observing bands. Second, poorly localized GW events will include thousands of potential hosting galaxies, thus decreasing their ability to constrain cosmological parameters.

The galaxy catalog method has been used with events associated with the second and third GW transient catalogs.^[^{11, 32}^] However, a deeper galaxy survey that covers more expansive sky areas is needed to enhance the possibility of studying cosmology with this method.

2.3 Methods Based Only on GWs Observations

The source redshift cannot be measured directly in the most common scenario where the GW detection is not associated with an EM counterpart. However, while GW observations give no information on the redshift of the source, they are sensitive to the so-called “redshifted mass” $M_z=(1+z)M$ (i.e., there is a complete degeneracy between mass and redshift). Therefore, the source redshift can be inferred if one provides an independent method to constrain the mass.

Two approaches can be taken to break the degeneracy and measure the redshift. The first, which can be applied only to those binary systems containing at least one neutron star, relies on the knowledge of the neutron star equation of state (EOS) to break the mass-redshift degeneracy via the tidal deformability. The second uses prior knowledge of the (redshift dependent) mass distribution and merger rate density of the dark sirens. The common denominator of these two methods is that they use only GW observations supplied with an additional hypothesis on the EOS or the redshift dependent mass and merger rate of GW sources.

2.3.1 Neutron Star Equation of State Method

Neutron stars that merge with another compact object, may experience a tidal deformation as they approach their companion. This tidal deformation is imprinted in the emitted GW with and additional phase^[^33-35^]

\begin{align} \psi ^{\rm tidal}(f)&=\sum _{a=1,2} \frac{3 \lambda _a (1+z)^5}{128 \eta } \Bigg[-\frac{24}{\chi _a} {\left(1+\frac{11\eta }{\chi _a}\right)}\frac{x^{5/2}}{M^5_z}\nonumber\\ &\quad -\frac{5}{28 \chi _a}\frac{x^{7/2}}{M^5_z} (3179-919 \chi _a -2286 \chi _a^2+260\chi _a^3) \Bigg] \end{align}

(4)

Here

M_z

is the redshifted mass at the detector, f the GW frequency, and the symmetric mass ratio is given in terms of the heavier mass m₁ and lighter mass m₂ by

\eta =m_1 m_2/M^2

; the mass ratios

\chi _a=m_{a,z}/M_z

are defined from the masses of the two components; the dimensionless factor

x=(\pi M_z f)^{2}

; and finally

\lambda _a

characterizes the quadrupole deformation of the neutron star which is subject to a tidal force. The tidal deformation parameter

\lambda _a

is a function of the neutron star radius R_NS and tidal Love number k₂. Provided an EOS, the tidal Love number and radius of the neutron star,

\lambda _a

only depends on the mass of the neutron star in the source frame, such that

\begin{equation} \lambda _a (m_a|{\rm EOS}) = \frac{2}{3}k_2(m_a|{\rm EOS}) R^5_{\rm NS}(m_a|{\rm EOS}) \end{equation}

(5)

That is why, if provided with a measure of

\lambda _a

and a good knowledge of the EOS, one can estimate the source frame mass M and later the redshift from the relation

M_z=(1+z)M

The additional tidal terms in Equation (4) are of post-Newtonian (PN) order 5 and 6, and so they can be hard to measure during the last moments of the inspiral stage. However, their order of magnitude is $\mathcal {O}(R_{\rm NS}/M)^5\approx 10^5$ , they are hence comparable in magnitude with the 3 PN and 3.5 PN orders (of the classical quadrupole waveform).

Current constraints on the NS deformability, and hence of the allowed EOS, have been obtained from the high-SNR event GW170817.^[³⁶^] While the constraints on the tidal deformability were poor for GW190425 given its low SNR.^[³⁷^] In both of these cases, cosmology was fixed and hence it is not possible to infer the redshift value from these observations.

2.3.2 The Mass and Redshift Merger Rates Method

Another way in which it is possible to overcome the mass-redshift degeneracy is via the prior knowledge of at least one between the dark siren mass distribution and the merger rate. In this method, each detected binary system is described by a set of parameters θ. Denoting with

\mathcal {H} = \lbrace H_0,\Omega _m, \Omega _\lambda ,\ldots \rbrace

the set of cosmological (hyper)parameters we are interested in inferring, and

\mathcal {D} = \lbrace d_1,\ldots ,d_n\rbrace

a set of GW observations, the posterior on the hyper parameters can be written as

\begin{equation} p(\mathcal {H}|\mathcal {D}) = \frac{p(\mathcal {D}|\mathcal {H})p(\mathcal {H})}{p(\mathcal {D})}\, \end{equation}

(6)

Under the assumption of independent observations, the likelihood

p(\mathcal {D}|\mathcal {H})

becomes the product of N single-event likelihoods

p(d_i|\mathcal {H})

. The observed gravitational data

d_i

depends on the population-level

\mathcal {H}

as well as source parameters such as masses M (for convention we use this notation to indicate the two binary masses) and redshift z. The single-event likelihood can be expressed as

\begin{equation} p(d_i|\mathcal {H}) = \int p(d_i|M, z, \mathcal {H})p(M,z|\mathcal {H}) \text{d}z \text{d}M \end{equation}

(7)

The implicit information of astrophysical masses and redshift is given by the prior term

p(M,z|\mathcal {H})

, which should be modeled to reproduce the dark sirens' mass and merger rates. A piece of additional redshift information is also arising from the GW likelihood

p(d_i|M, z, \mathcal {H})

, with which it is possible to measure the redshifted masses and the d_L of the source. Given the relation between redshifted masses and source masses, namely

M_z = (1+z)M

, prior knowledge of the source mass distribution would naturally provide implicit redshift information.

The prior

p(M,z|\mathcal {H})

vehicles the available astrophysical information on mass and redshift distributions of the GW event. A common factorization for this prior term is

\begin{equation} p(M,z|\mathcal {H},\Lambda )= C p(M|\Lambda ) \frac{R(z;\Lambda )}{1+z}\frac{\text{d} V_{\rm c}}{\text{d} z} \end{equation}

(8)

where

\frac{\text{d} V_{\rm c}}{\text{d} z}

is the differential of the comoving volume,

p(M|\Lambda )

a mass prior term,

R(z;\Lambda )

the dark sirens merger rate as function of redshift and C a normalization constant. In the above equation, the merger rate and mass distributions are often described using phenomenological models that are dependent on the parameters Λ. The population-level parameters Λ are also part of the statistical inference. In the following, we will briefly present three different applications of the rates method: two relying on the knowledge of the mass distribution and one relying on the merger rate density

R(z;\Lambda )

Before discussing the applications in detail, we note that this method strongly relies on the assumptions made for the compact objects' merger rates. In current studies, both the cosmological and population models are estimated jointly. However, this is still done by making assumptions, such as the independence of the BBHs mass distribution as a function of redshift. Therefore, keeping merger-rate models and assumptions updated with the most recent astrophysical simulations is essential.

Black Hole Mass Function

From a theoretical point of view, features that define a mass scale are expected in the black hole mass spectrum from many different formation channels—we refer the interested reader to ref. [ ^[³⁸^]] and references therein for a review of these processes. One of the most prominent for the inference of cosmological parameters is the pair-instability supernova (PISN) process.^[³⁹^] This process is expected to prevent black hole formation in the 50–120 $M_\odot$ mass range, resulting in a mass gap. The progenitors of BH forming just below the mass gap are expected to undergo a heavy mass loss due to the pulsational pair-instability supernova (PPISN) process. The presence of this phenomenon might lead to a pile-up in the mass distribution located at the lower end of the mass gap.

The upper limit for the black hole mass set by the PPISN process is used in ref. [40] to demonstrate that it is possible to constrain the Hubble constant at $z = 0.8$ with a simulated dataset from one to 5 years of Advanced LIGO and advanced Virgo at design sensitivity. The implications of wrong population assumptions are explored in ref. [41], demonstrating that, once the right population model is assumed, a joint inference of the population parameters Λ and cosmological parameters $\mathcal {H}$ is required to avoid incurring in biases. In refs. [23] an. [16] the authors apply this method to the GWTC–3.

Neutron Star Mass Function

The very same method can be applied to BNS observations. Differently from black holes, neutron stars are expected to span a narrower mass range. Several studies show the proof of principle of this method with current ground-based GW detectors^[⁴²^] and next-generation GW detectors such as the Einstein telescope.^[^{43, 44}^]

Merger Rate as a Function of Redshift

The third possibility is to use the dark sirens merger rate $\mathcal {R}(z;\Lambda )$ . An implicit redshift measure of the GW sources can be provided if the dark sirens merger rate shows a peak in redshift, as observed for the star formation rate at $z\approx \ 2$ .^[⁴⁵^] Considering a time delay due to the evolution of binary systems, the merger rate is expected to peak at $z < 2$ . Other works^[^{46, 47}^] suggest that the BBH formation is expected to follow the low-metallicity star formation history, which, in turn, is expected to peak above $z\approx 2$ ^[⁴⁸^]. Regardless of the detailed star formation history followed by the BBH merger rate, this fact provides a redshift scale within the observing range of third-generation ground-based interferometers. The authors in refs. [49] and [50] demonstrate the applicability of this method to a mock data set representative of 1 year of observations with the Einstein telescope.

2.3.3 Challenges for the GWs-Only Methods

The GWs-only methods presented in the previous sections offer a new avenue to probe cosmology but can be prone to systematics introduced by the models. This can be particularly important for future 3 $\text{rd}$ generation detectors that will observe GW at redshifts $2\text{--}3$ for BNSs and ≈10 for BBHs^[⁵¹^].

For NSs and the EoS method, accurately determining the EOS of neutron stars and using it for cosmology is indeed a challenge. In ref. [52] the authors discuss how several uncertainties and systematics on the determination of $\lambda _a$ can undermine our ability to measure H₀ with the neutron star EOS. It is found that if $\lambda _a$ is reasonably high and determined with an uncertainty of 15%, H₀ can still be measured with a precision of $\approx 50\%$ from a single event. However, the authors also note that a systematic bias (due to EOS modeling) on the determination of $\lambda _a$ could introduce a bias on the H₀ determination if more than 30 events are considered. Achieving a sub-percent precise cosmology using the EoS method would then require accurate modeling of the NSs EoS. We refer the reader to ref. [53] for a more in-depth description of EoS measures from BNSs.

Concerning the mass/redshift rate method for BBHs, a wrong model of the BBHs merger rate can introduce systematics in the determination of the cosmological parameters. In ref. [54] the authors show that a BBH population distribution modeling the $\approx 1\%$ of the detections would lead to a systematic bias of 1% on H₀ when ≈10⁴ BBHs are collected. It is therefore important to accurately model the BBHs merger rates as a function of cosmic time. In particular, a redshift-dependent mass spectrum can be present due to the BHs progenitors' metallicity and distribution of time delays between the BBH formation and its merger (see ref. [55] for a review). With current detections of GWs, there is no evidence that the mass spectrum of BBHs is evolving in redshift^[^{11, 56}^] and current H₀ measures are provided with redshift-independent mass models (see later). However, with future observing runs and $3\text{rd}$ generation GW detectors, we will be able to detect BBHs at higher and higher redshifts. It is therefore important, to develop parallel astrophysical simulations of BBHs synthesis and possibly corroborate GWs cosmology with other observations (e.g., star formation rate, etc.).

3 Cosmological Results from GW Observations

3.1 Results from GWs Observed Associated to EM Counterparts

The era of multi-messenger gravitational-wave astronomy began on August 17th 2017. The LIGO and Virgo interferometers observed GW170817, a gravitational-wave signal consistent with the merger of two neutron stars^[³^] and the Fermi gamma-ray burst monitor^[⁵⁷^] and International Gamma-Ray Astrophysics Laboratory^[⁵⁸^] detected a gamma-ray burst (GRB 170817A) ≈1.7 s after^[²⁴^] with a consistent position to that of GW170817. The open public alerts for GW170817 and GRB 170817A triggered multiple follow-up campaigns using ground and space-based telescopes to identify the expected kilonova electromagnetic counterpart.^[^{59, 60}^] These campaigns utilized the well-constrained 3D localization of the event to optimize their observing strategy, along, in some cases, with galaxy catalogs. After just ≈11 h, the 1-m two-hemisphere team first announced the identification of a bright optical transient consistent with the localization of GW170817. Confirmations from several other teams swiftly followed this ref. [24]. The counterpart, now known as AT 2017gfo, was confidently associated with the host Galaxy NGC 4993.

NGC4993 is a galaxy in the Hydra constellation with an average radial peculiar velocity of $\approx 310\text{ }\rm {km\text{ }s}^{-1}$ . The observed recessional velocity for NGC4993 is about $3327 \pm 72\text{ }\rm {km\text{ }s}^{-1}$ . By combining observations of the galaxy's proper motion and observed recessional velocity, it was possible to compute NGC escape velocity due to the expansion of the Universe, which was $v_{\rm r} = 3017 \pm 166 {\rm km\text{ }s^{-1}}$ . Furthermore, the recessional velocity can be converted to a measurement of the cosmological redshift, giving a value of the cosmological redshift of NGC4993 of $z= 0.0101 \pm 0.0005$ .^[³⁶^]

The maximum a posteriori luminosity distance information of GW170817 was estimated, fixing the sky position to that of NGC4993, as $43.8^{+2.9}_{-6.9} {\rm Mpc}$ at 68% confidence level.^[⁶¹^] By combining the cosmological redshift measurement from NGC4993 and the luminosity distance estimation from GW170817, it was possible to infer the value of the $H_0 = 70^{+12}_{-8} \ {\rm km} \, {\rm s}^{-1} \, {\rm Mpc}^{-1}$ .^[⁶¹^] The associated posterior distribution for this value is provided in Figure 1. However, this result has since been updated using an extended analysis at a lower frequency in the LIGO and Virgo sensitivity bands and using two different priors for the neutron star spins. The results are $H_0 = 70^{+13}_{-7} \ {\rm km} \, {\rm s}^{-1} \, {\rm Mpc}^{-1}$ using high-spin priors (magnitude of the dimensionless spin parameters ⩽0.89), and $H_0 = 70^{+19}_{-8} \ {\rm km} \, {\rm s}^{-1} \, {\rm Mpc}^{-1}$ using low-spin priors (magnitude of the dimensionless spin parameters ⩽0.05).^[³⁶^] Interestingly, the more restrictive low-spin prior (which is well justified based on inferences from the population of Galactic radio pulsars observed in binary neutron star systems^[⁶²^]) yields a broader constraint on the Hubble constant. This arises because the absence of strong precession in the high-spin prior analysis results in a tighter constraint on the inclination angle of the system. There is a strong degeneracy between the inferred luminosity distance and inclination angle of a binary merger^[^{61, 63}^] which constitutes the dominant source of uncertainty in the luminosity distance. Therefore, the tighter constraint on the inclination angle enabled by the high-spin prior yields a correspondingly narrower constraint on the luminosity distance and hence the Hubble constant. In the low-spin analysis, strong precession is ruled out a priori (which is consistent with the data), so there is no corresponding constraint on the inclination angle and hence a broader measurement of the Hubble constant itself. As a result, the narrower high-spin-prior results reflect our best constraint on the Hubble constant without additional information. Still, in future detections, where the observation of multiple polarization modes may itself break the distance–inclination degeneracy, the results from astrophysically motivated low-spin priors will be most relevant.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Hubble constant posterior from the BNS merger GW170817. The dashed vertical line corresponds to the 68% confidence level, and the dotted on to the 95% confidence level. The green and dashed shaded areas indicate the 1σ and 2σ contours reported from supernovae e CMB measures. Reproduced with permission.^[⁶¹^] Copyright 2017, Nature.

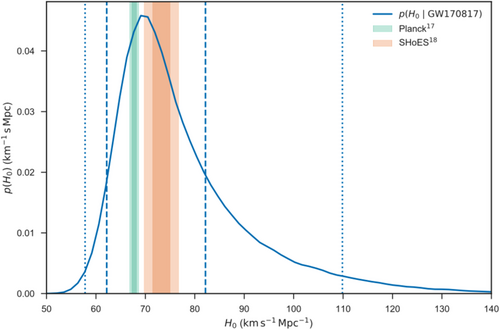
For GW170817, follow-up measurements of the EM afterglow enable an additional way to break the distance–inclination degeneracy and improve the estimation of H₀.^[⁶⁴^] From the 75th and 230th days after the BNS merger, radio band observations using very long baseline interferometry (VLBI) reported the observation of a narrow-collimated jet associated with the merger.^[⁶⁴^] The orbital inclination angle could then be determined by assuming that the jet is emitted perpendicularly to the orbital plane of the merger. This improves the d_L measure and provides an improved value for $H_0 = 68.4^{+4.7}_{-4.6} \ {\rm km} \, {\rm s}^{-1} \, {\rm Mpc}^{-1}$ ^[⁶⁵^] in contrast to the GW-alone value of $H_0 = 70^{+19}_{-8} \ {\rm km} \, {\rm s}^{-1} \, {\rm Mpc}^{-1}$ .

GW170817 remains the only gravitational-wave event with a confirmed electromagnetic counterpart (see, e.g., ref. [66] for a review of searches during the O3 observing run). However, it has recently been claimed that the BBH system GW190521 could be associated with a flare in an active galactic nuclei^[²⁵^] caused by the interaction of the kicked remnant black hole with the accretion of disk.^[⁶⁷^] If true, such a result yields another bright electromagnetic counterpart to measure the Hubble constant.^[^68-70^] However, we caution that the evidence of the claimed association is tentative.^[⁷¹^] Nevertheless, this opens an exciting prospect that future observing runs may yield firm counterparts to binary black hole signals, increasing the number of bright sirens and improving the Hubble constant's determination. Of particular interest, because at fixed detector sensitivity, black hole mergers can be observed at larger distances, such a population of counterparts offers a rich avenue for measuring the Hubble constant at larger redshifts than those available to BNS mergers.

3.2 Results from GWs Observations and Galaxy Surveys

The galaxy catalog method was used to infer the Hubble constant in several recent works using GW events from the GW transient catalogs.^[^{16, 17, 23, 32, 72, 73}^]

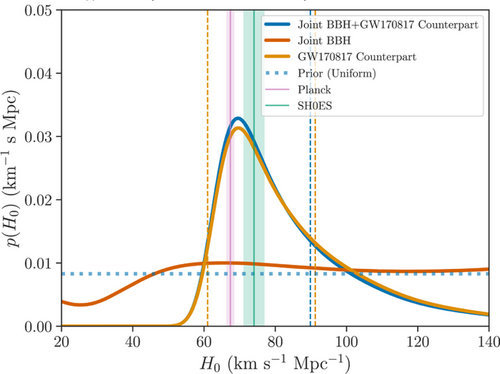
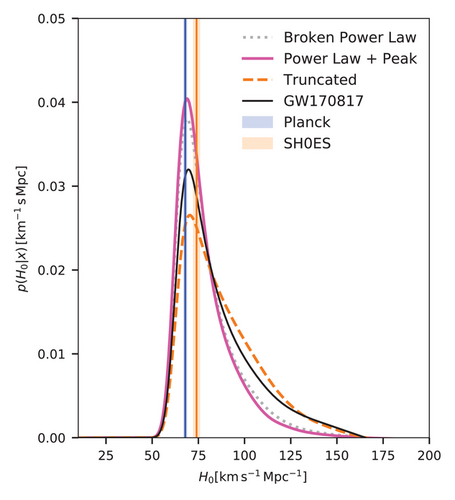
This analysis was performed for the first time with events detected during the first two runs of the LIGO and Virgo detectors and using the GLADE^[⁷⁴^] galaxy catalog for the majority of the events using the galaxies observed in the B-band. GLADE is a galaxy catalog with all-sky support and this makes it ideal for GW events with large estimated sky areas. For the event GW170814, the DES galaxy catalog^[⁷⁵^] was used since this event has a small estimated sky area and it is almost fully included in the sky area coverage of DES. The results from this analysis can be seen in Figure 2. The combined BBHs and GW170817-EM counterpart posterior gives an estimation of $H_0=68.7^{+17.0}_{-7.8} \ \rm {km \ s^{-1} \ Mpc^{-1}}$ . To generate this result, it has been used a set of six BBHs (without EM counterpart) and the H₀ estimation from the BNS GW170817 and its EM counterpart. As we will see later, the mass distribution of BBHs has a relevant role in assess possible systematics in the H₀ estimation. For this analysis, the heaviest mass component of the binary was chosen to be a power-law distribution with a slope of −1.6 between $m_{1,\text{min}}=5 \ \rm {M_\odot }$ and $m_{,\text{max}}=100 \ \rm {M_\odot }$ , whereas the distribution for the light component was selected to be uniform within the same range and with the condition $m_2\le m_1$ .

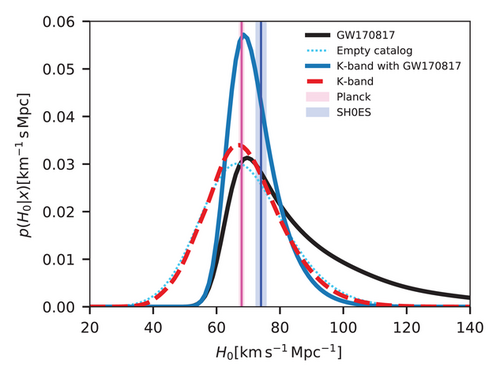
The galaxy catalog framework was used more recently for events detected during all three runs of the LIGO, Virgo, and KAGRA interferometers. In ref. [23], an analysis is performed using 47 compact binary coalescences and the GLADE+ galaxy catalog^[⁷⁷^] (a deeper and more complete version of the GLADE galaxy catalog). This work described the mass distribution of the BBHs with a more complex model. The primary component mass of BBHs was selected as a power law with an additional Gaussian peak; see ref. [23] for more details. The results can be seen in Figure 3. Considering just the 46 dark sirens, it was obtained a $H_0=67^{+13}_{-12} \ \rm {km \ s^{-1} \ Mpc^{-1}}$ . By combining this result with the H₀ estimation from GW170817 and its EM counterpart posterior (solid black curve) it is found $H_0=68^{+8}_{-6} \ \rm {km \ s^{-1} \ Mpc^{-1}}$ . This value represents an improvement of 40% with respect to the GW170817 case.^[⁶¹^] Figure 3 also reports an analysis assuming a 0% completeness for the GLADE+ galaxy catalog, referred to as “empty catalog.” As one can see from the posterior associated with this case, even if the galaxy catalog does not contain any galaxy, there is still implicit information on H₀ encoded in the observed BBHs. This information is given by the BBHs mass model assumed.

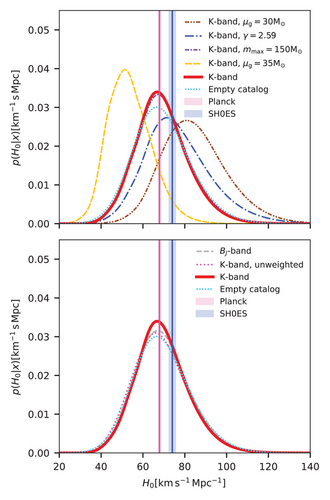
Indeed in refs. [23, 41], it has been shown that in the case that the galaxy catalog is not complete, the cosmological inference is strongly dependent on the population assumptions for masses and merger rates of BBHs. In ref. [23], possible systematics on the H₀ measure with respect to the BBHs population assumptions were explored. The BBH population parameter that is found to correlate the most with H₀ is the Gaussian peak in the BBHs mass spectra, referred to as μ_g. Varying this local excess of BBHs production strongly affects the H₀ posterior, as can be seen in Figure 4. In ref. [23], we also explore possible systematics introduced by the different treatments of the galaxy catalog, such as the choice of using galaxies observed in the B-band or the K-band from the GLADE+ catalog. It is found that the H₀ posterior is not strongly affected by the different treatments of the galaxy catalogs. This is because most of the current GW events are found at distances where the GLADE+ catalog is incomplete.

Additional searches have been performed with events currently detected. In ref. [17], the authors use GW events observed from the first two runs of LIGO and Virgo and the first half of their last run. By using the GLADE galaxy catalog and galaxies observed in the B-band, and a selection of GW events that are supported in a 70% complete region of GLADE, they infer $H_0=72.2^{+13.9}_{-7.5} \ {\rm km} \, {\rm s}^{-1} \, {\rm Mpc}^{-1}$ (in combination with GW170817 and its EM counterpart). The authors also explore additional systematics related to the selection associated with the galaxy catalog completeness and the galaxy observation bands, finding consistent results.

In refs. [72, 73] the authors use well-localized GW events from the three runs of the LIGO, Virgo, and KAGRA detectors to estimate H₀ with the dark energy survey imaging (DESI) Legacy survey catalog. DESI is a significantly deeper galaxy catalog, which is expected to be almost complete up to redshift 1. The authors report a value of $H_0=72.8^{+11.0}_{-7.6} \ {\rm km} \, {\rm s}^{-1} \, {\rm Mpc}^{-1}$ .

3.3 Results with the BBHs Mass Spectrum

In the previous sections, it became clear that population assumptions greatly affect the H₀ estimation made by cross-correlating GW data and galaxy catalogs, especially when galaxy catalogs are highly incomplete. As shown in refs. [40, 41] the correlation between population properties of BBHs can be used to probe cosmology using GWs alone.

In ref. [23] a joint analysis using 42 BBHs from GWTC–3 is used to jointly infer cosmology and population properties of the observed BBHs. The analysis uses three different population models for the mass distribution of BBHs (see ref. [23] for more details): a simple power-law and two more complex models consisting of a broken power-law and a power-law plus a Gaussian overdensity. It is found that, among all the mass models, the preferred ones are the power-law plus a Gaussian and the broken power law.

The estimation of the Hubble constant with the power-law plus Gaussian model resulted in $H_0= 50^{+37}_{-30} \ {\rm km} \, {\rm s}^{-1} \, {\rm Mpc}^{-1}$ , while the broken power-law model resulted in a consistent value of $H_0=44^{+52}_{-24} \ {\rm km} \, {\rm s}^{-1} \, {\rm Mpc}^{-1}$ . These constraints on H₀, as we will see later, arise from the ability of these models to fit an excess of BBHs with masses around $35\, M_{\odot }$ which sets a scale for the redshift distribution of the BBHs.

Figure 5 shows the joint posterior distribution between the cosmological parameters and the BBHs population parameters. In this figure, μ_g, m_max, and γ represent the BBHs excess (location of the Gaussian peak) in mass, the maximum mass for black hole production and the slope of the merger rate evolution in redshift ( $R(z)\propto (1+z)^\gamma$ ). As it can be seen from the plot, the BBH population presents an overdensity of BBHs produced at around 35M_⊙. The presence of an overdensity of BBHs sources allows us to set a characteristic source mass scale, which informs the cosmological inference and allows us to exclude higher values of H₀. In ref. [23] it is also found that other cosmological parameters such as the matter–energy density Ω_m and dark energy equation of state parameter w could not be constrained by current GW observations.

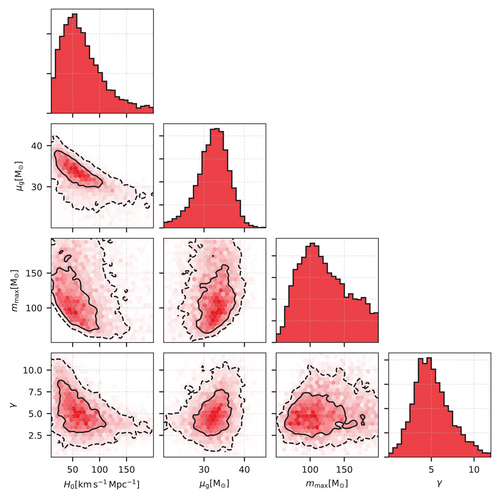
By combining the Hubble constant estimation found for the population of 42 BBHs in Figure 6 with the estimation from GW170817 a value of $H_0=68^{+12}_{-8} \ {\rm km} \, {\rm s}^{-1} \, {\rm Mpc}^{-1}$ is found. This represents an improvement of $\approx 17\%$ with respect to GW170817 alone.

A similar analysis using the population of BBHs from GWTC–3 is performed in ref. [16] finding similar constraints on the Hubble constant and providing new constraints on modifications of gravity on cosmological scales.

4 Conclusion

GW cosmology has started with the detection of GW170817 and its EM counterpart. After three observing runs and almost 100 GWs detected from compact binary coalesces, GWs are rapidly becoming a new tool to study the cosmological expansions of the Universe. In this review paper, we have summarized some of the methods that have been proposed and used in current literature to study cosmology with GWs.

We have discussed strong and weak points of methods that exploit GWs EM counterparts, use survey of galaxy catalogs, knowledge of the equation of state and tidal deformability of neutron stars, and assumptions about the population distribution of BBHs. We have then summarized the most recent GW-based H₀ measurements from sources observed in the third gravitational-wave transient catalog.

We have presented cosmological results from the binary neutron star merger GW170817 and its EM counterpart, showing that this type of event could provide a precise measure of the H₀. This measure can potentially be improved using the afterglow luminosity curve and the detection of collimated jets of ejected material.

We have also presented the most recent results that use dark sirens, namely populations of Compact binary coalescences observed without an EM counterpart. For these sources, we have discussed recent results that use the GLADE, GLADE+, and DESI galaxy catalogs, using galaxies observed in different bands. We have shown how the galaxy catalog method could be a powerful tool to study cosmology if the GW event is well localized and used in conjunction with a complete galaxy catalog.

We have also presented constraints on the cosmological parameters that use GWs alone. By using BBHs events from GWTC–3, we have also shown that it is possible to reconstruct jointly the distribution of masses of BBHs and the cosmological parameters.

With future observing runs of the global network of GW detectors, we will collect more and more GW detections from bright and dark standard sirens. These detections will make it possible to measure H₀ and other cosmological parameters with a new source type. On the one hand, bright sirens will offer rare but precise probes of the cosmological parameters.^[^78-82^] On the other hand, the numerous dark sirens will also make it possible to measure the cosmological parameters using population techniques such as cross-correlation techniques to infer the clustering redshift of GW sources^[^{20, 83}^] using spectroscopic galaxy surveys,^[⁸⁴^] the PISN mass scale of black holes,^[^{40, 41}^] the redshift distribution of the GW sources,^[^{49, 50}^] and the tidal distortion of neutron stars.^[^{33, 35}^] With the aid of more observations and further development of analysis techniques, we can reduce the current systematics and proceed toward accurate and precision gravitational-wave cosmology.

Acknowledgements

S.M. acknowledges the support of the ANR COSMERGE project, grant ANR-20-CE31-001 of the French Agence Nationale de la Recherche. G.D. acknowledges the support received through the iBOF-project BOF20/IBF/124.

Conflict of Interest

The authors declare no conflict of interest.

Biography

Dr. Simone Mastrogiovanni is a postdoctoral researcher at the Observatoire de Côte D'Azur in Nice, France. He works on astrophysical and cosmological interpretations for gravitational wave detections. He is a member of the Virgo collaboration. He obtained his PhD in Astronomy, Astrophysics and Space Science at Sapienza and Tor Vergata Universities of Rome and was a former postdoctoral researcher at the Observatoire de la Côte D'Azur, Nice, France.

References

1B. P. Abbott, R. Abbott, T. D. Abbott, M. R. Abernathy, F. Acernese, K. Ackley, C. Adams, T. Adams, P. Addesso, R. X. Adhikari, V. B. Adya, C. Affeldt, M. Agathos, K. Agatsuma, N. Aggarwal, O. D. Aguiar, L. Aiello, A. Ain, P. Ajith, B. Allen, A. Allocca, P. A. Altin, S. B. Anderson, W. G. Anderson, K. Arai, M. A. Arain, M. C. Araya, C. C. Arceneaux, J. S. Areeda, N. Arnaud, et al., (LIGO Scientific Collaboration and Virgo Collaboration), Phys. Rev. Lett. 2016, 116, 061102.
10.1103/PhysRevLett.116.061102
CAS PubMed Web of Science® Google Scholar
2R. Abbott, T. D. Abbott, S. Abraham, F. Acernese, K. Ackley, A. Adams, C. Adams, R. X. Adhikari, V. B. Adya, C. Affeldt, M. Agathos, K. Agatsuma, N. Aggarwal, O. D. Aguiar, L. Aiello, A. Ain, P. Ajith, S. Akcay, G. Allen, A. Allocca, P. A. Altin, A. Amato, S. Anand, A. Ananyeva, S. B. Anderson, W. G. Anderson, S. V. Angelova, S. Ansoldi, J. M. Antelis, S. Antier, et al., (LIGO Scientific Collaboration and Virgo Collaboration), Phys. Rev. D 2021, 103, 122002.
10.1103/PhysRevD.103.122002
CAS Web of Science® Google Scholar
3B. P. Abbott, R. Abbott, T. D. Abbott, F. Acernese, K. Ackley, C. Adams, T. Adams, P. Addesso, R. X. Adhikari, V. B. Adya, C. Affeldt, M. Afrough, B. Agarwal, M. Agathos, K. Agatsuma, N. Aggarwal, O. D. Aguiar, L. Aiello, A. Ain, P. Ajith, B. Allen, G. Allen, A. Allocca, P. A. Altin, A. Amato, A. Ananyeva, S. B. Anderson, W. G. Anderson, S. V. Angelova, S. Antier, et al., (LIGO Scientific Collaboration and Virgo Collaboration), Phys. Rev. Lett. 2017, 119, 161101.
10.1103/PhysRevLett.119.161101
CAS PubMed Web of Science® Google Scholar
4R. Abbott, T. D. Abbott, S. Abraham, F. Acernese, K. Ackley, A. Adams, C. Adams, R. X. Adhikari, V. B. Adya, C. Affeldt, D. Agarwal, M. Agathos, K. Agatsuma, N. Aggarwal, O. D. Aguiar, L. Aiello, A. Ain, P. Ajith, T. Akutsu, K. M. Aleman, G. Allen, A. Allocca, P. A. Altin, A. Amato, S. Anand, A. Ananyeva, S. B. Anderson, W. G. Anderson, M. Ando, S. V. Angelova, et al., (LIGO Scientific Collaboration and Virgo Collaboration), Astrophys. J. Lett. 2021, 915, L5.
10.3847/2041-8213/ac082e
CAS Web of Science® Google Scholar
5A. Buikema, C. Cahillane, G. L. Mansell, C. D. Blair, R. Abbott, C. Adams, R. X. Adhikari, A. Ananyeva, S. Appert, K. Arai, J. S. Areeda, Y. Asali, S. M. Aston, C. Austin, A. M. Baer, M. Ball, S. W. Ballmer, S. Banagiri, D. Barker, L. Barsotti, J. Bartlett, B. K. Berger, J. Betzwieser, D. Bhattacharjee, G. Billingsley, S. Biscans, R. M. Blair, N. Bode, P. Booker, R. Bork, et al., Phys. Rev. D 2020, 102, 062003.
10.1103/PhysRevD.102.062003
CAS Google Scholar
6M. Tse, H. Yu, N. Kijbunchoo, A. Fernandez-Galiana, P. Dupej, L. Barsotti, C. D. Blair, D. D. Brown, S. E. Dwyer, A. Effler, M. Evans, P. Fritschel, V. V. Frolov, A. C. Green, G. L. Mansell, F. Matichard, N. Mavalvala, D. E. McClelland, L. McCuller, T. McRae, J. Miller, A. Mullavey, E. Oelker, I. Y. Phinney, D. Sigg, B. J. J. Slagmolen, T. Vo, R. L. Ward, C. Whittle, R. Abbott, et al., Phys. Rev. Lett. 2019, 123, 231107.
10.1103/PhysRevLett.123.231107
CAS PubMed Web of Science® Google Scholar
7F. Acernese, M. Agathos, K. Agatsuma, D. Aisa, N. Allemandou, A. Allocca, J. Amarni, P. Astone, G. Balestri, G. Ballardin, F. Barone, J.-P. Baronick, M. Barsuglia, A. Basti, F. Basti, Th. S. Bauer, V. Bavigadda, M. Bejger, M. G. Beker, C. Belczynski, D. Bersanetti, A. Bertolini, M. Bitossi, M. A. Bizouard, S. Bloemen, M. Blom, M. Boer, G. Bogaert, D. Bondi, F. Bondu, et al., Class. Quant. Grav. 2015, 32, 024001.
10.1088/0264-9381/32/2/024001
Web of Science® Google Scholar
8F. Acernese, M. Agathos, L. Aiello, A. Allocca, A. Amato, S. Ansoldi, S. Antier, M. Arène, N. Arnaud, S. Ascenzi, P. Astone, F. Aubin, S. Babak, P. Bacon, F. Badaracco, M. K. M. Bader, J. Baird, F. Baldaccini, G. Ballardin, G. Baltus, C. Barbieri, P. Barneo, F. Barone, M. Barsuglia, D. Barta, A. Basti, M. Bawaj, M. Bazzan, M. Bejger, I. Belahcene, et al., (Virgo Collaboration), Phys. Rev. Lett. 2019, 123, 231108.
10.1103/PhysRevLett.123.231108
CAS PubMed Web of Science® Google Scholar
9B. P. Abbott, R. Abbott, T. D. Abbott, S. Abraham, F. Acernese, K. Ackley, C. Adams, R. X. Adhikari, V. B. Adya, C. Affeldt, M. Agathos, K. Agatsuma, N. Aggarwal, O. D. Aguiar, L. Aiello, A. Ain, P. Ajith, G. Allen, A. Allocca, M. A. Aloy, P. A. Altin, A. Amato, A. Ananyeva, S. B. Anderson, W. G. Anderson, S. V. Angelova, S. Antier, S. Appert, K. Arai, M. C. Araya, et al., Astrophys. J. Lett. 2019, 882, L24.
10.3847/2041-8213/ab3800
Web of Science® Google Scholar
10R. Abbott, T. D. Abbott, S. Abraham, F. Acernese, K. Ackley, A. Adams, C. Adams, R. X. Adhikari, V. B. Adya, C. Affeldt, M. Agathos, K. Agatsuma, N. Aggarwal, O. D. Aguiar, L. Aiello, A. Ain, P. Ajith, G. Allen, A. Allocca, P. A. Altin, A. Amato, S. Anand, A. Ananyeva, S. B. Anderson, W. G. Anderson, S. V. Angelova, S. Ansoldi, J. M. Antelis, S. Antier, S. Appert, et al., Astrophys. J. Lett. 2021, 913, L7.
10.3847/2041-8213/abe949
CAS Web of Science® Google Scholar
11R. Abbott, T. D. Abbott, S. Abraham, F. Acernese, K. Ackley, A. Adams, C. Adams, R. X. Adhikari, V. B. Adya, C. Affeldt, M. Agathos, K. Agatsuma, N. Aggarwal, O. D. Aguiar, L. Aiello, A. Ain, P. Ajith, S. Akcay, G. Allen, A. Allocca, P. A. Altin, A. Amato, S. Anand, A. Ananyeva, S. B. Anderson, W. G. Anderson, S. V. Angelova, S. Ansoldi, J. M. Antelis, S. Antier, et al., Phys. Rev. X 2021, 11, 021053.
CAS Google Scholar
12 Planck Collaboration, P. A. R. Ade, N. Aghanim, M. Arnaud, M. Ashdown, J. Aumont, C. Baccigalupi, A. J. Banday, R. B. Barreiro, J. G. Bartlett, N. Bartolo, E. Battaner, R. Battye, K. Benabed, A. Benoît, A. Benoit-Lévy, J.-P. Bernard, M. Bersanelli, P. Bielewicz, J. J. Bock, Astron. Astrophys. 2016, 594, A13.
10.1051/0004-6361/201525830
Web of Science® Google Scholar
13A. G. Riess, S. Casertano, W. Yuan, J. B. Bowers, L. Macri, J. C. Zinn, D. Scolnic, Astrophys. J. Lett. 2021, 908, L6.
10.3847/2041-8213/abdbaf
CAS Google Scholar
14E. Di Valentino, L. A. Anchordoqui, Ö. Akarsu, Y. Ali-Haimoud, L. Amendola, N. Arendse, M. Asgari, M. Ballardini, S. Basilakos, E. Battistelli, M. Benetti, S. Birrer, F. R. Bouchet, M. Bruni, E. Calabrese, D. Camarena, S. Capozziello, A. Chen, J. Chluba, A. Chudaykin, E. Ó Colgáin, F.-Y. Cyr-Racine, P. de Bernardis, J. de Cruz Pérez, J. Delabrouille, C. Escamilla-Rivera, A. Ferté, F. Finelli, W. Freedman, N. Frusciante, et al., Astropart. Phys. 2021, 131, 102605.
10.1016/j.astropartphys.2021.102605
Google Scholar
15S. Mastrogiovanni, L. Haegel, C. Karathanasis, I. Magaña Hernandez, D. A. Steer, J. Cosmol. Astropart. Phys. 2021, 2021, 043.
10.1088/1475-7516/2021/02/043
CAS Google Scholar
16M. Mancarella, E. Genoud-Prachex, M. Maggiore, arXiv:2112.05728 2021.
Google Scholar
17A. Finke, S. Foffa, F. Iacovelli, M. Maggiore, M. Mancarella, J. Cosmol. Astropart. Phys. 2021, 2021, 026.
10.1088/1475-7516/2021/08/026
CAS Google Scholar
18K. Leyde, S. Mastrogiovanni, D. A. Steer, E. Chassande-Mottin, C. Karathanasis, arXiv:2203.11680 2022.
Google Scholar
19O. A. Hannuksela, T. E. Collett, M. Çalışkan, T. G. F. Li, Mon. Not. R. Astron. Soc. 2020, 498, 3395.
10.1093/mnras/staa2577
CAS Web of Science® Google Scholar
20S. Mukherjee, B. D. Wandelt, S. M. Nissanke, A. Silvestri, Phys. Rev. D 2021, 103, 043520.
10.1103/PhysRevD.103.043520
CAS Google Scholar
21S. Mukherjee, A. Krolewski, B. D. Wandelt, J. Silk, 2022.
Google Scholar
22S. Mukherjee, B. D. Wandelt, J. Silk, Mon. Not. R. Astron. Soc. 2020, 494, 1956.
10.1093/mnras/staa827
CAS Web of Science® Google Scholar
23 The LIGO Scientific Collaboration, The Virgo Collaboration, The KAGRA Collaboration, R. Abbott, H. Abe, F. Acernese, K. Ackley, N. Adhikari, R. X. Adhikari, V. K. Adkins, V. B. Adya, C. Affeldt, D. Agarwal, M. Agathos, K. Agatsuma, N. Aggarwal, O. D. Aguiar, L. Aiello, A. Ain, P. Ajith, T. Akutsu, S. Albanesi, R. A. Alfaidi, A. Allocca, P. A. Altin, A. Amato, C. Anand, S. Anand, A. Ananyeva, S. B. Anderson, et al., arXiv:2111.03604 2021.
Google Scholar
24B. P. Abbott, R. Abbott, T. D. Abbott, F. Acernese, K. Ackley, C. Adams, T. Adams, P. Addesso, R. X. Adhikari, V. B. Adya, C. Affeldt, M. Afrough, B. Agarwal, M. Agathos, K. Agatsuma, N. Aggarwal, O. D. Aguiar, L. Aiello, A. Ain, P. Ajith, B. Allen, G. Allen, A. Allocca, P. A. Altin, A. Amato, A. Ananyeva, S. B. Anderson, W. G. Anderson, S. V. Angelova, S. Antier, et al., Astrophys. J. Lett. 2017, 848, L12.
10.3847/2041-8213/aa91c9
Web of Science® Google Scholar
25M. J. Graham, K. E. S. Ford, B. McKernan, N. P. Ross, D. Stern, K. Burdge, M. Coughlin, S. G. Djorgovski, A. J. Drake, D. Duev, M. Kasliwal, A. A. Mahabal, S. van Velzen, J. Belecki, E. C. Bellm, R. Burruss, S. B. Cenko, V. Cunningham, G. Helou, S. R. Kulkarni, F. J. Masci, T. Prince, D. Reiley, H. Rodriguez, B. Rusholme, R. M. Smith, M. T. Soumagnac, Phys. Rev. Lett. 2020, 124, 251102.
10.1103/PhysRevLett.124.251102
CAS PubMed Web of Science® Google Scholar
26E. Chassande-Mottin, K. Leyde, S. Mastrogiovanni, D. A. Steer, Phys. Rev. D 2019, 100, 083514.
10.1103/PhysRevD.100.083514
CAS Google Scholar
27K. Hotokezaka, E. Nakar, O. Gottlieb, S. Nissanke, K. Masuda, G. Hallinan, K. P. Mooley, A. T. Deller, Nat. Astron. 2019, 3, 940.
10.1038/s41550-019-0820-1
Web of Science® Google Scholar
28B. F. Schutz, Nature 1986, 323, 310.
10.1038/323310a0
Web of Science® Google Scholar
29R. Gray, I. M. Hernandez, H. Qi, A. Sur, P. R. Brady, H.-Y. Chen, W. M. Farr, M. Fishbach, J. R. Gair, A. Ghosh, D. E. Holz, S. Mastrogiovanni, C. Messenger, D. A. Steer, J. Veitch, Phys. Rev. D 2020, 101, 122001.
10.1103/PhysRevD.101.122001
CAS Web of Science® Google Scholar
30R. Gray, C. Messenger, J. Veitch, Mon. Not. R. Astropart. Soc. 2022.
Google Scholar
31K. Bundy, M. A. Bershady, D. R. Law, R. Yan, N. Drory, N. MacDonald, D. A. Wake, B. Cherinka, J. R. Sánchez-Gallego, A.-M. Weijmans, T. Daniel, T. Christy, C. Lodovico, A. M. Diamond-Stanic, A.-S. Alfonso, A.-R. Vladimir, B. Carles, F.-B. Jésus, B. Francesco, Astrophys. J. 2015, 798, 7.
10.1088/0004-637X/798/1/7
Web of Science® Google Scholar
32B. P. Abbott, R. Abbott, T. D. Abbott, F. Acernese, K. Ackley, C. Adams, T. Adams, P. Addesso, R. X. Adhikari, V. B. Adya, C. Affeldt, M. Afrough, B. Agarwal, M. Agathos, K. Agatsuma, N. Aggarwal, O. D. Aguiar, L. Aiello, A. Ain, P. Ajith, B. Allen, G. Allen, A. Allocca, P. A. Altin, A. Amato, A. Ananyeva, S. B. Anderson, W. G. Anderson, S. V. Angelova, S. Antier, et al., Astrophys. J. 2021, 909, 218.
10.3847/1538-4357/abdcb7
CAS Google Scholar
33C. Messenger, J. Read, Phys. Rev. Lett. 2012, 108, 091101.
10.1103/PhysRevLett.108.091101
CAS PubMed Web of Science® Google Scholar
34W. Del Pozzo, T. G. F. Li, C. Messenger, Phys. Rev. D 2017, 95, 043502.
10.1103/PhysRevD.95.043502
Google Scholar
35D. Chatterjee, A. H. K. R., G. Holder, D. E. Holz, S. Perkins, K. Yagi, N. Yunes, Phys. Rev. D 2021, 104, 083528.
10.1103/PhysRevD.104.083528
CAS Google Scholar
36B. P. Abbott, R. Abbott, T. D. Abbott, F. Acernese, K. Ackley, C. Adams, T. Adams, P. Addesso, R. X. Adhikari, V. B. Adya, C. Affeldt, B. Agarwal, M. Agathos, K. Agatsuma, N. Aggarwal, O. D. Aguiar, L. Aiello, A. Ain, P. Ajith, B. Allen, G. Allen, A. Allocca, M. A. Aloy, P. A. Altin, A. Amato, A. Ananyeva, S. B. Anderson, W. G. Anderson, S. V. Angelova, S. Antier, et al., (LIGO Scientific Collaboration and Virgo Collaboration), Phys. Rev. 2019, X9, 011001.
10.1103/PhysRevX.9.011001
Google Scholar
37B. P. Abbott, R. Abbott, T. D. Abbott, F. Acernese, K. Ackley, C. Adams, T. Adams, P. Addesso, R. X. Adhikari, V. B. Adya, C. Affeldt, M. Afrough, B. Agarwal, M. Agathos, K. Agatsuma, N. Aggarwal, O. D. Aguiar, L. Aiello, A. Ain, P. Ajith, B. Allen, G. Allen, A. Allocca, P. A. Altin, A. Amato, A. Ananyeva, S. B. Anderson, W. G. Anderson, S. V. Angelova, S. Antier, et al., Astrophys. J. Lett. 2020, 892, L3.
10.3847/2041-8213/ab75f5
CAS Web of Science® Google Scholar
38M. Zevin, S. S. Bavera, C. P. L. Berry, V. Kalogera, T. Fragos, P. Marchant, C. L. Rodriguez, F. Antonini, D. E. Holz, C. Pankow, Astrophys. J. 2021, 910, 152.
10.3847/1538-4357/abe40e
CAS Google Scholar
39J. R. Bond, W. D. Arnett, B. J. Carr, Astrophys. J. 1984, 280, 825.
10.1086/162057
CAS Web of Science® Google Scholar
40W. M. Farr, M. Fishbach, J. Ye, D. E. Holz, Astrophys. J. 2019, 883, L42.
10.3847/2041-8213/ab4284
CAS Google Scholar
41S. Mastrogiovanni, K. Leyde, C. Karathanasis, E. Chassande-Mottin, D. A. Steer, J. Gair, A. Ghosh, R. Gray, S. Mukherjee, S. Rinaldi, Phys. Rev. D 2021, 104, 062009.
10.1103/PhysRevD.104.062009
CAS Web of Science® Google Scholar
42S. R. Taylor, J. R. Gair, I. Mandel, Phys. Rev. D 2012, 85, 023535.
10.1103/PhysRevD.85.023535
Google Scholar
43S. R. Taylor, J. R. Gair, Phys. Rev. D 2012, 86, 023502.
10.1103/PhysRevD.86.023502
Google Scholar
44F. Iacovelli, A. Finke, S. Foffa, M. Maggiore, M. Mancarella, arXiv:2203.09237 2022.
Google Scholar
45P. Madau, M. Dickinson, Ann. Rev. Astron. Astrophys. 2014, 52, 415.
10.1146/annurev-astro-081811-125615
Web of Science® Google Scholar
46C. J. Neijssel, A. Vigna-Gómez, S. Stevenson, J. W. Barrett, S. M. Gaebel, F. S. Broekgaarden, S. E. de Mink, D. Szécsi, S. Vinciguerra, I. Mandel, Mon. Not. R. Astropart. Soc. 2019, 490, 3740.
10.1093/mnras/stz2840
CAS Web of Science® Google Scholar
47F. Santoliquido, M. Mapelli, N. Giacobbo, Y. Bouffanais, M. C. Artale, Mon. Not. R. Astropart. Soc. 2021, 502, 4877.
10.1093/mnras/stab280
CAS Web of Science® Google Scholar
48M. Chruślińska, G. Nelemans, L. Boco, A. Lapi, Mon. Not. R. Astropart. Soc. 2021, 508, 4994.
10.1093/mnras/stab2690
CAS Web of Science® Google Scholar
49X. Ding, M. Biesiada, X. Zheng, K. Liao, Z. Li, Z.-H. Zhu, J. Cosmol. Astropart. Phys. 2019, 2019, 033.
10.1088/1475-7516/2019/04/033
CAS Google Scholar
50C. Ye, M. Fishbach, Phys. Rev. D 2021, 104, 043507.
10.1103/PhysRevD.104.043507
CAS Google Scholar
51M. Maggiore, C. Van Den Broeck, N. Bartolo, E. Belgacem, D. Bertacca, M. A. Bizouard, M. Branchesi, S. Clesse, S. Foffa, J. García-Bellido, S. Grimm, J. Harms, T. Hinderer, S. Matarrese, C. Palomba, M. Peloso, A. Ricciardone, M. Sakellariadoun, J. Cosmol. Astropart. Phys. 2020, 2020, 050.
10.1088/1475-7516/2020/03/050
Web of Science® Google Scholar
52D. Chatterjee, A. Hegade K. R., G. Holder, D. E. Holz, S. Perkins, K. Yagi, N. Yunes, Phys. Rev. D 2021, 104, 083528.
10.1103/PhysRevD.104.083528
CAS Google Scholar
53L. Baiotti, Binary Neutron Stars, Springer Singapore, Singapore 2020, pp. 1–31.
Google Scholar
54H. Yu, B. Seymour, Y. Wang, Y. Chen, arXiv:2206.09984 2022.
Google Scholar
55M. Mapelli, in Handbook of Gravitational Wave Astronomy, Springer, Cham 2021.
Google Scholar
56M. Fishbach, Z. Doctor, T. Callister, B. Edelman, J. Ye, R. Essick, W. M. Farr, B. Farr, D. E. Holz, Astrophys. J. 2021, 912, 98.
10.3847/1538-4357/abee11
CAS Google Scholar
57C. Meegan, G. Lichti, P. N. Bhat, E. Bissaldi, M. S. Briggs, V. Connaughton, R. Diehl, G. Fishman, J. Greiner, A. S. Hoover, A. J. van der Horst, A. von Kienlin, R. M. Kippen, C. Kouveliotou, S. McBreen, W. S. Paciesas, R. Preece, H. Steinle, M. S. Wallace, R. B. Wilson, C. Wilson-Hodge, Astrophys. J. 2009, 702, 791.
10.1088/0004-637X/702/1/791
CAS Web of Science® Google Scholar
58A. von Kienlin, V. Beckmann, S. Covino, D. Götz, G. G. Lichti, D. Malesani, S. Mereghetti, E. Molinari, A. Rau, C. R. Shrader, S. J. Sturner, F. Zerbi, Astron. Astrophys. 2003, 411, L299.
10.1051/0004-6361:20031231
Web of Science® Google Scholar
59L.-X. Li, B. Paczynski, Astrophys.J. 1998, 507, L59.
10.1086/311680
Web of Science® Google Scholar
60B. Metzger, G. Martinez-Pinedo, S. Darbha, E. Quataert, A. Arcones, D. Kasen, R. Thomas, P. Nugent, I. V. Panov, N. T. Zinner, Mon. Not. R. Astron. Soc. 2010, 406, 2650.
10.1111/j.1365-2966.2010.16864.x
Web of Science® Google Scholar
61B. P. Abbott, R. Abbott, T. D. Abbott, F. Acernese, K. Ackley, C. Adams, T. Adams, P. Addesso, R. X. Adhikari, V. B. Adya, C. Affeldt, M. Afrough, B. Agarwal, M. Agathos, K. Agatsuma, N. Aggarwal, O. D. Aguiar, L. Aiello, A. Ain, P. Ajith, B. Allen, G. Allen, A. Allocca, P. A. Altin, A. Amato, A. Ananyeva, S. B. Anderson, W. G. Anderson, S. V. Angelova, S. Antier, et al., Nature 2017, 551, 85.
10.1038/551425a
PubMed Web of Science® Google Scholar
62X. Zhu, E. Thrane, S. Oslowski, Y. Levin, P. D. Lasky, Phys. Rev. D 2018, 98, 043002.
10.1103/PhysRevD.98.043002
CAS Web of Science® Google Scholar
63S. Nissanke, D. E. Holz, S. A. Hughes, N. Dalal, J. L. Sievers, Astrophys. J. 2010, 725, 496.
10.1088/0004-637X/725/1/496
Web of Science® Google Scholar
64K. Hotokezaka, E. Nakar, O. Gottlieb, S. Nissanke, K. Masuda, G. Hallinan, K. P. Mooley, A. T. Deller, Nat. Astron. 2019, 3, 940.
10.1038/s41550-019-0820-1
Web of Science® Google Scholar
65S. Mukherjee, G. Lavaux, F. R. Bouchet, J. Jasche, B. D. Wandelt, S. M. Nissanke, F. Leclercq, K. Hotokezaka, Astron. Astrophys. 2021, 646, A65.
10.1051/0004-6361/201936724
CAS Google Scholar
66M. W. Coughlin, Nat. Astron. 2020, 4, 550.
10.1038/s41550-020-1130-3
Web of Science® Google Scholar
67B. McKernan, K. E. S. Ford, I. Bartos, M. J. Graham, W. Lyra, S. Marka, Z. Marka, N. P. Ross, D. Stern, Y. Yang, Astrophys. J. Lett. 2019, 884, L50.
10.3847/2041-8213/ab4886
CAS Web of Science® Google Scholar
68H.-Y. Chen, C.-J. Haster, S. Vitale, W. M. Farr, M. Isi, MNRAS 2022, 513, 2152.
10.1093/mnras/stac989
CAS Web of Science® Google Scholar
69V. Gayathri, J. Healy, J. Lange, B. O'Brien, M. Szczepanczyk, I. Bartos, M. Campanelli, S. Klimenko, C. O. Lousto, R. O'Shaughnessy, Astrophys. J. Lett. 2021, 908, L34.
10.3847/2041-8213/abe388
CAS Google Scholar
70S. Mukherjee, A. Ghosh, M. J. Graham, C. Karathanasis, M. M. Kasliwal, I. Magaña Hernandez, S. M. Nissanke, A. Silvestri, B. D. Wandelt, arXiv:2009.14199 2020.
Google Scholar
71G. Ashton, K. Ackley, I. M. n. Hernandez, B. Piotrzkowski, Class. Quant. Grav. 2021, 38, 235004.
10.1088/1361-6382/ac33bb
CAS Web of Science® Google Scholar
72A. Palmese, J. deVicente, M. E. S. Pereira, J. Annis, W. Hartley, K. Herner, M. Soares-Santos, M. Crocce, D. Huterer, I. Magaña Hernandez, A. Garcia, J. Garcia-Bellido, J. Gschwend, D. E. Holz, R. Kessler, O. Lahav, R. Morgan, C. Nicolaou, C. Conselice, R. J. Foley, M. S. S. Gill, T. M. C. Abbott, M. Aguena, S. Allam, S. Avila, K. Bechtol, E. Bertin, S. Bhargava, D. Brooks, E. Buckley-Geer, et al., Astrophys. J. Lett. 2020, 900, L33.
10.3847/2041-8213/abaeff
CAS Google Scholar
73A. Palmese, C. R. Bom, S. Mucesh, W. G. Hartley, arXiv:2111.06445 2021.
Google Scholar
74G. Dálya, G. Galgóczi, L. Dobos, Z. Frei, I. S. Heng, R. Macas, C. Messenger, P. Raffai, R. S. de Souza, Mon. Not. R. Astrophys. Soc. 2018, 479, 2374.
10.1093/mnras/sty1703
CAS Web of Science® Google Scholar
75T. M. C. Abbott, F. B. Abdalla, S. Allam, A. Amara, J. Annis, J. Asorey, S. Avila, O. Ballester, M. Banerji, W. Barkhouse, L. Baruah, M. Baumer, K. Bechtol, M. R. Becker, A. Benoit-Lévy, G. M. Bernstein, E. Bertin, J. Blazek, S. Bocquet, D. Brooks, D. Brout, E. Buckley-Geer, D. L. Burke, V. Busti, R. Campisano, L. Cardiel-Sas, A. Carnero Rosell, M. Carrasco Kind, J. Carretero, F. J. Castander, et al., Astrophys. J. Suppl. 2018, 239, 18.
10.3847/1538-4365/aae9f0
CAS Google Scholar
76A. G. Riess, S. Casertano, W. Yuan, L. M. Macri, D. Scolnic, Astrophys. J. 2019, 876, 85.
10.3847/1538-4357/ab1422
CAS Web of Science® Google Scholar
77G. Dálya, R. Díaz, F. R. Bouchet, Z. Frei, J. Jasche, G. Lavaux, R. Macas, S. Mukherjee, M. Pálfi, R. S. de Souza, et al., arXiv:2110.06184 2021.
Google Scholar
78D. E. Holz, S. A. Hughes, Astrophys. J. 2005, 629, 15.
10.1086/431341
Web of Science® Google Scholar
79N. Dalal, D. E. Holz, S. A. Hughes, B. Jain, Phys. Rev. D 2006, 74, 063006.
10.1103/PhysRevD.74.063006
CAS Web of Science® Google Scholar
80S. Nissanke, D. E. Holz, S. A. Hughes, N. Dalal, J. L. Sievers, Astrophys. J. 2010, 725, 496.
10.1088/0004-637X/725/1/496
Web of Science® Google Scholar
81H.-Y. Chen, M. Fishbach, D. E. Holz, Nature 2018, 562, 545.
10.1038/s41586-018-0606-0
CAS PubMed Web of Science® Google Scholar
82S. M. Feeney, H. V. Peiris, A. R. Williamson, S. M. Nissanke, D. J. Mortlock, J. Alsing, D. Scolnic, Phys. Rev. Lett. 2019, 122, 061105.
10.1103/PhysRevLett.122.061105
CAS PubMed Web of Science® Google Scholar
83S. Bera, D. Rana, S. More, S. Bose, Astrophys. J. 2020, 902, 79.
10.3847/1538-4357/abb4e0
CAS Google Scholar
84C. C. Diaz, S. Mukherjee, Mon. Not. Roy. Astron. Soc. 2022, 511, 2782.
10.1093/mnras/stac387
CAS Web of Science® Google Scholar

Citing Literature

Volume536, Issue2

Special Issue:Gravitational Wave Physics and Astronomy

February 2024

2200180

Cosmology with Gravitational Waves: A Review

Abstract

1 Introduction