Center of mass mechanics of chimpanzee bipedal walking
ABSTRACT
Center of mass (CoM) oscillations were documented for 81 bipedal walking strides of three chimpanzees. Full-stride ground reaction forces were recorded as well as kinematic data to synchronize force to gait events and to determine speed. Despite being a bent-hip, bent-knee (BHBK) gait, chimpanzee walking uses pendulum-like motion with vertical oscillations of the CoM that are similar in pattern and relative magnitude to those of humans. Maximum height is achieved during single support and minimum height during double support. The mediolateral oscillations of the CoM are more pronounced relative to stature than in human walking when compared at the same Froude speed. Despite the pendular nature of chimpanzee bipedalism, energy recoveries from exchanges of kinetic and potential energies are low on average and highly variable. This variability is probably related to the poor phasic coordination of energy fluctuations in these facultatively bipedal animals. The work on the CoM per unit mass and distance (mechanical cost of transport) is higher than that in humans, but lower than that in bipedally walking monkeys and gibbons. The pronounced side sway is not passive, but constitutes 10% of the total work of lifting and accelerating the CoM. CoM oscillations of bipedally walking chimpanzees are distinctly different from those of BHBK gait of humans with a flat trajectory, but this is often described as “chimpanzee-like” walking. Human BHBK gait is a poor model for chimpanzee bipedal walking and offers limited insights for reconstructing early hominin gait evolution. Am J Phys Anthropol 156:422–433, 2015. © 2014 Wiley Periodicals, Inc.
Bipedal locomotion on extended limbs is a hallmark in the evolution of modern humans. Striding bipedalism confers many advantages relative to other forms of locomotion; in particular, the extended limb configuration allows the effective use of pendular mechanics during walking. Pendular walking can reduce the mechanical work required to lift and accelerate the center of mass (CoM) from one step to the next (Srinivasan and Ruina, 2006), enabling the recovery of up to 70% of the mechanical energy needed to lift and accelerate the CoM via transformations between kinetic and potential energies (Cavagna et al., 1976). Reconstructing the emergence of this efficiency in the hominin lineage is complicated by conflicting ideas of how the pelvis and CoM may have moved in fossil hominins.
In order to understand how early hominins may have utilized pendular mechanics, we must first gain a better understanding of the gait mechanics of our closest living, and facultatively bipedal relative, the chimpanzee. Humans and chimpanzees share a last common ancestor about 8–6 million years ago (Fabre et al., 2009), and thus serve as the phylogenetic bracket (sensu Witmer, 1995) for the last common ancestor of the two lineages. Studying chimpanzee bipedal locomotion can therefore be informative in attempting to reconstruct posture and gait of early bipedal hominins. In addition, the earliest fossils that can be safely attributed to the hominin clade, the australopithecines, resemble extant chimpanzees in numerous aspects of their locomotor skeleton (e.g., Stern and Susman, 1983; Lovejoy et al., 2009a, c), which would have placed constraints on their locomotor function similar, to a certain degree, to constraints that chimpanzees are subjected to when they walk bipedally. Although some authors have challenged the chimpanzee's validity as a model for any aspect of locomotion in the last common ancestor based on the skeleton of Ardipithecus ramidus (Lovejoy et al., 2009b), skepticism remains regarding the reconstruction and locomotor interpretation of this fossil (Harrison, 2010; Sarmiento, 2010; Wood and Harrison, 2011). In addition, many of the unambiguous postcranial features in the ischium, ankle, and foot of the A. ramidus skeleton show chimpanzee-like morphology (Lovejoy et al., 2009a, c). Chimpanzees, therefore, represent a very relevant outgroup for reconstructing the locomotor behavior of the last common ancestor of the panins and hominins, as well as early hominins like Australopithecus afarensis (Pilbeam, 2002; Stanford, 2012).
Chimpanzees are facultative bipeds in the wild (Doran, 1992, 1996; Hunt, 1992; Sarringhaus et al., 2014), and in the laboratory they can be easily enticed to walk on two legs. Indeed, multiple aspects of chimpanzee and bonobo bipedal gait have been explored with experimental data over several decades of research (e.g., Elftman, 1944; Jenkins, 1972; Taylor and Rowntree, 1973; Tuttle et al., 1978, 1979; Yamazaki et al., 1979; Fleagle et al., 1981; Stern and Susman, 1981; Kimura et al., 1985; Yamazaki, 1985; Tardieu et al., 1993; Kimura, 1996; D'Août et al., 2001, 2004; Thorpe et al., 2004; Sockol et al., 2007; Kimura and Yaguramaki, 2009; Pontzer et al., 2014). Despite this body of research, there are still unresolved issues, data gaps, and conflicting assumptions about chimpanzee bipedal gait. One area of uncertainty is how the chimpanzee whole body CoM moves, and whether these movements are governed by pendular mechanics.
Differing interpretations exist as to whether the CoM oscillates in height during chimpanzee locomotion, and this is largely a result of the indirect data upon which such interpretations are based. Chimpanzees do not have the two distinct peaks in the vertical ground reaction force of the stance limb that characterize human walking. This has been taken as an indication of a CoM trajectory that does not conform to pendulum-like motion and, thus, does not allow much transfer of kinetic and potential energies (e.g., Li et al., 1996; Pontzer et al., 2014). Human walking with flexed hind limbs (bent-hip, bent-knee (BHBK)) has often been equated with and called a chimpanzee-like gait (Li et al., 1996; Crompton et al., 1998; Wang et al., 2003; Foster et al., 2013). BHBK walking in humans results in a nearly flat CoM trajectory (Wang et al., 2003; Ortega and Farley, 2005; Gordon et al., 2009), suggesting that the CoM trajectory in chimpanzee bipedal walking is also flat. In such a gait, mechanical energy cannot be recovered through exchanges between kinetic and potential energies. On the other hand, force-plate studies of chimpanzee bipedal walking by Kimura (1996) and Kimura and Yaguramaki (2009) have found mechanical energy recoveries to vary widely, with an average exchange of ∼30%, and maximum values >60%. Although these values are lower than the mean and maximum reported for human walking (e.g., Cavagna et al., 1976), they nevertheless require a CoM path with fluctuations in height. Kimura (1996) concluded that in many cases “chimpanzees move their centre of gravity essentially in the same way as do humans.” However, he also speculated that the low energy recoveries in many strides indicate CoM trajectories that are more similar to those of monkeys, whose knees collapse into flexion during single support, thereby reducing CoM vertical fluctuations (Yamazaki et al., 1979, 1985; Hirasaki et al., 2004; Ogihara et al, 2007, 2010; see also Demes, 2011).
Most kinematic evidence strongly suggests that the CoM does fluctuate in height in chimpanzees. Jenkins (1972) pointed out, on the basis of cineradiographic recordings of two chimpanzee subjects, that the pelvis is highest in single support and lowest in double support, providing indirect evidence for vertical oscillations of the CoM similar to those in humans. He also recognized differences of pelvic movement during the single support phase, with the pelvis being elevated on the swing side in the chimpanzees, but depressed in humans. This swing side elevation may further enhance vertical CoM fluctuations. Yamazaki et al. (1979), based on computer modeling of bipedal gait, concluded that the CoM in chimpanzees moves in sinusoidal waves, with the peak CoM position occurring during the single support phase. Tardieu et al. (1993) attempted to quantify the CoM trajectory of a bipedally walking chimpanzee using a volumetric segmental model in combination with synchrophotographic images. They found that the CoM vertical displacements were slightly higher relative to stature in the chimpanzee than in a human, but with no regular periodicity.
Controversy also exists over the amount of side-to-side movements of the CoM during chimpanzee bipedal walking. Elftman (1944) provided the first detailed, but qualitative, kinematic description of a bipedally walking chimpanzee, emphasizing the broad track width and distinct trunk rotation and lateral sway. Jenkins (1972) characterized the lateral and rotational movements of the pelvis as pronounced and concluded that the CoM undergoes relatively larger lateral displacements in chimpanzees than in humans in order to maintain balance during single stance. Indeed, the notion of chimpanzees walking bipedally by “lurching from side to side” has become the textbook description of chimpanzee bipedalism (Fleagle, 2013). A number of researchers have also pointed out the large mediolateral forces during chimpanzee bipedal walking that likely produce large lateral displacements of the CoM away from midline (Kimura et al., 1985; Li et al., 1996; Pontzer et al., 2014). Large mediolateral CoM motions may be expected to increase the mechanical work performed in order to maintain steady locomotion. However, several studies have shown that in bipedally walking (“waddling”) birds the mediolateral motions of the CoM contribute to energy recovery, rather than detracting from it (Griffin and Kram, 2000; Usherwood et al., 2008; Paxton et al., 2013). In contrast, Tardieu et al. (1993), in the only experimental attempt to directly quantify transverse CoM movements in a chimpanzee, portrayed the mediolateral CoM displacements as smaller than in humans, because arm movements counterbalance the transverse trunk movements.
- quantify the vertical and mediolateral CoM fluctuations in chimpanzee bipedal walking;
- quantify exchanges between kinetic and potential energies;
- explore how vertical and mediolateral CoM displacements influence energy exchanges;
- quantify the work on the CoM and the mechanical cost of transport incurred by raising the CoM and accelerating it forward.
The results will be compared with similar published data on human normal and BHBK walking and with the facultative bipedal gaits of other primates. Finally, the relevance of these results for reconstructing early hominin gaits will be discussed.
METHODS
Animal subjects
Three subadult chimpanzees (Pan troglodytes) participated in this study. All procedures were approved by Stony Brook University's Institutional Animal Care and Use Committee. Data were collected over a period of 1½ years: Subject H (5.0–6.5 years, 20–31 kg), Subject L (5.5–6.5 years, 21–28 kg), and Subject C (6.0 years, 36 kg). The first two subjects contributed data during five recording sessions each, whereas data collection from Subject C was restricted to two recording sessions 1 week apart. Subjects contributed approximately the same number of bipedal strides to the sample (n = 26, 27, and 28, respectively). Chimpanzees mature faster than humans, and it is reasonable to assume that by age 5–6 years they have a mature gait; human children at that same chronological age already walk with adult-like gait parameters (Sutherland, 1997). At the time of first data collection, all three subjects had undergone daily training performing multiple locomotor modalities and were well accustomed to bipedal locomotion.
Kinematic and kinetic data collection and processing
Ground reaction forces were collected for complete strides using four BP400600 force plates (AMTI, Watertown, MA) integrated into the center of a wooden runway with a width of 1.2 m and a length of 11 m. Kinematic data were acquired using four digital cameras. A calibration fixture was filmed prior to trials to allow reconstruction of the 3-D positions of skin markers on the animals as they walked through the calibrated space that was centered over the force plates. Kinematic data and force data were acquired and synchronized using ProCapture software and processed in ProAnalyst (Xcitex, Wolburn, MA). Forces were recorded at 1,500 Hz, and videos at 150 Hz.
Kinematic data were extracted to obtain speed and to determine the beginning and end of strides (touchdown to touchdown of the same limb) as well as relative stance duration or duty factor. Prior to each data collection, nontoxic white paint was applied on the shaved skin overlying palpable bony landmarks. For speed, a marker over either the ischial tuberosity or the anterior superior iliac spine was digitized at the beginning and end of a stride, and average speed was calculated as the fore-aft distance covered by one of these pelvic markers in the stride divided by stride time. Two additional points were digitized at midstance: a marker over the greater trochanter for hip height, and crown height, the highest point on the vault of the head, for stature. Touchdowns were identified on videos as the first frame of the foot making contact with a force plate and verified using the synchronized force records.
Force recordings were exported from ProAnalyst and analyzed using a custom-written MatLab (The MathWorks, Natick, MA) script and processed in the following way: Vertical, fore-aft, and mediolateral forces were filtered using a fourth-order, low-pass Butterworth filter with a cut-off frequency of 75 Hz. Voltages were transformed to Newtons using calibration factors for the force plates, and then force traces from the four plates were summed and truncated to strides. All variables derived from the substrate reaction forces are listed in Table 1. Vertical and mediolateral displacements of the CoM were calculated over time, and the maximum displacements determined in both directions. Displacements are graphed as individual strides with subject averages overlaid. Stride durations were normalized to 0%–100% of the stride cycle and CoM displacements down-sampled to a constant number (1,001 points) for all strides. Maximum displacements are reported as absolute values as well as relative to stature (crown height at midstance).
| Average forward velocity (m s−1) |
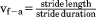 |
| Duty factor |
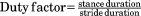 |
| Hip height (m) | h = vertical distance of greater trochanter to runway |
| Froude number |
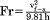 |
| Dimensionless velocity |
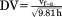 |
| Kinetic energy (J) |
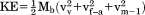 |
| Potential energy (J) |
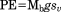 |
| Energy recovery |
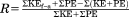 |
| PE/KE congruity (%) |
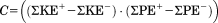 |
| PE/KE amplitude ratio |
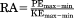 |
| CoM positive work (J) |
 |
| CoM positive power (W) |
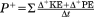 |
| Mechanical Cost of transport (J kg−1 m−1) |
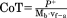 |
- Mb = body mass (kg); CoM = center of mass; sv and sm-l = CoM fluctuation amplitudes in the vertical and mediolateral directions; vv, vf-a, and vm-l = CoM velocities in the vertical, fore-aft, and mediolateral directions.
In order to evaluate whether strides were at or close to steady-state speeds, we calculated change in speed as the net horizontal impulse and divided it by body weight (Farley and Ko, 1997). Strides with a change in speed greater than 20% of average speed were excluded from further analyses, resulting in an average change in speed across the final sample (n = 81) of 6.9% ± 5.1%. Froude numbers were then calculated for each stride with hip height at midstance as the characteristic length (Alexander and Jayes, 1983). Dimensionless velocity was used for comparison of variables across animals and speeds and was calculated as the square root of the Froude number.
CoM mechanics were calculated from the ground reaction forces for complete strides following Cavagna et al. (1977). For kinetic and potential energy calculations it was assumed that the vertical and mediolateral CoM velocities average to zero over a stride, and that the fore-aft velocity is equal to the average forward speed. The pendulum-like nature of the strides was evaluated as percent energy exchange or recovery over a stride. Recovery was calculated using the total kinetic energy in three directions and then again, using only the vertical and fore/aft kinetic energies. Comparison of these two values allowed an evaluation of the contributions of mediolateral movements to the energy recovery rates. We also evaluated the energy recoveries in their relation to the congruity of the kinetic and potential energy fluctuations (Ahn et al., 2004) and in their relation to the amplitude ratio of the fluctuations (Vereecke et al., 2006). Recovery rates should be highest if the energies fluctuate out of phase (low congruity) and if their amplitude is similar (amplitude ratio ≈ 1; Table 1).
CoM external mechanical work per stride was calculated as the sum of all positive incremental changes in kinetic and potential energies (Cavagna et al., 1977). This calculation does not account for the internal work of moving body parts relative to the CoM, which can constitute up to 50% of the total mechanical work of human walking (Willems et al., 1995). We also calculated, but do not report, negative mechanical work, which is almost identical to the positive work (10.97 ± 4.17 J and −10.95 ± 4.19 J, respectively, across the entire sample)—as it should be in level walking on inelastic substrates with minimal energy dissipation in the environment (Kuo, 2007). Positive power was calculated as the rate at which positive work was performed on the CoM. The CoM positive power represents the “mechanical cost of locomotion” as it reflects the minimal mechanical energy generated per unit time to move the CoM. “Mechanical cost of transport” is the CoM positive work per unit mass and unit distance, and is calculated as the CoM power divided by the average forward speed and body mass (Table 1). Positive work calculations were also performed for the vertical, fore-aft, and mediolateral directions separately by adding the positive increments of the respective energy curves. These calculations included the kinetic energies by direction, and, additionally, the potential energy for the vertical direction. Finally, CoM work and power were also evaluated per kg body mass to account for differences in body mass between subjects and within subjects over the data collection period.
Statistical methods
Descriptive statistics (mean, standard deviation, and range) are reported for all variables and all animals combined, as well as for the individual animals. All variables were tested for normal distribution using the Kolmogorov–Smirnov statistics (n > 50) or the Shapiro–Wilk statistic (n < 50). Significance of correlations of variables with dimensionless speed was tested using either the parametric Pearson's product–moment correlation coefficient for normally distributed variables, or Spearman's ρ for variables that were not normally distributed. Pairwise comparisons of variables were conducted using Wilcoxon signed rank-sum tests (maximal vertical versus maximal mediolateral displacements of CoM, recoveries with and without mediolateral kinetic energy taken into account). Coefficients of variation were calculated to evaluate the variation in vertical and mediolateral CoM fluctuations, and a Fligner–Killeen test for equal coefficients was performed in the software package Past 3.02a (Hammer et al., 2001). Analysis of covariances with speed as covariate and Bonferroni post hoc tests were used to test for differences among animals in size-adjusted variables (work per kg, power per kg, and cost of transport). Analysis of variances was used for variables that were not significantly correlated with speed. Significance level for tests was P < 0.05, and tests were two-tailed. Statistical analyses other than the Fligner–Killeen test were executed in SPSS 20 (IBM, Chicago, IL).
RESULTS
Descriptive statistics for all variables across the entire sample are presented in Table 2, and for individual animals in Supporting Information Table S1. All bipedal strides are walking strides by kinematic definition (DF > 0.5). The average speed of 1.02 m s−1 is slower than the speed that corresponds to a Froude number of 0.5 (1.36 m s−1), at which humans and many animals tend to switch to a running, trotting, or cantering gait (Alexander and Jayes, 1983; Kram et al., 1997; O'Neill and Schmitt, 2012). For three strides, Froude numbers are above 0.5; however, these strides were retained in the analysis because of a lack of any apparent gait transition (see below; maximum Froude number = 0.58, maximum speed = 1.46 m s−1; Table 2).
| Variable | Mean | SD | Range |
|---|---|---|---|
| Speed (m s−1) | 1.02 | 0.17 | 0.56–1.46 |
| Duty factor | 0.65 | 0.04 | 0.60–0.77 |
| Hip height at midstance (m) | 0.38 | 0.02 | 0.34–0.41 |
| Crown height at midstance (m) | 0.89 | 0.03 | 0.81–0.95 |
| Froude number | 0.29 | 0.09 | 0.09–0.58 |
| Dimensionless velocity | 0.53 | 0.09 | 0.30–0.76 |
| Velocity at Froude of 0.5 (m s−1) | 1.36 | 0.04 | 1.29–1.41 |
| Recovery (%) | 15.37 | 10.00 | 2.00–45.49 |
| Recovery w/o m-l kinetic energy (%) | 18.48 | 9.60 | 4.33–47.39 |
| Congruity (%) | 54.66 | 5.34 | 43.98–66.23 |
| Positive work (J) | 10.97 | 4.17 | 2.50–21.76 |
| Work vertical (%) | 50.60 | 8.52 | 33.03–67.27 |
| Work fore-aft (%) | 39.08 | 8.61 | 17.04–54.89 |
| Work mediolateral (%) | 10.31 | 4.32 | 1.79–24.32 |
| Positive power (W) | 15.00 | 5.50 | 5.68–36.31 |
| Positive work per kg (J kg−1) | 0.40 | 0.13 | 0.12–0.72 |
| Positive power per kg (W kg−1) | 0.56 | 0.18 | 0.27–0.98 |
| Mechanical CoT (J kg−1 m−1) | 0.55 | 0.18 | 0.28–1.04 |
| Vertical CoM displacement (cm) | 2.32 | 0.94 | 0.75–4.66 |
| M-L CoM displacement (cm) | 3.48 | 1.07 | 0.42–5.90 |
| Relative vertical displacement (%) | 2.61 | 1.07 | 0.84–5.44 |
| Relative m-l displacement (%) | 3.91 | 1.18 | 0.49–6.72 |
| PE/KE amplitude ratio | 1.53 | 0.71 | 0.48–3.54 |
- Sample size for all variables: 81 strides across three subjects. See Table 1 for definitions of variables.
The CoM fluctuates in height as well as from side to side over a stride. The maximal mediolateral displacements were significantly higher than the vertical displacements (Z-score = −6.47, P < 0.001). The path of the CoM describes an approximately sinusoidal wave in the sagittal plane, with two maxima in the single support periods and two minima during double support periods (Fig. 1a). The magnitude of the CoM elevation was often not equivalent between each of the two steps of a stride. One animal, in particular (Subject C, dotted line in Fig. 1a), has a clear asymmetry with the CoM elevated much more during right side stance. This animal also moved with a sideways rotated trunk, with the right side in the lead. Oblique positioning of the trunk has also been observed in bipedally walking bonobos (D'Août et al., 2004). The mediolateral path of the CoM indicates a weight shift toward the support limb during single support. The deflections are very regular and symmetrical to either side (Fig. 1b). The frequency of the mediolateral motion is one-half the frequency of the vertical motion (Fig. 1a). The maximal magnitudes of the vertical fluctuations are more variable than those of the mediolateral fluctuations (CVs = 40.52 and 30.37, respectively; significantly different at P = 0.03). Maximal vertical and mediolateral displacements decrease with increasing dimensionless speed, but only the decrease in the mediolateral displacements is significant (Table 3).
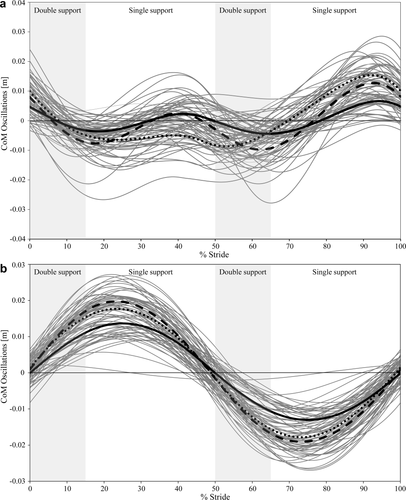
Vertical (a) and mediolateral (b) fluctuations of the CoM for complete strides. The bold lines are the mean values for the three animals. Animal H = dashed line, Animal L = solid line, and Animal C = dotted line. Stride duration is standardized to uniform length. The shaded and unshaded areas represent the average double support and single support phases, respectively.
| Variable | N | Pearson's r | Spearman's ρ | P |
|---|---|---|---|---|
| Max vertical displacements (cm) | 81 | −0.153 | 0.172 | |
| Max m-l displacements (cm) | 81 | −0.516 | <0.001 | |
| % recovery all | 81 | −0.319 | 0.004 | |
| Animal H | 26 | −0.091 | 0.657 | |
| Animal L | 27 | −0.418 | 0.030 | |
| Animal C | 28 | −0.508 | 0.006 | |
| Positive work all (J) | 81 | 0.285 | 0.010 | |
| Animal H | 26 | 0.681 | <0.001 | |
| Animal L | 27 | 0.298 | 0.131 | |
| Animal C | 28 | 0.751 | <0.001 | |
| Positive power all (W) | 81 | 0.436 | <0.001 | |
| Animal H | 26 | 0.743 | <0.001 | |
| Animal L | 27 | 0.459 | 0.016 | |
| Animal C | 28 | 0.722 | <0.001 | |
| Positive work per kg all (J kg−1) | 81 | 0.216 | 0.054 | |
| Animal H | 26 | 0.642 | <0.001 | |
| Animal L | 27 | 0.315 | 0.110 | |
| Animal C | 28 | 0.736 | <0.001 | |
| Positive power per kg all (W kg−1) | 81 | 0.353 | 0.001 | |
| Animal H | 26 | 0.619 | 0.001 | |
| Animal L | 27 | 0.612 | 0.001 | |
| Animal C | 28 | 0.744 | <0.001 | |
| CoT (J kg−1 m−1) | 81 | −0.145 | 0.196 | |
| Animal H | 26 | −0.209 | 0.306 | |
| Animal L | 27 | 0.278 | 0.160 | |
| Animal C | 28 | 0.643 | <0.001 |
- Significant correlations are in bold. See Table 1 for definition of variables.
When vertical and mediolateral displacements were combined to form path diagrams of the CoM in the coronal plane, it became apparent that these pathways are highly irregular. Some take up the shape of a “lazy 8” (Fig. 2), similar to that in humans walking at slow speeds (Fischer, 1899; Inman et al., 1981; Orendurff et al., 2004). However, unlike in humans, this shape is not confined to slow speeds, but can occur throughout the speed range. More often, the coronal pathways take the shape of a sweeping loop (Fig. 2). The U-shaped path that is found in fast walking humans and indicates that the maxima of both vertical and mediolateral fluctuations occur at the same time (Fischer, 1899; Inman et al., 1981; Orendurff et al., 2004) was not observed in any trials.
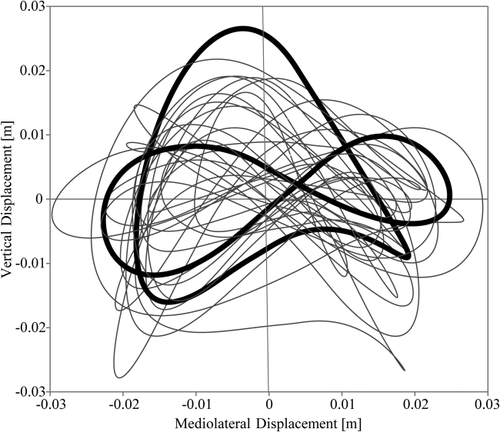
Frontal plane CoM trajectories of Animal H showing either the “lazy 8” shape that characterizes human CoM movements at slow walking speeds or a sweeping loop of variable shapes. Examples of these shapes are highlighted in bold.
Energy exchanges and recoveries are low, with an average of 15.37%, but highly variable across speeds and between chimpanzees (Fig. 3a; Table 2; Supporting Information Table S1). The highest recoveries occur at an intermediate speed, but low recoveries also happen at that speed. At slow and fast walking speeds, only low to moderate recoveries are found. Recovery rates are moderately, but significantly (Z = −7.37; P < 0.01), higher when calculated without taking the mediolateral kinetic energy into account (open symbols in Fig. 3a); i.e., the mediolateral movements reduce the energy exchanges. Although there are only a few strides at or above the speed at which a gait change is expected (Fr ≥ 0.5; Alexander and Jayes, 1983; vertical line in Fig. 3a), there is no indication of a change in gait mechanics for which an abrupt drop in recoveries would be indicative.
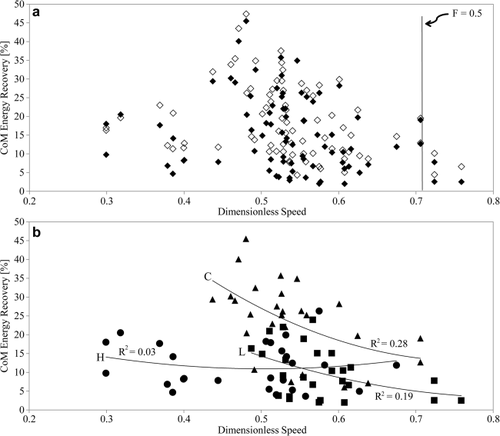
CoM mechanical energy recoveries as a function of dimensionless speed (a). Open symbols are recoveries calculated without taking the mediolateral kinetic energy into account. The vertical line indicates the dimensionless speed that corresponds to a Froude number of 0.5 at which humans and many animals tend to switch to nonpendular gaits. (b) Mechanical energy recoveries for individual animals. The trend lines are second-order polynomials. Animal H = circles, Animal L = squares, and Animal C = triangles.
Part of the variation in mechanical energy recovery is due to interindividual differences, with one animal achieving higher recovery rates than the other two (Animal C, triangles in Fig. 3b). Linear correlations of recovery rates with dimensionless speed are weak (Table 3). There is a significant decline in recovery rates in the combined sample, and a significant decline also for two animals individually; the third one walked with equally low recovery rates throughout the speed range (Animal H, circles in Fig. 3b; Table 3). The other two subjects are represented by strides in the medium to high walking speed range only. Curvilinear fits result in only marginally higher correlations (Fig. 3b). The lack of a denser speed sampling, particularly at lower speeds, does not allow us to conclusively address whether recovery rates peak at an intermediate speed.
As expected, energy recoveries decline with increasing congruity (Fig. 4a; Spearman's ρ = −0.402, P < 0.01). However, this relationship holds up only for Animal C individually (Pearson's r = −0.450, P = 0.02). Recovery rates are not significantly influenced by the amplitude ratio of the potential and kinetic energy fluctuations (Fig. 4b; Spearman's ρ = 0.131, P = 0.25), and this is also the case for the three animals individually.
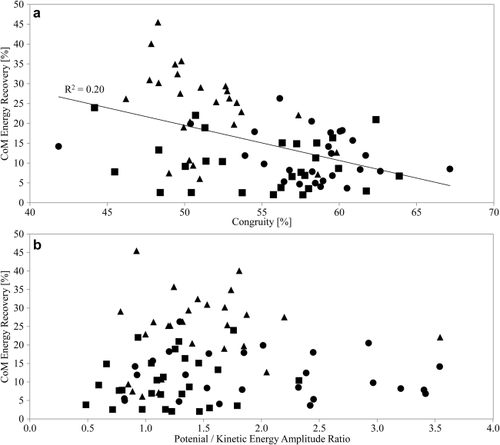
(a) CoM mechanical energy recoveries as a function of congruity. Energy recovery is significantly correlated with congruity, but the phase relationship explains only 20% of the variation in recovery. The trend line is a least-squares regression line. (b) CoM mechanical energy recoveries as a function of the PE/KE amplitude ratio. The relationship is not significant. Note that at the optimal ratio of one, both high and low recoveries are achieved. Animal H = circles, Animal L = squares, and Animal C = triangles.
CoM positive work and positive power were on average 10.97 ± 4.17 J and 15.00 ± 5.50 W per stride, respectively, with a peak power output of up to 36.31 W (Table 2). As with energy recoveries, both are highly variable, but they increase significantly with dimensionless speed in the combined sample as well as for animals individually, except for work in Animal L (Table 3). Work and power standardized per unit body mass display similar relationships with dimensionless speed, with the exception of work per kg across animals, which is borderline significant (Table 3 and Fig. 5a,b). The mechanical cost of transport is 0.55 ± 0.18 J kg−1 m−1 on average. This standardized work rate is unrelated to speed across the combined sample as well as for two animals individually (Fig. 5c and Table 3). For Subject C, cost of transport increases with speed (triangles in Fig. 3c). Animal H with the low energy recoveries throughout its speed range has the highest work and power per unit body mass as well as the highest cost of transport (circles in Figs. 3b and 5c, Supporting Information Table S1). Post hoc comparisons in analysis of covariances with speed as a covariate (or analysis of variances for CoT) reveal that the differences between this animal and the other two are significant at P < 0.01, whereas Subjects L and C do not differ in these variables.
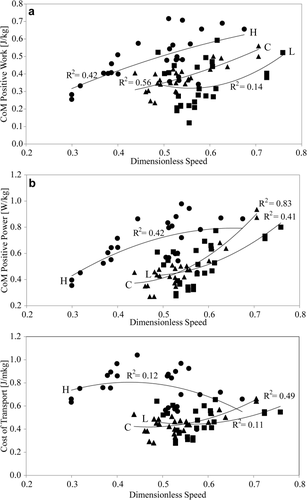
CoM positive work (a), power (b), and mechanical cost of transport (c) as a function of dimensionless speed. Animal H = circles, Animal L = squares, and Animal C = triangles. The trend lines are second-order polynomials. The R2 values for the curvilinear polynomial fits are only marginally higher than those for linear fits.
When the work on the CoM is broken down by direction, about 50% of it is for lifting the CoM, 40% for accelerating it in the fore-aft direction and 10% in the lateral direction (Table 2).
DISCUSSION
This study, for the first time, directly quantifies the vertical and mediolateral trajectories of the CoM in bipedally walking chimpanzees. In addition, it presents CoM energy exchanges and novel data on the mechanical work to lift and accelerate the CoM and the mechanical cost of transport.
Center of mass oscillations
The magnitudes of vertical and mediolateral CoM oscillations can be compared with those published by Orendurff et al. (2004) for human walking at a range of speeds (Table 4). These authors provide stature information, thus allowing comparison of relative fluctuations. Though their data on CoM oscillations are based on segmental kinematic, rather than ground reaction forces, it has been demonstrated that segmental CoM analysis is in good agreement with force plate-derived data (Gard et al., 2004; Gordon et al., 2009). Furthermore, CoM displacements at various speeds published by other authors are comparable with those of Orendurff et al. (Fischer, 1899; Saunders et al., 1953; Inman et al., 1981; MacKinnon and Winter, 1993; Tardieu et al., 1993; Kerrigan et al., 1995).
| Vertical CoM displacement (cm) | M-L CoM displacement (cm) | Average speed (m s−1) | Staturea (m) | Relative vertical displacement | Relative m-l displacement | |
|---|---|---|---|---|---|---|
| Chimpanzee | 2.32 ± 0.94 | 3.48 ± 1.07 | 1.02b | 0.89 ± 0.34 (0.80–0.95) | 2.61 ± 1.07 (0.85–5.44) | 3.91 ± 1.18 (0.49–6.72) |
| Humanc | 4.83 ± 1.03 | 3.29 ± 1.29 | 1.60b | 1.76 (1.68–1.85) | 2.74 (2.87–2.61) | 1.87 (1.96–1.78) |
| Humanc | 4.06 ± 0.72 | 4.41 ± 1.23 | 1.20 | 1.76 (1.68–1.85) | 2.31 (2.42–2.19) | 2.50 (2.62–2.38) |
- Values are mean ± standard deviation, and ranges (when available).
- a Stature for the chimpanzee sample is crown height at midstance, for the comparative human sample body height.
- b Self-selected speed.
- c Human data are from Orendurff et al., 2004, for two different walking speeds.
The mediolateral oscillations of the CoM for chimpanzee bipedal walking are similar in absolute magnitude to those of humans walking at a self-selected speed whereas the vertical oscillations are lower (Orendurff et al., 2004). Relative to stature, however, mediolateral oscillations are almost twice as high, whereas the vertical deflections are comparable in magnitude (Table 4). Both the relative vertical and mediolateral displacements are higher in chimpanzees when compared with humans walking at a slower speed of 1.2 m s−1 (Table 4). In humans and in chimpanzees the mediolateral CoM oscillations decrease with increasing speed, whereas the vertical oscillations are independent from speed in chimpanzees, but increase in humans (Table 3; Ortega and Farley, 2005).
Our data on mediolateral CoM oscillations support interpretations based on kinematic observations that the CoM in chimpanzee bipedal locomotion goes through considerable side-to-side excursions (Elftman, 1944; Jenkins, 1972). These shifts are most likely related to the lack of a bicondylar angle, resulting in a wide walking base. In order to balance the CoM over a laterally placed foot during the single support period, the CoM needs to shift toward the supporting foot. The lateral shift of the CoM in chimpanzees is augmented by abduction of the stance-side hip, causing the pelvis and trunk to list (rise) toward the stance limb (Elftman, 1944, Jenkins, 1972). The CoM mediolateral movements do not support the characterization of chimpanzee bipedal walking as similar to “tight-rope walking,” where compensatory arm movements mitigate the side sway of the trunk, therefore resulting in overall small lateral oscillations of the CoM (Tardieu et al., 1993). Note that the small mediolateral oscillations reported by these authors were estimated, rather than measured, because they were unsuccessful in differentiating between CoM lateral movements and lateral deviations of their chimpanzee subject's direction of movement.
Humans, on the other hand, possess a valgus knee angle and have a narrow walking base. The CoM oscillates between the medial borders of the supporting feet, rather than over the supporting foot, and the resultant small coronal plane moment is balanced by the hip abductors (MacKinnon and Winter, 1993; Knutson and Soderberg, 1995; Perry and Burnfield, 2010).
The sagittal trajectory of the chimpanzee CoM is similar to that of humans in that it follows two roughly sinusoidal oscillations per stride, with peaks during the single support period and troughs during double support (Fig. 1a). The CoM sagittal trajectory supports the notion that chimpanzees vault over the lower limb in a pendulum-like fashion during single support, even though the limb is flexed, and not extended as in humans. Kinematic data on knee flexion angle for the same three animals indeed show that the knee is highly flexed and that the flexion angle changes minimally during single support (O'Neill et al., in review). This is also the case in the two-dimensional kinematic data set of bipedally walking chimpanzees by (Fig. 6 of Pontzer et al., 2014) at the higher walking speed of 1.34 m s−1. The knee is maximally flexed during double support, when the CoM is at its deepest point. The rise of the CoM during single support is augmented by the list of the pelvis toward the supporting limb, a pattern that is opposite to pelvic list during human walking, where there is a slight drop on the swing side early during single limb support (Jenkins, 1972; Perry and Burnfield, 2010). The chimpanzee gait in this particular respect is similar to Trendelenburg gait in which patients with weakened hip abductors shift their weight over the support limb (Perry and Burnfield, 2010).
The vertical oscillations of the CoM clearly support the notion that chimpanzee bipedalism is a pendular gait, with the CoM fluctuating in height and reaching its maximum height during single support. The vertical force with only one peak during a stride in chimpanzees (Kimura et al., 1985; Pontzer et al., 2014) supports a simple inverted pendulum model (Roberts and Azizi, 2011). The double-peaked vertical force pattern in human walking results from the muscle actions that control hip drop early in the single support period and generate ankle push off late in single support which changes the effective length of the inverted pendulum (Gard and Childress, 1997; Kerrigan et al., 2000; Geyer et al., 2006).
The vertical oscillations of the CoM in chimpanzee bipedalism are distinctly different from those of humans walking with a BHBK gait, during which the CoM trajectory is essentially flat (Wang et al., 2003; Ortega and Farley, 2005; Gordon et al., 2009). A study by Foster et al. (2013) additionally reveals substantial differences in sagittal plane hip joint mechanics between human BHBK walking and chimpanzee bipedal walking. Based on these findings, the comparison of chimpanzee bipedal gait with the BHBK gait of humans with the CoM moving on a more or less flat trajectory is not warranted.
The highly irregular coronal paths of the CoM (Fig. 2) indicate that fluctuations in height and from side to side are not perfectly in-phase. The peak mediolateral CoM excursion regularly occurs at midsupport, whereas the peak vertical excursion is often after the mediolateral peak (Fig. 1a,b).
Limited data on CoM excursions of other nonhuman primates walking bipedally are available for comparison. The changes in height of the CoM over a stride in bipedally walking macaques are similar to those in the chimpanzees, with maximum height attained during the single support period (Fig. 8b of Ogihara et al., 2010). However, it is worth noting that the CoM path in that study was reconstructed from a musculoskeletal model, with potential energy profiles extrapolated from measured ground forces. Ground reaction force-derived vertical fluctuations of the CoM for bipedal macaques show a somewhat different pattern. Maximum height is around the start of the double support period (Ogihara et al., 2007). Kinematic tracking of the greater trochanter, a landmark used to track vertical CoM motion in humans (Gard et al., 2004), is suggestive of a drop in height during single support in bipedally walking capuchin monkeys (Demes, 2011). A minimum of CoM height during single support has also been reported for bipedally walking gibbons, based on measured ground forces (Fig. 3 of Vereecke et al., 2006). In this respect, CoM vertical oscillations of macaques and chimpanzees resemble those in human walking, whereas the vertical oscillations of gibbons and capuchin monkeys resemble those in human running.
Center of mass energy exchanges, work, and mechanical cost of transport
The muscular work to lift and accelerate the CoM constitutes a significant portion of total muscle work in human walking (Neptune et al., 2004). Although the chimpanzee CoM vertical fluctuations are comparable in relative magnitude with those in human bipedalism, exchanges between potential and kinetic mechanical energies are lower on average than in humans, are highly variable, and are not tightly correlated with speed. The lack of a tight correlation of recovery rates with congruity and overall low congruities indicate that the phasic relationships between kinetic and potential energy are poor. Although chimpanzees walk with vertical oscillations of the CoM comparable with those of humans (see above), they do not take advantage, to the same degree as humans do, of the energy exchanges and recoveries that these oscillations predispose for.
A comparison of recovery rates for primate bipedal walking is presented in Table 5. Our data are in good agreement with those previously published for adult and juvenile chimpanzees (Kimura, 1996; Kimura and Yaguramaki, 2009). These authors found a similarly large range in recoveries rates. A 3-D kinematics-based CoM analysis of macaque bipedalism found highly variable recovery rates (Ogihara et al., 2010), and so did the ground reaction force-based studies of gibbon and capuchin monkey bipedalism (Vereecke et al., 2006; Demes and O'Neill, 2013). It is reasonable to assume that the variable recovery rates are associated with variation in gait kinematics of animals that are not habitual bipeds. The resulting low average recovery rates are also lower than recoveries for quadrupedal gaits in those species in which both gaits have been measured at comparable speeds (capuchin monkeys: Demes and O'Neill, 2013; chimpanzees: unpublished data). The recovery rates of chimpanzee bipedal walking overlap widely with the low recoveries for human BHBK walking (Table 5). However, the underlying CoM mechanics are very different (see below).
| Mean (%) | Range (%) | Speed (m s−1) | |
|---|---|---|---|
| Chimpanzeea | 15 | 2–45 | 1.02 ± 0.17 (0.56–1.46) |
| Chimpanzee adultb | 24 | 15–35 | |
| Chimpanzee 0–8 yearsb | 10–31 | ||
| Macaquec | 5–62 | 0.83–1.39 | |
| Capuchin monkeyd | 2–17 | 1.13 ± 0.15 (0.86–1.43) | |
| Gibbone | 17 | ∼ 10–60 | |
| Humanf | ∼ 65 | ∼1.6 | |
| Humang | 63 | 60–63 | 0.7–1.8 |
| Human BHBKg | 21–41 | 0.7–1.8 |
- BHBK = bent hip, bent knee walking.
- (∼) indicates values extracted from figures.
- a This study.
- b Kimura and Yaguramaki, 2009.
- c Ogihara et al., 2010.
- d Demes and O'Neill, 2013.
- e Vereecke et al., 2006.
- f Cavagna et al., 1976.
- g Ortega and Farley, 2005.
The side-to-side movements of the CoM in chimpanzee bipedal walking are pronounced, but they are not passive. Mechanical energy recoveries including the mediolateral accelerations are significantly lower than those calculated without them (Fig. 3a); i.e., the lateral kinetic energy is not effectively converted into potential energy and vice versa. The pronounced frontal plane movements of chimpanzees require work on the CoM. When calculated separately, the work on the CoM in the mediolateral plane is about 10% of the total positive work (Table 2). The mediolateral CoM work component is much lower in human walking: for healthy children aged 10 years, it is less than 1% of the total work (van den Hecke et al., 2007). Donelan et al. (2001) have shown that in humans walking with greater step width and concomitantly greater mediolateral CoM movements and ground reaction forces recovery rates did not change much. However, the mechanical work at the step transition as well as the metabolic cost increased by 45% in comparison with walking at the preferred step width. It remains to be demonstrated whether the greater mechanical work associated with pronounced mediolateral CoM movements affects the metabolic costs of chimpanzee bipedalism.
Because of relatively high vertical and mediolateral oscillation amplitudes and the poor phasic coordination of energy fluctuations, the mechanical work required to lift and accelerate the CoM in chimpanzee bipedal locomotion is high. Correspondingly, so is the mechanical cost of transport and the work performed per unit body mass and unit distance. The mechanical cost of transport is about twice as high as that of human bipedal walking, but it is lower than that of the bipedal gaits of gibbons and capuchin monkeys (Table 6). The BHBK gait of humans is comparable in its mechanical cost of transport with normal human walking. The flat CoM trajectory in BHBK walking reduces the mechanical work required to lift the CoM, but it increases the costs to accelerate the CoM because energy exchanges are suppressed (Ortega and Farley, 2005). The metabolic cost of BHBK walking, on the other hand, is higher in comparison with normal walking (Carey and Crompton, 2005; Ortega and Farley, 2005; Gordon et al., 2009), probably due to increased force and work of muscles at the lower limb joints (Gordon et al., 2009; Foster et al., 2013). In chimpanzees, on the other hand, the CoM fluctuates in height and allows energy exchanges in bipedal walking, albeit not very effectively. Because of these differences in gait mechanics, comparisons of metabolic costs of chimpanzee bipedalism and human BHBK walking must not be undertaken with the expectation of equivalency of the two.
Unlike in human walking, recovery rates, work, power, and mechanical cost of transport of chimpanzee bipedalism are not tightly correlated with walking speed. Although there is a significant decline of recovery rates and an incline of work, power, and CoT in the higher speed range, our data are inconclusive as to whether recovery is highest and work and power lowest at an intermediate speed as it is in human walking (Fig. 5).
CONCLUSIONS
Our results demonstrate that chimpanzee bipedalism is not a smooth, flat-trajectory gait. The CoM does oscillate in height, reaching maximal height during the single support period. While the knees are flexed, the flexion angle does not change much during single support (Pontzer et al., 2014; O'Neill et al., in review), offering a somewhat rigid strut over which the CoM may vault, with additional changes in its height brought about by pelvic list toward the support side (Jenkins, 1972; O'Neill et al., in review). The CoM also oscillates mediolaterally, and the relative magnitude of these oscillations exceeds that of human walking. Energy recoveries in chimpanzee bipedal walking are low on average and highly variable, because the amplitudes of potential and kinetic energy fluctuations are dissimilar, the phasic relationship between the two is poor, and movements in the coronal and sagittal planes are variable and poorly coordinated. Humans, on the other hand, walk with high recovery rates due to the more similar amplitudes of potential and kinetic energy fluctuations that also display a better phasic relationship, and small mediolateral movements.
Human BHBK gait has been repeatedly likened with chimpanzee habitual bipedal locomotion, and it has also been used to model the gait of early hominins, in particular Au. afarensis as represented by “Lucy” (e.g., Li et al., 1996; Crompton et al., 1998; Wang et al., 2003, 2004; Carey and Crompton, 2005; Sellers et al., 2005; Raichlen et al., 2010). The BHBK gait of humans is characterized by a flat CoM trajectory and is a smooth, nonpendular gait. Thus, human BHBK and chimpanzee bipedal walking result in quite distinct CoM mechanics. As such, our results indicate that human BHBK walking does not capture the underlying CoM mechanics of chimpanzee bipedalism, as has been implied in some studies (e.g., Li et al., 1996; Crompton et al., 1998; Wang et al., 2003, 2004; Carey and Crompton, 2005; Sellers et al., 2005). These studies conclude that a BHBK gait is mechanically ineffective, energetically inefficient and maladaptive. And, indeed, optimizations of legged locomotion never converge on smooth, flat-trajectory gaits (Srinivasan and Ruina, 2006). Thus, human walking with flexed lower limbs is a poor model for chimpanzee bipedalism; further, it may have more limited utility for testing hypotheses about early hominin gait than has previously been appreciated.
Our data on chimpanzee CoM oscillations during bipedal walking lead us to believe that early hominin bipeds may have utilized pendular mechanics. As both bracket taxa rely on this fundamental mechanism of walking, it is likely that the last common ancestor and its early descendants in the hominin lineage would have been capable of supporting and accelerating an oscillating CoM. Use of a flat-trajectory gait like the BHBK gait of humans is less parsimonious. As the last common ancestor was in all likelihood a facultative biped, its form of bipedalism probably resembled that of facultative primate bipeds, particularly the chimpanzee, more than it resembled modern human bipedalism. The advent of walking with small mediolateral oscillations of the CoM was likely coupled with the appearance of a bicondylar valgus angle.
ACKNOWLEDGMENTS
The authors thank Kristin Lasek for animal training, and Nicholas Holowka for assistance with the experiments, and two anonymous reviewers and the associate editor for helpful comments on a prior version of this article.




