Observer error, dental wear, and the inference of new world sundadonty
ABSTRACT
Dental morphology provides important information on human evolution and interpopulation relationships. Dental wear is one of the major limitations of morphological data analysis. Wear figures heavily in existing debates about patterns of New World dental variation with some scholars finding evidence for a more generalized dentition in early New World populations (Powell: Doctoral Dissertation, Texas A&M University, TX (1995)) and others questioning these findings based on the probable effects of dental wear on trait scores (Turner, The First Americans: the Pleistocene Colonization of the New World. San Francisco: California Academy of Sciences (2002) 123–158; Turner: Am J Phys Anthropol 130 (2006) 455–461; Turner and Scott, Handbook of paleoanthropology, Vol. III: Phylogeny of Hominids. New York: Springer (2007) 1901–1941). Here we evaluate these competing claims using data from the Early Archaic Windover sample. Results confirm the dental distinctiveness of Windover with respect to other Old World Asian (i.e., sinodont/sundadont) populations. However, comparison of our results to those of Powell (1995) also highlights significant interobserver error. Statistical analysis of matched wear and morphology scores suggests trait downgrading for some traits. Patterns of missing data present a more challenging (and potentially serious) problem. Use of Little's MCAR test for missing data mechanisms indicates a complex process of data collection in which incidental and opportunistic recording of both highly worn and unerupted teeth introduce a “missing not at random” mechanism into our dataset that biases dental trait frequencies. We conclude that patterns of missingness and formal research designs for “planned missingness” are needed to help mitigate this bias. Am J Phys Anthropol 156:349–362, 2015. © 2014 Wiley Periodicals, Inc.
This article presents a study of dental wear, interobserver error, and dental morphology within the context of the Peopling of the Americas literature. Dental morphology provides important information on human population history and structure and links bioanthropology and bioarchaeology with the broader historical evolutionary sciences. As with other classes of phenotypic data, dental morphology is affected by environmental and epigenetic effects during development, thus blurring the genetic signal to an unknown extent. These challenges are compounded by concerns with inter- and intraobserver error, sexual dimorphism, inter-trait correlation, and issues with data scale and methods of analysis (Scott and Turner, 1997). Archaeological samples exhibit variable preservation and advanced rates of tooth wear, which also complicate morphological data collection. Despite these challenges, the dentition has provided important insights into the human past at a number of different scales, from interspecies comparisons (e.g., Kimbel and Delezene, 2009; Bailey and Hublin, 2013; Irish et al., 2013) to global, continental, and regional human interactions (Scott and Turner 1997; Turner and Scott, 2007; Hanihara, 2008; Stojanowski et al., 2013a, 2013b). One of the more visible areas of engagement has been the role of dental morphology for inferring the history of human migrations into the New World, an insight first noted by Hrdlička (1920), later expanded by Dahlberg (1945, 1951, 1959, 1963) and Hanihara (1968) and fully developed as part of the tripartite model by Turner (1971, 1983a, 1983b, 1985a, 1985b, 1986a, 1986b, 1992, 1994; see also Greenberg et al., 1986; Turner and Scott, 2007; Scott and Turner, 2008).
Turner's work recognized a common dental complex among New World populations that he termed sinodonty, comprising eight key crown and root features present at higher frequencies in modern northern Asian populations and in all modern and ancient Native American populations (Turner, 1985b, 1990). According to Turner, sinodonty evolved from a more generalized dentition (sundadonty), present in Southeast Asian and Oceanic populations, prior to the initiation of migrations into the New World during the late Pleistocene. The sinodont/sundadont distinction is a key component of Turner's long-term contributions to the First Americans literature and its validity impacts reconstructions of the timing and source(s) of migration events that contributed to the peopling of the Americas. The sinodont/sundadont dichotomy continues to anchor research questions on population history throughout the Pacific Rim (e.g., Potter et al., 2011) and is particularly relevant for framing questions of population affinity among Asian populations (e.g., Lee and Zhang, 2013; Matsumura and Oxenham, 2014).
Nevertheless, the pan-sinodont model's utility for explaining patterns of dental variation in the New World has varied in recent years (Stojanowski et al., 2013a). One reason for this is that the sundadont dental pattern has been identified by some authors in the New World, including very early material from the Archaic and Paleoindian periods (e.g., Lahr, 1995; Lahr and Haydenblit, 1996; Powell and Rose, 1999; Chatters, 2000; Powell, 1995, 2005; Sutter, 1997, 2005, 2009). Powell's (1995, 2005) work, in particular, documented the extent to which the dichotomy failed to capture the full range of morphological variation in New World populations. Findings of nonsinodont dentitions suggest that revision of Turner's pan-sinodont model, and all that it implies, might be needed. However, Turner (2002, 2006; Turner and Scott, 2007) continued to defend the model, claiming that other researchers failed to consider the effects of dental wear on observed trait frequencies. According to Turner, samples with worn dentitions, if not screened carefully, will exhibit less complex (sundadont) morphologies because of the tendency for slightly worn teeth to be scored as lacking a trait instead of as missing data (trait downgrading). This phenomenon was recently explored by Burnett et al. (2013) although not in the context of the Peopling of the Americas debate. For a variety of historical and methodological reasons, the issue of whether New World populations exhibit sundadont dentitions or just highly worn and improperly scored sinodont dentitions remains unresolved. This uncertainty might explain the decreased visibility of dental morphology in recent syntheses of the First Americans literature (Mazières, 2011; Pitblado, 2011; Stojanowski et al., 2013a).
Here we contribute to this literature by examining the relationship between dental wear, interobserver error, and dental trait frequencies in the Windover Pond sample (Doran and Dickel, 1988a, 1988b; Doran, 2002a, 2002b). The Windover sample is ideal for this study for a number of reasons. It is well preserved, includes mostly articulated primary burials, and includes all age ranges and wear grades. Most teeth are in situ, which minimizes identification errors. Most importantly, both the senior author (CMS) and Powell (1995) recorded dental morphological data from the site, thus allowing an assessment of interobserver error. We note that Windover was identified by Powell (1995) as either an outlier with respect to other Asian or New World populations or as sundadont in morphology. Therefore, reconsideration of the data from this site provides an opportunity to assess the effects of dental wear on inferences of New World sundadonty.
The frequency data presented in Powell (1995) are an invaluable source of information on Middle Holocene North American populations. Our initial goal was to use those published trait frequencies as comparative data; however, very high rates of observed interobserver error for the Windover sample initiated our consideration of how these differences arose. Here, we characterize the way in which Powell's (1995) frequencies differ from those collected by CMS, focusing on total sample size, total number of positive expressions of a trait, and the resulting trait frequencies. We pair these data with tooth specific wear scores to explore the relationship between wear and morphology and between trait downgrading and patterns of missing data to determine if observer error accounts for the sundadont dental frequencies identified by Powell (1995). Specifically, if Turner's assessment of claims of New World sundadonty was correct (2002, 2006; Turner and Scott, 2007) this suggests Powell included data from more highly worn teeth, which increased his 0 cell counts (trait absent) and reduced sample trait frequencies. If this is true, then comparing our data to Powell's should reveal the following: 1) our sample sizes should be smaller than those of Powell, 2) our positive trait expression counts should be similar to those of Powell, and 3) our sample frequencies should be higher than those of Powell. While this study will not evaluate all claims of sundadont dentition in the New World, it does evaluate a component of Powell's research, which is among the most visible and often cited as exemplary of New World sundadonty. This article also highlights important issues with the treatment of dental morphological data with respect to wear-related effects and patterns of missing data. This aspect of the article has far reaching consequences for basic practices of biodistance research.
AGE AT DEATH, DENTAL WEAR, AND MORPHOLOGICAL TRAIT SCORING
It is widely recognized that crown mineralization as well as crown wear negatively impact scoring of dental morphology (Hrdlička 1921; Morris, 1970; Scott, 1973; Nichol and Turner, 1986; Turner, 1987; Turner et al., 1991; Wu and Turner, 1993; Powell, 1995; Haeussler, 1996; Burnett, 1998; Hawkey, 1998; Burnett et al., 2013). For example, the inclusion of very young individuals who have yet to develop features specific to the enamel (e.g., deflecting wrinkles of the lower molars) or root (multiple roots may manifest toward the apex only) may artificially increase the zero cell counts and deflate reported sample frequencies. In addition, the inclusion of individuals whose crown morphology has either been completely removed by dental wear (erroneously scored as trait absent) or for which the trait is still discernible but scored incorrectly due to the loss of area or volume will impact trait frequencies either through trait downgrading (as wear progresses there is a tendency to score a feature as lower grade) or through trait upgrading (as wear progresses there is a tendency to score a feature as higher grade) (Burnett, 1998; Burnett et al., 1998, 2013). The relationship between obliteration due to wear and trait downgrading is intuitive, as crown size decreases so do most occlusal surface features. Trait upgrading effects are less clear. For example, depending on the specific shape and configuration of cusps, moderate to heavy wear could lead to trait upgrading for hypoconulid presence and size in a particularly bunodont human molar. Although the effects of wear on dental trait scoring have long been recognized (Hrdlička, 1921; Morris, 1970; Scott, 1973; Nichol and Turner, 1986; Turner, 1987; Turner et al., 1991; Wu and Turner, 1993; Haeussler, 1996; Hawkey, 1998), Burnett et al. (1998, 2013) were among the first to consider the topic explicitly.
Burnett (1998) considered the relationship between wear and maxillary premolar accessory ridges (MxPAR), which are prone to early obliteration based on their presence on the occlusal surface and lack of underlying dentine signature. Despite caution used in data collection, Burnett (1998) found that even slightly worn teeth were less likely than unworn teeth to exhibit positive expressions of the trait, an example of trait downgrading. Burnett et al. (1998, 2013) expanded this study to include I1 shoveling, maxillary canine distal accessory ridge, M2 cusp number, and M2 hypocone, each scored by two observers. Both I1 shoveling and maxillary canine distal accessory ridge scores exhibited strong relationships with wear grade, also reflective of trait downgrading. M2 cusp number showed frequency declines as wear increased due to trait downgrading or nonrandomly missing data. Finally, M2 hypocone scoring results varied by observer, with one presenting no evidence for wear-related effects and the second observer's scores exhibiting evidence of trait upgrading and violations of missing data assumptions (see below). As these authors are careful to note, the effect of wear on trait scoring can only truly be studied using longitudinal data collected from the same individuals. Samples conducive to such study are exceedingly rare. For example, the Dahlberg collection, identified by Burnett et al. (2013) as having considerable potential, is no longer available for study.
One of the more important insights of Burnett's (1998; Burnett et al., 1998, 2013) research on wear effects is the potential bias introduced by patterns of missing data. Rubin (1976) is credited with formalizing the different ways in which data can be missing and outlining the problems associated with the mechanisms that produce different missing data patterns. These are: missing completely at random (MCAR), missing at random (MAR), and missing not at random (MNAR). For dental data, missing data are MCAR if the reason for missingness is unrelated to the value of the trait or any other variable included in the analysis. MAR differs from MCAR in that the probability of missing data for a trait is related to some other variable in the dataset (e.g., wear score) but not related to the value of the variable itself. Graham (2009) notes that MAR is more accurately described as conditionally missing at random, since after controlling for measured variables the remaining missingness is completely unsystematic. Finally, data are MNAR if the probability of missingness is related to the trait's value, which introduces considerable bias into a dataset. For example, if the likelihood that incisor shoveling data are missing is related to the severity of shoveling (i.e., observations of shoveling scores 1–3 are more likely to be missing than shoveling scores 4–6) then incisor shoveling data violate the MCAR assumption and the patterning of missing data are consistent with MNAR. The repercussions for violating the assumptions of MCAR/MAR have been discussed in a number of sources (Allison, 2002; Little and Rubin, 2002; Schafer and Graham, 2002; Graham, 2009; Baraldi and Enders, 2010; Enders, 2010), including those specific to the evolutionary sciences (Nakagawa and Freckleton, 2008; Brown et al., 2012). The three mechanisms are not mutually exclusive within datasets and should be treated as assumptions applied to specific analyses that may or may not be applicable depending on which variables are selected for analysis (Baraldi and Enders, 2010). We note that of the three mechanisms, only MCAR can be empirically tested because evaluating MAR and MNAR requires knowing the values of the missing data points.
EVALUATING WEAR EFFECTS: CURRENT APPROACHES
Wear effects are commonly recognized as a limitation of research design and are addressed at the data collection and preanalysis data treatment phases of research (Morris, 1970; Scott, 1973; Nichol and Turner, 1986; Turner, 1987; Turner et al., 1991; Wu and Turner, 1993; Powell, 1995; Haeussler, 1996; Hawkey, 1998). While often glossed as “age effects” we note that it is not age that causes issues with dental morphology scoring (unlike cranial nonmetric features that present challenges due to developmental and senescent changes in appearance) but tooth crown wear specifically. Therefore, it is more appropriate to evaluate wear effects using corresponding data on tooth wear and not proxy measures such as skeletally-derived age at death. During data collection, scores are not recorded for teeth worn beyond the point at which a specific feature is observable, which varies for each trait depending on its position on the crown or root. Occlusal surface features with no dentine analog (e.g., deflecting wrinkles) will wear very quickly, followed by features of the occlusal crown surface that have dentine analogs (e.g., most primary cusps, odontomes), then features of the vertical mid-crown or cingulum (e.g., protostylids or interruption grooves), and finally root traits. Although ad hoc guidelines are provided for certain traits (cf. Turner et al., 1991) and broad guidelines have been suggested for suites of traits (e.g., occlusal crown vs. root traits, see Hawkey (1998)), currently there are no best practices guidelines defining the range of scorability based on standards for recording development stage (e.g., Moorees et al., 1963) or wear grade (e.g., Scott, 1979; Smith, 1984). As such, residual wear effects are often still apparent in a data set. Correlation or regression approaches are typically used to identify residual wear effects on a univariate basis (i.e., significant positive or negative correlations). Wear-biased variables are then removed from subsequent analyses to minimize the impact of nongenetic variance on inferences of population history and structure. It is unclear if this approach is optimal given that some data unaffected by wear are being excluded.
Because our focus here is on the Windover site it is useful to review Powell's (1995) research protocol. We note that Powell follows standard procedures in the collection and preparation of the Archaic period data, including collecting dental wear scores following Smith (1984). He states that care was taken to avoid recording false observations related to wear but also notes, “it is possible that some residual age effects remained in the middle Holocene data” (Powell, 1995; p. 154). Powell does not report wear scores, nor does he eliminate morphological traits due to wear-related missing data. Instead he evaluates wear effects by using skeletal age at death as a proxy. He pools all the Holocene samples, dichotomizes the morphological data, and uses three age bins (young 0–15 years, middle 16–35 years, old 35+ years) in a stepwise logistic regression. Using this technique he identified 11 age regressive traits and a single age progressive trait. Two traits that demonstrated an age or sex effect (single rooted P3, 4 cusped M2) were particularly relevant to the analysis as they comprise part of Turner's (1990) sinodont complex. Although this approach to dealing with wear is relatively common it is not infallible and ignores potential MCAR/MAR violations. Dichotomized trait scores may lack sensitivity to wear effects, the use of only three age bins may mask underlying issues with the data, and the pooling of samples may mask site-specific correlations based in regional patterns of dental attrition.
MATERIALS AND METHODS
The focus of this article is the Windover Pond site, an Early Archaic period cemetery located in Brevard County, Florida. The sample consists of approximately 168 individuals with subadults comprising 52% of the sample. Ages ranged from neonate to advanced. The burials vary in preservation based on soil and hydrological conditions within the lake catchment but were generally well preserved, with some approaching the condition of modern prepared specimens (Stojanowski et al., 2002). The majority of burials were primary interments with limited commingling of graves. Almost all teeth were preserved in situ, thus minimizing data recording errors due to tooth misidentification. This was especially relevant for highly worn dentitions.
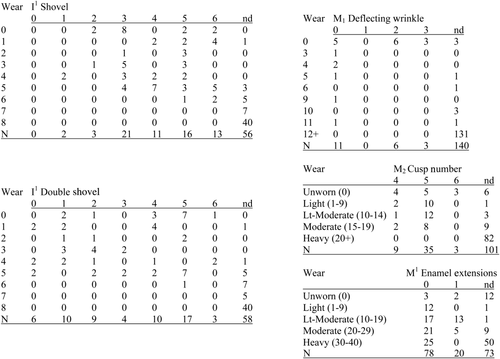
Data on 25 dental morphological traits were collected by CMS using the standards of the Arizona State University Dental Anthropology System (Turner et al., 1991) (Table 1). Several traits were recorded for all teeth within a tooth class, increasing the total number of variables to 42 (e.g., parastyles were scored for the M1, M2, and M3). Data were recorded under conditions of normal lighting and with the use of a standard hand lens for magnification. The scoring protocol was the same as that used by Powell (1995). The individual count method was used, and sides were collapsed using the highest degree of expression. Raw trait scores were dichotomized following Turner (1986, 1990) and Powell (1995) to ensure comparable frequency estimates. We present summary data on all 42 variables in Table 1, and then focus on five traits that are most relevant to the sinodont/sundadont dichotomy: I1 shoveling, I1 double shoveling, M1 deflecting wrinkle, M2 cusp number, and M1 enamel extensions. We do not discuss P3 root number and M1 root number for two reasons. First, CMS did not consistently score these traits because most teeth were in situ at the time of observation. Second, root traits are unlikely to be affected by wear and therefore contribute little to the present discussion. For this same reason we do not discuss data for M3 peg/reduced/absent, which both CMS and Powell record consistently (Table 2) and with very low frequencies that fall outside the range of sinodont populations.
| Trait (Breakpoint) | CMS | CMS | P-value | ||||||
|---|---|---|---|---|---|---|---|---|---|
| – | + | N | Freq | – | + | N | Freq | ||
| Winging I1 (1) | 7 | 11 | 18 | 0.61 | 49 | 11 | 60 | 0.18 | 0.001a |
| Labial Curve I1 (2–4) | 26 | 7 | 33 | 0.21 | 54 | 6 | 60 | 0.10 | 0.210 |
| Shovel I1 (3–6) | 3 | 36 | 39 | 0.92 | 6 | 54 | 60 | 0.90 | 1.000 |
| Shovel I2 (3–6) | 10 | 25 | 35 | 0.71 | 19 | 42 | 61 | 0.69 | 0.822 |
| Doub Shov I1 (2–6) | 9 | 27 | 36 | 0.75 | 8 | 47 | 55 | 0.85 | 0.178 |
| Doub Shov I2 (2–6) | 14 | 20 | 34 | 0.59 | 16 | 38 | 54 | 0.70 | 0.356 |
| Int Groove I1 (1) | 31 | 1 | 32 | 0.03 | 37 | 11 | 48 | 0.23 | 0.023a |
| Int Groove I2 (1) | 25 | 11 | 36 | 0.31 | 24 | 21 | 45 | 0.47 | 0.173 |
| TD I2 (1–6) | 30 | 6 | 36 | 0.17 | 19 | 30 | 49 | 0.61 | 0.000a |
| PM Cusps P1 (1) | 18 | 3 | 21 | 0.14 | 30 | 12 | 42 | 0.29 | 0.347 |
| Uto Azt P1 (1) | 30 | 1 | 31 | 0.03 | 43 | 5 | 48 | 0.10 | 0.395 |
| Metacone M2 (3–5) | 1 | 34 | 35 | 0.97 | 6 | 82 | 88 | 0.93 | 0.672 |
| Metacone M3 (3–5) | 2 | 18 | 20 | 0.90 | 22 | 52 | 74 | 0.70 | 0.088a |
| Hypocone M2 (2–5) | 6 | 27 | 33 | 0.82 | 4 | 82 | 86 | 0.95 | 0.027a |
| Hypocone M3 (2–5) | 8 | 12 | 20 | 0.60 | 11 | 65 | 76 | 0.86 | 0.023a |
| Cusp 5 M1 (1–5) | 24 | 8 | 32 | 0.25 | 33 | 25 | 58 | 0.43 | 0.112 |
| Cusp 5 M3 (1–5) | 18 | 2 | 20 | 0.10 | 48 | 13 | 61 | 0.21 | 0.336 |
| Carabelli M1 (2–7) | 32 | 15 | 47 | 0.32 | 17 | 34 | 51 | 0.67 | 0.001a |
| Parastyle M1 (1–5) | 48 | 2 | 50 | 0.04 | 55 | 27 | 82 | 0.33 | 0.000a |
| Parastyle M2 (1–5) | 46 | 0 | 46 | 0.00 | 65 | 13 | 78 | 0.17 | 0.002a |
| Parastyle M3 (1–5) | 34 | 0 | 34 | 0.00 | 59 | 6 | 65 | 0.09 | 0.091a |
| Enamel Ext M1 (1–3) | 43 | 13 | 56 | 0.23 | 31 | 41 | 72 | 0.57 | 0.000a |
| Enamel Ext M3 (1–3) | 31 | 13 | 44 | 0.30 | 22 | 40 | 62 | 0.65 | 0.001a |
| Peg/Red/Abs I2 (1) | 62 | 6 | 68 | 0.09 | 74 | 4 | 78 | 0.05 | 0.515 |
| Peg/Red/Abs M3 (1) | 59 | 11 | 70 | 0.16 | 74 | 0 | 74 | 0.00 | 0.000a |
| Shovel I1 (1–6) | 1 | 31 | 32 | 0.97 | 49 | 17 | 66 | 0.26 | 0.000a |
| Ling Cusps P2 (2–9) | 25 | 2 | 27 | 0.07 | 19 | 26 | 45 | 0.58 | 0.000a |
| Groove M1 (Y) | 3 | 27 | 30 | 0.90 | 18 | 37 | 55 | 0.67 | 0.033a |
| Cusp # M2 (5–6) | 22 | 6 | 28 | 0.21 | 63 | 10 | 73 | 0.14 | 0.351 |
| Cusp # M3 (5–6) | 17 | 0 | 17 | 0.00 | 14 | 54 | 68 | 0.79 | 0.000a |
| D Wrinkle M1 (1–3) | 6 | 5 | 11 | 0.45 | 10 | 26 | 36 | 0.72 | 0.148 |
| Protostylid M1 (1–7) | 24 | 8 | 32 | 0.25 | 13 | 52 | 65 | 0.80 | 0.000a |
| Protostylid M2 (1–7) | 17 | 9 | 26 | 0.35 | 14 | 39 | 53 | 0.74 | 0.001a |
| Protostylid M3 (1–7) | 12 | 6 | 18 | 0.33 | 17 | 42 | 59 | 0.71 | 0.006a |
| Cusp 5 M2 (2–5) | 7 | 14 | 21 | 0.67 | 8 | 44 | 52 | 0.85 | 0.112 |
| Cusp 5 M3 (2–5) | 1 | 12 | 13 | 0.92 | 11 | 49 | 60 | 0.82 | 0.680 |
| Cusp 6 M1 (1–5) | 24 | 9 | 33 | 0.27 | 29 | 26 | 55 | 0.47 | 0.075a |
| Cusp 6 M2 (1–5) | 24 | 2 | 26 | 0.08 | 32 | 19 | 51 | 0.37 | 0.006a |
| Cusp 6 M3 (1–5) | 12 | 2 | 14 | 0.14 | 35 | 20 | 55 | 0.36 | 0.198 |
| Enamel Ext M1 (1–3) | 33 | 18 | 51 | 0.35 | 14 | 57 | 71 | 0.80 | 0.000a |
| Enamel Ext M2 (1–3) | 25 | 23 | 48 | 0.48 | 12 | 68 | 80 | 0.85 | 0.000a |
| Enamel Ext M3 (1–3) | 28 | 14 | 42 | 0.33 | 21 | 45 | 66 | 0.68 | 0.001a |
- Break points after Powell (1995).
- a P ≤ 0.10.
| UI1 | UI1 | UM1 | UM3 | LM1 | LM2 | |
|---|---|---|---|---|---|---|
| Shovel | Doub shovel | Enam exta | Peg/agenesis | Def wrinkle | Cusp no. | |
| Sundadont weighted mean | 31.60 | 20.35 | 52.16 | 18.16 | 31.24 | 30.68 |
| Sinodont weighted mean | 70.28 | 46.31 | 74.86 | 28.95 | 49.40 | 11.55 |
| Abs (difference) | 38.68 | 25.95 | 22.70 | 10.80 | 18.17 | 19.14 |
| Sundadont mean | 30.82 | 22.72 | 47.90 | 16.33 | 29.54 | 30.74 |
| Sinodont mean | 71.08 | 55.80 | 72.80 | 32.38 | 45.53 | 15.50 |
| Abs (difference) | 40.27 | 33.08 | 24.90 | 16.05 | 15.99 | 15.24 |
| Powell (1995) | 90.0 | 85.5 | 56.9 | 0.0 | 72.2 | 13.7 |
| This study | 92.3 | 75.0 | 23.2 | 4.3 | 45.5 | 23.1 |
| Difference | −2.3 | 10.5 | 33.7 | −4.3 | 26.7 | −9.4 |
- Note: Weighted Means are weighted by reported sample size for each population in Turner (1990). Abs(Difference) is the absolute value of the difference between sinodont and sundadont mean frequencies.
- a Turner's published sinodont and sundadont frequencies for M1 enamel extensions (1990:304, Table 9) were calculated using a break point of 2+ (Turner, 1990; Table 4), although he indicates that “grade 1” was used (Turner, 1990). To compare our data with those of both Powell (1995) and Turner we recalculated Turner's frequencies using 1+ as a breakpoint (Turner, 1990; Table 4).
In addition to dental morphological traits a complete dental inventory was recorded using the standards set forth in Buikstra and Ubelaker (1994). Tooth presence was indicated using an 8-point scale, tooth development was scored following Moorees et al. (1963), and caries, calculus and abscesses were noted as per Buikstra and Ubelaker (1994). Wear was scored for each tooth using the Smith (1984) system for anterior dentition and the Scott (1979) system for molars. Anterior teeth scores ranged from 0 to 8 and molar tooth scores ranged from 0 to 40 with each quadrant receiving a score between 0 and 10.
We follow the approach of Burnett et al. (2013) in using exploratory data analysis and limited inferential statistics. For the five “sinodont” traits we document: 1) the maximum wear score for which any morphological data is recorded, and 2) the maximum wear score for which a positive expression is recorded. We also generate frequency tables of wear score by trait grade to evaluate the pattern of wear in relationship to the grade of trait expression. ANOVAs are used to test for differences in average trait score among wear grades using the raw, nondichotomized data. For these analyses, wear score categories were defined as follows. For I1 shoveling and double shoveling, three bins were used: light (0–1), moderate (2–3), heavy (4+). For M1 deflecting wrinkle, wear scores were divided into an unworn (0) and worn category (1–11). For M2 cusp number four categories were used: unworn, light wear (scored 1–9), light to moderate wear (scored 10–14), and moderate wear (scored 15–19). And for M1 enamel extensions five categories were used: unworn (scored 0), light wear (scored 1–9), light to moderate wear (scored 10–19), moderate wear (scored 20–29), and heavy wear (scored 30–40). To complement the ANOVAs we also used Fisher's Exact tests for 2 × 2 tables. Trait scores were dichotomized using the break points from Powell (1995) (see Table 1), and wear scores were dichotomized to maximize the difference between light and heavy wear as follows: I1 shoveling and double shoveling, light (0–1) versus heavy (4+); M1 deflecting wrinkle, light (0) versus heavy (1–11), M2 cusp number, light (0–9) versus heavy (10–19), and M1 enamel extension, light (0–19) versus heavy (20–40). The Fisher's Exact tests are most comparable to the approach of Burnett et al. (2013).
In addition, we use Little's (1998) MCAR test to evaluate the assumption that patterns of missing morphological data are independent of trait expression (i.e., ASUDAS score) and wear score. This test approximates a t-test for which wear score is the dependent variable and the two groups are defined as morphology score “missing” or “observed.” Because using the full range of wear grades produces a trivial test (i.e., incisors with a wear score of 8 have no crown so it is trivial to test whether shoveling score presence is independent of wear), we truncate the data set at the highest wear grade for which any morphological trait was recorded. For example, I1 shoveling was recorded as high as a wear score of 6. If the MCAR/MAR assumption is not violated within the truncated data set then missing data cells should be randomly distributed among wear grades of 6 and lower and not clustered toward either end of the distribution. Therefore, this truncated data set provides an independent test of missingness that complements the exploratory analysis of trait grades and wear. We then sequentially reduce the wear grade (for I1 shoveling we repeat the test for wear scores of 5 or less, then 4 or less, etc.) until an insignificant MCAR test P-value is achieved. This approach provides guidance on the relationship between wear, missing data patterns, and morphology in a way that can inform preanalysis data treatments. However, we stress that the effects of missing data will differ from sample to sample and among researchers, and as such the results we present should not be overextrapolated as indicative of a universal condition of the morphological scoring system for these traits. All statistical tests were performed using Systat v. 11.
RESULTS
Summary data for the complete list of 42 traits are presented in Table 1. Of these, half exhibited statistically significant trait frequency differences between observers. This is well beyond random expectation and reflects a significant observer error effect. We had predicted that a wear-based effect on reported trait frequencies would manifest in the following ways: 1) Powell's sample sizes would be larger than those of CMS, 2) raw counts of positive trait expression would be similar to those of CMS, and 3) Powell's sample frequencies would be lower than those of CMS. The third point would suggest that trait downgrading is occurring and biasing sample frequencies lower and into the sundadont range, as suggested by Turner (2002, 2006; Turner and Scott, 2007).
Results are mixed and indicate a much more complicated picture of interobserver error. First, Powell's reported sample sizes are larger for all 42 variables. Second, there was a moderate, positive correlation between both observers' counts of positive expressions of each trait (r = 0.647, P = 0.0001); however, there were notable exceptions to this overall trend (see Table 1) and the linearity in the data masks considerable differences in raw numbers. Third, Powell's frequencies are not uniformly lower than those of CMS. In fact, they were significantly higher than those of CMS for 18 of 21 traits that exhibited statistically significant differences. Although the stark differences speak poorly for using pooled samples collected by multiple observers, the specific patterning is contrary to Turner's suggestion that dental wear was causing the shift toward sundadont trait frequencies in the middle Holocene samples (including Windover).
Despite the stark differences in trait scores presented in Table 1, data collected by CMS and Powell (1995) produce consistent patterns of differentiation. We used mean trait scores for six key sinodont variables (I1 shoveling and double shoveling, M1 deflecting wrinkle, M1 enamel extension, M2 cusp number, and M3 reduced/agenesis) reported by Turner (1990) and combined them with comparable data from Windover as reported by Powell (1995) and CMS (Tables 1 and 2). PCA returned two eigenvectors with eigenvalues greater than one and the bivariate output of factor scores (Fig. 1) confirms that both Powell and CMS report data that falls outside of the two standard deviation range for the sinodont and sundadont samples. This confirms that both Powell and CMS recorded data that indicate Windover is an outlier with respect to Old World comparative populations. As such, more careful consideration of our data can speak to the broader issue of the relationship between dental wear and the inference of sinodonty or sundadonty. We present a trait-by-trait analysis below that focuses on how recording differences arise and relate to tooth wear and patterns of missing data.
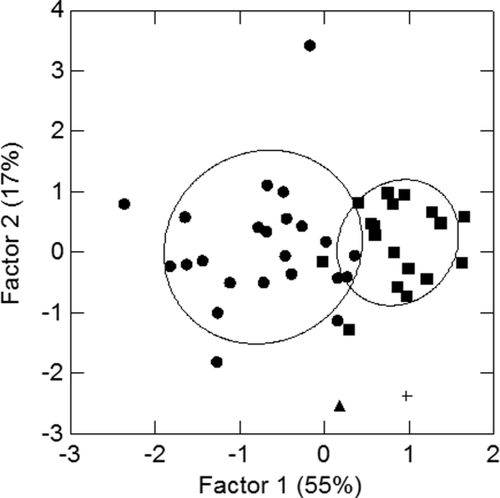
Bivariate plot of two factor scores extracted from PCA of sample means for sinodont (square) and sundadont (circle) populations reported in Turner (1990). Two standard deviation ellipses are drawn around the group means. The plus sign represents the Windover trait scores from Powell (1995) and the triangle represents the Windover trait scores from CMS. Note, the outlier in the top of plot is the Ainu 1 and 2 sample from Turner (1990).
Interobserver error
I1 shoveling and double shoveling are genetically linked expressions of the ectodysplasin A receptor gene (e.g., Kimura et al., 2009; Park et al., 2012). Sinodont populations exhibit significantly higher frequencies than sundadonts for both traits (Turner, 1990). The difference in the average frequency is large (∼39%) and there is little overlap among individual samples with respect to trait frequencies (see Table 2). Powell and CMS both record shoveling data for Windover that is on the extreme high end of the sinodont range of variation and do not contribute to the inference of New World sundadonty (contra Turner's suggestion regarding wear) but do contribute to the dental distinctiveness of Windover with respect to other Old and New World populations. That both Powell and CMS record similarly high frequencies suggests the result is robust to interobserver error. Differences in sample size reported in Table 1, however, do suggest an observer error effect. The added sample size reported by Powell may indicate that he scored more heavily worn teeth than CMS. A second explanation is that Powell's sample frequencies (1995, Table 7.1) report both sides rather than an individual count.1
The M1 deflecting wrinkle is the most susceptible trait to obliteration very early in the wear sequence (Turner, 1987; Turner et al., 1991). It is also a mass additive trait whose scoring is defined in terms of area and volume. As such it is highly susceptible to trait downgrading. According to Turner (1990) sundadonts have significantly lower frequencies of expression; however, the separation between sinodont and sundadont categories is not large (∼18%). Data recorded by CMS is within the range for sinodont populations, while the very high frequency noted by Powell (1995) is at the extreme high end of the sinodont range (Table 1). The differences between observers are not statistically significant (Table 1). The extreme values reported by Powell contribute to the inference that middle Holocene North American populations are neither sinodont nor sundadont but represent a third distinct phenotype (Powell, 1995, 2005). Data in Table 1 indicate that Powell reported five times as many positive expressions of the trait and three times the total number of observations as compared to CMS. We are unable to account for the 26 deflecting wrinkles he documents, especially considering that scoring more heavily worn teeth would increase the zero cell counts and deflate the sample frequency (the opposite of what is observed). As with shoveling and double shoveling, we suspect a tabulation error may be evident2.
Data for the frequency of 4-cusped M2s produces another complex pattern of interobserver error. Sundadonts have a significantly higher frequency of 4-cusped M2s (Turner, 1990), but there is little divergence between the sinodont and sundadont categories (∼19%). Powell's (1995) reported frequency falls within the range for sinodonts, while our reported frequency is higher and midway between the sinodont and sundadont means (Table 1). The differences between observers are not statistically significant (Table 1). As with the previous three traits, there is little evidence in either data set in support of Turner's assertion about the effects of wear downgrading on inferences of sundadonty. Nonetheless, despite the insignificant differences noted there are large variances in the data reported by Powell and CMS, which we suggest reflects a tabulation error in Powell (1995, Table 7.1) and the inclusion of more worn teeth in the total sample size.3
For M1 enamel extensions Turner (1990) reported significantly lower frequencies for sundadont populations; however, there is limited divergence between the sinodont and sundadont categories (∼19%). Powell's data are within the sinodont range and there is little support for Turner's hypothesis about trait downgrading and the appearance of sundadonty. Interestingly, data collected by CMS are within the sundadont range, and this is the only trait for which Powell and CMS differ significantly enough to change the allocation category (Table 1). Enamel extensions are unlikely to be affected by dental wear except at very advanced stages (composite scores of 35+) and we suspect data collected by CMS significantly under-report enamel extensions. The highest wear score for which a positive expression is recorded in our data is 22, about halfway into the wear sequence and well before the trait should be unobservable. Given this we suggest our low frequency of expression is attributable to under-reporting of positive trait expressions due to an overly conservative data collection protocol.
Dental wear and dental morphology
Although the previous section presented little evidence in support of a trait downgrading effect in Powell's data, there was considerable interobserver error with respect to total sample sizes recorded, the number of positive expressions recorded, and the resulting trait frequency. Trait downgrading resulting from scoring worn dentitions is a concern in studies of dental morphology generally (see Burnett et al., 2013), but it does not seem to account for the observation that middle Holocene samples are outliers with respect to the sinodont/sundadont framework. However, comparing Powell's frequencies to those recorded by CMS suggests a different wear effect is evident and implicates potential problems with missing data patterns. As with the preceding section we focus on I1 shoveling and double shoveling, M1 enamel extensions, M1 deflecting wrinkle, and M2 cusp number.
Burnett et al. (2013) provided data on dental wear and I1 shoveling for the Semna South collection of Nubian material. These authors documented a significant difference in trait frequencies across wear scores, noting that shoveling was not scored for any tooth with wear greater than Stage 4. There was a significant downgrading effect in their data. Comparable data on I1 shoveling and double shoveling from Windover Pond collected by CMS are presented in Table 3 and Figure 2. We discuss shoveling first. Data are reported up through wear Grades 5 and 6 for the right and left side, respectively, which is relatively far into the wear sequence and farther than that reported by Burnett et al. (Fig. 3). Contrary to the results of Burnett et al. (2013), there is no evidence for trait downgrading at Windover (see Fig. 2; ANOVA P-value = 0.67; Fisher's Exact Test P-value = 0.99). In fact, the opposite appears to be the case because the most highly worn teeth exhibit uniformly high degrees of shoveling, which suggests an MNAR mechanism is present in the dataset. Because shoveling was common and well developed at Windover, these data indicate highly worn teeth were only scored if the degree of shoveling was significant and affected the cingulum. Individuals with worn incisors that exhibited low grades of shoveling (who would otherwise be scored as low grades of expression or absent) were instead recorded as unobservable (i.e., missing data) because the incisal margin of the tooth was removed by dental wear. Therefore, there is a clear bias toward only scoring those teeth with higher grades of expression in these data (Fig. 2).
- Note: The nd column indicates the count of individuals with a recorded wear score but no recorded morphology score.
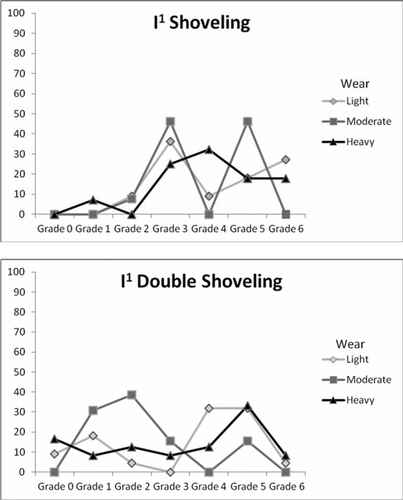
Percentage of each trait grade for different categories of wear. Each connected line should sum to 100%. For example, 50% of moderately worn incisors scored grade 3 shoveling and 50% of moderately worn incisors scored grade 5 shoveling, with all other grades being absent. Data are presented for I1 shoveling and double shoveling. To smooth the data wear scores were binned as follows: light (0–1), moderate (2–3), heavy (4+).
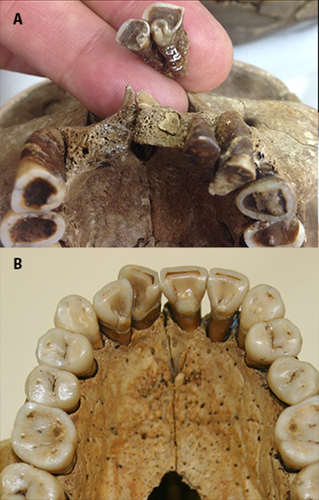
(A) Individual from Windover Pond, one of the only individuals to record an I1 shoveling score (shoveling = 6) with heavy wear (wear=6). Note how strongly developed the shoveling is near the cingulum and the shape of the exposed dentine that allows scoring of the trait. This tooth can be contrasted with (B) which is one of the lowest grades of shoveling recorded at Windover (shoveling = 3). Note the lack of cingulum involvement indicating that if this individual had a wear score of 6 the shoveling likely would be scored as missing data. Burial identifications: (A) Burial 154, (B) Burial 69A. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]
Little's MCAR statistic confirms this. Using all teeth with wear scores of 6 or less (6 is the maximum wear for which any tooth was scored for shoveling) returns a P-value of 0.003 indicating the data are not missing completely at random. Truncating the data to wear scores of 5 or less satisfies the MCAR assumption (P = 0.227). Interestingly, Burnett et al. (2013) documented a different relationship between wear and morphology because shoveling was relatively undeveloped in their study population. In this case patterns of missing data for incisor shoveling are related to the severity (i.e., value) of shoveling in the dataset, a clear example of an MNAR missing data mechanism (see also Burnett, 1998). Furthermore, the expectation of shoveling appears to affect whether more highly worn teeth are scored at all, and if so the evidence suggests they will only be scored for populations where shoveling is highly expressed.
The same basic pattern is observed for the double shoveling data (Table 3, Fig. 2). The trait was scored for individuals from Windover up through wear Grades 5 and 6 for the right and left sides, respectively. This is problematic given that double shoveling is generally expressed higher on the crown in comparison to shoveling (i.e., double shoveling does not involve the labial CEJ while shoveling can involve the cingulum at high grades of expression; but see Fig. 4). There is no evidence for systematic bias in the dataset (ANOVA P-value = 0.22; Fisher's Exact Test P-value = 0.99). As with shoveling there appears to be an MNAR mechanism in the dataset as indicated by the biased scores for individuals with wear Grade of 5 or 6, which show a tendency toward higher degrees of expression. Applying Little's test to the dataset with wear scores of 6 or less confirms this (P = 0.0001). Truncating the data to wear scores of 5 or less is still problematic (P = 0.020); however, scores of 4 or less satisfy the MCAR assumption (P = 0.502).
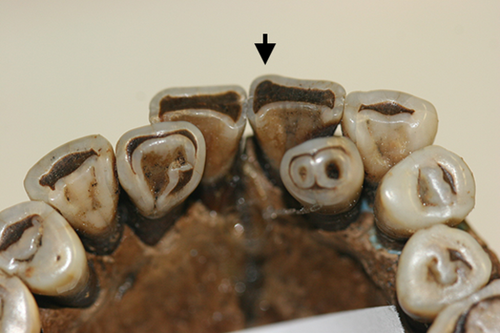
Individual from Windover Pond, one of the only individuals to record an I1 double shoveling score with heavy wear (wear = 5). Here the extent of double shoveling is evident by the shape of the exposed dentine, which demonstrates that only individuals with very strong double shoveling will be scored at this grade of wear. Burial identification: Burial 101. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]
Data for M1 deflecting wrinkle are very limited (Table 3, Fig. 5). The trait is obliterated early in life due to its position on the crown surface, and for this reason the overall sample size is quite small. The maximum wear score for which any morphological observation was recorded was only 11, roughly 25% into the wear sequence, reflecting blunted cusps that are not yet worn flat (Fig. 6). We noted earlier a very conservative pattern of data recording; however, consideration of even this small sample size suggests trait downgrading is apparent. For example, the only positive trait expressions are recorded for teeth that are completely unworn and unerupted (see Fig. 5) and there is a significant difference in trait scores among wear grades (Fisher's Exact Test P-value = 0.01; note there was no variation for the “worn” category so a t-test was not possible). For the five molars that exhibit any degree of wear deflecting wrinkle was scored as absent (lack of variation in the worn category precludes use of t-tests). Using all teeth with wear scores of 11 or less (P = 0.012) and 10 or less (P = 0.02) indicates an MNAR violation. However, using teeth with wear scores of 9 or less satisfies the MCAR assumption (see Table 4). Interestingly, using only unworn teeth results in a sample frequency of 64% (9 of 14), which is close to that reported by Powell (1995). However, we question the wisdom of including this trait in discussions of New World dental variation given how few molars actually can be scored and the clear tendency for trait downgrading to occur. For example, at Windover there were only 20 total M1s for which the trait could be scored and 140 M1s for which wear was observable but no deflecting wrinkle score was recorded (Table 3).
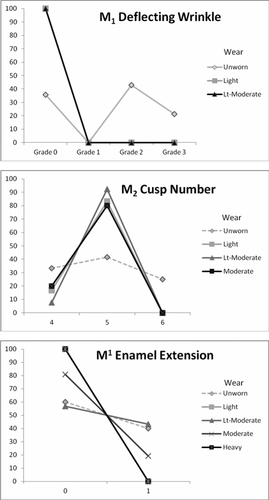
Percentage of each trait grade for different categories of wear. Each connected line should sum to 100%; see also Figure 2. Data are presented for three molar traits: M1 deflecting wrinkle, M2 cusp number, and M1 enamel extension. To smooth the data wear scores were binned as described in the text.
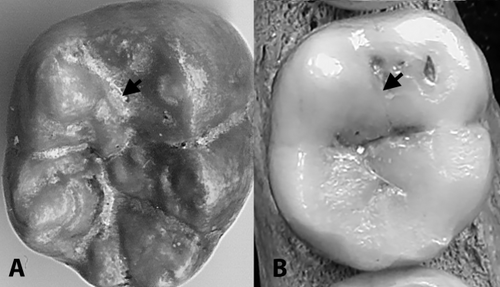
Two lower right first molars showing variation in the scoring of this trait. (A) Wear = 0 (unerupted), deflecting wrinkle = 3; (B) wear = 11, deflecting wrinkle not scored. This figure shows how any degree of wear can raise doubts about the scorability of this trait. Burial identifications: (A) Burial 51, (B) Burial 156.
| Wear score | M1 enamel extensions | M2 cusp number | M1 deflecting wrinkle |
|---|---|---|---|
| 40 | 0.0001 (98,73) | ||
| 39 | 0.0001 (97,64) | ||
| 38 | 0.0120 (97,63) | ||
| 37 | – | ||
| 36 | 0.0140 (95,57) | ||
| 35 | 0.2520 (92,45) | ||
| 34 | 0.5010 (92,42) | ||
| 33 | 0.9470 (88,36) | ||
| 32 | 0.8550 (87,35) | ||
| 31 | 0.0600 (77,25) | ||
| 30 | 0.0380 (75,24) | ||
| 29 | 0.0220 (73,23) | ||
| 28 | 0.0100 (72,22) | ||
| 27 | 0.0070 (69,21) | ||
| 26 | 0.0100 (67,21) | ||
| 25 | 0.0050 (65,20) | ||
| 24 | 0.0001 (64,18) | ||
| 23 | 0.0001 (62,16) | ||
| 22 | 0.0001 (61,16) | ||
| 21 | 0.0001 (57,16) | ||
| 20 | 0.0001 (52,14) | ||
| 19 | 0.0001 (47,14) | 0.279 (47,19) | |
| 18 | 0.0001 (42,14) | – | |
| 17 | 0.0001 (40,14) | 0.917 (45,15) | |
| 16 | 0.0001 (33,13) | 0.647 (42,15) | |
| 15 | 0.0001 (28,13) | 0.806 (39,12) | |
| 14 | 0.0001 (26,13) | 0.336 (37,10) | |
| 13 | 0.0001 (22,13) | 0.054 (34,8) | |
| 12 | 0.0001 (20,13) | 0.077 (32,8) | |
| 11 | 0.0001 (19,13) | 0.171 (28,8) | 0.017 (11,9) |
| 10 | 0.0001 (18,13) | 0.024 (26,7) | 0.013 (10,8) |
| 9 | – | – | 0.485 (10,5) |
| 8 | 0.0001 (17,13) | 0.020 (24,7) | – |
| 7 | – | 0.034 (23,7) | – |
| 6 | 0.0001 (15,13) | 0.050 (21,7) | 0.212 (9,5) |
| 5 | – | 0.064 (20,7) | 0.716 (9,4) |
| 4 | 0.0001 (11,13) | 0.085 (19,7) | 0.442 (8,3) |
| 3 | – | – | 0.649 (6,3) |
- Note: bold face indicates a significant P-value at the P = 0.05 level. Numbers in parentheses are the sample sizes for each test as follows: (number of observed morphology scores, number of missing data points).
Burnett et al. (2013) also considered M2 cusp number and identified a decline in the frequency of 5+ cusps with increasing wear, a pattern consistent with trait downgrading and/or MCAR/MAR violations. We document the opposite pattern here (the frequency of 5+ cusps increases in worn teeth); however, the wear-specific grade scores present a more complex and difficult to interpret overall pattern. Summary data are reported in Table 3 and Figure 5. We note that 6-cusped M2s are only found for wear scores of 0, which might suggest an MCAR/MAR violation or trait downgrading (Fig. 7). In fact, the unworn category has a very different data structure (more evenly divided among morphology scores) than any other wear grade categories (light, light-moderate, moderate, or heavy) for which the frequency of 5 cusped M2s dominate. This contrast between the distribution of scores for unworn and worn teeth supports an interpretation that dental wear is affecting the scoring of this trait for Windover Pond. However, ANOVA (P = 0.92) and Fisher's Exact Test (P = 0.46) P-values comparing morphology scores among wear grades were not significant, which might reflect the small samples sizes upon which these inferences are based.

Left and right second molars from the same individual at Windover Pond. This individual had one of the most worn dentitions for which M2 cusp number was scored. (A) left M2, wear = 19, 5-cusped. (B) Right M2, wear = 16, 5-cusped. Burial identification: Burial 109B. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]

Right M3 with well-developed enamel extension. Although this tooth is unworn it shows how wear might bias the scoring of this trait. For example, if this tooth was completely lacking a crown and part of the roots (wear = 40) one would still be able to score enamel extension data because the trait extends well down the roots. However, lower grade expressions might be obliterated by wear and scored as missing data. This shows how the value of a trait impacts its observability, a violation of the MCAR assumption. Burial identification: Burial 236. [Color figure can be viewed in the online issue, which is available at wileyonlinelibrary.com.]
Application of the MCAR test produces results different from those observed for the incisor traits and deflecting wrinkle. Using a wear score of 19 as the truncation point produces an insignificant P-value (P = 0.279), indicating the MCAR assumption is not violated for the complete data set. However, consideration of the pattern of MCAR test statistics in Table 4 suggests that unworn and unerupted teeth may also be affecting patterns of observability. Note that significant P-values are returned for wear scores of 10 or less, which is the point of truncation at which the number of unworn molars is greater than the number of worn molars in the sample. Observation of M2 cusp number may be impeded by teeth still in the crypt making it difficult to observe the distal portion of the tooth. It is unclear given this small sample how relevant this effect is compared to the likely influence of trait downgrading on observed frequencies.
Because of their position at the cervix of the tooth (Fig. 8), M1 enamel extensions provide data on a molar trait that is not expected to be affected by dental wear but may still suffer from MNAR mechanisms. We report summary data in Table 3 and Figure 5. These data are difficult to interpret and show considerable variation in frequencies of positive expression across wear bins; however, sample sizes are small for the “unworn” and “light wear” subsamples. In considering the “light-moderate,” “moderate,” and “heavy” wear subsamples there does appear to be a wear effect in the data. The subsample frequency and number of positive expressions decline sequentially as crown wear progresses (Fig. 5), a pattern that is statistically significant (ANOVA P-value = 0.001; Fisher's Exact Test P-value = 0.01). Sample sizes are roughly comparable and the difference in positive expressions counts is stark. Little's MCAR tests support this interpretation. Because we recorded data for enamel extensions throughout the full wear sequence (from 0 to 40) we used the full sample for the initial test. The P-value was significant (P = 0.0001). MCAR tests for truncation samples of wear scores of 38 or less (P = 0.012) and 36 or less (P = 0.014) were also statistically significant, which suggests that dental pathology (calculus accumulation) may be impacting the observability of this trait. However, as indicated in Table 4 missing data problems reemerge for truncation samples of wear scores of 30 or less, which also reflects an issue with the inclusion of unworn and unerupted teeth that dominate the sample. There is considerable missing data for enamel extensions; only 5 of 17 unworn, unerupted molars record a morphology score, two of these are positive expressions and the unworn subsample frequency is 40%. Although the dataset is small, this pattern suggests that CMS was more likely to score enamel extensions on unerupted teeth only if an enamel extension was visible, thereby unintentionally introducing an MNAR mechanism (and violation of the MCAR and MAR assumptions) into the dataset.
DISCUSSION AND CONCLUSIONS
In this article, we considered interobserver error, dental wear, and dental morphology within the context of debates about New World population history. We specifically evaluated competing claims about middle Holocene dental variation. In a series of articles, Powell (1995, 2005) noted that middle Holocene populations of North America do not conform to Turner's pan-sinodont model. Rather, eastern North American Archaic period populations presented dental trait frequencies that were either consistent with sundadont populations of the Old World, or were distinct enough from both sinodont and sundadont Old World samples to suggest a third grouping. Turner rebutted these claims on the grounds that Powell, and others who documented similar dental traits patterns in the New World (e.g., Lahr, 1995; Lahr and Haydenblit, 1995; Powell and Rose, 1999), failed to consider the effects of trait downgrading due to dental wear.
Here we considered interobserver error and the role of dental wear in generating scoring errors for the Windover sample using aggregate data reported in Powell (1995) and raw data collected by CMS. We focused on five of eight key traits that define the sinodont complex: I1 shoveling and double shoveling, M1 deflecting wrinkles, M2 cusp number, and M1 enamel extensions. These traits are located on different teeth within the arcade and on different locations on the crown and are, therefore, well suited for considering the effects of crown wear on trait frequencies. Three sinodont complex traits were omitted (P3 and M1 root number, M3 peg/reduce/absent) because they contribute little to the primary objective of the article - understanding the relationship between dental wear and morphology scores.
On the basis of our comparisons we conclude that there is little evidence that wear is affecting the inference of sundadonty for the Windover sample. Both Powell (1995, 2005) and CMS report sinodont or extreme sinodont frequencies for I1 shoveling, I1 double shoveling, and M1 deflecting wrinkle. Powell also reported sinodont frequencies for M1 enamel extension and M2 cusp number. The only traits for which Powell reported sundadont frequencies are M3 peg/reduced/absent and M1 root number; neither trait is likely to be affected by dental wear. The case for New World sundadonty, at least with respect to Windover Pond, is built ultimately on one trait, M1 root number. Therefore, Turner's wear-based explanation for the presence of sundadont dental frequencies in Archaic period populations of North America is not supported by our results.
Nevertheless, these analyses did reveal patterns that may suggest additional problems with the data. For example, some of Powell's (1995, 2005) results indicate that Archaic period populations formed a distinct subgrouping that was neither sinodont nor sundadont. This is the same pattern reproduced here (Fig. 1). Several traits considered in this article do show extreme sinodont values; however, we interpreted these values as resulting from counting variances in the data, a more confident approach to collecting data further into the wear sequence, and possible bias attributable to MCAR/MAR violations. The additional observations tabulated by Powell in comparison to CMS do not show evidence of trait downgrading because his frequencies were actually higher than those of CMS, which is contrary to expectations. Rather, a more complex process of observation protocol differences, dental wear effects, and tabulation variances was evident that seemed to vary on a trait-by-trait basis.
To explore this dynamic further, we used data collected by CMS to consider the relationship between trait and wear scores following the protocol of Burnett et al. (2013) and to consider evidence for missing data violations using Little's MCAR statistic. Results varied considerably by trait. I1shoveling and double shoveling demonstrated no downgrading effect but the dataset presented evidence for MCAR violations by including heavily worn teeth. M1 deflecting wrinkle was particularly problematic, returning a very small sample size, evidence of trait downgrading, and MCAR violations caused by the inclusion of worn molars. M2 cusp number demonstrated evidence for trait downgrading due to the inclusion of worn teeth and a possible MNAR missing data pattern resulting from the inclusion of unworn teeth. Finally, M1 enamel extensions were subject to a trifecta of bias effects. The data set exhibited evidence for trait downgrading and MCAR (and likely MAR) violations due to the inclusion of both heavily worn and unworn molars, this despite initial perceptions that a trait such as this would be relatively immune to wear effects.
Given these observations, we suggest that Turner (2002, 2006; Turner and Scott, 2007) was probably justified in his concern and skepticism about reports of nonsinodont morphology in middle Holocene Native American populations. However, this may not be due to trait downgrading but to other factors that impact patterns of missing data and, in particular, violations of the MCAR/MAR assumption. Nichol and Turner, (1986) first alluded to issues of trait observability in relation to wear and pathology. They note that knowing when to score (and when not to score) traits on teeth affected by wear and caries is “seemingly gained with experience” (Nichol and Turner, 1986; p. 312). Burnett et al. (Burnett, 1998; Burnett et al., 1998, 2013) were the first to draw attention to this problem in the dental morphology literature and it is a problem that deserves additional consideration in the future. Our data suggest MCAR violations can actually be more problematic than wear effects because they are difficult to identify and result from nonrandom inclusion and/or exclusion of teeth from both the heavily worn and unworn ends of the wear spectrum. For example, at Windover very high frequencies of incisor shoveling and double shoveling suggest that the sample is distinct from other New and Old World populations. However, in populations for which shoveling is well developed the effect of MCAR violations will bias the sample frequencies higher, which might explain the significantly higher trait frequencies for shoveling and double shoveling noted by Powell (1995, 2005) and reported in our dataset.
Although this article focuses specifically on traits relevant to the pan-sinodont model, it highlights issues of much broader significance to analysis of dental morphology. Researchers should consider a wider variety of issues related to missing data patterns; they should evaluate data for bias due to MCAR and MAR violations and use methods to mitigate that bias by removing it or incorporating it into analytical models. A singular approach to preanalysis data treatments ignores the ways in which dental anatomy interacts with the trait scoring process. Different traits likely need different standards for scorability beyond ad hoc suggestions based on chronological ages or coarse wear scores. This can be accomplished through a systematic study of morphology scores, patterns of missing data, and the relationship of both to dental wear, dental development, and dental pathology. In addition, research design requires a priori consideration of a sampling strategy that includes a protocol for “planned missingness” (Adèr, 2008). For frequency based approaches, maximum data recovery can be problematic at the limits of scorability unless a strict sampling frame is adopted.
ACKNOWLEDGMENTS
We thank Dr. Scott Burnett for engaging in productive discussions about the topic of dental wear, missing data, and dental morphology. We also thank Dr. Glen Doran for providing access to the Windover collection. Two anonymous reviewers also provided helpful commentary.