Gait-specific metabolic costs and preferred speeds in ring-tailed lemurs (Lemur catta), with implications for the scaling of locomotor costs
Abstract
Metabolic costs of resting and locomotion have been used to gain novel insights into the behavioral ecology and evolution of a wide range of primates; however, most previous studies have not considered gait-specific effects. Here, metabolic costs of ring-tailed lemurs (Lemur catta) walking, cantering and galloping are used to test for gait-specific effects and a potential correspondence between costs and preferred speeds. Metabolic costs, including the net cost of locomotion (COL) and net cost of transport (COT), change as a curvilinear function of walking speed and (at least provisionally) as a linear function of cantering and galloping speeds. The baseline quantity used to calculate net costs had a significant effect on the magnitude of speed-specific estimates of COL and COT, especially for walking. This is because non-locomotor metabolism constitutes a substantial fraction (41–61%, on average) of gross metabolic rate at slow speeds. The slope-based estimate of the COT was 5.26 J kg−1 m−1 for all gaits and speeds, while the gait-specific estimates differed between walking (0.5 m s−1: 6.69 J kg−1 m−1) and cantering/galloping (2.0 m s−1: 5.61 J kg−1 m−1). During laboratory-based overground locomotion, ring-tailed lemurs preferred to walk at ∼0.5 m s−1 and canter/gallop at ∼2.0 m s−1, with the preferred walking speed corresponding well to the COT minima. Compared with birds and other mammals, ring-tailed lemurs are relatively economical in walking, cantering, and galloping. These results support the view that energetic optima are an important movement criterion for locomotion in ring-tailed lemurs, and other terrestrial animals. Am J Phys Anthropol, 2012. © 2012 Wiley Periodicals, Inc.
Metabolic costs of resting and locomotion have been used to gain novel insights into the behavioral ecology and evolution of a wide range of primate species, including some fossil hominins (e.g., Altmann and Samuels,1992; Leonard and Robertson,1997; Steudel,2000; Pontzer et al.,2010). Locomotor costs have been of particular interest since they can reach 10–30 times higher (or more) than the cost of resting (Taylor et al.,1981; Hinds et al.,1993; Bishop,1999) or other non-locomotor activities (Coehl, 1976; Leonard and Robertson,1997). Such high costs could have a significant impact on daily energy expenditure and influence the decisions that primates must make about their foraging behavior.
Most previous studies of non-human primates have simply described locomotor costs as an increasing linear function of speed, and as a constant value per distance (Taylor and Rowntree,1973; Parsons and Taylor,1977; Mahoney,1980; Taylor et al.,1982). This relationship implies that there are no gait-specific effects on non-human primate costs per distance. That is, from the standpoint of locomotor costs, there is no reason to prefer one gait or speed to another. Yet it is well known that terrestrial mammals exhibit clear gait preferences and gait-specific preferred speeds in the wild (Pennycuick,1975; Kenagy and Hoyt,1989; Isbell et al., 1993) and in the laboratory (Hoyt and Taylor,1981; Perry et al.,1988; Wickler et al., 2000,2001; Watson et al., 2010). The reasons for these preferences may be complex, but one widely held view is that gait choice and gait-specific preferred speeds correspond to minima in locomotor cost per distance (Alexander,1989).
Experimental tests of this view have been limited in number, and no new locomotor cost data have been collected across speeds and gaits from non-human primates since the influential work of Taylor et al. (Taylor and Rowntree,1973; Parsons and Taylor,1977; Mahoney,1980; Taylor et al.,1982). In these earlier studies, a single linear function was used to represent the net cost of locomotion (COL) and the net cost of transport (COT), without consideration of gait (Taylor and Rowntree,1973; Parsons and Taylor,1977; Mahoney,1980; Taylor et al.,1982). This was a useful analytic approach at the time, since the main goal was to construct and compare large interspecific datasets; however, some ecologically relevant information on individual or species-specific locomotor costs may have been missed as a consequence. Indeed, more recent studies of a wide range of terrestrial mammals have identified gait-specific nonlinearities in the patterns of locomotor costs per speed and distance (Hoyt and Taylor,1981; Hurst et al.,1982; Williams et al.,1983; Parker et al.,1984; Luick and White,1986; Hoyt and Kenagy,1988; Langman et al.,1995; Minetti et al.,1999; Williams et al.,2002; Griffin et al.,2004; Maloiy et al.,2009). Further, it has long been known that the locomotor costs of humans are gait-specific, increasing in a curvilinear manner during walking and then linearly across running speeds [e.g., Margaria,1938; Ralston,1958; Saibene and Minetti,2003 (but see Steudel-Numbers and Wall-Scheffler,2009)]. This pattern results in minimum walking costs per distance that are about half those of running (e.g., Saibene and Minetti,2003; Rubenson et al.,2007).
Here, new measurements of the metabolic costs of resting and locomotion in ring-tailed lemurs (Lemur catta) are presented and used to test for gait-specific effects. Recent studies (e.g., Griffin et al.,2003; Rubenson et al.,2007; Weyand et al.,2009) have noted the importance of baseline quantities in partitioning gross from net costs, especially in walking. The effect of these different quantities on ring-tailed lemur COL and COT is evaluated, and the results considered in the context of earlier size-scaling studies of primate locomotor costs. Finally, laboratory-based measurements of overground travel speeds are compared with measurements of COT to determine if ring-tailed lemurs exhibit gait-specific preferred speeds, and whether those preferences correspond to locomotor cost minima.
METHODS
Animals
Three adult ring-tailed lemurs, Lemur catta, (two males, one female; mass: 2.31 ± 0.19 kg) were trained to walk, canter and gallop on a motorized treadmill. The animals were selected from a breeding colony maintained by Duke University at the Duke Lemur Center (DLC), Durham, NC, and housed in a system of large outdoor enclosures. The respirometry experiments were conducted in a climate-controlled research room, onsite at the DLC. The Duke Institutional Animal Care and Use Committee approved all procedures.
Respirometry
Metabolic measurements were made while each lemur exercised on a motorized variable-speed treadmill (Jog-A-Dog, Model DC5, Ottawa Lake, MI; belt area: 1.52 m × 0.36 m). A digital tachometer fastened to the axel of the rear drum tracked belt speed. Each animal was trained to exercise at seven speeds ranging from 0.25 to 2.25 m s−1. The training regime consisted of mixed periods of exercise and rest over approximately 1 hr d−1, 3–5 d wk−1 for at least 6 weeks. Training familiarized the animals with the treadmill and improved their fitness levels so that at the end of the training period all lemurs could sustain 6–10 min of steady-state locomotion at each speed.
Measurements of rate of oxygen consumption were collected using an open-circuit indirect calorimetry system (Fedak et al.,1981) as each lemur exercised in a custom-built metabolic chamber (Fig. 1). The metabolic chamber (0.87 m × 0.23 m × 0.51 m) was constructed of clear Plexiglas and rested on brackets 1 cm above the moving treadmill belt. A small ribbon of weather stripping was attached to the bottom of the chamber so that the chamber effectively slid across the belt surface and was only open to the room through a 0.15 m diameter intake cut into its back wall. The main pump pulled air through the chamber at a rate of 75–100 L min−1. These rates were high enough to ensure that all of the expired gas from the lemur was collected. A sub-sample of the mixed expired gas was pulled from the main flow using a small pump and regulator. The gas was then passed through columns of Drierite and Ascarite to remove H2O and CO2, respectively. Oxygen content was analyzed using a Sable Systems FC-1B Oxygen Analyzer (Sable Systems International, Las Vegas). The measurement system was calibrated using a nitrogen dilution technique (Fedak et al.,1981), which enabled calculation of oxygen consumption rate.
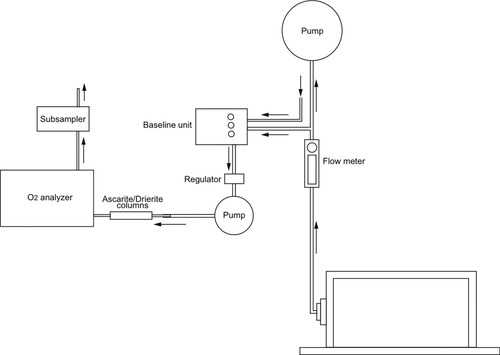
Schematic of the apparatus used to measure oxygen consumption. Arrows indicate the direction of airflow.
All locomotor trials lasted 6–10 min and oxygen consumption was measured throughout the trial. Rate of oxygen consumption (ml O2) was determined for the last 3–5 min of the trial after oxygen consumption had reached a steady-state plateau. During data collection, the order of the speeds was randomized and no more than five trials were collected from any one lemur on a single day, ensuring that the lemurs were sufficiently well rested for each locomotor trial. For each individual, 2–5 trials were measured at each of the seven speeds. Gross metabolic rate was calculated as 20.1 J ml O2−1 (Blaxter,1989).
The resting rate of oxygen consumption was measured using the same settings as during locomotion, with the principal modification being that air was drawn through the chamber at rates of 75–80 L min−1. During resting data collection, the room was darkened and remained quiet; typically, each lemur lay quietly on the tread surface throughout the experiment, although occasional grooming was observed. All resting measurements were recorded over a 10 min period in the morning before feeding to help ensure that each lemur was in a post-absorptive state. For each individual, 2–5 nonconsecutive resting trials were recorded.
Net locomotor costs
The net locomotor costs—calculated either per time or per distance—are partitioned from the gross metabolic rate by subtracting out some quantity representing the metabolic rate of tissue function not associated with the movement task (i.e., non-locomotor metabolism). Most previous studies of non-human primates have used the y-intercept of the gross metabolic rate versus speed linear regression as an estimate of this quantity (e.g., Taylor et al.,1982). However, a measure of resting metabolism, taken during quiet (motionless) standing, sitting or lying, has been used in more recent studies of humans and chimpanzees (e.g., Willis et al.,2005; Sockol et al.,2007; Weyand et al.,2010). Here, we used both approaches to calculate the mass-specific net COL and net cost of transport (COT), and consider their effects on the speed- and gait-specific estimates of locomotor costs.
For the COL (W kg−1), estimates for each individual were obtained by subtracting the y-intercept of a linear fit to the mean gross metabolic rate per speed (over the full speed range) (intercept baseline) and mean resting metabolic rate (RMR baseline) from the gross metabolic rate. The COT (J kg−1 m−1) was obtained by dividing the COL by tread speed. These values were compared with the COT estimated from the “slope approach” of earlier primate studies (Taylor and Rowntree,1973; Parsons and Taylor,1977; Mahoney,1980; Taylor et al.,1982), in which the mean gross metabolic rate versus speed for all three lemurs is fit using a single linear function and the slope is taken as the COT. This slope-based estimate of the COT is sometimes referred to as the “minimum” or “incremental” COT (Full,1991) and is directly comparable with the size-scaling equations of Taylor et al. (1982). In contrast, a COT estimated from the RMR baseline is comparable with Rubenson et al. (2007).
Overground speed measurements
All overground trials were conducted on a 9.0 m × 2.0 m × 2.3 m runway enclosed by fine-screen mesh strung from wooden posts that were fastened to the floor. The mesh closed the runway at both ends and along the top and sides to completely contain the animal. A canvas blind was set in the middle of the runway to divide it into two 1 m wide corridors, effectively creating an 18 m roundabout. The floor of the runway was smooth particleboard covered with a coating of polyurethane to seal it and prevent slipping by the animal. The lemurs were placed in the runway area, and then video recorded as they moved through the enclosure. Walking speeds were self-selected without prompting; cantering and galloping speeds were usually elicited by a DLC animal technician positioned at the end of the runway, taking a step toward the animal.
Trials were filmed in lateral view with a digital high-speed video camera (Redlake Motionscope PCI-500, San Diego, CA) recording at 125 Hz. The camera was positioned approximately 3 m from the runway to reduce parallax effects. The eye and tail base were digitized in MATLAB (R2008b, The MathWorks, Natick, MA) using DLT Dataviewer (Hedrick,2008). The coordinate data were filtered using a quintic smoothing spline (Woltring,1985,1986; Walker,1998) with a constant error tolerance (“spaps,” tolerance = 0.005; MATLAB, R2008b). The average horizontal velocities of the eye and tail base were used to calculate speed as the animal walked, cantered, or galloped through the camera field of view.
Model fitting and statistics
Linear mixed model (LMM) regressions were used to describe the changes in metabolic costs against speed, with all regression models fitted through the mean values per lemur per speed. For one lemur, it was not possible to collect metabolic costs during 0.25 m s−1 walks, and as a result the final dataset was unbalanced. In all models, speed was set as a fixed effect (N = 7) and individual lemur (N = 3) was set as a random effect.
To identify the best-fitting statistical model for changes in metabolic cost against speed within gaits, the Akaike Information Criterion (AIC) was used to compare the performance of linear, quadratic, and cubic regression fits. The lowest AIC indicates the best-fitting model (Akaike,1974; Sokal and Rohlf,2012). The goodness of fit of the LMM regressions was quantified using a modified coefficient of determination for mixed models (R12; Vonesh and Chinchilli,1997), which has been shown to perform well in simulations where LMMs were used for parameter estimation (Orelien and Edwards,2008).
Log-likelihoods (ln L) were calculated for the fit of single linear functions and for the fit of gait-specific functions to the gross metabolic rates, COL and COT against speed. Likelihood-ratio tests (LR tests, Λ; Sokal and Rohlf,2012) were then used to compare the single linear fit to the gait-specific fit, where the ln L from the single linear model fit and the sum of the ln L from the walking and cantering/galloping (gait-specific) model fits were used to compute the change in log-likelihood from one model to the other. The likelihood-ratio test probability distribution was approximated as a chi-square distribution (χ2) with degrees of freedom (df) equal to df2 – df1, where df2 is the number of free parameters in the gait-specific model and df1 is the number of free parameters in the single linear model (Sokal and Rohlf,2012). Model fitting and associated statistical testing were performed in R (version 2.9 for Mac OS) using the base, “nlme” and “lmmfit” libraries. Descriptive statistics given in the text are means ± s.d. In these cases, data were first averaged within each animal, and then averaged across animals for the species. Statistical significance was α = 0.05.
RESULTS
Gross metabolic rates
Gross metabolic rate increased with speed and across gaits for all individuals, consistent with most previous studies of terrestrial locomotion (Taylor et al.,1970,1982) (Fig. 2). Each lemur walked at speeds of 0.25 m s−1 to 1.0 m s−1, then cantered and galloped at speeds of 1.5 m s−1 and above. It is important to note that during treadmill locomotion at 1.0 m s−1, lemurs would switch from a walk to a canter then back to a walk for some strides. This is consistent with overground observations of ring-tailed lemur speeds and gaits, including a predicted gait transition at ∼1 m s−1 (Froude number; Fr = 0.5) (O'Neill and Schmitt,2012).
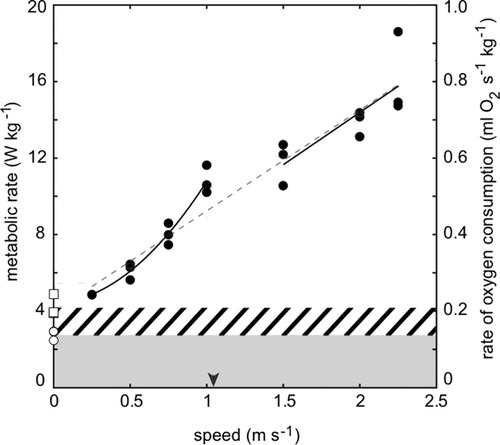
Mean mass-specific gross metabolic rates (Emet; left axis) and rates of oxygen consumption (right axis) of individual ring-tailed lemurs (N = 3) as a function of speed (v). Lines are LMM regression fits to the full dataset as well as the walking and cantering/galloping data separately: full, Emet = 4.05 + 5.26v (r2 = 0.915; gray dashed line); walking, Emet = 4.59 – 0.14v + 6.34v2 (r2 = 0.963); cantering/galloping, Emet = 3.46 + 5.47v (r2 = 0.648). The same equations in rates of oxygen consumption (ml O2 s−1 kg−1) are obtained by dividing each coefficient by 20.1 J ml O2−1. The y-intercepts for the individual-specific regression lines (intercept; white squares) and the individual RMRs (white circles) are shown at 0 m s−1. The shaded areas show the mean intercept (diagonal lines plus gray shaded area) and RMR baseline (gray shaded area) quantities for the species. The intercept baseline attributes a larger fraction of gross metabolic rate to non-locomotor costs than the RMR baseline. A black arrow shows the predicted walk-canter/gallop gait transition speed at Fr = 0.5 (as in O'Neill and Schmitt,2012).
A single linear regression captured much of the variation in gross metabolic rates over speed (LMM, R12 = 0.915). The slope-based estimate of the COT is 5.26 ± 0.35 J kg−1 m−1 for all gaits and speeds, with an intercept of 4.05 ± 0.56 W kg−1. Nevertheless, gait-specific trends were evident in the gross metabolic rates of ring-tailed lemurs. From the slowest walking speed at 0.25 m s−1 to the fastest walking speed at 1.0 m s−1, a quadratic model best fit the data (Table 1). In contrast, from the slowest canter at 1.5 m s−1 to the fastest gallop at 2.25 m s−1, a linear model best fit the data (Table 1). Comparing the single linear model with the gait-specific (piecewise) model, the gait-specific approach provided a significantly better fit to the data (Λ = 20.948; χ20.05 = 5.991) (Fig. 2). This suggests that the gait-specific model fits provide a more robust characterization of metabolic costs across speeds and gaits than a single linear regression.
| Model | AIC | ln L | R12 | ||
|---|---|---|---|---|---|
| Gross metabolic rate | |||||
| Walks | Linear | 26.706 | −9.353 | 0.935 | |
| Quadratic | 20.909 | −5.454 | 0.963 | ||
| Cubic | 22.888 | −5.444 | 0.963 | ||
| Canters/Gallops | Linear | 35.950 | −13.975 | 0.648 | |
| Quadratic | 36.394 | −13.197 | 0.677 | ||
| COLa | |||||
| Walks | Linear | 29.454 | −10.727 | 0.909 | |
| Quadratic | 23.101 | −6.550 | 0.940 | ||
| Cubic | 25.090 | −6.545 | 0.940 | ||
| Canters/Gallops | Linear | 36.236 | −14.118 | 0.590 | |
| Quadratic | 36.914 | −13.457 | 0.609 | ||
| COTa | |||||
| Walks | Linear | 40.499 | −16.249 | 0.004 | |
| Quadratic | 28.681 | −9.340 | 0.440 | ||
| Cubic | 27.599 | −7.800 | 0.467 | ||
| Canters/Gallops | Linear | 22.836 | −7.418 | 0.012 | |
| Quadratic | 23.093 | −6.546 | 0.060 | ||
- Boldface indicates the lowest AIC value.
- a The results shown are for RMR baseline subtraction. In all cases, the same model fits had the lowest AICs when an intercept baseline was subtracted, except for the walking COT, which was best fit by a quadratic model. The different model fits for the walking COT are shown in Fig. 4B.
- Results are shown for the different models fits. ln L, logarithm maximum likelihood; AIC, Akaike information criterion; R12, modified coefficient of determination for mixed models.
Baseline metabolism
The intercept metabolic rate was 4.05 ± 0.71 W kg−1, while the RMR was 2.77 ± 0.21 W kg−1. Both of these baseline values represent substantial percentages of the gross metabolic rate, especially at slow walking speeds (Fig. 3). At 0.25 m s−1, the intercept and the RMR were 81% and 55% of the gross metabolic rate, respectively. These values decreased with increasing speed. Across all four walking speeds, the percentages ranged from 81% to 39% when using the intercept baseline and from 55% to 26% when using the RMR baseline. On average, these two baselines accounted for 61% and 41% of the walking gross metabolic rate, respectively. Across the measured cantering and galloping speeds, the percentages ranged from 36% to 27% using the intercept and from 23% to 18% using RMR for the three speeds. These values were much less speed-dependent, and averaged 31% and 20% for the intercept and RMR subtractions, respectively. These data demonstrate that baseline quantities have a much larger effect on estimates of net walking costs than on net cantering and galloping costs in ring-tailed lemurs.
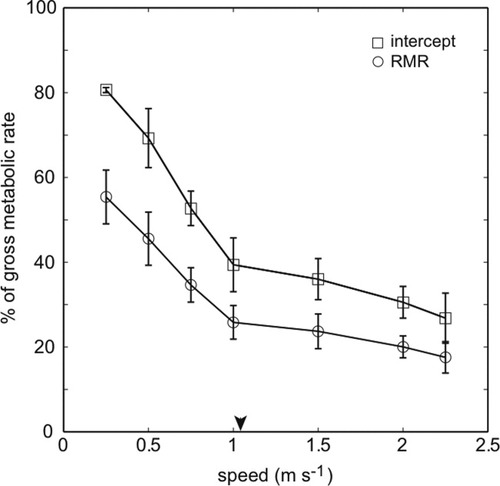
Representative percentage contributions of intercept (empty squares) and RMRs (empty circles) to the gross metabolic rates at different speeds and gaits. The % of gross metabolic rate = [(gross – baseline)/gross]·100. Circles are species means ± s.d. A black arrow shows the predicted walk-canter/gallop gait transition speed at Fr = 0.5 (as in O'Neill and Schmitt,2012).
Net locomotor costs
Mass-specific net locomotor costs (COL, COT) were calculated using both baseline quantities (Fig. 4A,B). As expected, the different values altered the magnitude, but not the slope of the COL (Fig. 4A). The linear fits across all gaits and speeds provide slope-based estimates of the COT of 5.24 J kg−1 m−1 using the intercept subtraction (LMM, R12 = 0.900) and 5.29 J kg−1 m−1 using the RMR subtraction (LMM, R12 = 0.899), almost identical to the values from gross metabolic rates. However, as before, gait-specific fits were evident in the dataset, and significantly improved on the single linear model fits (COL: Λ = 19.744; χ20.05 = 5.991; COT: Λ = 53.584; χ20.05 = 9.488).
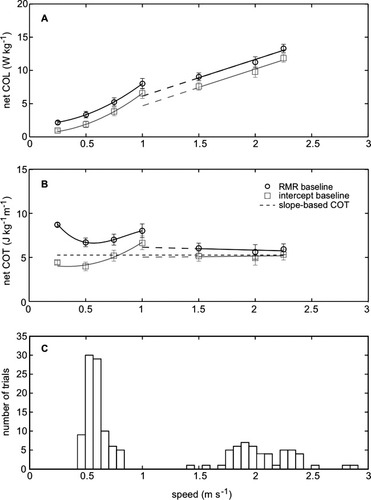
(A) Mass-specific net COL calculated using intercept (gray squares) and RMR (black circles) baseline quantities. (B) Mass-specific net cost of transport (COT) calculated from the “slope approach” (small dashed line), as well as intercept (gray squares) and RMR (black circles) baselines. The “slope approach” provides a much closer approximation of the subtraction-based estimates of the cantering and galloping COT, than of walking COT. The solid lines show the best-fit LMM functions based on the AIC (Table 1) for the gait-specific measurements. The black and gray large dashed lines extrapolate the canter/gallop gait-specific fits to the slowest cantering speed range for comparative purposes. (C) Histogram showing the frequency distribution (i.e., number of trials) recorded at different speeds for ring-tailed lemurs moving freely through an 18 m roundabout.
The COT calculated from the slope of gross metabolic rates assumes no change in cost across gaits and speeds, while the COT from an intercept or RMR baseline subtraction found distinct, gait-specific patterns (Fig. 4B). In particular, the slope-based estimate of COT missed the curvilinear functions across walking speeds apparent from the intercept and RMR subtraction estimates. Not surprisingly, the slope approach provided a good approximation of cantering and galloping costs estimated from an intercept baseline, but tended to overestimate the COT at 0.25–0.5 m s−1 and underestimate the COT at 1.0 m s−1. In contrast, the slope approach underestimated the COT at all speeds based on an RMR baseline. Using either the intercept or RMR baseline quantity, a curvilinear function best fit the walking data, while a linear function best fit the cantering/galloping data (Table 1). In both cases, the minimum COT measurement was 6.69 J kg−1 m−1 during walking at 0.5 m s−1. It is notable that the highest walking costs were at the slowest walking speeds and near the ∼1 m s−1 transition from a walk to a canter. In contrast, the slopes of the LMM fits to the cantering and galloping data were not different from zero, indicating that there is no effect of speed on cost per distance traveled, at least within the measured 1.5 m s−1 to 2.25 m s−1 range.
Overground speeds
A total of 140 overground trials were recorded in which the ring-tailed lemurs walked, cantered, or galloped along an indoor runway (Fig. 4C). The walking speeds of ring-tailed lemurs were tightly clustered between 0.5 and 0.6 m s−1, with a mean speed of 0.59 ± 0.09 m s−1 (median = 0.57 m s−1; mode = 0.49 m s−1). The ring-tailed lemurs almost never traveled at speeds between 0.75 and 1.5 m s−1. Above 1.5 m s−1, ring-tailed lemurs used a much wider range of speeds, but some clustering was evident around 2.0 m s−1. For cantering and galloping, the mean speed was 2.06 ± 0.28 m s−1 (median = 2.01 m s−1; mode = 1.92 m s−1).
Interspecific comparisons
Compared with the predictions from scaling studies of terrestrial birds and mammals, ring-tailed lemurs have low COTs for their body mass (Fig. 5), suggesting that their terrestrial locomotion is relatively economical. The general vertebrate scaling equation of Taylor et al. [1982; Eq. (8)] predicted 8.22 J kg−1 m−1 at all speeds and gaits, while their “primate equation” predicted 8.19 J kg−1 m−1. Both predictions were 36% higher than the measured COT of 5.26 J kg−1 m−1 for ring-tailed lemurs. The gait-specific equations of Rubenson et al. [2007; Eqs. (2)–(4)], which are based on an RMR subtraction, similarly overestimated ring-tailed lemur locomotor costs, with predictions of 9.66 J kg−1 m−1 for canters/gallops, and 12.0 or 11.62 J kg−1 m−1 for walks (using either the minimal cost or preferred-speed criteria, respectively). These predictions overestimated the COT of preferred speed canters/gallops (2.0 m s−1) by 42% (5.61 J kg−1 m−1), and the minimum/preferred speed walking (0.5 m s−1) by 42 and 44% (6.69 J kg−1 m−1), respectively.
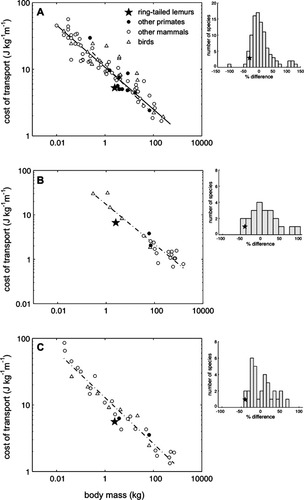
The mean net cost of transport (COT) for ring-tailed lemurs (gray star) compared with general size-scaling trends. (A) The trend lines for all birds and mammals (black solid line) and for primates alone (black dashed line) are from Taylor et al. (1982). The mean COT for ring-tailed lemurs is a slope-based estimate. (B) The trend line for birds and mammals walking (black dashed-dot line) is from Rubenson et al. (2007). The mean COT for ring-tailed lemurs is for walks at 0.5 m s−1 based on an RMR baseline. (C) The trend line for all birds and mammals using “running” gaits (e.g., running, trotting, galloping) (black dash-dot line) is from Rubenson et al. (2007). The mean COT for ring-tailed lemurs is for canter/gallops at 2.0 m s−1 based on an RMR baseline. In all three comparisons, ring-tailed lemurs fall below the regression line. For each figure, an associated inset shows the frequency distribution (i.e., number of species) of the percent difference [% difference = (estimate – mean/estimate)·100] of the species COTs used to build each scaling equation.
DISCUSSION
Metabolic cost increased across speed and gait for all three ring-tailed lemurs, consistent with most other studies of terrestrial locomotion in birds and mammals (Schmidt-Nielsen,1972; Taylor et al.,1970,1982); however, in contrast to all previous studies of non-human primates (Taylor and Rowntree,1973; Parsons and Taylor,1977; Mahoney,1980; Taylor et al.,1982), gait-specific effects, especially with regards to the COT, were evident. Importantly, these results indicate that gait-specific functions better describe locomotor costs than a single linear function fit across all speeds and gaits, when sufficient speeds are measured and gaits are known. While the ubiquity of these patterns across non-human primates is unclear, the results herein suggest that the use of gait-specific functions fit to locomotor cost data should be evaluated, as they may contain important ecological, behavioral, or biomechanical information. The gross metabolic rate, COL and COT were all curvilinear functions across walking speeds, and linear functions over the cantering and galloping speed range. These findings are relevant to understanding gait choice and the preferred (self-selected) speeds within gaits in ring-tailed lemurs. In addition, the gait-specific differences in preferred walking and canter/galloping costs have implications for the scaling of the COT.
Baseline subtractions
Of particular importance in the estimation of locomotor costs is how to partition the net from the gross metabolic cost, which (when determined from O2) is necessarily an aggregate measurement. Direct determinations of the metabolic rates of non-locomotor tissues are quite difficult (Stainsby et al.,1980; Marsh and Ellerby,2006), and different baseline quantities make different assumptions regarding non-locomotor metabolism (Full,1991; Rubenson et al.,2007).
For ring-tailed lemurs, the intercept baseline is 1.46 times higher than the RMR baseline. This is consistent with other studies of terrestrial animals, which report 1.3–1.7 times higher values (Taylor et al.,1970; Schmidt-Nielsen,1972; Taylor,1977). This higher value likely reflects the statistical dependence of the intercept and is not necessarily linked to non-locomotor metabolic processes at 0 m s−1. This is most apparent in studies where the intercept is negative (e.g., Chassin et al.,1976; Bransford and Howley,1977; Saunders et al.,2004). In contrast, RMR is independent of the locomotor sample.
Of course, RMR has been measured under several different conditions, including quiet (motionless) standing, sitting, and lying. Most recent locomotor studies have used the cost of standing (e.g., Griffin et al.,2003; Rubenson et al.,2007; Sockol et al.,2007; Maloiy et al.,2009); however, standing costs can be 10–25% higher than the cost of sitting or lying (e.g., Parsons and Taylor,1977; Parker et al.,1984; Levine et al.,2000). It has been suggested that this higher metabolism reflects the cost of balance, posture, and bodyweight support, which should be included in the net locomotor costs (Weyand etal.,2009,2010). For ring-tailed lemurs, the 1.46 times difference between intercept versus RMR baseline quantities implies that earlier estimates of the COL and COT that used an intercept baseline (Taylor et al.,1982) would have underestimated the cost of skeletal muscle function during locomotion, especially at walking speeds. This is of particular relevance for studies on the determinants of locomotor costs, which seek to link skeletal muscle function to metabolism.
Net locomotor costs, preferred speeds, and lemur biology
Ring-tailed lemurs have relatively low costs for walking, cantering, and galloping. Specifically, the 5.26 Jkg−1 m−1 COT is 36% below the predictions of Taylor et al. (1982), and the 6.69 J kg−1 m−1 (walk) and 5.61 J kg−1 m−1 (canter/gallop) are 42–44% below the predictions of Rubenson et al. [2007; Eqs. (2)–(4)]. These percentages are the lowest deviations among non-human primates (Fig. 5A–C).
These results are relevant to the view that both gait choice and gait-specific preferred speeds correspond to locomotor cost minima. First, these data suggest that the minimum COT for walking is higher than for cantering or galloping, using an RMR-based subtraction. This is consistent with the view that terrestrial animals below ∼20 kg have walking COTs that are greater than their COTs for faster-speed gaits (Rubenson et al.,2007). As a means of reducing the net locomotor contribution to daily energy expenditure then, it would be cheaper to canter/gallop than to walk a unit distance. Future studies might examine whether ring-tailed lemurs preferentially use cantering/galloping gaits in the wild. Unfortunately, current behavioral data on ring-tailed lemur travel and foraging do not differentiate among quadrupedal gaits (Sussman,1974; Simmen et al.,2010). Second, preferred speeds correspond well to the locomotor cost minima within the walking gait, indicating that ring-tailed lemurs prefer to walk at their most economical speeds. For cantering and galloping, it was not possible to sample locomotor costs over the full speed range, and therefore the linear function must be viewed as provisional. If a more complete sampling of the cantering/galloping speed range revealed a nonlinear function, as in the galloping gait of horses (Hoyt and Taylor,1981; Minetti et al.,1999), then the mean speed of 2.0 m s−1 may indeed correspond to locomotor cost minima. At present though, it can only be stated that the preferred speed is similar to the speed of lowest measured cantering/galloping COT. Finally, it is notable that ring-tailed lemurs avoid their slowest speeds as well as the speed at which they transition from a walking to a cantering gait, where their measured COTs are highest.
Implications for COT scaling
The gait-specific approach indicates that ring-tailed lemurs have different COTs for walking and cantering/galloping gaits. This contrasts with earlier studies (Taylor and Rowntree, 1972; Parsons and Taylor,1977; Mahoney,1980; Taylor et al.,1982), but corroborates the more recent finding that small animals have higher COTs for walking than for other, higher-speed gaits (Rubenson et al.,2007). This is opposite the pattern in humans, for which minimum walking costs are nearly half those of running (e.g., Saibene and Minetti,2003; Rubenson et al.,2007).
The overall pattern of changing COT with gait from a small primate (e.g., ring-tailed lemur) to a larger one (e.g., human) seems to reinforce several limitations of earlier scaling studies of the COT. First, as noted by Rubenson et al. (2007), the Mb−0.316 COT scaling slope reported in Taylor et al. (1982) is more representative of the cost of intermediate and high-speed gaits, such as running, trotting, and galloping, than the cost of walking. Second, studies that use a mass-scaling exponent alone to predict locomotor cost (reviewed in Pontzer et al.,2010) likely underestimate the cost attributable to active skeletal muscle function. This bias may be corrected, in part, by estimating the total COT from the sum of the intercept and slope exponents, and then performing a post-hoc RMR subtraction, in a manner similar to Marsh et al. (2006). However, only a few studies of non-human primates report both resting and locomotor costs for their animals. These two issues represent important limitations to the general use of the “primate equation” of Taylor et al. (1982), especially with regards to studies of walking. The criticisms of Steudel-Numbers (2003), who noted the use of tree shrews, some juvenile subjects and an atypical human running cost value as potential limitations should also be considered.
CONCLUSIONS
Gait-specific measurements of metabolic costs suggest ecologically relevant variation across speed and gait in ring-tailed lemurs. In particular, gross metabolic rate, COL and COT are curvilinear functions across walking speeds, and (at least provisionally) linear functions over the cantering and galloping speed range. These patterns may have been obscured in some earlier studies, which assumed a linear relation of locomotor cost and speed, and relied on an intercept rather than RMR baseline for partitioning net from gross metabolism. The results of these new gait-specific measurements indicate that ring-tailed lemur locomotor costs are 36-44% below expectations based on general vertebrate size scaling (Taylor et al.,1982; Rubenson et al.,2007), and that the COT for walking is higher than cantering/galloping costs. The preferred speeds of ring-tailed lemurs correspond well to the speeds that minimize the COT, especially during walking. This has previously been documented for humans, horses, and large birds. While more data are needed on gait choice in the wild, these results support the view that gait-specific preferred speeds correspond to locomotor cost minima and, more generally, that metabolic cost is an important movement criterion for primates and other terrestrial animals.
Acknowledgements
I thank B. Demes, W. Jungers, S. Larson, T. Roberts, C. Ruff, D. Schmitt, M. Teaford, and two anonymous reviewers for helpful comments on earlier versions of this article. I am grateful to the DLC staff, especially D. Brewer, W. Hess, and S. Zehr who provided expert animal handling and assistance with treadmill training. Thanks also to T. Griffin for advice on experimental set-up and data collection, and J. Rohlf for helpful discussions on statistical model fitting. This is Duke Lemur Center publication no. 1226.




