Applied Economic Perspectives and Policy
Early View
SUBMITTED ARTICLE
Open Access

Quantifying the land-use change due to soybean-based biodiesel in the United States

Ruiqing Miao, 

Ruiqing Miao

Department of Agricultural Economics and Rural Sociology, Auburn University, Auburn, Alabama, USA

Search for more papers by this author
Yijia Li, 

Yijia Li

Department of Agricultural and Consumer Economics, University of Illinois, Urbana-Champaign, Urbana, Illinois, USA

Search for more papers by this author
Madhu Khanna, 

Corresponding Author

Madhu Khanna

Department of Agricultural and Consumer Economics, University of Illinois, Urbana-Champaign, Urbana, Illinois, USA

Institute for Sustainability, Energy and Environment, University of Illinois, Urbana-Champaign, Urbana, Illinois, USA

Correspondence

Madhu Khanna, Department of Agricultural and Consumer Economics, University of Illinois, Urbana-Champaign, 1101 W. Peabody Drive (NSRC), Suite 350 MC-635, Urbana, IL 61801, USA.

Email: [email protected]

Search for more papers by this author
Christopher Clark, 

Christopher Clark

Office of Senator Klobuchar, Washington, DC, USA

Search for more papers by this author
Dallas Burkholder, 

Dallas Burkholder

US Environmental Protection Agency, Office of Transportation and Air Quality, Washington, DC, USA

Search for more papers by this author
Luoye Chen, 

Luoye Chen

Carbon Neutrality and Climate Change Thrust, Society Hub, The Hong Kong University of Science and Technology (Guangzhou), Guangdong, China

Search for more papers by this author
First published: 16 July 2025
https://doi.org/10.1002/aepp.70005

Editor in charge: Jerome Dumortier

Abstract

We quantify the impact of soybean oil-based biodiesel production on US cropland, using a method that accounts for the intermediate effect of soybean crushing facilities. Based on U.S. Environmental Protection Agency data for biodiesel production and proprietary data for soybean crushing facilities over 2011–2020, we find that the elasticities of soybean acreage and total cropland acreage with respect to soybean oil-based biodiesel production are 0.011 and 0.002, respectively. The direct land-use effect of soybean oil-based biodiesel is about 0.96 million acres of cropland expansion per billion gallons, about twice as high as some estimates for corn ethanol from previous studies.

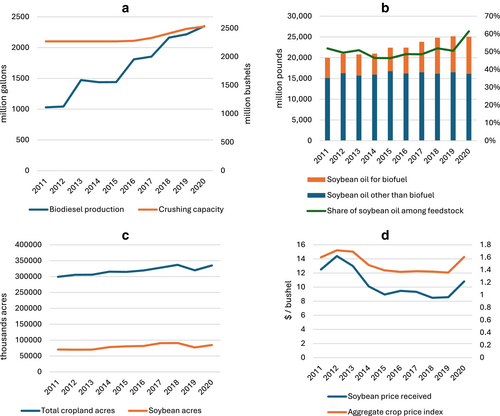
Biodiesel production in the United States has experienced significant growth from negligible levels in 2002 to about 1.8 billion gallons in 2020, and renewable diesel production has also increased 20-fold from 0.04 to 0.69 billion gallons over 2010–2020 (Figure 1a). These increases are anticipated to continue due to incentives from the Renewable Fuel Standard (RFS), the Sustainable Aviation Fuel Grand Challenge, and state-level low carbon fuel programs such as California's Low Carbon Fuel Standard (Department of Energy [DOE], 2022). Soybean oil has become the primary feedstock, accounting for about 44% of biodiesel production in the United States (Energy Information Administration [EIA], 2022). Similar to corn ethanol, soybean oil-based biodiesel production raises concerns about land-use changes as increasing demand for soybeans drives up demand for soybean acreage and creates incentives to expand total cropland. The increase in total cropland acreage can lead to the release of carbon stored in soils and vegetation on non-cropland and thus create a carbon debt that may take years to pay back through displacement of petroleum diesel by biodiesel.

Details are in the caption following the image
FIGURE 1
Open in figure viewerPowerPoint
Trends of variables over 2011–2020. (a) US biodiesel production and soybean crushed capacity; (b) US use of soybean oil and share of soybean oil among the feedstock for biodiesel and renewable diesel; (c) US aggregate cropland acreage (sum of 106 crops) and soybean acreage; (d) US soybean received price and aggregate crop price index. As explained in the text, we omit years prior to 2011 when production was lower and before the RFS2, and omit years after 2020 to avoid confounding factors such as COVID-19.

Unlike the extensive literature on the land-use effects of corn ethanol, which includes general equilibrium models (e.g., Hertel et al., 2010; Taheripour & Tyner, 2020), partial equilibrium models (e.g., X. Chen & Khanna, 2018), and empirical studies (e.g., Lark et al., 2022; Li et al., 2019; Miao, 2013; Motamed et al., 2016) analyzing ethanol-induced land-use changes, there are relatively few studies that have quantified the land use impact of soybean oil-based biodiesel. While general equilibrium modeling studies estimate the induced land-use effect of biodiesel to be 0.02–0.07 million acres per billion gallons (R. Chen et al., 2018; Zhao et al., 2021), a partial equilibrium modeling study by W. Wang and Khanna (2023) reports a much higher effect (0.78–1.5 million acres per billion gallons), which is about twice as large as that of corn ethanol. On the other hand, based on an assumed technical relationship between soybeans and biodiesel, a recent American Enterprise Institute report shows that producing 1 billion gallons of sustainable aviation fuel, a fuel similar to renewable diesel chemically, could require about 11.7–16.7 million acres of soybeans (Swanson & Smith, 2024).

The empirical assessment of the spatial pattern of land-use change effects of soybean oil-based biodiesel is more complex compared with that of corn ethanol, because the latter is derived directly from corn kernels at biorefineries and thus incentivizes corn acreage expansion in the immediate proximity of the biorefineries. Soybean oil-based biodiesel, however, is not directly produced from soybeans. Instead, it is produced from soybean oil, historically a byproduct from soybean crushing facilities. Therefore, the demand for soybeans created by biodiesel production is not in the proximity of the biorefinery. Instead, biodiesel production increases demand for soybean oil, which in turn increases the demand for soybeans in the vicinity of soybean crushing facilities. Additionally, demand for soybean biodiesel can also affect land use by increasing demand for soybeans and other crops, which in turn increases crop prices and can lead to cropland expansion more broadly even in areas that are not in the vicinity of crushing facilities or refineries. Whether, to what extent, and where soybean biodiesel influences farmers' land-use decisions depends on the spatial and economic association between crop acreage, crushing facilities, biorefineries, and crop prices which imposes high data requirements on any study that aims to understand the effect. Unfortunately, production or capacity data for biodiesel refineries and soybean crushing facilities are not publicly available, and neither are the soybean oil transaction data between the refineries and crushing facilities.

We obtained data for facility-level biodiesel production from the U.S. Environmental Protection Agency (USEPA) and proprietary data for facility-level soybean crushing from CrushTraders (a private trade information company in the United States) and developed an analytical framework to quantify the effect of soybean oil-based biodiesel production on soybean acreage and total cropland acreage in the United States, while recognizing that biodiesel production influences land use mainly through its effect on demand for soybean crush. This framework led to a two-stage model that consists of first estimating the association between soybean crushing and biodiesel production, and then estimating the effects of crushing facilities and crop prices on land use in their vicinity. We infer the effects of biodiesel production on land-use changes based on combining the outcomes of the two stages.

Our analysis focuses on the period 2011–2020, covering the years during which soybean oil used for biodiesel production almost doubled from 4874 million pounds in 2011 to 8920 million pounds in 2020 (see Figure 1b). We assign biodiesel production to counties (to be discussed below) and combine that with the county-level cropland acreage, state-level crop prices, national input price indices, as well as other county-level controls for the analysis. We also control for fixed effects using a static panel data approach and account for crop rotations using a dynamic panel approach. An instrumental variable (IV) approach is employed to address the endogeneity issues of crushing facility production and crop prices, as crushing facilities are often located in areas with substantial soybean acreage, and crop prices may be influenced by planted acreage. We also examine the spatial distribution of land use changes based on the location of biodiesel and crush facilities as well as the elasticity of soybean acreage and total cropland acreage with respect to changes in biodiesel production and crop prices.

The rest of this paper is organized as follows: The next section presents the empirical strategy and estimation methods and is followed by the section describing the dataset and variable construction. The regression results are presented and discussed in the subsequent section and are followed by the conclusions and discussion of policy implications.

ECONOMETRIC METHOD

The conceptual framework developed by early studies (e.g., Miao, 2013; Motamed et al., 2016) about the impact of ethanol plant proximity on crop acreage was based on the premise that the establishment of an ethanol plant forms a terminal market for corn grain that potentially increases local corn price or reduces transportation costs of bringing nearby corn to markets, or both. This phenomenon, termed the “direct ethanol production effect,” was hypothesized to incentivize farmers located near ethanol plants to expand corn acreage. Li et al. (2019) expanded this framework by recognizing the possibility of an “indirect ethanol production effect” because national-level growth in ethanol production in the United States raises corn and other crop prices across regions, leading to increased corn acreage even in nonproximity areas. Both effects can lead to an expansion in corn acreage by substituting corn for other crops and create incentives to convert noncropland into crop production, thereby increasing total cropland acreage.

In the case of soybean biodiesel, as discussed above, the “direct effect” is unlikely to occur near the biodiesel plants, because soybeans are not directly shipped to these plants as feedstock. Instead, the “direct effect” is more likely to occur around the crushing facilities as they serve as terminal markets for soybeans. The “indirect effect” of soybean oil-based biodiesel can arise because the surge in demand for soybean oil, and thus soybeans, can drive up overall crop prices and lead to expansion of cropland in other regions.

To capture these dynamics between biodiesel production, soybean crushing, and soybean production, we develop a two-stage model reflecting the soybean oil-based biodiesel production supply chain: the first stage quantifies the association between the demand from biodiesel plants and the quantity of crush at nearby facilities, and the second stage estimates the effects of crushing facilities and crop prices on land-use change in the vicinity of those facilities. We represent the relationship between biodiesel production, soybean crushing, and soybean acreage through the following equations:
κ ijt = γ 0 + γ 1 d ijt + γ 2 Γ ijt + γ 3 Z ijt + v ij + ε ijt , $$ {\kappa}_{\mathrm{ij}\mathrm{t}}={\gamma}_0+{\gamma}_1{d}_{\mathrm{ij}\mathrm{t}}+{\boldsymbol{\gamma}}_{\mathbf{2}}{\boldsymbol{\varGamma}}_{\mathbf{ijt}}+{\boldsymbol{\gamma}}_{\mathbf{3}}{\boldsymbol{Z}}_{\mathbf{ijt}}+{v}_{\mathrm{ij}}+{\varepsilon}_{\mathrm{ij}\mathrm{t}}, $$ ()
A ijt s = β 0 + β 1 κ ̂ ijt + β 2 p ̂ it + β 3 f ̂ t + β 4 Γ ijt + α ij + ϵ ijt , $$ {A}_{\mathrm{ij}\mathrm{t}}^s={\beta}_0+{\beta}_1{\hat{\kappa}}_{\mathrm{ij}\mathrm{t}}+{\beta}_2{\hat{p}}_{\mathrm{it}}+{\beta}_3{\hat{f}}_t+{\boldsymbol{\beta}}_{\mathbf{4}}{\boldsymbol{\varGamma}}_{\mathbf{ijt}}+{\alpha}_{\mathrm{ij}}+{\epsilon}_{\mathrm{ij}\mathrm{t}}, $$ ()
where in Equation (1), the first stage regression, κ $$ \kappa $$ is soybeans crushed; d $$ d $$ is biodiesel production; Γ $$ \varGamma $$ represents the vector of other control variables, including population density, monthly precipitation in March to May, and time trends; v ij $$ {v}_{ij} $$ is county-fixed effects, and ε ijt $$ {\varepsilon}_{ijt} $$ is the error term. In Equation (2), A s $$ {A}^s $$ is the soybean acreage; κ ̂ $$ \hat{\kappa} $$ is the predicted value of soybeans based on Equation (1); p ̂ $$ \hat{p} $$ and f ̂ $$ \hat{f} $$ are the predicted value of soybean price and fertilizer price index, respectively, by using the same independent variables in Equation (1); α ij $$ {\alpha}_{ij} $$ is the county fixed effects; ϵ ijt $$ {\epsilon}_{ijt} $$ is the error term; and subscripts i $$ i $$ , j $$ j $$ , t $$ t $$ stand for state i $$ i $$ , county j $$ j $$ , and year t $$ t $$ , respectively; Z $$ Z $$ is a vector of other IVs, including lagged crop stocks, RFS mandate, and lagged natural gas price (to be discussed below in detail). Finally, γ's and β's are parameters of interests. Note that price variables are constructed at the state-year level because that is the finest level that we could obtain, and thus their subscripts do not include county subscript j $$ j $$ . Similarly, the fertilizer price index is at the national level, thus it does not have state or county subscript. A detailed description of variable construction is presented in Data and variables section.

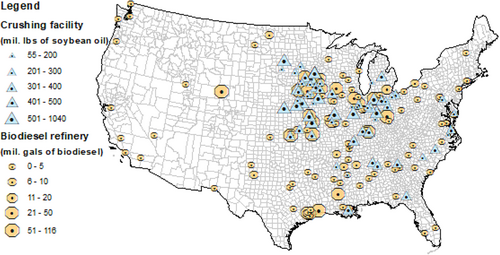
Estimation of Equations (1) and (2) is carried out using the two-stage least squares approach. This approach not only enables estimation of the impact of biodiesel production on soybean acreage through crushing facility operations, but also addresses endogeneity issue associated with the location and amount of soybean crush production. Since soybean crushing facilities are primarily clustered in the traditional soybean-producing belt from Ohio to Minnesota and a smaller concentration along the southeast seaboard (Figure 2), their presence is likely to be influenced by local soybean acreage. To assess the extent of this impact, we use effective biodiesel production within a specified radius of each crushing facility as an IV for soybean crush. By combining the regression results from the first stage (Equation 1) and second stage (Equation 2), we can calculate the marginal impact of one unit increase in biodiesel production on soybean acreage by multiplying γ1 by β 1 $$ {\beta}_1 $$ .

Details are in the caption following the image
FIGURE 2
Open in figure viewerPowerPoint
Locations of biodiesel refineries and crushing facilities.

Biodiesel production is a valid IV for soybean crush because our dataset only includes biodiesel plants that were consistently utilizing soybean oil as the feedstock, which in turn can affect the production of soybean crushing facilities. From 2011 to 2020, soybean oil accounted for about 55.4% of feedstocks used for biodiesel production, with a notable rise in both total soybean oil production and the use for biodiesel purposes (Figure 1b). This significant reliance on soybean oil has remained relatively stable over time, establishing a link between biodiesel production and the demand for soybean oil from crushing facilities. Biodiesel plants do not directly consume soybeans for production; instead, they rely on soybean oil processed at crushing facilities. Therefore, after controlling for crop price, input price, and many other variables as in Equation (2), it is reasonable to expect that the expansion of biodiesel production influences local soybean acreage only through its impact on crushing facility operations. This indirect pathway ensures that biodiesel production is not directly correlated with the error term in the acreage equation, thereby mitigating endogeneity concerns in the analysis.

To address different pathways of influence and evaluate the validity of the IVs, we also include the RFS annual volumetric mandate for biomass-based diesel as an IV for crush production. The USEPA establishes yearly volume requirements within the RFS program for renewable fuel with statutory targets. The two major types of biomass-based diesel fuels can generate Renewable Identification Numbers (RINs) to ensure compliance with the RFS. It is evident that the biofuel mandate is correlated with biodiesel production given the large incentives provided by these mandates and observed RIN prices (Miller et al., 2024). The RFS mandate directly affects the demand for biodiesel, which in turn impacts the demand for soybean oil and thus crush production. Since the mandate is set at the national level based on various policy objectives and market factors, it is exogenous to local factors that influence soybean acreage. Further, because the mandates are typically finalized preceding the compliance year, it is reasonable to believe that conditional on other control variables including input and output prices, the mandates are unlikely to be correlated with the error terms in Equation (2). There could be concern that the RFS mandate is correlated with some macro factors that influence farmers' planting decisions and are not controlled for in our model; this could render the RFS mandate an invalid IV. As the mandated volume of soybean biodiesel for a year is predetermined, the correlation between the mandate and the current year macro factors is expected to be weak. Furthermore, the impact of the macro factors may have been well captured by crop prices and fertilizer prices. Therefore, given the predetermined nature of the mandate and the controls for output and input prices, we do not expect macro factors to influence the estimates through the mandate. We find support for this through our robustness checks.

For total cropland acreage, we adopt similar models as those in Equations (1) and (2):
κ ijt = θ 0 + θ 1 d ijt + θ 2 Λ ijt + θ 3 Z ijt + v ij + μ ijt , $$ {\kappa}_{\mathrm{ij}\mathrm{t}}={\theta}_0+{\theta}_1{d}_{\mathrm{ij}\mathrm{t}}+{\theta}_2{\boldsymbol{\varLambda}}_{\mathbf{ijt}}+{\theta}_3{\boldsymbol{Z}}_{\mathbf{ijt}}+{v}_{\mathrm{ij}}+{\mu}_{\mathrm{ij}\mathrm{t}}, $$ ()
A ijt a = η 0 + η 1 κ ̂ ijt + η 2 p ̂ it + η 3 f ̂ t + η 4 Λ ijt + α ij + ξ ijt , $$ {A}_{\mathrm{ij}\mathrm{t}}^a={\eta}_0+{\eta}_1{\hat{\kappa}}_{\mathrm{ij}\mathrm{t}}+{\eta}_2{\hat{p}}_{\mathrm{it}}+{\eta}_3{\hat{f}}_t+{\boldsymbol{\eta}}_{\mathbf{4}}{\boldsymbol{\varLambda}}_{\mathbf{ijt}}+{\alpha}_{\mathrm{ij}}+{\xi}_{\mathrm{ij}\mathrm{t}}, $$ ()
where Equation (3) is the first stage model similar to Equation (1), A a $$ {A}^a $$ is total cropland acreage; κ ̂ $$ \hat{\kappa} $$ , p ̂ $$ \hat{p} $$ , and f ̂ $$ \hat{f} $$ are the predicted soybean crushed based, predicted Laspeyres price index (to be discussed below, and predicted fertilizer price index, based on Equation 3); Λ $$ \Lambda $$ is the vector of other control variables including population density and time trends; Z $$ Z $$ is a vector of other IVs, including lagged crop stocks, RFS mandate, and lagged natural gas price; a ij $$ {a}_{ij} $$ is the county fixed effects, and ξ ijt $$ {\xi}_{ijt} $$ is the error term. Here θ's and η's are parameters of interest. Similar to the soybean acreage models, we can calculate the impact of one unit increase in biodiesel production on total cropland acreage by calculating the product of θ 1 $$ {\theta}_1 $$ and η 1 $$ {\eta}_1 $$ .

The price variables (i.e., crop prices and fertilizer price index) in Equations (2) and (4) are likely to be correlated with the error terms, indicating endogeneity of these variables. This is because crop price in year t is partially determined by the crop acreage planted in that year and in previous years. Moreover, fertilizer price index can be correlated with other input prices left in the error term that could affect farmers' acreage decisions.

To address the possible endogeneity of prices, we use lagged crop stocks as IVs for crop prices by following Li et al. (2019), Miao et al. (2016), and Roberts and Schlenker (2013). The rationale is that crop stocks from the previous year can influence the current year's crop supply, thereby correlating with anticipated crop prices. The lagged crop stocks will affect cropland acreage only through affecting crop prices. Specifically, we use lagged soybean stock as an IV for soybean price, and use lagged aggregate crop stock as an IV for the Laspeyres price index. The aggregate crop stock is calculated by following the approach described in Li et al. (2019).

Furthermore, we use natural gas price as an IV for fertilizer price index by following Li et al. (2019). Since natural gas is a major feedstock for producing ammonia a key component for nitrogen fertilizer, we expect that natural gas price is highly correlated with fertilizer price index. Moreover, natural gas price is unlikely to affect crop acreage through channels other than affecting fertilizer prices. This is because the major energy sources for soybean farming are diesel, gasoline, and electricity, with electricity mainly being used for irrigation, cooling, and lighting (Hitaj & Suttles, 2016). Given that over 90% of US soybean production is dryland-based, and that cooling and lighting on the farm are part of fixed costs accounting for a relatively small share of overall expenses, it is unlikely that natural gas price would affect cropland acreage through its effects on electricity price. However, the correlation between natural gas price and other energy prices that affect crop acreage, such as diesel, could be a concern. The correlation coefficient between natural gas price and diesel price is about 0.3 (calculated based on the annual price data over 1997–2024 obtained from the U.S. Energy Information Administration). Based on the estimates by the Cooperative Extension Service at Purdue University (Parsons, n.d.), a similar amount of diesel is consumed per acre for corn and for soybean production (6.12 and 5.77 gallons per acre, respectively). Diesel prices are therefore unlikely to influence corn versus soybean acreage. Given that natural gas prices and diesel prices are weakly correlated and that the difference in diesel requirement between corn and soybean production is small, we expect that the channel through which natural gas price affects crop acreage by influencing diesel prices is weak as well.

Alternative specification—Dynamic panel estimation

Since crop rotation practices may influence planting decisions, we extend our analysis to incorporate a dynamic panel approach by including the previous year's crop acreage as an explanatory variable. This approach enables us to account for the temporal dynamics and potential endogeneity present in the data, thereby enhancing the robustness of our analysis. To accomplish this, we employ the Arellano-Bond estimator as described in Equations (5) and (6). Following Arellano and Bond (1991), who introduced the use of a generalized method of moments estimator in short panels, further lagged levels of dependent acreage can serve as IVs for the lagged dependent variable, provided there is no serial correlation in the error term. In this framework, we use a 4-year lagged cropland acreage variable as IVs for the lagged cropland acreage variables considering the number of lagged dependent variables and the total length of the panel data. In order to calculate the effects of biodiesel, we continue to use biodiesel production as the IV for soybean crush, and also include the RFS mandate, lagged crop stocks, and lagged natural gas price as the IVs for soybean crush, crop prices, and fertilizer price index, respectively. The dynamic specification can be written as:
A ijt s = δ 0 + δ 1 A ijt − 1 s + δ 2 A ijt − 2 s + β 1 κ ̂ ijt + β 2 p it + β 3 Γ ijt + w ij + θ ijt , $$ {A}_{\mathrm{ij}\mathrm{t}}^s={\delta}_0+{\delta}_1{A}_{\mathrm{ij}\mathrm{t}-1}^s+{\delta}_2{A}_{\mathrm{ij}\mathrm{t}-2}^s+{\beta}_1{\hat{\kappa}}_{\mathrm{ij}\mathrm{t}}+{\beta}_2{p}_{\mathrm{it}}+{\boldsymbol{\beta}}_{\mathbf{3}}{\boldsymbol{\varGamma}}_{\mathbf{ijt}}+{w}_{\mathrm{ij}}+{\theta}_{\mathrm{ij}\mathrm{t}}, $$ ()
A ijt a = η 0 + η 1 A ijt − 1 a + η 2 κ ̂ ijt + η 3 p it + η 4 Λ ijt + α ij + ξ ijt , $$ {A}_{\mathrm{ij}\mathrm{t}}^a={\eta}_0+{\eta}_1{A}_{\mathrm{ij}\mathrm{t}-1}^a+{\eta}_2{\hat{\kappa}}_{\mathrm{ij}\mathrm{t}}+{\eta}_3{p}_{\mathrm{it}}+{\boldsymbol{\eta}}_{\mathbf{4}}{\boldsymbol{\varLambda}}_{\mathbf{ijt}}+{\alpha}_{\mathrm{ij}}+{\xi}_{\mathrm{ij}\mathrm{t}}, $$ ()
where the notation is the same as those in Equations (1-4).

DATA AND VARIABLES

This section documents the data and methods used to construct the variables for the analysis. As discussed above, we construct a county-level panel dataset over 2011–2020 across the contiguous United States.

Crop acreage

Data for the soybean acreage and total cropland acreage are obtained from the Cropland Data Layer (CDL) compiled by USDA NASS for each year over the period 2011–2020. Total cropland acreage is the sum of acreage under 106 crops excluding idle or fallow land. The use of CDL data on crop acreage raises concerns about measurement errors in the data. Various assessments have noted that the probability that the CDL correctly classifies corn or soybeans is roughly 95% on average for some major producing states (Hendricks et al., 2014), and that the measurement errors with CDL data were more likely to have been present in the early years of the data. For instance, Lark et al. (2017) documented that the CDL understated aggregate cropland area by nearly 11% relative to National Resources Inventory (NRI) and the Census of Agriculture estimates in the early years, but this gap shrank by 2012 to within 1% and 3%, suggesting that the accuracy of the CDL data has improved over time. This is also supported by the Metadata of the CDL in both 2011 and 2024, which include this note: “Classification accuracy is generally 85%–95% correct for the major crop-specific land cover categories.” (NASS, 2025). This indicates that over our sample period (2011–2020), the measurement accuracy of the CDL data about major crops and total cropland acreage was high and consistent. Additionally, we expect that classification error in the CDL data will be further mitigated through aggregation from the pixel level to a county or higher level and from individual crops to aggregate measures of cropland acreage. This is because, for instance, mistakenly classifying crop A as crop B does not affect total cropland acreage. Overall, we believe that measurement error issue in the CDL data over our sample period is not a major concern.

Although CDL offers land-use information at a fine resolution, we aggregate crop acreage up to the county level for several reasons. First, unlike an analysis at the field level where land-use status in the previous year must be considered when explaining current year land use to reflect the influence of crop rotation, this is not as much of a concern in an aggregate level (e.g., the county-level) analysis. This is because, as discussed above, a county consists of many farms and thus the impact of crop rotation on crop acreage in the county is likely to be small: some farms rotate out soybeans in a year but other farms rotate in this crop in the same year, masking the effect of rotation on total soybean acreage in the county. Second, some of the other control variables in our analysis are only available at the county level or even higher levels (e.g., population density, crop prices, and fertilizer prices). Thus, conducting the analysis at the grid level will not offer much gain in terms of harnessing variable variation. Third, similar to the county-level analysis, conducting grid-level analysis does not avoid the need to make arbitrary assumptions about the feedstock catchment area for a biorefinery. For example, studies that have utilized grid-level data to examine the effects of proximity to an ethanol plant on acreage have arbitrarily identified a geographic market size for the feedstock produced in a grid and assumed that the entire capacity of the ethanol plant within a given radius of a grid is assigned to that grid (e.g., Motamed et al., 2016).

Effective crush production

We obtained proprietary, facility-level data for the soybean crushing industry from CrushTraders (CrushTraders, 2023), a US market information company with specialty in soybeans, soybean meal, and soybean oil. Figure 2 depicts the locations of the 63 crushing facilities in the United States. Effective crush production at the county level is constructed by allocating the annual crush of each crushing facility to counties located within a 50-mile radius of the facility. Specifically, let k ft $$ {k}_{ft} $$ denote the quantity of soybeans (in million bushels per year) crushed (m) by crushing facility f in year t, and S jf $$ {S}_{jf} $$ denote the overlap area of county j $$ j $$ and the 50-mile-radius circle of crushing facility f. The soybean crush of facility f $$ f $$ in year t assigned to county j in year t is k jft c = k ft · S jf / π · 50 2 $$ {k}_{jf t}^c={k}_{ft}\cdotp {S}_{jf}/\left(\pi \cdotp {50}^2\right) $$ . For instance, if a crushing facility crushes 60 million bushels of soybeans per year, and if a county has 300 square miles located within the 50-mile radius of this crushing plant, then the county's effective soybean crush delivered to this facility is calculated as 60 × 300 / π · 50 2 ≈ 2.29 $$ 60\times 300/\left(\pi \cdotp {50}^2\right)\approx 2.29 $$ million bushels of soybeans. If a county j is in the catchment area of n crushing facilities, the total effective soybean crushed in the county in year t is then k jt c = ∑ f = 1 n k jft c $$ {k}_{jt}^c={\sum}_{f=1}^n{k}_{jft}^c $$ . Here, we choose 50-miles radius for two reasons. First, the average minimum distance from a soybean farm to a crushing plant is about 40 miles (Informa Economics, 2016). Second, a 50-mile radius feedstock catchment area is large enough to meet the demand from a crushing facility covered in our sample. To ensure the robustness of our estimates, we also constructed this variable using 25-mile and 100-mile radius. The related estimates are discussed in Robustness check section.

Crop prices

Soybean price is represented by 1-year lagged, state-level received soybean price obtained from the USDA NASS Quick Stats. The underlying assumption is that, as discussed in Li et al. (2019) and Miao et al. (2016), farmers may form their price expectation based on the received prices in the previous year. For the total cropland acreage model, crop price is represented by the 1-year lagged Laspeyres price index, which is constructed based on the state-level received prices for 10 major crops in the United States. Let p st L $$ {p}_{st}^L $$ denote the Laspeyres price index for state s in year t (i.e., the variable p it $$ {p}_{it} $$ in Equation 4), p lst $$ {p}_{lst} $$ denote the received price for crop l in state s in year t, and q lst $$ {q}_{lst} $$ the production of crop l in state s and year t. Then we have p st L ≡ ∑ l = 1 10 p lst q ls 2000 / ∑ l = 1 10 p ls 2000 q ls 2000 $$ {p}_{st}^L\equiv {\sum}_{l=1}^{10}{p}_{ls t}{q}_{ls2000}/{\sum}_{l=1}^{10}{p}_{ls2000}{q}_{ls2000} $$ , where state-level production of crop l in year 2000 is used as weight for the calculation. Similarly, if we use county-level production in year 2000 as weight, we can obtain a Laspeyres price index for each county c in state s as p cst L ≡ ∑ l = 1 10 p lst q lcs 2000 / ∑ l = 1 10 p ls 2000 q lcs 2000 $$ {p}_{cst}^L\equiv {\sum}_{l=1}^{10}{p}_{ls t}{q}_{lcs2000}/{\sum}_{l=1}^{10}{p}_{ls2000}{q}_{lcs2000} $$ . In our analysis, crop prices are deflated by using the GDP Implicit Price Deflator with 1996–2000 as the base year.

Other control variables

We control for national level fertilizer price index, county-level monthly precipitation in spring, county-level population density, and time trends as in Li et al. (2019). Fertilizer prices reflect general crop production costs and therefore affect farmers' land-use decisions. Even though N-based fertilizers are not used as much on soybean (because it is a legume), fertilizer price is a useful variable to include because most farmers who grow soybean also grow corn, and thus the price of fertilizer may incentivize more soybean relative to corn when prices are high. The national-level fertilizer price index (base year 1979) is obtained from the U.S. Bureau of Labor Statistics (2023). We use the one-year lagged price index as an independent variable because fertilizers are typically purchased in the fall prior to the next planting season.

Spring precipitation is expected to affect crop acreage due to the possibility of prevented planting caused by excessive rainfall. We therefore control county-specific monthly precipitation in March, April, and May. The data are obtained from the National Center for Environmental Information of the National Oceanic and Atmospheric Administration. Since we expect that higher population density would reduce the availability of agricultural land and therefore cropland acreage, we control for population density in our estimation. County-level population data are obtained from the datasets of “County Population Totals: 2010–2019” and “County Population Totals: 2020–2021” created by the U.S. Census Bureau. County-level population density is calculated by using county total population divided by county total area. Both linear and quadratic time trends are included to capture technological changes.

Instrumental variables

Data for the refinery-level biodiesel production based on soybean oil over 2011–2020 are obtained from the EPA. The dataset includes 116 unique biodiesel refineries that used soybean oil as feedstock to produce biodiesel or renewable diesel in the United States. The county-level effective biodiesel production (measured in million gallons) is used as the IV for soybean crushed for biodiesel. To construct this IV, we first match a biorefinery with a crushing facility based on the distance between them. Specifically, biorefinery A is matched with crushing facility B if and only if, within a 50-mile distance, A is the nearest biorefinery to B, and B is the nearest crushing facility to A. We assume that a biorefinery will obtain soybean oil first from its matched crushing facility, and that if the soybean oil demand of the biorefinery is larger than the production of the matched crushing facility, then the biorefinery will procure the shortfall from its second nearest crushing facility within the 50-mile radius, and so on. We also assume that a crushing facility prioritizes supplying soybean oil to its matched biodiesel refinery. Surplus after meeting the demand from the matched biodiesel refinery can be used to meet the demand from its second nearest biorefinery, and so on. Once we specify the quantity of biodiesel production associated with each crushing facility, we then assign the biodiesel production to a crushing facility's surrounding counties located in its 50-mile feedstock catchment areas using the same approach for calculating the county-level crushing production discussed in Effective crush production.

We acknowledge that these are strong assumptions due to data limitation, since information about soybean oil sources for individual biodiesel refineries is unavailable. Since transportation cost is non-trivial and is directly determined by distance, we expect that, all else being equal, cost-minimizing firms would prefer procuring feedstock from nearest sources, which provides a microeconomic foundation for this allocation algorithm.

The RFS annual volume requirements for biomass-based diesel each year over 2011–2020 are obtained from EPA. The crop stocks data are obtained from NASS Quickstats of the USDA. We use 2-year lagged soybean stocks to instrument soybean prices and 2-year lagged weighted aggregate crop stocks to instrument the Laspeyres Price Index. Specifically, the weighted aggregate crop stocks are a weighted sum of state-level stocks of the 10 major crops considered in this study, where the weight is the production share of a crop within a state over the year 1996–2000. Finally, the fertilizer price index is instrumented by the annual natural gas price (industrial price), which is obtained from the U.S. Energy Information Administration.

Table 1 presents the summary statistics of the variables used in the sample. An average county in our sample has about 29.6 thousand soybean acres and 104.7 thousand acres of total cropland. Figure 1c shows that both soybean acreage and total cropland acreage have been increasing during 2011–2020. Soybean acreage increased from around 70 million acres in 2011 to 90 million acres in 2017–2018, with a decrease in 2019 due to the United States-China trade war and excessive rainfall in the spring of that year, but largely returned to pre-2019 levels in 2020. Total cropland acreage increased from 300 to 330 million acres during the 2011–2020 period. The sample mean of effective soybean crushed in a county is 0.56 million bushels, and the biodiesel production assigned to a county is 0.17 million gallons. Average soybean received price is 7.6 dollars per bushel, and average crop price index is about 1.4. Crop prices increased slightly from 2011 to 2012 but decreased and then remained relatively stable from 2014 to 2018 (Figure 1d), followed by large fluctuations over 2019–2020.

TABLE 1. Summary statistics of variables.
Variables Mean SD Min. Max.
Dependent variables
Soybean acreage (in 1000 acres) 29.6 486 0.0 605.2
Total cropland acreage (in 1000 acres) 104.7 127.4 0.0 1138.6
Independent variables
Soybean crushed (million bushels) 0.56 1.5 0.0 17.4
Soybean received price ($/bushel, base year: 1996–2000) 7.6 1.7 5.2 11.1
Laspeyers price index (state, base year: 2000) 1.4 0.4 0.3 2.5
Fertilizer price index (base year 1979) 222.8 87.7 193.7 310
Population density (persons/square mile) 262.0 1850.7 0.1 74,064
March precipitation (inches) 3.1 2.4 0.0 26.6
April precipitation (inches) 3.9 2.5 0.0 18.0
May precipitation (inches) 4.2 2.5 0.0 24.7
Instrumental variables
Effective biodiesel production (million gallons) 0.17 0.8 0 10.7
Biomass-based mandate (billion gallons) 1.7 0.5 0.8 2.4
Soybean stocks (bushels) 92,261.6 130,069 31 669,369
Weighted aggregate crop stocks (weighted by state production share) 1.0 0.3 0.3 1.6
Natural gas price ($/1000 cubic feet, base year: 1996–2000) 3.0 0.6 2.2 4.1
  • Note: The sample is summarized at the county level over the period of 2011–2020.

RESULTS

We estimated the following model specifications: a fixed effects model without considering the endogeneity issue (see results in Column [1] FE in Tables 2 and 4), fixed effects models addressing the endogeneity issue using the IV approach (see results in Columns [2]–[4] FE-IV of Tables 2 and 4), and Arellano-Bond estimator (Column [5] A–B in Tables 2 and 4). The results from Hausman's endogeneity tests for soybean crushed, crop price, and fertilizer price index show that all three variables are endogenous in both soybean acreage and total cropland acreage models (p-value < 0.001). By comparing results from Column (1) and those from Columns (2) to (4), we can see the importance of addressing the endogeneity issue. Model specifications in Columns (3) and (4) are the same as that in Column (2) except that Column (3) excludes soybean crushed as an explanatory variable whereas Column (4) excludes crop prices. Estimating model specifications in Columns (3) and (4) allows us to examine the presence of omitted variable bias when either crop prices or soybean crushed are excluded as determinants of crop acreage over the 2011–2020 period. Model specification in Column (5), based on the Arellano-Bond (A-B) estimator, allows us to control for the effects of previous year planting decisions (crop rotation) while addressing endogeneity issues.

TABLE 2. Determinants of soybean acreage.
Soybean acreage (1) FE (2) FE-IV (3) FE-IV (4) FE-IV (5) A-B
L.Soybean price 0.277*** 0.926*** −0.394 0.303
(0.0836) (0.205) (0.587) (0.805)
Soybean crushed (mil. bu.) 0.825 6.895*** 5.857*** 2.622***
(2.233) (2.070) (2.013) (0.476)
Lagged fertilizer price −0.0499*** 0.0268*** −0.0749 0.0269*** −0.0555
(0.00613) (0.00885) (0.0500) (0.00904) (0.0445)
Population density −0.00589** −0.00580** −0.00573* −0.00590** −0.000291*
(0.00280) (0.00230) (0.00295) (0.00240) (0.00016)
March precipitation 0.432*** 0.433*** 0.376*** 0.351*** −0.184
(0.0699) (0.0683) (0.0759) (0.0646) (0.0139)
April precipitation −0.327*** −0.404*** −0.245* −0.330*** −0.0622
(0.0583) (0.0681) (0.129) (0.0627) (0.089)
May precipitation −0.231*** −0.244*** −0.231*** −0.245*** −0.389***
(0.0556) (0.0549) (0.0570) (0.0542) (0.091)
Linear time trend 2.880*** 5.486*** 1.433 4.357***
(0.333) (0.597) (2.095) (0.500)
Quadratic time trend −0.241*** −0.321*** −0.190** −0.271***
(0.0270) (0.0347) (0.0741) (0.0306)
L.Soybean acreage 1.387***
(0.407)
L2.Soybean acreage −0.532
(0.421)
Constant 34.99*** 16.73***
(2.618) (5.633)
Observations 24,147 24,147 24,147 24,147 21,464
Kleibergen-Paap rk LM statistic (p-value) - <0.0001 <0.0001 <0.0001 <0.0001
Cragg-Donald Wald F statistic - 849.08 321.52 922.37 0.616
Kleibergen-Paap rk Wald F statistic - 71.926 54.531 70.125 -
Hansen J statistic (p-value) - 0.5128 - <0.0001 <0.0001
  • Note: Robust and clustered standard errors in parentheses, and (1)–(4) are clustered to the crop reporting district level. Specifications of the models: (1) Fixed Effects (FE) model; (2) FE-IV (Instrumental variables: state-level lagged soybean stocks, effective biodiesel production assuming 50 miles from a crushing facility, Renewable Fuel Standard (RFS) mandated volume of biomass-based diesel, lagged natural gas price); (3) FE-IV (Instrumental variables: state-level lagged soybean stocks, lagged natural gas price); (4) FE-IV (Instrumental variables: effective biodiesel production assuming 50 miles from a crushing facility, RFS mandated volume of biomass-based diesel, lagged natural gas price); (5) Arellano-Bond estimator: use lagged 4 to instrument lagged dependent variables.
  • a The test statistics are Arellano-Bond test for AR(1) and AR(2) in first differences, respectively.
  • *p < 0.1; **p < 0.05; ***p < 0.01.

Note that all the FE-IV models in Table 2 and Table 4 pass the under-identification test and weak instrument tests. The p-values of the Kleibergen-Paap rk LM statistic are much smaller than the critical value of 0.01, indicating that we can reject the null of no correlation between the endogenous variables and the IVs at the 1% significance level. The two weak identification test statistics, the Cragg-Donald F Wald statistic and the Kleibergen-Paap Wald rk F statistic, are both greater than 10. This implies that we can reject the null hypothesis that the IVs are weakly correlated with the endogenous variables (Stock & Yogo, 2005). These test results support the use of FE-IV models as our preferred approach. For the Arellano-Bond estimators, we include 2-year lagged soybean acreage and 1-year lagged total cropland acreage as explanatory variables based on the test statistics of Arellano-Bond tests for AR(1) and AR(2) in first differences. We include Hansen J overidentification test for Arellano-Bond estimators; however, the test statistics reject the null hypothesis that all IVs are valid in the model. We, therefore, use results in Column (2) of Tables 2 and 4 as our preferred model specification, which passes the Hansen J overidentification test at the 10% significance level (p-value = 0.5128).

Soybean acreage

Table 2 presents the regression results for soybean acreage models. By comparing Columns (1) and (2) we can see that ignoring the endogeneity of soybean crushed and of soybean price will result in a nearly 10-fold underestimation of the true effects of crushing. Results in Column (2) of Table 2, our main results, show that soybean crushed and lagged soybean price have positive and statistically significant effects on soybean acreage. Holding all other factors constant, a 0.1-million-bushel increase in effective soybean crushed in a county (about 18% of the sample mean) corresponds to an increase of about 689.5 acres in soybean acreage (equivalent to around 2.3% of the sample mean of soybean acreage per county). A one-dollar increase in soybean received price, which represents about a 13% increase in average soybean price, will increase soybean acreage in a county by 926 acres, about 3.1% of average soybean acreage in a county. The short-run effect of crushing on soybean acreage based on the Arellano-Bond estimator (Column [5]) is smaller than the FE-IV results, showing that a 0.1-million increase in soybean crushed contributes to a 262.2-acre increase in soybean acreage in a county (less than 1% average soybean acreage in a county). However, the long-run effect of a 0.1-million increase in soybean crushed is much larger: a 1808-acre increase in soybean acreage. Note that the results in the Arellano-Bond estimators should be interpreted with caution because the Hansen J overidentification test rejects the null hypothesis that all IVs are valid in the model.

The fertilizer price index has a positive and statistically significant impact on soybean acreage, as soybean does not need as much fertilizer as corn. Increased fertilizer prices may make growing corn less appealing than growing soybean. Also, we find that March precipitation increases soybean acreage, whereas April and May precipitation does the opposite. A plausible explanation is that excessive rainfall in March may prevent farmers from planting corn or other crops that are usually planted in early spring, while excessive rainfall in April, or especially in May, prevents soybean planting (Bastidas et al., 2008). Population density has a negative and statistically significant effect, indicating that all else being equal, higher population density in a county will reduce cropland acreage in that county. The coefficients of both linear time trend and quadratic time trend are statistically significant, with the coefficient of the former being positive and the latter negative, indicating an inverse-U-shaped relationship between crop acreage and time trend.

Next, we combine the first stage results (i.e., results from models illustrated in Equations 1 and 3) with those from the second stage to examine the effects of biodiesel production. Table 3 shows the first stage results of preferred specification in Column (2) of Table 2. From Table 3 we find that, everything else being equal, a 0.1-million-gallon increase in effective biodiesel production in a county contributes to a 0.028-million-bushel increase in soybeans crushed in that county. This crushing-to-biodiesel responsiveness ratio is smaller than the current technical conversion rate from soybeans to biodiesel (1 bushel of soybeans can be converted to 1.5 gallons of biodiesel; Hay, 2019) and could reflect the possibility that some of the demand for additional crush for biodiesel is being met by reducing the amount of crushing for meeting needs for food and feed. Combined with the second-stage results, we calculate that soybean acreage increases by approximately 193.1 acres in a county for a 0.1-million-gallon increase in biodiesel production. Nationally, this suggests that a 1-billion-gallon increase in soybean oil-based biodiesel will increase soybean acreage by 1.93 million acres.

TABLE 3. First stage results of the preferred specification in Column (2) of Table 2.
(1) (2) (3)
Lagged soybean price Soybean crushed (mil. bu.) Lagged fertilizer price
Biodiesel production 0.0492*** 0.280*** −0.827**
(0.0226986) (0.0205799) (0.5541302)
Population density −0.0000826 −0.0000411** 0.00648**
(0.0000848) (0.0000387) (0.0017328)
March precipitation −0.0990*** 0.00685*** −0.512***
(0.0077853) (0.0014103) (0.1484237)
April precipitation 0.0670*** −0.00668*** 1.016***
(0.0114449) (0.0014646) (0.1241532)
May precipitation 0.0172*** 0.00110** 0.572***
(0.0054503) (0.0008576) (0.1528645)
Linear time trend −2.357*** −0.0452*** −62.95***
(0.0344632) (0.0203371) (0.9006509)
Quadratic time trend 0.0950*** 0.00198*** 2.083***
(0.0012862) (0.0010432) (0.0324991)
Lagged soybean stocks 0.00000122*** 0.00000119*** 0.000101***
(4.25e-07) (2.19e-07) (0.0000147)
RFS mandate 3.035*** 0.199*** 128.6***
(0.1134965) (0.0538761) (2.77938)
Lagged natural gas price −0.917*** 0.00721*** 8.796***
(0.0138045) (0.0032499) (0.1862604)
Observations 24,147 24,147 24,147
  • Abbreviation: RFS, Renewable Fuel Standard.
  • *p < 0.1; **p < 0.05; ***p < 0.01.

Total acreage

Results for the total cropland acreage models are presented in Table 4. Column (1) of the table shows that when the endogeneity issue is ignored, one would obtain a highly biased estimate (i.e., −9.558), with the sign of the coefficient even changing for the soybean crushed. Similar to Table 2, results in Column (2) in Table 4 are our main results, and they show that a 0.1-million-bushel increase in soybean crushed in a county increases the aggregate cropland acreage of that county by 321.8 acres (about 0.3% of the sample mean of aggregate crop acreage in a county). The magnitude is smaller than the impact on soybean acreage, which implies that there is some displacement across crops. The results of the Arellano-Bond estimator (see Column [5]) show similar but smaller short-run effects of soybean crushed on total cropland acreage, with a 0.1-million-gallon increase in soybean crushed in a county increasing the aggregate cropland acreage of that county by 220.7 acres. Again, the long-run effect is much larger (about 2982 acres). Similar to that in Table 2, the Arellano-Bond estimation in Column (5) of Table 4 does not pass the overidentification test, indicating that its results should be interpreted with caution. Using the first stage results (see Table 5) of our preferred specification (Column [2] of Table 4), we find that total cropland acreage increases by approximately 96.2 acres in a county for every 0.1-million-gallon increase in biodiesel production (calculated by using 0.1 × 3.218 × 0.299 × 1000). Nationally, this suggests that a 1-billion-gallon increase in soybean oil-based biodiesel will increase total cropland acreage by 0.96 million acres.

TABLE 4. Determinants of total cropland acreage.
Total cropland acreage (1) FE (2) FE-IV (3) FE-IV (4) FE-IV (5) A-B
Lagged price index 0.449 5.999* 5.646* 4.753***
(1.806) (3.576) (3.372) (1.421)
L.Soybean crushed (mil. bu.) −9.558** 3.218* 1.040 2.207***
(4.418) (1.952) (1.539) (0.438)
Lagged fertilizer price −0.0625*** 0.0514** 0.0292 0.0382** −0.0578***
(0.0103) (0.0232) (0.0347) (0.0182) (0.0116)
Population density −0.0100* −0.00980* −0.01000* −0.00948** −0.000432**
(0.00541) (0.00506) (0.00519) (0.00472) (0.000181)
Linear time trend 266.0 980.8*** 895.1*** 480.8***
(178.6) (341.4) (337.3) (130.5)
Quadratic time trend −0.0659 −0.243*** −0.221*** −0.119***
(0.0443) (0.0845) (0.0835) (0.0323)
L.Total CDL acreage 0.926***
(0.0162)
Constant −268283.4 15.67***
(180129.0) (2.444)
Observations 27,281 27,281 27,281 27,281 27,281
Kleibergen-Paap rk LM statistic (p-value) - <0.0001 <0.0001 <0.0001 <0.0001
Cragg-Donald Wald F statistic - 675.08 3588.49 1123.84 <0.0001
Kleibergen-Paap rk Wald F statistic - 215.08 2596.55 213.11 -
Hansen J statistic (p-value) - 0.071 - <0.0001 <0.0001
  • Note: Robust and clustered standard errors in parentheses, and (1)–(4) are clustered to the crop reporting district level. Specifications of the models: (1) Fixed Effects (FE) model; (2) FE-IV (Instrumental variables: state-level lagged weighted crop stocks, effective biodiesel production assuming 50 miles from a crushing facility, Renewable Fuel Standard (RFS) mandated volume of biomass-based diesel, lagged natural gas price); (3) FE-IV (Instrumental variables: state-level lagged weighted crop stocks, lagged natural gas price); (4) FE-IV (Instrumental variables: effective biodiesel production assuming 50 miles from a crushing facility, RFS mandated volume of biomass-based diesel, lagged natural gas price); (5) Arellano-Bond estimator: use lagged 4 to instrument lagged dependent variables.
  • Abbreviation: CDL, Cropland Data Layer.
  • a The test statistics are Arellano-Bond test for AR(1) in first differences, Arellano-Bond test for AR(2) in first differences.
  • *p < 0.1; **p < 0.05; ***p < 0.01.
TABLE 5. First stage results of the preferred specification in Column (2) of Table 4.
(1) (2) (3)
Lagged price index Soybean crushed (mil. bu.) Lagged fertilizer price
Biodiesel production −0.0117** 0.299*** 1.654***
(0.00476) (0.0123) (0.345)
Population density 0.0000288 −0.0000651*** −0.00161
(0.0000220) (0.0000156) (0.00200)
Linear time trend −84.32*** 2.082 −7450.1***
(0.586) (1.623) (54.53)
Quadratic time trend 0.0209*** −0.000521 1.841***
(0.000145) (0.000402) (0.0135)
Lagged crop stocks −0.751*** 0.418*** −42.29***
(0.0113) (0.0185) (0.951)
RFS mandate −0.357*** 0.143*** 86.23***
(0.00929) (0.0239) (0.786)
Lagged natural gas price −0.160*** 0.0300*** 8.714***
(0.00270) (0.00171) (0.174)
Observations 27,281 27,281 27,281
  • Abbreviation: RFS, Renewable Fuel Standard.
  • *p < 0.1; **p < 0.05; ***p < 0.01.

Our results in Table 4 also show that a one-unit increase (or, equivalently, about a 71.4% increase from the sample mean) in the lagged crop price index contributes to about 5999 acres (or, equivalently, about 5.7%) of increase in aggregate cropland acreage in a county. The first stage results of the crop price index regression in Column (1) of Table 5 show that the coefficients of biodiesel production and RFS mandate are negative (−0.0117 and −0.357, respectively). The coefficient of biodiesel production is negligible: a 0.1-million-gallon (about 59% of sample mean) increase in biodiesel production in a county is associated with a decrease in state-level aggregated price index by about 0.08% (calculated by using 0.1 × 0.0117/1.4, where 1.4 is the sample mean of crop price index). The negative sign of the RFS mandate can be partially explained by the fact that we use the RFS mandate for biomass-based diesel, which can be produced from soybean oil, waste oil, and animal fats. According to EIA (2022), soybean oil accounts for about 44% of feedstock for biomass-based diesel, and the remaining part is largely supplied by waste oil or animal fats. It is likely that, holding the soybean-oil-based biodiesel production constant, the use of waste oil and animal fats dampens the demand for crops and thus decreases the crop price index.

Robustness check

We first examine the robustness of our results to the inclusion of year fixed effects. Column (1) in Tables S1 and S2 respectively presents the results of soybean and total acreage models while controlling for year fixed effects. Note that due to limited spatial variation in state-level prices and no spatial variation in the national-level fertilizer price index, these price variables are excluded when we include year fixed effects, following the practice in Y. Wang et al. (2020). The results show that the estimate of the coefficient of soybean crushed is quite close to the estimate in our main model (6.974 with year fixed effects vs. 6.895 without year fixed effects for the soybean acreage regression and 2.103 vs. 3.218 for the total acreage regression).

Using lagged crop price is equivalent to assuming that farmers have naïve expectations. Futures price, allowing more sophisticated expectation behavior for farmers, can be a reasonable alternative to lagged received price. We have, therefore, included an additional robustness check that controls for futures price of soybeans in the regression and found that the results remain robust (see Column [2] in Table S1). For instance, the estimate of soybean crushed coefficient is now 7.809, comparable to the estimate of 6.895 in our main model, and both are statistically significant. The coefficient of soybean price reduces from 0.926 to 0.561 when we switch from received price to futures price. However, the 95% confidence intervals of the two estimates overlap ([0.524, 1.328] vs. [0.291, 0.832]), indicating that the difference between the two may not be statistically significant.

The US crop market is well integrated, and the national-level stock may play a larger role in determining crop prices than does the state-level stock. We, therefore, include a robustness check using national-level stocks as the IV for crop prices. These results are provided in Column (3) in Table S1 for the soybean acreage regression and Column (2) in Table S2 for the total acreage regression. The results remained largely consistent with those obtained using state-level stocks, with the new estimate of soybean crushed coefficient at 6.026 versus 6.895 in our main model that uses state-level stock as the IV, and the new estimate of soybean price coefficient at 0.540 versus 0.926 in our main model. These results suggest that our findings are robust to the use of state-level or national-level stocks as IVs. For total acreage models, the estimated coefficient of soybean crushed with national stock as an IV is 2.301, whereas, the estimate with state-level stock as an IV is 3.218. For the estimates of price coefficients, the two corresponding numbers are 6.485 and 5.999, respectively. Note that because national stock lacks spatial variation, the estimates from models with national stock as an IV have larger standard errors.

The validity of the RFS mandate as an IV may be questionable because it could be correlated with some macroeconomic factors that also affect farmers' planting decisions. To address this concern, we re-estimated our preferred regression models by excluding the RFS mandate as an IV (see Column [4] in Table S1 and Column [3] in Table S2). We find that the estimate of the coefficient of soybean crushed in the soybean acreage model (6.604) is also quite close to the estimate in our main model (6.895). The same finding holds for the estimates of the soybean price coefficients (0.614 vs. 0.926). For total acreage regressions, the estimate of the soybean crushed coefficient under this new specification is 2.785, slightly smaller than the estimate under our preferred model, 3.218; and the estimate of the price index coefficient is 6.541, slightly larger than the estimate under our preferred model, 5.999.

In Tables S3 and S4 we examine the robustness of the results of the preferred model specifications (i.e., Column [2] in Table 2 and Table 4) by examining a different catchment area assumption for crushing facilities. We use 25-mile and 100-mile radii for the catchment areas, respectively, to check spatial reach and influence of soybean crushing facilities on surrounding land use. The impact from using a 25-mile radius gives a slightly smaller effect of soybean crushed, while the results from 100 miles give a larger effect. The direction and statistical significance do not change compared with our preferred models.

We also construct the county-level effective biodiesel production assuming a different maximum transportation distance between a biodiesel refinery and a crushing facility. Recall that in the main specification in Tables 2 and 4, this maximum transportation distance is assumed to be 50 miles. Results with the assumption of a maximum distance of 25 and 100 miles are presented in Tables S5 and S6, respectively. For the soybean acreage models, the coefficients of soybean crushed under the two alternative distance assumptions are 8.436 and 6.108, close to the corresponding coefficient, 6.895, under the original assumption. For total cropland acreage models, the coefficient of soybean crushed under the 25-mile assumption is close to the coefficient under the original assumption (4.016 vs. 3.218). However, the coefficient of soybean crushed under the 100-mile assumption is positive but statistically insignificant.

DISCUSSION

To contextualize the land-use change effects of biodiesel and crop prices, we compute the own-price acreage elasticities and the acreage elasticity with respect to soybean crushed and biodiesel production at the sample means based on the results from our preferred model specification (Column [2] in Tables 2 and 4). The results are presented in Table 6. The soybean acreage elasticity with respect to soybean crush is approximately 0.13, suggesting that a 1% increase in a county's effective soybean crushing production would result in a 0.13% increase in soybean acreage in that county. The elasticity of soybean acreage with respect to biodiesel production is about 0.011, which is much smaller than the corresponding value of 0.1 for corn ethanol calculated by Li et al. (2019). The total acreage elasticity with respect to biodiesel production is about 0.002, which is smaller than that of corn ethanol of 0.024. The elasticity of total cropland acreage with respect to soybean crushed is much smaller than the elasticity of soybean acreage with respect to soybean crushed (0.017 vs. 0.13). The elasticity of aggregate cropland acreage with respect to the Laspeyres price index is about 0.079. This magnitude is consistent with the estimates of 0.077–0.089 from existing studies (e.g., Li et al., 2019; Roberts & Schlenker, 2013).

TABLE 6. Elasticities and cropland expansion over 2011–2020 based on preferred models.
Values
Soybean acreage elasticity w.r.t.
Soybean crushed 0.130
Soybean received price 0.237
Biodiesel production 0.011
Soybean acreage expansion due to
Increase in local effective biodiesel production over 2011–2020 (mil. acres) 1.24
Biodiesel-driven increase in soybean price over 2011–2020 (mil. acres) 0.73
Total expansion (sum of the above two items, mil. acres) 1.97
Total acreage elasticity w.r.t.
Soybean crushed 0.017
Price index 0.079
Biodiesel production 0.002
Cropland expansion due to
Increase in local effective biodiesel production over 2011–2020 (mil. acres) 0.62
Biodiesel-driven increase in aggregated crop price index over 2011–2020 (mil. acres) 0.58
Total expansion (sum of the above two items, mil. acres) 1.20
  • Note: For soybean acreage, the elasticities under the preferred specification are calculated based on regression results under Column (2) in Table 2. For total acreage, the elasticities under the preferred specification are calculated based on regression results under Column (2) in Table 4. The price increase assumption is based on tab. 3 of W. Wang and Khanna (2023), where soybean price increases by 8.2% under their Scenario 3 with the addition of the soybean and corn oil biodiesel.

The predicted changes in county-level soybean acreage and total cropland acreage attributable to biodiesel production while holding all other variables constant are shown in Table 6 and Figure 3. The changes are calculated based on the coefficients from our preferred specifications and their corresponding first-stage results (i.e., Column [2] in Tables 2–5). Given the increase in soybean oil-based biodiesel production over 2011–2020 (640 million gallons in our dataset), the soybean acreage expansion directly attributable to this local effective biodiesel production change, termed “direct effect,” is about 1.24 million acres, the increase in soybean acres observed mainly in the heartland region because this is where most crushing plants are located (Figure 3a). The aggregate cropland acreage increases by 0.62 million acres over this period due to the direct effect, indicating that land-use changes occurred mainly at the intensive margin instead of the extensive margin.

Details are in the caption following the image
FIGURE 3
Open in figure viewerPowerPoint
Changes in soybean acreage (a, b) and total cropland acreage (c, d) due to the increase in biodiesel production and crop price (in 1000 acres). Maps (a) and (c) are for changes attributable to local effective biodiesel production change over the 2011–2020 period; maps (b) and (d) represent changes attributable to price change caused by biodiesel production over the 2011–2020 period.

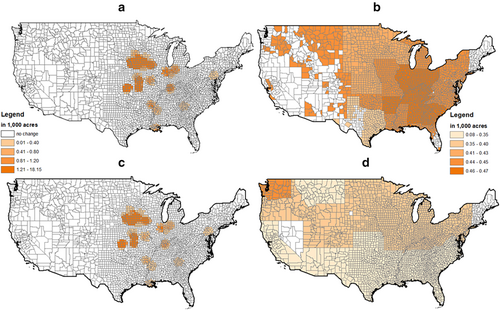
With the growing production of soybean-based biodiesel, soybean prices, and overall crop prices would increase in both soybean-producing regions and other crop-producing areas. W. Wang and Khanna (2023) estimated that soybean price and aggregate crop price increased by 8.2% and 4.56% respectively, compared with a no-biodiesel scenario due to the increase in annual biodiesel production from 91 million gallons in 2005 to 1.282 billion gallons in 2018. Applying these estimates, we find that compared with the case of no biodiesel expansion, soybean acreage increased by about 0.73 million acres due to the biodiesel-production-driven soybean price increase, termed “indirect effect” while aggregate cropland acreage expanded by about 0.58 million acres due to the indirect effect of biodiesel production expansion. When examining changes spatially, we find a relatively even distribution across all the soybean-producing counties given the increase in crop prices (Figure 3b). We also find that the southern states experience smaller overall land-use change than other crop-producing regions, as the overall crop price change in this region is relatively small (Figure 3d).

We convert our estimates into cropland change in million acres per billion gallons of biodiesel produced and compare our results with those from simulation studies (see Figure 4; more details are included in Table S8). Based on results in Table 6, one can readily check that the direct and indirect effects of 1 billion gallons of biodiesel production are 0.96 and 0.91 million acres, respectively, resulting in a total land-use effect of 1.87 million acres. Note that the general equilibrium models, primarily the Global Trade Analysis Project (GTAP) models, reported increases of 0.01–0.07 million acres in total cropland per billion gallons of biodiesel production. The partial equilibrium model developed by W. Wang and Khanna (2023) estimated a much larger effect, ranging from 0.78 to 1.5 million acres per billion gallons. Our estimate of total cropland expansion per billion gallons of biodiesel is close to the range reported by W. Wang and Khanna (2023) and is significantly larger than the estimates from GTAP and other computable general equilibrium models. This is consistent with the literature on corn ethanol, where in a review Austin et al. (2022) found that empirical results were comparable to results from partial equilibrium models, both of which were larger than results from computable general equilibrium models like GTAP. Our results for soybean biodiesel are also consistent with the EPA's Model Comparison Exercise, which found that across four models (two general equilibrium models and two partial equilibrium models) an increase in soybean biodiesel production by 1 billion gallons increased soybean acreage in the United States by 0.7–6.7 million acres across models, and increased total cropland by 0.2–1.7 million acres (EPA, 2023).

Details are in the caption following the image
FIGURE 4
Open in figure viewerPowerPoint
Reported aggregate cropland expansion due to biodiesel production expansion among existing studies. The direct effect indicates acreage expansion due to an increase in local effective biodiesel production, and the indirect effect indicates acreage expansion due to an increase in the aggregated crop price index caused by soybean-oil-based biodiesel production. The total effect is the sum of the direct and indirect effects. The Wang and Khanna (2023) (BEPAM [a]) estimate refers to the scenario with no pastureland, while the Wang and Khanna (2023) (BEPAM [b]) scenario includes pastureland. Here GLOBIOM stands for Global Biosphere Management Model, GCAM for Global Change Analysis Model, GTAP for Global Trade Project, ADAGE for Applied Dynamic Analysis of the Global Economy, BEPAM for Biofuel and Environmental Policy Analysis Model, GTAP-BIO for GTAP-Biofuel, and CARB for California Air Resources Board.

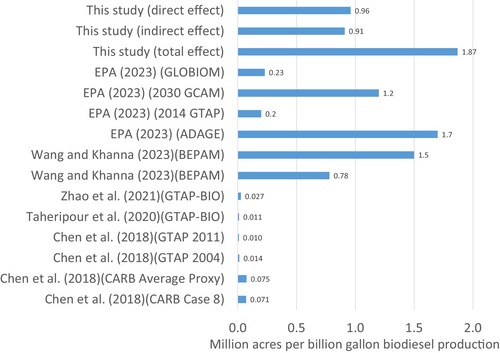
To better understand the land-use intensity of biodiesel, we also compare it with that of corn ethanol. Li et al. (2019) empirically estimated 0.599 million acres of total cropland expansion per billion gallons of corn-based ethanol via the direct effect, while Lark et al. (2022) estimated 0.94 million acres per billion gallons. Our estimate indicates that on a gallon-to-gallon basis, the direct land-use effect of biodiesel production is approximately 1.6 times the direct land-use effect of corn ethanol estimated by Li et al. (2019), and slightly more than that estimated by Lark et al. (2022).

Given that the production capacity of biofuels (particularly renewable diesel) continues to expand (Buckner & Peterson, 2023), our findings have direct policy implications. First, the land-use intensity of soybean oil-based biodiesel production identified in this study can assist policymakers in establishing practical and ecologically sound targets for soybean-based renewable energy production such as biodiesel and sustainable aviation fuels. Second, the comparison between biodiesel and ethanol in terms of land-use intensity illustrated above may provide policymakers with support to better balance the current biofuel portfolio and thus enhance its sustainability. Third, by identifying areas where land-use change is associated with soybean oil-based biodiesel production, our findings can facilitate the establishment of area-specific safeguard measures to monitor or to prevent non-cropland from being converted, improving the environmental sustainability of biodiesel production.

CONCLUSION

This study develops an empirical framework to quantify the impact of soybean biodiesel production on both soybean acreage and total cropland acreage, using EPA data for biodiesel production and proprietary data for soybean crushing facilities. Our two-stage model, which estimates the relationship between biodiesel production and soybean crush in the first stage and then evaluates the local land-use effects of crushing facilities in the second stage, offers a nuanced understanding of these interactions. This method allows us to infer the broader impacts of biodiesel production on land-use changes and control for the endogeneity of crush at the same time.

Our analysis reveals a positive and significant relationship between local effective biodiesel production, soybean crushed, and cropland acreage at the county level. Over 2011–2020, the soybean acreage expansion and total cropland expansion attributable to the 640-million-gallon increase in local effective soybean oil-based biodiesel production are 1.24 and 0.62 million acres, respectively. Thus, on a national basis, we find that a 1-billion-gallon increase in soybean biodiesel production triggers an increase of 1.93 million acres of soybean acres and 0.96 million acres of total cropland, excluding the land-use change caused by biodiesel-driven price increase. Our estimated biodiesel-induced land-use change is smaller than the level expected simply based on technical coefficients of crop yield and conversion of feedstock to fuel, estimated to be 11.7–16.7 million acres of soybean acreage per 1-billion-gallon increase in soybean-based biofuels (Swanson & Smith, 2024). We also find that aggregate cropland remains relatively insensitive to crop prices. While the land-use change intensity (i.e., on a per gallon basis) of soybean-based biodiesel is larger than that of corn ethanol, the acreage elasticity with respect to biodiesel production is smaller. Possible reasons include the smaller total biodiesel production volume and soybean oil demand compared with corn ethanol and the intertwined markets for soybean oil and meal, which may dampen the direct responsiveness of land-use change to biodiesel production.

Our results are largely consistent across various model specifications and robustness checks, corroborating previous findings and extending the understanding of biodiesel impacts on agricultural land use. Our empirical estimates are larger than those of computable general equilibrium simulation models; this is consistent with a recent synthesis of literature on estimates of the effects of corn ethanol production on land use, which found that empirical estimates were comparable with partial equilibrium-based estimates, and both were higher than computable general equilibrium model-based estimates like GTAP (Austin et al., 2022). Future research can explore more deeply the nuanced interactions between biodiesel production, soybean oil, and land use. Current crop prices highlight soybeans as an economically attractive feedstock option. There is a growing literature developing algorithms to correct the potential measurement error before using the CDL data to quantify the impact of bioenergy development on land-use changes (e.g., Pates et al., 2025). We leave it to future research to analyze the implications of increased accuracy in CDL data and to explore alternative datasets such as MODIS and Landsat data when examining the land-use impact of bioenergy development. Furthermore, investigating the sustainability and environmental impacts of biodiesel production, alongside comparisons of different biofuel pathways, will deepen our understanding of their effects on land use. This study establishes a robust basis for future research and policy discussions on land-use impacts of biofuels.

ACKNOWLEDGMENTS

This work was partly supported by the U.S. EPA under contract 68HERD20A0004. Ruiqing Miao gratefully acknowledges the support from the Alabama Agricultural Experiment Station and the Hatch Program of the National Institute of Food and Agriculture, U.S. Department of Agriculture. Madhu Khanna also gratefully acknowleges support from the Hatch Program of the National Institute of Food and Agriculture, U.S. Department of Agriculture. We thank Kent Woods from Crush Traders for providing the data for this research. We also thank Jennifer Phelan for coordinating the project, and Robert Sabo and David Smith at the U.S. EPA for their review of an earlier draft. Comments from Andrew Hultgren, Nicholas Paulson, two anonymous referees, and the 2023 AAEA Annual Conference participants are much appreciated. The views expressed in this manuscript are those of the authors and do not necessarily represent the views or policies of the U.S. Environmental Protection Agency. All remaining errors are our own.

    CONFLICT OF INTEREST STATEMENT

    The authors declare no conflicts of interest.

    Endnotes

  1. 1 In subsequent discussion, we will use the term “biodiesel” as a concise reference including both biodiesel and renewable diesel in our analysis. Although biodiesel and renewable diesel have distinct end-product characteristics, they are both made from same types of feedstocks, for example, vegetable oils or animal fats. In this paper, we focus on the facilities using soybean oil as feedstock, so combining the two renewables does not change the implications of this study.
  2. 2 Note that all comparisons between ethanol and biodiesel focus on land-use intensity and are not adjusted based on the energy content of these two fuels.
  3. 3 Lack of facility level data from the USEPA for those early years precluded the inclusion of data prior to 2011. There was much less production in that interval as well, and likely none due to the RFS Program (Miller et al., 2024), thus effect on land prior to 2011 are assumed to be small. Data for the years following 2020 is not included to avoid confounding effects of the spike in oil prices and fertilizer prices due to the Ukraine war. The data trends do not show significant changes in cropland acreage, soybean crushing, biodiesel production, or other variables in 2020, suggesting that the impact of COVID-19 on our 2011–2020 study is minimal. Although the United Staes-China trade war and the excessive rainfall in early spring of 2019 reduced soybean planted acreage significantly in that year, the acreage largely recovered in 2020 and after (Vaiknoras & Hubbs, 2023).
  4. 4 Some studies use the difference-in-differences (DID) approach to examine the impact of biofuel production on land-use changes (e.g., Arora et al., 2016; Ifft et al., 2019; Pates et al., 2025). While the DID approach has clear advantages such as simplicity and capacity to control for unobserved time-invariant factors and aggregate policy or price shocks, its core identifying assumption (parallel trends between treatment and control groups) is often difficult to satisfy (see Arora et al., 2016; Pates et al., 2025 for detailed discussions). Moreover, the DID approach usually cannot identify the impact of crop prices on land-use change, because the treatment and control groups are typically exposed to the same prices. Therefore, we choose to follow the majority of the empirical literature on this topic (e.g., Li et al., 2019; Miao, 2013; Motamed et al., 2016; Wang et al., 2020), and use the fixed effects models with instrumental variables (FE-IV) to identify the land-use effect of both biodiesel production and soybean price. This choice is mainly driven by the goal of identifying the impact of soybean prices on cropland acreage. We acknowledge that both the DID and FE-IV approaches rely on assumptions that may be challenging to satisfy, and that it is unclear a priori which approach yields less biased estimates when these assumptions are violated.
  5. 5 The complete set of first-stage equations includes three equations, with soybeans crushed, crop price, and fertilizer price index as dependent variables, respectively. All these three first-stage equations have the same independent variables. In other words, the first-stage models for crop price and fertilizer price index are exactly the same as Equation (1) except that we replace κ $$ \kappa $$ with p $$ p $$ for the first-stage model for crop price, and replace κ $$ \kappa $$ with f $$ f $$ for the first-stage model for the fertilizer price index.
  6. 6 Here, we do not explicitly consider demand for feed from livestock production. This is partially because the demand for feed can be reflected in crop prices. Since we use county-level data for crop acreage, the crop rotation is implicitly included. This is because a county includes many farms, the impact of rotation on crop acreage change is likely to cancel out over these many farms. In later sections, we incorporate lagged cropland acreage to account for rotation effects in an alternative specification, and we find that our results remain robust across different model specifications.
  7. 7 Similar to the soybean acreage models discussed above, here the first-stage models for the Laspeyres price index and fertilizer price index are exactly the same as Equation (3) except that we replace κ $$ \kappa $$ with p $$ p $$ for the first-stage model for the Laspeyres price index, and replace κ $$ \kappa $$ with f $$ f $$ for the first-stage model for the fertilizer price index.
  8. 8 Farmers' decision on soybean acreage is affected by both corn and soybean prices. As corn and soybean prices are correlated, the exclusion of corn price from the soybean acreage model may lead to omitted variable bias. However, multicollinearity between corn and soybean prices (with a correlation coefficient of 0.87 in our sample) prevents us from including both prices in the soybean acreage model. This issue has also been noted in early studies by Li et al. (2019) and Miao et al. (2016). We, therefore, rely on the IV approach applied here to control for unobserved factors that affect both soybean price and soybean acreage. We then assess the robustness of the estimates with various robustness checks.
  9. 9 The correlation coefficient between fertilizer price index and natural gas price is 0.678 in our sample.
  10. 10 Economic Research Service, Commodity Costs and Returns, https://www.ers.usda.gov/data-products/commodity-costs-and-returns/commodity-costs-and-returns (accessed June 28, 2024).
  11. 11 We choose CDL data over NASS survey data primarily due to a decrease in the number of counties reporting acreages after 2014, which could introduce bias to the estimates.
  12. 12 In our sample, the maximum annual crushing capacity is about 100 million bushels. Suppose half of the 50-mile-radius catchment area is planted with soybeans and the soybean yield is 50 bushels per acre, then the total soybean production in the catchment area is about 126 million bushels per year, sufficient to meet the demand from the largest crushing facility in our dataset.
  13. 13 The 10 crops are: barley, corn, cotton, oats, peanuts, rice, rye, soybeans, sorghum, and wheat.
  14. 14 The data are publicly available at: https://www.ncei.noaa.gov/pub/data/cirs/climdiv/ (accessed April 10, 2024).
  15. 15 The datasets are publicly available at: https://www.census.gov/programs-surveys/popest/data/data-sets.All.html (accessed April 10, 2024).
  16. 16 This indicates that the distance between a biorefinery and its paired crushing facility is no larger than 50 miles. In other words, if there is no crushing facility within 50 miles of a biodiesel plant, the biodiesel plant is not paired with any crushing facility and is thus excluded from the sample. We vary this distance limit from 25 to 100 miles in our robustness checks.
  17. 17 Available at: https://www.epa.gov/renewable-fuel-standard-program/renewable-fuel-annual-standards (accessed June 28, 2024).
  18. 18 The data are available at: https://www.eia.gov/dnav/ng/hist/n3035us3A.htm (accessed April 10, 2024).
  19. 19 Tab. 5.1 in Stock and Yogo (2005) provides critical values for the Cragg-Donald statistic based on the number of endogenous variables (1 to 3) and IVs (3–30). The maximum critical value is 11.32, indicating a tolerance for IV estimator bias up to 10% compared with OLS.
  20. 20 As the analysis is based on county-level data, the rotation effect is less salient. The positive effect of previous soybean acreage indicated in the Arellano-Bond model results may instead reflect the overall upward trend in soybean acreage over the sample period.
  21. 21 For results of Arellano-Bond models, the short-run effect of crushing on soybean acreage can be read from the coefficient of soybean crushed. The long-run effect is calculated by using the coefficient of soybean crushed divided by 1 minus the coefficients of the two lagged dependent variables.
  22. 22 Calculated by using 0.1 × 6.895 × 0.280 × 1000, where 6.895 is the coefficient of soybean crushed in Column (2) of Table 2, 0.280 is the coefficient of biodiesel production in Column (2) of Table 3, and 1000 is the unit of soybean acreage in the analysis.
  23. 23 A similar robustness check is not conducted for the total acreage model because not all crops have futures prices.
  24. 24 Details of the calculation are included in Table S7.
  25. 25 Weiwei Wang generously provided price impact estimates based on the simulation in Wang and Khanna (2023) for the 10 major crops considered in the present study except rye. As the sample period and biodiesel production increase differ from those in Wang and Khanna (2023), for simplicity we assume that the impact of biodiesel production increase on crop prices is proportional to that in Wang and Khanna (2023). Specifically, the simulations in Wang and Khanna (2023) show that an annual biodiesel production increase by 1.19 billion gallons increased soybean price by 8.2% and aggregate crop price by 4.56%. We, therefore, assume that the 0.64-billion-gallon biodiesel production expansion in our sample period would increase soybean price by 4.4% and aggregate crop price by 2.45%, calculated by multiplying the ratio of 0.64 to 1.19 by 8.2% and 4.56%, respectively.
  26. 26 Note that the spatial variation in Figure 3 is not driven by spatial heterogeneity in the effect of biodiesel production or of crop prices on crop acreage. Instead, it only reflects spatial variation in biodiesel production change or crop price change over 2011–2020.
  27. 27 The higher end of their estimate is obtained in the scenario that assumes that grasslands can be converted to crop production while the lower end of the estimate was based on the assumption that crop expansion in response to higher prices was limited to marginal land acres (land that is frequently in and out of crop production). They show that the lower estimate was based on a model that was better validated.

      28. The full text of this article hosted at iucr.org is unavailable due to technical difficulties.