Implications of comorbidity and ascertainment bias for identifying disease genes
Abstract
Comorbidity, the co-occurrence of disorders, is frequently observed to occur at higher rates in clinically ascertained samples than in population-based samples. An explanation for this finding is that subjects suffering from multiple illnesses are more likely to seek medical care and receive a diagnostic evaluation. We refer to the component of the comorbidity between illnesses due to such ascertainment bias as “spurious comorbidity.” When spurious comorbidity is present, an apparent association between a candidate locus and the phenotype of interest may actually be attributable to an association between the locus and a comorbid phenotype. This phenomenon, which we call “spurious comorbidity bias,” could thus produce misleading association findings. In this article, we describe this phenomenon and demonstrate that it may produce marked bias in the conclusions of family-based association studies. Because of the extremely high rates of comorbidity among psychiatric disorders in clinical samples, this problem may be particularly salient for genetic studies of neuropsychiatric disorders. We conclude that ascertainment bias may contribute to the frequent difficulty in replicating candidate gene study findings in psychiatry. Am. J. Med. Genet. (Neuropsychiatr. Genet.) 96:817–822, 2000. © 2000 Wiley-Liss, Inc.
INTRODUCTION
A number of obstacles to identifying the genetic basis of complex diseases have been overcome with the use of nonparametric linkage and family-based association methods. For example, the use of allele-sharing methods obviates the need to specify parameters required by parametric lod score linkage analysis, and family-based association approaches avoid the problem of population stratification that can confound case-control association studies. Here, we highlight a potential source of bias that has received little attention in gene mapping studies of complex traits. The essence of this phenomenon is that, in the presence of ascertainment bias, a finding of apparent association to one phenotype may actually be attributable to a second, comorbid phenotype. Using the transmission/disequilibrium test (TDT) [Spielman et al., 1993], we demonstrate that this type of spurious comorbidity due to ascertainment bias can readily produce misleading results in association studies. We refer to the resulting bias as “spurious comorbidity bias.”
In a given individual, comorbidity between two disorders, A and B, may occur for a variety of reasons [Klein and Riso, 1993]. For example, the two disorders may co-occur by chance; A may be a cause of B, B may be a cause of A, or both may be caused by a common third factor such as shared genetic or environmental influences. In addition, spuriously high rates of comorbidity may occur among clinically ascertained individuals due to at least two types of sampling bias [Galbaud du Fort et al., 1993]. First, if each comorbid condition has independent, additive effects on treatment-seeking, individuals with both conditions will be more likely to present for treatment than will individuals with only one. This phenomenon, known as Berkson's bias [Berkson, 1946], means that even if two disorders are independent in the population, they may be associated in clinical samples. Second, the greater burden of illness due to having two comorbid disorders may increase the probability that a person will seek treatment for either individual disorder. This “clinical bias” could further increase the prevalence of comorbidity in clinical samples beyond the purely mathematical effect of Berkson's bias [Galbaud du Fort et al., 1993]. We refer to these two instances of comorbidity due to ascertainment bias as spurious comorbidity. Imagine a genetic association study of a trait (“study phenotype”) which may or may not have a genetic basis. If the probability of ascertainment is increased by the presence of a second phenotype trait (“comorbid phenotype”), we will have spurious comorbidity. Now imagine that the comorbid phenotype is genetically influenced by a candidate locus we are testing. We may now observe an apparent association to the study phenotype that is wholly or partly due to the presence of the association between the candidate locus and the comorbid phenotype. This result would be a kind of “false-positive” in that the association would apply to a phenotype other than the one under study.
Here, we model the effect of ascertainment bias and demonstrate that it may substantially bias the TDT over a range of prevalence values for the study and comorbid phenotypes. Although this issue applies to the study of any disorder, we use an example from psychiatry as an illustration because we believe that psychiatric genetics may be particularly vulnerable to this type of bias. For example, comorbidity of mood and anxiety disorders is common, even in population-based samples [Kessler et al., 1994]. This is due in part to the fact that these disorders are highly prevalent. Psychiatric comorbidity is even more common in clinical samples, most likely due to the combined effects of Berkson's bias and “clinical bias” [Galbaud du Fort et al., 1993]. Genetic studies that recruit subjects in clinical settings may thus be prone to spurious comorbidity, a circumstance that we demonstrate can bias hypothesis testing in association studies.
In this article, we examine the effects of this type of sampling bias in order to determine how likely is it that a study using a realistic sample size would detect association that was related to a correlated or comorbid phenotype, rather than the phenotype of interest. We use the TDT to illustrate this phenomenon because its resistance to confounding due to population structure has led to increasingly widespread use. However, analogous calculations could be made for case-control association studies and other designs.
MATERIALS AND METHODS
Figure 1 presents the causal diagram [Greenland et al., 1999] which we used to simulate the effects of ascertainment bias on the TDT [Spielman et al., 1993], a family-based association test which examines whether a marker allele present in heterozygous parents is transmitted to affected offspring significantly more (or less) often than expected by chance (i.e., 50% of the time). The study phenotype, P, and a comorbid phenotype, C, take the value 1 when present and 0 when absent. The variable A records whether a subject has been ascertained. We assume all ascertained subjects (A = 1) have the study phenotype (P = 1). The arrow from C to A indicates that the comorbid phenotype increases the probability of ascertainment, and thus represents spurious comorbidity. The variable U represents shared genetic and/or environmental causes of P and C. The arrow from P to C implies that the study phenotype may also cause the comorbid phenotype. However, we assume that the comorbid phenotype does not cause the study phenotype (although that possibility is considered in the Discussion section). A gene G, which can be a cause of C, is the candidate gene being tested in the association study of P. The variable G takes the value 0, 1, or 2 depending on the subject's number of copies of the susceptibility allele of the candidate gene. For several variations of the model in Figure 1, we simulated 1,000 replicate datasets consisting of 300 child–parent trios in which the child has the study phenotype.
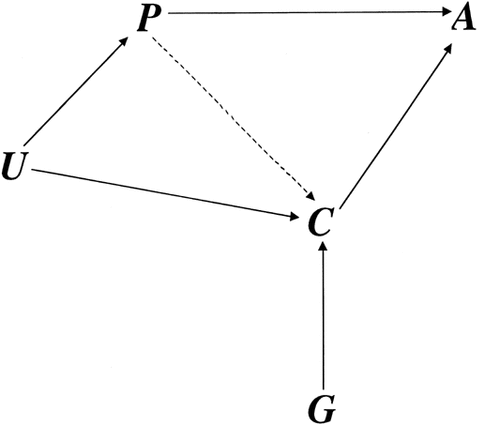
Causal diagram for the general model used to illustrate the phenomenon of spurious comorbidity bias in genetic association studies. All ascertained subjects (A) are affected with the study phenotype (P). A comorbid phenotype (C) increases the likelihood of ascertainment. In this model, P can also be a cause of C. Each allele of a candidate gene (G) increases the expression of C in a multiplicative fashion, but G is not a cause of P. Finally, a set of unspecified factors (U) may be causes of both P and C.
Simulation Models
Distribution of the variables G, U, P, and C used in our simulations.
For all models, we assumed that the population frequency of U is 0.3. Among individuals with U, the prevalence of the study phenotype (P) is 0.16 [P(P = |U = 1) = 0.16]; among those without U, the prevalence is 0.08 [P(P = |U = 0) = 0.08]. Hence, the overall prevalence of P is 0.104. We chose these probabilities for U and P to give an overall prevalence for P similar to that observed in studies of social phobia (see Results). The gene G has two alleles with susceptibility allele frequency p. Genotype frequencies are assumed to conform to Hardy-Weinberg expectations. We varied p between 0.01 and 0.9. The baseline penetrance ϕPU for individuals with G = 0 susceptibility alleles depends on P and U status; that is, ϕPU = P(C = |G = 0, U,P). We chose a simple model where ϕPU = 0.01 + 0.01U + 0.02P. The fact that the coefficient of U is nonzero implies that U causes C. The fact that the coefficient of P is nonzero implies that P causes C. Thus, there is true comorbidity in the population. Since the coefficient for P is greater than the coefficient for U, we are assuming that the effect of the study phenotype on penetrance is greater than the effect of U. To test the effect of this assumption, we also simulated under models where the coefficient for P is 0 (see Discussion). It follows from our model that the minimum baseline penetrance, for individuals without P or U is ϕ00 = 0.01. For individuals with both P and U, ϕ11 = 0.04. The population prevalence of the comorbid phenotype (C) depends on P, U, and the number of copies of the susceptibility allele G. We assume a multiplicative genotype relative risk (GRR) model, with multiplier θ0 + θ1P. In other words, P(C = | P,U,G) = ϕPU(θ0 + θ1P)G, where G is the number of copies of the susceptibility allele; if θ1 = 0, the GRR multiplier is the same for all individuals. If θ1 > 0, the GRR multiplier depends on P status.
Model for Ascertainment Bias
Whether an individual is ascertained depends on P and C status. We assume that all ascertained individuals are affected with the study phenotype; that is, P = 1 for all ascertained individuals. Furthermore, we assume P(A = |C, P = 1) = αγC, where α is the probability of ascertainment among affected individuals with C = 0, and the parameter γ describes the multiplicative increase in ascertainment probability for individuals with C = 1 and P = 1 over individuals with C = 0 and P = 1. If γ = 1, all individuals with the study phenotype have equal ascertainment probability, and there is no ascertainment bias; if γ = 2, individuals who have the comorbid phenotype are ascertained at two times the rate of individuals without. Note that since all ascertained subjects have P = 1 and among subjects with P = 1, P(C = |G, U) = ϕ1U βG with β = θ0 + θ1, the effect of G on C among the ascertained can be summarized in the single parameter β.
We simulated under five basic GRR models, defined by β = 1 (no genetic effect), 2, 3, 4, 5. For each basic model, we simulated 1,000 replicate datasets for 10 different susceptibility allele frequencies (p = 0.01, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9) and four levels of ascertainment bias (γ = 1 (no bias) and γ = 2, 3, 4). Thus, we simulated 1,000 replicate datasets of 300 trios under a total of 200 (5 × 10 × 4) different models.
-
p = allele frequency of the putative susceptibility allele.
-
G = number of copies of the susceptibility allele of the tested candidate gene (0, 1, or 2).
-
ϕPU = penetrance for given combinations of P and U, when G = 0.
-
α = probability of ascertainment among affected individuals with C = 0.
-
γ = multiplicative increase in ascertainment probability due to the presence of comorbid phenotype C.
-
θ0 + θ1 P = the genotypic risk ratio, i.e., the increase in risk for each additional copy of the susceptibility allele, where:
-
θ0 = genotypic risk ratio for patients without study phenotype (P = 0), and
-
β = θ0 + θ1 = the genotypic risk ratio for patients with study phenotype (P = 1).
RESULTS
Figure 2 shows plots of the simulation results for all models. The four plots are for the four levels of ascertainment bias, γ. The proportion of the 1,000 replicates in which a significant TDT test was obtained [P(sig TDT)] is plotted by allele frequency for the five GRR models. In each plot, a line through 0.05 is plotted for reference. When there is no ascertainment bias and thus no spurious comorbidity (γ = 1), and/or when there is no genetic effect (β = 1 for any γ) the proportion of significant replicates for a test with type I error rate α = 0.05 falls near the expected 0.05 level even though there is true comorbidity in the population. For γ > 1, the proportion of replicates yielding a significant TDT depends on the strength of ascertainment bias (γ), the strength of the genetic association between the gene and C (β) and the susceptibility allele frequency (p). For low allele frequency (p = 0.01), the bias is minor; the proportion of significant replicates does not exceed 0.09, even for ascertainment bias of γ = 4. For a gene with weak effect on the comorbid phenotype among the ascertained patients (β = 2), the bias is also low when γ = 2: the proportion of significant replicates does not exceed 0.08, even for high allele frequencies. For stronger ascertainment bias, the proportion of significant replicates increases moderately. For genes with a stronger effect on the comorbid phenotype among the ascertained patients (β ≥ 3) the bias can be quite severe for allele frequencies of 0.1 or greater. For example, when β = 4 and γ = 4, the probability of a false-positive TDT exceeds 50% for susceptibility allele frequencies greater than 0.2.
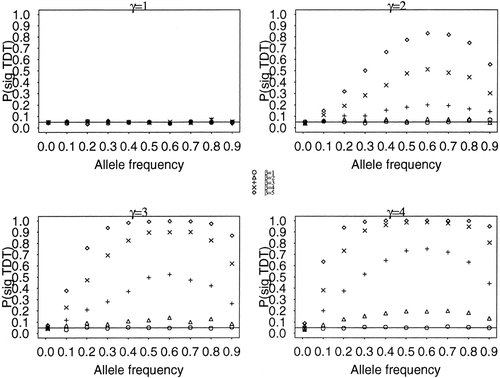
Type I error rate in 1,000 replicates of a TDT test (n = 300 trios) of the association between candidate gene G and study phenotype P. The proportion of replicates in which a significant TDT test was obtained [P(sig TDT)] when α = 0.05 is plotted by allele frequency. The five panels represent models with different values of γ, the multiplicative increase in ascertainment probability when comorbid phenotype C is present. For each level of γ, we vary the strength of the effect (β) of candidate gene G on the comorbid phenotype (C). A solid line through the assumed alpha level of the test (0.05) is presented for reference.
Application: Comorbidity of Social Phobia and Depression
To demonstrate the relevance of this phenomenon to genetic studies of complex disorders, we apply the model to a hypothetical study of the genetics of social phobia, an anxiety disorder which is defined by excessive fear and avoidance of social or performance situations. There is evidence that genetic factors influence the susceptibility to social phobia [Smoller and Tsuang, 1998], making it a plausible subject for genetic association studies. Major depression is frequently comorbid with social phobia. In population-based samples, the lifetime prevalence of depression has been estimated to be 5–17% in the general population [Kessler et al., 1994; Weissman et al., 1996] but 17–37% among individuals with social phobia [Magee et al., 1996; Schneier et al., 1992]. In clinical samples, the lifetime comorbidity between social phobia and major depression can be as high as 70% [Van Ameringen et al., 1991], suggesting that comorbid depression is overrepresented in clinically ascertained samples of individuals with social phobia by a factor of approximately 2–4. Therefore, both social phobia (P) and depression (C) appear to be causes of “ascertained social phobia” (A), as depicted in Figure 1. Also consistent with the causal model shown in Figure 1, depression may be in part a secondary complication of social phobia among patients with this comorbidity [Kessler et al., 1999; Van Ameringen et al., 1991]. All of the presented simulations were based on a study phenotype prevalence of 0.104, which is within the range (2.4–13.3%) of prevalence estimates of social phobia from population-based studies [Magee et al., 1996; Schneier et al., 1992; Wittchen et al., 1999]. Several of the models simulated also closely match the observed lifetime prevalence of depression in the population and in individuals with social phobia. For example, for β = 4 and allele frequencies from 0.4 to 0.8, the prevalence of the comorbid phenotype is between 5–17% in the population, and between 16–38% among patients with the study phenotype. With ascertainment bias γ = 2, the prevalence among clinical samples ranges from 27–55%; for γ = 4, from 43–71%. Under these models, with a sample size of 300 trios, there is high probability of detecting a spurious association between social phobia and the candidate gene even in the low-bias situation. For example, for ascertainment bias γ = 2 and genotype relative risk β = 3, the probability of detecting an association is greater than 0.15; for γ = 4, the probability is greater than 0.63. For genotype relative risk β = 4, the corresponding probabilities are 0.37 and 0.94, respectively. Given our current understanding of the pathophysiology of psychiatric disorders, genes which are candidates for depressive disorders (e.g., those related to serotonergic neurotransmission) are also plausible candidates for anxiety disorders. If our candidate locus were indeed a cause of depression, allelic association might be observed even if social phobia itself did not have a genetic basis. Without attention to the issue of comorbidity due to ascertainment bias, an investigator testing such a candidate might erroneously conclude that a susceptibility gene for social phobia had been identified.
DISCUSSION
Our analyses suggest that genetic association studies may produce misleading results when the study phenotype is comorbid with a genetically influenced phenotype that increases the probability of ascertainment. In this context, an apparent association between a candidate locus and the study phenotype may actually be attributable to an association with the comorbid phenotype. In fact, in the model we examined, for most simulations in which when the genotypic risk ratio among ascertained patients (β) is > 1 and there is any degree of ascertainment bias (γ > 1), the TDT was an invalid test (i.e., had an incorrect alpha level).
The simulation models we presented assume that the study phenotype can be a cause of the comorbid phenotype. We chose this model because it may apply to the example of social phobia and depression that we used to illustrate the phenomenon of spurious comorbidity bias. However, our results are more general: We have performed simulations (not shown) in which P is not a cause of C (i.e., in which there is no arrow between P and C in the causal model so that ϕPU = ϕU is not a function of the study phenotype and θ1 = 0), and found the results to be strikingly similar to those for the model shown in Figure 1. Other simulations with lower or higher baseline penetrance functions (ϕPU) also gave similar results. Thus, a general result is that the bias in the TDT appears to be a function primarily of the amount of ascertainment bias, the strength of the genetic association (as measured by β), and the allele frequency p.
The engine driving this phenomenon, selection bias, can result from at least two mechanisms, and Galbaud du Fort et al. [1993] have shown that both can produce spurious comorbidity in psychiatric studies of clinical samples. The first is the purely mathematical effect of Berkson's bias: individuals suffering from two disorders can seek treatment for either one of the disorders. The independent, additive effect of treatment-seeking for either disorder can result in an overrepresentation of comorbid cases among individuals in clinical settings. The second mechanism has to do with the clinical impact of comorbidity: the probability of seeking treatment for a specific disorder can be increased by the clinical burden of suffering from a comorbid disorder. As a result of these two phenomena, clinically ascertained samples may be enriched for probands who are affected by a comorbid, genetically influenced disorder.
The spurious finding that can result from this bias is perhaps best characterized as a “misattributed” association rather than a false-positive association. That is, if an apparent association between the study phenotype and a particular allele results from comorbidity with another phenotype, this association would still represent a valid association with the comorbid phenotype. The danger, however, is that this association will be misattributed to the study phenotype unless the possibility of spurious comorbidity bias is recognized.
If it were suspected, the presence of ascertainment bias in a clinical sample could be investigated by comparing the prevalence of comorbid phenotypes to their expected frequency based on available population-based estimates. If spurious comorbidity bias seems likely, any associations found using the TDT must be suspected to be misattributed. One might hope to eliminate this bias by restricting the analysis to probands who do not suffer from the comorbid disorder C. However, this hope is misplaced, since such a restriction will itself create bias [Robins et al., 2000]. Similarly, restricting the analysis to probands suffering from the comorbid disorder creates bias. Finally, selecting a biased sample of probands in such a way as to ensure that the prevalence of comorbidity among the probands is equal to that found in the population fails to eliminate the bias.
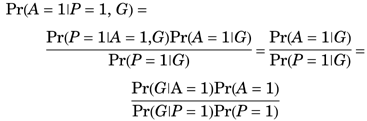
We note that there are at least two scenarios in which a comorbid phenotype would not bias an analysis of the study phenotype. First, if the comorbid phenotype C caused the study phenotype P, then a susceptibility gene for C can legitimately be considered a susceptibility gene for the other phenotype, and we would wish the TDT to reject the null. For example, the metabolic consequences of obesity often result in the development of Type II diabetes mellitus. If a gene-mapping study of obesity included a large proportion of obese subjects with Type II diabetes, a candidate locus could be conferring susceptibility to both obesity and Type II diabetes because of a common metabolic derangement. Second, a genetic lesion may actually contribute to the occurrence of two separate disorders via different pathways. For example, the pleiotropic (i.e., variably expressed) APO-ϵ4 allele may be a cause of both atherosclerotic heart disease and Alzheimer disease. Hence, the association between APO-ϵ4 and Alzheimer disease would be a true-positive even if APO-ϵ4-related heart disease increased the probability of ascertainment for a study of Alzheimer disease.
In summary, spurious comorbidity bias is only a problem if: 1) there is a comorbid phenotype which increases the probability of ascertainment for the study phenotype; 2) the comorbid phenotype is substantially influenced by the genetic locus being tested (or there is sufficient linkage disequilibrium between the candidate locus and a disease locus that influences the comorbid phenotype); 3) the comorbid phenotype is not a cause of the study phenotype; and 4) the comorbidity is not due to a shared (pleiotropic) effect of the candidate locus on the phenotypes. In studies of psychiatric disorders, the first condition may be commonly met: the comorbidity of disorders observed in the clinical samples used for genetic studies is often markedly higher than that observed in population-based samples. For example, the conditional probability of lifetime major depression among individuals with panic disorder was 55% in the large, population-based National Comorbidity Survey [Kessler et al., 1998], but 80% in a recent genetic association study of a clinically referred sample [Peroutka et al., 1998]. Typically, investigators do not know whether the other conditions are met.
In conclusion, we have explored the impact of spurious comorbidity bias on hypothesis testing in genetic association studies. Under some circumstances, we conclude that association statistics including the TDT can be substantially affected by ascertainment bias. It must be acknowledged that we have illustrated this phenomenon with a particular genetic model, sample size, and set of parameter values; the frequency of finding a misleading association may vary under alternative models. Nevertheless, the possibility that ascertainment bias can lead to misattributed associations may have important implications for psychiatric genetic research. A vexing issue in psychiatry genetics has been the difficulty in replicating many reported associations between psychiatric disorders and candidate genes. Varying degrees of spurious comorbidity bias among clinical samples may be contributing to the discrepant results of genetic studies in psychiatry.
Acknowledgements
The authors thank Jed Rubenfeld for his contributions to this work.




