Forward-looking experimentation of correlated alternatives
Abstract
This paper studies how a forward-looking decision maker experiments on unknown alternatives of correlated utilities. The utilities are modeled by a Brownian motion such that similar alternatives yield similar utilities. Experimentation trades off between the continuation value of exploration and the opportunity cost of exploitation. The optimal strategy is to continuously explore unknown alternatives and then exploit the best known alternative when the one being explored is found to be sufficiently worse than the best one. The decision maker explores unknown alternatives more quickly as they prove to be worse than the best known one. Applied to firm experimentation, my model predicts a conditional version of Gibrat's law and a linear relation between firm size and profitability.
1 Introduction
This paper studies the experimentation problem of a long-lived decision maker who chooses alternatives of unknown correlated utility. The decision maker learns the utility of her chosen alternative, which informs her future choices. To capture the correlation, I model utility as a Brownian motion over a continuum of alternatives such that similar alternatives yield similar utilities. Prior work on correlated utility, including Jovanovic and Rob (1990) and Callander (2011), studies short-lived agents who can exploit a better alternative based on past explorations. My innovation is to study a long-lived decision maker who can also continue to explore.
The optimal experimentation strategy describes how quickly the decision maker continuously explores unknown alternatives and when she stops to exploit the best known one (Theorem 1). The speed of exploration depends on the drawdown, i.e., the utility difference between the best known alternative and the one being explored, and the decision maker exploits the best alternative when the drawdown exceeds a threshold.
The innovation of my analysis is the application of time change to the domain of alternatives. A time change indexes a stochastic process by an increasing sequence of stopping times. The experimentation literature on finitely many risky arms, such as Karatzas (1984), Moscarini and Smith (2001), and Keller, Rady, and Cripps (2005), performs time change in the domain of information that accumulates at a controlled rate. The most up-to-date information is a sufficient statistic because it encompasses past information. In my model, the decision maker controls the speed of exploring new alternatives. The alternative being explored is not a sufficient statistic because previously explored alternatives could be better. I show that the optimal strategy also takes the best known alternative into account.
The trade-off between the continuation value of exploration and the flow opportunity cost of exploitation implies faster exploration for more negative drawdowns (Proposition 1). On the one hand, faster exploration acquires information more quickly and realizes the continuation value sooner. When the drawdown becomes more negative, the impatient decision maker finds it less pressing to realize the decreased continuation value. On the other hand, faster exploration shortens the duration of exploration as the flow opportunity cost of exploitation accrues. When the drawdown is more negative, the increased flow opportunity cost prompts the decision maker to explore in a shorter time. I show that the opportunity cost incentive always dominates the continuation value incentive. This is because the option to exploit partially insures the decision maker from the drawdown, and so the continuation value is less sensitive to the drawdown than the flow opportunity cost.
In the time series, i.e., how experimentation evolves over time, the speed's monotonicity with respect to drawdown implies that the speed of exploration increases over time under conditions on model parameters (Corollary 1).
I study the comparative statics of the optimal strategy (Proposition 2). Intuitively, the value of exploration increases when the decision maker is more patient, the cost of exploration is lower, or the utility has a more positive drift. To realize the increased value, the decision maker explores alternatives more quickly for any given drawdown and tolerates more negative drawdowns, i.e., the drawdown threshold increases. The comparative statics also hold when the utility is more volatile because of the option value of exploitation.
My model applies to a firm that experiments on its firm size to maximize profits. I interpret the log number of employees as a proxy for firm size and log profit as a proxy for profitability. Under the Brownian specification, firm-size elasticity of profitability is modeled to be independent and identically distributed over all firm sizes.
In the cross section, i.e., how experimentation differs across Brownian realizations, I derive two results that correspond to predictions on firm dynamics. The first result is that as the decision maker explores more alternatives, the speed of exploration converges asymptotically in distribution (Proposition 3). In terms of firm dynamics, this translates to a conditional version of Gibrat's law: among large firms, the percentage change in firm size conditional on growth follows essentially the same distribution that is invariant to absolute firm size. The percentage change depends on absolute size only through the extensive margin, i.e., firms that stop growing, but not the intensive margin, i.e., firms that keep growing. By comparison, the original, unconditional version of Gibrat's law states that the distribution is invariant at both the extensive margin and the intensive margin.
The second result is that the exploited alternative and its utility are asymptotically linear (Proposition 4). In the context of firm experimentation, this result means that long-run profitability is proportional to long-run firm size among large firms. The result highlights an endogenous selection effect: firms choose to operate at large sizes because they experience increasing profits along the growth path. Therefore, the regression of firm size on profits may overestimate average profit elasticity.
Related literature
My paper incorporates a long-lived decision maker into the experimentation problem where the utilities of unknown alternatives are modeled by a Brownian motion. Jovanovic and Rob (1990) analyze such a problem with overlapping generations of short-lived agents, each of whom can learn the Brownian realization of one alternative before choosing another for utility. Callander (2011) examines myopic agents who reveal the utility of an alternative to their choice. Garfagnini and Strulovici (2016) extend Callander (2011) to agents who live for two periods.1 In these papers, the agents acquire information at most once before exploitation and, therefore, do not incorporate the information value of continued exploration.2 By contrast, the long-lived decision maker in my model can continue to explore. As a result, past exploration becomes instrumental to future exploration, and the information value feeds back to the decision maker's experimentation strategy.
Urgun and Yariv (2025) considers a related search model in which an agent searches continuously among alternatives of Brownian utility. The objective is to maximize the expected discounted utility of the best alternative subject to a search cost. As in my model, their optimal strategy is to search continuously until the drawdown reaches a threshold. The optimal speed of search is driven by the continuation value. By contrast, the objective in my model is to maximize the expected discounted flow utility subject to a learning cost. The optimal speed of exploration is driven by the flow opportunity cost in addition to the continuation value.
The time change enables me to derive the time-series and cross-sectional results from the literature on Brownian motions that are stopped at a drawdown threshold. Taylor (1975) and Lehoczky (1977) characterize the joint distribution of the running maximum and the stopping time, for a Brownian motion whose drift and volatility may depend on its value. However, their framework does not accommodate my optimal strategy because both the drift and the volatility in my case depend on the drawdown. To leverage their results, I apply a time change to the Brownian utility, transforming it from the time domain to the domain of alternatives. Because the Brownian utility over alternatives has constant drift and volatility, their results can be applied to this process, as the threshold strategy remains invariant under the time change.
The remainder of the paper is organized as follows. Section 2 introduces the experimentation problem. Section 3 derives the optimal experimentation strategy. Section 4 studies the properties of optimal experimentation. Section 5 discusses key modeling assumptions. The Appendix provides proofs.
2 Experimentation problem
I study the experimentation problem of a forward-looking decision maker who continuously explores new alternatives of unknown and correlated utility subject to a learning cost.
An experimentation strategy specifies the choice of alternatives based on past experiments. In realization , the decision maker chooses alternative at time . As in Callander (2011) and Garfagnini and Strulovici (2016), the decision maker learns the realized utility upon her choice via learning-by-doing. Therefore, her information at time t consists of the history of calendar time, the chosen alternatives, and the corresponding utilities, i.e., , where denotes the generated sigma algebra. Let denote the augmented filtration and let denote the decision maker's discount rate. I define the strategy space as follows.
Definition 1.An experimentation strategy, , or simply , is a stochastic process that satisfies the following conditions.
- Initial condition. For each , .
- Continuous exploration condition. For each , the frontier is absolutely continuous.
- Measurability condition. Strategy is predictable with respect to the augmented filtration .
- Growth condition. There exists and such that for all and .
When the decision maker explores new alternatives, she incurs a flow learning cost , where is the speed of exploration. The cost function is twice continuously differentiable and strictly convex. It is assumed to satisfy , , and the Inada condition, . Note that the cost is increasing in the speed of exploration and is zero when the speed is zero, e.g., when the decision maker exploits a previously chosen alternative. Thus, the flow learning cost can be interpreted as the utility loss incurred by the decision maker when she first learns to extract utility from a given alternative.
Remark 1. (Key assumptions)I comment on the key assumptions in the model. First, the utility process with stationary independent increments allows the recursive formulation of the optimal strategy. In particular, the Brownian specification with constant drift and volatility lends itself to the well developed mathematics literature. Second, on the strategy space, the continuous exploration condition permits jumps to known alternatives and forbids jumps to unknown alternatives to the right of the frontier. I argue in Section 5.1 that this condition is without loss of optimality for convex learning costs. Third, the growth condition rules out strategies with explosive explorations that attain infinite utility at infinite cost.
3 Optimal experimentation strategy
I derive the optimal experimentation strategy in three steps. First, I show that the objective function is bounded. Second, I construct a candidate strategy based on several conjectures. Third, I prove the optimality of this strategy through verification. The primary departure from the standard argument is that the strategy cannot be characterized by a stochastic differential equation due to the possibility of exploitation.
3.1 Bounded objective function
Unlike myopic or short-lived agents, the long-lived decision maker might attain infinite utility by exploring an arbitrarily large set of alternatives for an arbitrarily good alternative. Because such a strategy would also incur an infinite learning cost, the objective function would be ill-defined as infinity minus infinity.3
The growth condition guarantees a bounded objective function by limiting exploration in finite time. The decision maker can choose from an exponentially growing, but bounded, set of alternatives whose running maximum increases at most exponentially in expectation. The restriction on in the condition guarantees that the running maximum grows at a slower rate than the exponential discounting, leaving the objective bounded from above.
Lemma 1. (Bounded objective function)Over the set of strategies that satisfy the growth condition with fixed constants and , the objective function (1) is bounded from above.
3.2 Verification argument
I construct a candidate strategy based on some conjectures and then verify the optimality of the strategy. The key observation is that, among the many explored alternatives, the utility of the best known alternative and that of the frontier (i.e., rightmost alternative) are state variables, due to the Markovian property of Brownian utility.
I first claim that exploitation is a lookback option that gives the running maximum, , when executed. A lookback option is an option with a backward-looking and history-dependent payoff.4 Because exploitation does not generate information or advance the frontier for future experiments, once the decision maker starts to exploit, she will continue to do so by recalling the best known alternative.
Together with the running maximum, the frontier utility, , characterizes the continuation value, i.e., . This is because all unknown alternatives are to the right of . Conditional on available information, the utility distribution of unknown alternatives depends only on due to the Markov property of Brownian motion.
Next, I claim that the option value is a function of the drawdown. The option value is the difference between the continuation value and the value of exploitation, i.e., , and the drawdown is the difference between the frontier utility and the running maximum, i.e., . Note that the drawdown is weakly negative by definition. Suppose that both the frontier utility and the running maximum increase by the same constant. The utility distribution of unknown alternatives then shifts upward by the same amount due to the stationary independent increments of Brownian utility. Therefore, both the value of exploration and the value of exploitation increase by the same amount, leaving the option value unchanged. The option value function can thus be written as .
I derive the laws of the frontier utility, running maximum, and drawdown by applying a time change to the utility process.
Lemma 2. (Time change)The frontier utility satisfies , where the process is a continuous square-integrable -martingale with quadratic variation .
By constructing a candidate strategy that satisfies these conditions, I characterize the value function and the unique optimal strategy by a verification argument.
Theorem 1. (Optimal experimentation)
- (i) The continuation value satisfies . The option value function v is the unique solution to (3) subject to boundary conditions (5)–(7), with extension for . Moreover, v is increasing and convex.
- (ii) The optimal experimentation strategy is unique and is given by
where (2) defines exploitation time τ and (4) defines speed of exploration s.
4 Properties of optimal experimentation
I analyze how optimal experimentation evolves over time, depends on model parameters, and differs in the cross section.
4.1 Time-series properties
Proposition 1.The speed of exploration s is higher for the more negative drawdown y.
The intertemporal trade-off between the flow opportunity cost of exploitation and the continuation value of exploration determines the optimal speed of exploration. On the one hand, the decision maker incurs the flow opportunity cost, , when she explores new alternatives instead of exploiting the best known one. To avert the flow cost, she would like to explore quickly over a short period of time, and more so for more negative drawdowns when the opportunity cost is higher. On the other hand, the impatient decision maker would like to realize the continuation value, v, sooner by acquiring more information. For less negative drawdowns, the value is higher and, therefore, prompts faster exploration.
The speed of exploration is higher for more negative drawdowns because the opportunity cost is more sensitive to the drawdown than the continuation value, i.e., . When the drawdown experiences a negative shock at frontier , the utilities of all alternatives to the right of decrease, while those to the left, including the best alternative, remain unchanged. As a result, the flow opportunity cost increases by the size of the shock.
However, the continuation value decreases by a smaller amount because the option to exploit partially insures against the shock. Given optimal execution of the option to exploit, the envelope theorem implies6 . In words, the shock at the current frontier is relevant to the continuation value only when the chosen alternative in the future, , lies to the right of . If the frontier utility reaches the drawdown threshold before marking a new maximum, the decision maker will exploit the best alternative, which lies to the left of , and, therefore, she insulates herself from the negative shock. Only when , is alternative the best, and so all future alternatives chosen during exploration and exploitation will lie to its right. The negative shock at factors in the decision maker's flow utility permanently, implying that .
I provide a sufficient condition for the speed of exploration to increase on average in the time series.
Corollary 1.If and is decreasing over , then the speed of exploration is a submartingale over .
4.2 Comparative statics
I derive the comparative statics of the option value function, the speed of exploration, and the drawdown threshold with respect to model parameters. I write that c increases if increases and increases pointwise, and that v and, respectively, s increase if v and s increase pointwise. Moreover, a set of parameters is said to be more favorable if either the drift μ is higher, the volatility is higher, the discount rate r is lower, or the cost function c is lower.
Proposition 2. (Comparative statics)Option value v, speed of exploration s, and drawdown threshold are increasing in the drift μ and the volatility of the utility process, and are decreasing in the discount rate r and the learning cost function c.
Intuitively, the decision maker derives higher value from exploration when it yields higher utility, the decision maker is more patient, or learning is less costly (Figure 1). As a result, she also tolerates a more negative drawdown threshold. Moreover, she is motivated to explore at a higher speed at any given drawdown so as to realize the increased value more quickly. The comparative statics hold when the utility process is more volatile as well, because the option to exploit insures against negative shocks.
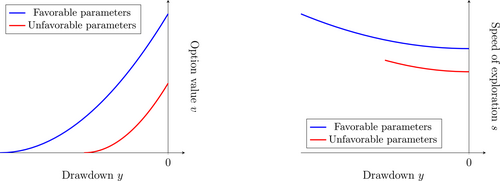
The option value functions and the speed of exploration functions for two sets of parameters.
4.3 Cross-sectional properties
In the application of firm experimentation, a firm experiments on its size, , to maximize expected discounted profitability, . I use the log number of employees as a proxy for firm size and use log profit for profitability. The Brownian specification means that over all firm sizes, the firm-size elasticity of profitability is independent and identically distributed. I interpret the learning cost, c, as the loss in profits when a firm first operating at a given firm size fails to allocate human resources to maximize profit. Starting at the minimal firm size, the optimal strategy is to grow continuously until the percentage drawdown, y, exceeds a threshold and then to scale down to exploit the most profitable size in the long run. The percentage growth rate, s, depends on the percentage drawdown.
Stochastic utility generates heterogeneous experimentation behaviors in the cross section under the optimal strategy. In the context of firm experimentation, I obtain two cross-sectional predictions on firm dynamics: the conditional version of Gibrat's law and the linear relation between long-run firm size and profitability.
First, I present the asymptotic convergence of the speed of exploration, which corresponds to the conditional version of Gibrat's law. With a slight abuse of notation, I index the drawdown and speed of exploration by the alternative rather than calendar time, i.e., and , by undoing the time change . This is possible because whether the drawdown has exceeded the threshold is invariant to the continuous time change, i.e., .
Proposition 3. (Asymptotic convergence)As , the speed of exploration conditional on exploration, , converges in distribution.
The conditional version of Gibrat's law can explain an empirical deviation from the original law, which states that the percentage growth in firm size is (unconditionally) invariant to absolute firm size. Daunfeldt and Elert (2013) reject the original, unconditional version of Gibrat's law on the aggregate level for Swedish firms during 1998–2004 because small firms on average grow more quickly than large firms. By contrast, the conditional version of Gibrat's law suggests that its deviation from the original law derives from the extensive margin: large and old firms are more likely to have stopped exploration and growth. Moreover, the conditional law weakens the original law parsimoniously in that the intensive margin—the percentage growth in firm size conditional on growth—is invariant.
The proof of Proposition 3 also implies that the decision maker quickly stops exploring.
Corollary 2. (Short exploration)There exist such that for all .
My second cross-sectional result is that the exploited alternative is linear in its utility. This result corresponds to the linear relation between long-run firm size and profitability. To present a stark contrast, I restrict attention to a driftless utility process, i.e., , which means that the average elasticity of profit is zero. Denote the exploited alternative by and its utility by .
Proposition 4. (Linear relation)For , the pair satisfies the linear relation
Proposition 4 highlights an endogenous selection effect: large firms choose to operate at large sizes because they experience increasing profits along the growth path. As a result, the naïve regression of profitability on firm size would estimate a positive average elasticity despite the zero mean in the profit process, because the estimation overlooks the selection bias. The proposition implies that the bias persists even for very large firms.
5 Discussions on modeling assumptions
In this section, I discuss how my analysis depends on three modeling assumptions: the continuous exploration condition, the Inada condition, and the learning cost.
5.1 Continuous exploration condition
The continuous exploration condition in Definition 1 is without loss of optimality under convex learning costs. The idea is that in continuous time, fast continuous exploration approximates discontinuous jumps, and small but frequent jumps can approximate continuous explorations.
Suppose that the decision maker can explore discontinuously subject to a discrete learning cost , where is the distance of the chosen alternative from previous explorations and is the discrete cost function. I assume that and that C is convex as in Garfagnini and Strulovici (2016). This formulation is consistent with the flow learning cost of continuous exploration because the speed of exploration measures the infinitesimal distance from previous explorations.
I claim that the discrete cost function is effectively linear. Because C is convex, it suffices to show subadditivity, i.e., for . Instead of exploring an alternative at distance D in one step, the decision maker can first explore the middle point at distance and then explore the chosen alternative, now at distance . Over an arbitrarily short time lapse, the two-step exploration reveals additional information at the middle point while accumulating zero flow utility. The cost therefore bounds the effective learning cost from below.
Remark 2.The above argument fails if C is not convex. When the decision maker explores discontinuously, the (closure of the) set of explored alternatives may no longer be an interval. In addition to the utility at the rightmost alternative, the decision maker also needs to take the utility at each boundary point into account. The number of state variables grows with each discontinuous exploration, leaving the recursive analysis intractable.
5.2 Inada condition
The Inada condition guarantees an interior solution to (4). If the learning cost function c fails the condition, it may be optimal to explore at infinite speed. Such instantaneous exploration realizes the continuation value immediately and, therefore, averts the flow opportunity cost. The decision maker does so over an interval of alternatives until the drawdown reaches the threshold or becomes less negative, whereupon the optimal speed becomes finite again.11 Despite the more involved technicalities, such instantaneous explorations yield the same economic insights.
5.3 Learning cost
My analysis extends to the experimentation problem with an adjustment friction in place of the learning cost. I model the adjustment friction by restricting the chosen alternative to be continuous, with a given Lipschitz constant; in other words, the speed of change is uniformly bounded. The key difference is that the decision maker can no longer exploit the best known alternative instantaneously, but can only take time to backtrack from the frontier.
I denote the highest value from backtracking from a given alternative by the exploitation value. The exploitation value–frontier utility pair can be shown to be a Markov process over the domain of alternatives.
Similar to the case with a learning cost, the optimal strategy is to explore until the generalized drawdown—i.e., the difference between the exploitation value and the frontier utility—exceeds a threshold, and then backtrack to exploit the alternative that attains the exploitation value. While the maximum utility increases monotonically during exploration, the exploitation value decreases at a rate proportional to the generalized drawdown, reflecting the lower flow utility when backtracking from the frontier. As a result, the exploited alternative may differ from the best one.
Appendix: Proofs
A.4 Proof of Lemma 1
A.5 Proving Lemma 2
This lemma adapts Proposition 1.1.5 in Chapter V of Revuz and Yor (2013) to my setting where is defined over t instead of x. The time change may remind the reader of the celebrated Dambis–Dubins–Schwarz theorem (see, for example, Theorem 1.1.6 in Chapter V of Revuz and Yor (2013)). However, my model specifies a standard Brownian motion (and utility process ) as a primitive and then constructs its time-change . By comparison, the theorem specifies a continuous martingale and then shows the existence of a Brownian motion in a possibly enlarged probability space such that the martingale is a time-change of that Brownian motion. In particular, my lemma does not require such enlargement.
Proof of Lemma 2.Define . The process Z is continuous by composition and is adapted to by the definition of . For , its expectation satisfies
The same argument shows that is an -martingale, because is a uniformly integrable -martingale on for all . Therefore, Z is squared-integrable and its quadratic variation is by definition. □
A.6 Proving Theorem 1
Following the conjectures in the main text, I construct a candidate strategy (Proposition 5 and Corollary 3) and then verify its optimality and uniqueness.
Proposition 5.There exist constants and , and a convex function with such that v satisfies HJB (3) and boundary conditions (5), (6), and (7). For such v, the unique maximizer is given by the FOC (4).
Proof.I prove the existence to the free boundary problem by the shooting method. First, I transform the HJB to an autonomous ordinary differential equation (ODE) by a change of variables. Second, I prove the existence to an initial value problem that omits the value matching condition and the smooth pasting condition (Lemma 3). Third, I derive the monotonicity (Lemma 4) and asymptotic properties (Lemma 5 and Lemma 6) of such solutions. Fourth, I show the two omitted conditions hold for one such solution, which, therefore, solves the free boundary problem (Lemma 7).
Consider the change of variables . By substituting the speed of exploration (8) into HJB (3), I obtain
Define to be 0 for and for . For so that , consider the initial value problem of ODE (9) with initial conditions and . Such exists because .
Lemma 3.There exists a unique solution ϕ to the initial value problem. Moreover, .
Proof.By the Picard–Lindelöf theorem, there exists a unique solution to the initial value problem on , where is well defined.
To show by contradiction, I suppose . For , I have because by continuity. The supremum is attained also by continuity. Moreover, I have and, thus, . Differentiating ODE (9) at , I obtain
Because implies , the solution exists and is unique on . □
Lemma 4.The function is continuously differentiable with respect to , and its derivative is positive and strictly decreasing in y.
Proof.Because , the derivative of ϕ with respect to is the solution to the variational equation
To obtain a contradiction, I suppose . The supremum is attained because . I have for and for . At , I have as . Therefore, for sufficiently small , which is a contradiction. □
Lemma 5.For sufficiently close to , the solution intersects with the 45-degree line, −y.
Proof.For the case of , I have . The initial conditions satisfy and . Moreover, and so ϕ exists and is unique in a neighborhood of 0. I have for some close enough to zero.
For the case of , I have . The solution is the constant function . It satisfies for some .
In either case, I have for some . By the continuity of ϕ with respect to , I have for sufficiently small . Because , intersects with −y by the intermediate value theorem. □
Lemma 6.For sufficiently large , the solution does not intersect with the 45-degree line, −y.
Proof.For the case of , define
For the case of , define
Lemma 7.There exist and such that on with equality at and .
Proof.Let be the supremum of solutions of initial values that intersect with the 45-degree line. It exists by Lemma 5 and Lemma 6. Let denote the corresponding solution. Let denote a maximizing sequence. For each n, let denote the solution for and let denote the first intersection. The sequence is uniformly bounded by L by the proof of Lemma 6 and, therefore, admits a converging subsequence. With a slight abuse of notation, let denote the converging subsequence. Define .
For all n, I have because intersects −y from above. In addition, is uniformly bounded from below by −1 on , because is increasing in the initial value and decreasing in y by Lemma 4.
The first derivative is uniformly bounded by and so is uniformly Lipschitz. Moreover, is uniformly bounded by on because . The Arzelà–Ascoli theorem therefore implies that the sequence admits a uniformly converging subsequence. The uniqueness of the initial value problem further implies that the limit is . Moreover, the uniform convergence implies ; i.e., intersects with the 45-degree line. It also implies that on
I show that is uniformly bounded on . For the case of , I have
The uniformly bounded implies that is uniformly Lipschitz. Because the first derivative is uniformly bounded between , the Arzelà–Ascoli theorem implies that admits a uniformly converging subsequence. By the uniqueness of the initial value problem, the limit is . Moreover, the uniform convergence implies .
It remains to show . Suppose . I have for sufficiently small . By the continuity of the initial value problem, , so intersects the 45-degree line, which contradicts the fact that is the supremum. □
Because solves ODE (9) and the corresponding boundary conditions, I obtain the desired function v by reverting the change of variables via . □
Proposition 5 allows me to extend the construction from to .
Corollary 3.Any function v defined in Proposition 5, with the extension of value 0 for , solves the HJB equation
Remark 3.When , the solution to the free boundary problem can also be characterized by
Proof of Part (i) of Theorem 1.Define the candidate continuation value function as for . Note that the function is convex. Recall that .
For any strategy , Itô's lemma gives
Taking expectation (over ) of (10), I obtain
Including the flow utility and learning costs over and taking expectations, I obtain
For , the chosen alternative is at the frontier and so . In this case, Corollary 3 implies that the integrand is weakly negative. For , I have . The integrand is also weakly negative since v is weakly positive.
By construction, attains the maximum integrand (at zero) over all s because it satisfies the HJB equation in Corollary 3. For this strategy, the speed is bounded and so the learning cost is uniformly integrable. As , the terminal value, , vanishes and so the value of is given by .
Consider an arbitrary strategy . The growth condition implies that is uniformly integrable. Fatou's lemma gives
Proof of Part (ii) of Theorem 1.For any optimal strategy, the integrand in (11) is zero t-almost everywhere with probability 1. Within the threshold , it is uniquely maximized by . Beyond the threshold , the integrand is maximized if and only if and . Therefore, the process is unique. Within the threshold, and is, therefore, unique. For the unique X, the threshold is reached only when . Then is unique almost surely. □
A.7 Proof of Proposition 2
The proof of Proposition 2 relies on two single-crossing lemmata about the solution to initial value problem (9) with respect to model parameters (Lemma 9 and Lemma 10). They imply the monotonicity of and (Corollary 4 and Corollary 5). Given the monotonic endpoints, the single-crossing lemmata strengthen the monotonicity results to the functions v (Lemma 11) and s pointwise (Lemma 12).
Consider two sets of parameters labeled by that are identical except either , , , or . Recall that .
Lemma 8.If , then pointwise.
For the proof, see the proof of Proposition 5(c) in Moscarini and Smith (2001).
For , let denote the solution to ODE (9) subject to initial condition and from until , for parameters i.
Lemma 9. (Single crossing, starting from 0)
- If , then and for all .
- If , then there is at most one such that . Moreover, and for all .
Proof.I first prove the lemma for either or . By Lemma 8, pointwise.
For the case of , I prove on by showing there. Suppose to the contrary that . It is attained by continuity of s and in the neighborhood of 0, because . Moreover, on because there. At , I have
For the case of , I show that and crosses at most once. Let denote the first crossing. Because , I have . Whenever , I have , and so for sufficiently small .12 I continue to show for all by showing there. Suppose to the contrary that . It is attained by continuity of ϕs. In addition, I have either or and . Moreover, on because there. At , I have
The proofs for single crossing with respect to μ and are analogous: the only difference lies in the derivation of the ordering between s. For μ, I obtain the ordering by noting and, thus, for all interior y. For , I note and so . □
Corollary 4.Let denote the option value at 0 for parameters i. Then .
Proof.Suppose otherwise. I have by Lemma 9. Because touches the 45-degree line, the function will never intersect the line, which is a contradiction. □
For , let denote the solution to ODE (9) for parameters i from until , subject to initial conditions and , where . The solution exists at least for by construction in Proposition 5.
Lemma 10. (Single crossing, starting from )
- If , then and for .
- If , then there exists at most one such that . Moreover, and for .
The proof is analogous to Lemma 9. The only difference is the starting point y instead of 0. For , I have and by the convexity of . The reverse goes for .
Corollary 5.Let denote the drawdown threshold for parameter i. Then .
Proof.Suppose otherwise. I have , a contradiction. □
Lemma 11.Let denote the option value for parameters i. Then pointwise.
Proof.It suffices to show that pointwise.
Suppose otherwise. There exists such that by the intermediate value theorem. By Lemma 9, I have and so does not intersect the 45-degree line on . Moreover, and so the convex does not intersect the 45-degree line on . Therefore, does not intersect with the 45-degree line, which is a contradiction. □
Lemma 12.Let denote the speed of exploration for parameters i. Then pointwise.
A.8 Proof of Corollary 1
Define . It is increasing because g is increasing. Moreover, elementary calculus shows that is decreasing whenever is increasing.
A.9 Proof of Proposition 3
Lemma 13.Let z denote a Brownian motion with drift μ and volatility reflected at . Then the pairs of processes and share the same law, where is the local time of z at 0.
For the proof, see Peskir (2006).
Proof of Proposition 3.Lemma 13 implies that the measure is absolutely continuous and its density satisfies the Kolmogorov forward equation
This diffusion-drift problem with absorption/reflection boundary conditions can be solved by Fourier series. See Chapter 4 of Strauss (2007). The solution converges asymptotically to the leading eigenfunction, denoted by , exponentially at the rate of the leading eigenvalue, denoted by .
I note that for . □
A.10 Proof of Corollary 2
The proof of Proposition 3 implies that the distribution of decays to zero exponentially at rate λ. Because , I have . Therefore, the distribution of τ also decays to zero exponentially at rate λ.
A.11 Proof of Proposition 4
Similar to Proposition 3, I index the utility process U by the alternatives instead of time by undoing the time change . Because the threshold strategy is invariant to the continuous time change, the utility process is stopped at the alternative , where .
I prove Proposition 4 by establishing the linear relationship between and , and then translating the relationship from to . I first approximate the tail distribution of (Lemma 14). I continue to derive the expectation of conditional on , using that of conditional on (Lemma 15). I use this indirect method because is not adapted to the natural filtration , but is. Finally, I translate the conditional expectation to conditional on by the marginal distribution of approximated in Lemma 14 and the Markov inequality.
Lemma 14.Suppose . Then has an exponential tail with exponent λ.
Proof.Proposition 3 implies that has an exponential tail, and so there exist such that . Because , the tail probability of is bounded from above by .
The difference is independent of due to the strong Markov property. Recall that Brownian motion near an extrema follows a Bessel-3 process starting at zero. Therefore, z follows the distribution of hitting time at of that process. Its density follows an exponential distribution asymptotically.13 Because the stopping alternative is distributed as the hitting time at of a Bessel-1 process, i.e., reflected Brownian motion, z has a thinner exponential tail than . Because and z are independent and sum to , the tail of must be at least as thick as the tail of . □
Lemma 15.Suppose . Then and satisfy
Proof.Because by definition, is independent of due to the strong Markov property of Brownian motion. Therefore, it suffices to compute and .
First, I compute . To simplify notation, I will compute it under the normalization . For standard Brownian motion starting at , let H denote the exit time from . The expectation of conditional on exiting at z is14 . Because has finite expectation, the dominated convergence theorem applies and the conditional expectation of H is given by .
Due to the quadratic variation of Brownian motion, the escape time converges to almost surely as . By the dominated convergence theorem, the conditional expectation converges as well, i.e., .
Second, I compute . For a standard Brownian motion and , the conditional Laplace transform satisfies
Lehoczky (1977) shows that is exponentially distributed with mean . Using his result, I obtain the tail conditional expectation of by integrating the conditional expectation
For the utility process U with , the Brownian scaling property implies that the conditional expectation for volatility and threshold σz is
Proof of Proposition 4.Note that the coefficient of x is, in fact, . See the proof of Proposition 3.
I first show . The Markov inequality applied to Lemma 15 yields
I continue to show . For a standard Brownian motion stopped at drawdown , the Laplace transform of conditional on satisfies16
The independence between and implies
Given the distribution of in Lehoczky (1977), the density of conditional on is bounded by




