Power of personalized smoking cessation: A quantitative lifecycle framework for policy evaluation
Abstract
Evidence suggests that smokers' responsiveness to cessation medication depends on genotypes. Whether personalized treatment based on genotypes is cost effective compared to standard treatments, however, has been unexplored. We thus construct a lifecycle model with endogenous health evolution and life expectancy and with heterogeneities in genotypes, demographics, and adolescent smoking. We examine the cost effectiveness of three intervention policies: (i) a standard policy where all smokers receive counseling and medication, (ii) a standard policy where some smokers receive counseling and others receive counseling and medication, and (iii) a personalized policy based on genotypes. The personalized policy proves the most cost effective: every dollar of program cost generates about $29 and $40 in value measured over the lifecycle for smokers treated at age 37 and 52, respectively, about 16–22% higher than the two standard policies.
1 Introduction
Cigarette smoking is a leading preventable health threat. Evidence has shown large healthcare costs, morbidity (productivity) costs, and mortality losses associated with smoking, where the estimated total cost of smoking and value of life lost per death are sizable.1 Thus, smoking cessation can be valuable by reducing such health risks and economic costs. Recent medical research shows that using genetic markers helps predict the risk of developing nicotine dependence, delays in smoking cessation, and the responsiveness to medication treatment. Whether this personalized medicine treatment is cost effective, however, remains unexplored.
Genetic markers, including nicotinic acetylcholine receptor genes, nAChRs, matter for treatment effectiveness (cf. Kortmann, Dobler, Bizarro, and Bau (2010) and Chen et al. (2020)). Specifically, among the three common haplotypes spanning this gene region, H1, H2, and H3, Chen et al. (2012) find that the high-risk haplotype (H3) are unequivocally heavy smokers with strongest addiction, but typically respond well to medication. In contrast, smokers with the low-risk haplotype (H1) are usually light smokers and are more likely to quit with basic counseling, but do not benefit from medication. This suggests that identifying a smoker's genotype to treat those most likely to respond (i.e., the H2 and H3 types) is valuable.
We develop a lifecycle model with endogenous decisions on smoking and quitting, health investment and savings, and life expectancy. We consider the three main smoking costs: (i) rising demand for medical care (healthcare cost), (ii) lower labor income (morbidity cost), and (iii) shortened life expectancy (mortality cost). We build upon the health capital framework (Grossman (1972a,b)) and the health and life expectancy framework (Rosen (1988); Ehrlich and Chuma (1990); Jones (2016)), incorporating addicts' smoking habit formation (Carroll, Overland, and Weil (1997, 2000)) and bequest motives (De Nardi (2004)). Additionally, we consider behavioral aspects: peer, home, and workplace influences under which adolescent smoking need not be a fully rational decision2 and a rational addict may not be able to quit due to addiction. Moreover, even in adulthood, limited health valuation and incomplete health knowledge may also lead to excessive smoking.
A lifecycle model offers several improvements over existing approaches. In particular, the epidemiological literature focuses primarily on the morbidity and mortality hazard and the associated healthcare costs. A lifecycle model allows us to address (i) how a consumption-smoking trade-off affects the extensive (smoke or quit) and intensive (cigarettes smoked per day, or CPD) margins; (ii) how saving and bequest motives affect health investment and smoking behavior; (iii) how the health consequences affect productivities and incomes which in turn influence smoking and health investment; (iv) how the degrees of addiction measured by smoking habits and heterogeneities in genotypes and demographics matter for smoking behavior; (v) how the aforementioned channels change with age; and (vi) how such age-dependent channels affect the welfare gains from standard versus personalized smoking cessation treatments. In addition to various heterogeneities typically included in the literature (see a critical review by Chaloupka and Warner (2000)), we include genotypes, which affect smoking preferences, smoking habits, and treatment responsiveness.
We calibrate our model to fit key observations from US data. The set of targets include economic data, such as income, various expenditure and bequest ratios, and life expectancy, from the Panel Study of Income Dynamics (PSID) and other sources. We supplement it with medical data, most importantly, gene-dependent smoking cessation behavior by Chen et al. (2012) and differential life years gains from cessation by Jha et al. (2013). Our calibrated model fits well, particularly in life expectancy and quit rates that are critical in policy evaluation.
We propose three equal-cost smoking cessation policies: (i) a standard policy (S) where all smokers receive both counseling and medication, (ii) a standard policy () where some smokers receive counseling and others receive counseling and medication, and (iii) a personalized policy (P) based on genotypes, the highlight of this study. Policy S is the typical baseline. Policy is designed to mimic policy P in all aspects except not being gene-based. Thus, a comparison between policy P and isolates the effectiveness of personalized medication. Based on the resulting quit rates and other endogenous responses, we then compute two equivalent variation measures of welfare gains: the Consumption Equivalent variation (CE) and the Income Equivalent variation (IE). Based on these measures, we compute the expected value of a statistical life (VSL) gain from quitting and the equivalent one-time wealth transfer as a fraction of lifetime income. We further construct a unified measure, a cost/effectiveness ratio (C/E), based on the expected IE and on the transfer measure of a smoker, as well as on the policy coverage rates given the same program budget.
We find that, under the same program costs, personalized treatment provides coverage for more people and maintains higher effectiveness than standard treatments. The VSL gain under personalized treatment at age 37 is about $168 thousand dollars (in 2009 dollars) per quitter or, approximately, a 13% gain from the benchmark value without treatment. The gain when treating at 52 is 12% higher than at age 37. Per dollar of program cost, personalized treatment at age 37 generates almost $29 IE in effectiveness over the lifecycle, about 17–22% higher than the comparable figures under the standard treatments. As a result of a greater quit rate, this effectiveness measure is larger when personalized treatment is implemented at age 52, generating $40 IE over the lifecycle, about 16–22% higher than standard treatments. The transfer-based cost-effectiveness gains of personalized policy are of comparable magnitude. An unambiguous finding is that personalized treatment proves the most cost effective of all treatments in smoking cessation regardless of treatment age.
We further decompose the welfare gains (measured by CE and IE) from cessation into: (i) a pure income channel, (ii) a health-productivity channel, (iii) an endogenous health investment channel, and (iv) a bequest motive channel. We find that the health investment channel accounts for over three-fifths of the welfare gain from smoking cessation, as it incorporates the policy effects on health capital and on life expectancy. The health-productivity effect and bequest motive are equally important, together accounting for about one-third of the gain, though the contribution of the former diminishes and the contribution of the latter rises toward the later stage of one's life.
Our effectiveness measures are more general than quality-adjusted life years (QALYs) and the cost-effectiveness measures commonly used in the medical and public health literature. Specifically, our lifetime utility-based effectiveness measures account for time discounting, diminishing marginal valuation and differential utility weights. More importantly, our measures are obtained in a lifecycle framework in which health investment and health capital evolution interact with many other decisions over the lifecycle. We are thus able to more thoroughly investigate individual responses to different policies over time. While the purpose of this study is to evaluate smoking cessation policies, our theoretical framework and quantitative method readily apply to other addictions, such as alcohol and illicit drugs, as well as to evaluating the efficacy of other precision medicines.
The Supplemental Appendix (Chen, Wang, and Yao (2025)) contains details on data, model solution and algorithm, various measures, and robustness analyses.
2 Background and evidence
2.1 On genotype-demographic heterogeneities and smoking
The health economics literature finds that male smokers typically smoke more cigarettes per day (CPD) than female smokers and that blacks are less likely to smoke and smoke less than whites. There exists a substantially positive effect of education on health, in particular, better-educated smokers are more likely to quit smoking than less-educated smokers. By using a more precise gene-related measure, addicts may raise smoking intensity in response to higher cigarette taxes in contrast to the conventional predictions, whereas there is an adverse effect of smoking bans on passive (second-hand) smokers (Adda and Cornaglia (2006, 2010)).
We identify several stylized facts based on cross-sectional data from PSID (1999–2011): (i) about 1 out of 4 of the US adult population (whites and blacks at age above 18) smokes, with the average CPD almost one and a half packs (14);3 (ii) the average expenditure on tobacco accounts for an nonnegligible share (6.5%) of an addict's labor income; (iii) while the share of smokers differs little across genders and races, it varies substantially by education, with almost 30% of non-college educated but less than 10% of college educated being smokers; (iv) males smoke more than females, whites smoke more than blacks, and the noncollege educated smoke more than college educated; (v) while the noncollege educated white males have the highest average CPD, the noncollege educated black females have the highest smoking expenditure to labor income share.4
Figure 1 plots lifecycle smoking behavior, using the average data moments of each age group by regarding the data as multiple waves of cross-sections.5 First, the left panel of Figure 1 shows that the share of smokers in the population declines with age, indicating quitting by smokers over time. While the reduction in smoking prevalence is commonly identified in both economics and medicine literature, it is noted that as the sample size is trimmed down sharply due to deaths, the average outcomes become more volatile for age cohort beyond 65. Second, two smoking intensity measures that incorporate quitting and survival probability are presented in the middle panel (smoking expenditure to labor income ratio) and in the right panel (population average CPD). The smoking expenditure share declines sharply before age 30 and the downward trend continues through the remaining life course. The population average CPD exhibits a relatively stable pattern up to age 50 and then a downward trend, which is consistent with the smoking likelihood pattern discovered by Darden, Gilleskie, and Strumpf (2018).6
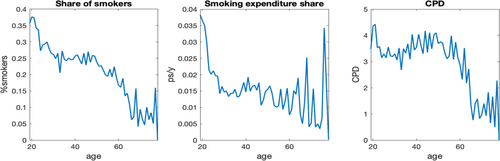
Lifecycle smoking behavior in PSID data. Note: Smoking expenditure share (as a ratio to labor income, ps/y) and cigarette smoked per day (CPD) are both measured as the population average with cohort and year effects being teased out.
Turning now to the cessation data (Chen et al. (2012)) to be used in our quantitative analysis,7 we note that the share of H1, H2, and H3 genotypes among smokers is about 25%, 43%, and 32%, respectively. While the shares of the three genotypes do not vary significantly by gender or education, they do by race. In particular, panel A of Table 1 shows that whites have a much larger share of the H3 haplotype than blacks and blacks have a much larger share of the H1 haplotype than whites, while the share of the H2 haplotype is similar for both. Additionally, panel B of Table 1 summarizes the smoking behavior of the three genotypes in terms of CPD, indicating that H1 smokers are the lightest smokers, whereas H3 smokers the heaviest smokers.8
|
H1 |
H2 |
H3 |
|
|---|---|---|---|
|
A. Population shares (%) |
|||
|
all |
25 |
43 |
32 |
|
whites |
21 |
44 |
35 |
|
blacks |
51 |
43 |
6 |
|
B. CPD |
20.7 |
21.1 |
22.5 |
|
C. Quit rates (%) |
|||
|
counseling only |
34.9 |
25.3 |
16.8 |
|
college |
44.0 |
32.3 |
21.8 |
|
noncollege |
32.3 |
23.1 |
15.5 |
|
counseling and medication |
34.9 |
36.0 |
35.5 |
|
college |
44.0 |
46.0 |
46.0 |
|
noncollege |
32.3 |
32.9 |
32.9 |
- Note: Quit rates are relapse-adjusted and reported for college educated and noncollege educated smokers and their averages.
2.2 On smoking cessation and treatment effectiveness
Extensive research supports the effectiveness of counseling and pharmacological interventions in increasing smoking cessation rates among smokers. Successful counseling boosts the motivation to quit by personalizing the costs and risks of the patient's tobacco use. Seven medications are also approved by the Food and Drug Administration (FDA) for treating nicotine dependence.
Medical studies suggest that, among the three genotypes, H3 smokers (the high-risk haplotype) are less able to quit, more likely to smoke longer or inhale more deeply; thus, the risk in mortality is higher for H3 (cf. Kortmann et al. (2010) and Chen et al. (2015a)). Panel C of Table 1 presents the quitting behavior of the three genotypes. The quit rates are taken from the experiment data in Chen et al. (2012),9 adjusted by a 25% relapse rate.10 Interestingly, despite belonging to the high risk group, H3-type smokers are most responsive to medication treatment compared with the other two genotypes. The quit rate is only 16.8% for H3-type smokers if only counseling is provided and 35.5% with medication and counseling. This quit rate, however, is essentially unchanged for H1-type smokers (34.9% regardless of the provision of medication), and for H2 smokers, it is 25.3% without medication and 36.0% with medication. Moreover, conditional on genotype and treatment, college educated smokers have a substantially higher quit rate than noncollege educated smokers.11
3 The model
We model smoking behavior and its health consequences within a lifecycle framework of consumption-smoking-health investment-bequest trade-offs with three key features: (i) endogenous health evolution and life expectancy, (ii) endogenous smoking habits, and (iii) endogenous labor productivity. We consider heterogeneities in demographics (gender/race/education) to affect work efficiency and heterogeneities in genotypes to affect smoking preferences, habits, and responses to smoking cessation treatments (counseling/medication).
First, we allow better health to improve the quality of life, and hence, lifetime utility (cf. Murphy and Topel (2006)).12 This is important because QALYs is a standard effectiveness measure in cost-effectiveness analysis in medicine and health (cf. Gold, Siegel, Russell, and Weinstein (1996)). Second, by allowing health capital to evolve endogenously (cf. Grossman (1972a,b)), smoking enjoyment is at the expense of health deterioration at an increasing rate over time. Third, while individuals value health, such valuation rises with age; moreover, they have imperfect health knowledge. Fourth, we incorporate into an addict's preference a smoking habit whose formation depends on the flow smoking intensity.13 Fifth, departing from the literature, we consider heterogeneities in individuals' tastes for smoking and responses to smoking cessation treatments based on genetic markers, which permits us to evaluate precision medicine with personalized treatments.14
3.1 The basic environment
Time is continuous. An individual's life starts at when she acts as a decision maker (who may be referred to as a young adult).15 Her life ends at T, which is endogenous.
3.1.1 Preferences, smoking habits, and bequests
Denote as the (constant) preference parameter for full health valuation. We assume that health valuation rises with age, which is consistent with arguments by behavioral macroeconomists (e.g., Gabaix (2023)): when health issues have not become a threat, an individual values health less.16 Specifically, we propose: , where captures the fact that individuals undervalue health when young.
Health raises an individual's lifetime utility directly via two channels: higher quality of life (through ) and longer life expectancy (through T). Two remarks are in order. First, in order for longevity to raise lifetime utility, it is necessary to ensure that the flow utility be positive. Given the log functional form, this is met when we choose the scale of health, income, and smoking habit properly, so that their logged values are sufficiently greater than zero. This strategy follows Murphy and Topel (2006), by assuming consumption bundles exceed “subsistence” levels (which are, in our case, and for smokers).17 Second, although consumption and health have the same income elasticity under the simple log functional form, the positive health effect on life expectancy makes health a luxury good relative to consumption, consistent with the literature on health and life (Hall and Jones (2007); Jones (2016)).
3.1.2 Income, spending, and asset accumulation
3.1.3 Health evolution and life expectancy
Finally, the terminal date of an individual's life, T, is reached when her health drops below a minimum surviving threshold (i.e., ). This setting is natural based on the medical literature, where may be viewed as the biological requirement for a human body to function. Because the evolution of an individual's health capital depends on her decisions, her life expectancy is thereby endogenous, depending particularly on smoking behavior and health investment.21
3.1.4 Smoking cessation without treatment
Remarks
We model an individual's decision over the life course in a deterministic setting. One might argue for inclusion of shocks to health and income as in the macro-health literature. It is thereby informative to justify our modeling choice for the purposes of this study. Particularly, while smoking does not necessarily lead to bad health outcomes and productivity losses, it does raise the probability of detrimental consequences based on genetics (cf. Levine and Crimmins (2016)). For the vast majority of the population, health degradation as a result of smoking is almost definite and cumulative. Therefore, in our model, we capture such consequences in a deterministic structure, as the genetic nature of health effects of smoking makes it inappropriate to model health evolution as stochastic. Cutler and Glaeser (2005) find that genetics and behavioral-specific situational factors (such as peers and families) play far more important roles in driving health behaviors than health news or health shocks. Accordingly, we consider both genetic and initial habit heterogeneities that capture in spirit their genetic and situational factors. We also allow interactive effects of health deterioration and income evolution over the lifecycle to affect smoking behavior. Empirical evidence shows that the positive psychology effect (more intense smoking due to the stress of unanticipated job loss or income reduction) and the negative wealth effect (due to the financial hardship) tend to drive the inconclusive response of smoking to income shocks.22 We thus believe that, once we allow for expected health deterioration and income evolution over the lifecycle, uncertainty would not play a primary role in smoking and cessation decisions. It is particularly so because our focus is on contrasting personalized with standard cessation treatments where the income risk differential under different treatments is unlikely to be critical.
3.2 Optimization
Consider an individual of type that summarizes genotypes, work efficiency driven by gender/race/education, natural health deterioration rate by gender, and initial smoking habit (=0 for nonsmokers). The baseline dynamic optimization problem in the absence of treatment can be conveniently divided into three steps.
3.2.1 Step I: Optimization given life expectancy T
For a given life expectancy T and initial smoking status (= 1 if smoking or 0 if nonsmoking), we consider separately the optimization problem facing a particular type of agent who is retired or working with their constraints, (2), (5), and (7), to be modified accordingly.
Retiree's problem
Worker's problem
Equation (11) governs the dynamic path of health investment. Note that when an individual is older, health capital deteriorates ( is lower) and health investment exhibits diminishing returns with age ( is lower). Thus, health investment may increase sharply at later ages to maintain health capital above the survival threshold. Meanwhile, the consumption-perceived health capital ratio () is expected to increase, at least for older individuals, implying that health investment is likely to decrease eventually when approaching the end of life. These two forces on balance may generate complicated health investment path. From (12), we see that, for an addict, and also enter with the opposite effects on smoking dynamics, though now health deterioration suppresses the smoking trend and a rising consumption-perceived health capital ratio raises the trend. While health investment may enable an individual to smoke more without harming health as much (when ), the effect of the health stock on smoking is generally ambiguous; for the retired (), however, a higher health stock discourages the individual from smoking (recall that ); that is, there is a reinforcing effect between health buildup and smoking holdback to an old retired addict. In addition, changes in smoking depends positively on smoking intensity () but negatively on the smoking habit stock ().
3.2.2 Step II: Determination of life expectancy
3.2.3 Step III: Health perception consistency
Along the optimal trajectory, , we impose for all , that is, no one is surprised along the equilibrium path, which is hereafter referred to as health perception consistency, despite misperception about the true source of health hazard from natural deterioration versus smoking .
3.3 Responses to treatment under voluntary take-up and government intervention
As documented in the medical literature, smoking cessation is difficult to achieve, especially for noncasual smokers.24 As shown by Koçak et al. (2015), although 70% of smokers desire to quit, only 46% of them have made an attempt to quit and less than 10% quit for an extended period. Government interventions, however, by providing financial incentives, can significantly increase the probability of participating in and completing a smoking cessation program by smokers, thereby enhancing cessation success (Volpp et al. (2009)). Moreover, this literature suggests take-up of cessation treatment as nonbehavioral, and hence, we shall view take-up rates as exogenous probabilities and instead focus on modeling responses to treatment, given a cessation program. We shall not model smoking relapse either because medical evidence also suggests it most likely nonbehavioral.25 Thus, we simply adjust the quit rates from Chen et al. (2012) by a relapse probability (25%) to be used as the targeted moments in our numerical applications.
4 Calibration and numerical solution
We begin with calibrating the baseline model, taking into account all dimensions of heterogeneity—initial smoking habit, smoking-associated genotypes, and demographics. We then calibrate the smoking cessation treatment effects under voluntary take-up and under policy-induced participation. We discretize the life span so that 1 year corresponds to one period. Since adolescent smoking involves nonfully rational behavior depending primarily on environment and social comparison, we assume life starts at age 18 (i.e., ) and individual choice starts at age .26
4.1 Baseline calibration
We calibrate the model to fit targeted moments of both smokers and nonsmokers. While we consider demographics as the only source of heterogeneity for nonsmokers, smokers are also allowed to be heterogeneous in initial smoking habits and smoking-associated genotypes. In particular, we categorize smokers into 6 groups based on initial habits, , determined by adolescent smoking (at age 18). Smokers with different genotypes, indicated by , differ in their preference for smoking, α, and habit scaling parameter, . We also incorporate heterogeneous work efficiency, θ, for eight demographic groups (by gender/race/education) as well as differential natural health deterioration rates, δ, by gender. Accordingly, there are 144 () groups of smokers and 8 groups of nonsmokers in total.
Some parameters are determined outside the model, by normalization or by direct data measurement. We normalize the efficiency wage rate, w, to one and set the subjective time discount rate, ρ, to 0.02 to fit the average US wealth-income ratio of about 7 (Glover, Heathcote, Krueger, and Ríos-Rull (2020)). The growth rate of consumption, g, is set to equal to that of output per capita in the US (1.8%) to ensure long-run balanced growth, and hence, the real interest rate becomes . Lacking good panel data on wealth, we set initial wealth to be 15% of average initial labor income as permanent flow income converted to capitalized value: .
The initial stock of health at age is normalized to under which the threshold health level at death is calibrated at to match the average mortality rate and average life expectancy of the US population.27 The health investment curvature parameter ϵ is set to 0.3, following Hall and Jones (2007), to produce a reasonable health investment profile.
Because smoking drops by half at age 65, we apply the half-life formulation to compute the habit adjustment parameter: . To capture individuals' incomplete knowledge about the detrimental health effect of smoking, we use the empirical finding by Kenkel (1991) that for 7 illnesses that can be caused by smoking, respondents surveyed (including both smokers and nonsmokers) are aware of 5.5 on average. We therefore assume that individuals' belief of , that is, , to be 1/4 lower than .28 Moreover, recall that measures the detrimental health effect resulting from second-hand smoke. We set q to be 0.125 based on the finding in Pickett et al. (2006) that, even in US counties with extensive smoke-free law coverage, the exposure to second-hand smoke for nonsmokers is about 12.5%.
Based on the PSID data, initial smoking habits are given by .29 The correspondent population shares of the six groups are . We set the gender (male-to-female) ratio of to be 1.6 within each group, based on the PSID data on youth's CPD, and compute for each gender in each group accordingly. Notably, to which group a smoker belongs is assumed independent of genotype, to be consistent with the medical evidence that the formation of initial smoking habits is largely influenced by environment rather than by genes.
In the labor economics literature, the wage-tenure profile estimation usually yields an experience return at 3–5%. We thus use the average to set . Then to align health-based and experience-based human capital, we jointly calibrate κ and to match income peak age of around 52 and the peak to initial income ratio of about 2.27, as documented in Guvenen, Karahan, Ozkan, and Song (2021). This yields and . Regarding the extent to which bequest is a luxury good, we match our figure with that in De Nardi (2004), which gives .
We calibrate θ for each of the eight demographic groups using PSID labor income of household heads aged between 23 and 26, normalized to an average of one. We do this for three reasons. First, the vast majority of people have completed education and started working by age 23. Second, their health may have not been significantly affected by smoking by age 26. Third, the experience may have yet contributed much to their labor income. In Table 2, we report the population share of each group among smokers and the calibrated value of θ for each group. As can be seen, the college educated all have higher than average work efficiency and are thus expected to have higher labor income, controlling for age. Blacks with no college degree, on the contrary, have much lower work efficiency, and hence, lower labor income within the same age cohort. In addition, there is a gender gap that leads to higher labor income for males than for females. Such gaps are larger for whites than for blacks. These implied patterns are in line with the labor economics literature.30
|
Gender |
Race |
Education |
Share Within Smokers (%) |
Work Efficiency θ |
|---|---|---|---|---|
|
female |
black |
noncollege |
5 |
0.63 |
|
female |
white |
noncollege |
45 |
0.79 |
|
female |
black |
college |
0 |
1.13 |
|
female |
white |
college |
5 |
1.13 |
|
male |
black |
noncollege |
7 |
0.78 |
|
male |
white |
noncollege |
34 |
1.10 |
|
male |
black |
college |
1 |
1.36 |
|
male |
white |
college |
3 |
1.46 |
- Note: Population shares are within active smokers.
Denote y as labor income and Y as total income (labor plus interest income, which is of greater relevance, especially for the retired). There are three functional forms to be specified: (i) health valuation: ; (ii) detrimental health effects of smoking: (where ensures that rises with age); (iii) health investment efficacy: . We are thus left with 20 parameters to be calibrated within the model: , χ, , B, η, , , , ν, , p, μ, α, and by genotype, and δ by gender. They are jointly calibrated to meet the quitting threshold expression (8), as well as the 19 targeted moments: (i) 4 expenditure/bequest shares: consumption expenditure share (), health investment share (), smoking expenditure to labor income share (), and bequest-asset ratio measured by the share of total assets that come from bequests (); (ii) 1 smoking and 2 health investment gradients: age 50 to 25 smoking ratio (), health investment at age 38 and 60 to initial investment ratio ; (iii) 2 smoking population shares: shares of smokers at age 50 and 65 ( and ); (iv) 7 life year measures: the average life expectancy for nonsmokers and smokers (, ) and for males and females (, ), and 3 age-dependent life year gains as a result of smoking cessation at age 30, 40, and 50 (, , and ); and (v) 3 average smoking levels by genotype ().
All expenditure and income measures are based on the US data averaged across individuals and over time. The consumption share is measured by the ratio of consumption (excluding tobacco consumption and private health expenditure) to GDP, from Penn World Table 6.3 (average over 1998–2007). The health investment share is measured by the average healthcare cost-to-GDP ratio, from the World Bank 1998–2010. We find an average individual invests about 15% of her income in health. The smoking expenditure ratio is computed as an average household head's smoking expenditure over labor income, using data from PSID (1999–2011).31 More specifically, smoking expenditure ps is computed by multiplying (tax-included) price of per pack of cigarettes, CPD from PSID, and 365 days in a year. We find an average individual (weighted average of smokers and nonsmokers) spends about 1.6% of her labor income on smoking. We set the bequest-asset ratio to 0.6, following De Nardi (2004). The smoking gradient (age 50 to 25) is set to 0.46, based on Holford et al. (2014);32 and the two smoking population shares are computed from PSID. The two health investment gradients are based on Hall and Jones (2007). The average life expectancy of the US population is 78 years, based on the World Bank data (1998–2011), and females live about 5 years longer than males on average. From Jha et al. (2013), the gap of life expectancy between smokers and nonsmokers is 12 years, and the average life year gain for smokers who quit at the ages 30, 40, and 50, respectively, are 10, 9, and 6 years. These give us life expectancy and life year gain figures. Finally, the smoking intensity of three genotypes is based on the CPD data from Chen et al. (2012) converted to model units.
We calibrate the 20 parameters jointly within the model by minimizing the distance between the model and the targeted values given the threshold expression (8). The algorithm for calibrating these parameters is as follows. We first choose a set of values for the parameters (initial guesses), and then solve the model for the 144 groups of smokers and 8 groups of nonsmokers. Next, given the population share of each group, we compute the weighted average of the targets from the model and compare them with the corresponding targeted values. The process reiterates until the sum of all gaps between model and data moments converges. Table 3 summarizes the parametrization, with panel A reporting predetermined parameters and panel B reporting parameters calibrated within the model. Table 4 presents the model fit, data versus model moments, showing a good fit overall.
|
A. Determined outside the model |
||
|---|---|---|
|
Parameter |
Value |
Target |
|
time discount and interest rates |
ρ = 0.02, r = 0.038 |
wealth-income ratio, BGP |
|
health stock boundaries |
h0 = 100, |
normalized, computed |
|
habit adjustment |
ς = 0.015 |
computed |
|
experience return |
ϕ1 = 0.04 |
match literature |
|
initial wealth |
a0 = 395 |
preset |
|
health investment curvature |
ϵ = 0.3 |
match literature |
|
bequest luxuriousness |
b1 = 11.6 |
match literature |
|
B. Calibrated within the model |
||
|---|---|---|
|
Parameter |
Value |
Target |
|
Experience scaling/curvature |
κ = 355, ϕ2 = −0.00059 |
joint targets of peak income year and peak-to-initial income ratio |
|
Health cost of smoking |
γ0 = 0.0135, γ1 = −0.000039, γ2 = 0.000039 |
joint targets of 4 expenditure bequest shares, 3 smoking and health investment gradients, 2 smoking population shares, 7 life year measures, 3 smoking intensity measures, and equation (8) |
|
Natural health deterioration |
δM = 1.08, δF = 1.02 |
|
|
Health investment efficacy |
Φ0 = 0.020, B = 1.51, η = 0.03 |
|
|
Health curvature |
μ = 0.01 |
|
|
Tastes for smoking |
αH1 = 2.36, αH2 = 2.69, αH3 = 3.23 |
|
|
Tastes for health quality |
, χ = 0.06 |
|
|
Bequest motive |
b0 = 13.49 |
|
|
Imputed cigarette price |
p = 2.44 |
|
|
Smoking habit |
S0H1 = 0.31, S0H2 = 0.41, S0H3 = 0.78, ν = 0.98 |
|
- Note: Consumption and health expenditure shares are ratios to total income (, ), smoking expenditure share to labor income (), and bequest share to total assets (). The smoking gradient is the age 50 to 25 smoking ratio () and the health investment gradients are age 38 and 60 to age 19 ratios . The smoking population shares are for those at ages 50 and 65 . Life year measures include average life expectancy for nonsmokers/smokers , that of males/females , and life year gains from quitting at ages 30/40/50 . Smoking intensity measures are CPD of three genotypes converted to model units.
|
Target |
Data |
Model |
|---|---|---|
|
peak income year, peak to initial income ratio |
52, 2.27 |
52, 2.27 |
|
consumption expenditure share () |
0.614 |
0.628 |
|
health investment share () |
0.149 |
0.143 |
|
smoking expenditure-labor income share () |
0.0159 |
0.0162 |
|
bequest-asset ratio () |
0.60 |
0.56 |
|
smoking gradient () |
0.46 |
0.40 |
|
health investment gradients |
1.73, 4.62 |
1.93, 4.49 |
|
smoking population shares (smk_fr50,smk_fr65) |
0.238, 0.112 |
0.308, 0.155 |
|
life expectancy of nonsmokers, smokers (LEnonsmoker,LEsmoker) |
81, 69 |
80.8, 68.9 |
|
life expectancy of males, females (LEM,LEF) |
75.5, 80.5 |
75.1, 80.5 |
|
life year gains from cessation (LEgain30,LEgain40,LEgain50) |
10, 9, 6 |
10.8, 7.9, 4.8 |
|
smoking intensity (save,H1,save,H2,save,H3) |
10.42, 10.64, 11.33 |
10.28, 10.55, 11.01 |
- Note: See Notes to Table 3 regarding the targeted moments.
The only imperfect match is the overestimation of smoking population shares, which is essentially due to the absence of cessation treatments in the baseline calibration. Recall that Koçak et al. (2015) show that despite 70% of smokers wanting to quit, only 46% of them have made such an attempt and less than 10% maintain abstinence for an extended period. Assume any such attempts include uses of formal treatments (counseling or counseling and medication), as well as usage of over-the-counter treatments (nicotine patch/inhaler/nasal spray/gum). Then we may view a general treatment rate, or a take-up rate (without a government intervention), as , and a share of smokers who quit with voluntary treatment as . Taking this into account would sufficiently close the gap in the share of smokers between the model and data.
4.2 Calibrating cessation treatment effects
We now calibrate the smoking cessation treatment effects under voluntary take-up and under policy-induced participation. According to Volpp et al. (2009), smokers receiving sufficient financial incentives have significantly higher rates of participating in and completing a smoking cessation program, and hence, have a significantly higher quit rate. Our calibration of treatment responses is based on the experimental data from Chen et al. (2012), which involves quit rates by genotype, education, age, and treatment (i.e., counseling or counseling plus medication). We use these quit rates as the targets for calibrating policy-induced treatment effects because their experiment provided free cessation treatment.33 To back out the quit rates under voluntary take-up, we borrow the numbers from Koçak et al. (2015) and estimate the average quit rate under voluntary treatment to be 21.7%.34 We then compute the ratio of average quit rates under policy-induced treatment and under voluntary treatment to be 1.6 and use it to back out the quit rates under voluntary take-up for smokers by genotype, education, age, and treatment.
Since the experimental data from Chen et al. (2012) contains only heavy smokers, we exclude light smokers and focus on smokers with initial smoking habits given by ; the correspondent population shares of the five groups are .35 To calibrate heterogeneous responses to different types of treatment, namely counseling versus counseling plus medication, we need more within the genotype-demographic cell variations in – with only five groups of , the quitting response may be too lumpy, leading to imprecise calibration outcomes. It is known that self-reported CPD figures are concentrated on a quarter pack, half a pack, one pack, and one pack and a half (5, 10, 20, and 30). As such, it is uninformative to use the distribution of directly. We instead interpolate 3 additional data points in between each pair of figures (one-quarter, half, and three-quarters). This gives us 17 data points in within each of the 24 cells by genotype and demographics: , with corresponding population shares given by {0.024, 0.037, 0.050, 0.063, 0.076, 0.076, 0.076, 0.076, 0.076, 0.074, 0.072, 0.069, 0.067, 0.057, 0.046, 0.036, 0.025}. Again, the gender ratios of are set to be the same across all 17 grids. Moreover, Chen et al. (2012) focus on two major age groups, 25–44 (average 37) and 45–66 (average 52), and show differential quit rates across the two groups. We follow by examining the quitting responses of young (37) and old (52) addicts.
4.2.1 Voluntary treatment effects
We have the following parameters associated the voluntary treatment effects to calibrate—6 counseling effect parameters by genotype and education at age 37 (), 3 medication effect parameters by genotype at age 37 (), and a habit duration parameter (), where the last one refers to the duration for which the smoking habit persists after quitting. In addition, medical evidence suggests that treatment effects depend on age and that this age effect varies across genotypes. We thus specify 6 parameters to be associated with differential age effects of treatment, 3 age ratios (age 52 to 37) of the counseling effect by genotype (), and 3 age ratios (age 52 to 37) of the medication effect by genotype (). Since medication does not affect H1 haplotype at any age (i.e., ), the total number of parameters to be calibrated is 14. We calibrate these parameters jointly to match 14 targeted moments associated with quit rates of smokers by genotype, education, age, and treatment. The parameter values are reported in Table 5, panel A and the model fit in panel B, showing a good fit of the model.
|
A. Calibrated parameters |
|||
|---|---|---|---|
|
H1 |
H2 |
H3 |
|
|
college taste response to counseling ϖτ,college |
0.16 |
0.17 |
0.05 |
|
noncollege taste response to counseling ϖτ,noncollege |
0.21 |
0.19 |
0.07 |
|
habit survival response to medication ϰτ |
0 |
1.08 |
1.40 |
|
52–37 ratio of taste response to counseling ϖτ,ratio |
1.50 |
1.70 |
3.04 |
|
52–37 ratio of habit survival response to medication ϰτ,ratio |
n.a. |
0.15 |
2.00 |
|
after-quitting habit duration parameter Tk |
15 |
||
|
B. Model fit |
||||||
|---|---|---|---|---|---|---|
|
Data |
Model |
|||||
|
H1 |
H2 |
H3 |
H1 |
H2 |
H3 |
|
|
college quit rate after counseling (%) |
26.8 |
19.7 |
13.3 |
25.2 |
21.3 |
14.7 |
|
noncollege quit rate after counseling (%) |
19.7 |
14.1 |
9.5 |
19.5 |
15.8 |
11.4 |
|
quit rate ratio at age 52 to 37 after counseling |
1.11 |
2.14 |
1.87 |
1.09 |
2.08 |
1.77 |
|
college quit rate after counseling & medication (%) |
26.8 |
28.0 |
28.0 |
25.2 |
31.2 |
26.5 |
|
noncollege quit rate after counseling & medication (%) |
19.7 |
20.0 |
20.0 |
19.5 |
20.3 |
22.8 |
|
quit rate ratio at age 52 to 37 after counseling & medication |
1.11 |
1.13 |
1.25 |
1.09 |
1.42 |
1.21 |
4.2.2 Policy-induced treatment effects
Next, we calibrate the cessation treatment effects under policy-induced participation. There are 13 parameters to calibrate: an additional counseling effect by genotype and education at age 37 (), an additional medication effect by genotype at age 37 (), changes in age 52 to 37 ratios of the counseling effect and the medication effect by genotype (, ). The smoking habit duration remains unchanged and medication continues to have no effect on the H1 haplotype. These 13 parameters are calibrated to match the various quit rates in the experimental data from Chen et al. (2012), as reported in Table 6.
|
A. Calibrated parameters |
|||
|---|---|---|---|
|
H1 |
H2 |
H3 |
|
|
change in college taste response to counseling Δϖτ,college |
0.06 |
0.02 |
0.02 |
|
change in noncollege taste response to counseling Δϖτ,noncollege |
0.05 |
0.03 |
0.02 |
|
change in habit survival response to medication Δϰτ |
0 |
0.03 |
0.28 |
|
change in 52–37 ratio of taste response to counseling Δϖτ,ratio |
−0.15 |
0.01 |
0.76 |
|
change in 52–37 ratio of habit survival response to medication Δϰτ,ratio |
n.a. |
0.05 |
−0.32 |
|
B. Model fit |
||||||
|---|---|---|---|---|---|---|
|
Data |
Model |
|||||
|
H1 |
H2 |
H3 |
H1 |
H2 |
H3 |
|
|
college quit rate after counseling (%) |
44.0 |
32.3 |
21.8 |
43.9 |
32.2 |
20.7 |
|
noncollege quit rate after counseling (%) |
32.3 |
23.1 |
15.5 |
32.3 |
24.4 |
18.1 |
|
quit rate ratio at age 52 to 37 after counseling |
1.11 |
2.14 |
1.87 |
1.08 |
2.16 |
1.91 |
|
college quit rate after counseling & medication (%) |
44.0 |
46.0 |
46.0 |
43.9 |
47.5 |
46.7 |
|
noncollege quit rate after counseling & medication (%) |
32.3 |
32.9 |
32.9 |
32.3 |
32.5 |
36.0 |
|
quit rate ratio at age 52 to 37 after counseling & medication |
1.11 |
1.13 |
1.25 |
1.08 |
1.15 |
1.32 |
4.3 Lifecycle pattern
Before turning to the main policy evaluation task, it is informative to illustrate how genotype heterogeneity affects individual smokers' lifecycle choices and to compare the lifecycle pattern of several key indicators to the data.
Table 7 presents a comparison in key indicators for each genotype of smokers, nonsmokers, and the respective population weighted averages. As can be seen, life expectancy of smokers is 11–12 years shorter than nonsmokers. H3-haplotype smokers live slightly shorter than other haplotypes, consistent with medical evidence that CHRNA5 is associated with increased mortality (Halldén et al. (2016)). Smokers spend about 6–7% of labor income on tobacco, thus having a lower share of other consumption than nonsmokers.
|
H1 |
H2 |
H3 |
Nonsmoker |
Mean |
|
|---|---|---|---|---|---|
|
share of population (%) |
6.2 |
10.6 |
7.8 |
75.4 |
|
|
life expectancy T |
69.4 |
69.0 |
68.4 |
80.8 |
77.9 |
|
consumption expenditure share |
0.616 |
0.627 |
0.598 |
0.632 |
0.628 |
|
smoking expenditure share |
0.065 |
0.065 |
0.067 |
0 |
0.016 |
|
health investment share |
0.132 |
0.125 |
0.120 |
0.149 |
0.143 |
|
health investment share , LY fixed |
0.110 |
0.103 |
0.090 |
0.093 |
0.095 |
- Note: See notes to Table 3 regarding expenditure shares. Population shares are with respect to total population. In the last row, with life years (LY) fixed at the lower bound, the average is over age 19–60.
The health expenditure ratio in row 5 may seem to be low for smokers compared with nonsmokers, given that more health maintenance is needed by addicts. This arises from the large life year gap between smokers and nonsmokers, and the sharply increasing health care expenditure at very advanced ages when diminishing returns kick in. This raises the average healthcare expenditure ratio of nonsmokers over the life span. If we trim everyone's life span to 60 years (i.e., the shortest life years among all groups of smokers), then smokers' average health investment share becomes 7 percentage points higher than nonsmokers' (see the last row of Table 7).36
Figure 2 displays the lifecycle pattern of several key indicators, contrasting an average nonsmoker and an average smoker. First, while nonsmokers have higher labor income than smokers, the total income gap is even more substantial because of greater asset accumulation toward later stages of life. Second, health investment share of smokers is slightly higher than that of nonsmokers until the late 60s, since smoking-deteriorated health requires stronger effort to maintain; the health investment share, however, rises substantially for nonsmokers at more advanced ages due to their longevity.37 Third, the death hazard, defined as the mortality rate at a given age conditional on survival up to that age, is higher for smokers than for nonsmokers at any point in life. At age 37, the death hazard is 0.0163 for smokers and 0.0154 for nonsmokers; the gap widens to 0.0518 versus 0.0383 at age 65. For most periods of life, smoking contributes to over half of the death hazard of a smoker (see details in Supplemental Appendix D).
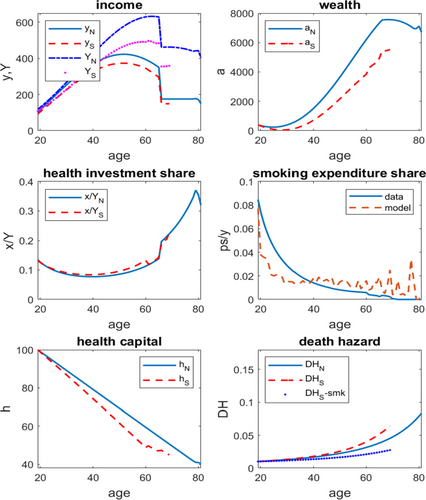
Lifecycle profiles of income, wealth, health investment and smoking expenditure shares, health capital and death hazard. Note: All lifecycle profiles are from age 19 until death, with subscript N denoting a nonsmoker and S denoting a smoker. Incomes reported are labor income (y) and total income (Y). Wealth is measured by total assets (a) and smoking expenditure share is with respect to labor income (ps/y) of the population. Health capital (h) is from the initial normalized level of 100 to the minimum (), and death hazard includes overall death hazards (DH) and a smoking-led death hazard for smokers (DHS−smk). For all panels that contrast smokers and nonsmokers, quitters are excluded from smokers after quitting, as are those no longer alive.
To compare model predictions with the data, we report in Table 8 three gradients of total income, health investment share, and health capital at age 37, 52, and 65 (relative to age 23 for the income and health gradients). The first two ages are the two treatment ages used for policy evaluation. Because these are untargeted moments, they serve as an additional validation of our calibrated model.38
|
Key Ratios |
At Age t |
|||||
|---|---|---|---|---|---|---|
|
37 |
52 |
65 |
||||
|
Data |
Model |
Data |
Model |
Data |
Model |
|
|
total income gradient |
||||||
|
nonsmokers |
2.4 |
2.3 |
3.0 |
3.5 |
2.8 |
3.8 |
|
smokers |
1.7 |
2.1 |
2.0 |
3.2 |
2.1 |
3.3 |
|
health investment share |
||||||
|
nonsmokers (%) |
6.9 |
7.8 |
8.2 |
8.9 |
16.7 |
13.8 |
|
smokers (%) |
8.4 |
8.4 |
13.4 |
10.1 |
6.2 |
14.4 |
|
health capital gradient |
||||||
|
nonsmokers |
n.a. |
0.86 |
n.a. |
0.70 |
n.a. |
0.57 |
|
smokers |
n.a. |
0.82 |
n.a. |
0.62 |
n.a. |
0.49 |
- Note: The total income and health capital gradients are a ratio of the indicator at age t to that at age 23.
The results indicate that smokers have a flatter total income gradient than nonsmokers and that our model prediction of the pattern is correct despite over prediction at older ages (due to our simplified setting of asset income). Meanwhile, the health investment share gradient is steeper at older ages, in line with the literature (e.g., De Nardi, French, and Jones (2010)). While the overall prediction for nonsmokers captures the rising pattern with a sharp increase toward the end of a lifetime, that of smokers is somewhat of—the model underpredicts an average smoker's health investment share at age 52 but overpredicts it at age 65. This might be due to smoking-led serious diseases occurring at the 50s, and sample trimming of older smokers as a result of death (with the surviving ones being increasing representative of those biologically resilient to cigarette exposure). Since we do not model large health shocks or the small biologically resilient group, we end up fitting the average smoker's hump-shaped health investment share in the data with a smooth and positive trend that more reasonably captures a representative smoker's lifecycle pattern of health investment. Overall, our model yields a downward health capital gradient: to an average nonsmoker, health capital drops at an increasing rate from age 23 to age 65 and an average smoker's health falls by even more, especially at older ages.
5 Policy evaluations
By calibrating the theoretical model to fit the data with heterogeneous responses to different treatments, we have a numerical model that can be readily used for policy evaluation. We focus on evaluating personalized versus standard treatments within an integrated dynamic framework that suits for a systematic cost-effectiveness analysis of precision medicine. We consider policy intervention in the form of subsidizing smokers to receive cessation treatment. We begin with policy analysis under the benchmark setup where smoking cessation policies are implemented at two benchmarking ages, 37 and 52, corresponding to the mean ages of the two age groups (25–44 and 45–64) in the experimental data. We then examine the sources of welfare gains from quitting and evaluate the role of each behavioral factor and second-hand smoke played in policy effectiveness by performing counterfactual experiments.
5.1 Method
We compare the effectiveness of the following three government policies, two standard medication policies (S, ), and one personalized medication policy (P), all under the same budgetary cost. Thus, whichever policy yields greater value of effectiveness is by construction more cost effective. The three smoking cessation policies are specified as follows:
- 1. S: Subsidize 10% of smokers randomly with $1400 cash for completing both counseling and medication treatment, regardless of genotype.
- 2. : Subsidize 12.2% of smokers randomly with two types of subsidies: a $392 cash subsidy for completing counseling only, given to 3.1% of smokers, and a $1400 cash subsidy for completing both counseling and medication treatment, given to 9.1% of smokers, both regardless of genotype.
- 3. P: Offer rebate to 12.2% of smokers who have taken a genetic test to identify their genotype associated with smoking addiction and have completed a gene-based treatment. The rebate consists of three parts. R1: $224 cash for completing the genetic test; R2: $168 cash for completing counseling; R3: $1008 cash for completing medication. All subsidized smokers receive R1 and R2, but only those identified as H2 and H3 genotypes receive R3.
Policy S is a proxy for the standard policy that recommends that all smokers receive counseling and medication, whereas policy is a proxy for some real world policy under which some smokers only receive counseling, while others receive counseling and medication. Neither policy takes smokers' genotypes into account. By contrast, policy P is personalized based on the genotype: (i) smokers receive a rebate only if they have taken a genetic test, and (ii) only those with genotypes responsive to medication would receive a rebate for medication treatment.
Several remarks regarding the treatment policies are in order.
First, the size of the subsidy in the benchmark case under policy S ($1400 per person) is adequate for covering the full cost of the counseling and medication treatment ($1050; see the detailed breakdown below) and for compensating the time cost of taking treatment ($350, about 1% of an average smoker's labor income, since treatment takes about 1% of average annual working hours). The inflation-adjusted amount matches with the subsidy offered in the cessation experiment conducted by Chen et al. (2012) that provides free treatment and compensates for the time cost.39
Second, while the size of the budget regarding 10% coverage of smokers in the benchmark case under policy S is only for illustrative purposes, the total budget figure is feasible in practice and the subsidy rate in our experiment is viewed a feasible, conservative figure.40
Third, the three policies have equal total budgets. Given that the shares of the three genotypes among smokers are 0.25, 0.43, and 0.32 for H1, H2, and H3 (Chen et al. (2012); Bergen et al. (2013)), we compute the fraction of smokers to be subsidized under policy P as 12.2% to meet the budget.
Fourth, the value of each type of rebate in policy P is based on the treatment or test cost. We estimate the monetary cost to be $150 for counseling, $900 for medication, and $200 for a genetic test. We thereby set the full rebate under policy P to be the same as policy S ($1400) to cover the test, counseling, and medication for H2 and H3 smokers, and then set the value of each type of rebate to be proportional to the cost of the corresponding treatment or test.
Fifth, policy is designed to mimic policy P, except not being gene-based. It covers not only the same fraction of smokers as policy P (12.2%), but also the same fraction to receive counseling (3.1%) and to receive both counseling and medication (9.1%) as policy P. Moreover, those subsidized only for counseling under receive the same amount of subsidy as the H1 smokers under P, and those subsidized for both counseling and treatment under receive the same amount of subsidy as the H2 and H3 smokers under P. A comparison between policies and P, therefore, isolates the effectiveness of personalized medication.
We carry out the policies on smokers aged 37 or 52. We solve the model for each group of smokers with different genotypes, demographics, and initial smoking habits (thus, groups in total) when they are subsidized by a policy at 37 or 52. When modeling the cost of treatment or the genetic test, we also consider time cost (i.e., time needed for traveling, waiting, and receiving treatment), and convert the time cost into labor income losses using the hourly wage of each group (using PSID data). Based on medical practice, we estimate that it takes about 9 hours to receive counseling, 7.5 hours for medication, and 2 hours for a genetic test.
We employ six measures for policy comparison: (Measure 1) share of smokers that can be subsidized, (Measure 2) quit rates of subsidized smokers, (Measure 3) Consumption Equivalent (CE) of subsidized smokers, (Measure 4) Income Equivalent (IE) of subsidized smokers, (Measure 5) value of a statistical life (VSL) gains of quitters, and (Measure 6) one-time wealth transfer as a fraction of lifetime income for quitters and for subsidized smokers. While Measure 2 is standard, Measure 1 is an extra extensive margin that has often been overlooked in previous studies. The omission of this extensive margin effect would bias the cost-effectiveness analysis significantly, particularly because of the nature of personalized medical treatment. Measures 3–6 require further explanation.
Furthermore, we take into account voluntary take-up of treatment, since subsidizing smokers who would have taken up treatment even without subsidy would bias the overall policy effectiveness. We incorporate two margins into CE and IE to reflect policy effectiveness net of voluntary take-up. First, the policy induces smokers who would have not taken up treatment into cessation programs. According to Volpp et al. (2009), these are about 65% of smokers.41 Second, for those who would have taken treatment without intervention, the policy increases their probability of completing the cessation program, and hence, their probability of quitting—a margin that has been calibrated in Section 4.2. We assume all voluntary take-ups involve both counseling and medication treatments, which produces a conservative measure of net policy effectiveness.
Based on IE, we compute the VSL gain from quitting by multiplying a smoker's VSL without quitting (discussed below) by her IE with quitting. The gain measured by a one-time wealth transfer in the year of policy implementation can also be computed as IE (without adjustment for life years in this case) multiplied by her lifetime labor income.
Notably, our CE and IE measures are more general than the typical measure by QALYs in the literature of medicine and health. In contrast with QALYs, our lifetime utility-based effectiveness measures account for time discounting and diminishing marginal valuation. Moreover, our measures consider differential utility weights that are calibrated to the data. Furthermore, our measures incorporate heterogeneous individuals' dynamic responses. This is important because such responses vary across individuals over the life course.
5.2 Validating the quantitative model: Value of a statistical life
The value of a statistical life (VSL) helps validate our key measure of IE for constructing a dollar measure of effectiveness. By normalizing the value of death to zero (which can be simply obtained by setting for all individuals and for smokers, all at their subsistence levels), one may compute VSL as the dollar value of willingness to pay for a living status on average. This is done by first computing CE and IE as the percentage decrease in lifetime utility from life to death and then multiplying IE by average income of an individual to obtain a dollar measure. We finally convert permanent flow income to capitalized dollar value at age 45 (average age of a licensed driver in the US as we plan to compare our VSL with empirical estimates by Ashenfelter and Greenstone (2004)) based on the real interest rate of 3.8% and the life expectancy of smokers and nonsmokers.42
We estimate VSL for smokers and nonsmokers of all subgroups and their population-weighted average. Since smokers have lower average work efficiency than nonsmokers ( vs. 1.03), lower average labor or replacement income (277 vs. 289 efficiency wage units) and lower life expectancy (69 vs. 81 years), their VSL is lower than nonsmokers. The VSLs for type H1, H2, and H3 smokers are estimated as 2.125, 2.209, and 2.187 million US dollars, largely comparable across genotypes. Given the population weights for the three genotypes, the (weighted) average VSL of a smoker becomes 2.181 million US dollars. The VSL of an average nonsmoker is computed as 2.665 million US dollars. Thus, VSL of an average smoker is 18% lower than that of an average nonsmoker, indicating a large gain from smoking cessation. Given the population weights (24.6% smokers and 75.4% nonsmokers), the (weighted) average VSL in our model is 2.546 million US dollars, in line with the empirical literature.43
5.3 Findings
5.3.1 Gains in life years
Table 9 reports the expected gain in life years (LY) for smokers (by genotype) who endogenously quit at age 37 or 52 under the standard policy S. The LY gains by demographic groups are reported in Supplemental Appendix Table A3.44
|
Gain in LY at Age 37 |
Gain in LY at Age 52 |
|
|---|---|---|
|
mean |
10.08 |
4.87 |
|
H1 |
10.23 |
5.02 |
|
H2 |
10.64 |
4.78 |
|
H3 |
9.13 |
4.88 |
- Note: Gains in life years (LY) of smokers who are treated and quit at age 37 and 52 under policy are reported for each genotype group.
When the policy is implemented at age 37, we find that, across the three genotypes, the gain in LY is the largest for H2 smokers and is the smallest for H3 smokers who are typically strong addicts. For every demographic group, the LY gains are large, ranging from 8.7 (noncollege-educated black males) to 12.1 (college-educated black females) years. The college-educated gain more LY than the non-college educated, given gender, because cessation increases the lifetime income and, hence, health investment more for the former group than for the latter group. Women, facing a lower natural health deterioration rate, gain more LY than men, given race and education. When treatment is received at 52, the aforementioned patterns continue to hold true, except that the gain in LY is now higher for H3 than H2 smokers. On average, treatment at this older age results in about 5.2 years less LY gain than treatment at age 37, or 11% less LY gain over adulthood.
5.3.2 Lifecycle profiles: Quitters versus nonquitters
To compare lifecycle profiles between a quitter and a nonquitter, we consider a quitter as one who stops smoking after treatment at age 37 or 52, under a particular policy, with a nonquitter as the counterfactual case of the same person who did not quit. For illustrative purposes, we focus on two demographic groups: (i) white females with no college degree (the largest group of smokers with work efficiency far below one) and (ii) white males with a college degree (constituting a small share of smokers but with the highest work efficiency). For both groups, we choose the H2 haplotype, which constitutes the largest fraction of smokers in both demographic groups.
Figure 3 plots the lifecycle profiles of the smoking expenditure share and the health investment share, and Figure 4 plots the lifecycle profiles of health capital and total income. Both are for quitting at 37, while we relegate the similar pattern for quitting at 52 to Supplemental Appendix Figures A1–A2. Several observations are in order.
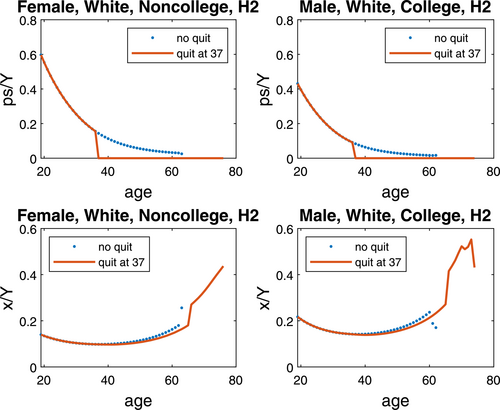
Lifecycle profile of smoking and health investment when quitting at 37. Note: For comparison, smoking and health expenditure shares of total income (ps/Y and x/Y) for nonquitters/quitters at age 37 in two genotype-demographic groups.
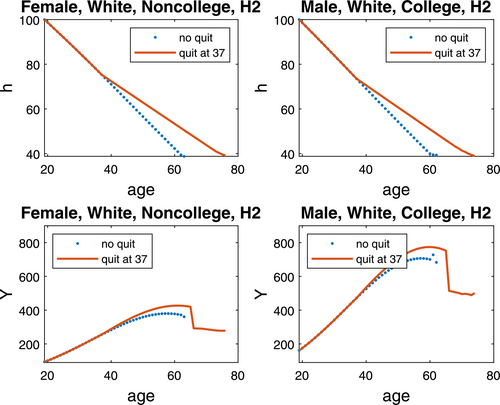
Lifecycle profile of health capital and labor income when quitting at 37. Note: Health capital (h) and total income (Y) are depicted for nonquitters/quitters at age 37 in two genotype-demographic groups.
First, while the smoking expenditure share declines over the lifecycle for both groups of smokers, that of the white males with a college degree is much lower than that of the white females with no college degree, because the former group has higher income and higher opportunity cost of smoking than the latter group.
Second, both groups have U-shaped health investment shares, which increase sharply after retirement; smoking cessation reduces the health investment share in the short run while increases it in the long run due to increased life years. Throughout the life time, the health investment share is higher for white males with a college degree than white females with no college degree, since the positive health effect on life expectancy makes health a luxury good relative to consumption.
Third, smoking cessation slows down health deterioration, boosting up health capital by a large margin. While the health capital of white female nonquitters with no college degree and white male nonquitters with a college degree deplete by half at ages 54 and 53, respectively, quitters in both groups are able to prolong the half-life by 8–9 years. At 52, both groups have about 14% higher health capital by quitting.
Fourth, for both groups of smokers, total income reaches the peak 3 years earlier for nonquitters than for quitters. At the respective peak-income ages, white female quitters with no college degree and white male quitters with a college degree have 12.3% and 9.5% higher total income than their nonquitter counterparts. Such gains drop substantially when quitting at 52, to 0.7% and 1.6%, suggesting a larger smoking cessation effect on income enhancement when quitting earlier.
5.3.3 Policy effectiveness
We now report our main findings obtained by comparing the key measures under the three proposed policies.45
Share of smokers that can be subsidized
Equal-budget policy comparison implies that 12.2% of smokers can be subsidized under policy P or . This means policy P covers 22% more smokers for treatment than the standard policy S by minimizing the “number needed to treat” (NNT) emphasized by the medical literature (see Chen, Horton, and Bierut (2018)). That is, due to personalized medications, there is an extensive margin effect to cover more addicts with differential treatments based on genotypes.
Quit rates
Table 10 reports the quit rates of subsidized smokers under the three policies.
|
Treated at Age 37 |
Treated at Age 52 |
|||||
|---|---|---|---|---|---|---|
|
S |
S′ |
P |
S |
S′ |
P |
|
|
mean |
31.7 |
28.5 |
31.7 |
35.6 |
34.0 |
35.6 |
|
H1 |
32.0 |
32.0 |
32.0 |
28.5 |
28.5 |
28.5 |
|
H2 |
32.7 |
28.7 |
32.7 |
34.1 |
33.7 |
34.1 |
|
H3 |
30.0 |
25.4 |
30.0 |
43.6 |
38.8 |
43.6 |
- Note: Quit rates by smokers treated at age 37 and 52 under policies are reported for the 3 genotype groups.
Quit rates under S and P are similar, since every H2 or H3 smoker is treated with both counseling and medication. Quit rates under are lower, as some H2 and H3 smokers only receive counseling, which is less effective than if it is combined with medication. Note that H1 smokers must have the same quit rates under all policies because medication does not have any additional effect on their cessation outcome. Moreover, treatment received at age 52 results in higher cessation success than treatment received at age 37 by 13% (under S and P) to 19% (under ). Notably, the success rate is enhanced substantially for H3 smokers when they are treated at 52, compared to when they are treated at 37 and compared to other genotypes treated at 52.
Consumption equivalent (CE) and income equivalent (IE)
Table 11 reports the expected CE and IE for subsidized smokers treated at age 37 or 52 by genotype, net of voluntary treatment effects. The same measures by demographic group are reported in Supplemental Appendix Table A4. To compute the expected CE for subsidized smokers net of voluntary treatment effects, we first compute the expected CE of subsidized smokers without considering voluntary take-up (denoted as ) and then compute CE for smokers who would have taken up treatment without policy (denoted as ). Assuming the fraction of voluntary take-up to be 35% of smokers and identical across all groups of smokers, based on evidence from Volpp et al. (2009), we compute CE net of voluntary treatment as . The IE net of voluntary take-up is computed similarly.
|
Consumption Equivalent CE |
Income Equivalent IE |
|||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
Treated at Age 37 |
Treated at Age 52 |
Treated at Age 37 |
Treated at Age 52 |
|||||||||
|
S |
S′ |
P |
S |
S′ |
P |
S |
S′ |
P |
S |
S′ |
P |
|
|
mean |
3.27 |
2.81 |
3.26 |
3.58 |
3.10 |
3.57 |
1.97 |
1.68 |
1.97 |
2.75 |
2.37 |
2.74 |
|
H1 |
3.07 |
3.07 |
3.07 |
0.75 |
0.75 |
0.75 |
1.72 |
1.72 |
1.71 |
0.57 |
0.57 |
0.57 |
|
H2 |
2.84 |
2.42 |
2.83 |
1.54 |
1.47 |
1.54 |
1.57 |
1.33 |
1.57 |
1.17 |
1.12 |
1.17 |
|
H3 |
4.00 |
3.14 |
4.00 |
8.62 |
7.21 |
8.62 |
2.72 |
2.11 |
2.71 |
6.65 |
5.53 |
6.65 |
- Note: Smokers' gains in Consumption Equivalent (CE) and Income Equivalent (IE) from 3 policies are reported for the 3 genotype groups.
The average CE (IE) over all subsidized smokers treated at 37, net of voluntary treatment, is about 3.3% (2.0%) under policy S or P, but about 0.5 (0.3) percentage points less under . That policy is not as effective as S or P is due to the inclusion of the worse-off H2 and H3 smokers, some of whom do not receive medication under . This is reflected in the comparison of CE and IE by genotype over different policies, where we see a large relative gain of policy S and P over for H2 and H3 smokers, with no gain for H1 smokers. Effectiveness gains are much larger for quitters. For a subsidized quitter treated at 37, CE (IE) is about 13% (8%) under the three policies, four times of the average figures for all subsidized smokers. The advantage of policy S and P over policy remains when smokers are subsidized at 52.
Among subsidized smokers and quitters, CE (IE) is the highest for the H3 group, regardless of the treatment age. In addition, H3 smokers receive the largest relative gain under S and P versus . These results indicate that smoking cessation policy, especially the personalized one, can generate particularly large welfare gains for the strongest addicts.
Across demographic groups, males receive a relatively large gain measured in CE and IE when treated at 37 while females receive a relatively large gain when treated at 52. Moreover, demographic groups with a larger share of H2 and H3 genotypes (i.e., the white groups) benefit relatively more from S and P than from .
Cost/effectiveness ratio
We now construct a unified measure of effectiveness. First, consider the measure without voluntary take-up of treatment. View the 10% or 12.2% subsidy rate as a lottery draw for subsidized treatment with probability or 0.122. With probability , a smoker would not be subsidized and her decision remains unchanged, and by construction her CE and IE are zero. One can then compute the expected CE of a smoker as . Similarly, the expected IE of a smoker is . We next construct a dollar measure of effectiveness, by multiplying IE by average smokers' income, which is US$36,048 in 2009 dollars. The expected flow gain is over the life course corresponding to the formula (18). To have a unified figure, we use the average adult life years of subsidized smokers (which exclude the lightest smokers), , and estimate the expected gain as . Since average subsidy per smoker is in 2009 dollars, the cost/effectiveness (C/E) ratio is simply .46
Second, we take into account voluntary take-up of treatment. As mentioned above, 35% of the subsidized smokers would have taken up treatment even without subsidy, and they would have had lower quit rates had there been no subsidy policy. Using the CE and IE measures for voluntary take-up computed in the previous subsection, we construct the value of expected gain for voluntary take-up, denoted as , using the same method as above. Then the expected gain of policy net of voluntary treatment becomes , and the corresponding cost/effectiveness (C/E) ratio is . The C/E ratio based on the one-time wealth transfer measure is computed similarly.
5.3.4 Taking stock
We find that, while policies S and P have similar effects in terms of the quit rate and CE or IE for subsidized smokers, policy P is able to cover 22% more smokers than policy S, since it saves the budget by not subsidizing H1 smokers for medication while not reducing the effectiveness of treatment.47 Policy has the least effectiveness measured by CE and IE, but it is also able to cover 22% more smokers than policy S by not subsidizing some smokers for medication.
We report two VSL gain measures, two wealth transfer measures, and the unified measures in Table 12. We show that, under the same program costs, personalized treatment provides coverage for more, and maintains high effectiveness. The expected VSL gain under P is (in 2009 dollars) per quitter when treated at age 37, or a 13% gain from the benchmark value, comparable to the gain under S but higher than that under . Similarly, the expected one-time wealth transfer is about 8% of their lifetime income per quitter under P, close to the gain under S.
|
Treated at Age 37 |
Treated at Age 52 |
|||||
|---|---|---|---|---|---|---|
|
S |
|
P |
S |
|
P |
|
|
% subsidized |
10 |
12.22 |
12.22 |
10 |
12.22 |
12.22 |
|
expected gain in life years LEgain (years) |
10.08 |
9.98 |
10.08 |
4.87 |
4.85 |
4.87 |
|
quit rate (%) |
31.7 |
28.5 |
31.7 |
35.6 |
34.0 |
35.6 |
|
VSL gain of a quitter (2009 US$) |
168,230 |
165,624 |
167,937 |
187,666 |
174,415 |
187,459 |
|
VSL gain of a quitter (%) |
13.31 |
13.25 |
13.29 |
10.98 |
10.24 |
10.97 |
|
expected CE of a quitter (%) |
13.28 |
13.19 |
13.26 |
12.45 |
11.66 |
12.44 |
|
expected IE of a quitter (%) |
7.98 |
7.85 |
7.97 |
9.52 |
8.87 |
9.51 |
|
expected transfer to a quitter (%) |
8.25 |
8.11 |
8.23 |
8.93 |
8.29 |
8.92 |
|
expected CE of a subsidized smoker—net (%) |
3.27 |
2.81 |
3.26 |
3.58 |
3.10 |
3.57 |
|
expected IE of a subsidized smoker—net (%) |
1.97 |
1.68 |
1.97 |
2.75 |
2.37 |
2.74 |
|
expected transfer to a subsidized smoker—net (%) |
1.83 |
1.57 |
1.82 |
2.64 |
2.28 |
2.64 |
|
cost/effectiveness ratio (C/E)—net |
1/23.61 |
1/24.54 |
1/28.79 |
1/32.94 |
1/34.72 |
1/40.20 |
|
cost/effectiveness ratio (C/E)—net, transfer-based |
1/21.91 |
1/22.96 |
1/26.72 |
1/31.66 |
1/33.42 |
1/38.63 |
- Note: The subsidy rates, an average quitter's gains in life year (LEgain), quit rates, value of statistical life (VSL) gain in 2009 US$, Consumption Equivalent (CE), Income Equivalent (IE), wealth transfer as a fraction of lifetime income, and cost/effectiveness ratios (C/E), from 3 policies implemented at ages 37 and 52, are reported.
For every dollar of subsidy, standard policies S and , respectively, generate 23.61 and 24.54 dollars IE in effectiveness over adulthood.48 Such effectiveness measure rises to 28.79 dollars under the personalized medication policy P. Thus, the cost effectiveness of policy P is 22% higher than policy S and 17% higher than policy . The transfer-based cost-effectiveness gains of personalized policy are of comparable magnitude. Since policy mimics policy P in every aspect except not being gene-based, the latter figure implies that, by identifying the genotype and treating only 19% more subsidized smokers correctly with medication than policy , policy P generates a sizable effectiveness relative to policy .49
When treated at age 52, a quitter incurs 12% larger VSL gains or 8% larger transfer gains under S and P than when treated at age 37, and IE in effectiveness over adulthood for subsidized smokers rises even more by about 40%. To understand this, we decompose changes in effectiveness measures into an extensive margin from life year gains, an extensive margin from successful cessation, and an overall intensive margin. Because of a strong extensive margin gain from successful cessation, a strong intensive margin gain (especially for H3), and a moderate extensive margin loss from life years, we find higher effectiveness under treatment at age 52 than at age 37. When treatment is at 52, the cost effectiveness of personalized policy P turns out to be 16–22% higher than standard policies.
5.4 Sources of welfare gains
We begin by verifying the essentiality of endogenous life expectancy and smoking habits for the working of smoking cessation policies. Our counterfactual exercises indicate that the endogenous life expectancy effect is a necessary driver for health investment: without it, individuals would have not had sufficient incentives to invest in health for higher earnings (i.e., in all circumstances). The detrimental effect of smoking habits on utility is also a necessary driver for quitting under treatment: without it, addicts would have not had sufficient incentives to quit smoking. That is, they are quintessential channels for welfare gains from any smoking cessation policy, which will be included throughout the decomposition analysis below.
There are four additional channels through which the smoking cessation policy may yield welfare gains: (i) a pure income channel (PI) due to subsidy received by each participant net of the out-of-pocket cost to participate the program, which would not affect any decision margins; (ii) a health-productivity channel (HP) resulting from higher labor income due to better health; (iii) a health investment channel (HI) that raises health capital and life expectancy but is accompanied with higher out-of-pocket expenditure; and, (iv) a bequest motive channel (BM) due to greater wealth accumulation induced by better health. Once these channels are considered, the smoking cessation effect on consumption is automatically accounted for, via pure and labor income channels (PI and HP) as well as consumption-health investment and consumption-bequest trade-offs (captured by HI and BM).
To perform counterfactuals, we focus on the quitters in the benchmark policy experiments under policy P and recompute their CE and IE by solving the model with one of the channels above shut down. In particular, the net income effect with policy () is simply a once-and-for-all term at the time of policy implementation (): per participant subsidy—per participant program cost. Because by construction the net income effect without policy () is zero, to shut down PI, we set at . To shut down HP, we set the labor income path to the no-policy benchmark and set to zero.50 To shut down HI, we restore the health investment path under policy to the no-policy benchmark.51 To shut down BM, we set . We compute the contribution of each channel j as: of benchmark—CE of . By renormalizing total contribution to 100%, we obtain the following decomposition results: , summarized in Table 13.
|
Channels |
Treated at 37 |
Treated at 52 |
||
|---|---|---|---|---|
|
CE |
IE |
CE |
IE |
|
|
1. pure income (PI) |
−0.4 |
−0.4 |
−0.4 |
−0.4 |
|
2. health-productivity (HP) |
18.5 |
17.6 |
0.4 |
0.8 |
|
3. health-investment (HI) |
62.4 |
67.7 |
65.6 |
67.2 |
|
4. bequest motive (BM) |
19.6 |
15.1 |
34.5 |
32.5 |
- Note: Table reports %contribution of each of channels (i)–(iv) to welfare gains for quitters, measured by CE and IE, from policy P at age 37 and 52.
Overall, the endogenous health investment (HI) is most important, accounting for over 60% of the welfare gain from the smoking cessation policy. This is because HI incorporates not only the policy effects on health capital throughout life but also the consequent impact on life expectancy. The health-productivity (HP) channel is also important, but only when treatment occurs at a young age. On the contrary, bequest motive (BM) is equally important as HP when one takes the treatment and quits at a young age, but its contribution rises at an old age because its lifesaving effect on wealth accumulation to be used by the descendants becomes more prominent when incremental labor income in-flows start to decline. Regardless of the treatment age, the pure income channel (PI) is inconsequential.
5.5 Further discussion
We further conduct three counterfactuals to investigate the roles played by (i) second-hand smoke, (ii) incomplete knowledge about the detrimental health effect of smoking, and (iii) undervaluation of health, in the effectiveness of policy P. In particular, we set, respectively, (absence of second-hand smoke), (complete health knowledge), and (full valuation of health). The results are reported in Supplemental Appendix Table A6.
Second-hand smoke is found to cause lower life year gains from quitting and lower quit rates for old addicts but higher quit rates for young addicts. At both ages, however, welfare gains from smoking cessation policy for quitters are lower. The presence of second-hand smoke would yield a stronger role played by smoking cessation policy for mitigating smoking-induced negative externalities. Thus, it is expected that second-hand smoke can lead to greater cost effectiveness (lower C/E ratios), but our result indicates it is so only when the policy is implemented for young addicts. This latter finding is mainly due to the lower quit rate for the old addicts with second-hand smoke: the old have already reduced smoking before treatment, so the presence of second-hand smoke makes quitting a less important margin; on the contrary, the young smoke more heavily, so quitting becomes more important given the detrimental effect of second-hand smoke.
The presence of incomplete knowledge yields higher life year gains from quitting. Similar to second-hand smoke, it lowers quit rates for old addicts due to weakened incentives for quitting, but higher quit rates for the young who are more vulnerable. Yet, for quitters, the welfare gains from smoking cessation policy are higher for old quitters but lower for young quitters. Because quitting is the main driver quantitatively, cost effectiveness is lower for old smokers in the presence of incomplete knowledge, though more modest than second-hand smoke.
Undervaluation of health always results in smaller life year gains from quitting and lower quit rates, regardless of the treatment age. While it lowers welfare gains of a young quitter, it raises that of an old quitter due to the lesser degree of undervaluation ( increases over the lifecycle. Nonetheless, undervaluation of health causes smoking cessation policy less cost effective for both ages. Our results are in line with empirical findings in Adda and Lechene (2013) in which individuals who have poorer nonsmoking related health (and thus tend to undervalue health) are more likely to start smoking and to smoke more cigarettes than those with better nonsmoking related health, and that smoking has a lower effect on mortality for the former group than for the latter group.
One might also wonder whether there is an optimal age for policy intervention? Unfortunately, limited samples in the clinical trials prohibit us from conducting the exercises at all ages. Nonetheless, we may gain further insight by constructing an overlapping group under age 45 (mean age of the 35–54 age group, covering half of the 25–44 age group and half of the 45–64 age group). In Supplemental Appendix Tables A7–A8, we report the counterparts of calibrated figures to Tables 5–6 and Table 12 in the main text. As can be seen, quit rates and equivalent measures often exhibit nonmonotonic patterns over ages 37, 45, and 52, where some patterns are even U-shaped.52 Thus, it becomes difficult to pin down a reasonable range for the optimal age of policy intervention.
We conduct two sets of robustness checks, one considering the net deadweight cost of medical treatment and the other considering a lump-sum tax imposed on all agents to finance the government subsidy. A summary of the results is presented in Supplemental Appendix Table A9. In short, we find that such variations do not alter much of our main findings, neither qualitatively nor quantitatively.
6 Conclusions
We have developed a lifecycle model with endogenous smoking and quitting, health investment and savings, and life expectancy to explore the cost effectiveness of personalized versus standard smoking cessation treatments. Under the same program costs, personalized treatment has been shown to provide broader coverage and maintain high effectiveness. The key channel for the welfare gains from smoking cessation is the endogenous health investment response to policy, a factor largely ignored by the medical literature. The quantitative results have revealed that it is never too late to provide smoking cessation treatment, which is useful because in medical practice both patients and physicians tend to feel a low need for cessation treatment for those who have smoked for a long time. We have further verified that personalized treatment is always more cost effective than standard treatments in smoking cessation regardless of treatment age. This is of great policy relevance because, while personalized treatment has been much desired by patients in practice, our paper presents the first systematic evidence for it being cost effective relative to standard treatments under model-based policy evaluation. As genetic tests are becoming increasingly common in medical care and as more evidence becomes available to guide medical treatments, this work lays out a study paradigm in gene-guided precision medicine which extends beyond smoking cessation treatments.




