Adaptive Maximization of Social Welfare
Abstract
We consider the problem of repeatedly choosing policies to maximize social welfare. Welfare is a weighted sum of private utility and public revenue. Earlier outcomes inform later policies. Utility is not observed, but indirectly inferred. Response functions are learned through experimentation.
We derive a lower bound on regret, and a matching adversarial upper bound for a variant of the Exp3 algorithm. Cumulative regret grows at a rate of T2/3. This implies that (i) welfare maximization is harder than the multiarmed bandit problem (with a rate of T1/2 for finite policy sets), and (ii) our algorithm achieves the optimal rate. For the stochastic setting, if social welfare is concave, we can achieve a rate of T1/2 (for continuous policy sets), using a dyadic search algorithm.
We analyze an extension to nonlinear income taxation, and sketch an extension to commodity taxation. We compare our setting to monopoly pricing (which is easier), and price setting for bilateral trade (which is harder).
1 Introduction
Consider a policymaker who aims to maximize social welfare, defined as a weighted sum of utility across individuals. The policymaker can choose a policy parameter such as a sales tax rate, an unemployment benefit level, a health-insurance copay rate, etc. The policymaker does not directly observe the welfare resulting from their policy choices. They do, however, observe behavioral outcomes such as consumption of the taxed good, labor market participation, or health care expenditures. They can revise their policy choices over time in light of observed outcomes. How should such a policymaker act? To address this question, we bring together insights from welfare economics (in particular optimal taxation, Ramsey (1927), Mirrlees (1971), Baily (1978), Saez (2001), Chetty (2009)) with insights from machine learning (in particular online learning and multiarmed bandits, see Slivkins (2019), Lattimore and Szepesvári (2020) for recent reviews, and Thompson (1933), Lai and Robbins (1985) for classic contributions).
In our baseline model, individuals arrive sequentially and make a single binary decision. In each period, the policymaker chooses a tax rate that applies to this binary decision, and then observes the individual's response. They do not observe the individual's private utility. Social welfare is given by a weighted sum of private utility and public revenue. Later, we extend our model to nonlinear income taxation, where welfare weights vary as a function of individual earnings capacity, and sketch an extension to commodity taxation, where individual decisions involve a continuous consumption vector.
Our goal is to give guidance to the policymaker. We propose algorithms to maximize cumulative social welfare, and we provide (adversarial and stochastic) guarantees for the performance of these algorithms. In doing so, we also show that welfare maximization is a harder learning problem than reward maximization in the multiarmed bandit setting. Private utility in our baseline model is equal to consumer surplus, which is given by the integral of demand. In order to learn this integral, we need to learn demand for counterfactual, suboptimal tax rates. This drives the difficulty of the learning problem.
Why Welfare, Why Adversarial Guarantees?
Our algorithms are designed to maximize social welfare, which is not directly observable, rather than maximizing outcomes that are directly observable. The definition of social welfare as an aggregation of individual utilities is at the heart of welfare economics in general, and of optimal tax theory in particular. The distinction between utility and observable outcomes is important in practice. To illustrate, consider the example of a policymaker who chooses the level of unemployment benefits, where the observable outcome is employment. The policymaker could use an algorithm that adaptively maximizes employment. The problem with this approach is that employment might be maximized by making the unemployed as miserable as possible. This is not normatively appealing. Such an algorithm would minimize the utility of the unemployed, rather than maximizing social welfare. Similar examples can be given for many domains of public policy, including health, education, and criminal justice. In contrast to observable outcomes such as employment, welfare is improved by increasing the choice sets of those affected, not by reducing these choice sets.
Our theoretical analysis provides not only stochastic but also adversarial guarantees, which hold for arbitrary sequences of preference parameters. Adversarial guarantees for algorithms promise robustness against deviations from the assumption that heterogeneity is independently and identically distributed over time. Possible deviations from this assumption include autocorrelation, trends, heteroskedasticity, more general nonstationarity, and other concerns of time-series econometrics. In the employment example, such deviations might for instance be due to the business cycle. One might fear that adversarial robustness is achieved at the price of worsened performance for the i.i.d. setting, relative to less robust algorithms. That this is not the case follows from our theoretical characterizations.
Lower and Upper Bounds on Regret
Our main theorems provide lower and upper bounds on cumulative regret. Cumulative regret is defined as the difference in welfare between the chosen sequence of policies and the best possible constant policy. We consider both stochastic and adversarial regret. A lower bound on stochastic regret satisfies that, for any algorithm, there exists some stationary distribution of preference parameters for which the algorithm has to suffer at least a certain amount of regret. An upper bound on adversarial regret has to hold for a given algorithm and any sequence of preference parameters.
For a given algorithm, stochastic regret, averaged over i.i.d. sequences of preference parameters, is always less or equal than adversarial regret, for the worst-case sequence. A lower bound on stochastic regret (for any algorithm) therefore implies a corresponding lower bound on adversarial regret, and an upper bound on adversarial regret (for a given algorithm) immediately implies an upper bound on stochastic regret. When an adversarial upper bound coincides with a stochastic lower bound, in terms of rates of regret, it follows that the proposed algorithm is rate efficient, for both stochastic and adversarial regret. It follows, furthermore, that the bounds are sharp.
A Lower Bound on Stochastic Regret
We first prove a stochastic (and thus also adversarial) lower bound on regret, for any possible algorithm in the welfare maximization problem. Our proof of this bound constructs a family of possible distributions for preferences. This family is such that there are two candidate policies, which are potentially optimal. The difference in welfare between these two policies depends on the integral of demand over intermediate policy values. In order to learn which of the two candidate policies is optimal, we need to learn behavioral responses for intermediate policies, which are strictly suboptimal. Because of the need to probe these suboptimal policies sufficiently often, we obtain a lower bound on regret, which grows at a rate of , even if we restrict our attention to settings with finite, known support for preference parameters and policies. This rate is worse than the worst-case rate for bandits of .
A Matching Upper Bound on Adversarial Regret for Modified Exp3
We next propose an algorithm for the adaptive maximization of social welfare. Our algorithm is a modification of the Exp3 algorithm (Auer, Cesa-Bianchi, Freund, and Schapire (2002)). Exp3 is based on an unbiased estimate of cumulative welfare for each policy. The probability of choosing a given policy is proportional to the exponential of this estimate of cumulative welfare, times some rate parameter. Relative to Exp3, we require two modifications for our setting. First, we need to discretize the continuous policy space. Second, and more interestingly, we need additional exploration of counterfactual policies, including some policies that are clearly suboptimal, in order to learn welfare for the policies, which are contenders for the optimum. This need for additional exploration again arises because of the dependence of welfare on the integral of demand over counterfactual policy choices. For our modified Exp3 algorithm, we prove an adversarial (and thus also stochastic) upper bound on regret. We show that, for an appropriate choice of tuning parameters, worst-case cumulative regret over all possible sequences of preference parameters grows at a rate of , up to a logarithmic term. The algorithm thus achieves the best possible rate. Since the rates for our stochastic lower and adversarial upper bound coincide, up to a logarithmic term, we have a complete characterization of learning rates for the welfare maximization problem.
Improved Stochastic Bounds for Concave Social Welfare
The proof of our lower bound on regret is based on the construction of a distribution of preferences which delivers a nonconcave social welfare function. If we restrict attention to the stochastic setting, where preferences are i.i.d. over time, and if we assume that social welfare is concave, then we can improve upon this bound on regret. We prove a lower bound on stochastic regret, under the assumption of concavity, which grows at the rate of . We then propose a dyadic search algorithm, which achieves this rate, up to logarithmic terms. This dyadic search algorithm maintains an “active interval,” containing the optimal policy with high probability, which is narrowed down over time. Only policies within the active interval are sampled.
Extensions to Nonlinear Income Taxation and to Commodity Taxation
Our discussion up to this point focuses on a minimal, stylized case of an optimal tax problem, where individual actions are binary, and the policy imposes a tax on this binary action. Our arguments generalize, however, to more complicated and practically relevant settings. This includes optimal nonlinear income taxation, as in Mirrlees (1971) and Saez (2001), and commodity taxation for a bundle of goods, as in Ramsey (1927). For nonlinear income taxation, different tax rates apply at different income levels, and welfare weights depend on individual earnings capacity. In Section 5, we discuss an extension of our tempered Exp3 algorithm to nonlinear income taxation, and characterize its regret. For commodity taxation, different tax rates apply to different goods, and consumption decisions are continuous vectors. In Section 6, we sketch an extension of our algorithm to commodity taxation, but leave its characterization for future research.
Roadmap
The rest of this paper proceeds as follows. We conclude this introduction with a discussion of some related work and relevant references. Section 2 introduces our setup, formally defines the adversarial and stochastic settings, and compares our setup to related learning problems. Section 3 provides lower and upper bounds on regret in the adversarial and stochastic settings. Section 4 restricts attention to the stochastic setting with concave social welfare, and provides improved regret bounds for this setting. Section 5 discusses an extension of our baseline model to nonlinear income taxation. Section 6 sketches another extension of our baseline model to commodity taxation. Section 7 concludes, and discusses some possible applications of our algorithm, as well as an alternative Bayesian approach to adaptive welfare maximization. The proofs of Theorem 1 and Theorem 2 can be found in Appendix A. The proofs of our remaining theorems and proofs of technical lemmas are discussed in the Online Supplement (Cesa-Bianchi, Colomboni, and Kasy (2025)).
1.1 Background and Literature
To put our work in context, it is useful to contrast our framework with the standard approach in public finance and optimal tax theory, and with the frameworks considered in machine learning and the multiarmed bandit literature.
Optimal Taxation
Optimal tax theory, and optimal policy theory more generally, is concerned with the maximization of social welfare, where social welfare is understood as a (weighted) sum of subjective utility across individuals (Ramsey (1927), Mirrlees (1971), Baily (1978), Saez (2001), Chetty (2009)). A key tradeoff in such models is between, first, redistribution to those with higher welfare weights, and second, the efficiency cost of behavioral responses to tax increases. Such behavioral responses might reduce the tax base.
Optimal tax problems are defined by normative parameters (such as welfare weights for different individuals), as well as empirical parameters (such as the elasticity of the tax base with respect to tax rates). The typical approach in public finance uses historical or experimental variation to estimate the relevant empirical parameters (causal effects, elasticities). These estimated parameters are then plugged into formulas for optimal policy choice, which are derived from theoretical models. The implied optimal policies are finally implemented, without further experimental variation.
Multiarmed Bandits
The standard approach of public finance, which separates elasticity estimation from policy choice, contrasts with the adaptive approach that characterizes decision-making in many branches of AI, including online learning, multi-armed bandits, and reinforcement learning. Multiarmed bandit algorithms, in particular, trade off exploration and exploitation over time (Slivkins (2019), Lattimore and Szepesvári (2020)). Exploration here refers to the acquisition of information for better future policy decisions, while exploitation refers to the use of currently available information for optimal policy decisions at the present moment. The goal of bandit algorithms is to maximize a stream of rewards, which requires an optimal balance between exploration and exploitation. Bandit algorithms for the stochastic setting are characterized by optimism in the face of uncertainty: Policies with uncertain payoff should be tried until their expected payoff is clearly suboptimal.
Bandit algorithms (and similarly, adaptive experimental designs for informing policy choice, as in Russo (2020), Kasy and Sautmann (2021)) are not directly applicable to social welfare maximization problems, such as those of optimal tax theory. The reason is that bandit algorithms maximize a stream of observed rewards. By contrast, social welfare as conceived in welfare economics is based on unobserved subjective utility.
Adversarial Decision-Making
Adversarial models for sequential decision-making find their roots in repeated game theory (Hannan (1957)), while related settings were independently studied in information theory (Cover (1965)) and computer science (Vovk (1990), Littlestone and Warmuth (1994)). Regret minimization, also in a bandit setting, was investigated as a tool to prove convergence of uncoupled dynamics to equilibria in N-person games (Hart and Mas-Colell (2000, 2001))—the exponential weighting scheme used by Exp3 is also known as smooth fictitious play in the game-theoretic literature (Fudenberg and Levine (1995)). Recent works (Seldin and Slivkins (2014), Zimmert and Seldin (2021)) show that simple variants of Exp3 simultaneously achieve essentially optimal regret bounds in adversarial, stochastic, and contaminated settings, without prior knowledge of the actual regime. This suggests that algorithms designed for adversarial environments can behave well in more benign settings, whereas the opposite is provably not true.
Bandit Approaches for Economic Problems
Bandit-type approaches have been applied to a number of other economic and financial scenarios in the literature where rewards are observable. These include monopoly pricing (Kleinberg and Leighton (2003)) (see also the survey by den Boer (2015)), second-price auctions (Weed, Perchet, and Rigollet (2016)), first-price auctions (Han, Zhou, and Weissman (2020), Han, Zhou, Flores, Ordentlich, and Weissman (2020), Achddou, Cappé, and Garivier (2021)); see also Kolumbus and Nisan (2022), Feng, Podimata, and Syrgkanis (2018), Feng, Guruganesh, Liaw, Mehta, and Sethi (2021), and combinatorial auctions (Daskalakis and Syrgkanis (2022)). Bandit-type approaches have also been applied to some settings where rewards are not directly observable, including bilateral trading (Cesa-Bianchi, Cesari, Colomboni, Fusco, and Leonardi (2024a, 2024b), and the newsvendor problem (Lugosi, Markakis, and Neu (2023)).
Bandit algorithms are widely used in online advertising and recommendation. Online learning methods are successfully used for tuning the bids made by autobidders (a service provided by advertising platforms) (Lucier, Pattathil, Slivkins, and Zhang (2024)). While these algorithms are analyzed in adversarial environments, the extent to which they are deployed in commercial products remains unclear.
2 Setup
Notation
2.1 Regret
The Adversarial Case
The Stochastic Case
2.2 Comparison to Related Learning Problems
Lipschitzness and Information Requirements
The difficulty of the learning problem in each of these models critically depends on (i) the Lipschitz properties of the welfare function, and (ii) the information required to evaluate welfare at a point.
We say that a generic welfare function is one-sided Lipschitz if for all and all . One-sided Lipschitzness allows us to bound the approximation error of a learning algorithm operating on a finite subset of the set of policies. One-sided Lipschitzness is an intrinsic property of both the monopoly pricing and the optimal taxation problem; it is not an assumption that is additionally imposed. To see this for monopoly pricing, note that, for , . For social welfare, .
We say that learning requires only pointwise information if is a function of , and does not depend on otherwise. Pointwise information allows us to avoid exploring policies that are clearly suboptimal, when we aim to learn the optimal policy.
Table I summarizes the Lipschitz properties and information requirements in each of the three models; the following justifies the claims made in Table I:
- 1. For monopoly pricing, welfare is one-sided Lipschitz and only depends on pointwise.
- 2. For optimal taxation, welfare is one-sided Lipschitz and depends on both at the given x (pointwise), and on an integral of for a range of values of (nonpointwise).
- 3. For bilateral trade, welfare is not one-sided Lipschitz and depends on both and (pointwise), as well as the integrals of and (nonpointwise).
These properties suggest a ranking in terms of the difficulty of the corresponding learning problems, and in particular in terms of the rates of divergence of cumulative regret: The information requirements of optimal taxation are stronger than those of monopoly pricing, but its continuity properties are more favorable than those of bilateral trade. This intuition is correct, as shown by Table I. The rates for monopoly pricing and for bilateral trade are known (or can be easily adapted) from the literature. In this paper, we prove corresponding rates for optimal taxation.
|
Policy Space |
Objective Function |
|||
|---|---|---|---|---|
|
Model |
Discrete |
Continuous |
Pointwise |
One-Sided Lipschitz |
|
Monopoly price setting |
T1/2 |
T2/3 |
Yes |
Yes |
|
Optimal taxation |
T2/3 |
T2/3 |
No |
Yes |
|
Bilateral trade |
T2/3 |
T |
No |
No |
- Note: This table shows the efficient rates of regret for different learning problems. Rates are up to logarithmic terms, and apply to both the stochastic and the adversarial setting. Regret rates are shown for the discrete case, where the space of policies x is restricted to a finite set, and the continuous case, where x can take any value in . The columns on the right describe the properties of the objective function in each problem, which drive the differences in regret rates.Rates for the optimal taxation case are proven in this paper. Rates for the continuous monopoly price setting case are from Kleinberg and Leighton (2003); the discrete case reduces to a standard bandit problem. Rates for the continuous bilateral trade case are from Cesa-Bianchi et al. (2024a); the discrete case can be deduced by adapting the arguments in the same paper (for the stochastic i.i.d. case with independent sellers' and buyers' valuations), or by adapting the techniques in Cesa-Bianchi et al. (2024b) (for the adversarial case, allowing the learner to use weakly budget balanced mechanisms).
In comparing optimal taxation and monopoly pricing to conventional multiarmed bandits, it is worth emphasizing that there are two distinct reasons for the slower rate of convergence. First, the continuous support of x, as opposed to a finite number of arms, which is shared by optimal taxation and monopoly pricing. Second, the requirement of additional exploration of suboptimal policies for the optimal tax problem. As shown in Table I, the continuous support alone is enough to slow down convergence, with no extra penalty for the additional exploration requirement, in terms of rates. If, however, we restrict our attention to a discrete set of feasible policies x, then monopoly pricing reduces to a multiarmed bandit problem, with a minimax regret rate of . The optimal tax problem, by contrast, still has a rate of , even if we restrict our attention to the case of finite known support for v and x, as shown by the proof of Theorem 1 below.
Hannan Consistency
The cumulative regret of any nonadaptive algorithm necessarily grows at a rate of T. This includes, in particular, randomized experiments where the policy is chosen uniformly at random, from a fixed policy set, in every period. Algorithms for which adversarial regret (and thus also stochastic regret) grows at a rate less than T, so that per period regret goes to 0 as T increases, are known as Hannan consistent. Nonadaptive algorithms are not Hannan consistent. Table I implies that Hannan consistent algorithms exist in all settings considered, with the exception of Bilateral trade and continuous policy spaces.
3 Stochastic and Adversarial Regret Bounds
We now turn to our main theoretical results, lower and upper bounds on stochastic and adversarial regret for the problem of social welfare maximization. We first prove a lower bound on stochastic regret, which applies to any algorithm, and which immediately implies a lower bound on adversarial regret. We then introduce the algorithm Tempered Exp3 for Social Welfare. We show that, for an appropriate choice of tuning parameters, this algorithm achieves the rates of the lower bound on regret, up to a logarithmic term. Formal proofs of these bounds can be found in Appendix A.
3.1 Lower Bound
Theorem 1. (Lower Bound on Regret)Consider the setup of Section 2. There exists a constant such that, for any randomized algorithm for the choice of and any time horizon , the following holds:
- 1. There exists a distribution μ on with associated demand function G for which the stochastic cumulative expected regret is at least .
- 2. There exists a sequence for which the adversarial cumulative expected regret is at least .
The proof of Theorem 1 can be found in Appendix A. The adversarial lower bound follows immediately from the stochastic lower bound, since worst-case regret (over possible sequences of ) is bounded below by average regret (over i.i.d. draws of ), for any distribution of .
Sketch of Proof
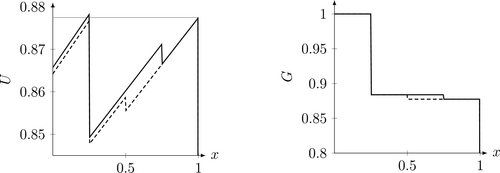
Construction for proving the lower bound on regret. Notes: This figure illustrates our construction for proving the lower bound on regret. The relative social welfare of policies 1 and .25 depends on the sign of ϵ. The solid line corresponds to ϵ = −1, the dashed line to ϵ = 1. In order to distinguish between these two, we must learn demand in the intermediate interval [0.5,0.75].
The difference in welfare of the two candidate optimal policies and 1 depends on the sign of ϵ. In order not to suffer expected regret that grows as , any learning algorithm needs to sample policies from points that are informative about the sign of ϵ. The only points that are informative are those in the region , where welfare is bounded away from optimal welfare.
More specifically, the learning algorithm has to sample on the order of times from the region , to be able to detect the sign of ϵ, incurring regret on the order of in the process. Any learning algorithm therefore incurs regret on the order of , which for , leads to the conclusion.
3.2 An Algorithm That Achieves the Lower Bound
We next introduce Algorithm 1, which allows us to essentially achieve the lower bound on regret, in terms of rates.

Tempered Exp3 for Social Welfare.
Conventional Exp3
Algorithm 1 is a modification of the Exp3 algorithm. Conventional Exp3 (Auer et al. (2002)) is designed to maximize the standard bandit objective, . Exp3 maintains an unbiased running estimate of the cumulative payoff of each arm k, calculated using inverse probability weighting, . In period i, arm k is chosen with probability , where η and γ are tuning parameters. is thus increasing in the estimated average performance of arm k in prior periods. Because is not normalized by the number of time periods i, more weight is given to the best performing arms over time, as estimation uncertainty for average performance decreases. In both these aspects, Exp3 is similar to the popular Upper Confidence Bound algorithm (UCB) for stochastic bandit problems (Lai (1987), Agrawal (1995), Auer, Cesa-Bianchi, and Fischer (2002)). In contrast to UCB, Exp3 is a randomized algorithm. Randomization is required for adversarial performance guarantees. This is analogous to the necessity of mixed strategies for zero-sum games.
Modifications Relative to Conventional Exp3
Relative to this algorithm, we require three modifications. First, we discretize the continuous support of x, restricting attention to the grid of policy values . Second, since welfare is not directly observed for the chosen policy x, we need to estimate it indirectly. In particular, we first form an estimate of cumulative demand for each of the policy values , using inverse probability weighting. We then use this estimated demand, interpolated using a step-function, to form estimates of cumulative social welfare, . Third, we require additional exploration, relative to Exp3. Since social welfare depends on demand for counterfactual policy choices, we need to explore policies that are away from the optimum, in order to learn the relative welfare of approximately optimal policy choices. The mixing weight γ, which determines the share of policies sampled from the uniform distribution, needs to be larger relative to conventional Exp3, to ensure sufficient exploration away from the optimum.
Theorem 2. (Adversarial Upper Bound on Regret of Tempered Exp3 for Social Welfare)Consider the setup of Section 2, and Algorithm 1. Assume that .
Then for any sequence expected regret is bounded above by
Tuning
Unknown Time Horizon
Note that the proposed tuning depends crucially on knowledge of the time horizon T at which regret is to be evaluated. In order to extend our rate results to the case of unknown time horizons, we can use the so-called doubling trick; cf. Section 2.3 of Cesa-Bianchi and Lugosi (2006): Consider a sequence of epochs (intervals of time periods) of exponentially increasing length, and rerun Algorithm 1 for each time period separately, tuning the parameters over the current epoch length. This construction converts Algorithm 1 into an “anytime algorithm,” which enjoys the same regret guarantees of Theorem 2, up to a multiplicative constant factor. Another more efficient strategy to achieve the same goal is to modify Algorithm 1, allowing the parameters η and γ to change at each iteration, and splitting each bin associated with the discretization parameter K whenever more precision is required.
The Extra Term
There is a rate discrepancy between our our upper and lower bounds on regret, corresponding to the term in our upper bound. We conjecture the existence of an alternative algorithm that can eliminate this extra logarithmic term, albeit at the cost of reduced computational efficiency and a less transparent theoretical analysis. Our conjecture is based on known results for the standard multi-armed bandit problem with K arms. The Exp3 algorithm achieves an upper bound of order for this problem, which includes an extra logarithmic factor compared to the known lower bound of order . Exp3 is an instance of the Follow-The-Regularized-Leader (FTRL) algorithm with importance weighting and the negative entropy as the regularizer. It is known that using the -Tsallis entropy as the regularizer in the FTRL algorithm with importance weighting results in regret guarantees of order for the bandit problem (Lattimore and Szepesvári (2020)). However, unlike Exp3, FTRL with Tsallis entropy involves a more complex proof. Analogous statements might be true for our setting.
Numerical Example
For illustration, Figure 2 plots the cumulative average regret of Tempered Exp3 for Social Welfare for the case where is sampled uniformly at random from each time period. Initially, the performance of our algorithm is, by construction, equal to the performance of choosing a policy uniformly at random. Over time, however, the average regret of our algorithm drops by more than half, in this numerical example. Note that the rate at which cumulative regret declines in Figure 2 (for i.i.d. sampling from a fixed distribution) is unrelated to the regret rate of Theorem 2 (for the worst-case sequence of , for each time horizon T).
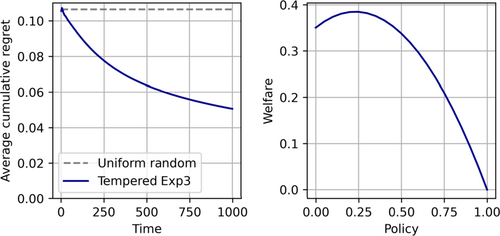
Tempered Exp3 for Social Welfare—numerical example. Notes: This figure illustrates the performance of our algorithm for the stochastic case, where vi is drawn uniformly at random from [0,1] for all i, the weight λ equals .7, and the tuning parameters are K = 20,η = 0.025,γ = 0.1. The left plot shows the cumulative average regret of our algorithm, averaged across 4000 simulations. The right plot shows expected social welfare U(x) as a function of the policy x.
Alternative Algorithms
Theorem 2 shows that Tempered Exp3 for Social Welfare achieves the lower bound for adversarial regret. The same might be true for other algorithms. Any alternative algorithm that shares this property needs to be randomized. The need for randomization parallels the need for mixed strategies in both static and dynamic zero-sum games; it excludes deterministic algorithms such as UCB. For the bandit setting, the Tsallis-INF algorithm (Zimmert and Seldin (2021)), of which Exp3 is a special case, is furthermore the only algorithm known to be rate optimal in both stochastic and adversarial regimes.
For our adaptive welfare problem, any algorithm that achieves the optimal rate is not only required to randomize; any such algorithm also needs to sample suboptimal policies at a sufficient rate; cf. the proof of Theorem 1. Tempered Exp3 for Social Welfare does so by sampling policies uniformly at random, with probability γ. In the conclusion, we propose a similar modification for Thompson sampling.
A possible improvement to uniform sampling across all policies, as in Tempered Exp3 for Social Welfare, could be to only sample policies uniformly at random from the range of potentially optimal policies: Demand outside this range is irrelevant for welfare comparisons within this range. This idea is implemented in the algorithm that we introduce in Section 4 for the stochastic concave setting.
4 Stochastic Regret Bounds for Concave Social Welfare
Theorem 1 in Section 3 provides a lower bound proportional to for adversarial and stochastic regret in social welfare maximization. The proof of this lower bound constructs a distribution for the . This distribution is such that expected social welfare is nonconcave, as a function of x; two global optima are separated by a region of lower welfare. In order to learn which of two candidates for the globally optimal policy is actually optimal, it is necessary to sample policies in between. These intermediate policies yield lower welfare, and sampling them contributes to cumulative regret. This construction is illustrated in Figure 1.
Given that the construction relies on nonconcavity of expected social welfare, could we achieve lower regret if we knew that social welfare is actually concave? The answer turns out to be yes, for the stochastic setting (in the adversarial setting, cumulative welfare is necessarily nonconcave). One reason is that concavity ensures that the function is unimodal. To estimate the difference in social welfare between two policies, it therefore suffices to sample policies that lie in the interval between them. These in-between policies yield social welfare exceeding the minimum of the two boundary policies. A second reason is that concavity prevents unexpected spikes in social welfare. This property allows us to test carefully chosen triples of points for extended periods, to ensure that one of them is suboptimal, without incurring significant regret.
For the stochastic setting with concave social welfare, we present an algorithm that achieves a bound on regret of order , up to logarithmic terms. Before describing our proposed algorithm, Dyadic Search for Social Welfare, let us formally state the improved regret bounds. The proofs of these lower and upper bounds can be found in the Online Supplement.
Theorem 3. (Lower bound on regret for the concave case)Consider the setup of Section 2. There exists a constant such that, for any randomized algorithm for the choice of and any time horizon , the following holds.
There exists a distribution μ on with associated demand function G and concave social welfare function U, for which the stochastic cumulative expected regret is at least .
Theorem 4. (Stochastic Upper Bound on Regret of Dyadic Search for Social Welfare)Consider the stochastic setup of Section 2 and time horizon . If Algorithm 2 is run with confidence parameter , and if the social welfare function U is concave, then the expected regret is of order at most , up to logarithmic terms.

Dyadic Search for Social Welfare.
Dyadic Search
Our algorithm is based on a modification of dyadic search, as discussed in Bachoc, Cesari, Colomboni, and Paudice (2022a, 2022b). At any point in time, this algorithm maintains an active interval , which contains the optimal policy with high probability. Only policies within this interval are sampled going forward. As evidence accumulates, this interval is trimmed down, by excluding policies that are suboptimal with high probability.
The algorithm proceeds in epochs τ. At the start of each epoch, a subinterval is formed, with mid-point . The points are in a dyadic grid, that is, they are of the form . After sampling from , we calculate confidence intervals , , and for the welfare differences , , and , where .
If the confidence interval or lies above 0, concavity implies that the optimal policy cannot lie to the left of l; we can thus trim the active interval by dropping all points to the left of l. Symmetrically, if the confidence interval or lies below 0, we can trim by dropping all points to the right of r.
Confidence Intervals for Welfare Differences
Before concluding this section, we highlight two features of Algorithm 2. First, two of the three points , and the corresponding estimates of demand, are kept from each epoch to the next. Second, estimation of the integral term is performed by querying points following a fixed and balanced design on the dyadic grid—instead of, for example, using a randomized Monte Carlo procedure, which may lead to unbalanced exploration. This implies that the points queried to estimate the integral terms can be easily reused to obtain other integral estimates from each epoch to the next. These two features combined ensure that Algorithm 2 recycles information very efficiently to prune the active interval as quickly as possible, which leads to better regret.
5 Income Taxation
We discuss two extensions of the baseline model of optimal taxation that we introduced in Section 2. These extensions incorporate features that are important in more realistic models of optimal taxation. For both of these extensions, we propose a properly modified version of Algorithm 1. The first extension, discussed in this section, is a variant of the Mirrlees model of optimal income taxation (Mirrlees (1971), Saez (2001, 2002)). The second extension, discussed in Section 6 is a variant of the Ramsey model of commodity taxation (Ramsey (1927)).
Our model of income taxation generalizes our baseline model by allowing for heterogeneous wages , welfare weights , extensive-margin labor supply responses determined by the cost of participation , and nonlinear income taxes . Two simplifications are maintained in this model, relative to a more general model of income taxation. First, only extensive margin responses (participation decisions) by individuals are allowed; there are no intensive margin responses (hours adjustments). Second, as in the baseline model of Section 2, there are no income effects. In imposing these assumptions, our model mirrors the model of optimal income taxation discussed in Section II.2 of Saez (2002).
Setup
At each time , one individual arrives who is characterized by (i) a potential wage , and (ii) an unknown cost of participation . This individual makes a binary labor supply decision . If they participate in the labor market (), they earn , but pay a tax according to the tax rate on their earnings . They furthermore incur a nonmonetary cost of participation .
Their optimal labor supply decision is therefore given by , and private welfare equals . The implied public revenue is equal to the tax on earnings if , and 0 otherwise.
Piecewise Constant Tax Schedules
Algorithm
Algorithm 3 generalizes Algorithm 1 to this setting. As before, we form an unbiased estimate of using inverse probability weighting, map this estimate into a corresponding estimate of , based on Equation (18), and cumulate across time periods to obtain . Note that is observed whenever . This implies that the estimate is in fact a function of observables, and the same holds for .

Tempered Exp3 for Optimal Income Taxation.
Algorithm 3 keeps track of estimated demand and social welfare for each bin (“tax bracket”), as defined by the grid points . The algorithm then constructs a distribution over tax rates given w, using the tempered Exp3 distribution. The tax schedule is sampled according to these (marginal) distributions of tax rates for each bracket. Though immaterial for the following theorem, we choose the perfectly correlated coupling, across brackets, of these marginal distributions, which is implemented using the random variable in Algorithm 3.
Theorem 5. (Adversarial Upper Bound on Regret of Tempered Exp3 for Optimal Income Taxation)Consider the setup of Section 5, and Algorithm 3. Assume that , and that for all w.
Then for any sequence expected regret is bounded above by
6 Commodity Taxation
In this section, we generalize our baseline model of optimal taxation to a model of commodity taxation with multiple goods and continuous demand functions , where is a vector of tax rates. We again assume that there are no income effects. Our setup is a version of the classic Ramsey model (Ramsey (1927)). We propose a generalization of Tempered Exp3 for Social Welfare to this setting. In the following, we use to denote the Euclidean inner product between x and y.
Setup

Tempered Exp3 for Commodity Taxation.
Mapping Demand to Welfare
7 Conclusion
Possible Applications
The setup introduced in Section 2 was deliberately stylized, to allow for a clear exposition of the conceptual issues that arise when adaptively maximizing social welfare. The algorithm that we proposed for this setup, and the generalizations discussed later in the paper, are nonetheless directly practically relevant. They remain appropriate in economic settings that are considerably more general than the setting described by our model.
The reasons for this generality have been elucidated by the public finance literature, cf. Chetty (2009), building on the generality of the envelope theorem; cf. Milgrom and Segal (2002), Sinander (2022). By the envelope theorem, the welfare impact of a marginal tax change on private welfare can be calculated ignoring any behavioral responses to the tax change. This holds in generalizations of our setup that allow for almost arbitrary action spaces (including discrete and continuous, multidimensional, and dynamic actions), and for arbitrary preference heterogeneity. The expressions for social welfare that justify our algorithms remain unchanged under such generalizations. That said, the validity of these expressions does require the absence of income effects and of externalities. If there are income effects or externalities, the algorithms need to be modified.
Our approach is motivated by applications of algorithmic decision-making for public policy, where a policymaker cares about welfare, but also faces a government budget constraint. Possible application domains of our algorithm include the following. In public health and development economics, field experiments such as Cohen and Dupas (2010) vary the level of a subsidy for goods such as insecticide-treated bed nets (ITNs), estimating the impact on demand. Our algorithm could be used to find the optimal subsidy level quickly and apply it to experimental participants. A term capturing positive externalities of the use of ITNs could be added to social welfare, leaving the algorithm otherwise unchanged. In educational economics, many studies evaluate the impact of financial aid on college enrollment (Dynarski, Page, and Scott-Clayton (2023)). An adaptive experiment might vary the level of aid provided, where aid is conditional on college attendance and conditional on pre-determined criteria of need or merit. In such an experiment, a variant of our algorithm for optimal income taxation might be used, where the welfare weights ω are a function of need or merit, and the outcome y is college attendance. In environmental economics, many experiments (e.g., Lee, Miguel, and Wolfram (2020)) study the impact of electricity pricing on household electricity consumption. Once again, our baseline algorithm (for binary household decisions about connecting to the grid) or our algorithm for commodity taxation (for continuous household decisions about consumption levels) could be applied, to learn optimal prices, taking into account both distributional considerations and externalities.
These examples are all drawn from public policy, where there is an intrinsic concern for social welfare. This contrasts with commercial applications, where the goal is typically to maximize (directly observable) profits by monopolist pricing (den Boer (2015)), or more generally by reserve price setting in auctions (Nedelec, Calauzènes, El Karoui, and Perchet (2022). Adaptive pricing algorithms are used in applications such as online ad auctions. A concern for welfare might enter in such commercial settings if there is a participation constraint that needs to be satisfied for consumers. Suppose, for example, that consumers or service providers need to first sign up for a platform, say for e-commerce or for gig work, and then repeatedly engage in transactions on this platform. To sign up in the first place, their expected welfare needs to exceed their outside option. This constraint might then enter the platform provider's objective, in Lagrangian form, adding a term for welfare, and leading to objectives such as those maximized by our algorithms.
An Alternative Approach: Thompson Sampling
The main algorithm proposed in this paper, Tempered Exp3 for Social Welfare, is designed to perform well in the adversarial setting. In the construction of this algorithm, no probabilistic assumptions were made about the distribution of . In the stochastic framework, a sampling distribution is assumed, for instance, that the be i.i.d. over time. The Bayesian framework completes this by assuming a prior distribution over the parameters, which govern the sampling distribution.
One popular heuristic for adaptive policy choice in the Bayesian framework is Thompson sampling (Thompson (1933), Russo, Van Roy, Kazerouni, Osband, and Wen (2018)), also known as probability matching, which assigns a policy with probability equal to the posterior probability that this policy is optimal. In our setting, Thompson sampling could be implemented as follows. First, form a posterior for the demand function , based on all the data available from previous periods . Sample one draw from this posterior. Map this draw into a draw from the posterior for via . Find the maximizer . This is the policy recommended by Thompson sampling. We conjecture that this algorithm will outperform random assignment, but will underexplore relative to the optimal algorithm. Adding further forced exploration to this algorithm might improve cumulative welfare. A formal analysis of algorithms of this type is left for future research.
A natural class of priors for G are Gaussian process priors (Williams and Rasmussen (2006)). If outcomes y are conditionally normal (rather than binary, as in our baseline model), then the posterior for demand is available in closed form, and the posterior mean is equal to the best linear predictor given past outcomes . Furthermore, since social welfare is a linear transformation of demand, the posterior for U is then also linear and available in closed form. For details, see Kasy (2018).
Appendix A: Proofs
A.1 Theorem 1 (Lower Bound on Regret)
Defining a Family of Distributions for v
Explicit Lower Bound on Regret That Will Be Proven
Fix a randomized algorithm to choose the policies , and fix a time horizon .
Number of Mistakes and Lower Bound on Regret
Intuition for the Remainder of the Proof
Low Regret Cannot Be Achieved for Both Positive and Negative ϵ
A.2 Theorem 2 (Adversarial Upper Bound on Regret)
The proof of this theorem builds upon the proof of Theorem 6.5 in Cesa-Bianchi and Lugosi (2006). Relative to this theorem, we need to additionally consider the discretization error introduced by Algorithm 1, and explicitly control the variance of estimated welfare.
Recall our notation and for realized cumulative welfare, and for cumulative welfare for the counterfactual, fixed policy x. We further abbreviate . Throughout this proof, the sequence is given and conditioned on in any expectations.
- 1.
Discretization
Recall that . Let
(this is rounded down to the next grid point ), and denoteas well as . Then it is immediate that ,and and, therefore, - 2.
Unbiasedness
At the end of period i, is an unbiased estimator of for all k. Therefore, for all i and k.
- 3.
Upper bound on optimal welfare
Define , and .
It is immediate that
Furthermore,Given our initialization of the algorithm, . - 4.
Lower bound on estimated welfare
Denote , where ,
so that , and .
By definition of ,
Since for all k, for all i and k and, therefore, (where the last inequality holds by assumption). Using for any yieldsTherefore,The second inequality follows from . - 5.
Connecting the first-order term to welfare
Note that, by definition, . Therefore,
and thuswhere we have used the fact that for all k, given our definition of Ũ, and the fact that is distributed according to , by construction. - 6.
Bounding the second moment of estimated welfare
It remains to bound the term . As in the preceding item, we have
We can rewrite
Bounding immediately gives
and, therefore, - 7.
Collecting inequalities
Combining the preceding items, we get
Multiplying by and dividing by η, adding to both sides and subtracting , bounding , and (from Item 1), yields
(36)This proves the first claim of the theorem. - 8.
Optimizing tuning parameters
Suppose now that we choose the tuning parameters as follows:
Substituting we getThe second claim of the theorem follows.




