A Comment on: “Autoregressive Conditional Duration: A New Model for Irregularly Spaced Transaction Data”
Abstract
Based on the GARCH literature, Engle and Russell (1998) established consistency and asymptotic normality of the QMLE for the autoregressive conditional duration (ACD) model, assuming strict stationarity and ergodicity of the durations. Using novel arguments based on renewal process theory, we show that their results hold under the stronger requirement that durations have finite expectation. However, we demonstrate that this is not always the case under the assumption of stationary and ergodic durations. Specifically, we provide a counterexample where the MLE is asymptotically mixed normal and converges at a rate significantly slower than usual. The main difference between ACD and GARCH asymptotics is that the former must account for the number of durations in a given time span being random. As a by-product, we present a new lemma which can be applied to analyze asymptotic properties of extremum estimators when the number of observations is random.
1 Introduction
ER noted that the likelihood function in ( 3 ) is identical to the likelihood function of the GARCH(1,1) model with Gaussian innovations. In line with this, for their main result (p. 1135), ER referred to Lee and Hansen ( 1994 , LH henceforth) to conclude that under the condition of strict stationarity and ergodicity of the durations , that is, , is consistent and asymptotically normal at the usual rate.
As we argue in this paper, the machinery in LH cannot be applied to the ACD setup unless additional arguments are used and further assumptions imposed. In particular, with such that the strict stationarity and ergodicity condition holds, that is, , we argue that, in contrast to the GARCH case, the behavior of the QML estimator depends on whether (i) , (ii) , or (iii) . Specifically, results regarding rates of convergence, asymptotics of the QMLE, convergence of the score, and sample information all depend on which of the three cases above holds. Key is that modifications of arguments are needed due to randomness of the number of durations .
This paper makes the following contributions.
First, we provide a new lemma which can be applied to analyze asymptotic properties of extremum estimators when the number of observations is random. The arguments in its proof use renewal theory and are thus different from LH/ER.
Second, we apply this result and show in Section 2 that under the additional condition , which implies , and T are proportional in the sense that . The latter result can be used to prove that normalizing the score by either , , or the sample information, , leads to asymptotic normality, establishing asymptotic normality of , , and ; see Theorem 2 .
Third, to illustrate that these results do not hold in general, we present in Section 3 a counterexample, with stationary and ergodic, but where , and hence . With exponential innovations , we show that converges at the rate for some , which is significantly slower than the usual rate. Moreover, has a mixed normal (MN) limiting distribution. Hence, the limiting distribution of the MLE differs from the classical, LH/ER form . Importantly, the MN limit theory implies that different normalizations lead to distinct asymptotic distributions.
Finally, we note that the arguments in the counterexample are specific to the MLE, and hence there is no guarantee that they can be generalized to the QMLE for the case of , and neither to the ‘unit root’ case of .
2 Main Result
To derive the asymptotic distribution of the QMLE presented in Theorem 2 , we make use of the following general lemma which extends the results in LH to allow for a random number of observations.
Lemma 1.Let be a random function of the parameter , indexed by . Assume that is three times continuously differentiable, and that for in the interior of Φ, as :
- (C.1) , ,
- (C.2) ,
- (C.3) ,
where is a k-dimensional Brownian motion, is a closed neighborhood of , and . Moreover, with a counting process defined on the same probability space as , assume that for some constant :
- (C.4) as .
With , there exists an open neighborhood , such that, as :
- (i) With probability tending to 1, there exists a unique maximum point of in , is concave on , and ;
- (ii) ;
- (iii) , .
All proofs of the results in this paper are provided in Section 4 . Note that Assumption (C.4) can be replaced by and , .
Our main result is as follows.
Theorem 2.For the ACD model ( 1 )–( 2 ) with true parameter , assume:
- (i) is an i.i.d. sequence of random variables with support , pdf bounded away from zero on compact subsets of , , and ,
- (ii) is an interior point satisfying .
As , the maximizer of in ( 3 ) is consistent and asymptotically normal:
Remark 1.Theorem 2 shows that, if the strict stationarity condition is strengthened with the additional restriction , then is asymptotically normal as . In particular, . In this case, using as normalization instead, Theorem 2 and ( 8 ) jointly imply that . Hence, up to a scaling factor, and have the same asymptotic distribution. Likewise, when normalizing by the sample information, we find for the MLE as then .
Remark 2.The proof of Theorem 2 relies on the new Lemma 1 , which may also be used to establish asymptotic theory for the more general ACD() models mentioned in ER (p. 1133) which allow lags of and lags of in ( 2 ), including the simple stylized ACD model considered in Cavaliere, Mikosch, Rahbek, and Vilandt ( 2024 ).
Remark 3.Asymptotic normality of the estimator is not guaranteed to hold when Assumption (ii) does not hold; see Section 3 for a counterexample.
3 Non-Standard Asymptotics
We present here a counterexample which shows that if , implying , the asymptotic distribution of is not normal, even under strict stationarity and ergodicity. Specifically, different normalizations (e.g., using a deterministic function of T, or a random normalization such as the sample information) may lead to different asymptotics.
Consider the ACD model given by ( 1 )–( 2 ), under the assumption that the 's are exponentially distributed with . We have the following result.
Theorem 3.Consider the exponential ACD model with true parameter being an interior point satisfying the strict stationarity condition and . As , the maximizer of in ( 3 ) is consistent and asymptotically mixed normal:
In line with Remark 1 , the following corollary for normalized by the sample information or by holds.
Corollary 1.Under the assumptions of Theorem 3 , and as .
Remark 4.Consider a drifting sequence of true parameters of the form (). Using the same arguments as in the proof of Theorem 3 , it holds that , which is mixed normal with (deterministic) non-centrality parameter −s. In contrast, for normalized by the sample information as in Corollary 1 , we find , where the non-centrality parameter is now random. The latter result implies that when , the asymptotic local power of t-ratios is random in the limit, which contrasts with the case in Theorem 2 .
To shed some light on the mixed normality in Theorem 3 , note that when , the limiting distribution of does not have exponential tails; in particular, it has infinite variance. To see this, write the right-hand side of ( 9 ) as with standard normal, independent of , and let for any vector norm . Then, since is a -stable random variable with (see Lemma 4 ), it follows by Breiman's lemma (see, e.g., Lemma 3.1.11 in Mikosch and Wintenberger ( 2024 )) that for x large, with c a positive constant, using the tail asymptotics of (see Remark 6 ).
To further emphasize the different asymptotic behavior of when , consider here a small Monte Carlo study where i.i.d. realizations of are generated for large T. In particular, we consider the kernel density estimates for and against the normal density function which matches the (sample) median and interquartile range across Monte Carlo realizations. Specifically, we set , corresponding to approximately . This particular value is shown in Figure 1 , where we also show the values of corresponding to (), , as well as those satisfying (boundary of the non-stationarity region). The sample size T is calibrated such that the median number of durations in is about .
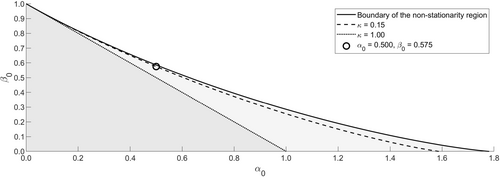
The stationarity region (gray) with lines indicating tail indices κ0 = 1.00 and κ0 = 0.15.
Figure 2 shows that, as predicted by Theorem 3 , the large sample distributions of both and display fatter tails than the Gaussian pdf.
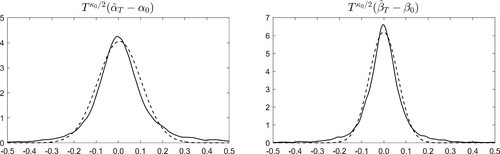
Estimated densities (solid lines) against the Gaussian pdf (dashed lines).
Remark 5.It is important to note that for the case of , which is not ruled out by the ER conditions, the limiting behavior of is unknown (for both types of normalizations), even when is exponential (MLE). The key challenge in this case is that the large sample behavior of has not been established at present; see, for example, Mikosch and Resnick ( 2006 ). Also, we note that the results in Theorem 3 and its corollary hold only for the MLE. Further research is needed to understand the QMLE case.
4 Proofs and Additional Results
4.1 Proof of Lemma 1
We first consider the asymptotic behavior as for the score, the second-order derivative, and the third-order derivatives of . Next, we use these results to establish (i)–(iii).
Establishing (i)–(iii): These hold by using ( 11 )–( 13 ) together with the arguments in the proof of Lemma 1 in Jensen and Rahbek ( 2004 ), replacing T there by , and setting . Specifically, ( 11 ) replaces condition (A.1) in Jensen and Rahbek ( 2004 ), ( 12 ) replaces their condition (A.2), and ( 13 ) replaces their condition (A.3). Q.E.D.
4.2 Proof of Theorem 2
In order to establish (C.4), note that since , we have , where the last term tends to zero a.s. (as , and hence, ). Hence, up to a negligible term, equals , which by Gut ( 2009 , Theorem 2.1) and the strong LLN converges a.s. to , as desired. Q.E.D.
4.3 Proof of Theorem 3
To establish ( 14 ), we apply Theorem 3.1 in Sweeting ( 1992 ) which holds under the regularity conditions D1 and D2 therein. Specifically, condition D1 holds if (a.s.), under a sequence of data generating processes (DGPs) with true parameter value , . Let with . Condition D2 holds if, for any , , under the -sequences of DGPs.
4.4 Proof of Corollary 1
By the proof of Theorem 3 , , where Z is independent of . Moreover, , where ; this implies the desired result. Q.E.D.
4.5 Additional Lemma
Lemma 4.If and ,
Remark 6.We note that a κ-stable random variable is given via its characteristics function. It has right tail of the asymptotic order as ; see, for example, Samorodnitsky and Taqqu ( 1994 , Chapter 1) for more details.




