RCTs to Scale: Comprehensive Evidence From Two Nudge Units
Abstract
Nudge interventions have quickly expanded from academic studies to larger implementation in so-called Nudge Units in governments. This provides an opportunity to compare interventions in research studies, versus at scale. We assemble a unique data set of 126 RCTs covering 23 million individuals, including all trials run by two of the largest Nudge Units in the United States. We compare these trials to a sample of nudge trials in academic journals from two recent meta-analyses. In the Academic Journals papers, the average impact of a nudge is very large—an 8.7 percentage point take-up effect, which is a 33.4% increase over the average control. In the Nudge Units sample, the average impact is still sizable and highly statistically significant, but smaller at 1.4 percentage points, an 8.0% increase. We document three dimensions which can account for the difference between these two estimates: (i) statistical power of the trials; (ii) characteristics of the interventions, such as topic area and behavioral channel; and (iii) selective publication. A meta-analysis model incorporating these dimensions indicates that selective publication in the Academic Journals sample, exacerbated by low statistical power, explains about 70 percent of the difference in effect sizes between the two samples. Different nudge characteristics account for most of the residual difference.
1 Introduction
Thaler and Sunstein (2008) defined nudges as “choice architecture that alters people's behavior in a predictable way without forbidding any options or significantly changing their economic incentives.” These light-touch behavioral interventions—including simplification, personalization, and social-norm comparison—have become common in the literature, spanning hundreds of papers in fields such as economics, political science, public health, decision-making, and marketing.
Soon after researchers embraced these interventions, nudges also went mainstream within governments in larger-scale applications. While behavioral interventions were already being used on a case-by-case basis within government, the launch of ideas42 in the United States in 2008, the UK's Behavioural Insights Team (BIT) in 2010 (see, e.g., Halpern (2015)), and the Office of Evaluation Sciences (OES) in 2015 spurred an explosion of government teams dedicated to using behavioral science to improve government services. As of last count, there are more than 200 such units globally (Figure A.1, OECD (2017)).
The rapid expansion of behavioral interventions through Nudge Units offers a unique opportunity to compare the impact of interventions as implemented by researchers to the larger roll-out of similar interventions “at scale” (Muralidharan and Niehaus (2017)). Do nudges impact, for example, take-up of vaccinations, contribution to retirement plans, or timely payment of fines similarly in interventions by academic researchers and in larger-scale implementations within governments? Understanding how RCTs scale is a key question, as researchers and policy-makers build on the results of smaller interventions to plan larger implementations. To the best of our knowledge, this comparison of Nudge Unit experiments to the papers in the literature has not been possible so far, given the lack of comprehensive data on Nudge Unit interventions.
In this paper, we present the results of a unique collaboration with two major “Nudge Units”: BIT North America, which conducts projects with multiple U.S. local governments, and OES, which collaborates with multiple U.S. Federal agencies. Both units kept a comprehensive record of all trials from inception in 2015. As of July 2019, they conducted a total of 165 trials testing 347 nudge treatments and affecting almost 37 million participants. In a remarkable case of administrative transparency, each trial had a trial report, including in many cases a pre-analysis plan. The two units worked with us to retrieve the results of all trials, 87 percent of which have not been documented in working papers or academic publications.
This evidence differs from a traditional meta-analysis in two ways: (i) the large majority of these findings have not previously appeared in academic journals; (ii) we document the entirety of trials run by these units, with no scope for selective publication.
We restrict our data set to RCTs (excluding 13 natural experiments and difference-in-differences) and require that the trials have a clear control group (excluding 15 trials), do not use financial incentives (excluding 3 trials), and have a binary outcome as dependent variable (excluding 8 trials). The last restriction allows us to measure the impact with a common metric—the percentage point difference in outcome, relative to the control. Finally, we exclude interventions with default changes (excluding 2 nudges in 1 trial). This last restriction ensures that the nudge treatments are largely comparable, consisting typically of a combination of simplification, personalization, implementation intention prompts, reminders, and social-norm comparisons introduced in administrative communication. Examples of such interventions include a letter encouraging service-members to re-enroll in their Roth Thrift Savings Plans, and a post-card from a city encouraging people to fix up their homes in order to meet code regulations. Our final sample includes 126 trials, involving 241 nudges and collectively impacting over 23 million participants.
We compare these trials to nudges in the literature, leaning on two recent papers summarizing over 100 published nudge RCTs across many settings, Benartzi et al. (2017) and Hummel and Maedche (2019). We apply identical restrictions as in the Nudge Units sample, leaving a final sample of 26 RCTs, including 74 nudge treatments collectively affecting 505,337 participants. While this sample is fairly representative of the type of nudges in the literature, the features of these interventions do not perfectly match with the treatments implemented by the Nudge Units, a difference to which we return below.
What do we find? In the 26 papers in the Academic Journals sample, we compute the average (unweighted) impact of a nudge across the 74 nudge interventions. On average, a nudge intervention increases take-up by 8.7 (s.e. = 2.5) percentage points (pp.), a 33.4 percent increase over the average control group take-up of 26.0 percent.
Turning to the 126 trials by Nudge Units, we estimate an unweighted impact of 1.4 pp. (s.e. = 0.3), an 8.0 percent increase over an average control group take-up of 17.3 percent. While this impact is highly statistically significantly different from 0 and sizable, it is about one sixth the size of the estimate in academic papers, and we can reject the hypothesis of equal effect sizes in the two samples.
What accounts for this large difference? We document three key dimensions (although others may also play a role): (i) statistical power of the trials; (ii) characteristics of the nudge interventions; and (iii) selective publication. We then propose a model that accounts for these dimensions, and explore the relative role of each. While the model is aimed at our specific setting, it likely has implications for other contexts in which experimental evidence is collected by researchers, and then rolled out “at scale.”
First, we document a large difference in the sample size and thus statistical power of treatment arms within the trials. The median nudge intervention in the Academic Journals sample has a treatment arm sample size of 484 participants and a minimum detectable effect size (MDE, the effect size that can be detected with 80% power) of 6.3 pp. In contrast, the interventions in the Nudge Units have a median treatment arm sample size of 10,006 participants and MDE of 0.8 pp. Thus, the statistical power in the Academic Journals sample is an order of magnitude smaller.
We propose one way to interpret this difference. In economics, 80% statistical power calculations are commonplace and constitute, for example, the large majority of formal power calculations on the AEA Registry. Holding this criterion constant, the differences in sample size may arise optimally if academic researchers expect much larger effect sizes and therefore are comfortable with a larger MDE ex ante. While we do not observe whether the academic trials in our sample were designed based on power calculations, we were able to collect forecasts on expected nudge effect sizes from a survey of academic researchers and nudge practitioners. The median nudge practitioner expects an average impact of 1.95 pp. for the Nudge Unit trials, remarkably in line with our findings and with the MDE for that sample. Conversely, the median academic researcher expects a larger effect size of 4.0 pp. for the Nudge Units sample and of 7.0 pp. for the Academic Journals sample. This suggests that academics' optimistic expectations about nudge effect sizes may shape their trial design, and thus the differences in statistical power. Further, we document that, in the Academic Journals sample, researchers run more treatment arms per trial than in the Nudge Units sample, further diluting the (smaller) initial sample. Thus the smaller sample per arm in the Academic Journals sample does not merely reflect a capacity constraint.
Second, the nudge interventions in the two samples have different features, and some of these differences may account for the effect size discrepancy. We consider differences in (i) the degree of academic involvement; (ii) the types of behavioral mechanism used, such as Academic Journal nudges having more in-person contact and choice design; (iii) the policy area, with the Academic Journal studies being more likely to tackle, for example, environmental policy questions; and (iv) the characteristics of the trials, such as institutional constraints. We document differences in all the above dimensions, with varying impacts on effect size. Differences in the type of behavioral mechanism used and in the policy area account for a sizable share of the difference in effect sizes, while other differences, such as in academic involvement, do not. We return below to a full decomposition of the effect size differences.
Third, we consider selective publication as a function of statistical significance. In the Academic Journals sample, there are over 4 times as many studies with a t statistic between 1.96 and 2.96 for the most significant arm in a paper, versus studies where the most significant arm has a t between 0.96 and 1.96. Therefore, part of the different effect sizes in the two samples may come from the truncation of statistically insignificant trials in published papers. We stress that with “selective publication” we include not only whether a journal would publish a paper, but also whether a researcher would write up a study (the “file drawer” problem, e.g., Franco, Malhotra, and Simonovits (2014)). In the Nudge Units sample, all these selective steps are removed.
Building on this evidence, we estimate a model based on Andrews and Kasy (2019) which allows for selective publication of the Academic Journal trials, different effect sizes in the two samples, and, in some models, different nudge characteristics. This model also takes as inputs differences in statistical power. We find strong evidence of publication bias: we estimate that trials with no significant results are ten times less likely to be written up and published than trials with a significant result. We estimate that if there were no publication bias, the average effect of a nudge in the Academic Journals sample would be 3.9 pp. (s.e. = 1.9) and thus publication bias in the Academic Journals sample explains about 60–70 percent of the difference in effect sizes. If we include key nudge characteristics as predictors of the effect size, these characteristics explain most of the remaining difference, since the characteristics of nudges in the Academic Journals are more often associated with larger effect sizes.
We use these estimates to produce simulated counterfactuals of the average effect size of a nudge if one were to alter each of the dimensions separately and in combination. Selective publication has the largest impact on the point estimate, but statistical power also plays a role, in that under-powered studies exacerbate the impact of selective publication. The two elements are interlinked in that low statistical power would not bias the effect size in the absence of selective publication.
These results also suggest that the 1.4 pp. estimate for the Nudge Unit trials is a reasonable estimate for the average impact of a nudge at scale on government services, with likely higher impacts for nudge interventions in the absence of the “at scale” constraints. While a cost-benefit analysis is not the focus of this paper (see Benartzi et al. (2017)), we stress that this 1.4 pp. impact comes with a marginal cost that is typically zero or close to zero, thus suggesting a sizable return on investment.
Within the literature on effectiveness of nudges (e.g., Laibson (2020), Milkman et al. (2021)) we contribute, to our knowledge, the first comprehensive evaluation of the RCTs from a Nudge Unit. The 1.4 pp. estimate likely is a lower bound of the impact of behavioral science for three reasons. First, the Nudge Units face institutional constraints that make their RCTs less likely to have characteristics typically associated with larger impacts, such as default changes (Jachimowicz et al. (2019)). Second, the trials we consider typically have multiple arms; while we estimate the average impact of each arm, organizations can adopt the most successful nudge in the trial. Third, researchers can build on the most successful results in the design of later interventions.
This paper is also related to the literature on publication bias (e.g., Simonsohn, Nelson, and Simmons (2014), Brodeur et al. (2016), Oostrom (2021)) and research transparency (Miguel et al. (2014); Christensen and Miguel (2018)). We show encouraging evidence of best practices in Nudge Units, which ran appropriately powered trials and kept track of all the results, thus enabling a comprehensive evaluation. In comparison, we document a large role of selective publication in published papers. We also apply the publication-bias correction of Andrews and Kasy (2019) and show that the normality assumption traditionally used in meta-analyses is too restrictive and would lead to biased estimates.
Bringing these two literatures together, a key question is the extent to which selective publication leads to bias in the estimate of the impact of behavioral science. On the one hand, it leads to the publication of results with large effect sizes due to luck or p-hacking, especially given the many under-powered interventions. These results are unlikely to replicate at the same effect size, thus inducing bias. Indeed, replications (in other settings) typically yield smaller point estimates than the original results, for example, for laboratory experiments (Camerer et al. (2016)) or TV advertising impacts (Shapiro, Hitsch, and Tuchman (forthcoming)). On the other hand, selective publication may also highlight the interventions that turn out to be truly successful at inducing a behavior; these “good ideas” would presumably replicate. Our results cannot measure the magnitude of the two forces, given that the Nudge Unit interventions are not exact replications of the Academic Journal nudges.
Finally, the paper is related to the literature on scaling RCT evidence (Banerjee and Duflo (2009); Allcott (2015); Bold et al. (2018); Dehejia, Pop-Eleches, and Samii (2019); Meager (2019); Vivalt (2020)). In our case, “scaling” nudges did not entail the examination of, for example, general-equilibrium effects (e.g., Muralidharan and Niehaus (2017)), which are important in other contexts. Rather, the key aspects of scaling in our setting are the ability to conduct adequately powered interventions, within the institutional constraints that are more likely to arise at scale. The latter aspect echoes the findings on scaling in Bold et al. (2018) and Vivalt (2020).
2 Setting and Data
2.1 Trials by Nudge Units
Nudge Units
We analyze the trials conducted by two large “Nudge Units” operating in the United States: the Office of Evaluation Sciences (OES), which collaborates with federal government agencies; and the Behavioral Insights Team's North America office (BIT-NA), which worked primarily with local government agencies during the period in question.
OES was launched in 2015 under the Obama Administration as the core of the White House Social and Behavioral Sciences Team (SBST). The formal launch was coupled with a Presidential Executive Order in 2015, which directed all government agencies to “develop strategies for applying behavioral science insights to programs and, where possible, rigorously test and evaluate the impact of these insights.” OES staff work with federal agencies to scope, design, implement, and test a behavioral intervention. Also in 2015, the UK-based Behavioural Insights Team (BIT) opened its North American office (BIT-NA), aimed at supporting local governments to use behavioral science. Mainly through the What Works Cities initiative, BIT-NA has collaborated with over 50 U.S. cities to implement behavioral experiments within local government agencies.
The two units have shared goals: to use behavioral science to improve the delivery of government services through rigorous RCTs, and to build the capacity of government agencies to use RCTs. In interviews with the leadership of both units, both teams noted that their primary goal is to measure what changes will make a measurable difference on key policy outcomes. The vast majority of their projects are similar in scope and methodology. They are almost exclusively RCTs, with randomization at the individual level; they often involve a low-cost nudge using a mode of communication that does not require in-person interaction (such as a letter or email); and they aim to either increase or reduce a behavioral variable, such as increasing take-up of a vaccine, or reducing missed appointments. Furthermore, the two units embrace practices of good trial design and research transparency. All trial protocols, including power calculations, and results are documented in internal registries irrespective of the results. All data analyses go through multiple rounds of code review. Moreover, OES has taken the additional step of making all trial results public, and recently, posting pre-analysis plans for every project.
These units are central to the process of taking nudge RCTs to scale in a meaningful way. In this case, scaling means two things. First, “scaling” occurs in the numerical sense, because government agencies often have access to larger samples than the typical academic study, and so the process of scaling nudge interventions tells us how an intervention fares when the sample is an order of magnitude larger than the original academic trial. Second, the selection of trials that Nudge Units conduct also tells us something about which academic interventions are politically, socially, and financially feasible for a government agency to implement—“scalable” in the practical sense.
Figure 1(a)–(b) shows an intervention from OES aimed to increase service-member savings plan re-enrollment. The control group received the status quo email (Figure 1(a)), while the treatment group received a simplified, personalized email with loss framing and clear action steps (Figure 1(b)). The outcome is measured as the rate of savings plan re-enrollment. Figure A.2(a) presents two additional examples of OES interventions, focused respectively on increasing vaccine uptake among veterans and improving employment services for UI claimants in Oregon. Figure A.2(b) presents a nudge intervention run by BIT-NA encouraging utilities customers to enroll in AutoPay and e-bill.

Figures 1(a) and 1(b) present an example of a nudge intervention from OES. This trial aims to increase service-member savings plan re-enrollment. The control group received the status quo email (reproduced in Figure 1(a)), while the treatment group received a simplified, personalized reminder email with loss framing and clear action steps (reproduced in Figure 1(b)). The outcome in this trial is measured as savings plan re-enrollment rates.
Sample of Trials
As Figure 2(a) shows, from the universe of 165 trials conducted by the units, we limit our sample to projects with a randomized controlled trial in the field, removing 13 trials. We then remove 15 trials without a clear “control” group, such as horse races between two behaviorally-informed interventions. We then remove 3 trials with monetary incentives, and limit the scope further to trials with a primary outcome that is binary, removing 8 trials. We also remove trials where the “treatment” is changing the default, since they are the rare exception among Nudge Unit interventions in our sample (only two treatment arms of one trial), and substantively different.
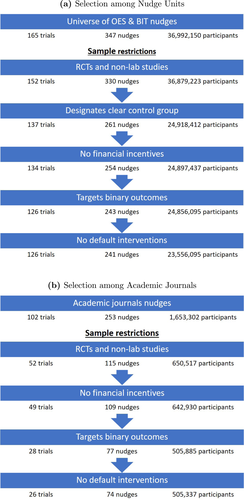
This figure shows the number of trials, treatments, and participants remaining after each sample restriction.
Our final sample consists of 126 randomized trials that include 241 nudges and involve 23.5 million participants. For each trial, we observe the sample size in the control and treatment groups and the take-up of the outcome variable in each group, for example, the vaccination rate or enrollment in a savings plan. Whenever there are multiple dependent variables specified in the pre-analysis or trial report, we take the primary binary variable specified. We do not observe the individual-level micro data, though, arguably, given the 0–1 dependent variable, this does not lead to much loss of information. We discuss additional details in Appendix A.1 of the Supplemental Material (DellaVigna and Linos (2022)). To our knowledge, only 16 of these trials (listed in Table A.I(a)) have been written or published as academic papers; we discuss the results for this subset in Appendix A.2 of the Supplemental Material.
2.2 Trials in Academic Journals
Sample of Trials
We aim to find broadly comparable published nudge studies, without hand-picking individual papers. In a recent meta-analysis, Hummel and Maedche (2019) selected 100 papers screened out of over 2000 initial papers identified as having “nudge” or “nudging” in the title, abstract, or keyword. We report their selection criteria in Appendix A.3 of the Supplemental Material. The papers cover a number of disciplinary fields, including economics, public health, decision-making, and marketing. A second meta-analysis that covers several areas is Benartzi et al. (2017), which does a cost-benefit comparison of a few behavioral interventions to traditional incentive-based interventions. Hummel and Maedche (2019) reviewed 9 other meta-analyses, which we do not include because they focus exclusively on one policy area or topic. We thus combine the behavioral trials in Hummel and Maedche (2019) and in Benartzi et al. (2017), for a total of 102 trials.1
We apply parallel restrictions as for the Nudge Units sample, as Figure 2(b) shows. First, we exclude lab experiments, survey experiments with hypothetical choices, and non-RCTs (e.g., changes in a cafeteria menu over time, with no randomization), for a remaining total of 52 studies. Second, we exclude treatments with financial incentives, removing 3 trials. Third, we require binary dependent variables, dropping 21 trials. Finally, we exclude default interventions, dropping just 2 trials. This leaves a final sample of 26 RCTs, listed in Table A.I(b,) including 74 nudge treatments with 505,337 participants. For each paper, we code the sample sizes and the outcomes in the control and the nudge treatment groups, as well as features of the interventions.
2.3 Comparison of Two Samples and Author Survey
Categories of Nudges
We categorize each nudge by its policy area, communication channel, and behavioral mechanisms, as highlighted in Tables I and A.II, and Figure A.3.
A typical “revenue & debt” trial involves nudging people to pay fines after being delinquent on a utility payment, while an example of a “benefits & programs” trial encourages individuals to enroll in a government program, such as pre- and post-natal care for Medicaid-eligible mothers. The “workforce and education” category includes prompting job-seekers to plan their job search strategy. One “health” intervention urges people to get vaccinated or sign up for a doctor's appointment. A “registration” nudge asks business owners to register their business online as opposed to in-person, and a “community engagement” intervention motivates community members to attend a local town hall meeting. Compared to the Nudge Units sample, the Academic Journals sample has a larger share of trials about health outcomes and environmental choices and fewer about revenue and debt, benefits, and workforce and education.
The medium of communication with the treatment group tends to be through email, letter, or postcard in the Nudge Units sample, as opposed to in-person interactions, which are common in the Academic Journals sample. In 61% of the Nudge Unit trials and in 43% of the Academic Journal trials, the researchers do not send the control group any communication within the field experiment (although the control group may still be receiving communication about the specific program through other means).
We also code the behavioral mechanisms, with details in Appendix A.4 of the Supplemental Material. In the Nudge Units sample, the most frequent mechanisms include: simplification of a letter or notice; drawing on personal motivation such as personalizing the communication or using loss aversion to motivate action; using implementation intentions or planning prompts; exploiting social cues or building social norms into the communication; adjusting framing or formatting of existing communication; and nudging people towards an active choice or making some choices more salient. In the Academic Journals sample, there are fewer cases that explicitly feature simplification and information as one of the main levers, and more cases that feature personal motivation and social cues, changes in framing and formatting, or choice re-design (e.g., active choice).
Features of Trials
While Table I categorizes the nudges on several descriptive dimensions, Table II summarizes broader features of the trial, such as the degree of academic involvement, the difficulty of changing the selected behavior, trial design decisions, and features of implementation. We draw on a combination of information from the papers and trial reports, as well as from a short survey of authors and of the Nudge Unit leadership teams. We present details of the survey in Appendix A.5 of the Supplemental Material.
|
Nudge Units |
Academic Journals |
|||||
|---|---|---|---|---|---|---|
|
Freq. (%) |
Nudges (Trials) |
ATE (pp.) |
Freq. (%) |
Nudges (Trials) |
ATE (pp.) |
|
|
Date |
||||||
|
Early* |
46.06 |
111 (49) |
1.88 |
48.65 |
36 (14) |
7.10 |
|
Recent* |
53.94 |
130 (77) |
0.97 |
51.35 |
38 (12) |
10.18 |
|
Policy area |
||||||
|
Revenue & debt |
29.05 |
70 (30) |
2.43 |
17.57 |
13 (4) |
3.60 |
|
Benefits & programs |
22.41 |
54 (26) |
0.89 |
10.81 |
8 (3) |
14.15 |
|
Workforce & education |
18.67 |
45 (24) |
0.49 |
9.46 |
7 (2) |
2.56 |
|
Health |
12.45 |
30 (18) |
0.73 |
28.38 |
21 (9) |
8.98 |
|
Registration & regulation compliance |
8.71 |
21 (16) |
2.18 |
12.16 |
9 (2) |
3.16 |
|
Community engagement |
7.88 |
19 (10) |
0.74 |
4.05 |
3 (2) |
2.80 |
|
Environment |
0.83 |
2 (2) |
6.83 |
13.51 |
10 (3) |
22.95 |
|
Consumer behavior |
0 |
0 (0) |
– |
4.05 |
3 (1) |
3.19 |
|
Medium of communication |
||||||
|
|
39.83 |
96 (47) |
1.09 |
12.16 |
9 (6) |
3.75 |
|
Physical letter |
29.88 |
72 (44) |
2.41 |
16.22 |
12 (4) |
1.67 |
|
Postcard |
21.58 |
52 (22) |
0.82 |
6.76 |
5 (1) |
10.46 |
|
Website |
2.90 |
7 (4) |
−0.04 |
12.16 |
9 (3) |
6.24 |
|
In person |
0.83 |
2 (2) |
3.05 |
28.38 |
21 (5) |
14.82 |
|
Other |
10.37 |
25 (15) |
1.30 |
24.32 |
18 (9) |
9.38 |
|
Control group receives |
||||||
|
No communication |
61.41 |
148 (66) |
1.42 |
43.24 |
32 (9) |
10.91 |
|
Some communication |
38.59 |
93 (62) |
1.34 |
56.76 |
42 (17) |
6.99 |
|
Mechanism |
||||||
|
Simplification & information |
58.51 |
141 (73) |
1.19 |
5.41 |
4 (2) |
16.34 |
|
Personal motivation |
57.26 |
138 (76) |
1.77 |
32.43 |
24 (9) |
9.59 |
|
Reminders & planning prompts |
31.54 |
76 (49) |
2.54 |
35.14 |
26 (11) |
5.02 |
|
Social cues |
36.51 |
88 (58) |
0.87 |
21.62 |
16 (7) |
13.81 |
|
Framing & formatting |
31.95 |
77 (47) |
1.38 |
32.43 |
24 (8) |
13.53 |
|
Choice design |
6.22 |
15 (12) |
7.01 |
20.27 |
15 (9) |
8.85 |
|
Total |
100 |
241 (126) |
1.39 |
100 |
74 (26) |
8.68 |
- Note: This table shows the number of nudges and trials in each category, and the average treatment effect within each category. Frequencies for Medium and Mechanism are not mutually exclusive and frequencies may not sum to 1.
- * Early refers to trials implemented between 2015 and 2016 for Nudge Units, and to papers published in 2014 or before for Academic Journals. Recent refers to trials and papers after these dates.
|
Academic Journals |
Nudge Units |
||||
|---|---|---|---|---|---|
|
Mean [Std. Dev.] |
Mean [Std. Dev.; p-Value of Difference From Column 1] |
||||
|
All |
BIT |
OES |
Academic-Affiliated OES |
||
|
(1) |
(2) |
(3) |
(4) |
(5) |
|
|
Academic faculty involvement |
100% |
19% |
0% |
50% |
100% |
|
Outcome features |
|||||
|
Control group take-up (%) |
26.0 |
17.3 |
15.6 |
19.5 |
26.4 |
|
[19.9] |
[23.2; p = 0.10] |
[23.9; p = 0.05] |
[22.2; p = 0.29] |
[24.0; p = 0.94] |
|
|
Outcome time-frame (days) |
68.7 |
60.2 |
38.6 |
101.7 |
141.5 |
|
[91.7] |
[74.5; p = 0.59] |
[38.0; p = 0.11] |
[104.9; p = 0.25] |
[110.9; p = 0.04] |
|
|
Trial design |
|||||
|
Mechanisms per treatment arm |
1.5 |
2.2 |
2.0 |
2.5 |
2.3 |
|
[0.7] |
[1.0; p = 0.00] |
[1.0; p = 0.00] |
[0.9; p = 0.00] |
[0.9; p = 0.00] |
|
|
Treatment arms per trial |
2.8 |
1.9 |
1.7 |
2.3 |
1.9 |
|
[2.1] |
[1.7; p = 0.03] |
[1.0; p = 0.01] |
[2.5; p = 0.31] |
[1.5; p = 0.06] |
|
|
Minimum detectable effect (pp.) |
8.2 |
1.7 |
2.2 |
1.2 |
1.7 |
|
[6.4] |
[2.2; p = 0.00] |
[2.6; p = 0.00] |
[1.6; p = 0.00] |
[2.2; p = 0.00] |
|
|
Institutional constraints rating (1–5) |
4.0 |
3.0 |
3.0 |
3.0 |
2.8 |
|
[0.9] |
[0.6; p = 0.00] |
[0.5; p = 0.00] |
[0.7; p = 0.01] |
[1.3; p = 0.00] |
|
|
Planning and implementation |
|||||
|
Total duration (months) |
21.3 |
11.1 |
8.6 |
15.0 |
17.0 |
|
[16.1] |
[3.9; p = 0.00] |
[1.3; p = 0.00] |
[3.3; p = 0.09] |
[8.3; p = 0.24] |
|
|
Planning (including IRB) |
6.6 |
4.6 |
4.0 |
5.6 |
5.1 |
|
[6.1] |
[2.3; p = 0.17] |
[1.1; p = 0.06] |
[3.4; p = 0.61] |
[2.5; p = 0.28] |
|
|
Intervention and data collection |
6.7 |
4.5 |
3.4 |
6.2 |
6.5 |
|
[7.1] |
[2.0; p = 0.16] |
[1.2; p = 0.03] |
[1.8; p = 0.77] |
[2.3; p = 0.91] |
|
|
Data analysis and write-up |
7.8 |
2.0 |
1.3 |
3.2 |
3.9 |
|
[7.0] |
[1.2; p = 0.00] |
[0.5; p = 0.00] |
[1.1; p = 0.00] |
[2.9; p = 0.01] |
|
|
Personnel full-time equivalent months |
14.9 |
5.8 |
4.3 |
8.3 |
6.2 |
|
[18.1] |
[4.9; p = 0.03] |
[2.8; p = 0.01] |
[6.9; p = 0.17] |
[2.8; p = 0.02] |
|
|
Number of survey responses |
25 |
13* |
8* |
5* |
24 |
|
Number of trials |
26 |
126 |
78 |
48 |
24 |
- Note: Data on the institutional constraints rating, duration, and personnel FTE months were collected from a survey of the researchers involved in the trials (see text and Section A.5 of the Supplemental Material for details). Outcome duration is capped at 360 days, which only affects one trial in each of the Academic Journal and Nudge Unit samples.
- * In columns 2 to 4, the number of survey responses corresponds to the number of Nudge Unit staff members in leadership roles whom we surveyed.
The first feature is the degree of academic involvement. While all studies in the Academic Journals sample (Column 1) are led by academics, there is significant heterogeneity in the Nudge Units sample (Column 2). BIT North America employs behavioral scientists and other researchers directly, and so BIT-NA trials (Column 3) are designed by internal staff in collaboration with government partners. In comparison, OES interventions (Column 4) are often designed in coordination with academic fellows, PhD students, academics on sabbaticals at OES, and university faculty who collaborate on individual trials. The 50% of OES trials that record a full-time faculty member as lead or affiliate (Column 5) are therefore more similar in this respect to the Academic Journal trials, and we will consider them separately.
Second, we consider the difficulty of moving a behavioral outcome. Differences in treatment effects could arise if trials in either the Nudge Units or the Academic Journals sample tackle behaviors that are harder to shift. While we do not observe this directly (e.g., through a measure of elasticity), we lean on two proxies. A first proxy is the control group take-up, given that outcomes with very low take-up may be especially hard to shift. The average control group take-up is 26.0% in the Academic Journals sample, and 17.3% in the Nudge Units sample, a difference that is only marginally statistically significant, suggesting that the two samples are reasonably comparable in this dimension. As a second proxy, we measure the time horizon of the outcome variable, that is, the number of days between the receipt of the intervention and the recorded behavior. For example, if the outcome is whether the recipient clicks a link in the email on the day it is sent, we record a 1-day time frame, and if the outcome is re-enrollment in college six months after the receipt of a letter, we record 180 days. Short-run responses are presumably easier to affect with a nudge. The OES interventions have a longer time frame than the Academic Journals trials, though the difference is not statistically significant
Third, we consider differences in trial design. Trials in the Academic Journals sample have fewer behavioral mechanisms per treatment arm: an average of 1.5, compared to an average of 2.2 in Nudge Unit trials (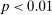 ). At the same time, the average trial in the Academic Journals sample evaluates more treatment arms, 2.8 versus 1.9. The typical treatment arm in the Academic Journals sample is also less statistically powered with a larger MDE, a point we revisit below. Trial design may also be affected by institutional constraints, where the implemented design may differ from the ideal design initially envisioned. We therefore asked survey respondents to indicate on a Likert scale from 1 (vastly different) to 5 (exactly the same) how close the final intervention was to the ideal one they had hoped to implement. We find a clear difference: while most Academic Journal RCTs have a rating of 4 or 5, the BIT or OES interventions are typically rated 3, indicating a stronger impact of institutional constraints.
). At the same time, the average trial in the Academic Journals sample evaluates more treatment arms, 2.8 versus 1.9. The typical treatment arm in the Academic Journals sample is also less statistically powered with a larger MDE, a point we revisit below. Trial design may also be affected by institutional constraints, where the implemented design may differ from the ideal design initially envisioned. We therefore asked survey respondents to indicate on a Likert scale from 1 (vastly different) to 5 (exactly the same) how close the final intervention was to the ideal one they had hoped to implement. We find a clear difference: while most Academic Journal RCTs have a rating of 4 or 5, the BIT or OES interventions are typically rated 3, indicating a stronger impact of institutional constraints.
A fourth trial feature is decision-making around trial planning and implementation. The Academic Journal interventions may involve a more extensive planning and design process, which may impact the effect size. We thus asked authors of the papers in the Academic Journals sample to indicate the approximate number of months of total duration of the RCT, as well as the months of planning, of intervention and data collection, and of data analysis and write-up. We also asked for the full-time staff or PI months spent on a project. We asked parallel questions to the BIT and OES staff, and we contacted the academic fellows for the Academic-Affiliated OES trials. As Table II shows, the answers are closer than one may have thought. The average duration of the planning and intervention periods is similar for the Academic Journals sample and the OES sample (11–13 months), and somewhat shorter for the BIT sample (around 7 months). The average personnel time is higher for the Academic Journals sample than for the Nudge Units sample (14.9 months vs. 5.8 months), but this difference is amplified by a couple of outliers in the Academic Journals sample: the difference in the medians is quite modest (9 vs. 6 months). The data analysis and write-up period is shorter for the Nudge Unit interventions, given that most are not written up as academic papers.
Overall, we identified a few differences in trial features between the Academic Journals sample and the Nudge Units sample. The Nudge Unit interventions are less likely to be led by academics, tend to face higher institutional constraints, and involve fewer personnel. These features (or at least the first two) seem typical of an “at scale” intervention. Nudge Unit trials also include fewer arms per trial, a larger sample, and more behavioral mechanisms per arm. This may suggest a different objective function, where more emphasis is placed on moving the policy outcome and less on disentangling the exact mechanism. We return to these differences in Section 4.2.
3 Impact of Nudges
We present the unweighted impact of the nudges in the two samples.
Academic Journals
As Column 1 in Table III shows, the average treatment effect for the 74 nudges in 26 trials in the Academic Journals sample is 8.68 pp. (s.e. = 2.47), a large increase relative to the average control group take-up of 25.97 percent.
|
Academic Journals |
Nudge Units |
||||
|---|---|---|---|---|---|
|
All |
BIT |
OES |
Academic-Affiliated OES |
||
|
(1) |
(2) |
(3) |
(4) |
(5) |
|
|
Average treatment effect (pp.) |
8.682 |
1.390 |
1.698 |
1.023 |
0.978 |
|
(2.467) |
(0.304) |
(0.528) |
(0.206) |
(0.408) |
|
|
Nudges |
74 |
241 |
131 |
110 |
45 |
|
Trials |
26 |
126 |
78 |
48 |
24 |
|
Observations |
505,337 |
23,556,095 |
2,008,289 |
21,547,806 |
8,923,186 |
|
Average control group take-up (%) |
25.97 |
17.33 |
15.60 |
19.47 |
26.45 |
|
Distribution of treatment effects |
|||||
|
25th percentile |
1.05 |
0.06 |
0.00 |
0.15 |
0.10 |
|
50th percentile |
4.12 |
0.50 |
0.40 |
0.60 |
0.42 |
|
75th percentile |
12.00 |
1.40 |
1.64 |
1.22 |
1.20 |
- Note: This table shows the average treatment effect of nudges. Standard errors clustered by trial are shown in parentheses. pp. refers to percentage point.
Figure 3(a) shows the estimated nudge-by-nudge treatment effect together with 95% confidence intervals, plotted against the take-up in the control group. The figure shows that there is substantial heterogeneity in the estimated impact, but nearly all the estimated effects are positive, with some very large point estimates. The plot also shows suggestive evidence that the treatment effect seems to be highest in settings in which the control take-up is in the 20%–60% range.
This figure plots the treatment effect relative to control group take-up for each nudge with the quadratic fit. Some of the outliers are labeled for context. Error bars show 95% confidence intervals.
Nudge Units
Column 2 in Table III shows the unweighted average impact of the 241 nudge treatments in the 126 Nudge Unit trials. The estimated impact is 1.39 pp. (s.e. = 0.30), compared to an average control take-up of 17.33 pp. This estimated treatment effect is still sizable and precisely estimated to be different from zero, but is one-sixth the size of the point estimate in Column 1 for the Academic Journal papers.
Figure 3(b) shows the estimated treatment effect plotted against the control group take-up. The treatment effects are mostly concentrated between −2pp. and +8pp., with a couple of outliers, both positive and negative. Among the positive outliers are treatments with reminders for a sewer bill payment and emails prompting online AutoPay registration for city bills. One trial that produced a negative effect is a redesign of a website aimed to encourage applications to a city board.
The comparison between Figures 3(a) and 3(b), which are set on the same x- and y-axis scale, visually demonstrates two key differences between published academic papers and Nudge Unit interventions. The first, which we already stressed, is the difference in estimated treatment effects, which are generally larger, and more dispersed, in the Academic Journals sample. But another equally striking difference is the statistical precision of the estimates: the confidence intervals are much tighter for the Nudge Unit studies, which are typically run with a much larger sample.
Robustness
Tables A.III(a)–(b) and A.IV(a)–(b) display additional information on the treatment effects. As Table A.III(a) shows, the difference in treatment effects between the two samples is parallel in log odds terms (which can be approximately interpreted as percent effects): 0.50 log points (s.e. = 0.11) for the Academic Journals sample, compared to 0.27 log points (s.e. = 0.07) in the Nudge Units sample. The impact in log odds point is larger than the impact that one would have computed in percent terms from Table III, given that treatment effects with lower control take-up are larger in log odds. Table A.III(b) shows that the average treatment effect for the Nudge Unit trials that have been published in academic journals is 0.97 pp. (s.e. = 0.23), similar to the entire Nudge Units sample, albeit slightly smaller (see Appendix A.2 of the Supplemental Material for details). Table A.IV(a) displays the number of treatments that are statistically significant, split by the sign of the effects.
Table A.IV(b) shows that the estimates in both samples are slightly larger if we include the default interventions, with the caveat that these are just 3 arms in the Academic Journals sample and 2 arms in the Nudge Units sample. Next, while we cannot fully capture the “importance” of the outcome variable in each nudge, in Table A.IV(b) we consider the subset of nudges with “high-priority” outcomes, as rated by a team of undergraduates, which aims to capture variables closer to the policy of interest (e.g., measuring actual vaccination rates as opposed to appointments for a vaccination). The estimated nudge impact for this subset is somewhat lower for the Academic Journal nudges at 6.5 pp., but at least as high for the Nudge Unit ones, at 1.6 pp. We then consider the subset of Nudge Unit interventions that are low-cost, that is, either relying on email contact or on existing means of communication with the control group. We replicate the same effect size. Finally, estimates weighted by citations for the Academic Journals sample yield slightly lower point estimates.
4 Nudge Units versus Academic Journal Nudges
We sketch a model of decision-making around nudge experimentation, highlighting features of experimental design (as in, e.g., Frankel and Kasy (forthcoming), and Azevedo et al. (forthcoming)), as well as selective publication (as in Andrews and Kasy (2019)).
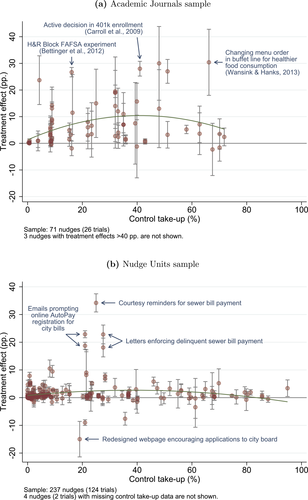
We assume that researchers and nudge units alike design experiments aiming to provide evidence on a particular treatment, in our case a nudge. Our model makes three key sets of assumptions, capturing the trial design, underlying effect size, and selective publication. First, both academic researchers and Nudge Units design an experiment to detect an effect size d with 0.80 statistical power. Second, there is a true effect size of the nudge intervention β distributed with a random effect. Third, results that are not statistically significant are published by academic researchers with some probability 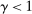 , while results that are statistically significant are published with probability 1.
, while results that are statistically significant are published with probability 1.
We propose that the observed differences between our two samples can be largely explained by differences in those three components, d, β, and γ. First, the samples differ in the expected effect size d, with 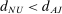 , resulting in differences in statistical power and number of treatment arms. Second, they differ in the average effectiveness of the nudges, with
, resulting in differences in statistical power and number of treatment arms. Second, they differ in the average effectiveness of the nudges, with 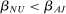 , with some of the differences explained by different characteristics X, that is,
, with some of the differences explained by different characteristics X, that is, 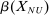 versus
versus 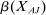 . Third, they differ in selective publication, that is,
. Third, they differ in selective publication, that is, 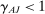 , but not for (this sample of) Nudge Units (i.e.,
, but not for (this sample of) Nudge Units (i.e., 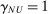 ). We discuss these differences in turn below, as well as a few possible alternative explanations of the findings.
). We discuss these differences in turn below, as well as a few possible alternative explanations of the findings.
4.1 Experimental Design
Models of optimal experimental design typically center on the goal of collecting evidence on the effectiveness of an intervention. Frankel and Kasy (forthcoming), for example, modeled a researcher who decides the optimal sample size for a treatment (and whether to run an experiment) as a function of the prior, the cost of collecting evidence, and other factors. Azevedo et al. (forthcoming) discussed the trade-off for a given sample between running fewer treatment arms with a larger sample, or more treatment arms with less power per arm, as a function of the fatness of the tails in the distribution of treatment effects.
For simplicity, we assume a simple, rule-of-thumb experimentation rule, based on the Cohen (1965) convention, that researchers aim for statistical power of 0.80, given an expected effect size d for a treatment arm. This is a descriptive model and we do not see it as normative, given the need to take into account the cost of collecting observations, the priors, etc. Still, aiming for 0.80 power is widespread. We collected the power calculations for all pre-registrations on the AEA Registry, the largest data set we know with systematic power calculations. Among the 267 that were registered prior to the start of their intervention and provided a minimum detectable effect with a targeted level of power, 240 use a power target of 0.80 (Table A.V). The senior leadership of the Nudge Units also reported to us that in their power calculations, 80% power was used as the default.
In our setting, given the binary dependent variable, the implicit MDE d for 80 percent power can be computed using just the control take-up and the sample sizes in the control and treatment groups, all of which we observe.2 As Figure 4(a) shows, the Academic Journals sample has a median MDE 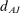 of 6.30 pp. and an average MDE of 8.18 pp.; most of these studies are powered to detect only quite large treatment effects. In contrast, the Nudge Units sample has a median MDE
of 6.30 pp. and an average MDE of 8.18 pp.; most of these studies are powered to detect only quite large treatment effects. In contrast, the Nudge Units sample has a median MDE 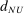 of 0.80 pp. and an average MDE of 1.73 pp. Thus, the statistical power is an order of magnitude larger in the Nudge Units sample than in the Academic Journals sample. Figure A.4(a) shows the corresponding difference in sample size per treatment arm: a median of 484 in the Academic Journals sample versus 10,006 in the Nudge Units sample.
of 0.80 pp. and an average MDE of 1.73 pp. Thus, the statistical power is an order of magnitude larger in the Nudge Units sample than in the Academic Journals sample. Figure A.4(a) shows the corresponding difference in sample size per treatment arm: a median of 484 in the Academic Journals sample versus 10,006 in the Nudge Units sample.
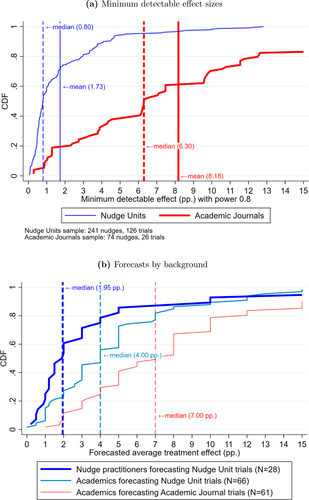
Figure 4(a) plots the CDF of the minimum detectable effects (MDE), or the size of the treatment effect that each treatment arm is powered to statistically detect 80% of the time given the control group take-up rate and the sample size. For 4 nudges (2 trials) in the Nudge Units sample that are missing control take-up data, the MDE is calculated assuming a conservative control group take-up of 50%. Control take-up is bounded below at 1% when calculating MDE. Figure 4(b) shows various distributions of forecasts made by Nudge Unit practitioners and academics (university faculty and post-docs) on the treatment effect of nudges.
Is it plausible that the Nudge Units were expecting effect sizes of, on average, around 1 pp., while academics were expecting effect sizes closer to 8 pp.? While we did not ask this question exactly, we surveyed academic researchers and nudge practitioners about their expectation for the findings of our study, as in DellaVigna and Pope (2018) and along lines outlined by DellaVigna, Pope, and Vivalt (2019). Specifically, we created a 10-minute survey eliciting forecasts using a convenience sample through email lists and Twitter ( ). The survey explained the methodology of our analysis, described the two samples, showed participants three nudge interventions randomly drawn out of 14 exemplars, and asked for predictions (in percentage point units) of: (a) the average effect size for the Nudge Units sample; and (b) the average effect size for the Academic Journals sample. Among the respondents, 28 self-identify as Nudge Unit practitioners, and 66 as academic researchers. We focus on the predictions of these two samples, with more detail in Appendix A.6 of the Supplemental Material.
). The survey explained the methodology of our analysis, described the two samples, showed participants three nudge interventions randomly drawn out of 14 exemplars, and asked for predictions (in percentage point units) of: (a) the average effect size for the Nudge Units sample; and (b) the average effect size for the Academic Journals sample. Among the respondents, 28 self-identify as Nudge Unit practitioners, and 66 as academic researchers. We focus on the predictions of these two samples, with more detail in Appendix A.6 of the Supplemental Material.
In Figure 4(b), the blue continuous line indicates the distribution of forecasts by (self-identified) nudge practitioners about the effect size finding for the Nudge Unit interventions. The median nudge practitioner expects an average impact of 1.95 pp., which is remarkably in line not only with our findings, but also with the calculation of the projected effect size 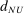 implied by the observed sample size.
implied by the observed sample size.
Do researchers expect a larger effect size? Figure 4(b) shows two predictions by academics: for the Nudge Units sample, and for the Academic Journals sample. The researchers significantly overestimate the findings for the Nudge Units sample: the median academic expects an effect size of 4.0 pp. As for the Academic Journals sample, the median academic expects an effect size of 7.0 pp., close to the observed average effect size in this sample and also close to the effect size  implied by the power calculations.
implied by the power calculations.
Put differently, when asked about the same sample, and given the same information, academic researchers expect a larger effect size than nudge practitioners. We take these results as suggestive of the fact that academics' expectations about the effect size of their own trial may shape their trial design, and can at least partially explain differences in statistical power between the two samples.3 We acknowledge that, while we attribute this difference in MDE between the two samples to different expected effect sizes, it may also be due to different views of what is a policy-relevant or publishable effect size.
A reasonable objection is that sample sizes, to a large extent, may be fixed, leaving experimenters with little choice (other than deciding whether to run the experiment altogether). One decision, though, that they clearly have is how many treatment arms to run: the more arms, the lower the statistical power per arm. If researchers actively aim for a higher MDE d (at the cost of lower statistical power), we would observe it in this dimension. As Figure A.4(b) and Table II show, the number of arms is significantly larger in the Academic Journals sample than in the Nudge Units sample, despite academic researchers having (on average) a smaller sample size to start with.
Figure A.4(c) and Table II document an additional trial design feature. Academic researchers have fewer behavioral mechanisms per arm (as coded in our categorization). Plausibly, they are more concerned with establishing a mechanism for the potential findings, thus requiring multiple arms, each with a different mechanism. Nudge Units, instead, may be mostly focused on studying combinations of mechanisms to yield higher policy impact. Nudge Unit leadership confirmed that this was their primary concern when designing trials, and as one interviewee noted, “You only get to add more treatment arms if you can show with certainty that you are powered well enough to detect an effect between one treatment and control.”
Overall, we find a major difference in trial design: much larger sample sizes per treatment arm in the Nudge Units sample. We propose a simple explanation: academic researchers expect or target larger effect sizes and therefore are comfortable with a larger MDE. While we cannot prove this directly, we document that this difference in sample size is in line with differences in forecasts of effect sizes in survey predictions. Below, in Section 4.4, we consider the implications of these differences in statistical power.
4.2 Differences in Nudge and Trial Features
A second potential difference between the two samples is in the average effect size β. We now examine a number of observable features of the trials and of the nudges that may explain why the two samples could have a different β.
4.2.1 Academic Involvement
As we documented in Table II, while BIT trials are typically designed by internal staff, the OES interventions are typically designed in collaboration with academic fellows. The two sets of trials also differ in other dimensions: the OES trials have a longer planning and intervention duration and higher personnel FTE involvement.
Thus, in Table III we revisit the effect size separately for the two Nudge Units. The average effect size for BIT interventions (1.70 pp., s.e. = 0.53, Column 3) is similar to, and in fact slightly larger than, the effect size for the OES interventions (1.02 pp., s.e. = 0.21, Column 4). Furthermore, for the 24 OES trials with explicit academic involvement, the point estimate is essentially the same as for the overall OES sample (0.98 pp., s.e. = 0.41, Column 5). Thus, differences in academic involvement and in the setup of the two Nudge Units per se do not appear to explain our findings.
4.2.2 Categories of Nudges
Next, we separate the impact of nudge treatments by category. As Table I shows, the average treatment effect (ATE) varies substantially across interventions: for example, in-person interventions or nudges on the environment policy area have larger effect sizes. Both types of interventions are more common in the Academic Journals sample, and could thus contribute to the different effect sizes.
In Column 2 of Table IV, we thus include in the effect size specification the nudge features controls in Table I, as well as two additional variables: a quadratic of the average take-up in the control group, which could proxy for the difficulty in affecting a behavior (e.g., the persuasion rate), and the outcome time frame, which could capture harder-to-affect longer-run outcomes.4 The point estimate is larger for studies focused on the environment, for cases with no previous communication, and for cases in which the contact takes place in-person, as opposed to via email or mail; also framing and formatting and especially choice design appear to have the largest effects.5
|
Full Sample |
Academic-Affiliated Only |
||||||
|---|---|---|---|---|---|---|---|
|
Dep. Var.: Treatment Effect (pp.) |
(1) |
(2) |
(3) |
(4) |
(5) |
(6) |
(7) |
|
Constant |
1.390 |
4.316 |
1.031 |
2.878 |
0.978 |
4.117 |
1.970 |
|
(0.304) |
(2.152) |
(0.342) |
(2.008) |
(0.405) |
(4.884) |
(4.405) |
|
|
Omitted group: Nudge Units |
|||||||
|
Academic Journals |
7.292 |
2.381 |
−0.915 |
0.030 |
7.704 |
6.122 |
−1.778 |
|
(2.450) |
(1.605) |
(1.930) |
(1.956) |
(2.487) |
(1.972) |
(2.693) |
|
|
Publication bias controls (Egger's test) |
|||||||
|
Minimum detectable effect (MDE) |
0.207 |
0.233 |
−0.084 |
||||
|
(0.247) |
(0.273) |
(0.168) |
|||||
|
Academic Journals×MDE |
0.840 |
0.342 |
1.076 |
||||
|
(0.386) |
(0.375) |
(0.372) |
|||||
|
Nudge categories |
|||||||
|
Policy area |
|||||||
|
Benefits & programs |
−0.266 |
−0.267 |
|||||
|
(1.006) |
(0.927) |
||||||
|
Workforce & education |
−2.319 |
−2.474 |
|||||
|
(1.003) |
(0.940) |
||||||
|
Health |
−0.876 |
−1.812 |
|||||
|
(1.555) |
(1.469) |
||||||
|
Registrations & regulation compliance |
−1.027 |
−1.014 |
|||||
|
(1.358) |
(1.349) |
||||||
|
Community engagement |
−1.625 |
−1.457 |
|||||
|
(1.595) |
(1.289) |
||||||
|
Environment |
9.287 |
5.491 |
|||||
|
(4.961) |
(4.872) |
||||||
|
Consumer behavior |
−10.959 |
−7.402 |
|||||
|
(3.670) |
(3.578) |
||||||
|
Medium of communication |
|||||||
|
|
−1.883 |
−1.537 |
|||||
|
(1.429) |
(1.392) |
||||||
|
Physical letter |
−0.844 |
−0.308 |
|||||
|
(1.204) |
(1.153) |
||||||
|
Postcard |
0.125 |
−0.019 |
|||||
|
(1.514) |
(1.360) |
||||||
|
Website |
−2.236 |
−1.513 |
|||||
|
(3.180) |
(2.745) |
||||||
|
In person |
7.210 |
5.373 |
|||||
|
(3.146) |
(3.417) |
||||||
|
Other |
−0.438 |
−0.185 |
|||||
|
(1.727) |
(1.678) |
||||||
|
Control group receives |
|||||||
|
Some communication |
−1.223 |
−1.225 |
|||||
|
(0.953) |
(0.892) |
||||||
|
Mechanism |
|||||||
|
Simplification & information |
0.878 |
0.872 |
|||||
|
(1.119) |
(1.209) |
||||||
|
Personal motivation |
−0.502 |
−0.330 |
|||||
|
(0.856) |
(0.916) |
||||||
|
Reminders & planning prompts |
0.349 |
0.789 |
|||||
|
(0.840) |
(0.785) |
||||||
|
Social cues |
0.040 |
0.233 |
|||||
|
(0.959) |
(0.920) |
||||||
|
Framing & formatting |
1.245 |
0.998 |
|||||
|
(0.934) |
(0.912) |
||||||
|
Choice design |
6.226 |
5.528 |
|||||
|
(2.356) |
(2.315) |
||||||
|
Trial features |
|||||||
|
Control take-up (%) |
0.108 |
0.046 |
|||||
|
(0.059) |
(0.056) |
||||||
|
Control take-up2 |
−0.001 |
−0.001 |
|||||
|
(0.001) |
(0.001) |
||||||
|
Log(outcome time-frame days) |
−0.692 |
−0.309 |
|||||
|
(0.409) |
(0.367) |
||||||
|
Ideal nudge implemented rating (1–5) |
0.979 |
0.467 |
|||||
|
(1.291) |
(0.731) |
||||||
|
Log(personnel FTE months) |
0.671 |
0.902 |
|||||
|
(0.857) |
(0.711) |
||||||
|
Log(planning & implementation months) |
−2.721 |
−1.419 |
|||||
|
(1.562) |
(1.548) |
||||||
|
Nudges |
315 |
315 |
315 |
315 |
119 |
119 |
119 |
|
Trials |
152 |
152 |
152 |
152 |
50 |
50 |
50 |
|
R-squared |
0.18 |
0.46 |
0.38 |
0.49 |
0.14 |
0.22 |
0.45 |
- Note: This table shows OLS estimates with standard errors clustered by trial in parentheses. The MDE (minimum detectable eff ect) is calculated in pp. at power 0.8. Observations with missing data for outcome time-frame, control take-up result, trial duration, institutional constraints rating, or personnel FTE months are included with separate dummies.
These controls reduce the difference in point estimate between the samples by two thirds, from 7.3 pp. (Column 1) to 2.4 pp. (Column 2), suggesting an important contribution of nudge characteristics. At the same time, some of these nudge categories may be capturing differences in effect sizes due to selective publication, for example, in-person nudges have smaller sample sizes, with potentially biased effect sizes in the presence of selective publication. We evaluate the contribution of nudge characteristics together with other factors in Section 4.4.6
4.2.3 Features of Trials
While so far we controlled for the type of nudge, next we control for general features of the trial described in Table II. In Columns 5–7 of Table IV, we hold academic involvement constant and consider only the Nudge Unit trials with an academic affiliate, as well as the Academic Journal trials. In this subsample, we replicate the large difference in effect size, with a 7.7 pp. larger effect size in the Academic Journals sample (Column 5).
Adding controls for the features of trials in Column 6, we find that the Likert rating for how close the intervention was to the planned one has a positive impact, but is not significant. The measure of personnel involvement also has a positive, but not statistically significant, impact. Altogether, these features have only modest explanatory power for the effect size difference between the two samples.
Overall, we can explain some of the gap between our two samples as a difference in β, where β is determined by nudge features including the policy outcome, the behavioral mechanism used, and the mode of communication. We recognize that these nudge features are not exogenously selected and that at least some of these differences in observables, such as lack of in-person interventions, may be part of going to scale. We return to differences in effect size below when modeling jointly with selective publication.
4.3 Selective Publication
The third component of our model is selective publication. Following the literature (e.g., Andrews and Kasy (2019)), we include any channel leading to selective publication out of the sample of all studies run, including decisions by journal editors on which papers to publish, but also by researchers of which studies to write up and submit for publication (the file drawer effect). We expect some publication bias in the Academic Journals sample, but not in the Nudge Units sample where we access all trials.
4.3.1 Graphical Evidence on Publication Bias
As a first test, following Card and Krueger (1995), in Figure 5(a) we plot each point estimate for the nudges in the Academic Journals sample as a function of the statistical precision of the estimate, in our case measured with the statistical power (MDE). The plot shows evidence of two phenomena. First, there is a fanning out of the estimates: the less-powered studies (studies with larger MDE) have a larger variance of the point estimates, just as one would expect even without any selective publication. Second, the less-powered studies also have a larger point estimate for the nudge. Indeed, a simple linear regression estimate displayed on the figure documents a strong positive relationship: 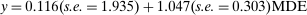 . This second pattern is consistent with publication bias: to the extent that only statistically significant results are published, less imprecise studies will lead to a (biased) inference of larger treatment effects. We observe similar patterns when we plot the treatment effect against the standard error, another measure of precision, as shown in Figure A.5.
. This second pattern is consistent with publication bias: to the extent that only statistically significant results are published, less imprecise studies will lead to a (biased) inference of larger treatment effects. We observe similar patterns when we plot the treatment effect against the standard error, another measure of precision, as shown in Figure A.5.
This panel displays tests for publication bias in the Academic Journals sample. Figure 5(a) plots the relationship between the minimum detectable effect and the treatment effect size. The estimated equation is the linear fit with standard errors clustered at the trial level. Figure 5(b) shows the distribution of t-statistics (i.e., treatment effect divided by standard error) for all nudges, and Figure 5(c) shows the distribution for only the max t-stat within each trial. Figure 5(c) excludes one trial in which the most significant treatment arm uses financial incentives.
As a second test, following Brodeur et al. (2016), in Figure 5(b) we plot the distribution of t statistics around the standard 5% significant threshold ( ) for the nudge treatments in the Academic Journals sample. We detect no bunching in t statistics to the right of the
) for the nudge treatments in the Academic Journals sample. We detect no bunching in t statistics to the right of the  threshold. Behavioral studies, however, often employ multiple treatment arms in one trial, compared to a control group, often in a horse race of alternative behavioral levers. In such a setting, arguably, for publication what matters is that at least one nudge or treatment arm be statistically significant, not all of them.
threshold. Behavioral studies, however, often employ multiple treatment arms in one trial, compared to a control group, often in a horse race of alternative behavioral levers. In such a setting, arguably, for publication what matters is that at least one nudge or treatment arm be statistically significant, not all of them.
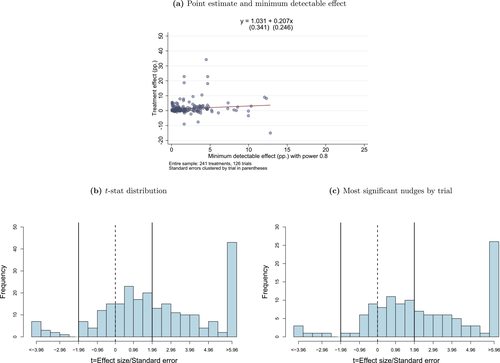
In Figure 5(c), thus, we plot the distribution of the most significant t-statistic across the different nudge treatments in a trial. There are 9 papers with a (max) t statistic between 1.96 and 2.96, but only 2 papers with (max) t statistic between 0.96 and 1.96. This suggests that the probability of publication for papers with no statistically significant results is only a fraction of the probability of publication for studies with at least one significant result.7 Zooming in closer around the threshold, there is only 1 study with a max t statistic between 1.46 and 1.96, versus 6 between 1.96 and 2.46.
In Figure 6, we produce the same plots for the Nudge Unit trials. The contrast of Figure 6(a) with Figure 5(a) is striking: in the Nudge Units sample, there is no evidence that the less-powered studies have larger point estimates. Indeed, a linear regression of point estimate on MDE returns 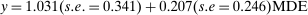 , providing no evidence of a positive slope. Further, Figures 6(b) and 6(c) show there is no discontinuity in the distribution of the t-statistic, nor in the max of the t-statistic by trial. This is consistent with the fact that we observe the universe of completed trials.
, providing no evidence of a positive slope. Further, Figures 6(b) and 6(c) show there is no discontinuity in the distribution of the t-statistic, nor in the max of the t-statistic by trial. This is consistent with the fact that we observe the universe of completed trials.
This panel displays tests for publication bias in the Nudge Units sample. Figure 6(a) plots the relationship between the minimum detectable effect and the treatment effect size. The estimated equation is the linear fit with standard errors clustered at the trial level. Figure 6(b) shows the distribution of t-statistics (i.e., treatment effect divided by standard error) for all nudges, and Figure 6(c) shows the distribution for only the max t-stat within each trial. Figure 6(c) excludes two trials in which the most significant treatment arm uses defaults/financial incentives.
As a further piece of evidence, in Figures A.5(c)–(f) we present funnel plots as in Andrews and Kasy (2019), plotting the point estimate and the standard errors, with bars indicating the results that are statistically significant. These plots indicate an apparent missing mass for the Academic Journal papers when considering the max t-statistics (Figure A.5(d)), and no evidence of a missing mass for the Nudge Unit trials (Figure A.5(f)).
This evidence thus points to selective publication in the nudge experiments run by academic researchers. This evidence adds to the publication bias literature in two ways. First, it suggests that the maximal t-statistic may play an even larger role in determining publication than all individual t-statistics. Second, our result appears to differ from the findings of Brodeur, Cook, and Heyes (2020), who did not find statistically significant evidence of p-value manipulation for experimental studies (as opposed to in difference-in-differences or instrumental variable studies) using the universe of papers in top-25 economics journals in 2015 and 2018. In Figure A.6, we reconsider the data in Brodeur, Cook, and Heyes (2020) comparing the evidence of manipulation when we consider each t-stat on its own, as opposed to the max t-stat in a paper. We focus on t-statistics from the main table in each paper. Figure A.6(a) replicates the finding of bunching around 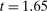 (
(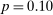 ) and
) and 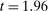 (
(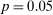 ) for individual t-statistics. When considering the maximal t-statistic, Figure A.6(b) shows a sizable jump in the distribution around
) for individual t-statistics. When considering the maximal t-statistic, Figure A.6(b) shows a sizable jump in the distribution around 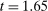 (
(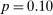 ): there are 10 studies with maximal t-stat just above this threshold, but only 2 just below it. There is, however, no obvious jump at
): there are 10 studies with maximal t-stat just above this threshold, but only 2 just below it. There is, however, no obvious jump at 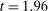 . When restricting the sample to only experimental studies, the evidence is suggestive given the much smaller sample, but still there is an apparent gap in the distribution of the maximal t-statistic below
. When restricting the sample to only experimental studies, the evidence is suggestive given the much smaller sample, but still there is an apparent gap in the distribution of the maximal t-statistic below 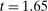 , as opposed to above, qualitatively consistent with the findings in our sample of published nudge interventions (Figures A.6(c)–(d)).8
, as opposed to above, qualitatively consistent with the findings in our sample of published nudge interventions (Figures A.6(c)–(d)).8
4.3.2 Reduced-Form Evidence on Impact of Publication Bias
Before we turn to our full model of selective publication, we consider reduced-form evidence in the spirit of Egger's test. Returning to Table IV, in Column 3 we control for statistical power (MDE) in both the Nudge Units sample and in the Academic Journals sample. The idea of this test is to obtain the predicted effect size for experiments with a very large sample size (and thus no role for sampling error or publication bias). The nudge effect size is strongly increasing with the MDE in the Academic Journals sample, but not in the Nudge Units sample, consistent with the pattern in Figures 5(a) and 6(a). Adding these controls can explain the entire difference in effect size: for trials with, hypothetically, zero MDE, the effect size is indistinguishable in the two samples, and is 1 pp. in the Nudge Units sample. We replicate this result in Table A.VII with alternative specifications for this test. In Column 1, we use the exact Egger's test with standard errors as regressors and inverse-variance weights, and in Column 2, we present results weighted by 1/MDE instead of regressing on MDE. An important caveat to these results is that the MDE can itself be endogenous to nudge characteristics and to the researcher expectations about effect sizes (as we emphasized above).
4.4 Meta-Analysis Model With Publication Bias Correction
Bringing these components together, we now turn to our meta-analytic model of treatment effect sizes with publication bias based on Andrews and Kasy (2019). The model allows for all three key dimensions: (i) (statistical power) the model takes as input the precision of the estimates implied by the differences in statistical power; (ii) (effect size) the model allows for different effect sizes β for academic researchers and Nudge Unit interventions; (iii) (publication bias) papers with no statistically significant results in the Academic Journals sample have a probability of publication 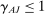 .
.
The Andrews and Kasy (2019) model builds on traditional random-effects meta-analysis models, and adds selective publication. In a meta-analysis, the researcher collects a sample of studies (indexed by i), each with an observed effect size 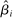 that estimates the study's true effect size
that estimates the study's true effect size 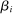 , and an observed standard error
, and an observed standard error 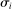 . A random-effects model allows the true effect
. A random-effects model allows the true effect 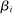 to vary around the grand true average effect
to vary around the grand true average effect 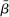 with some variance
with some variance 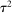 . The parameter τ may represent differences in context, populations, design features, etc. In our setting, there are multiple treatment arms in nearly each study. Thus, we introduce a within-trial random effect variance. This allows for different nudges within the same trial (i.e., study) to have more similar results than nudges across different studies, since they share a setting, a behavioral outcome, and basic design. Formally, the trial-level base effect
. The parameter τ may represent differences in context, populations, design features, etc. In our setting, there are multiple treatment arms in nearly each study. Thus, we introduce a within-trial random effect variance. This allows for different nudges within the same trial (i.e., study) to have more similar results than nudges across different studies, since they share a setting, a behavioral outcome, and basic design. Formally, the trial-level base effect 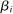 is drawn from
is drawn from  , and the treatment-level true effect
, and the treatment-level true effect  is drawn from
is drawn from 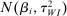 . Finally, the observed treatment effect
. Finally, the observed treatment effect 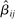 is drawn around
is drawn around 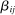 from
from 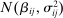 .
.
To start with, in Panel A of Table V, we present maximum likelihood estimates from such traditional meta-analysis (other than allowing for a separate within-trial variance).9 The estimated effect sizes 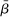 are very close to the unweighted estimates in Table III, at 8.58 pp. for the Academic Journals sample and 1.50 pp. for the Nudge Units sample.
are very close to the unweighted estimates in Table III, at 8.58 pp. for the Academic Journals sample and 1.50 pp. for the Nudge Units sample.
|
Normal 1 |
Normal 2 |
|||||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
ATE (pp.) |
|
|
|
|
|
|
|
|
−Log Likelihood |
|
|
Panel A. Traditional parametric normal-based meta-analysis |
||||||||||
|
Academic Journals |
8.58 |
1 (fixed) |
8.58 |
7.89 |
5.65 |
– |
– |
– |
1 (fixed) |
267.69 |
|
(1.98) |
(1.98) |
(1.99) |
(2.86) |
|||||||
|
Nudge Units |
1.50 |
1 (fixed) |
1.50 |
3.04 |
2.38 |
– |
– |
– |
1 (fixed) |
647.26 |
|
(0.34; p=0.00) |
(0.34) |
(1.24) |
(1.20) |
|||||||
|
Panel B. Generalized mixture model with selective publication |
||||||||||
|
Academic Journals |
3.89 |
0.10 |
1.30 |
2.70 |
0.05 |
19.18 |
5.86 |
12.73 |
0.86 |
211.25 |
|
(1.88) |
(0.13) |
(0.97) |
(1.00) |
(0.17) |
(4.81) |
(3.19) |
(3.06) |
(0.07) |
||
|
Nudge Units |
1.38 |
1 (fixed) |
0.35 |
0.41 |
0.23 |
5.09 |
4.64 |
6.40 |
0.78 |
395.04 |
|
(0.33; p=0.19) |
(0.10) |
(0.12) |
(0.09) |
(1.72) |
(3.53) |
(3.41) |
(0.06) |
|||
|
Difference in observed ATE explained by publication bias: 66% (26%) |
||||||||||
|
Panel C. Generalized mixture model with selective publication and heterogeneity based on observables |
||||||||||
|
Parsimonious model of observables (see Column 3 of Table A.IX(c)): |
||||||||||
|
Difference in observed ATE explained by: publication bias 77% (19%), observable characteristics 21% (14%) |
||||||||||
|
Richer model of observables (see Column 4 of Table A.IX(c)): |
||||||||||
|
Difference in observed ATE explained by: publication bias 77% (19%), observable characteristics 20% (11%) |
||||||||||
-
Note: This table shows the estimates from a traditional normal-based meta-analysis method in Panel A, and from generalized models with a mixture of normals in Panels B and C. Under the traditional normal-based meta-analysis assumptions, trial base effects
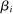 are drawn from a normal distribution centered at
are drawn from a normal distribution centered at 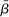 with between-trial standard deviation
with between-trial standard deviation  . Then, each treatment arm j within a trial i draws a base treatment effect
. Then, each treatment arm j within a trial i draws a base treatment effect 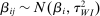 , where
, where 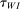 is the within-trial standard deviation. Each treatment arm also has some level of precision given by an independent standard error
is the within-trial standard deviation. Each treatment arm also has some level of precision given by an independent standard error 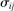 . The observed treatment effect is
. The observed treatment effect is 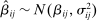 . In Panel B, the mixture of two normals model is a generalization of the normal-based meta-analysis, and allows trial base effects to be drawn from a second normal distribution. The model in Panel C adds a third normal, and also allows the probability of drawing effects from each normal to vary depending on observable trial characteristics (see Table A.IX(c) for details). To capture the extent of selective publication, the probability of publication is allowed to differ depending on whether trials have at least one significant treatment arm. In particular, trials without any significant results at the 95% level are γ times as likely to be published as trials with significant results. Estimates are obtained using maximum likelihood. Bootstrap standard errors are shown in parentheses. The p-value of the difference in the estimated average treatment effect (ATE) between the Academic Journals and Nudge Units samples is shown in the parentheses below the Nudge Unit ATE.
. In Panel B, the mixture of two normals model is a generalization of the normal-based meta-analysis, and allows trial base effects to be drawn from a second normal distribution. The model in Panel C adds a third normal, and also allows the probability of drawing effects from each normal to vary depending on observable trial characteristics (see Table A.IX(c) for details). To capture the extent of selective publication, the probability of publication is allowed to differ depending on whether trials have at least one significant treatment arm. In particular, trials without any significant results at the 95% level are γ times as likely to be published as trials with significant results. Estimates are obtained using maximum likelihood. Bootstrap standard errors are shown in parentheses. The p-value of the difference in the estimated average treatment effect (ATE) between the Academic Journals and Nudge Units samples is shown in the parentheses below the Nudge Unit ATE.
Figure 7(a) shows the distribution of treatment effect for the Academic Journals sample and the fit of this model (blue dotted line). This normal-based estimator provides a poor fit, given the nearly bi-modal distribution of the underlying data: most treatment effects are in the range between 0 and 10 pp., but there is also a right tail above 10 pp., with no corresponding left tail. The substantial right skew, which a normal distribution cannot fit, leads to an upward bias in the estimate for 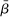 and a very large estimate for
and a very large estimate for 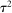 ; this implies that the meta-analysis estimate is very close to the unweighted average.
; this implies that the meta-analysis estimate is very close to the unweighted average.

This figure plots the empirical histogram of observed nudge effects and compares the fit of a normal-based meta-analysis model (Panel A of Table V) to the fit of a mixture of two normals model (Panel B of Table V) for the Academic Journals sample in Figure 7(a) and for the Nudge Units sample in Figure 7(b). One nudge in the Nudge Units sample with an effect less than −10 pp. and three nudges in the Academic Journals sample with effects greater than 35 pp. are not shown.
Figure 7(b) displays the distribution of treatment effects for the Nudge Unit trials. Once again, this normal-based model (blue dotted line) does not fit the data well: there are more effect sizes in the right tail than under the estimated distribution.
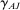 times as likely to be published as studies with a significant intervention. Selective publication in favor of significant results would imply that
times as likely to be published as studies with a significant intervention. Selective publication in favor of significant results would imply that 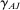 is less than 1. We assume that publication bias occurs at the level of the most significant nudge j within a paper i, consistent with the evidence from Figures 5(b)–(c), that is,
is less than 1. We assume that publication bias occurs at the level of the most significant nudge j within a paper i, consistent with the evidence from Figures 5(b)–(c), that is,
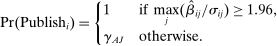
The estimates for the Nudge Units sample, in Panel B, have a drastically improved log likelihood. We estimate that the treatment effects come from two distributions, one centered at 0.35 pp., a second one centered at 5.09 pp., with 78% of trials drawing from the first distribution. The overall estimated treatment effect, at 1.38 pp. (the weighted average of the means from the two normal distributions), is very similar to the estimate from the traditional meta-analysis, but now, as the continuous red line in Figure 7(b) shows, we have a much better fit of the distribution of treatment effects.
For the Academic Journals sample, we estimate a very significant (and quite precisely estimated) degree of publication bias: papers with no statistically significant results only have one-tenth the probability of being published as studies with significant results ( , s.e. = 0.13). This parallels the non-parametric estimate from the t-statistics distribution in Figure 5(c) of
, s.e. = 0.13). This parallels the non-parametric estimate from the t-statistics distribution in Figure 5(c) of 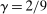 . Accounting for publication bias has a vast impact on the estimated average impact of the nudges, which falls to 3.89 pp., quite a bit lower than the unweighted estimate of 8.7 pp., but still higher (though not significantly so) than the estimated Nudge Unit ATE. Thus, publication bias accounts for two-thirds of the difference in effect sizes between the two samples. As Figure 7(a) shows (continuous red line), this model fits the distribution of treatment effects much better.
. Accounting for publication bias has a vast impact on the estimated average impact of the nudges, which falls to 3.89 pp., quite a bit lower than the unweighted estimate of 8.7 pp., but still higher (though not significantly so) than the estimated Nudge Unit ATE. Thus, publication bias accounts for two-thirds of the difference in effect sizes between the two samples. As Figure 7(a) shows (continuous red line), this model fits the distribution of treatment effects much better.
Allowing for a flexible distribution of treatment effects is critical. Assuming a normal distribution even with a correction for selective publication (Panel A of Table A.IX(a)) would lead to a biased estimate of the parameters, as apparent from the poor fit displayed in Figure A.7(b). Conversely, a further non-parametric extension allowing for a mixture of three normals (Panel C of Table A.IX(a)) leads to similar results, confirming that a mixture of two normals provides enough parametric flexibility.
So far, we have not modeled the impact of nudge characteristics. In Panel C of Table V, we take an alternative approach that explicitly models the role of characteristics, detailed in Appendix A.7 of the Supplemental Material. We assume that the Academic Journal trials and the Nudge Unit trials come from the same underlying distribution of effect sizes, modeled with a mixture of three normals, but that the two sets of trials are drawn with different probabilities from those normals. We model the probability of assignment into the three normals in an ordinal probit, which takes as inputs observable characteristics X. As before, we estimate a high degree of selective publication and an ATE for the Academic Journals sample at 3.05 pp. (Columns 3 and 4, Table A.IX(c)). In this model, nudge characteristics explain much of the gap that is not already explained by publication bias.
Summary
For the Nudge Unit trials, the meta-analytic estimate is consistent with the unweighted estimate of 1.4 pp. For the Academic Journal trials, selective publication accounts for about 70 percent of the larger effect size relative to the Nudge Unit trials. If we include key nudge characteristics as predictors, these characteristics explain most of the remaining difference, since the observable characteristics of nudges in the Academic Journals are more often associated with larger effect sizes.
4.5 Counterfactuals
The model in Panel B of Table V allows us to present counterfactuals to illustrate the role of each of the three dimensions of our model on the average effect size. In Row 1 of Table VI, we simulate the average treatment effect (ATE) for the Academic Journals sample given the estimated distribution of effect size, the observed statistical power, and the estimated degree of selective publication (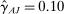 ) from Panel B of Table V. We reproduce the observed large impact of nudges, at 7.33 pp.
) from Panel B of Table V. We reproduce the observed large impact of nudges, at 7.33 pp.
|
Effect Size Distribution |
Statistical Power |
Selective Publication |
Simulated ATE (pp.) |
|
|---|---|---|---|---|
|
(1) Acad. J. as observed |
Acad. J. |
Acad. J. |
Yes (as in Acad. J.) |
7.33 (1.16) |
|
Counterfactuals—Academic Journal effect sizes with: |
||||
|
(2) High power |
Acad. J. |
Nudge Units |
Yes (as in Acad. J.) |
6.26 (1.11) |
|
(3) No pub. bias |
Acad. J. |
Acad. J. |
No (as in Nudge Units) |
3.81 (0.77) |
|
(4) High power & no pub. bias |
Acad. J. |
Nudge Units |
No (as in Nudge Units) |
3.78 (0.87) |
|
Counterfactuals—Nudge Unit effect sizes with: |
||||
|
(5) Low power & pub. bias |
Nudge Units |
Acad. J. |
Yes (as in Acad. J.) |
3.35 (0.69) |
|
(6) Pub. bias |
Nudge Units |
Nudge Units |
Yes (as in Acad. J.) |
2.43 (0.57) |
|
(7) Low power |
Nudge Units |
Acad. J. |
No (as in Nudge Units) |
1.39 (0.38) |
|
(8) Nudge Units as observed |
Nudge Units |
Nudge Units |
No (as in Nudge Units) |
1.40 (0.38) |
-
Note: This table shows estimates for counterfactual simulated average treatment effects using the generalized model in Panel B of Table V. Each counterfactual exercise draws 1000 samples of 152 simulated trials from the estimated mixture distribution for the sample of nudges indicated under “Effect size distribution”. The number of experimental arms and their standard errors for these simulated trials are drawn with replacement from the sample listed under “Statistical power”. Under selective publication, simulated trials without any positively significant treatment arms at the 95% level are “published” with probability
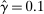 (as estimated in Panel B of Table V). Simulated trials with at least one positively significant treatment arm are published with probability 1. When selective publication is suppressed, all simulated trials are published. The “Simulated ATE (pp.)” column reports the average treatment effect in percentage points for all “published” treatment arms from the
(as estimated in Panel B of Table V). Simulated trials with at least one positively significant treatment arm are published with probability 1. When selective publication is suppressed, all simulated trials are published. The “Simulated ATE (pp.)” column reports the average treatment effect in percentage points for all “published” treatment arms from the 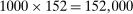 simulated trials. The standard deviation of the observed ATE in the 1000 simulated samples is reported in parentheses.
simulated trials. The standard deviation of the observed ATE in the 1000 simulated samples is reported in parentheses.
In the next series of counterfactuals, we change each component individually, and report the implied effect size. In Row 2, we change only the statistical power of the estimates: if the Academic Journal nudges had the same distribution of effect size and were still subject to publication bias, but had more precise standard errors (due to larger sample sizes) as in the Nudge Units sample, would the observed point estimate change? The point estimate would indeed be lower, at 6.26 pp., as the more precise estimate would blunt to some extent the impact of selective publication, albeit not by much.
In Row 3, we show the impact of instead removing only publication bias: the impact in this case is very sizable, since it would reveal the true average effect size, which is 3.81 pp. (as in Table V, Panel B). With no publication bias, improving the statistical power would not have a further impact (Row 4).
In the next counterfactuals, we consider the Nudge Unit trials, but add features of the Academic Journals sample. With both low statistical power and publication bias (Row 5), the observed effect size would be 3.35 pp., more than twice the observed effect size (reproduced in Row 8). With publication bias but high statistical power (Row 6), the observed effect size would still be biased upward, but less so, at 2.43 pp. This further clarifies the potential of selective publication to bias average effect sizes, especially when the studies are not well-powered. Finally, in the absence of publication bias (Row 7), having lower statistical power would not bias the average point estimate.
These counterfactuals point to the critical role of publication bias, compounded by low statistical power, in explaining the large effect size in the Academic Journals sample.
4.6 Additional Differences
While we have focused on three main components—statistical power, effect size, and selective publication—there are other differences in the nudge experimentation model between the two samples that could affect the effect sizes. We consider here some of the possible alternatives, weaving in anecdotal evidence on how Nudge Units make decisions.
First, it is possible that Nudge Units, more than researchers, can do repeated experiments with one partner, and thus finesse their design (leading to larger effect sizes over time), or vice versa, run out of creative nudge solutions to a problem (leading to smaller effect sizes over time). Series of collaborations with one government partner, however, are not too common. In 62% of cases, there are at most two experiments with a given government partner (in our sample). Furthermore, in cases in which there are at least two experiments with the same partner, we do not see differences in nudge effect sizes between experiments run earlier versus later, as Figure A.8(a) shows.
Another possibility is that the extent of subsequent experiments with one government unit may depend on the effect size in the first intervention. For example, if government units persist in experimenting in easier-to-affect settings in which the initial nudge effect size is large, this may potentially upward bias the point estimate. Figure A.8(b), though, shows that there is no systematic relationship between the effect size in the first intervention and the total number of collaborations.
These findings match anecdotal evidence from interviews with the leadership of both Nudge Unit teams. The likelihood of working on an additional trial with a given government partner seems to be largely orthogonal to the results of any given trial, and is often decided before final results on one trial are completed. For example, at BIT, contracts on how many trials to run per city partner were set in advance of conducting those trials. Both Nudge Units noted that the decision to run a trial depends more on feasibility, such as availability of administrative data, technical feasibility to nudge, a large enough sample size, as well as funding constraints. This would not appear to bias the estimate of the difference in effect sizes in an obvious way.
5 Discussion and Conclusion
An ongoing question in both policy circles and in academia asks: what would it look like if governments began using the “gold standard of evaluation”—RCTs—more consistently to inform policy decisions? While this has not yet happened at scale, nudge interventions have been used frequently and consistently through Nudge Units in governments, thus creating an opportunity to measure what taking nudges to scale might look like.
By studying the universe of trials run across two large Nudge Units in the United States, covering over 23 million people, and comparing our results to published meta-analyses, we make progress on this question. We find that, on average, nudge interventions have a meaningful and statistically significant impact on the outcome of 1.4 pp. This estimated effect is significantly smaller than in academic journal articles (8.7 pp.). Using a meta-analysis model, we decompose this difference. We show that the largest source of the discrepancy is selective publication in the Academic Journals sample, exacerbated by low statistical power in that sample. If we include key nudge characteristics as predictors of the effect size, these characteristics explain most of the remaining difference, since the characteristics of nudges in the Academic Journals are more often associated with larger effect sizes.
We hope that future research will expand on our work in a number of directions. First, we do not observe the micro-data for each trial, limiting the ability to, for example, estimate which outcome is more elastic to different interventions. Second, it will be interesting to see whether other Nudge Units achieve different effect sizes, especially if they use a different mix of interventions, such as changing defaults or changing the choice architecture. Third, it would be valuable to examine determinants of which government departments decide to select into working with Nudge Units, and why they do so. Fourth, we hope that future research will evaluate the extent to which the results of the Nudge Unit interventions are implemented by the government units.
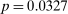 . This may even understate the extent of publication bias. Among the three Academic Journals trials with statistically insignificant results (see Table A.I(b)), two actually emphasize statistically significant results, either on a subsample or on a different outcome.
. This may even understate the extent of publication bias. Among the three Academic Journals trials with statistically insignificant results (see Table A.I(b)), two actually emphasize statistically significant results, either on a subsample or on a different outcome.



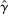 (Pub. Bias)
(Pub. Bias)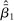
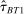
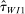
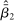
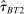
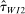
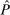 (Normal 1)
(Normal 1)
