Preferences for Truth-Telling
Abstract
Private information is at the heart of many economic activities. For decades, economists have assumed that individuals are willing to misreport private information if this maximizes their material payoff. We combine data from 90 experimental studies in economics, psychology, and sociology, and show that, in fact, people lie surprisingly little. We then formalize a wide range of potential explanations for the observed behavior, identify testable predictions that can distinguish between the models, and conduct new experiments to do so. Our empirical evidence suggests that a preference for being seen as honest and a preference for being honest are the main motivations for truth-telling.
0 Introduction
Reporting private information is at the heart of many economic activities, for example, a self-employed shopkeeper reporting her income to the tax authorities (e.g., Allingham and Sandmo (1972)), a doctor stating a diagnosis (e.g., Ma and McGuire (1997)), or an expert giving advice (e.g., Crawford and Sobel (1982)). For decades, economists made the useful simplifying assumption that utility only depends on material payoffs. In situations of asymmetric information, this implies that people are not intrinsically concerned about lying or telling the truth and, if misreporting cannot be detected, individuals should submit the report that yields the highest material gains.
Until recently, the assumption of always submitting the payoff-maximizing report has gone basically untested, partly because empirically studying reporting behavior is by definition difficult. In the last years, a fast growing experimental literature across economics, psychology, and sociology has begun to study patterns of reporting behavior empirically and a string of theoretical papers has been built on the assumption of some preference for truth-telling (e.g., Kartik, Ottaviani, and Squintani (2007), Matsushima (2008), Ellingsen and Östling (2010), Kartik, Tercieux, and Holden (2014)).
In this paper, we aim to deepen our understanding of how people report private information. Our strategy to do so is threefold. We first conduct a meta study of the existing experimental literature and document that behavior is indeed far from the assumption of payoff-maximizing reporting. We then formalize a wide range of explanations for this aversion to lying and show that many of these are consistent with the behavioral regularities observed in the meta study.1 Finally, in order to distinguish among the many and varied explanations, we identify new empirical tests and implement them in new experiments.
In order to cleanly identify the motivations driving aversion to lying, we focus on a setting without strategic interactions. We thus abstract from sender-receiver games or verification of messages, such as audits. We do so because the strategic interaction makes the setting more complex, especially if one is interested in studying the underlying motives of reporting behavior, as we are. We therefore use the experimental paradigm introduced by Fischbacher and Föllmi-Heusi (2013): subjects privately observe the outcome of a random variable, report the outcome, and receive a monetary payoff proportional to their report (for related methods using inferences about the population, see Batson, Kobrynowicz, Dinnerstein, Kampf, and Wilson (1997) and Warner (1965)). While no individual report can be identified as truthful or not (and subjects should thus report the payoff-maximizing outcome under the standard economic assumption), the researcher can judge the reports of a group of subjects. This paradigm is the one used most widely in the literature and several recent studies have shown that behavior in it correlates well with cheating behavior outside the lab (Hanna and Wang (2017), Cohn and Maréchal (2019), Cohn, Maréchal, and Noll (2015), Gächter and Schulz (2016c), Potters and Stoop (2016), Dai, Galeotti, and Villeval (2018)).2
In the first part of our paper (Section 1 and Appendix A, Abeler, Nosenzo, and Raymond (2019)), we combine data from 90 studies that use setups akin to Fischbacher and Föllmi-Heusi (2013), involving more than 44,000 subjects across 47 countries. Our study is the first quantitative meta analysis of this experimental paradigm. Interactive versions of the analyses can be found at www.preferencesfortruthtelling.com. We show that subjects forgo on average about three-quarters of the potential gains from lying. This is a very strong departure from the standard economic prediction and comparable to many other widely discussed non-standard behaviors observed in laboratory experiments, like altruism or reciprocity.3 This strong preference for truth-telling is robust to increasing the payoff level 500-fold or repeating the reporting decision up to 50 times. The cross-sectional patterns of reports are extremely similar across studies. Overall, we document a stable and coherent corpus of evidence across many studies, which could potentially be explained by one unifying theory.4
In the second part of the paper (Section 2 and Appendices B, C, D, and E), we formalize a wide range of explanations for the observed behavior, including the many explanations that have been suggested, often informally, in the literature. The classes of models we consider cover three broad types of motivations: a direct cost of lying (e.g., Ellingsen and Johannesson (2004), Kartik (2009)); a reputational cost derived from the belief that an audience holds about the subject's traits or action (e.g., Mazar, Amir, and Ariely (2008)), including guilt aversion (e.g., Charness and Dufwenberg (2006)); and the influence of social norms and social comparisons (e.g., Weibull and Villa (2005)). We also consider numerous extensions, combinations, and mixtures of the aforementioned models (e.g., Kajackaite and Gneezy (2017)). For all models, we make minimal assumptions on the functional form and allow for heterogeneity of preference parameters, thus allowing us to derive very general conclusions.
Our empirical strategy to test the validity of the proposed explanations proceeds in two steps. First, we check whether each model is able to match the stylized findings of the meta study. This rules out many models, including models where the individual only cares about their reputation of having reported truthfully. In these models, individuals are often predicted to pool on the same report, whereas the meta study shows that this is never the case. However, we also find eleven models that can match all the stylized findings of the meta study. These models offer very different mechanisms for the aversion to lying with very different policy implications. It is therefore important to be able to make sharper distinctions between the models. In the second step, we thus design four new experimental tests that allow us to further separate the models. We show that the models differ in (i) how the distribution of true states affects one's report; (ii) how the belief about the reports of other subjects influences one's report;5 (iii) whether the observability of the true state affects one's report; (iv) whether some subjects will lie downwards, that is, report a state that yields a lower payoff than their true state, when the true state is observable. Our predictions come in two varieties: (i) to (iii) are comparative statics while (iv) concerns properties of equilibrium behavior.
We take a Popperian approach in our empirical analysis (Popper (1934)). Each of our tests, taken in isolation, is not able to pin down a particular model. For example, among the models we consider, there are at least three very different motives that are consistent with the behavior we find in test (i), namely, a reputation for honesty, inequality aversion, and disappointment aversion. However, each test is able to cleanly falsify whole classes of models and all tests together allow us to tightly restrict the set of models that can explain the data. Since we formalize a large number of models, covering a broad range of potential motives, the set of surviving models is more informative than if we had only falsified a single model, for example, the standard model. The surviving set obviously depends on the set of models and the empirical tests that we consider. However, the transparency of the falsification process allows researchers to easily adjust the set of non-falsified models as new evidence becomes available.
In the third part of the paper (Section 3 and Appendices F and G), we implement our four tests in new laboratory experiments with more than 1600 subjects. To test the influence of the distribution of true states (test (i)), we let subjects draw from an urn with two states and we change the probability of drawing the high-payoff state between treatments. Our comparative static is 1 minus the ratio of low-payoff reports to expected low-payoff draws. Under the assumption that individuals never lie downwards, this can be interpreted as the fraction of individuals who lie upwards. We find a very large treatment effect. When we move the share of true high-payoff states from 10 to 60 percent, the share of subjects who lie up increases by almost 30 percentage points. This result falsifies direct lying-cost models because this cost only depends on the comparison of the report to the true state that was drawn, but not on the prior probability of drawing the state.
To test the influence of subjects' beliefs about what others report (test (ii)), we use anchoring, that is, the tendency of people to use salient information to start off one's decision process (Tversky and Kahneman (1974)). By asking subjects to read a description of a “potential” experiment and to “imagine” two “possible outcomes” that differ by treatment, we are able to shift (incentivized) beliefs of subjects about the behavior of other subjects by more than 20 percentage points. This change in beliefs does not affect behavior: subjects in the high-belief treatment are slightly less likely to report the high state, but this is far from significant. This result rules out all the social comparison models we consider. In these models, individuals prefer their outcome or behavior to be similar to that of others, so if they believe others report the high state more often, they want to do so, too.
To test the influence of the observability of the true state (test (iii)), we implement the random draw on the computer and are thus able to recover the true state. We use a double-blind procedure to alleviate subjects' concerns about indirect material consequences of lying, for example, being excluded from future experiments. We find significantly less over-reporting in the treatment in which the true state is observable compared to when it is not. This finding is again inconsistent with direct lying-cost models and social comparison models since, in those models, utility does not depend on the observability of the true state. Moreover, we find that no subject lies downwards in this treatment (test (iv)).
In Section 4, we compare the predictions of the models to the gathered empirical evidence. The main empirical finding is that our four tests rule out almost all of the models previously suggested in the literature. Of the models we propose and consider, only two cannot be falsified by our data. Both models combine a preference for being seen as honest with a preference for being honest. This combination is also present in the concurrent papers by Khalmetski and Sliwka (forthcoming) and Gneezy, Kajackaite, and Sobel (2018). Both papers assume that individuals want to be perceived as honest and suffer from a lying cost related to the material gain from lying. A distinct intuition is explored in another concurrent paper by Dufwenberg and Dufwenberg (2018), who supposed that individuals care about the perception about by how much they have cheated, that is, lied for material gain. We discuss how these studies relate to ours in the Conclusions. We then turn to calibrating a simple, linear version of one of our non-falsified models, showing that it can quantitatively reproduce the data from the meta study as well as the patterns in our new experiments. In the model, individuals suffer a fixed cost of lying and a cost that is linear in the probability that they lied (given their report and the equilibrium report). Both cost components are important.
Section 5 concludes and discusses policy implications. Three key insights follow from our study. First, our meta analysis shows that the data are not in line with the assumption of payoff-maximizing reporting but rather with some preference for truth-telling. Second, our results suggest that a preference for being seen as honest and a preference for being honest are the main motivations for truth-telling. Finally, policy interventions that rely on voluntary truth-telling by some participants could be very successful, in particular if it is made hard to lie while keeping a good reputation.
1 Meta Study
1.1 Design
The meta study covers 90 experimental studies containing 429 treatment conditions that fit our inclusion criteria. We include all studies using the setup introduced by Fischbacher and Föllmi-Heusi (2013) (which we will refer to as “FFH paradigm”). Subjects conduct a random draw and then report their outcome of the draw, that is, their state. We require that the true state is unknown to the experimenter (i.e., we require at least two states) but that the experimenter knows the distribution of the random draw. We also include studies in which subjects report whether their prediction of a random draw was correct (as in Jiang (2013)). The payoff from reporting has to be independent of the actions of other subjects, but the reporting action can have an effect on other subjects. The expected payoff level must not be constant, for example, no hypothetical studies, and subjects are not allowed to self-select into the reporting experiment after learning about the rules of the experiment. We only consider distributions that either (i) have more than two states and are uniform or symmetric single-peaked, or (ii) have two states (with any distribution). This excludes only a handful of treatments in the literature. For more details on the selection process, see Appendix A.
We contacted the authors of the identified papers and obtained the raw data of 54 studies. For the remaining studies, we extract the data from graphs and tables shown in the papers. This process does not allow to recover additional covariates for individual subjects, like age or gender, and we cannot trace repeated decisions by the same subject. However, for most of our analyses, we can reconstruct the relevant raw data entirely in this way. The resulting data set thus contains data for each individual subject. Overall, we collect data on 270,616 decisions by 44,390 subjects. Experiments were run in 47 countries which cover 69 percent of world population and 82 percent of world GDP. A good half of the overall sample are students; the rest consists of representative samples or specific non-student samples like children, bankers, or nuns. Table I lists all included studies. Studies for which we obtained the full raw data are marked by *.
|
Study |
|
|
Country |
Randomization Method |
True Distribution |
|
|---|---|---|---|---|---|---|
|
this study* |
7 |
1124 |
United Kingdom |
multiple |
multiple |
|
|
4 |
1102 |
Germany |
coin toss |
multiple |
||
|
1 |
60 |
China |
draw from urn |
1D10 |
||
|
3 |
507 |
Germany |
draw from urn |
1D10 |
||
|
11 |
403 |
Israel |
coin toss |
20D2 |
||
|
2 |
200 |
Germany |
die roll |
1D6 |
||
|
Arbel, Bar-El, Siniver, and Tobol (2014)* |
2 |
399 |
Israel |
die roll |
1D6 |
|
|
Ariely, Garcia-Rada, Hornuf, and Mann (2014) |
1 |
188 |
Germany |
die roll |
1D6 |
|
|
Aydogan, Jobst, D'Ardenne, Muller, and Kocher (2017) |
2 |
120 |
Germany |
coin toss |
2D2 |
|
|
8 |
672 |
India |
die roll |
1D6 |
||
|
Barfort, Harmon, Hjorth, and Leth Olsen (2015) |
1 |
862 |
Denmark |
die roll |
asy. 1D2 |
|
|
3 |
272 |
Germany |
die roll |
1D6 |
||
|
Beck, Bühren, Frank, and Khachatryan (2018)* |
6 |
128 |
Germany |
die roll |
1D6 |
|
|
2 |
103 |
Colombia |
die roll |
1D6 |
||
|
7 |
342 |
Germany |
die roll |
1D2 |
||
|
3 |
269 |
USA |
coin toss |
1D2 |
||
|
2 |
182 |
Italy |
coin toss |
1D2 |
||
|
1 |
90 |
China |
die roll |
1D6 |
||
|
Cappelen, Fjeldstad, Mmari, Sjursen, and Tungodden (2016)* |
2 |
1473 |
Tanzania |
coin toss |
6D2 |
|
|
Charness, Blanco-Jimenez, Ezquerra, and Rodriguez-Lara (2019) |
4 |
338 |
Spain |
die roll |
1D10 |
|
|
1 |
117 |
Czech Republic |
die roll |
1D6 |
||
|
2 |
98 |
Madagascar |
die roll |
1D6 |
||
|
8 |
563 |
coin toss |
1D2 |
|||
|
4 |
375 |
Switzerland |
coin toss |
1D2 |
||
|
1 |
162 |
Switzerland |
coin toss |
1D2 |
||
|
4 |
468 |
Switzerland |
coin toss |
1D2 |
||
|
Conrads, Irlenbusch, Rilke, and Walkowitz (2013)* |
4 |
554 |
Germany |
die roll |
1D6 |
|
|
4 |
246 |
Germany |
coin toss |
4D2 |
||
|
Conrads, Ellenberger, Irlenbusch, Ohms, Rilke, and Walkowitz (2017) |
1 |
114 |
Germany |
die roll |
1D2 |
|
|
2 |
384 |
France |
die roll |
1D3 |
||
|
1 |
288 |
Germany |
die roll |
1D6 |
||
|
Dieckmann, Grimm, Unfried, Utikal, and Valmasoni (2016) |
5 |
1015 |
multiple (5) |
coin toss |
1D2 |
|
|
1 |
466 |
Switzerland |
die roll |
1D6 |
||
|
Di Falco, Magdalou, Masclet, Villeval, and Willinger (2016) |
1 |
1080 |
Tanzania |
coin toss |
1D2 |
|
|
1 |
252 |
Germany |
draw from urn |
asy. 1D2 |
||
|
4 |
170 |
Germany |
coin toss |
4D2 |
||
|
3 |
3400 |
multiple (3) |
die roll |
1D6 |
||
|
8 |
2151 |
USA |
coin toss |
1D2 |
||
|
5 |
979 |
Switzerland |
die roll |
1D6 |
||
|
Foerster, Pfister, Schmidts, Dignath, and Kunde (2013)* |
1 |
28 |
Germany |
die roll |
12D8 |
|
|
1 |
505 |
Denmark |
die roll |
2D6 |
||
|
4 |
209 |
Denmark |
coin toss |
1D2 |
||
|
23 |
2568 |
multiple (23) |
die roll |
1D6 |
||
|
4 |
262 |
United Kingdom |
die roll |
1D6 |
||
|
3 |
978 |
USA |
coin toss |
multiple |
||
|
8 |
304 |
USA |
die roll |
1D6 |
||
|
2 |
207 |
Germany |
draw from urn |
multiple |
||
|
2 |
1511 |
USA |
coin toss |
4D2 |
||
|
1 |
51 |
Netherlands |
die roll |
1D6 |
||
|
2 |
826 |
India |
die roll |
1D6 |
||
|
1 |
415 |
Rwanda |
coin toss |
30D2 |
||
|
6 |
765 |
Germany |
die roll |
asy. 1D2 |
||
|
4 |
342 |
Germany |
multiple |
asy. 1D2 |
||
|
3 |
740 |
Germany |
coin toss |
1D2 |
||
|
Houser, List, Piovesan, Samek, and Winter (2016)* |
2 |
72 |
USA |
coin toss |
asy. 1D2 |
|
|
8 |
223 |
multiple (6) |
die roll |
1D2 |
||
|
Hugh-Jones (2016)* |
30 |
1390 |
multiple (15) |
coin toss |
1D2 |
|
|
3 |
148 |
Denmark |
die roll |
1D6 |
||
|
2 |
39 |
Netherlands |
die roll |
1D2 |
||
|
4 |
224 |
multiple (4) |
die roll |
1D2 |
||
|
17 |
1303 |
multiple (2) |
multiple |
multiple |
||
|
7 |
384 |
Germany |
die roll |
1D6 |
||
|
Lowes, Nunn, Robinson, and Weigel (2017) |
1 |
499 |
DR Congo |
die roll |
30D2 |
|
|
2 |
192 |
France |
die roll |
1D2 |
||
|
Mann, Garcia-Rada, Hornuf, Tafurt, and Ariely (2016) |
10 |
2179 |
multiple (5) |
die roll |
1D2 |
|
|
Meub, Proeger, Schneider, and Bizer (2016) |
2 |
94 |
Germany |
die roll |
1D2 |
|
|
1 |
108 |
Germany |
die roll |
1D6 |
||
|
Muñoz-Izquierdo, Gil-Gómez de Liaño, Rin-Sánchez, and Pascual-Ezama (2014)* |
3 |
270 |
Spain |
coin toss |
1D2 |
|
|
48 |
1440 |
multiple (16) |
coin toss |
1D2 |
||
|
6 |
316 |
Germany |
die roll |
1D2 |
||
|
2 |
102 |
Netherlands |
draw from urn |
1D2 |
||
|
3 |
240 |
Switzerland |
die roll |
1D6 |
||
|
1 |
156 |
Israel |
die roll |
1D6 |
||
|
1 |
427 |
Israel |
die roll |
1D6 |
||
|
2 |
300 |
USA |
coin toss |
1D2 |
||
|
Shalvi, Dana, Handgraaf, and De Dreu (2011)* |
2 |
129 |
USA |
die roll |
1D6 |
|
|
2 |
178 |
Netherlands |
coin toss |
20D2 |
||
|
4 |
144 |
Israel |
die roll |
1D6 |
||
|
2 |
126 |
Israel |
die roll |
1D6 |
||
|
4 |
120 |
Netherlands |
coin toss |
1D2 |
||
|
Shen, Teo, Winter, Hart, Chew, and Ebstein (2016) |
1 |
205 |
Singapore |
die roll |
1D6 |
|
|
3 |
90 |
Czech Republic |
die roll |
1D6 |
||
|
3 |
674 |
multiple (2) |
die roll |
multiple |
||
|
Thielmann, Hilbig, Zettler, and Moshagen (2017)* |
1 |
152 |
Germany |
coin toss |
asy. 1D2 |
|
|
2 |
31 |
Germany |
die roll |
1D6 |
||
|
4 |
416 |
Germany |
coin toss |
5D2 |
||
|
9 |
178 |
multiple (2) |
die roll |
asy. 1D2 |
||
|
Wibral, Dohmen, Klingmuller, Weber, and Falk (2012) |
2 |
91 |
Germany |
die roll |
1D6 |
|
|
Zettler, Hilbig, Moshagen, and de Vries (2015)* |
1 |
134 |
Germany |
coin toss |
asy. 1D2 |
|
|
1 |
189 |
Israel |
coin toss |
1D2 |
- a Studies for which we obtained the full raw data are marked by *. 1DX refers to a uniform distribution with X outcomes. A coin flip would thus be 1D2. ND2 refers to the distribution of the sum of N uniform random draws with two outcomes. Asymmetric 1D2 refers to distributions with two outcomes for which the two outcomes are not equally likely.
Having access to the (potentially reconstructed) raw data is a major advantage over more standard meta studies. We can treat each subject as an independent observation, clustering over repeated decisions and analyzing the effect of individual-specific covariates. We can separately use within-treatment variation (by controlling for treatment fixed effects), within-study variation (by controlling for study fixed effects), and across-study variation for identification. Most importantly, we can conduct analyses that the original authors did not conduct. For other meta studies using the full individual subject data (albeit on different topics), see, for example, Harless and Camerer (1994), Weizsäcker (2010), or Engel (2011).

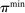 is the payoff from reporting the lowest possible state,
is the payoff from reporting the lowest possible state, 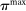 is the payoff from reporting the highest state, and
is the payoff from reporting the highest state, and 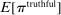 is the expected payoff from truthful reporting. For example, a roll of a six-sided die would result in standardized reports of −1, −0.6, −0.2, +0.2, +0.6, or +1.
is the expected payoff from truthful reporting. For example, a roll of a six-sided die would result in standardized reports of −1, −0.6, −0.2, +0.2, +0.6, or +1.In general, without making further assumptions, one cannot say how many people lied or by how much in the FFH paradigm. We can only say how much money people left on the table. An average standardized report greater than 0 means that subjects leave less money on the table than a group of subjects who report fully honestly.
To give readers the possibility to explore the data in more detail, we have made interactive versions of all meta-study graphs available at www.preferencesfortruthtelling.com. The graphs allow restricting the data, for example, only to specific countries. The graphs also provide more information about the underlying studies and give direct links from the plots to the original papers.
1.2 Results
Finding 1.The average report is bounded away from the maximal report.
Figure 1 depicts an overview of the data. Standardized report is on the y-axis and the maximal payoff from misreporting, that is,  , is on the x-axis (converted by PPP to 2015 USD). As payoff, we take the expected payoff, that is, the nominal payoff used in the experiment times the probability that a subject receives the payoff, in case not all subjects are paid. Each bubble represents the average standardized report of one treatment. The size of the bubble is proportional to the number of subjects in that treatment. The baseline treatment of Fischbacher and Föllmi-Heusi (2013) is marked in the figure. It replicates quite well.
, is on the x-axis (converted by PPP to 2015 USD). As payoff, we take the expected payoff, that is, the nominal payoff used in the experiment times the probability that a subject receives the payoff, in case not all subjects are paid. Each bubble represents the average standardized report of one treatment. The size of the bubble is proportional to the number of subjects in that treatment. The baseline treatment of Fischbacher and Föllmi-Heusi (2013) is marked in the figure. It replicates quite well.
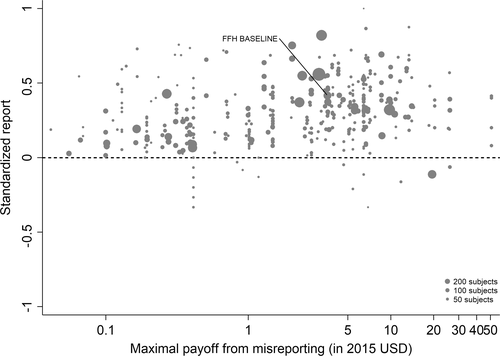
Average standardized report by incentive level. Notes: The figure plots standardized report against maximal payoff from misreporting. Standardized report is on the y-axis. A value of 0 means that subjects realize as much payoff as a group of subjects who all tell the truth. A value of 1 means that subjects all report the state that yields the highest payoff. The maximal payoff from misreporting (converted by PPP to 2015 USD), that is, the difference between the highest and lowest possible payoff from reporting, is on the x-axis (log scale). Each bubble represents the average standardized report of one treatment, and the size of a bubble is proportional to the number of subjects in that treatment. “FFH BASELINE” marks the result of the baseline treatment of Fischbacher and Föllmi-Heusi (2013).
If all subjects were monetary-payoff maximizers and had no concerns about lying, all bubbles would be at +1. In contrast, we find that the average standardized report is only 0.234. This is significantly (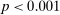 ) lower than 0.25 or any higher threshold (clustering on subject; 0.38 when clustering on study) and thus bounded away from 1. This means that subjects forego about three-quarters of the potential gains from lying. This is a very strong departure from the standard economic prediction.
) lower than 0.25 or any higher threshold (clustering on subject; 0.38 when clustering on study) and thus bounded away from 1. This means that subjects forego about three-quarters of the potential gains from lying. This is a very strong departure from the standard economic prediction.
This finding turns out to be quite robust. Subjects continue to refrain from lying maximally when stakes are increased. Figure 1 shows that an increase in incentives affects behavior only very little. In our sample, the potential payoff from misreporting ranges from cents to 50 USD (Kajackaite and Gneezy (2017)), a 500-fold increase. In a linear regression of standardized report on the potential payoff from misreporting, we find that a one dollar increase in incentives changes the standardized report by −0.005 (using between-study variation as in Figure 1) or 0.003 (using within-study variation). See Appendix A for more details and for a comparison of our different identification strategies. This means that increasing incentives even further is unlikely to yield the standard economic prediction of +1. In Appendix A, we also show that subjects still refrain from lying maximally when they report repeatedly. In fact, repetition is associated with significantly lower reports. Learning and experience thus do not diminish the effect. Reporting behavior is also quite stable across countries, and adding country fixed effects to our main regression (see Table A.2) increases the adjusted 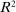 only from 0.370 to 0.457.
only from 0.370 to 0.457.
We next analyze the distribution of reports within each treatment.
Finding 2.For each distribution of true states, more than one state is reported with positive probability.
Figure 2 shows the distribution of reports for all experiments using uniform distributions with six or two states, for example, six-sided die rolls or coin flips. We exclude the few studies that have nonlinear payoff increases from report to report. The figure covers 68 percent of all subjects in the meta study (the vast majority of the remaining subjects are in treatments with non-uniform distributions—where Finding 2 also holds). The size of the bubbles is proportional to the number of subjects in a treatment. The dashed line indicates the truthful distribution. The bold line is the average across all treatments, the gray area around it the 95% confidence interval of the average. As one can see in Figure 2, all possible reports are made with positive probability in almost all treatments. More generally, for each distribution of true states we have data on, the likelihood of the modal report is significantly (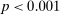 ) lower than 0.79 (or any higher threshold), and thus bounded away from 1. We have enough data to cluster on study for the two distributions in Figure 2 and the result is robust to such clustering.
) lower than 0.79 (or any higher threshold), and thus bounded away from 1. We have enough data to cluster on study for the two distributions in Figure 2 and the result is robust to such clustering.
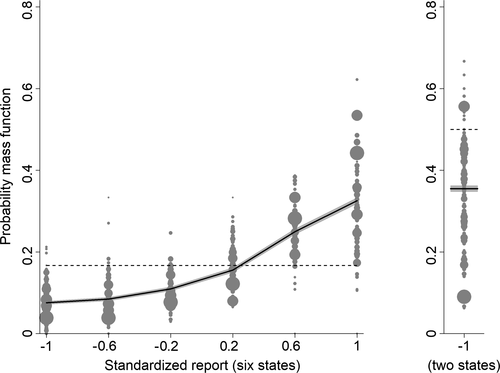
Distribution of reports (uniform distributions with six and two outcomes). Notes: The figure depicts the distribution of reports by treatment. The left panel shows treatments that use a uniform distribution with six states and linear payoff increases. The right panel shows treatments that use a uniform distribution with two states. The right panel only depicts the likelihood that the low-payoff state is reported. The likelihood of the high-payoff state is 1 minus the depicted likelihood. The size of a bubble is proportional to the total number of subjects in that treatment. Only treatments with at least 10 observations are included. The dashed line indicates the truthful distribution at 1/6 and 1/2. The bold line is the average across all treatments; the gray area around it the 95% confidence interval of the average.
Finding 3.When the distribution of true states is uniform, the probability of reporting a given state is weakly increasing in its payoff.
The figure also shows that reports that lead to higher payoffs are generally made more often, both for six-state and two-state distributions. The right panel of Figure 2 plots the likelihood of reporting the low-payoff state (standardized report of −1) for two-state experiments. The vast majority of the bubbles are below 0.5, which implies that the high-payoff report is above 0.5. This positive correlation between the payoff of a given state and its likelihood of being reported holds for all uniform distributions we have data on (OLS regressions, all 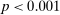 ). We have enough data for the distributions with two, three, six, and 10 states to test report-to-report changes, and find that the reporting likelihood is strictly increasing for two, three, and six states (all
). We have enough data for the distributions with two, three, six, and 10 states to test report-to-report changes, and find that the reporting likelihood is strictly increasing for two, three, and six states (all 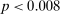 ) and weakly increasing for 10 states. We have enough data to cluster on study for two- and six-state distributions and the result is robust to such clustering.
) and weakly increasing for 10 states. We have enough data to cluster on study for two- and six-state distributions and the result is robust to such clustering.
Finding 4.When the distribution of true states has more than three states, some non-maximal-payoff states are reported more often than their true likelihood.
Interestingly, some reports that do not yield the maximal payoff are reported more often than their truthful probability; in particular, the second highest report in six-state experiments is more likely than 1/6 in almost all treatments. Such over-reporting of non-maximal states occurs in all distributions with more than three states we have data on (see Figure A.7 for the uniform distributions). We test all non-maximal states that are over-reported against their truthful likelihood using a binomial test. The lowest p-value is smaller than 0.001 for all distributions (we exclude distributions for which we have very little data, in particular, only one treatment). We have enough data to cluster on study for the uniform six state distribution and the result is robust to such clustering.
We relegate additional results and all regression analyses to Appendix A.
2 Theory
The meta study shows that subjects display strong aversion to lying and that this results in specific patterns of behavior as summarized by our four findings. In this section, we use a unified theoretical framework to formalize various ways that could potentially explain these patterns (introduced in Section 2.1). In order to address the breadth of plausible explanations and to be able to draw robust conclusions, we consider a large number of potential mechanisms, most of them already discussed, albeit often informally, in the literature. Indeed, one key contribution of our paper is to formalize in a parallel way a variety of suggested explanations. There are three broad types of explanations of why subjects seem to be reluctant to lie: subjects face a lying cost when deviating from the truth; they care about some kind of reputation that is linked to their report (e.g., they care about the beliefs of some audience that observes their report); or they care about social comparisons or social norms which affect the reporting decision. In Section 2.2, we discuss one example model for each of the three types of explanations, including one of the two models that our empirical exercise will not be able to falsify. We discuss the remaining models in the appendices.
To test the models against each other, we first check whether they are able to explain the stylized findings of the meta study (Section 2.3). We find that many different models can do so. We therefore use our theoretical framework to develop four new tests that can distinguish between the models consistent with the meta study (Section 2.4). Table II lists all models and their predictions. For comparison purposes, we also state the results of our experiments in the row labeled Data.
|
New Tests |
||||||
|---|---|---|---|---|---|---|
|
Model |
Can Explain Meta Study |
Shift in True Distribution F |
Shift in Belief About Reports |
Observability of True State ω |
Lying Down Unobs./Obs. |
Section |
|
Lying Costs (LC) |
Yes |
f-invariance |
|
o-invariance |
No/No |
|
|
Social Norms/Comparisons |
||||||
|
Conformity in LC* |
Yes |
drawing out |
affinity |
o-invariance |
No/No |
|
|
Inequality Aversion* |
Yes |
f-invariance |
affinity |
o-invariance |
Yes/Yes |
B.1 |
|
Inequality Aversion + LC* |
Yes |
drawing in |
affinity |
o-invariance |
-/- |
B.2 |
|
Censored Conformity in LC* |
Yes |
f-invariance |
affinity |
o-invariance |
No/No |
B.3 |
|
Reputation |
||||||
|
Reputation for Honesty + LC* |
Yes |
drawing in |
- |
o-shift |
-/No |
|
|
Reputation for Being Not Greedy* |
Yes |
f-invariance |
- |
o-invariance |
Yes/Yes |
B.4 |
|
LC-Reputation* |
Yes |
drawing in |
- |
o-shift |
-/- |
B.5 |
|
Guilt Aversion* |
Yes |
f-invariance |
affinity |
o-invariance |
Yes/Yes |
B.6 |
|
Choice Error |
Yes |
f-invariance |
|
o-invariance |
Yes/Yes |
B.7 |
|
Kőszegi–Rabin + LC |
Yes |
- |
|
o-invariance |
No/No |
B.8 |
|
Data |
drawing in |
|
o-shift |
?/No |
||
- a
The details of the predictions are explained in the text. “-” means that, depending on parameters, any behavior can be explained. The predictions for shifts in F and
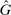 are for two-state distributions, that is,
are for two-state distributions, that is, 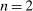 . Models that do not necessarily have unique equilibria are marked with an asterisk (*). For these models, the predictions of f-invariance and o-invariance mean that the set of possible equilibria is invariant to changes in F or observability. The predictions of drawing in/out are based on the assumption of a unique equilibrium.
. Models that do not necessarily have unique equilibria are marked with an asterisk (*). For these models, the predictions of f-invariance and o-invariance mean that the set of possible equilibria is invariant to changes in F or observability. The predictions of drawing in/out are based on the assumption of a unique equilibrium.
2.1 Theoretical Framework
An individual observes state 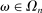 , drawn i.i.d. across individuals from distribution F (with probability mass function f). We will suppose, except where noted, that the drawn state is observed privately by the individual. We suppose
, drawn i.i.d. across individuals from distribution F (with probability mass function f). We will suppose, except where noted, that the drawn state is observed privately by the individual. We suppose 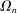 is a subset of equally spaced natural numbers from
is a subset of equally spaced natural numbers from  to
to  , ordered
, ordered 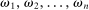 with
with 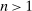 . As in the meta study, we only consider distributions F that have
. As in the meta study, we only consider distributions F that have 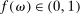 for all
for all 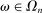 and that either (i) have more than two states and are uniform or symmetric single-peaked, or (ii) have two states (with any distribution). Call this set of distributions
and that either (i) have more than two states and are uniform or symmetric single-peaked, or (ii) have two states (with any distribution). Call this set of distributions 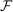 .6 After observing a state, individuals publicly give a report
.6 After observing a state, individuals publicly give a report 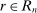 , where
, where 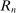 is a subset of equally spaced natural numbers from
is a subset of equally spaced natural numbers from 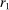 to
to 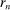 , ordered
, ordered 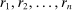 . Individuals receive a monetary payment which is equal to their report r. We suppose that there is a natural mapping between each element of
. Individuals receive a monetary payment which is equal to their report r. We suppose that there is a natural mapping between each element of 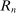 and the corresponding element of
and the corresponding element of 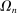 .7 For example, imagine an individual privately flipping a coin. If they report heads, they receive £10; if they report tails, they receive nothing. Then
.7 For example, imagine an individual privately flipping a coin. If they report heads, they receive £10; if they report tails, they receive nothing. Then 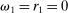 , and
, and 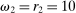 . We denote the distribution over reports as G (with probability mass function g). An individual is a liar if they report
. We denote the distribution over reports as G (with probability mass function g). An individual is a liar if they report 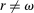 . The proportion of liars at r is
. The proportion of liars at r is 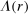 .
.
We denote a utility function as ϕ. For clarity of exposition, we suppose that ϕ is differentiable in all its arguments, except where specifically noted, although our predictions are true even when we drop differentiability and replace our current assumptions with the appropriate analogues (we do maintain continuity of ϕ). We will also suppose, except where specifically noted, that sub-functionals of ϕ are continuous in their arguments.
We suppose that individuals are heterogeneous. They have a type 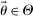 , where
, where  is a vector with J entries, and Θ is the set of potential types
is a vector with J entries, and Θ is the set of potential types 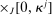 , with
, with 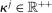 . Each of the J elements of
. Each of the J elements of 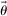 gives the relative trade-off experienced by an individual between monetary benefits and specific non-monetary, psychological costs (e.g., the cost of lying, or reputational costs). When we introduce specific models, we will only focus on the subvector of
gives the relative trade-off experienced by an individual between monetary benefits and specific non-monetary, psychological costs (e.g., the cost of lying, or reputational costs). When we introduce specific models, we will only focus on the subvector of 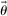 that is relevant for each model (which will usually contain only one or two entries). We suppose that
that is relevant for each model (which will usually contain only one or two entries). We suppose that 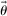 is drawn i.i.d. from H, a non-atomic distribution on Θ. Each entry
is drawn i.i.d. from H, a non-atomic distribution on Θ. Each entry 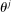 is thus distributed on
is thus distributed on 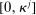 .8 In Appendix E, we show that the set of non-falsified models does not change if we assume that H is degenerate. The exogenous elements of the models are thus the distribution F over states and the distribution H over types, while the distribution G over reports and thus the share of liars at r,
.8 In Appendix E, we show that the set of non-falsified models does not change if we assume that H is degenerate. The exogenous elements of the models are thus the distribution F over states and the distribution H over types, while the distribution G over reports and thus the share of liars at r, 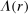 , arise endogenously in equilibrium.
, arise endogenously in equilibrium.
We assume that individuals only report once and there are no repeated interactions. We suppose a continuum of “subject” players and a single “audience” player (the continuum of subjects ensures that any given subject has a negligible impact on the aggregate reporting distribution). The subjects are individuals exactly as described above. The audience takes no action, but rather serves as a player who may hold beliefs about any of the subjects after observing the subjects' reports. The audience could, for example, be the experimenter or another person the subject reveals their report to. Subjects do not observe each others' reports. Utility may depend on the distribution of others' reports, the drawn state-report combinations of others, or beliefs.9 Because subjects take a single action, we can consider a strategy as mapping type and state combinations (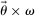 ) into a distribution over reports r.10 When an individual's utility depends on the beliefs of other players, we consider the Sequential Equilibria of the induced psychological game, as introduced by Battigalli and Dufwenberg (2009). (The original psychological game theory framework of Geanakoplos, Pearce, and Stacchetti (1989) cannot allow for utility to depend on updated beliefs.) When utility does not depend on others' beliefs, the analysis can be simplified and we assume the solution concept to be the set of standard Bayes Nash Equilibria of the game. In some of our models, an individual's utility depends only on their own state and report. In this case, our solution concept is simply individual optimization, but for consistency, we also use the words equilibrium and strategy to describe the outcomes of these models.
) into a distribution over reports r.10 When an individual's utility depends on the beliefs of other players, we consider the Sequential Equilibria of the induced psychological game, as introduced by Battigalli and Dufwenberg (2009). (The original psychological game theory framework of Geanakoplos, Pearce, and Stacchetti (1989) cannot allow for utility to depend on updated beliefs.) When utility does not depend on others' beliefs, the analysis can be simplified and we assume the solution concept to be the set of standard Bayes Nash Equilibria of the game. In some of our models, an individual's utility depends only on their own state and report. In this case, our solution concept is simply individual optimization, but for consistency, we also use the words equilibrium and strategy to describe the outcomes of these models.
2.2 Modeling Preferences for Truth-Telling
In this section, we introduce one example for each of the three main categories of lying aversion: lying costs (Section 2.2.1), social norms/comparisons (2.2.2), and reputational concerns (2.2.3). The remaining models are described in Appendix B. Some of these models represent other ways of formalizing the effect of descriptive norms and social comparisons on reporting, including a model of inequality aversion (Appendix B.1); a model that combines lying costs with inequality aversion (B.2); and a social comparisons model in which only subjects who could have lied upwards matter for social comparisons (B.3). Other models build on the idea of reputational concerns and include a model where individuals want to signal to the audience that they place low value on money (B.4); a model where individuals want to cultivate a reputation as a person who has high lying costs (B.5); and a model of guilt aversion (B.6). Finally, we include a model of money maximizing with errors (B.7), and a model that combines lying costs with expectations-based reference-dependence (B.8). In addition, Appendix C describes several models that fail to explain the findings of the meta study and that are therefore not further considered in the body of the paper. Most prominently, we discuss a model in which individuals only care about the audience's belief about their honesty (Appendix C.2).
2.2.1 Lying Costs (LC)
A common explanation for the reluctance to lie is that deviating from telling the truth is intrinsically costly to individuals. The fact that individuals' utility also depends on the realized state, not just their monetary payoff, could come from moral or religious reasons; from self-image concerns (if the individual remembers ω and r);11 from “injunctive” social norms of honesty, that is, norms that are based on a shared perception that lying is socially disapproved; or from the unwillingness to defy the authority of the person or institution who asks for the private information. Such “lying-cost” (LC) models have wide popularity in applications and represent a simple extension of the standard model in which individuals only care about their monetary payoff. Our formulation of this class of models nests all of the lying cost models discussed in the literature, including a fixed cost of lying, a lying cost that is a convex function of the difference between the state and the report, and generalizations that include different lying-cost functions.12
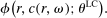
 , which is not necessarily unique. (For some specifications, for example fixed costs of lying, c will not be differentiable in its arguments.) For our calibrational exercises, we normalize
, which is not necessarily unique. (For some specifications, for example fixed costs of lying, c will not be differentiable in its arguments.) For our calibrational exercises, we normalize 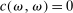 , so that individuals experience no cost when they tell the truth. In order to make the model non-trivial, we suppose that there is at least one non-maximal state ω such that there exists an
, so that individuals experience no cost when they tell the truth. In order to make the model non-trivial, we suppose that there is at least one non-maximal state ω such that there exists an  where
where 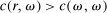 (otherwise, no one would ever pay any costs to lying). The only element of
(otherwise, no one would ever pay any costs to lying). The only element of  that affects utility is the scalar
that affects utility is the scalar 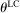 which governs the weight that an individual applies to the lying cost. We make a few assumptions on ϕ. First, ϕ is strictly increasing in the first argument, fixing all the other arguments; this captures the property that utility is increasing in the monetary payment received. Second, ϕ is decreasing in the second argument, fixing all the other arguments, capturing the property that utility falls as the cost of lying increases. In particular, it is strictly decreasing for all
which governs the weight that an individual applies to the lying cost. We make a few assumptions on ϕ. First, ϕ is strictly increasing in the first argument, fixing all the other arguments; this captures the property that utility is increasing in the monetary payment received. Second, ϕ is decreasing in the second argument, fixing all the other arguments, capturing the property that utility falls as the cost of lying increases. In particular, it is strictly decreasing for all 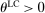 . Third and fourth, fixing all other arguments, ϕ is (weakly) decreasing in
. Third and fourth, fixing all other arguments, ϕ is (weakly) decreasing in 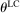 , and the cross partial of ϕ with respect to c and
, and the cross partial of ϕ with respect to c and 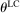 is strictly negative, while other cross partials are 0. This captures the properties that an individual with a higher draw of
is strictly negative, while other cross partials are 0. This captures the properties that an individual with a higher draw of 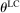 has both a higher utility cost of lying, for the same “sized” lie, and faces a higher marginal cost of lying. In other words, utility exhibits increasing differences with respect to c and
has both a higher utility cost of lying, for the same “sized” lie, and faces a higher marginal cost of lying. In other words, utility exhibits increasing differences with respect to c and 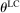 .13 The solution to LC models can be found by simply solving a single decision maker's optimization problem.
.13 The solution to LC models can be found by simply solving a single decision maker's optimization problem.2.2.2 Social Norms: Conformity in LC
Another potential explanation for lying aversion extends the intuition of the LC model. It posits that individuals care about social norms or social comparisons which inform their reporting decision. The leading example is that individuals may feel less bad about lying if they believe that others are lying, too. Importantly, the norms here are “descriptive” in the sense that they are based on the perception of what others normally do, rather than “injunctive,” which are instead based on the perception of what ought to be done and do not depend on the behavior of others (injunctive norms are better captured by LC models). We call such a model “Conformity in LC.” Such concerns for social norms are discussed, for example, in Gibson, Tanner, and Wagner (2013), Rauhut (2013), and Diekmann, Przepiorka, and Rauhut (2015). Our model follows the intuition of Weibull and Villa (2005). We suppose that an individual's total utility loss from misreporting depends both on an LC cost (as described in the previous model), but also on the average LC cost in society. The latter depends not just on players' actions, but on the profile of joint state-report combinations across all individuals. Because we can think of any individual's drawn state as part of their privately observed type, we use the framework of Bayes Nash Equilibrium.14
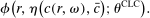
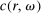 has the same interpretation and assumptions as in the LC model and types are heterogeneous in the scalar
has the same interpretation and assumptions as in the LC model and types are heterogeneous in the scalar 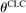 (where CLC denotes the “Conformity in LC” model specific parameter; analogous abbreviations are used for the rest of the models); the rest of the vector
(where CLC denotes the “Conformity in LC” model specific parameter; analogous abbreviations are used for the rest of the models); the rest of the vector  again does not affect utility.
again does not affect utility.  is the average incurred LC cost in society. This average cost is determined in equilibrium, and thus all individuals know what it is; for notational ease, we suppress the dependence of
is the average incurred LC cost in society. This average cost is determined in equilibrium, and thus all individuals know what it is; for notational ease, we suppress the dependence of  on the other parameters of the model. η captures the “normalized cost of lying,” that is, the cost of lying conditional on the incurred LC cost in society (for our calibrational exercises, we suppose
on the other parameters of the model. η captures the “normalized cost of lying,” that is, the cost of lying conditional on the incurred LC cost in society (for our calibrational exercises, we suppose 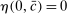 ) and is strictly increasing in its first argument. For
) and is strictly increasing in its first argument. For 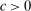 , η is strictly falling in the second argument so that the normalized cost is increasing in the individual's own personal lying cost and falling in the aggregate LC cost, that is, their lying costs are falling as others lie more (for
, η is strictly falling in the second argument so that the normalized cost is increasing in the individual's own personal lying cost and falling in the aggregate LC cost, that is, their lying costs are falling as others lie more (for 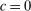 , the partial of η with respect to its second argument is 0). As in the previous model, ϕ is strictly increasing in its first argument, and decreasing in the second argument (strictly so for all
, the partial of η with respect to its second argument is 0). As in the previous model, ϕ is strictly increasing in its first argument, and decreasing in the second argument (strictly so for all 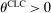 ). ϕ is (weakly) decreasing in
). ϕ is (weakly) decreasing in 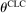 fixing the first two arguments, and the cross partial of ϕ with respect to η and
fixing the first two arguments, and the cross partial of ϕ with respect to η and 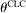 is strictly negative, while other cross partials are 0. These assumptions are analogous to the ones presented in the previous models and capture the same intuitions.
is strictly negative, while other cross partials are 0. These assumptions are analogous to the ones presented in the previous models and capture the same intuitions.2.2.3 Reputation for Honesty + LC
A different way to extend the LC model is to allow individuals to experience both an intrinsic cost of lying, as well as reputational costs associated with inference about their honesty (e.g., Khalmetski and Sliwka (forthcoming), Gneezy, Kajackaite, and Sobel (2018)). We suppose that an individual's utility is falling in the belief of the audience player that the individual's report is not honest, that is, has a state not equal to the report. Akerlof (1983) provided the first discussion in the economics literature that honesty may be generated by reputational concerns, and many recent papers have built on this intuition.15 Thus, an individual's utility is belief-dependent, specifically depending on the audience player's updated beliefs. Thus, we must use the tools of psychological game theory to analyze the game. We use the framework of Battigalli and Dufwenberg (2009) in our analysis.16 Of course, the audience cannot directly observe whether a player is lying, and has to base their beliefs on the observable report r. Utility is thus a decreasing function of the audience's belief about whether an individual lied. Because the audience player makes correct Bayesian inference based on observing the report and knowing the equilibrium strategies, their posterior belief about whether an individual is a liar, conditional on a report r, is 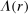 , the fraction of liars at r in equilibrium. We therefore directly assume that utility depends on
, the fraction of liars at r in equilibrium. We therefore directly assume that utility depends on 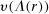 , with υ a strictly increasing function.
, with υ a strictly increasing function.
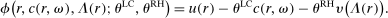
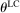 and
and 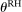 and the rest of
and the rest of 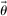 does not affect utility. c is as described in the LC model. υ is a strictly increasing function of
does not affect utility. c is as described in the LC model. υ is a strictly increasing function of 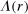 with a minimum at 0 (and in calibrational exercises, we normalize
with a minimum at 0 (and in calibrational exercises, we normalize  . Thus, the individual likes more money, but dislikes lying and being perceived as a liar by the audience. The functional form implies analog patterns for the cross partials as the previous models.18
. Thus, the individual likes more money, but dislikes lying and being perceived as a liar by the audience. The functional form implies analog patterns for the cross partials as the previous models.182.3 Distinguishing Models Using the Meta Study
We now turn to understanding how our models can be distinguished in the data. The first test is whether the models can match the four findings of the meta study. We find that the three models presented in the previous section, as well as all those listed in Appendix B, can do so.
Proposition 1.There exists a parameterization of the LC model, the Conformity in LC model, the Reputation for Honesty + LC model, and of all other models listed in Appendix B (i.e., Inequality Aversion; Inequality Aversion + LC; Censored Conformity in LC; Reputation for Being Not Greedy; LC-Reputation; Guilt Aversion; Choice Error; and Kőszegi and Rabin + LC) which can explain Findings 1–4 for any number of states n and for any 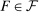 .
.
All proofs for the results in this section are collected in Appendix D. The proof for the LC model constructs one example utility function, combining a fixed cost and a convex cost of lying, and then shows that it yields Findings 1–4 for any n and any 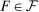 . Many of the other models considered in this paper contain the LC model as limit case and can therefore explain Findings 1–4. However, there are several models, for example, the Inequality Aversion model (Appendix B.1) or the Reputation for Being Not Greedy model (B.4), which rely on very different mechanisms and can still explain Findings 1–4.
. Many of the other models considered in this paper contain the LC model as limit case and can therefore explain Findings 1–4. However, there are several models, for example, the Inequality Aversion model (Appendix B.1) or the Reputation for Being Not Greedy model (B.4), which rely on very different mechanisms and can still explain Findings 1–4.
2.4 Distinguishing Models Using New Empirical Tests
Proposition 1 shows that the existing literature, reflected in the meta study, cannot pin down the mechanism which generates lying aversion. The meta study does falsify quite a few popular models, which we discuss in Appendix C, but the data are not strong enough to narrow the set of surviving models further down. This motivates us to devise four additional empirical tests which can distinguish between the models that are in line with the meta study. Three of the four new tests are “comparative statics” and one is an equilibrium property: (i) how does the distribution of true states affect the distribution of reports; (ii) how does the belief about the reports of other subjects influence the distribution of reports; (iii) does the observability of the true state affect the distribution of reports; (iv) will some subjects lie downwards if the true state is observable. As a prediction (iv′), we also derive whether some subjects will lie downwards if the true state is not observable, as in the standard FFH paradigm. We cannot test this last prediction in our data but state it nonetheless as it is helpful in building intuition regarding the models as well as important for potential applications.19
We derive predictions for each model and for each test using very general specifications of individual heterogeneity and the functional form. We present predictions for an arbitrary number of states n and for the special case of 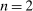 . On the one hand, allowing for an arbitrary number of states generates predictions that are applicable to a larger set of potential settings. On the other hand, restricting
. On the one hand, allowing for an arbitrary number of states generates predictions that are applicable to a larger set of potential settings. On the other hand, restricting 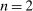 allows us to make sharper predictions, and thus potentially falsify a larger set of models. For example, for models where individuals care about what others do (e.g., social comparison models), it does not matter whether individuals care about the average report or the distribution of reports when
allows us to make sharper predictions, and thus potentially falsify a larger set of models. For example, for models where individuals care about what others do (e.g., social comparison models), it does not matter whether individuals care about the average report or the distribution of reports when 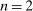 . For models that rule out downwards lying, the binary setting also allows us to back out the full reporting strategy of individuals without actually observing the true state: the high-payoff state will be reported truthfully, so we can deduct the expected number of high-payoff states from the number of observed high-payoff reports and we are left with the reports made by the subjects who have drawn the low-payoff state. Moreover, conducting our new tests with two-state distributions is simpler and easier to understand for subjects. Recall that across all results, we only consider distributions
. For models that rule out downwards lying, the binary setting also allows us to back out the full reporting strategy of individuals without actually observing the true state: the high-payoff state will be reported truthfully, so we can deduct the expected number of high-payoff states from the number of observed high-payoff reports and we are left with the reports made by the subjects who have drawn the low-payoff state. Moreover, conducting our new tests with two-state distributions is simpler and easier to understand for subjects. Recall that across all results, we only consider distributions 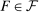 .
.
The models, as well as the predictions they generate in each of the tests, are listed in Table II. We report the two-state predictions in the columns describing the effect of shifts in the distributions of true states F and beliefs about others' reports 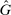 (see below for details), since we use two-state distributions in our new experimental tests of these predictions. Some of the models we consider do not guarantee a unique reporting distribution G without additional parametric restrictions. We discuss below in more detail how we deal with potential non-uniqueness for each prediction and we mark the models which do not necessarily have unique equilibria with an asterisk (*) in Table II. Importantly, no model is ruled out solely on the basis of predictions that are based on an assumption of uniqueness. Similarly, the models that cannot be falsified by our data are not consistent solely because of potential multiplicity of equilibria.
(see below for details), since we use two-state distributions in our new experimental tests of these predictions. Some of the models we consider do not guarantee a unique reporting distribution G without additional parametric restrictions. We discuss below in more detail how we deal with potential non-uniqueness for each prediction and we mark the models which do not necessarily have unique equilibria with an asterisk (*) in Table II. Importantly, no model is ruled out solely on the basis of predictions that are based on an assumption of uniqueness. Similarly, the models that cannot be falsified by our data are not consistent solely because of potential multiplicity of equilibria.
We now turn to discussing our four empirical tests. The first test is about how the distribution of reports G (recall that 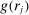 gives the unconditional fraction of individuals giving report
gives the unconditional fraction of individuals giving report 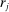 ) changes when the higher states are more likely to be drawn (but while maintaining the same set of support for the distribution). Specifically, we suppose that we induce a shift in the distribution of states F (recall that
) changes when the higher states are more likely to be drawn (but while maintaining the same set of support for the distribution). Specifically, we suppose that we induce a shift in the distribution of states F (recall that 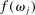 gives the probability that state
gives the probability that state 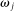 is drawn) that satisfies first-order stochastic dominance. We then look at 1 minus the ratio of the observed number of reports of the lowest state to the expected number of draws of the lowest state:
is drawn) that satisfies first-order stochastic dominance. We then look at 1 minus the ratio of the observed number of reports of the lowest state to the expected number of draws of the lowest state: 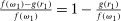 . For those models in which no individual lies downwards, we can interpret the statistic as the proportion of people who draw
. For those models in which no individual lies downwards, we can interpret the statistic as the proportion of people who draw 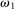 but report something higher, that is
but report something higher, that is 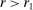 .
.
Definition 1.Consider two pairs of distributions: 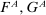 and
and 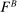 ,
, 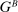 , where
, where 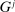 is the reporting distribution associated with
is the reporting distribution associated with 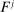 , and where
, and where 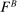 strictly first-order stochastically dominates
strictly first-order stochastically dominates 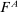 and they all have full support. A model exhibits drawing in/drawing out/f-invariance if
and they all have full support. A model exhibits drawing in/drawing out/f-invariance if 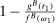 is larger than/smaller than/the same as
is larger than/smaller than/the same as 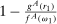 .
.
Thus, the term “drawing in” means that the lowest state is even more under-reported when higher states become more likely. “Drawing out” refers to the opposite tendency. As we will show below, several very different motivations can lead to drawing in. For example, increasing the true probability of high states increases the likelihood that a high report is true, leading subjects who care about being perceived as honest, as in our Reputation for Honesty + LC model (Section 2.2.3), to make such reports more often. But increasing the true probability of high states also increases the likelihood that other subjects report high, pushing subjects who dislike inequality (Appendix B.2) to report high states. And subjects who compare their outcome to their recent expectations (Appendix B.8) could also react in this way.20
The second test looks at how an individual's probability of reporting the highest state will change when we exogenously shift their belief about the distribution of reports. We will refer to 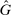 as the beliefs of players about the distribution of reports. In equilibrium, given correct beliefs about others,
as the beliefs of players about the distribution of reports. In equilibrium, given correct beliefs about others, 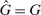 . Our experiment focuses on manipulating the beliefs about others, that is,
. Our experiment focuses on manipulating the beliefs about others, that is, 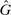 , so that they may no longer be correct, and then observing the resulting actual reporting distribution G. We focus on situations where there is full support on all reports in both beliefs and actuality.
, so that they may no longer be correct, and then observing the resulting actual reporting distribution G. We focus on situations where there is full support on all reports in both beliefs and actuality.
Definition 2.Fix a distribution over states F and consider two pairs of distributions 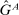 ,
, 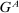 and
and 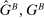 , where
, where 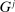 is the reporting distribution induced by F and by the belief that others will report according to
is the reporting distribution induced by F and by the belief that others will report according to 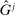 . Moreover, suppose all exhibit full support and
. Moreover, suppose all exhibit full support and 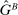 strictly first-order stochastically dominates
strictly first-order stochastically dominates 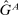 . A model exhibits affinity/aversion/
. A model exhibits affinity/aversion/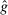 -invariance if
-invariance if 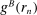 is larger than/smaller than/the same as
is larger than/smaller than/the same as 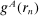 .
.
Thus, the term “affinity” means that reporting of the highest state increases when the subject believes that higher states are more likely to be reported by others. The term “aversion” refers to the opposite tendency. Such an exercise allows us to test the models in one of three ways. First, in some models, for example, Inequality Aversion (Appendix B.1), individuals care directly about the reports made by others and thus 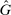 (or a sufficient statistic for it) directly enters the utility. Therefore, we can immediately assess the effect of a shift in
(or a sufficient statistic for it) directly enters the utility. Therefore, we can immediately assess the effect of a shift in  on behavior.21 For these models, shifting an individual's belief about
on behavior.21 For these models, shifting an individual's belief about  directly alters their best response (and since subjects are best responding to their
directly alters their best response (and since subjects are best responding to their  , which may be different from the actual G, we may observe out-of-equilibrium behavior). These models all predict affinity.
, which may be different from the actual G, we may observe out-of-equilibrium behavior). These models all predict affinity.
Second, in some other models (Conformity in LC and Censored Conformity in LC), individuals care about the profile of joint state-report combinations across other individuals (i.e., the amount of lying by others). In these models, no individual lies downwards and so, for binary states,  contains sufficient information about the joint state-report combinations. Thus, shifting
contains sufficient information about the joint state-report combinations. Thus, shifting  directly alters an individual's best response. These models again predict affinity.
directly alters an individual's best response. These models again predict affinity.
Finally, this exercise allows us, albeit indirectly, to understand what happens when beliefs about H (the distribution of 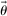 ) change. Directly changing this belief is difficult since this requires identifying
) change. Directly changing this belief is difficult since this requires identifying 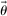 for each subject and then conveying this insight to all subjects. However, for models with a unique equilibrium, because G is an endogenous equilibrium outcome, shifts in
for each subject and then conveying this insight to all subjects. However, for models with a unique equilibrium, because G is an endogenous equilibrium outcome, shifts in 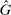 can only be rationalized by subjects as shifts in some underlying exogenous parameter—which has to be H, since our experiment fixes all other parameters (e.g., F and whether states are observable).22 For many of these models, the conditions defining the unique equilibrium reporting strategy are invariant to shifts in
can only be rationalized by subjects as shifts in some underlying exogenous parameter—which has to be H, since our experiment fixes all other parameters (e.g., F and whether states are observable).22 For many of these models, the conditions defining the unique equilibrium reporting strategy are invariant to shifts in 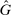 and H, which means that our treatment should not affect behavior. For another set of models, in particular Reputation for Being Not Greedy, Reputation for Honesty + LC, and LC-Reputation, there is no simple mapping from
and H, which means that our treatment should not affect behavior. For another set of models, in particular Reputation for Being Not Greedy, Reputation for Honesty + LC, and LC-Reputation, there is no simple mapping from 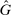 to beliefs about H and a shift in
to beliefs about H and a shift in 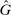 could lead to affinity, aversion, or
could lead to affinity, aversion, or 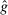 -invariance.
-invariance.
Our third test considers whether or not it matters for the distribution of reports that the audience player can observe the true state. In particular, we will test whether individuals' reports change if the experimenter can observe not only the report, but also the state for each individual.
Definition 3.A model exhibits o-shift if G changes when the true state becomes observable to the audience, and o-invariance if G is not affected by the observability of the state.
In some of the models we consider, the costs associated with lying are internal and therefore do not depend on whether an audience is able to observe the state or not. In other models, however, the costs depend on the inference the audience is able to make, and so observability of the true state affects predictions.23
Our fourth test comes in two parts. Both parts try to understand whether or not there are individuals who engage in downwards lying, that is, draw 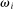 and report
and report  with
with 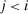 . The first is whether downwards lying can occur in an equilibrium with observability of the state by the audience and where G features full support. The second is an analogous test but in the situation where the state is not observed by the audience. We will only focus on the former test in our experiments.
. The first is whether downwards lying can occur in an equilibrium with observability of the state by the audience and where G features full support. The second is an analogous test but in the situation where the state is not observed by the audience. We will only focus on the former test in our experiments.
Definition 4.Fix a distribution over states F and an associated full-support distribution G over reports. The model exhibits downwards lying if there exists some individual who draws 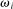 but reports
but reports 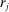 where
where 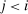 . The model does not exhibit downwards lying if there is no such individual.
. The model does not exhibit downwards lying if there is no such individual.
Although lying down may seem counterintuitive, as we will show below, there can be a number of reasons why individuals may want to lie downwards. In models where individuals are concerned with reputation, lying downwards may be beneficial if low reports are associated with a better reputation than high reports. Alternatively, in models of social comparisons, such as the inequality aversion models, downwards lying may arise because individuals aim to conform to others' reports.
The following proposition summarizes the predictions for the three models described above.
Proposition 2.
- • Suppose individuals have LC utility. For an arbitrary number of states n, we have f-invariance,
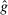 -invariance, o-invariance, and no lying down when the state is unobserved or observed.
-invariance, o-invariance, and no lying down when the state is unobserved or observed. - • Suppose individuals have Conformity in LC utility. For arbitrary n, depending on parameters, we may have drawing in, drawing out or f-invariance, we may have affinity, aversion or
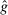 -invariance, we have o-invariance and no lying down when the state is unobserved or observed. For
-invariance, we have o-invariance and no lying down when the state is unobserved or observed. For 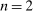 , we have drawing out when the equilibrium is unique and we have affinity.
, we have drawing out when the equilibrium is unique and we have affinity. - • Suppose individuals have Reputation for Honesty + LC utility. For arbitrary n, depending on parameters, we may have drawing in, drawing out or f-invariance, we may have affinity, aversion or
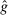 -invariance, we have o-shift, depending on parameters, we may have lying down or not when the state is unobserved, and we have no lying down when the state is observed. For
-invariance, we have o-shift, depending on parameters, we may have lying down or not when the state is unobserved, and we have no lying down when the state is observed. For 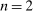 , we have drawing in when the equilibrium is unique.
, we have drawing in when the equilibrium is unique.
“Depending on parameters” refers to the distribution over states F, the distribution H over types, any sub-functions that might be introduced in a model definition, for example, the cost function c in the LC model, and when considering affinity, aversion, and 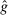 -invariance,
-invariance, 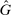 (as this is something we experimentally manipulate). In the cases when predictions depend on parameters, the proofs will provide examples for each possible behavior. If the statement is unqualified, it means that it holds for any
(as this is something we experimentally manipulate). In the cases when predictions depend on parameters, the proofs will provide examples for each possible behavior. If the statement is unqualified, it means that it holds for any 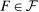 , any H, sub-functions, and
, any H, sub-functions, and  .
.
Before moving on, we provide some intuition for the results. For simplicity, we focus on two-state/report distributions. In the LC model, individuals never lie downwards, because they (weakly) pay a lying cost and also receive a lower monetary payoff when doing so. Since only their own state and their own report matter for utility, conditional on drawing the low state, for a fixed  , an individual will always make the same report, regardless of F or
, an individual will always make the same report, regardless of F or  . Thus, we observe both f-invariance and
. Thus, we observe both f-invariance and  -invariance. Last, the lying cost is an internal cost and does not depend on the inference others are making about any given person. Thus, individuals do not care whether their state is observed.
-invariance. Last, the lying cost is an internal cost and does not depend on the inference others are making about any given person. Thus, individuals do not care whether their state is observed.
In the Conformity in LC models, individuals will never lie downwards since, as in the LC model, they would face a lower monetary payoff as well as a weakly higher cost of lying. Morever, with a unique equilibrium, as 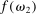 increases, more individuals draw the high state and can report
increases, more individuals draw the high state and can report 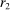 without having to lie. Thus, the average incurred cost of lying falls. This increases the normalized cost of lying (η) for all individuals. Thus, an individual who draws
without having to lie. Thus, the average incurred cost of lying falls. This increases the normalized cost of lying (η) for all individuals. Thus, an individual who draws 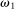 , and was indifferent before between
, and was indifferent before between 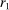 and
and 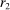 , will now strictly prefer
, will now strictly prefer 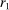 . This implies drawing out. In the Conformity in LC model, because G enters directly into the utility function and because no one lies downwards, we can tell how the individual's best response changes with shifts in expected G, that is,
. This implies drawing out. In the Conformity in LC model, because G enters directly into the utility function and because no one lies downwards, we can tell how the individual's best response changes with shifts in expected G, that is, 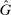 . Fixing F, if
. Fixing F, if 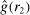 increases, more people draw the low state but say the high report. This means that more individuals are expected to lie, and so the normalized cost of lying (η) decreases. Thus, individuals who draw the low report will be more likely to say the high report, that is, we have affinity. Last, as in the LC model, these costs do not depend on any inference others are making, and so individuals do not care whether their state is observed.
increases, more people draw the low state but say the high report. This means that more individuals are expected to lie, and so the normalized cost of lying (η) decreases. Thus, individuals who draw the low report will be more likely to say the high report, that is, we have affinity. Last, as in the LC model, these costs do not depend on any inference others are making, and so individuals do not care whether their state is observed.
In the Reputation for Honesty + LC model, because individuals have a concern for reputation and also have lying costs, they may or may not lie down if the state is unobserved. If an individual is motivated relatively more by reputational concerns, then they will lie down if the state is unobserved. In contrast, if lying costs dominate as a motivation, they will not lie down. If the state is observed, no one lies downwards. Although multiple equilibria may occur, whenever the equilibrium is unique, the Reputation for Honesty + LC model exhibits drawing in. As 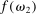 increases, some individuals who previously drew
increases, some individuals who previously drew 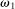 will now draw
will now draw 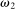 . Those individuals now face a lower LC cost when giving the high report (which is in fact zero). Fixing the reputational cost, this implies some of them will now give the high report (instead of the low report). Fixing the behavior of others, this reduces the fraction of liars giving the high report and thus the reputational cost of the high report decreases; and similarly, increases the fraction of liars giving the low report. This reduces the (relative) cost of giving the high report even more. Therefore, we observe drawing in. Our intuition here relies on partial equilibrium reasoning, but the formal proof shows how to extend this to full equilibrium reasoning. Even with a unique equilibrium, we may observe either aversion, affinity, or
. Those individuals now face a lower LC cost when giving the high report (which is in fact zero). Fixing the reputational cost, this implies some of them will now give the high report (instead of the low report). Fixing the behavior of others, this reduces the fraction of liars giving the high report and thus the reputational cost of the high report decreases; and similarly, increases the fraction of liars giving the low report. This reduces the (relative) cost of giving the high report even more. Therefore, we observe drawing in. Our intuition here relies on partial equilibrium reasoning, but the formal proof shows how to extend this to full equilibrium reasoning. Even with a unique equilibrium, we may observe either aversion, affinity, or 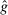 -invariance since it depends on how the distribution of H is perceived to have changed when
-invariance since it depends on how the distribution of H is perceived to have changed when 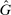 shifts.24 Because the model includes reputational costs, whether or not the audience observes just the report, or also the state, matters for behavior.
shifts.24 Because the model includes reputational costs, whether or not the audience observes just the report, or also the state, matters for behavior.
In Appendix F, we provide additional evidence regarding predictions of the Kőszegi–Rabin + LC model which are not listed in the table. We also test specific f-invariance predictions for the LC model in a 10-state experiment, where we show that drawing-in like behavior also obtains in an experiment with 10 states.
3 New Experiments
In this section, we report a large-scale (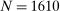 ) set of experiments designed to implement the four tests outlined above. The experiments were conducted with students at the University of Nottingham and University of Oxford. Subjects were recruited using ORSEE (Greiner (2015)). The computerized parts of the experiments were programmed in z-Tree (Fischbacher (2007)). All instructions and questionnaires are available in Appendix G.
) set of experiments designed to implement the four tests outlined above. The experiments were conducted with students at the University of Nottingham and University of Oxford. Subjects were recruited using ORSEE (Greiner (2015)). The computerized parts of the experiments were programmed in z-Tree (Fischbacher (2007)). All instructions and questionnaires are available in Appendix G.
3.1 Shifting the Distribution of True States F
We test the effect of a shift in the distribution of true states F using treatments with two-state distributions. Subjects are invited to the laboratory for a short session in which they are asked to complete a questionnaire that contains some basic socio-demographic questions as well as filler questions about their financial status and money-management ability that serve to increase the length of the questionnaire so that the task appears meaningful. Subjects are told that, they would receive money for completing the questionnaire and that the exact amount would be determined by randomly drawing a chip from an envelope. The chips have either the number 4 or 10 written on them, representing the amount of money in GBP that subjects are paid if they draw a chip with that number. Thus, drawing a chip with 4 on it represents drawing 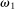 and drawing a chip with 10 represents drawing
and drawing a chip with 10 represents drawing 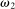 . Reports of 4 and 10 are similarly
. Reports of 4 and 10 are similarly 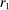 and
and 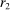 . The chips are arranged on a tray on the subject's desk such that subjects are fully aware of the distribution F (see Appendix G for a picture of the lab setup). Subjects are told that, at the end of the questionnaire, they need to place all chips into a provided envelope, shake the envelope a few times, and then randomly draw a chip from the envelope. They are told to place the drawn chip back into the envelope and to write down the number of their chip on a payment sheet. Subjects are then paid according to the number reported on their payment sheet by the experimenter who has been waiting outside the lab for the whole time.
. The chips are arranged on a tray on the subject's desk such that subjects are fully aware of the distribution F (see Appendix G for a picture of the lab setup). Subjects are told that, at the end of the questionnaire, they need to place all chips into a provided envelope, shake the envelope a few times, and then randomly draw a chip from the envelope. They are told to place the drawn chip back into the envelope and to write down the number of their chip on a payment sheet. Subjects are then paid according to the number reported on their payment sheet by the experimenter who has been waiting outside the lab for the whole time.
We conduct two between-subject treatments, varying the distribution of chips that subjects have on their trays. In one treatment, the tray contains 45 chips with the number 4 and 5 chips with the number 10. In the other treatment, the tray contains 20 chips with the number 4 and 30 chips with the number 10. We label the two treatments F_LOW and F_HIGH, respectively, to indicate the different probabilities of drawing the high state (10 percent vs. 60 percent). Note that the distribution used in F_HIGH first-order stochastically dominates the distribution in F_LOW in line with Definition 1. We select samples sizes such that the expected number of low states is the same (and equal to 131) in the two treatments. Thus, we have 146 subjects in F_LOW and 328 subjects in F_HIGH. Most of the sessions were conducted in Nottingham and some in Oxford between June and December 2015.
3.2 Results
Finding 5.We observe drawing in, that is, the statistic 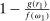 is significantly higher in F_HIGH than F_LOW.
is significantly higher in F_HIGH than F_LOW.
Figure 3 shows the values of the statistic 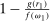 across the two treatments. In F_LOW, we expect 131 subjects to draw the low £4 payment and we observe 80 subjects actually reporting 4, that is, our statistic is equal to
across the two treatments. In F_LOW, we expect 131 subjects to draw the low £4 payment and we observe 80 subjects actually reporting 4, that is, our statistic is equal to 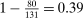 . In F_HIGH, we also expect 131 subjects to draw 4, but only 43 subjects report to have done so, so our statistic is equal to 0.67 (this means that 45 percent of subjects in F_LOW and 87 percent in F_HIGH report 10). This difference of almost 30 percentage points is very large and highly significant (
. In F_HIGH, we also expect 131 subjects to draw 4, but only 43 subjects report to have done so, so our statistic is equal to 0.67 (this means that 45 percent of subjects in F_LOW and 87 percent in F_HIGH report 10). This difference of almost 30 percentage points is very large and highly significant ( , OLS with robust SE;
, OLS with robust SE; 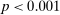 ,
, 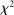 test).25
test).25
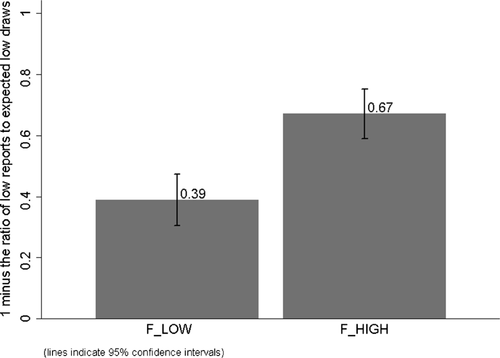
Effect of shifting the distribution of true states.
3.3 Shifting Beliefs About the Distribution of Reports 
Our next set of treatments is designed to test predictions concerning the effects of a shift in subjects' beliefs about the distribution of reports, that is,  . There are three other studies testing the effect of beliefs on reporting (Rauhut (2013), Diekmann, Przepiorka, and Rauhut (2015), and Gächter and Schulz (2016a)). These studies affect beliefs by showing to subjects the actual past behavior of participants. Diekmann, Przepiorka, and Rauhut (2015) and Gächter and Schulz (2016a) found no effect and Rauhut (2013) found a positive effect. Rauhut (2013), however, compared subjects who have initially too high beliefs that are then updated downwards to subjects who have initially too low beliefs that are updated upwards. The treatment is thus not assigned fully randomly.
. There are three other studies testing the effect of beliefs on reporting (Rauhut (2013), Diekmann, Przepiorka, and Rauhut (2015), and Gächter and Schulz (2016a)). These studies affect beliefs by showing to subjects the actual past behavior of participants. Diekmann, Przepiorka, and Rauhut (2015) and Gächter and Schulz (2016a) found no effect and Rauhut (2013) found a positive effect. Rauhut (2013), however, compared subjects who have initially too high beliefs that are then updated downwards to subjects who have initially too low beliefs that are updated upwards. The treatment is thus not assigned fully randomly.
We use an alternative and complementary method. Our strategy to shift beliefs is based on an anchoring procedure (Tversky and Kahneman (1974)): we ask subjects to think about the behavior of hypothetical participants in the F_LOW experiment and we anchor them to think about participants who reported the high state more or less often. The advantage of our design is that we do not need to sample selectively from the distribution of actual past behavior of other subjects. This could be problematic because, if the past behavior is highly selected but presented as if representative, it could be judged as implicitly deceiving subjects and could confound results of an experimental study on deception. We are not aware of other studies that have used anchoring to affect beliefs before.
In our setup, subjects are asked to read a brief description of a “potential” experiment which follows the instructions used in the F_LOW experiment, that is, 90 percent probability of the low payment and 10 percent probability of the high payment. Subjects also have on their desk the tray with chips and envelope that subjects in the F_LOW experiment had used. Subjects are then asked to “imagine” two “possible outcomes” of the potential experiment. There are two between-subject treatments, varying the outcomes subjects are asked to imagine. In treatment G_LOW, the outcomes have 20 percent and 30 percent of hypothetical participants reporting to have drawn a 10, while in treatment G_HIGH, these shares are 70 percent and 80 percent. Subjects are then asked a few questions about these outcomes.26 Subjects are then told that the experiment has actually been run in the same laboratory in the previous year and they are asked to estimate the fraction of participants in the actual experiment who have reported a 10. Subjects are paid £3 if their estimate is correct (within an error margin of ±3 percentage points). This mechanism is very simple and easier to explain and understand than proper scoring rules. It elicits in an incentive-compatible way the mode (or more precisely, the mid-point of the 6-percentage point interval with the highest likelihood) of a subject's distribution of estimates. We use subjects' estimates to check whether our anchoring manipulation is successful in shifting subjects' beliefs.27
Finally, after answering a few additional socio-demographic questions, subjects are told that they will be paid an additional amount of money on top of their earnings from the belief elicitation. To determine how much money they are paid, subjects are asked to take part in the F_LOW experiment themselves. The procedure is identical to the description of F_LOW in the previous section. The experiments were conducted in Nottingham between March and May 2016 with a total of 340 subjects (173 in G_LOW, 167 in G_HIGH).
3.4 Results
We start by showing the effect of the anchors on subjects' beliefs.
Finding 6.The anchors significantly shift beliefs. Estimates of the fraction of participants reporting a 10 are more than 20 percentage points higher in G_HIGH than G_LOW.
Figure 4 shows the distributions of estimates of the proportion of reported 10's made by subjects across the two treatments. The distribution of the G_HIGH treatment is strongly shifted to the right relative to G_LOW, and practically first-order stochastically dominates it, in line with Definition 2. On average, subjects in G_LOW believe that 41 percent of participants in the F_LOW experiment have reported a 10. In G_HIGH, the average belief is 62 percent (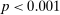 , OLS with robust SE;
, OLS with robust SE; 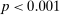 , Wilcoxon rank-sum test).
, Wilcoxon rank-sum test).
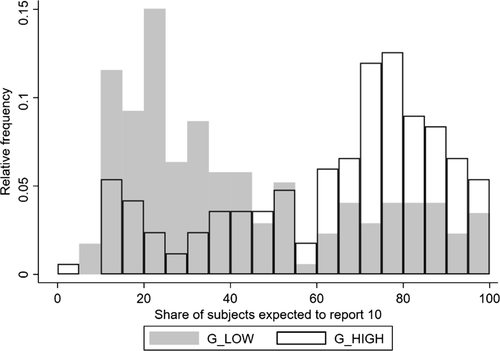
Distribution of beliefs about proportion of reported 10's.
Having established that our manipulation is successful in shifting beliefs about reports in the expected direction, our next step is to examine the effects of this shift in beliefs on subjects' actual reporting behavior.
Finding 7.The fraction of subjects reporting a 10 is not significantly different between G_HIGH and G_LOW, that is, we cannot reject the null hypothesis of 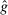 -invariance. The point estimate is in the direction of aversion.
-invariance. The point estimate is in the direction of aversion.
Figure 5 shows the share of subjects reporting a 10 across the two treatments. Recall that, in both treatments, the true probability of drawing a 10 is 10 percent (this is indicated by the dashed line in the figure). We observe 55 percent of subjects reporting a 10 in G_LOW, and 49 percent in G_HIGH. This difference is not significant (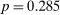 , OLS with robust SE;
, OLS with robust SE; 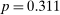 , 2SLS regressing report on belief with treatment as instrument for belief;
, 2SLS regressing report on belief with treatment as instrument for belief;  ,
, 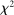 test). Taken together, our study and the previous literature provide converging evidence that manipulating beliefs about others' reports has a limited impact on reporting.
test). Taken together, our study and the previous literature provide converging evidence that manipulating beliefs about others' reports has a limited impact on reporting.
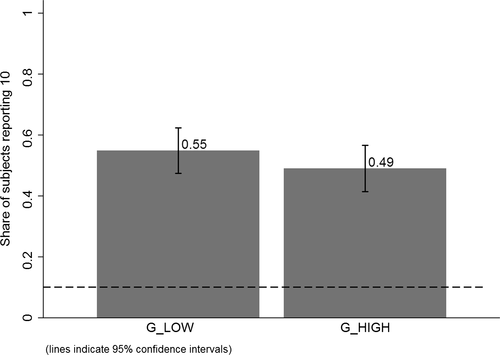
Effect of shifting beliefs about the distribution of reports.
One word of caution is warranted. Even though the point estimate of the effect of the 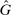 treatments is quite close to zero, we cannot reject (small) positive or negative effects of a change in beliefs. A power analysis shows that we can only detect treatment differences of 15 percentage points or larger at the 5% level and with 80% power, but we are not sufficiently powered to detect small differences like that observed in Figure 5. This may raise the concern that our rejection of many models, in particular the social comparisons models, which all predict affinity, is driven by a lack of power. However, these models typically predict quite large responses to shifts in
treatments is quite close to zero, we cannot reject (small) positive or negative effects of a change in beliefs. A power analysis shows that we can only detect treatment differences of 15 percentage points or larger at the 5% level and with 80% power, but we are not sufficiently powered to detect small differences like that observed in Figure 5. This may raise the concern that our rejection of many models, in particular the social comparisons models, which all predict affinity, is driven by a lack of power. However, these models typically predict quite large responses to shifts in 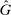 . For example, a simple, calibrated version of the Conformity in LC model implies that 21 percent of subjects should increase their reports across our
. For example, a simple, calibrated version of the Conformity in LC model implies that 21 percent of subjects should increase their reports across our  treatments, which we do have power to detect. In fact, our data show that (in net) 6 percent of subjects decrease their report.28
treatments, which we do have power to detect. In fact, our data show that (in net) 6 percent of subjects decrease their report.28
3.5 Changing the Observability of States
A final set of treatments tests whether observability of the subject's true state by the experimenter affects reporting behavior, in line with Definition 3. The experiments use a setup similar to the one described above. Subjects are invited to the lab to fill in a questionnaire and are paid based on a random draw that they perform privately. There are two between-subject treatments. Differently from the previous experiments, in both treatments the draw is performed out of a 10-state uniform distribution. In our UNOBSERVABLE treatment, the draw is performed using the same procedures described for the previous experiments: subjects draw a chip at random out of an envelope, report the outcome on a payment sheet, and are paid based on this report. Thus, in this treatment, the experimenter cannot observe the true state of a subject and cannot tell for any individual subject whether they lie or tell the truth.
In our OBSERVABLE treatment, we maintain this key feature of the FFH paradigm, but make subjects' true state observable to the experimenter. In order to do so, the procedure of the OBSERVABLE treatment differs from the UNOBSERVABLE treatment in two ways. First, the draw is performed using the computer instead of the physical medium of our other experiments (the chips and the envelope).29 Second, we introduce a payment procedure that makes it impossible for the experimenter to link a report to an individual subject. Before the start of the experiment, the experimenter places an envelope containing 10 coins of £1 each on each subject's desk. Subjects are told to sit “wherever they want” and sit down unsupervised. The experimenter does thus not know which subject is at which desk. After the computerized draw, instead of writing the number on their chip on the payment sheet, subjects are told to take as many coins from the envelope as the number of their chip. Subjects then leave the lab without signing any receipt for the money taken or meeting the experimenter again. At the end of the experiment, the experimenter counts the number of coins left by subjects on each desk to reconstruct their “report” and compares it to the true state drawn on the corresponding computer without being able to link any report to the identity of a subject.30 We ran these experiments at the University of Nottingham with 288 subjects (155 in UNOBSERVABLE; 133 in OBSERVABLE). Experiments were conducted between May and October 2015.
3.6 Results
Figure 6 shows the distribution of reports in the UNOBSERVABLE and OBSERVABLE treatments. The dashed line in the figure indicates that, in both treatments, the truthful probability of drawing each state is 10 percent.
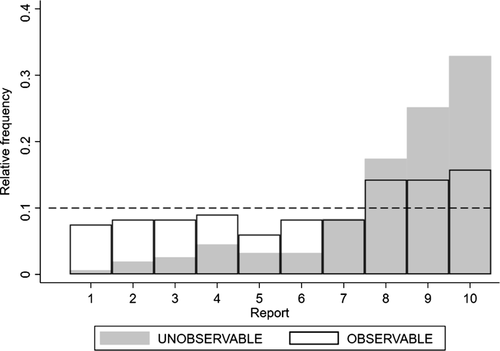
Effect of changing the observability of states.
Finding 8.Introducing observability has a strong and significant effect on the distribution of reports.
Reports in the UNOBSERVABLE treatment are considerably higher than in the OBSERVABLE treatment (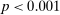 OLS with robust SE;
OLS with robust SE; 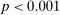 Kolmogorov–Smirnov test;
Kolmogorov–Smirnov test;  , Wilcoxon rank-sum test; see Kajackaite and Gneezy (2017) for a similar result).
, Wilcoxon rank-sum test; see Kajackaite and Gneezy (2017) for a similar result).
This result also demonstrates that it would be misleading to rely on evidence from settings in which the true state is observable by the researcher if one is actually interested in understanding a setting in which the true state is truly unobservable.
We can also use the OBSERVABLE treatment to examine our prediction about the existence of downwards lying when the state is observable (Definition 4). Importantly, we may not have the same result in a setting where the true state is unobservable (see Table II).
Finding 9.There is no downwards lying when the true state is observable.
Figure 7 shows a scatter plot of subjects' reports and true draws in the OBSERVABLE treatment. The size of the bubbles reflects the underlying number of observations. No subject reported a number lower than their true draw, that is, lied downwards. About 60 percent of the subjects who lie report the highest possible number; the remaining 40 percent of liars report non-maximal numbers.
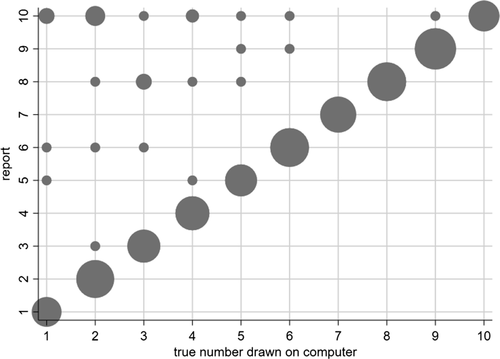
Reports and true draws in OBSERVABLE.
4 Relating Theory to Data
In this section, we compare the predictions derived in Section 2 and Appendix B with our experimental results and show that only two closely-related models are able to explain the data. We then discuss a simple, parameterized utility function for one of the surviving models which is able to quantitatively reproduce the data from the meta study as well as those from our experiments.
4.1 Overall Result of the Falsification Exercise
Recall that our four empirical tests, in addition to the meta study, concern (i) how the distribution of true states affects one's report (we find drawing in); (ii) how the belief about the reports of other subjects influences one's report (we find 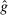 -invariance); (iii) whether the observability of the true state affects one's report (we find it does); (iv) whether some subjects will lie downwards if the true state is observable (we find they do not). Taking all evidence together, we find the following:
-invariance); (iii) whether the observability of the true state affects one's report (we find it does); (iv) whether some subjects will lie downwards if the true state is observable (we find they do not). Taking all evidence together, we find the following:
Finding 10.Only the Reputation for Honesty + LC and the LC-Reputation models cannot be falsified by our data.
Table II summarizes the predictions of all models. The two models that cannot be falsified by our data, Reputation for Honesty + LC and LC-Reputation, combine a preference for being honest with a preference for being seen as honest. In Reputation for Honesty + LC, individuals care about lying costs and about the probability of being a liar given their report. In LC-Reputation, individuals care about lying costs and about what an audience observing the report deduces about their lying cost parameter  .
.
All other models fail at least one of the four tests. Looking at Table II, one can discern certain patterns. The LC model, which is most widely used in the literature, fails two tests, predicting f-invariance and o-invariance. The Conformity in LC model, which is our preferred way to model the effect of descriptive norms, fails three tests, predicting drawing out (when the equilibrium is unique), affinity, and o-invariance. All other social comparisons models also predict affinity and o-invariance. Moreover, as we discuss in Appendix C, several popular models, like the standard model and models that assume that subjects only care about their reputation for having been honest, cannot even explain the findings of the meta study (and also fail our new tests).
We find no significant effect of a change in beliefs, that is,  -invariance. As we discussed in Section 3.4, our study is sufficiently powered to detect treatment differences implied by reasonably parameterized versions of the social comparison models, for example, Conformity in LC. We cannot, however, rule out (small) positive or negative effects of a change in beliefs. Regardless of whether our
-invariance. As we discussed in Section 3.4, our study is sufficiently powered to detect treatment differences implied by reasonably parameterized versions of the social comparison models, for example, Conformity in LC. We cannot, however, rule out (small) positive or negative effects of a change in beliefs. Regardless of whether our  treatments have enough power or not, even if we interpreted our data on this test as inconclusive and thus disregard the
treatments have enough power or not, even if we interpreted our data on this test as inconclusive and thus disregard the  -invariance result, we can still reject all the social comparisons models because they fail at least one other experimental test.
-invariance result, we can still reject all the social comparisons models because they fail at least one other experimental test.
Importantly, non-uniqueness of equilibria does not affect our overall falsification. Recall that the first and third test might not work when there is more than one equilibrium. All those models that fail the first or third test and could feature multiple equilibria also fail additional tests. Similarly, the models that our data cannot falsify are consistent with the data when the equilibrium is unique.
4.2 A Calibrated Utility Function
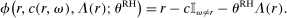
As before, r is the report, ω the true state, and  the fraction of liars at r. c is a fixed cost of lying and
the fraction of liars at r. c is a fixed cost of lying and  is an indicator function of whether an individual lied. We suppose all individuals experience the same fixed cost of lying (this utility function is thus a limit case of the Reputation for Honesty + LC model). The individual-specific weight on reputation,
is an indicator function of whether an individual lied. We suppose all individuals experience the same fixed cost of lying (this utility function is thus a limit case of the Reputation for Honesty + LC model). The individual-specific weight on reputation, 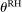 , is drawn from a uniform distribution on
, is drawn from a uniform distribution on 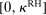 . The average
. The average 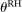 is thus
is thus 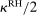 . Additional details of the calibration are in Appendix H.2.31
. Additional details of the calibration are in Appendix H.2.31
We calibrate the model to match the leading example in the literature, a simple die-roll setting, that is, a uniform distribution F over six possible states with payoffs ranging from 1 to 6, where the audience cannot observe the state. We set 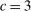 and
and  . We find that in the equilibrium, no individual lies down. Moreover,
. We find that in the equilibrium, no individual lies down. Moreover, 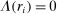 for
for 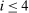 ,
, 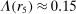 , and
, and 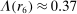 . We find a reporting distribution similar to that found in our meta study:
. We find a reporting distribution similar to that found in our meta study: 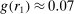 ,
, 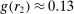 ,
, 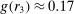 ,
, 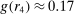 ,
, 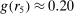 , and
, and 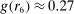 . Figure 8 compares the predicted reporting distribution of this calibrated model to the data. The fit is quite good, in particular given the simple functional form, and the model matches all four findings of the meta study.
. Figure 8 compares the predicted reporting distribution of this calibrated model to the data. The fit is quite good, in particular given the simple functional form, and the model matches all four findings of the meta study.
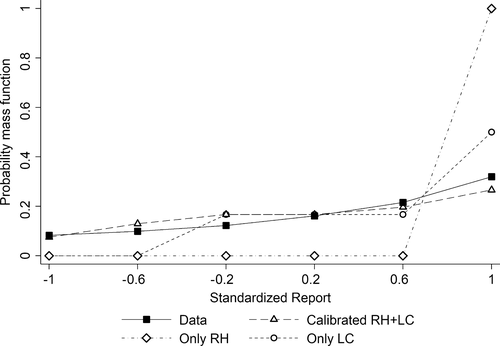
Calibrated Reputation for Honesty + LC.
It also matches up with our experimental findings. In a setting where the state is observable, the model predicts no downwards lying, as in our data (this is true for all Reputation for Honesty + LC utility functions), and much more truth-telling. Under observability, all liars report the maximal report, similar to our data.
The model also generates the large amount of drawing in we observe. We consider two states like in our F treatments, and in order to keep the payoff scale the same as the previous calibration, we suppose they pay 1 and 6. When 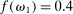 , the equilibrium features no lying down and so
, the equilibrium features no lying down and so 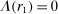 . Moreover,
. Moreover, 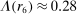 and the share of low reports is
and the share of low reports is 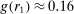 . When
. When 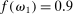 , we find two equilibria. One of the equilibria features no lying down, and in this case
, we find two equilibria. One of the equilibria features no lying down, and in this case 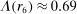 and
and 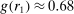 . The other equilibrium features lying down; here
. The other equilibrium features lying down; here 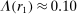 ,
, 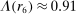 , and
, and 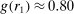 . Thus, in the last equilibrium, approximately 8 out of every 10 individuals who draw the high state give the low report. For comparison, our experiments yield
. Thus, in the last equilibrium, approximately 8 out of every 10 individuals who draw the high state give the low report. For comparison, our experiments yield 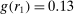 and
and 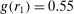 , respectively. Regardless of which of these two equilibria is selected, we observe significant amounts of drawing in. Moreover, the model can generate almost any behavior in our
, respectively. Regardless of which of these two equilibria is selected, we observe significant amounts of drawing in. Moreover, the model can generate almost any behavior in our  treatments, because those treatments do not pin down the belief about H (and thus
treatments, because those treatments do not pin down the belief about H (and thus  , on which utility in the model depends). Depending on the new beliefs, aversion,
, on which utility in the model depends). Depending on the new beliefs, aversion,  -invariance, or affinity could result, as the new belief could either imply a positive, no, or negative change in the gap between
-invariance, or affinity could result, as the new belief could either imply a positive, no, or negative change in the gap between  and
and 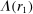 (see the Reputation for Honesty + LC part of the proof of Proposition 2 for details).
(see the Reputation for Honesty + LC part of the proof of Proposition 2 for details).
Both components of the utility function are important. In Figure 8, we also plot the predicted reporting distributions for the utility function when we shut down the LC or the RH part. The Only-RH model is far away from the data. The Only-LC model is closer, but this model does not generate drawing in or o-shift.32
5 Conclusion
Our paper attempts to understand the constituent mechanisms that drive lying aversion. Drawing on the extensive experimental literature following the FFH paradigm, we establish some “stylized” findings within the literature, demonstrating that even in one-shot anonymous interactions with experimenters, many subjects do not lie maximally. Our new experimental results, combined with our theoretical predictions, demonstrate that a preference for being seen as honest and a preference for being honest are the main motivations for truth-telling. While we focus on a situation of individual decision making, the utility functions we consider should be present in all situations that involve the reporting of private information, for example, sender-receiver games, and would there form the basis for the strategic interaction.33
Three concurrent papers also present models that incorporate a desire to appear honest in the utility function. The utility functions proposed by Khalmetski and Sliwka (forthcoming) and Gneezy, Kajackaite, and Sobel (2018) are similar in spirit to our Reputation for Honesty + LC model. Both papers combine a desire to appear honest with a desire to be honest. Khalmetski and Sliwka (forthcoming) showed that a calibrated version of their model reproduces the data patterns observed in the FFH paradigm. Similarly to two of our new tests, Gneezy, Kajackaite, and Sobel (2018) presented experiments that manipulate the true distribution of the states as well as the observability of the state, with similar results to our tests. Taken together, the results of these two studies are in line with the two non-falsified models we propose that also combine lying costs and reputational costs. In another concurrent paper, Dufwenberg and Dufwenberg (2018) presented a different, more nuanced formalization of the desire to appear honest; in particular, they assumed that individuals care about the beliefs that an audience has about the degree of over-reporting (rather than the simple chance of being a liar). Dufwenberg and Dufwenberg (2018) showed that this model can explain the results of the original Fischbacher and Föllmi-Heusi (2013) setup (six-sided die roll). Future research could investigate whether reputational concerns regarding honesty are more often captured by the assumptions in the models of Khalmetski and Sliwka (forthcoming), Gneezy, Kajackaite, and Sobel (2018), and our paper or by the Dufwenberg and Dufwenberg (2018) assumption of perceived cheating aversion.
What lessons can we draw for policy? The size and robustness of the effect we document suggest that mechanisms that rely on voluntary truth-telling by some participants could be very successful. They could be easier or cheaper to implement and they could achieve outcomes that are impossible to achieve if incentive compatibility is required. Moreover, if the social planner wants to increase truth-telling in the population, our preferred model suggests that lying costs and concerns for reputation are important. Thus, whatever created the lying costs in the first place, for example, education or a Hippocratic oath-type professional norm, is effective and should be strengthened. In addition, one should try to make it harder to lie while keeping a good reputation, for example, via transparency, naming-and-shaming, or reputation systems (e.g., Bø, Slemrod, and Thoresen (2015)).
There are at least four potential caveats for these policy implications. First, we would not normally base recommendations on a single lab experiment. Given that our meta study provides very strong, large-scale evidence, however, we feel confident that truth-telling is a robust phenomenon. Second, lab experiments are not ideal to pin down the precise value of policy-relevant parameters. We would thus not put much emphasis on the exact value of, say, the average amount of lying, which we measure as 0.234. However, it is clear that, whatever the exact value is, it is far away from 1. Third, none of our results suggests that all people in all circumstances will shy away from lying maximally. Any mechanism that relies on voluntary truth-telling will need to be robust to some participants acting rationally and robust to self-selection of rational participants into the mechanism. Finally, the FFH paradigm does not capture several aspects that could affect reporting. Subjects have to report and they have to report a single number. This excludes lies by omission or vagueness (Serra-Garcia, Van Damme, and Potters (2011)). From the viewpoint of the subject, there is also little ambiguity about whether they lied or not. In reality, a narrative for reporting a higher state while still maintaining a self-image of honesty might be easier to generate (Bénabou, Falk, and Tirole (2018), Mazar, Amir, and Ariely (2008)).
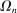 and
and 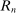 . A simpler (albeit slightly less general) conceptualization is that a report is the identity function from
. A simpler (albeit slightly less general) conceptualization is that a report is the identity function from 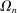 to itself.
to itself.
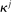 and H imply that our framework for more general models does not nest, strictly speaking, the standard model, where individuals only care about their monetary payoff. Instead, the standard model is a limit case of our models (where the κ's go to 0, or the support of H becomes concentrated on 0). This allows the predictions generated by more general models to be sharply distinguished from the predictions of the standard model (as opposed to nesting them). The same reasoning applies to other “nested” models; for example, the lying-cost (LC) model is a limit case of the Reputation for Honesty + LC model.
and H imply that our framework for more general models does not nest, strictly speaking, the standard model, where individuals only care about their monetary payoff. Instead, the standard model is a limit case of our models (where the κ's go to 0, or the support of H becomes concentrated on 0). This allows the predictions generated by more general models to be sharply distinguished from the predictions of the standard model (as opposed to nesting them). The same reasoning applies to other “nested” models; for example, the lying-cost (LC) model is a limit case of the Reputation for Honesty + LC model.
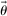 and the non-monetary costs in the models we consider (detailed below), if an individual of type
and the non-monetary costs in the models we consider (detailed below), if an individual of type 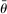 is indifferent between the two reports, then no other type can be indifferent. Because subjects in the experiment are anonymous to each other, we also only focus on equilibria where strategies cannot depend on the identity of the player (but of course, it can depend on their preference parameters).
is indifferent between the two reports, then no other type can be indifferent. Because subjects in the experiment are anonymous to each other, we also only focus on equilibria where strategies cannot depend on the identity of the player (but of course, it can depend on their preference parameters).
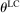 , only that the restriction on the cross partials hold. We make the assumption that utility is weakly decreasing in
, only that the restriction on the cross partials hold. We make the assumption that utility is weakly decreasing in  as it allows for a natural interpretation of
as it allows for a natural interpretation of  (the same applies to the following models). Our results also do not depend on individuals all having the same functional form c so long as the assumptions regarding
(the same applies to the following models). Our results also do not depend on individuals all having the same functional form c so long as the assumptions regarding  hold. So, for example, our results hold when some individuals have fixed and others convex costs of lying.
hold. So, for example, our results hold when some individuals have fixed and others convex costs of lying.
 ). Observe that we suppose in this model that individuals' utility depends on the actual costs of others. An alternative framing would be where the utility for an individual depends on their own beliefs about others' costs. With a continuum of agents, and correct beliefs, these equal the realized costs.
). Observe that we suppose in this model that individuals' utility depends on the actual costs of others. An alternative framing would be where the utility for an individual depends on their own beliefs about others' costs. With a continuum of agents, and correct beliefs, these equal the realized costs.
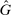 (and G). In a more complete model, individuals would think many different possible H distributions to be possible, and hold a prior over these different distributions. Thus, observing a different
(and G). In a more complete model, individuals would think many different possible H distributions to be possible, and hold a prior over these different distributions. Thus, observing a different 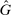 would induce a shift in the inferred distribution over the different possible H's. Given reasonable assumptions about the prior distribution over H, our results will continue to hold.
would induce a shift in the inferred distribution over the different possible H's. Given reasonable assumptions about the prior distribution over H, our results will continue to hold.
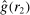 will be interpreted as more individuals who drew
will be interpreted as more individuals who drew 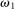 being willing to give the high report. This decreases the proportion of truth-tellers at the high report, driving aversion. In contrast, suppose the change is interpreted as a shift by individuals who have medium LC costs, but relatively high reputational costs. This means that it is interpreted as a shift in the reports of individuals who drew the high state (since individuals who drew the low state and have medium LC costs are unlikely to ever give the high report). An increase in
being willing to give the high report. This decreases the proportion of truth-tellers at the high report, driving aversion. In contrast, suppose the change is interpreted as a shift by individuals who have medium LC costs, but relatively high reputational costs. This means that it is interpreted as a shift in the reports of individuals who drew the high state (since individuals who drew the low state and have medium LC costs are unlikely to ever give the high report). An increase in 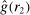 is then interpreted as individuals who drew
is then interpreted as individuals who drew 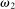 as being more willing to pay the reputation cost of reporting
as being more willing to pay the reputation cost of reporting 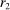 . Thus, the fraction of truth-tellers at
. Thus, the fraction of truth-tellers at 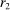 increases, driving affinity.
increases, driving affinity.
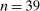 1), we find a treatment difference of 28 percentage points (
1), we find a treatment difference of 28 percentage points (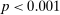 , OLS with robust SE;
, OLS with robust SE; 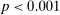 ,
, 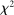 test). Using only the Oxford subsample (
test). Using only the Oxford subsample (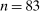 ), we find a treatment difference of 27 percentage points (
), we find a treatment difference of 27 percentage points (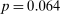 , OLS with robust SE;
, OLS with robust SE; 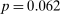 ,
, 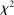 test).
test).
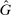 treatments is from 0.049 to −0.165. We focus on the Conformity in LC model as it provides a baseline utility function for modeling social comparisons and cleanly demonstrates the fact that we should expect to see large shifts in our
treatments is from 0.049 to −0.165. We focus on the Conformity in LC model as it provides a baseline utility function for modeling social comparisons and cleanly demonstrates the fact that we should expect to see large shifts in our 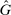 treatments. For details of this calibration, see Appendix H.1.
treatments. For details of this calibration, see Appendix H.1.
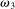 are indifferent between reporting
are indifferent between reporting 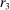 and
and  . We suppose for the figure that they say
. We suppose for the figure that they say  . Shifting these to
. Shifting these to  only worsens the fit.
only worsens the fit.



 Treatments
Treatments Subjects
Subjects
 -invariance
-invariance -invariance
-invariance -invariance
-invariance -invariance
-invariance
