Linking Growth of Juvenile Sockeye Salmon to Habitat Temperature in Alaskan Lakes
Present address: University of Victoria, Department of Biology, Post Office Box 3020, Station CSC, Victoria, British Columbia V8W 3N5, Canada.
Abstract
We examined the influence of temperature on the size of age-1 smolts of sockeye salmon Oncorhynchus nerka relative to that of food availability and density dependence across a variety of Alaskan lakes. We analyzed data from 36 lakes providing 134 lake years (annual means) of data. These lakes represent clear, organically stained, and glacially turbid lake types. They produce age-1 sockeye salmon smolts exhibiting a threefold variation in average length (52–145 mm) and a 30-fold variation in average weight (1–30 g). We used simple regression analysis to test for linkages between age-1 smolt size and the independent variables zooplankton biomass (mg/m2), smolt density (number/km2), length of the growing season, and mean water column temperature. Zooplankton biomass (ZB) was the strongest single predictor of smolt size, accounting for 52% of the variation in mean age-1 smolt fork length (FL) and weight (W). Individually, smolt density (SMD) accounted for only 10% of the variance in age-1 smolt size; however, mean water column temperature (Ts) explained 24% of the variation in FL and 19% of the variation in W. Smolt size was unrelated to the length of the growing season (S); however, growth rate indexed by length varied inversely with S while growth in terms of weight did not. Subsequently, we combined all factors into a multivariate model of age-1 smolt size and the population's biological and thermal environment. Taken together, the factors ZB, SMD, and Ts accounted for 70% of the variation in FL and W. The influence of temperature on smolt size appeared to be more direct (through its effect on metabolic rates) than indirect (through limiting food availability (plankton)). Our results may influence fishery management objectives and serve as a template to project future trends in juvenile sockeye salmon growth under different climatic conditions.
Introduction
Ocean temperatures strongly influence the physiology and ecology of adult sockeye salmon Oncorhynchus nerka. For instance, the distribution and age at maturity of sockeye salmon are influenced by sea surface temperatures in the North Pacific, suggesting that warmer temperatures increase metabolic demand or alter food resource availability and thereby lead to lower growth rates and limit the southern oceanic distribution of these fish (Welch et al. 1995). Lakes experience larger seasonal temperature fluctuations than northern Pacific Ocean waters. In addition, coastal lakes, which are strongly influenced by ocean winds, can exhibit different mixing patterns and stratification than interior lakes (Stockner 1987; LaPerriere 1997). Stockner (1987) speculated that differences in epilimnetic temperature, heat content, and plankton abundance between the coastal and interior lakes of British Columbia accounted for some of the variation in the size of sockeye salmon smolts; however, this variation was not quantified. Yet despite the significance of temperature and heat in lakes (Hutchinson 1957) and the fact that the relationships between temperature and plankton are largely viewed as important (Beauchamp et al. 1989; Levy 1990a; Luecke et al. 1996; Stockwell and Johnson 1999), the use of temperature, stratification, and heat budget variables to characterize juvenile sockeye salmon growth patterns has not been fully explored.
The relationships between a lake's thermal environment and its freshwater production have been viewed in the context of changing meteorological conditions and broad latitudinal (temperature) gradients. For instance, Scavia et al. (1986) associated lower phytoplankton densities (chlorophyll-a concentration) in Lake Michigan with a protracted winter and the subsequent delay in vernal heating of the water column. The species composition, size distribution, and biomass of pelagic zooplankton in Lake Windermere were also strongly influenced by climatic changes (George and Harris 1985). In particular, it was spring epilimnetic temperatures and not grazing by planktivorous fish that determined zooplankton abundance in that lake. On a global scale, primary production (Brylinski and Mann 1973; France 1992) and fish yield (Schlesinger and Rieger 1982) have been correlated with mean annual air temperature. Plante and Downing (1993) derived an inverse relationship between mean annual air temperature and adult sockeye salmon production (biomass) for a number of Pacific Northwest and British Columbia stocks. Although there is a close correlation between mean air and lake surface temperatures, the particular relevance of atmospheric temperature to biological standing stock is obscure (Quiros 1990; Hartman 1995). Correlations between climate and fish (e.g., year-class strength) may also be unpredictable because of density-dependent factors such as predation and competition (Lehtonen and Lappalainen 1995).
In the case of juvenile sockeye salmon, most of the temperature-related work to date has focused on metabolic efficiency, feeding, and reproduction. The pioneering work of Brett (1971) showed that the growth rates of age-0 sockeye salmon were directly proportional to temperature when food supply was in excess; however, if less food was available, the temperature for maximum growth was lower. In addition, the diel vertical migration patterns exhibited by juvenile sockeye salmon (Narver 1970) have been related to growth rates and bioenergetic efficiency through temperature selection (Levy 1990b; Bevelhimer and Adams 1993) and predator avoidance (Eggers 1978; Stockwell and Johnson 1999). Therefore, the interactions between food and temperature underlie the variation observed in the population characteristics and growth patterns of juvenile sockeye salmon.
Salmon-producing lakes span a broad geographic range in Alaska, extending from the southeastern panhandle westward to the Alaska Peninsula and Bristol Bay, and they exhibit a variety of limnological characteristics and productivity differences (Koenings et al. 1986; Koenings et al. 1990; Koenings and Edmundson 1991; Schmidt et al. 1994; LaPerriere 1997; Edmundson and Carlson 1998). Because temperature and stratification seem to influence most of the physical, chemical, and biological processes in lakes (Hutchinson 1957), we hypothesize that among morphologically different lakes, the variability in the size of sockeye salmon smolts of a given age-class reflects variations in freshwater thermal regimes. In this paper, we attempt to quantify the influence of temperature on the size of age-1 sockeye salmon smolts relative to that of food resource availability (zooplankton biomass) and density-dependent effects (fish density). Our multiple-lake approach centers on evaluating limnological and fisheries data collected from a variety of Alaskan lakes representing clear, organically stained (colored), and glacially turbid lake types. Such an approach may be useful to fishery managers in predicting broad patterns or regional responses in sockeye salmon production in the context of climatic variability.
Study Lakes
The 36 Alaskan lakes in our study are distributed between approximately 55°N and 65°N and between 130°W and 145°W (Table 1; Figure 1). Most of the lakes support anadromous populations of sockeye salmon; however, five of them (the most southeastern of the two Crescent lakes [Crescent SE] and Esther Pass, Port Dick, Spiridon, and Speel lakes) have barriers to fish migration and are stocked with sockeye salmon fry. The lakes are situated at elevations ranging from near sea level to 914 m. Lakes in the southeastern panhandle and those on the Kodiak Archipelago lie within the maritime zone. In the southcentral regions (e.g., the Kenai Peninsula), lakes have a more transitional type of climate. A few lakes included in our study lie within the Copper River drainage, which experiences more of a continental climatic effect. Finally, the two northernmost lakes included in the study are located on the Seward Peninsula and fall within the transitional−continental zone. As a group, these lakes exhibit a wide range of morphometric characteristics. The smallest lake has a surface area of less than 1 km2, while the largest has one of nearly 300 km2. There are deep, fjordlike lakes, ones with glacially scoured U-shaped basins, and ones with relatively shallow bathymetry and a more extensive littoral zone. In the deepest lake, the maximum depth is 290 m, while the shallowest lake has a mean depth of only 3 m. A clear distinguishing feature among many of these lakes is the presence of color or turbidity caused by different water sources. Stained lakes are brownish or yellowish from the presence of high concentrations of dissolved organic material. In contrast, glacial lakes are highly turbid from large inputs of meltwater containing inorganic silt particles. The average water color exceeds 40 platinum-cobalt (Pt) units in those lakes containing the most organic material. Lakes receiving silty glacial meltwater have an average turbidity of 18 nephelometric turbidity units (NTU). On the other hand, clear lakes are those lacking appreciable amounts of color (<12 Pt units) and turbidity (< 5 NTU). Our data set was composed of 18 clear lakes, 9 stained lakes, and 9 glacial lakes (Table 1).

General locations of the study lakes: (A) Badger, Hugh-Smith; (B) McDonald, Redoubt, Sweetheart; (C) Auke, Crescent, Speel; (D) Crosswind, Klutina, Summit, Tazlina, Tonsina; (E) Coghill, Esther Pass; (F) Bear, Delight, Desire, Hidden, Packers, Port Dick, Skilak, Tustumena, Upper Russian; (G) Afognak, Akalura, Frazer, Karluk, Red, Spiridon, Upper Station; (H) Chelatna; (I) Crescent; (J) Chenik; and (K) Glacial, Salmon
Methods
Fisheries data
We obtained data on sockeye salmon smolts from a variety of regional information and technical data reports published by the Alaska Department of Fish and Game (ADF&G), along with some unpublished ADF&G data. In Alaska, sockeye salmon smolts begin their seaward migration in early spring (April−May), and the migration is usually completed by the end of June. Our data originated from a variety of ADF&G fishery studies dealing with stock assessment, juvenile stocking, and lake fertilization. We included the five stocked lakes (Crescent SE, Esther Pass, Port Dick, Spiridon, and Speel) in our analysis because juvenile sockeye salmon were planted as unfed fry in early spring (April−May) when they were of similar size to newly emergent wild fry. Smolt length and weight data were available from 36 lakes (134 lake years). Fork length was measured from the tip of the snout to the fork of the tail to the nearest 0.1 mm, and mass was measured to the nearest 0.1 g. For smolt enumeration (census) projects, sizes were weighted by the number of fish that out-migrated during each sampling period over the course of the out-migration to give mean population fork length (FL) and weight (W). Size data were also available for smolts from several lakes for which there were no estimates of total smolt abundance. In these cases, smolts were sampled periodically throughout the spring migration period (i.e., early, middle, and late). For each system we computed arithmetic means for each sample and weighted these by the number of smolts captured per sample period. Before out-migrating as smolts, young sockeye salmon spend a period of one, two, or sometimes three winters in freshwater. However, in our analysis of size at age, we considered only one age-class of smolts, those that reared for 1 year in their natal lake. Age was determined by reading smolt scale samples mounted on glass slides or impressions, using a microfiche reader. A fish with one freshwater annulus was designated as an age-1 smolt. Of the 36 lakes (N = 134 lake years [see below]), total smolt out-migration (abundance) estimates were available for 21 lakes (N = 84 lake years). Smolt counts or estimates were made using smolt fences, calibrated fyke nets, or inclined-plane traps. Smolt abundances were typically estimated from mark–recapture experiments (Rawson 1984; Carlson et al. 1999) carried out throughout the migration period. For our analysis, we considered the total smolt abundance of all age-classes and standardized the abundance estimates to a common spatial unit (number/km2). Standardizing abundance by unit area reflects a potential for intraspecific competition and has been used in multilake studies as a predictor of density-dependent salmonid growth (e.g., Rieman and Meyers 1992). Thus, smolt density (SMD) is our index of density-dependent factors (competition among cohorts of juvenile sockeye salmon) affecting juvenile growth.
Limnological data
Limnological data were obtained from systematic surveys carried out by the ADF&G statewide limnology program during the 1980s and 1990s. Detailed field and laboratory methodologies can be found in Koenings et al. (1987). For the 36 lakes, we compiled information on water temperature and zooplankton biomass, typically from monthly (every 3−4 weeks) sampling trips over the ice-free season. Vertical measurements of temperature were made at intervals of 1–5 m with a combined temperature−oxygen probe (Yellow Springs Instruments). We used a third- to fifth-order polynomial (Shuter et al. 1980) to model changes in water temperatures over time (°C versus day of the year) to estimate the seasonal temperature trend. Maximum surface temperature (Tmax) was taken as the corresponding y-intercept, where the instantaneous slope of the polynomial regression equals zero. The duration of the growing season (S) was calculated as the difference between the projected days of the year for the respective x-intercepts of the polynomial regression where f(x) = 4°C (i.e., S is the number of days between spring and fall 4°C isothermy). For the most part, observed temperature data for each year extended from less than 4°C in the spring to more than 4°C in the fall. However, in our polynomial curve fitting, we excluded data series in which the spring and fall surface temperatures were above 5°C to avoid unnatural deviations from the characteristic seasonal temperature profile.
We calculated Birgean summer heat budgets (θs), which incorporate the change in volume with depth, as the difference between maximum heat content (kcal/km2; 1 kcal = 4.2 kJ) and the amount of heat stored at maximum density (Wetzel and Likens 1991). We also computed the seasonal mean (May−October) volume-weighted mean temperature (Ts) as a method of comparing lake thermal conditions. We integrated the polynomial function (as described above) for selected depths over S to obtain the number of degree days (°C × d). Dividing this quantity by S yields the seasonal average temperature for a selected depth (t̄d). The mean temperature for a volume increment (t̄v) was taken as the average t̄d of two selected depths. We then computed Ts using volume increments as the weighting factor, that is,
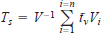
where V is the total lake volume, Vi is a volume increment, and n is the number of volume increments.
Zooplankton samples were collected by vertical tows from a maximum depth of 50 m (or, if the lake was shallower, from 0.5 m above the bottom) to the surface using a 153-μm-mesh conical net 0.2 or 0.5 m in diameter. Individual dry weight was estimated by means of mass–length regression equations for zooplankton, as reported in Koenings et al. (1987). For each lake, the instantaneous biomass measurements were averaged over all sampling stations for each sample date and then averaged over all dates in each year. We expressed mean zooplankton biomass (ZB) on the basis of per-unit lake area (mg/m2) rather than on a volumetric basis because the latter implies a uniform vertical distribution. Use of area estimates of crustacean abundance and biomass in regression analyses of fish production, biomass, or yield is commonly reported (e.g., Hanson and Leggett 1982; Quiros 1990; Cyr and Peters 1996). Herein, ZB is used as our index of food resource availability for rearing sockeye salmon juveniles (fry).
Statistical analysis
We could have used the multiyear averages from individual lakes for our analyses. Instead, we used the annual averages from each lake (lake years) as individual data points because interannual variability within lakes is an important characteristic of sockeye salmon and their habitat. While between-lake variability is generally greater than between-year variability, there can be large interannual differences in fry density, macrozooplankton abundance, and phytoplankton density as a result of fluctuating escapement and subsequent juvenile recruitment. Since the purpose of our study was to capture the average behavior of a lake or population of juvenile sockeye salmon, we considered the yearly data from each lake as our primary observational unit. Analyses using lake-year data are prevalent in aquatic studies (France and Peters 1989; Koenings and Edmundson 1991; Mazumder 1994; Edmundson and Carlson 1998; Mazumder and Havens 1998). Because of their heteroscedasticity, the data for FL, W, and ZB were log10 transformed to improve the fitted relationships. We used one-way analysis of variance (ANOVA) with lake type as a categorical variable followed by Tukey's pairwise comparisons to test for differences in thermal characteristics, smolt size, and zooplankton biomass among lake types. Least-squares regression analysis was used to test the functional relationships between pairs of variables. We also used analysis of covariance (ANCOVA) to test for differences in the slopes and intercepts among lake types, with a significance level of α = 0.05. A significant effect of lake type indicates different y-intercepts, and a significant interaction term (lake type × covariate) suggests different slopes (Neter et al. 1990).
To develop the multivariate models to predict smolt size, we initially used the best-subsets regression approach (Neter et al. 1990) to select a small group of best subsets for further statistical analysis. After the variables are specified, the procedure provides a comparison of models with different numbers of predictors. Goodness of fit (adjusted-R2) was used to compare models of the same size, and both adjusted-R2 and Mallows Cp statistic were used to compare models of different sizes (Neter et al. 1990). We considered a model to be good when the adjusted-R2 was high and the Cp was close to the number of parameters (including the y-intercept) in the model. For variables that were considered functionally dependent on more than one other variable, we used backward elimination, a stepwise regression technique (Neter et al. 1990). Interaction terms were suppressed in the multiple-regression analysis. The significance level for retaining variables was α = 0.1. For all multiple-regression equations, we computed partial correlation coefficients (partial r) to measure the contribution of each independent variable while the effects of the other independent variables were held constant. We conducted all statistical tests using SYSTAT (SPSS 1998).
Results
Limnological Characteristics
Mean limnological conditions varied considerably among lakes (Table 2). Turbidity ranged from less than 1 to more than 40 NTU, and color varied from 4 to 28 Pt units. All of the lakes had fairly low conductivity, with most being below 100 μmhos/cm. The lakes were oligotrophic, with chlorophyll-a concentrations varying by an order of magnitude; average concentrations never exceeded 5 μg/L, however. Zooplankton biomass ranged from 22 to 2,223 mg/m2, a variation of two orders of magnitude. Mean water column (Ts) and maximum temperatures (Tmax) were not very consistent among lakes, varying by nearly 6°C and 10°C, respectively. The summer heat budget ranged from 2.5 to 18.8 kcal/cm2, and S varied from 130 to 224 d, a difference of 3 months.
We also considered the effect of lake typology on the variables of interest. Based on Tukey's comparisons, differences in S were statistically significant between the stained and glacial lakes (P = 0.033) but not between the clear and glacial lakes (P = 0.264) (Table 3). In addition, the ANOVA post hoc tests indicated that Tmax was 3°C warmer (P < 0.001) in stained lakes than in clear lakes, whereas glacial lakes were 3°C colder (P < 0.001) than clear lakes. The variable Ts was significantly higher (by about 2°C) in the clear lakes than in the glacial lakes (P = 0.002), but there were no statistically significant differences between the clear and stained lakes (P = 0.491) or between the stained and glacial lakes (P = 0.087). The ANOVA suggested that there were no differences in lake type associated with the magnitude of θs (P = 0.094) or with chlorophyll concentration (P = 0.154). However, the reported P-value for ZB (P = 0.059) was only slightly greater than our prescribed significance level). Therefore, ZB may be affected by lake typology.
Smolt Population Characteristics
Alaskan sockeye nursery lakes exhibit a great deal of variation in smolt size (Table 4). In the 36 lakes that we studied, mean population fork length ranged from 52 to 145 mm, averaging 87 mm. In comparison, mean weight (W) ranged from approximately 1.0 to 30.0 g, averaging 7.6 g. As expected, FL and W were strongly correlated (r2 = 0.99), and the curvilinear relationship conformed well to a power function (Figure 2). Among 21 lakes, average smolt abundance (all age-classes) varied from 13,485 to more than 7 million per year, and smolt density ranged from approximately 13,000 to 450,000/km2 (Table 4). Following log10 transformation of the size data, the ANOVA post hoc tests indicated that stained and glacial lakes produced significantly smaller smolts than clear lakes (P < 0.001; Table 5). However, there were no significant differences between the stained and glacial lakes with respect to FL (P = 0.879) or W (P = 0.121). Mean smolt abundance was higher in glacial lakes than in clear and stained lakes (P < 0.001); however, the our post hoc tests indicated that the stained lakes had higher SMD than the clear (P = 0.002) and glacial (P = 0.001) lakes. In contrast, there was no significant difference in SMD between the clear and glacial lakes (P = 0.579).
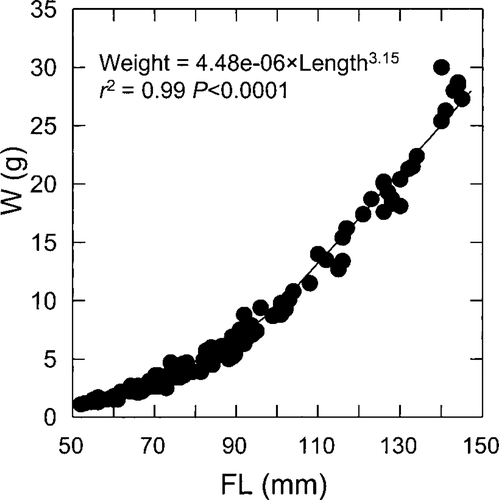
Relationship between mean population length (FL) and weight (W) for age-1 sockeye salmon smolts from 36 Alaskan lakes (N = 134 lake years)

Factors Related to Smolt Size
Initially, we used simple regression analysis to test for linkages between the dependent variables FL and W and the independent variables ZB, SMD, Ts, and S by pooling the data across lake types. The single variable ZB accounted for 52% of the variation in FL and 51% of the variation in W (Table 6). There was a positive relationship between smolt size and ZB. The variable Ts explained about 20% of the variation in both FL and W, while, contrary to our expectations, FL (P = 0.44) and W (P = 0.99) were not significantly related to S. However, there was a significant inverse relationship (r2 = 0.25; P < 0.001) between growth (FL/S; mm/d) and S (Figure 3A). Yet no relationship (P = 0.427) was evident between W/S and S (Figure 3B) despite the close correlation (r2 = 0.85) between the two growth parameters (Figure 4A). Nonetheless, beyond a growth rate of approximately 0.6 mm/d there was considerably more variation about the LOWESS fit. Furthermore, the residuals of the FL/S − W/S relationship appeared to have a sigmoidal shape as a function of ZB, as the response had a tentatively positive slope between 100 and 1,000 mg/m2 (Figure 4B).
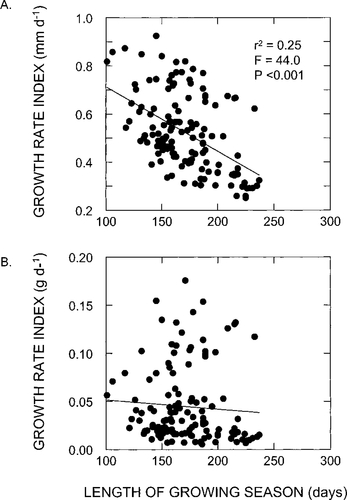
Relationships between (A) age-1 smolt growth as indexed by length (FL/S) and length of the growing season (S) and (B) age-1 smolt growth as indexed by weight (W/S) and length of the growing season
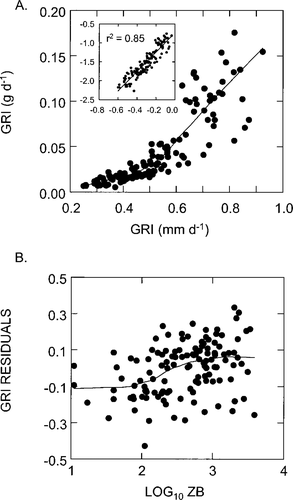
Relationship between the growth rate (GRI) indexed by length and the growth rate indexed by weight; the inset shows the results of linear regression with log10-transformed data. (B) Relationship between the growth rate equation residuals and log10-transformed zooplankton biomass (ZB)
Both FL and W were inversely related (P = 0.003) to SMD, and the negative sign suggested density effects on growth (Table 6). However, SMD accounted for only about 10% of the variation in FL and W. Because the univariate models included at least three different lake types, we considered the possibility that the FL and W responses differed according to lake typology influences. An ANCOVA with FL as the response variable, lake type as a category variable, and (individually) the independent variables ZB, SMD, and Ts as covariates indicated similar slopes (P > 0.05; Table 7). However, with FL as the dependent variable and ZB as a covariate, the reported probability for the interaction term (P = 0.058) was close to our prescribed significance level, so we could not emphatically declare that there were different slopes in that case. In addition, in both models involving SMD as the covariate, the reported P-values for the effect of lake type were close to our 5% significance level. Based on tests of the interaction terms, we felt that pooling the data across different lake typologies in the single-factor regression models was reasonable. Nonetheless, we could not entirely discount the importance of lake typology influences. For this reason, we retained color (COLOR) and turbidity (TURB) as continuous variables rather than using lake type as a categorical variable in our subsequent combined analyses of all lakes.
Combined Biological and Temperature Models
Because mean age-1 smolt size (FL and W) was significantly related to ZB, SMD, and Ts, we attempted to develop a more accurate model for estimating smolt size through multiple-regression analysis. The 21 lakes used in this regression analysis were a subset of the 36 used to derive the previous FL−W relationship. Subsequently, we considered the factors ZB, SMD, Ts, S, Tmax, θs, COLOR, and TURB using the best-subsets procedure to identify subsets of independent variables that provided a best fit to the underlying structure of the data (Table 8). We looked for a subset with the highest adjusted-R2 value and a Cp statistic close to the number of model predictors. From this variable selection method, we preferred the parsimonious subset (ZB, SMD, and Ts) for predicting both FL and W. For the FL and W best subsets, respectively, the adjusted-R2 values were 0.68 and 0.69, and the Cp statistics were 3.2 and 3.1. The procedure did not select any subset with the variables Tmax, θs, COLOR, or TURB, as none of these variables fulfilled the statistical criteria. Therefore, we selected the variables ZB, SMD, and Ts for further analysis using the stepwise multiple-regression procedure to predict smolt size.

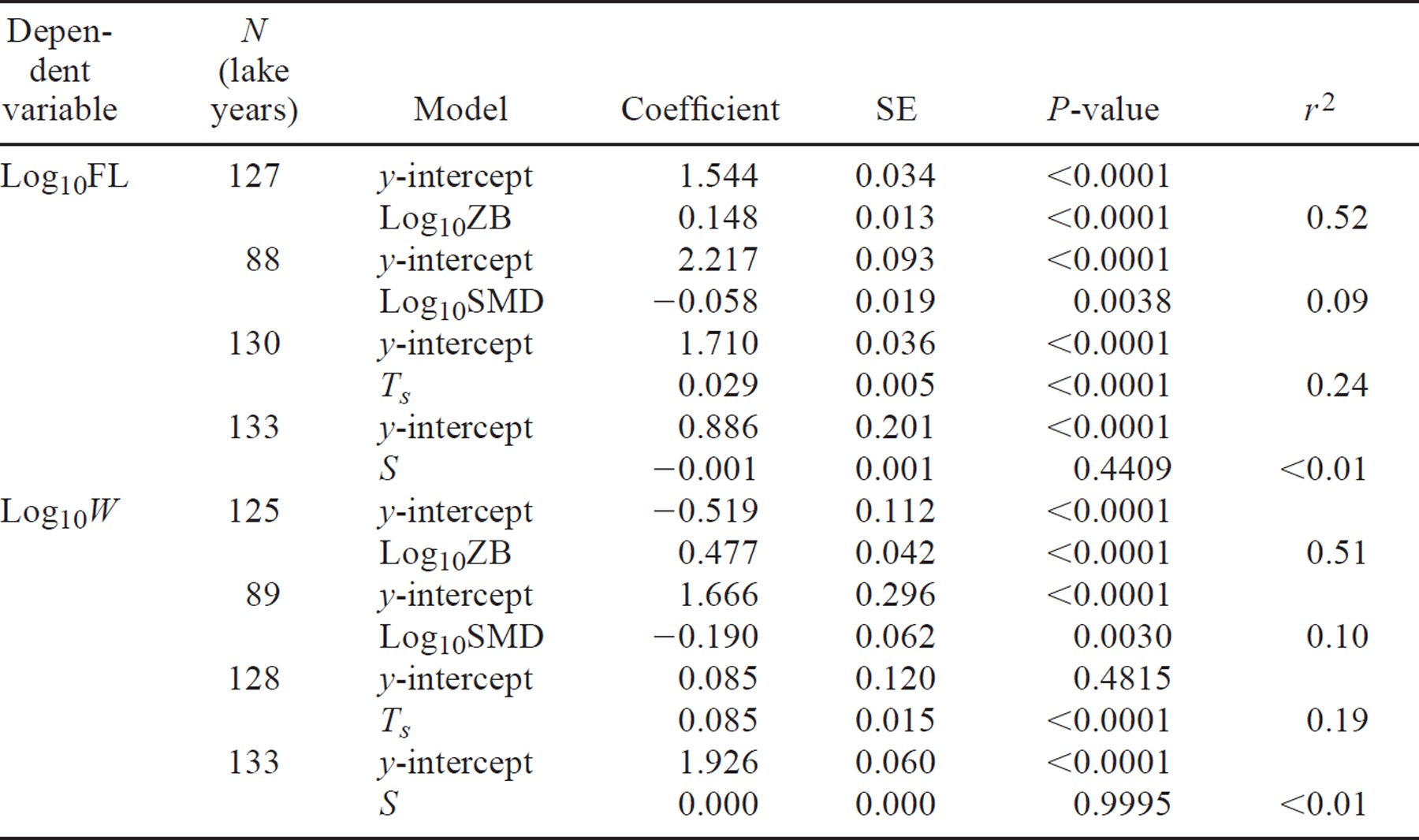
Taken together, the factors ZB, SMD, and Ts accounted for 70% of the variation in FL and W (Table 9). The variables S (P = 0.227), Tmax (P = 0.979), θs (P = 0.362), COLOR (P = 0.236), and TURB (P = 0.392) failed to meet the minimum significance requirements for inclusion in the model. Thus, the explanatory variables retained by the stepwise procedure were in exact agreement with our best-subset regression results. The regression coefficients had the expected signs (i.e., positive for ZB and Ts and negative for SMD), and their magnitudes were similar to those of the coefficients in the single-factor models. In the multiple-regression models predicting FL and W, the independent variables were all highly significant (P < 0.001). While our model predicting FL had a significant intercept (P < 0.001), the W model did not (P = 0.575). The coefficients of partial determination indicated that Ts accounted for a substantial amount (26%) of the variation in age-1 smolt size when both ZB and SMD were included in the models. Examination of a plot of the residuals against the fitted values showed that both the FL and W models were diagnostically well behaved, in that the data were randomly distributed above and below zero. This pattern indicated no apparent bias by lake type or the presence of influential outliers, which was confirmed by plots of the predicted versus observed log10FL and log10W values (Figure 5A, B). However, after fitting the multiple regressions, we were concerned about possible collinearity among ZB, SMD, and Ts. The partial r values between ZB and Ts in the FL (r = 0.07, P = 0.557) and W (r = 0.04, P = 0.710) models were not significant (Figure 6). In comparison, the partial r values between Ts and SMD were higher in both models (r = 0.27) and the correlations were significant (P < 0.015), but we considered this multicollinearity to be minor. Also, the correlations between ZB and SMD in the FL (r = 0.30, P = 0.007) and W (r = 0.33; P = 0.002) models were not too large, though the partial correlations were significant. Nonetheless, the coefficients had the expected signs and their magnitudes seemed reasonable, so we concluded that any collinearity among the independent variables was probably slight and of little consequence.

Plots of the observed and predicted values from (A) the regression of log10-transformed age-1 smolt length (FL) on zooplankton biomass, smolt density, and mean water column temperature and (B) the regression of log10-transformed age-1 smolt weight (W) on those independent variables

Path analysis with partial correlation coefficients (r) among (A) log10-transformed age-1 smolt length (FL), zooplankton biomass (ZB), smolt density (SMD), and mean water column temperature (Ts) and (B) log10-transformed age-1 smolt weight (W) and the other three variables. Arrows indicate the hypothesized relational effects between all pairs of variables; P < 0.05*, P < 0.01**
Discussion
Defining Juvenile Sockeye Salmon Thermal Habitat
Thermal conditions in aquatic environments have a profound impact on organisms by affecting the rate of physiological processes and growth (Wootton 1990). For salmonids, density-independent growth depends on the length of the growing season and water temperature (Thorpe 1994). The length of the growing season indirectly affects the growth and survival of juvenile fish by controlling the rates of embryonic development (Sabo and Orth 1995), species distribution (Shuter et al. 1980; Hubert 1988; Minns and Moore 1995), reproductive success (Serns 1982; Sabo and Orth 1995), and abundance (Kallemeyn 1987). Jansen and Johnsen (1986) found a strong positive correlation between the size of Atlantic salmon Salmo salar smolts and the length of the growing season, but growth rates were faster in colder rivers than in warmer ones. We found no significant relationship between S and the size of sockeye salmon smolts (Table 5). This implies that fry grow more rapidly in lakes with short growing seasons than in those with long seasons. There is empirical evidence for such countergradient variation in growth rates among other fish species (Conover 1990; Conover and Present 1990; Conover et al. 1997). Their studies suggest that there is a genetic propensity for fish in higher latitudes (i.e., regions with shorter growing seasons) to grow faster, perhaps to achieve a larger size for enhanced overwinter survival.
We also found that the growth rate (in terms of length) of sockeye salmon smolts varied inversely with the duration of the growing season, albeit weakly (Figure 3A). However, when growth was indexed by weight, a similar pattern did not emerge (Figure 3B). We believe that this apparent discrepancy results from a decoupling of the two growth rate indices caused by differences in food levels. Beyond a growth rate of about 0.6 mm/d there is little correspondence between FL/S and W/S (Figure 4A), suggesting that length is at a maximum earlier in the season while weight continues to increase or decrease as a function of the changing conditions of the forage base. Indeed, the underlying pattern in the residuals of the regression of FL/S on W/S only showed a strong positive trend with values of ZB ranging from about 100 to 1,000 mg/m2 (Figure 4B); below and above these forage levels the response was flat. We contend that these upper and lower average levels of the standing stock of macrozooplankton may represent threshold conditions of starvation and food satiation, respectively. That is, we suggest that fish rearing under these conditions change little in length over time but experience substantial changes in weight in response to prey availability. Thus, if temporal variations in length and weight are asynchronous, then the lack of correlation between W/S and S in our data set has a plausible explanation. If there is countergradient variation (Conover 1990; )Conover et al. 1997) in the growth of sockeye salmon smolts, our data suggest that it is heavily masked by the influences of food resources and temperature.
Although the length of the growing season might provide a reasonable means for assessing regional and annual variations in thermal regimes among lakes, it does not seem to summarize very well the average in-lake thermal conditions imposed on juvenile sockeye salmon. On the other hand, the size of Atlantic salmon smolts was strongly related to the length of the growing season (indexed as the number of rearing days above 7°C; Jansen and Johnsen 1986). Because of the close correlation between air and surface water temperatures (Shuter et al. 1980), thermal indices based on mean air temperature have been used to assess the variation in freshwater fish production or yield (Schlesinger and Rieger 1982). Unfortunately, detailed water temperature data are seldom available to assess the potential mechanisms of the meteorological−fish relationships. Many freshwater fish experience large changes in water temperature because they migrate between the littoral and limnetic zones or between the epilimnion and the hypolimnion. Hence, using climatic variables such as air temperature as proxies for surface water temperature or the length of the growing season may not accurately reflect a fish's thermal environment.
Young sockeye salmon typically reside in their natal lake for 1–3 years, feeding on pelagic plankton before migrating out to sea as smolts. Rearing juveniles commonly exhibit diel vertical migration (Narver 1970) to exploit foraging opportunities, avoid predators (Eggers 1978), and (probably) to optimize bioenergetic efficiency (Beauchamp et al. 1989; Levy 1990a; Bevelhimer and Adams 1993; Luecke et al. 1996). In terms of abiotic factors, turbidity appears to dampen diel vertical migration in sockeye salmon (Levy 1990b), whereas the diel vertical migration of kokanee (lacustrine sockeye salmon) in Blue Mesa Reservoir, Colorado, shifted in response to the temporal development of stratification (Stockwell and Johnson 1999). From our perspective, we might infer that based on light attenuation, diel vertical migration would be weakest in glacial lakes. Schmidt et al. (1994) found that sockeye salmon juveniles migrated to great depths (>50 m) during the day in moderately turbid (5–10 NTU) Skilak Lake, Alaska, whereas in the nearby and highly turbid (50 NTU) Tustumena Lake they were surface (<10 m) oriented even though the latter lake had much lower food (zooplankton biomass) levels. On the other hand, Yanusz (1989) found that for much of the growing season sockeye salmon fry remained in the surface layers during the day and night in Packers Lake, Alaska, a strongly stratified and stained system. It is likely then that the pattern and amplitude of diel vertical migration at a regional scale would follow a complex thermal and food resource gradient. Such a gradient would be affected not only by changes in latitude (length of the growing season) but also by the influences of lake typology (color and turbidity) on light penetration (Koenings and Edmundson 1991) and primary (Edmundson and Carlson 1998) and secondary (Koenings et al. 1990) production. Thus, quantifying the relative effect of temperature on juvenile sockeye salmon growth among a variety of natural populations is problematic.
Ideally, one would like to know the amount of time sockeye salmon spend at selected temperatures (depths) during their freshwater life history, along with having detailed information on food (zooplankton) availability. Several investigators have developed such data (Beauchamp et al. 1997; Stockwell and Johnson 1999). However, it is rare for sockeye salmon distribution data of this sort to be coupled with limnological measures, at least for a large number of lakes. Thus, the initial question raised is how we can more easily define and quantify the thermal habitat or temperature regime experienced by rearing sockeye salmon juveniles in the absence of concomitant hydroacoustic and temperature information. In order to assess the potential temperature niche available for young sockeye salmon relative to their size at smoltification, we considered the variable Ts because it incorporates both the length of the growing season and the corresponding seasonal changes in temperature at different depths. Furthermore, we think that Ts, which represents the average temperature of the water column over the entire growing season, probably captures much of the spatial and temporal range in temperature experienced by rearing juvenile fry. Therefore, we suggest that the variable Ts is a good index of the overall thermal conditions imposed on lake-rearing fry.
Model Evaluation and Applications
To isolate the effect of temperature (e.g., Ts) on fish growth, one also needs to consider the concomitant effects of biotic factors such as food abundance and density-dependent forces (Lehtonen and Lappalainen 1995). In our analysis, we examined these additional factors through the variables ZB (food) and SMD (fish density). Of the three variables, ZB was the strongest single predictor of smolt size (mean length and weight), followed by Ts and SMD (Table 6). Despite differences in temperature regimes in the different lake types (Table 3), the relationships between smolt size and the independent variables are consistent with respect to sign and magnitude across lake types (Table 7). That is, the growth of juvenile sockeye salmon is directly related to zooplankton availability and temperature and inversely related to fish population density. Hence, pooling the data across lake types in the single-factor regression analysis was a reasonable statistical method. From the standpoint of the goodness-of-fit criterion (r2), the influence of Ts by itself on smolt size was relatively weak (about 20%; Table 6). However, temperature interacting with food availability mediates the population growth rates of juvenile sockeye salmon (Beauchamp et al. 1989; Levy 1990a, 1990b; Bevelhimer and Adams 1993; Luecke et al. 1996). Thus, we considered a multiple-regression approach to better assess the effects of temperature on smolt size relative to those of food resource availability and fry density.
The empirical models that we derived for the Alaskan lakes predicted smolt size with a relatively high degree of accuracy (R2 = 0.70). There was no apparent covariation in our models because the partial regression coefficients were of much the same magnitude as those in the single-factor regression models and none of the independent variables were strongly correlated with each other (Figure 6). Despite the significance of temperature in the models, the idea that Ts might affect smolt size indirectly by limiting plankton production seemed to be a reasonable assumption. Zooplankton is the principal component of the diet of young sockeye salmon, and their growth and densities are strongly related to temperature (Shuter and Ing 1997). However, the partial correlations between ZB and Ts in our multivariate models were negligible (Figure 6). We do not disregard the important influence of temperature on crustacean zooplankton but concede that within the 10°C range of Ts our variable ZB might simply be too robust to detect a temperature effect on zooplankton metabolism (e.g., molting rate, growth, and reproduction). In addition, zooplankton species composition is an important consideration because cladocerans exhibit a greater capability for responding to temperature through faster growth and generation time than copepods (Shuter and Ing 1997). Indeed, our data set includes not only clear and stained lakes that have both cladoceran and copepod zooplankters, but also glacial lakes that do not support populations of cladocerans (Koenings et al. 1990). Nonetheless, we interpret our models as indicating that increasing energy input (indexed as Ts) affects vital metabolic rates, causing more rapid growth and larger smolt size. It is not our intention, however, to discuss sockeye salmon energetics, as the interactions of temperature and ration on metabolism are outside the scope of this paper. Instead, our empirical model simply quantifies a significant effect of temperature in conjunction with food availability and fish density on the growth of rearing sockeye salmon juveniles as indexed by age-1 smolt size.
Several possibilities exist for the use of this kind of model in fishery resource management. For instance, recruitment into a stock is not independent of other biotic and abiotic components, and to assume that the factors regulating sockeye salmon populations in their natal lakes remain relatively constant is naïve (Rigler 1982; Koenings and Burkett 1987; Schmidt et al. 1997). Recruitment variability is a critical issue in the management of Pacific salmon. In Alaska, sockeye salmon fisheries are managed with defined spawner-escapement goals and stock–recruitment analysis. However, there is strong evidence that the smolt-to-adult survival of sockeye salmon increases with smolt size (Henderson and Cass 1991; Koenings et al. 1993). Thus, the dependence of sockeye salmon smolt size on lake temperature as well as on forage availability and the magnitude of density-dependent growth (Table 9; Figure 6) argues for combining limnological data with stock and recruitment information to develop or refine escapement goals. Although Koenings and Burkett (1987) developed the first model of carrying capacity for sockeye salmon production in Alaska based on freshwater conditions (euphotic volume), reliable limnological and smolt (or perhaps fall fry) information, with corresponding stock recruitment data, needs to be obtained from multiple sockeye salmon lakes in order to develop relationships between the species' trophodynamics, smolt demographics, size of spawning stocks, and adult recruits. This will provide a more refined method for estimating system carrying capacity, optimum escapement, and yield.
The empirical models we developed might also be helpful in assessing the general effects of climate change on lakes producing sockeye salmon, particularly on a regional basis or in the context of multiple lake types. For example, simulated increases in water temperature based on a doubling of atmospheric CO2 projected decreases in available habitat for coldwater fishes among deep, well-mixed, oligotrophic systems (Stefan et al. 1995), though the lakes studied are of a more southerly distribution. Our model suggests that temperature increases would accelerate freshwater growth and presumably also the production of juvenile sockeye salmon. Schindler et al. (1996) suggested that the lower precipitation associated with warmer temperatures would decrease the loading of dissolved organic material, resulting in greater transparency, deeper thermoclines, and presumably greater heat content in smaller, humic, stained lakes. On the other hand, King et al. (1997) found that warmer climatic conditions produced earlier stratification, thinner epilimnions, and steeper thermal gradients in Lake Huron. Furthermore, warmer conditions, coupled with an earlier onset of stratification, accelerated the growth of northern populations of warmwater fishes such as smallmouth bass and yellow perch, whereas the growth of coldwater species such as lake trout declined (King et al. 1999). We suggest that the increased glacier melt associated with warmer air temperatures would probably increase inorganic turbidity because of increased reflectance (Koenings and Edmundson 1991) and lower surfaces temperatures in glacially influenced lakes. Thus, predicted freshwater growth patterns of sockeye salmon under changing temperature regimes may be complicated by lake typology influences. Whatever the response, from a regional or multilake perspective, such climate change scenarios may yield new ecological insights for future research on freshwater sockeye salmon production and pose major challenges for fishery managers.
Acknowledgments
This is contribution PP-188 of the Alaska Department of Fish and Game, Commercial Fisheries Division, Juneau.











