Volume 2025, Issue 1 5689716

Research Article

Open Access

Optimization and Vibration Response Analysis of Vehicle Suspension Structure With Inerter

Haiqing Lu,

Haiqing Lu

School of Machinery and Automation , Weifang University , Weifang , 261061 , China , wfu.edu.cn

Search for more papers by this author

Fanjie Li,

Corresponding Author

Fanjie Li

[email protected]

orcid.org/0000-0002-2883-7596

School of Machinery and Automation , Weifang University , Weifang , 261061 , China , wfu.edu.cn

Search for more papers by this author

Xiaopeng Li,

Xiaopeng Li

orcid.org/0000-0003-4161-2727

School of Mechanical Engineering and Automation , Northeastern University , Shenyang , 110819 , China , neu.edu.cn

Search for more papers by this author

Haozhe Wang,

Haozhe Wang

School of Mechanical Engineering and Automation , Northeastern University , Shenyang , 110819 , China , neu.edu.cn

Search for more papers by this author

Haiqing Lu,

Haiqing Lu

School of Machinery and Automation , Weifang University , Weifang , 261061 , China , wfu.edu.cn

Search for more papers by this author

Fanjie Li,

Corresponding Author

Fanjie Li

[email protected]

orcid.org/0000-0002-2883-7596

School of Machinery and Automation , Weifang University , Weifang , 261061 , China , wfu.edu.cn

Search for more papers by this author

Xiaopeng Li,

Xiaopeng Li

orcid.org/0000-0003-4161-2727

School of Mechanical Engineering and Automation , Northeastern University , Shenyang , 110819 , China , neu.edu.cn

Search for more papers by this author

Haozhe Wang,

Haozhe Wang

School of Mechanical Engineering and Automation , Northeastern University , Shenyang , 110819 , China , neu.edu.cn

Search for more papers by this author

First published: 19 May 2025

https://doi.org/10.1155/vib/5689716

Academic Editor: Angelo Marcelo Tusset

Share a link

Email
Wechat
Bluesky

Abstract

The structural composition and component parameters of the suspension will have an impact on the vibration reduction and handling performance of the vehicle. This paper innovatively proposes a suspension structure using an inerter and mathematically models it. To further improve the comprehensive performance of the designed suspension, the component parameters are optimized and the bushing is selected based on merit. The influence of parameters on suspension response is obtained using numerical methods, and the damping effect and handling performance of the suspension are deeply studied. Based on the analysis results of this paper, the designed suspension structure and its optimized design have effectively improved the overall performance of the vehicle. In addition to optimizing the parameters of suspension components, optimizing the selection of suspension bushings also has a positive impact on the overall performance of the vehicle. Therefore, this study provides a new design approach for improving the overall performance of suspension systems.

1. Introduction

Suspension, as a bridge between the vehicle body and axle transmission, has always been a key research object for improving driving safety and comfort. After the invention of the inerter, a new type of mechanical isolation system constructed by the inerter, spring, and damper emerged. Therefore, studying the suspension composed of inerter, spring, and damper has both forward-looking and practical value.

The invention of the inerter is aimed at improving the theory of mechanical–electrical similarity, enabling mechanical and electrical components to correspond one-to-one. Cao et al. [1] ingeniously applied the inerter to the vibration control of seat suspensions, and using the inerter to generate controllable damping forces is a highly innovative research work. Shen et al. [2] proposed a hydropneumatic suspension to enhance comfort, which significantly improved comfort by combining the inerter with the suspension. Yang et al. [3] explored the vibration isolation performance of energy-saving suspension using the inerter from the perspective of energy recovery and proved the effectiveness of inerters in the field of energy recovery. They used optimization algorithms to improve the design of vibration reduction structures. Ge et al. [4] used parameter optimization methods based on analytical solutions to optimize suspension parameters, simplifying the optimization process and solving the inherent inertia problem of actuators. Although analytical solutions can simplify the optimization process, the numerical solutions of multiobjective optimization algorithms are more accurate. Wei and Su [5] optimized the switching function during active suspension control using a particle swarm optimization algorithm, improving the dynamic performance of the suspension. Gao and Han [6] optimized the stiffness of the bushing, improving the stability of the vehicle during operation. However, the impact of the damping coefficient of the bushing, an important indicator, on stability has not been considered. Nie et al. [7] used a vehicle equivalent model to analyze the response of the suspension through theoretical and experimental research, demonstrating the load adaptability of the designed structure during operation. Zhang et al. [8] studied a new type of viscous damper device related to displacement and analyzed the mathematical and dynamic relationship of the device through theory and experiment. The adaptability of the mem-damper to loads is analyzed using vehicle suspension as the carrier. Zhang et al. [9] combined the inerter with application controllers for suspension and simulated and analyzed the designed suspension damping structure using the vertical acceleration and its rate of change of the vehicle body as input signals. Chen et al. [10] used the LQR control algorithm to control the coefficients of the damping components of the ISD suspension, making both adjustable simultaneously, further optimizing the overall performance of the suspension during operation. Wang et al. [11] studied the performance of suspension structures using inerters under the influence of nonlinear factors and investigated the nonlinear factors. To explore the application potential of the diamond-shaped structure inerter, Zhang et al. [12] established a structure of the seat suspension using numerical methods and studied the mechanism of seat suspension load adaptation. Kuznetsov et al. [13] established a suspension structure using inerters to improve ride comfort and optimized the parameters using weighted acceleration as the evaluation index. Hu and Chen [14] discussed the improvement effect of different combinations of inerters, springs, and dampers on the behavior of suspension during operation. Li et al. [15, 16] discussed the damping effect of two-stage vehicle suspensions and analyzed the variation law of damping performance after the combination of inerter and traditional suspensions. Hu et al. [17–19] analyzed the performance of suspension systems with control strategies in terms of vibration reduction and stability and proposed a switching method to adjust the state of the suspension during operation, thereby better achieving stability during vibration suppression. Shi et al. [20] analyzed the characteristics of suspension using inerters in nonlinear behavior and studied the inducing effects of factors such as friction and clearance on nonlinear behavior. In this paper, the optimization design of the suspension structure using the inerter is carried out. By optimizing the parameters of the damping components and optimizing the selection of bushings, the overall performance of the suspension has been further optimized.

The structure of the paper is as follows. In Section 2, the mathematical model of the vehicle suspension system is established. In Section 3, the optimization design of the vehicle suspension system has been carried out. In Section 4, the dynamic response of the suspension is discussed, the influence of bushing parameters on power transmission is studied, and the comparative analysis of vehicle handling stability is explored. Finally, the conclusions are given in Section 5.

2. Mathematical Modeling of the Vehicle Suspension System

To study the vibration response of a vehicle suspension structure using an inerter containing damping components, the model of the vehicle suspension system is established as shown in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The model of the vehicle suspension system.

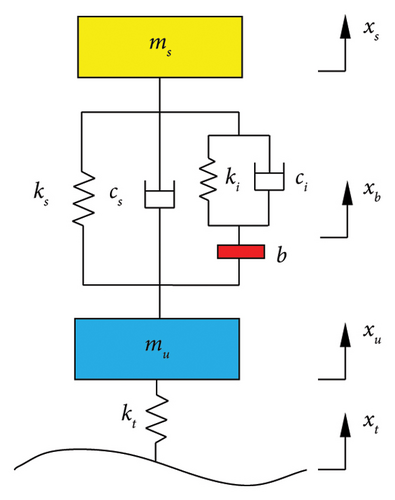
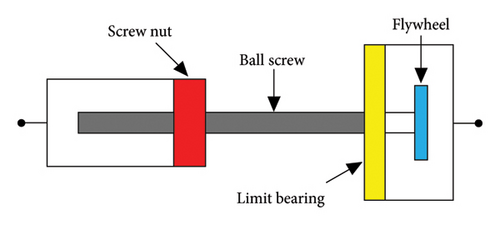
The physical implementation structures of inerters mainly include ball screw inerter, gear rack inerter, and hydraulic inerter. The ball screw type inerter is shown in Figure 2.

The dynamic equation of the vehicle suspension model is

\begin{matrix} \{\begin{matrix} m_{s} x_{s}^{″} + k_{s} (x_{s} - x_{u}) + c_{s} (x_{s}^{'} - x_{u}^{'}) + F = 0, \\ {m_{u} x}_{u}^{″} + k_{t} (x_{u} - x_{t}) - k_{s} (x_{s} - x_{u}) - c_{s} (x_{s}^{'} - x_{u}^{'}) = F, \\ F = b (x_{b}^{″} - x_{u}^{″}) = k_{i} (x_{s} - x_{b}) + c_{i} (x_{s}^{'} - x_{b}^{'}), \end{matrix} \end{matrix}

(1)

where m_s is the spring-loaded mass, m_u is the nonspring-loaded mass, k_s is the main spring stiffness, c_s is the main damping coefficient, k_t is the tire stiffness, b is the inertance, k_i is the secondary spring stiffness, and c_i is the secondary damping coefficient. F is the force acting on both ends of the inertial container.

The mathematical model for simulating random road excitation can be written as

\begin{matrix} x_{t}^{'} (t) = - 22 π f_{0} x_{t} (t) + π \sqrt{G_{0} v} w (t), \end{matrix}

(2)

where G₀ is the road roughness coefficient, v is the vehicle speed, w(t) is a Gaussian white noise matrix with a mean of zero, and f₀ is the lower cutoff frequency.

The general representation of the state space equation is

\begin{matrix} \{\begin{cases} X^{'} = A X + B U, \\ Y = C X, \end{cases} \end{matrix}

(3)

where A, B, and C are coefficient matrices.

The state variables of the system can be written as

\begin{matrix} X = {(\begin{matrix} x_{1} & x_{2} & x_{3} & x_{4} & x_{5} & x_{6} & x_{7} \end{matrix})}^{T} . \end{matrix}

(4)

We define them as follows:

\begin{matrix} x_{1} = x_{s}^{'}, \\ x_{2} = x_{u}^{'}, \\ x_{3} = x_{b}^{'}, \\ x_{4} = x_{s}, \\ x_{5} = x_{u}, \\ x_{6} = x_{b}, \\ x_{7} = x_{t} . \end{matrix}

(5)

The state equation can be written as

\begin{matrix} \{\begin{matrix} x_{1}^{'} = - \frac{1}{m_{s}} [k_{s} (x_{4} - x_{5}) + c_{s} (x_{1}^{'} - x_{2}^{'}) + k_{i} (x_{4} - x_{6}) + c_{i} (x_{1}^{'} - x_{3}^{'})]; \\ x_{2}^{'} = - \frac{1}{m_{u}} [k_{t} (x_{5} - x_{7}) - k_{s} (x_{4} - x_{5}) - c_{s} (x_{1}^{'} - x_{2}^{'}) - k_{i} (x_{4} - x_{6}) - c_{i} (x_{1}^{'} - x_{3}^{'})]; \\ x_{3}^{'} = - \frac{1}{b} [k_{i} (x_{6} - x_{4}) + c_{i} (x_{3}^{'} - x_{1}^{'})] + x_{2}^{'}; \\ x_{4}^{'} = x_{1}; \\ x_{5}^{'} = x_{2}; \\ x_{6}^{'} = x_{3}; \\ x_{7}^{'} = - 22 π f_{0} x_{7} + π \sqrt{G_{0} v} w (t) . \end{matrix} \end{matrix}

(6)

The coefficient matrix A can be written as

\begin{matrix} A = (\begin{matrix} a_{11} & a_{12} & a_{13} & a_{14} & a_{15} & a_{16} & 0 \\ a_{21} & a_{22} & a_{23} & a_{24} & a_{25} & a_{26} & a_{27} \\ a_{31} & a_{32} & a_{33} & a_{34} & a_{35} & a_{36} & a_{37} \\ 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & - 2 π f_{0} \end{matrix}), \end{matrix}

(7)

where

\begin{matrix} \{\begin{matrix} a_{11} = - \frac{c_{s} + c_{i}}{m_{s}}, \\ a_{12} = \frac{c_{s}}{m_{s}}, \\ a_{13} = \frac{c_{i}}{m_{s}}, \\ a_{14} = - \frac{k_{s} + k_{i}}{m_{s}}, \\ a_{15} = \frac{k_{s}}{m_{s}}, \\ a_{16} = \frac{k_{i}}{m_{s}}, \\ a_{21} = \frac{c_{i} + c_{s}}{m_{u}}, \\ a_{22} = - \frac{c_{s}}{m_{u}}, \\ a_{23} = - \frac{c_{i}}{m_{u}}, \\ a_{24} = \frac{k_{i} + k_{s}}{m_{u}}, \\ a_{25} = - \frac{k_{s} + k_{t}}{m_{u}}, \\ a_{26} = - \frac{k_{i}}{m_{u}}, \\ a_{27} = \frac{k_{t}}{m_{u}}, \\ a_{31} = \frac{c_{i}}{b} + \frac{c_{i} + c_{s}}{m_{u}}, \\ a_{32} = - \frac{c_{s}}{m_{u}}, \\ a_{33} = - \frac{c_{i}}{b} - \frac{c_{i}}{m_{u}}, \\ a_{34} = \frac{k_{i}}{b} + \frac{k_{i} + k_{s}}{m_{u}}, \\ a_{35} = - \frac{k_{s} + k_{t}}{m_{u}}, \\ a_{36} = - \frac{k_{i}}{b} - \frac{k_{i}}{m_{u}}, \\ a_{37} = \frac{k_{t}}{m_{u}} . \end{matrix} \end{matrix}

(8)

The coefficient matrix B can be written as

\begin{matrix} B = {(\begin{matrix} 0 & 0 & 0 & 0 & 0 & 0 & 2 π \sqrt{G_{0} v} \end{matrix})}^{T} . \end{matrix}

(9)

The coefficient matrix C can be written as

\begin{matrix} C = (\begin{matrix} c_{11} & c_{12} & c_{13} & c_{14} & c_{15} & c_{16} & 0 \\ 0 & 0 & 0 & 1 & - 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & k_{t} & 0 & - k_{t} \end{matrix}), \end{matrix}

(10)

where

\begin{matrix} \{\begin{matrix} c_{11} = - \frac{c_{s} + c_{i}}{m_{s}}, \\ c_{12} = \frac{c_{s}}{m_{s}}, \\ c_{13} = \frac{c_{i}}{m_{s}}, \\ c_{14} = - \frac{k_{s} + k_{i}}{m_{s}}, \\ c_{15} = \frac{k_{s}}{m_{s}}, \\ c_{16} = \frac{k_{i}}{m_{s}} . \end{matrix} \end{matrix}

(11)

The input variable can be written as follows:

\begin{matrix} U = w (t) . \end{matrix}

(12)

The output variable can be written as follows:

\begin{matrix} Y = {(x_{s}^{″} x_{s} - x_{u} (x_{u} - x_{t}) k_{t})}^{T} . \end{matrix}

(13)

3. Optimization Design of the Vehicle Suspension System

To achieve the goal of suspension optimization design, the parameters used for numerical simulation were first selected.

The model parameters of the vehicle suspension system are shown in Table 1 [21–23].

Table 1. The model parameters of the vehicle suspension system.

Item	Notation	Value
Spring-loaded mass	m_s	320 kg
Nonspring-loaded mass	m_u	45 kg
Tire stiffness	k_t	190 kN·m⁻¹
Main spring stiffness	k_s	22 kN·m⁻¹
Main damping coefficient	c_s	1 kN·s·m⁻¹
Inertance	b	288 kg
Secondary spring stiffness	k_i	6.64 kN·m⁻¹
Secondary damping coefficient	c_i	1.608 kN·s·m⁻¹
Road roughness coefficient	G₀	5 × 10⁻⁶ m³·cycle⁻¹
Vehicle speed	v	20 m·s⁻¹
Lower cutoff frequency	f₀	0.01 Hz

3.1. Optimization of Suspension Parameters

To improve the comprehensive performance, a genetic algorithm is used to optimize the parameters of inertance b, secondary spring stiffness k_i, and secondary damping coefficient c_i. In the optimization process, more emphasis should be placed on ride comfort and safety, while also considering tire dynamic loads to a certain extent. Based on this, we select values of 0.4, 0.4, and 0.2, respectively. The fitness function is

\begin{matrix} \min J = 0.40.40.2 A {(x)}^{2} + L {(x)}^{2} + T {(x)}^{2}, \end{matrix}

(14)

where J is the fitness function value.

A group of individuals in the optimization process can be written as

\begin{matrix} x = (b, k_{i}, c_{i}) . \end{matrix}

(15)

To ensure that the optimized parameters meet the actual production requirements, optimization ranges were set for the inertance b, secondary spring stiffness k_i, and secondary damping coefficient c_i, as shown in the following equation:

\begin{matrix} \{\begin{matrix} 10400 kg < b < kg, \\ 1010000 N \cdot m^{- 1} < k_{i} < N \cdot m^{- 1}, \\ 102000 N \cdot s \cdot m^{- 1} < c_{i} < N \cdot s \cdot m^{- 1} . \end{matrix} \end{matrix}

(16)

The set constraints can be written as

\begin{matrix} s . t \{\begin{matrix} A (x) < A {(x)}_{past}, \\ L (x) < L {(x)}_{past}, \\ T (x) < T {(x)}_{past}, \end{matrix} \end{matrix}

(17)

where A(x)_past, L(x)_past, and T(x)_past are the root mean square values under the optimized parameters.

3.2. Power Flow Analysis of ISD Suspension

The model in Figure 3 introduces bushings based on the model in Figure 1 and establishes the mechanical mesh of the vehicle with bushings.

The equivalent impedance on the left is

\begin{matrix} Z_{e q} = i ω m_{s} + \frac{1}{(i ω / k_{b} + i ω c_{b}) + (k_{s} / i ω) + c_{s}} . \end{matrix}

(18)

The equivalent impedance on the right side is

\begin{matrix} Z_{L} = \frac{1}{(1 / (k_{b} / i ω) + c_{b}) + (1 / i ω b) + (1 / (k_{i} / i ω) + c_{i})} . \end{matrix}

(19)

The force at connection point A can be written as

\begin{matrix} F_{L} = \frac{Z_{L}}{Z_{e q} + Z_{L}} F_{c}, \end{matrix}

(20)

where F_c is a constant force source, and F_c is taken as the harmonic unit force.

The speed at connection point A can be written as

\begin{matrix} V_{L} = \frac{F_{L}}{Z_{L}} . \end{matrix}

(21)

The power flow passing through point A can be written as

\begin{matrix} P = \frac{1}{2} Re (F_{L} {V_{L}}^{*}) . \end{matrix}

(22)

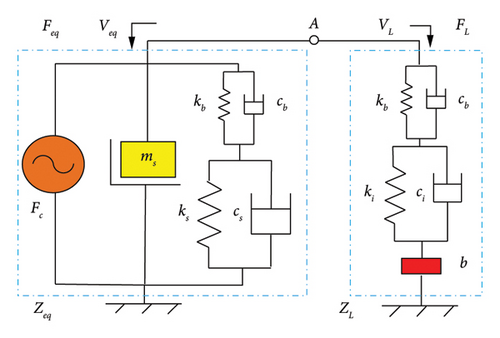
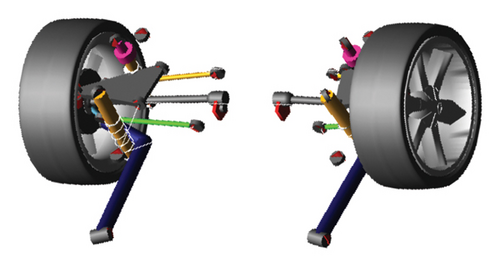
To verify the correctness of the established suspension system model, a multibody dynamic model of the suspension system illustrated in Figure 4 is established in the simulation software ADAMS/car, and the parameter k_b = 450 N/mm and c_b = 0.50 N·s·mm⁻¹ are selected.

The comparison of power flow obtained through theoretical calculation and simulation data is illustrated in Figure 5.

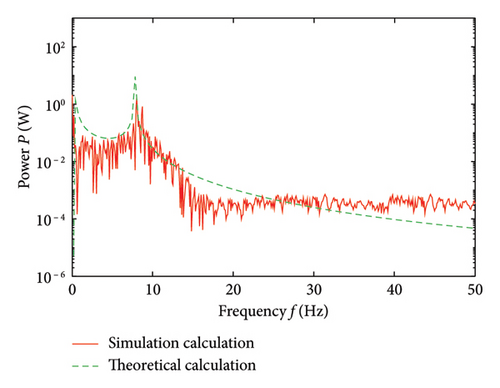
In Figure 5, as the frequency increases, the trend of the power flow spectrum obtained through theoretical calculation and simulation data is basically consistent, and the error is not large, which proves the correctness of the constructed model.

4. Results and Discussion

4.1. Dynamic Response of Vehicle Suspension

To characterize the impact of suspension parameters optimized by a genetic algorithm, the dynamic response of the vehicle suspension system under the design parameters before optimization is compared. The dynamic response of the vehicle suspension system before and after parameter optimization is illustrated in Figure 6.

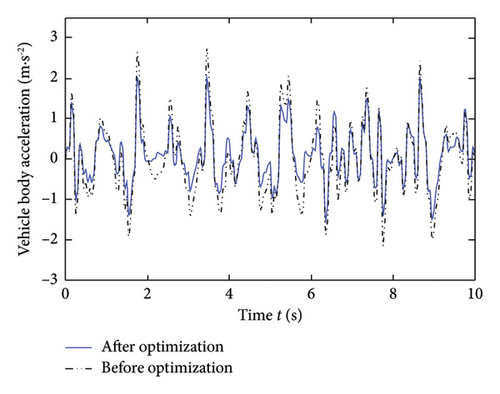
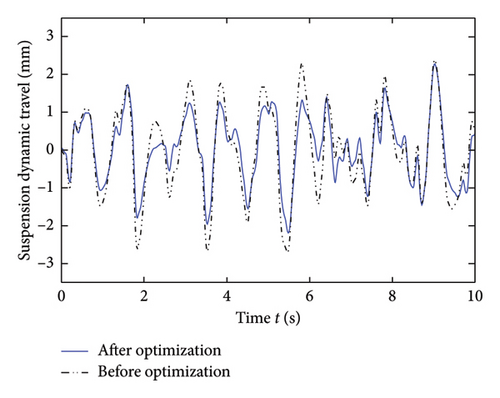
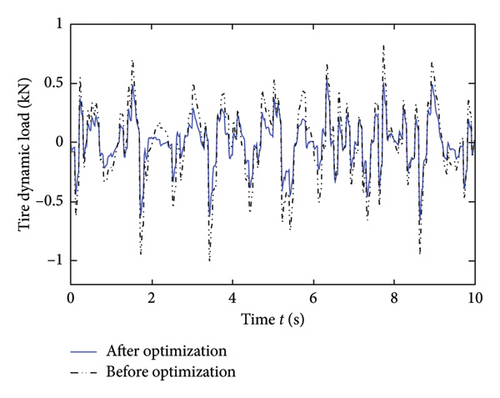
In Figure 6, compared to before optimization, the optimized vehicle body acceleration, suspension working space, and tire dynamic load indicators have all been significantly improved. The parameters obtained through genetic algorithm optimization are significantly better than the design parameters before optimization.

The comparison of peak-to-peak values before and after optimization is shown in Table 2. In Table 2, the peak-to-peak value of vehicle body acceleration improved by 25.8%. The peak-to-peak value of suspension dynamic travel improved by 11.2%. The peak-to-peak value of the tire dynamic load improved by 34.9%. The comprehensive damping performance of the optimized vehicle suspension system has been improved.

Table 2. The comparison of peak-to-peak values.

Evaluation indicator	Before optimization	After optimization	Improvement level (%)
Vehicle body acceleration	4.93 m·s⁻²	3.66 m·s⁻²	25.8
Suspension dynamic travel	5.08 mm	4.51 mm	11.2
Tire dynamic load	1.89 kN	1.23 kN	34.9

4.2. The Influence of Bushing Parameters on Power Transmission

Blindly optimizing the parameters according to optimization methods may result in parameters that are not suitable for production or have a long production cycle, and the optimization design lacks practical significance. Therefore, in the actual application process, optimization and selection of existing bushing parameters are carried out to complete the optimization and matching of suspension bushing parameters.

The bushing parameters of the three mainstream vehicle suspensions in the market are shown in Table 3.

Table 3. Bushing parameters table.

Bushing type	Stiffness (N/mm)	Damping coefficient (N·s·mm⁻¹)
Type 1	450	0.50
Type 2	800	0.15
Type 3	300	2.00

Based on the stiffness and damping coefficients of different types of bushings in Table 3, this study investigates the influence of bushing parameters on the vibration power of suspension systems based on vibration power flow theory. The power flow spectra under different stiffnesses are shown in Figure 7.

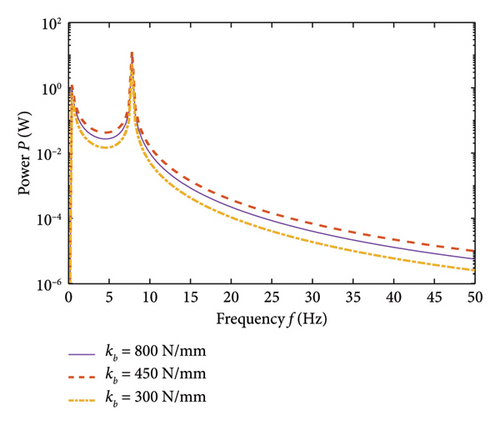
In Figure 7, the stiffness variation of the bushing has a relatively small impact on the vibration power flow transmitted to the body. In 0–50 Hz, the power flow spectrum at k_b = 300 N/mm is always lower than the other two types of power flow spectra.

The power flow spectrum with different damping is shown in Figure 8.

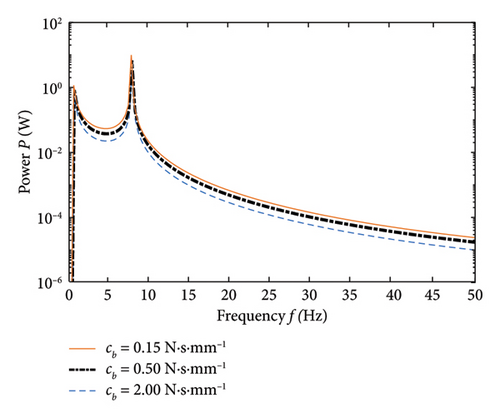
In Figure 8, when the damping coefficient of the bushing increases to a small extent, the amplitude difference of the power flow spectrum is small. However, as the damping coefficient increases from 0.50 to 2.00 N·s·mm⁻¹, the amplitude difference of the power flow spectrum becomes apparent. In 0–50 Hz, the power flow spectrum of the bushing with a damping coefficient of c_b = 2.00 N·s·mm⁻¹ is always lower than the power flow spectra of the other two types. In summary, compared to Type 1 and Type 2, Type 3 is more suitable for reducing the energy transmitted through the suspension to the body, enabling the suspension to achieve better vibration reduction effects.

4.3. Comparative Analysis of Vehicle Handling Stability

The handling stability of the vehicle is also an important performance evaluation indicator. To fully demonstrate the superiority of the ISD suspension proposed in this manuscript in terms of comprehensive damping performance, the manuscript introduces a comparative analysis of vehicle handling stability between traditional suspension and ISD suspension.

As the body roll changes, the change in toe angle will directly reflect the stability when encountering obstacles during straight-line driving and the magnitude of the lateral force on the tires. The toe angle variation curve between ISD suspension and traditional suspension is shown in Figure 9.

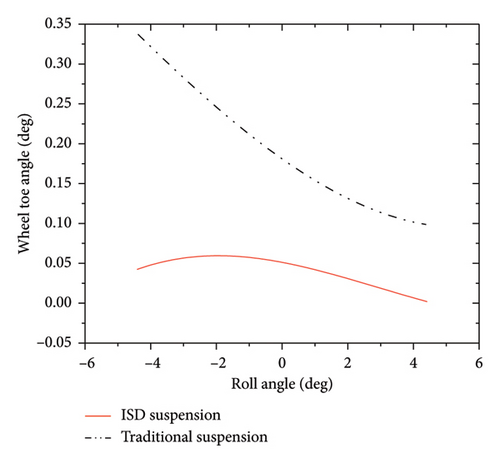
In Figure 9, ISD suspension shows obvious advantages in roll motion, indicating that its performance significantly improves when facing complex working conditions, ensuring good driving stability of the vehicle. From the perspective of the coefficient of variation, ISD suspension has decreased by 13.6% compared to traditional suspension. Overall analysis shows that the ISD suspension has a smaller variation during roll motion. When the vehicle tilts, there is a significant height difference between the left and right wheels. The ball screw converts the linear displacement difference into the rotation of the flywheel, which unleashes the potential of inertia.

The variation curve of the kingpin inclination angle between ISD suspension and traditional suspension under the condition of dual wheel same direction jumping is shown in Figure 10.

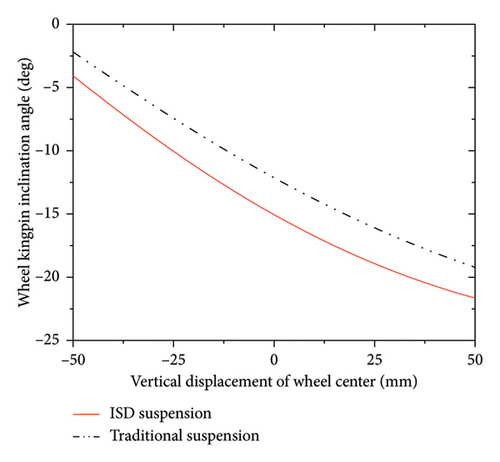
In Figure 10, when jumping up, it should be at a negative camber angle as much as possible. To ensure the same total angle, the inclination angle of the main pin should be increased. At this time, the change in the inclination angle of the main pin of the ISD suspension meets this requirement, and the linearity of the inclination angle of the ISD suspension is good.

5. Conclusions

The innovation of this paper lies in the comprehensive use of a genetic algorithm to optimize the parameters of suspension and the optimal selection of bushings to improve suspension performance. The contribution of this study is mainly reflected in providing new ideas for the optimization design of vehicle suspension.

1.
Using a genetic algorithm to optimize suspension parameters, after about 25 generations, the optimal value of the fitness function is basically stable. Most of the data generated by 100 generations are concentrated at a point, which corresponds to the optimal parameter.
2.
The optimized parameters are significantly better than the design parameters before optimization, and the comprehensive damping performance of the vehicle suspension system has been improved after optimization.
3.
The trend of the power flow spectrum of the vehicle suspension system obtained through theoretical calculations and simulation data is basically consistent, which verifies the correctness of the constructed model.
4.
ISD suspension shows obvious advantages in roll motion, indicating that its performance significantly improves when facing complex working conditions, ensuring good driving stability of the vehicle.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This study was supported by the National Natural Science Foundation of China (Grant no. 52275090).

Open Research

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

1 Cao J., Liu P. F., Ning D. H., Sun S. S., and Liu G. J., Vibration Control of the Seat Suspension With a Magnetorheological Damper-Based Controllable Inerter, Journal of Vibration and Control. (2025) 31, no. 1-2, 92–103, https://doi.org/10.1177/10775463241297739.
10.1177/10775463241297739
Google Scholar
2 Shen Y. J., Qiu D. D., Yang X. F., Chen J. J., Guo Y., and Zhang T. Y., Vibration Isolation Performance Analysis of a Nonlinear Fluid Inerter-Based Hydro-Pneumatic Suspension, International Journal of Structural Stability and Dynamics. (2024) 26, https://doi.org/10.1142/S0219455426500793.
10.1142/S0219455426500793
Google Scholar
3 Yang X. F., Zhang T. Y., Shen Y. J., Liu Y. L., Bui V., and Qiu D. D., Tradeoff Analysis of the Energy-Harvesting Vehicle Suspension System Employing Inerter Element, Energy. (2024) 308, https://doi.org/10.1016/j.energy.2024.132841.
10.1016/j.energy.2024.132841
Google Scholar
4 Ge Z., Wang W. R., Li G. P., and Rao D. G., Design, Parameter Optimisation, and Performance Analysis of Active Tuned Inerter Damper (TID) Suspension for Vehicle, Journal of Sound and Vibration. (2022) 525, https://doi.org/10.1016/j.jsv.2022.116750.
10.1016/j.jsv.2022.116750
Google Scholar
5 Wei S. W. and Su X. Y., Sliding Mode Control Design for Active Suspension Systems Using Quantum Particle Swarm Optimisation, International Journal of Vehicle Design. (2019) 81, no. 1/2, 93–114, https://doi.org/10.1504/IJVD.2019.110734.
10.1504/IJVD.2019.110734
Google Scholar
6 Gao J. and Han P. F., Collaborative Optimization of Bushing Installation Angle and Bushing Stiffness of Torsion Beam Suspension to Improve the Handing Stability of the Whole Vehicle, Advances in Mechanical Engineering. (2022) 14, no. 5, https://doi.org/10.1177/16878132221101022.
10.1177/16878132221101022
Google Scholar
7 Nie J. M., Liu X. B., Huang X. R., and Zhang X. L., Load Adaptivity of the Mem-Spring and Its Performance Benefits in Vehicle Suspensions, Nonlinear Dynamics. (2024) 112, no. 24, 21645–21666, https://doi.org/10.1007/s11071-024-10161-5.
10.1007/s11071-024-10161-5
Google Scholar
8 Zhang X. L., Zhang S. J., Wang F. L., and Nie J. M., Understanding the Inherently Self-Adjusting Mechanism and Load Adaptability of the Mem-Damper, International Journal of Structural Stability and Dynamics. (2024) 25, https://doi.org/10.1142/S0219455426500240.
10.1142/S0219455426500240
Google Scholar
9 Zhang X. J., Ahmadian M., and Guo K. H., On the Benefits of Semi-Active Suspensions With Inerters, Shock and Vibration. (2012) 19, no. 3, 257–272, https://doi.org/10.1155/2012/640275.
10.3233/SAV-2011-0628
Web of Science® Google Scholar
10 Chen M. Z. Q., Hu Y., Li C., and Chen G., Semi-Active Suspension With Semi-Active Inerter and Semi-Active Damper, IFAC Proceedings Volumes. (2014) 47, no. 3, 11225–11230, https://doi.org/10.3182/20140824-6-ZA-1003.00138.
10.3182/20140824-6-ZA-1003.00138
Google Scholar
11 Wang F. C., Hong M. F., and Lin T. C., Designing and Testing a Hydraulic Inerter, Proceedings of the Institution of Mechanical Engineers—Part C: Journal of Mechanical Engineering Science. (2011) 225, no. 1, 66–72, https://doi.org/10.1243/09544062JMES2199, 2-s2.0-79251470110.
10.1243/09544062JMES2199
Web of Science® Google Scholar
12 Zhang X. L., Cheng X. B., Liu J. C., Yang J. X., and Nie J. M., Load Adaptivity of Seat Suspensions Equipped With Diamond-Shaped Structure Mem-Inerter, Journal of Vibration Engineering & Technologies. (2024) 12, no. 7, 8707–8724, https://doi.org/10.1007/s42417-024-01385-1.
10.1007/s42417-024-01385-1
Google Scholar
13 Kuznetsov A., Mammadov M., Sultan I., and Hajilarov E., Optimization of Improved Suspension System With Inerter Device of the Quarter-Car Model in Vibration Analysis, Archive of Applied Mechanics. (2011) 81, no. 10, 1427–1437, https://doi.org/10.1007/s00419-010-0492-x, 2-s2.0-80053568741.
10.1007/s00419-010-0492-x
Web of Science® Google Scholar
14 Hu Y. and Chen M. Z. Q., Performance Evaluation for Inerter-Based Dynamic Vibration Absorbers, International Journal of Mechanical Sciences. (2015) 99, 297–307, https://doi.org/10.1016/j.ijmecsci.2015.06.003, 2-s2.0-84934946840.
10.1016/j.ijmecsci.2015.06.003
Web of Science® Google Scholar
15 Li X. P., Li F. J., and Shang D. Y., Dynamic Characteristics Analysis of ISD Suspension System Under Different Working Conditions, Mathematics. (2021) 9, no. 12, https://doi.org/10.3390/math9121345.
10.3390/math9121345
PubMed Web of Science® Google Scholar
16 Li F. J., Li X. P., Shang D. Y., and Wang Z. H., Dynamic Modeling and Damping Performance Improvement of Two Stage ISD Suspension System, Proceedings of the Institution of Mechanical Engineers—Part D: Journal of Automobile Engineering. (2021) 236, no. 10-11, 2259–2271, https://doi.org/10.1177/09544070211059955.
10.1177/09544070211059955
Google Scholar
17 Hu Y. L., Hua T. Y., Chen M. Z. Q., Shi S., and Sun Y. H., Inherent Stability Analysis for Multibody Systems With Semi-Active Inerters, Journal of Sound and Vibration. (2022) 535, https://doi.org/10.1016/j.jsv.2022.117073.
10.1016/j.jsv.2022.117073
Google Scholar
18 Hu Y. L., Hua T. Y., Chen M. Z. Q., Shi S., and Sun Y. H., Application of Semi-Active Inerter in a Two-Body Point Absorber Via Force Tracking, Transactions of the Institute of Measurement and Control. (2021) 43, no. 12, 2809–2817, https://doi.org/10.1177/01423312211009374.
10.1177/01423312211009374
Google Scholar
19 Hu Y. L., Hua T. Y., Chen M. Z. Q., Shi S., and Sun Y. H., Instability Analysis for Semi-Active Control Systems With Semi-Active Inerters, Nonlinear Dynamics. (2021) 105, no. 1, 99–112, https://doi.org/10.1007/s11071-021-06555-4.
10.1007/s11071-021-06555-4
Web of Science® Google Scholar
20 Shi B. Y., Dai W., and Yang J., Performance Enhancement of Vehicle Suspension System With Geometrically Nonlinear Inerters, Archive of Applied Mechanics. (2024) 94, no. 1, 39–55, https://doi.org/10.1007/s00419-023-02502-4.
10.1007/s00419-023-02502-4
Google Scholar
21 Zhang X. L., Zhang T., Nie J. M., and Chen L., A Semiactive Skyhook-Inertance Control Strategy Based on Continuously Adjustable Inerter, Shock and Vibration. (2018) 2018, 1–8, https://doi.org/10.1155/2018/6828621, 2-s2.0-85044073322.
10.1155/2018/6828621
Google Scholar
22 Nie J. M., Zhao Y., Zhang X. L., and Zhang T., Design and Test of Lateral Interconnected Hydro-Pneumatic ISD Suspension, Proceedings of the Institution of Mechanical Engineers—Part D: Journal of Automobile Engineering. (2022) 238, no. 4, 633–645, https://doi.org/10.1177/09544070221140982.
10.1177/09544070221140982
Google Scholar
23 Shen Y. J., Shi D. H., Chen L., Liu Y. L., and Yang X. F., Modeling and Experimental Tests of Hydraulic Electric Inerter, Science China Technological Sciences. (2019) 62, no. 12, 2161–2169, https://doi.org/10.1007/s11431-019-9546-y.
10.1007/s11431-019-9546-y
Google Scholar

All articles

Optimization and Vibration Response Analysis of Vehicle Suspension Structure With Inerter

Abstract

1. Introduction

2. Mathematical Modeling of the Vehicle Suspension System

3. Optimization Design of the Vehicle Suspension System

3.1. Optimization of Suspension Parameters

3.2. Power Flow Analysis of ISD Suspension

4. Results and Discussion

4.1. Dynamic Response of Vehicle Suspension

4.2. The Influence of Bushing Parameters on Power Transmission

4.3. Comparative Analysis of Vehicle Handling Stability

5. Conclusions

Conflicts of Interest

Funding

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Optimization and Vibration Response Analysis of Vehicle Suspension Structure With Inerter

Abstract

1. Introduction

2. Mathematical Modeling of the Vehicle Suspension System

3. Optimization Design of the Vehicle Suspension System

3.1. Optimization of Suspension Parameters

3.2. Power Flow Analysis of ISD Suspension

4. Results and Discussion

4.1. Dynamic Response of Vehicle Suspension

4.2. The Influence of Bushing Parameters on Power Transmission

4.3. Comparative Analysis of Vehicle Handling Stability

5. Conclusions

Conflicts of Interest

Funding

Open Research

Data Availability Statement

References

Figures

References

Related

Information