In recent years, increasing slope instability accidents caused by rainfall occur. In order to quantitatively analyze the influence of rainfall infiltration on slope stability more accurately, based on the traditional Green–Ampt infiltration model, the influence of the slope’s angle and the characteristics of unsaturated loess were considered and the saturated zone and unsaturated zone were calculated separately in this paper. Through the energy conservation equation, this paper transferred the influence of rainfall infiltration into generalized penetration force and changed the penetration force and composite soil nailing wall supporting force into vertical article point method using the Bishop internal force hypothesis. The slope was divided into two parts, which were calculated, respectively, and integrated by the weighted solving method, and the calculation formula of overall stability of composite soil nailing wall retaining structure was deduced under the action of rainfall. For example, the difference of 1.165 obtained in this paper’s formula is 0.122 compared with the traditional Bishop method (1.043), which not only verifies the correctness of the formula in this paper but also reflects the weakening of the stability coefficient caused by rainfall. Since the soil parameters of unsaturated soil are weakened by rainfall, there may be some errors, and the result provides reference for similar support under special natural environment.

1. Introduction

Rainfall infiltration is the most common cause of slope instability. Every year, many geological disasters occur, such as collapse of foundation pit, landslides, and debris flow, and many of them are related to rainfall. In recent years, scholars have done a lot of research on the problem of slope deformation and failure caused by rainfall infiltration from different perspectives [1].

In the early stage, most of the research stayed in saturated seepage; for example, Darcy’s law was usually used as the rainfall infiltration model, which ignored the existence of unsaturated soil. In reality, saturated soil is very rare. For the soft soil area along the southeast coast in China and some places with high groundwater levels, the study of saturated seepage is relatively meaningful. But for the northwest area in China, most of the loess is unsaturated, and forcing the saturated seepage idea to apply to the unsaturated region may produce a large error [2]. Therefore, many scholars began to change their thinking and try to consider the characteristics of unsaturated soil in the permeability model [3, 4].

The instability of unsaturated soil is mainly due to the presence of gas in the soil, and the water in the soil is difficult to saturate. When rainfall infiltration leads to an increase in pore water pressure, the matric suction and shear strength of the soil decrease, which will lead to the instability and failure of the slope.

Nowadays, the commonly used rainfall infiltration models include the Green–Ampt infiltration model, Philip infiltration model [5], Kostiyacov infiltration model, and Horton infiltration model [6]. Both of the Kostiyacov infiltration model and the Horton infiltration model are empirical equations, and the parameters are basically obtained by fitting. The Philip infiltration model needs to solve the vertical infiltration series, which may lead to the inaccuracy of its results. The Green–Ampt infiltration model has been widely recognized for its advantages of simple form, excellent expansibility, and clear concept. It is not only the most widely used model to solve the infiltration problem of the saturated soil but also suitable for the infiltration problem of unsaturated soil [7]. Liu et al. [8] concluded that the unsaturated soil slope would suffer multiple short-term failures when the cohesion reduced through the saturated infiltration principle and the Green–Ampt infiltration model. Lei et al. [9] substituted the inclination angle of the infinite slope into the traditional Green–Ampt infiltration model and found that when other parameters were unchanged, the larger the inclination angle, the smaller the infiltration potential energy of rainwater. Combined with various conditions, Pan et al. [10] proposed an improved infiltration model that could be used under different rainfall conditions. Using this model, they found that the migration velocity of the wetting front was an exponential function. Tsai et al. [11] estimated matric suction at the wet front by calculating the infiltration process of the wet front with different particle sizes, considering the dynamic effect of capillary pressure. Based on the Green–Ampt infiltration model, Yao et al. [12] analyzed the variation process of the wet front in the slope during rainfall, considering the influence of the unsaturated layer above the wet front. By studying the effects of soil shrinkage and expansion on saturated water conductivity, Stewart [13] proposed a dynamic Green–Ampt seepage model. Compared with the traditional Green–Ampt model, the dynamic Green–Ampt seepage model can calculate infiltration and runoff at multiple scales.

In terms of the influence of rainfall on slope stability, scholars have found that the reason for slope instability induced by rainfall infiltration is that rainfall infiltration would increase soil moisture content and pore water pressure and reduce matric suction, which changes the mechanical properties of soil and weakens its shear strength, thus reducing the anti-sliding force [14, 15]. Lu, Wayllace, and Oh [16] found that rainfall infiltration increased the soil weight to a certain extent and then increased the sliding force of landslide, which was more likely to induce landslide. Carey and Petley [17] analyzed the Lowthervill Landslide and found that the increase of pore water pressure on the slope resulted in the decrease of effective stress, which is the main reason for the slope collapse. Tang et al. [18] generated random rainfall events according to average rainfall intensity and duration and calculated landslide failure probability under different rainfall conditions with the Monte Carlo method. Liang et al. [19] found that the influence of rainfall intensity on slope erosion was greater than that of slope angle and vegetation coverage. Based on the theoretical study of unsaturated soil, Herrada, Gutierrez-Martin, and Montanero [20] established a physical model of soil permeability characteristics in the research process and analyzed it with numerical theoretical methods. Tian et al. [21] proposed a new slope stability analysis method considering pore gas pressure and studied the influence of airflow on slope stability through the numerical method. Huang, Loveridge, and Satyanaga [22] established a new model to analyze shallow landslides, which not only retains the simplicity of the traditional infinite slope model but also significantly improves accuracy.

In summary, the quantitative effects of rainfall in unsaturated loess areas have not been considered when analyzing slope stability. To more accurately calculate the stability coefficient of a composite soil-nail wall-supported slope under rainfall, this paper modifies the traditional Green–Ampt rainfall infiltration model, considering the slope angle and the characteristics of unsaturated loess. The most significant novelty lies in the application of the principle of energy conservation to quantify rainfall infiltration as a mechanical concept, and the quantified values are then substituted into the vertical slice method to analyze slope stability. The author hopes that this paper will improve the calculation system for slope stability with soil nails in unsaturated soils. And we represent the results of independent research, and all references to other people’s work are clearly cited.

2. Seepage Force Calculation of Rainfall Infiltration Based on Energy Conservation Equation

2.1. Traditional Green–Ampt Infiltration Model

In 1911, Green and Ampt [23] proposed the traditional Green–Ampt infiltration model based on Darcy’s law through an infiltration test (Figure 1).

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Traditional Green–Ampt infiltration model.

As shown in Figure 1, the traditional infiltration model divides the soil layers into a saturated layer and a dry layer, and the infiltration front is the dividing line between dry and wet layers. The moisture content of saturated layer is θ_s, and the moisture content of dry layer is θ₁, so the infiltration rate is

\begin{matrix} v_{i} = \frac{d I}{d t} = K_{s} \frac{z_{f} + s_{f} + H}{z_{f}}, \end{matrix}

()

where K_s is the saturation permeability coefficient and s_f is matric suction.

At the same time, the cumulative infiltration volume is

\begin{matrix} I = (θ_{s} - θ_{1}) z_{f} . \end{matrix}

()

The relationship between infiltration front depth z_f and infiltration time t can be expressed as follows:

\begin{matrix} t = \frac{(θ_{s} - θ_{1})}{K_{s}} [z_{f} - (s_{f} + H) \ln \frac{z_{f} + s_{f} + H}{s_{f} + H}] . \end{matrix}

()

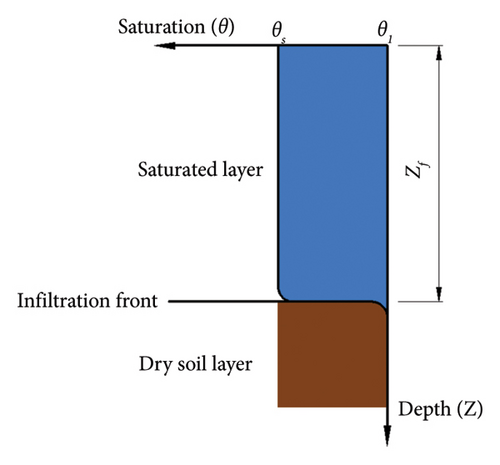
2.2. Modified Green–Ampt Infiltration Model

Generally speaking, Darcy’s law can be used to solve the seepage of saturated soil, without considering the complex matric suction problem. If the seepage problem of unsaturated soil needs to be solved, in most cases, the soil and water characteristic curve (SWCC) needs to be fitted to determine the seepage problem by fitting parameters, which is not suitable for the actual infiltration process [24]. In view of this, the Green–Ampt infiltration model is modified to be suitable for unsaturated soil areas.

As loess in Northwest China is also a kind of unsaturated soil, the gas in the void makes it difficult to completely saturate the water in the void during the infiltration process, and the slope seepage will also change due to slope inclination, so the traditional Green–Ampt model is modified as shown in Figure 2.

The soil is divided into a saturated layer, an infiltration layer, and a dry soil layer. The thickness of the saturated layer and infiltration layer is the same, and both are half of the depth of the infiltration front. According to the research results [25], when continuous rainfall occurs with intensity exceeding the soil infiltration capacity, the moisture content distribution in the loess infiltration layer can be described using an elliptical curve model. Under such conditions, surface runoff is generated immediately, with only partial rainfall infiltrating into the soil. Due to the steep slope gradient, water accumulation during the calculation process can be neglected as rainwater infiltration becomes significantly hindered. Then the cumulative infiltration volume I is modified as follows:

\begin{matrix} I = \int_{0}^{z} θ (z) d z = \frac{4 + π}{8} (θ_{2} - θ_{1}) z . \end{matrix}

()

According to Darcy’s law, the infiltration rates of the slope top and slope surface are, respectively:

\begin{matrix} v_{i 1} = K_{s} \frac{[(z / 2) + S_{f}]}{(z / 2)}, \end{matrix}

()

\begin{matrix} v_{i 2} = K_{s} \frac{[(z^{'} / 2) \cos α + S_{f}]}{(z^{'} / 2)} . \end{matrix}

()

And because of the definition of penetration rate:

\begin{matrix} v_{i} = \frac{d I}{d t} . \end{matrix}

()

If formula (5) is combined with formulas (6) and (7), the following can be obtained, respectively:

\begin{matrix} K_{s} d t = \frac{(z / 2) (θ_{2} - θ_{1})}{(z / 2) + S_{f}} \frac{4 + π}{8} d z, \end{matrix}

()

\begin{matrix} K_{s} d t = \frac{4 + π}{8} \frac{(z^{'} / 2) (θ_{2} - θ_{1})}{(z^{'} / 2) \cos α + S_{f}} d z^{'} . \end{matrix}

()

The implicit expression of the infiltration front z parallel to the slope top and the infiltration front z^′ parallel to the slope and the rainfall duration t can be obtained:

\begin{matrix} t = \frac{(4 + π) (θ_{2} - θ_{1})}{8 K_{s}} [z - 2 s_{f} \ln (\frac{2 s_{f} + z}{2 s_{f}})], \end{matrix}

()

\begin{matrix} t = \frac{(4 + π) (θ_{2} - θ_{1})}{8 K_{s} \cos α} [z^{'} - \frac{2 s_{f}}{\cos α} \ln (\frac{2 s_{f} + z^{'} \cos α}{2 s_{f}})], \end{matrix}

()

where s_f is the matric suction of loess and K_s is the saturation permeability coefficient of loess.

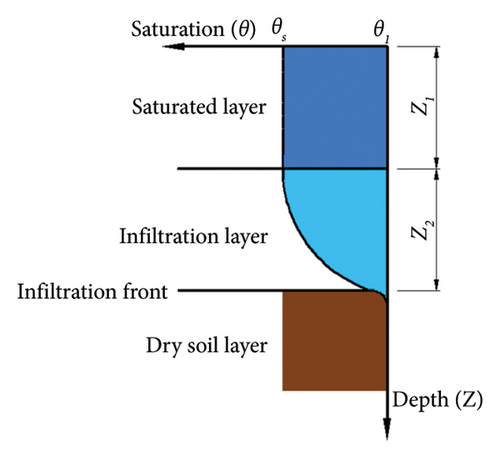
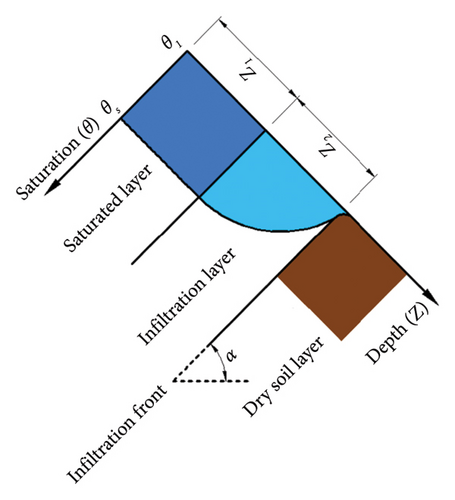
Equations (10) and (11) represent the seepage Green–Ampt infiltration model of unsaturated soil modified for the influence of slope dip on infiltration.

2.3. Generalized Seepage Force

In order to quantify the impact of rainfall infiltration on the unsaturated soil slope, the calculation model as shown in Figure 3 was established. Continuous rainfall was observed on the surface of the model, and the modified Green–Ampt model was used as the infiltration model.

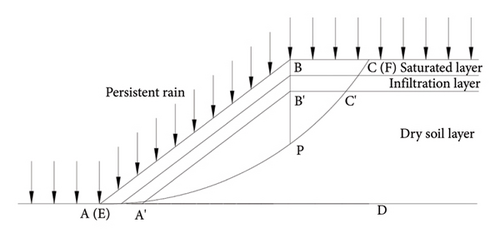
If the rainwater penetrates into the slope soil from the AB and BC surfaces and EF is the sliding crack surface, the deepest infiltration of rainwater will reach the boundary between the wetted layer and the dry soil layer, A^′B^′C^′ surface, which is the wet front. The rainwater flows in the direction parallel to the wet front in the saturated and unsaturated layers and flows out at the foot of the slope only at the same level. The seepage in the model can be divided into two parts, one is perpendicular to the slope, and the other is the general seepage along the wet front. In this model, the general seepage is combined with the vertical seepage as a mixed seepage.

The dead weight of rainwater exerting effective force on soil on the AB plane is the dead weight of total rainfall mg minus the component mgsinθ flowing along the slope. Therefore, the mass of rainwater exerting effective force on soil can be regarded as the ratio of mg(1−sin θ) and gravity acceleration g, divided by the density ρ_w of water, which can be simplified into the following formula:

\begin{matrix} m_{w} = qt l_{2} (1 - \sin θ), \end{matrix}

()

where m_w is effective rainwater mass; q is rainfall intensity; t is the duration of rainfall; l₂ is slope length; and θ is the slope angle.

At this point, we assume that the effect of rainwater infiltration is converted into a force, which is called seepage force for convenience. Then, the work done by the infiltration force generated by rainwater infiltration can be obtained by the law of conservation of energy:

\begin{matrix} Δ E = \frac{1}{2} m v_{1}^{2} - \frac{1}{2} m v_{2}^{2} + m g h \\ = \frac{1}{2} ρ_{w} q t l_{1} v_{1}^{2} + \frac{1}{2} ρ_{w} q t l_{2} (1 - \sin θ) {(v_{1} \cos θ)}^{2} \\ - \frac{1}{2} ρ_{w} q^{'} v_{2}^{2} + ρ_{w} q t g [l_{2} (1 - \sin θ) z^{'} + l_{1} z], \end{matrix}

()

where l₁ is the distance from the top of the slope to the entrance of the potential fracture surface; v₁ is the instantaneous velocity when rain falls on the ground; v₂ is the instantaneous velocity when rain flows out from the foot of the slope; and h is the rainfall infiltration depth, which is equal to z and z^′ calculated in Section 2.2. When the rainfall time is too long and the depth of z or z^′ exceeds the depth of the sliding fracture surface, the depth of the sliding fracture surface is h for calculation.

However, in actual engineering, the possibility of seepage from the slope foot is generally small, so the velocity v₂ at the slope foot can be approximately regarded as 0, and equation (13) can be simplified:

\begin{matrix} Δ E = \frac{1}{2} ρ_{w} q t l_{1} v_{1}^{2} + \frac{1}{2} ρ_{w} q t l_{2} (1 - \sin θ) {(v_{1} \cos θ)}^{2} \\ + ρ_{w} q t g [l_{2} (1 - \sin θ) z^{'} + l_{1} z] . \end{matrix}

()

To analyze the effect of seepage force on the soil at this time, in order to facilitate the analysis, vertical BP is made from the top of the slope to divide the whole soil slope into two parts, so that the water flowing in from the surface AB only acts on arc triangle ABP, while the water flowing in from surface BC acts on the whole slope, namely, arc triangle ABC. Suppose that the average percolation force per unit volume generated by the water flowing in from surface AB in the slope is j₁, and that the average percolation force per unit volume generated by the water flowing in from surface BC in the slope is j₂, and that the percolation forces are all at the centroid of the arc triangle and parallel to the direction of the sliding surface; then:

\begin{matrix} Δ E_{1} = \frac{1}{2} ρ_{w} q t l_{1} v_{1}^{2} + ρ_{w} q t g l_{1} z = j_{1} S_{C B P} \cdot 1, \end{matrix}

()

\begin{matrix} Δ E_{2} = \frac{1}{2} ρ_{w} q t l_{2} (1 - \sin θ) {(v_{1} \cos θ)}^{2} \\ + ρ_{w} q t g l_{2} (1 - \sin θ) z^{'} \\ = j_{2} S_{A C P} \cdot 1 . \end{matrix}

()

According to equations (15) and (16), the effect of rainfall infiltration can be quantified and acted on the slope, and then the seepage force can be substituted into the stability analysis for calculation.

3. Vertical Strip Division Method Considering Seepage Force and Supporting Force

3.1. Fundamental Assumption

1.
It is assumed that the slope soil mass is uniform, the slope top is smooth, the sliding surface is a circular arc, the radius is r, the center of the circle is above the slope, and the sliding surface passes the slope foot and extends to the top of the slope.
2.
It is assumed that the slope soil meets the Mohr–Coulomb yield criterion, and when the soil reaches the ultimate strength, the anchor solid also reaches the ultimate strength.
3.
It is assumed that when the slope soil is destroyed, the forces on both sides of the strip are equal, opposite in direction, and act on the same straight line, which can be ignored.

3.2. Stability Formula

As shown in Figure 4, the overall slope is evenly divided into countless small blocks of width b, among which the arc-shaped triangle CBP has i bars, and the arc-side triangle ABP has i^′ bars.

As shown in Figure 4, for the ith soil strip in the arc triangle CBP, the width is b_i, the length is H_i, and the gravity is w_i. Shear stress is T_i; normal stress is N_i; the supporting force is R_i produced by the composite soil nailing wall support on the strip, and the supporting distance is s. Uniform load qb_i caused by upper rain during rainfall; permeability is j_1i, its direction is basically consistent with tangential antisliding force T_i, and j_1i = j₁b_iH_i, if bar i is in equilibrium, then:

\begin{matrix} T_{i} = \frac{c_{i} b_{i} + N_{i} \tan ϕ_{i}}{F s}, \end{matrix}

()

\begin{matrix} q b_{i} + w_{i} + Δ H_{i} + j_{1 i} \sin θ_{i} + \frac{R_{i} \sin β_{i}}{s} = N_{i} \cos θ_{i} + T_{i} \sin θ_{i} . \end{matrix}

()

Let the stability coefficient of arc-edge triangle CBP be F_s1, and substitute equation (18) into (17), and the following equation can be obtained:

\begin{matrix} N_{i} = \frac{\begin{matrix} q b_{i} + w_{i} + Δ H_{i} + j_{1 i} \sin θ_{i} + \\ (R_{i} \sin β_{i} / s) - (c_{i} b_{i} \sin θ_{i} / F s 1) \end{matrix}}{\cos θ_{i} + (\tan ϕ_{i} \sin θ_{i} / F s 1)} = \frac{1}{m_{θ i}} (\begin{matrix} q b_{i} + w_{i} + Δ H_{i} + j_{1 i} \sin θ_{i} + \\ \frac{R_{i} \sin β_{i}}{s} - \frac{c_{i} b_{i} \sin θ_{i}}{F s 1} \end{matrix}), \end{matrix}

()

where

\begin{matrix} m_{θ i} = \cos θ_{i} + \frac{\tan ϕ_{i} \sin θ_{i}}{F s 1}, \end{matrix}

()

\begin{matrix} \sum R_{i} = m (π d_{1} q {}_{s k 1}L_{1}) + n (R_{s} + π d_{2} q_{s k 2} L_{2}) . \end{matrix}

()

The equilibrium condition of the moment of the strip is analyzed. The sum of the forces on the strip to the moment of the center of the sliding surface is 0. At this time, the forces between the strips cancel each other exactly, so there is no torque to the center of the circle. Meanwhile, when the normal stress N_i passes through the center of the circle, there is no torque. Assuming that the anchorage force through the soil strip passes the center of the strip surface, then:

\begin{matrix} \sum (w_{i} + q b_{i}) r \sin θ_{i} = \sum [T_{i} r + \frac{R_{i} r \cos (β_{i} + θ_{i})}{s} - j_{1 i} (r - \frac{H_{i}}{2} \cos θ_{i})] . \end{matrix}

()

By substituting equation (17) into equation (22), we get:

\begin{matrix} \sum (w_{i} + q b_{i}) \sin θ_{i} = \sum [\frac{c_{i} b_{i} + N_{i} \tan ϕ_{i}}{F s 1} + \frac{R_{i} \cos (β_{i} + θ_{i})}{s} - j_{1 i} (1 - \frac{H_{i}}{2 r} \cos θ_{i})] . \end{matrix}

()

Then substitute equation (19) into (23) to get:

\begin{matrix} F_{s 1} = \frac{\sum (1 / m_{θ i}) [c_{i} b_{i} \cos θ_{i} + (\begin{matrix} q b_{i} + w_{i} + Δ H_{i} + \\ j_{1 i} \sin θ_{i} + (R_{i} \sin β_{i} / s) \end{matrix}) \tan ϕ_{i}]}{\sum (w_{i} + q b_{i}) \sin θ_{i} - (R_{i} \cos (β_{i} + θ_{i}) / s) + j_{1 i} (1 - (H_{i} / 2 r) \cos θ_{i})} . \end{matrix}

()

In the above equation, ΔH_i = H_i+1 − H_i is still unknown. According to Bishop’s hypothesis, ΔH_i = 0, and because H_i ≪ 2r, the term H_i/(2r)cos θ_i in the denominator is omitted, and (24) can be simplified as follows:

\begin{matrix} F_{s 1} = \frac{\sum (1 / m_{θ i}) [c_{i} b_{i} \cos θ_{i} + (q b_{i} + w_{i} + j_{1 i} \sin θ_{i} + (R_{i} \sin β_{i} / s)) \tan ϕ_{i}]}{\sum (w_{i} + q b_{i}) \sin θ_{i} - (R_{i} \cos (β_{i} + θ_{i}) / s) + j_{1 i}} . \end{matrix}

()

Similarly, in an arc-side triangle, ABP, assume that the stability coefficient of arc-side triangle ABP is F_s2; then:

\begin{matrix} F_{s 2} = \frac{(1 / m_{θ i^{'}}) [c_{i^{'}} b_{i^{'}} \cos θ_{i^{'}} + (q b_{i^{'}} + w_{i^{'}} + (j_{1 i^{'}} + j_{2 i^{'}}) \sin θ_{i^{'}} + (R_{i^{'}} \sin β_{i^{'}} / s)) \tan ϕ_{i^{'}}]}{(w_{i^{'}} + q b_{i^{'}}) \sin θ_{i^{'}} - (R_{i^{'}} \cos (β_{i^{'}} + θ_{i^{'}}) / s) + j_{1 i^{'}} + j_{2 i^{'}}} . \end{matrix}

()

Assuming that the overall slope stability coefficient F_s can be obtained by F_s1 and F_s2 weighting, the stability coefficient is weighted according to the proportion of slope top and slope surface, and the overall stability calculation formula of the slope supported by composite soil nailing wall under the action of rainfall is obtained:

\begin{matrix} F_{s} = \frac{l_{1}}{l_{1} + l_{2} \cos θ} F_{s 1} + \frac{l_{2} \cos θ}{l_{1} + l_{2} \cos θ} F_{s 2} . \end{matrix}

()

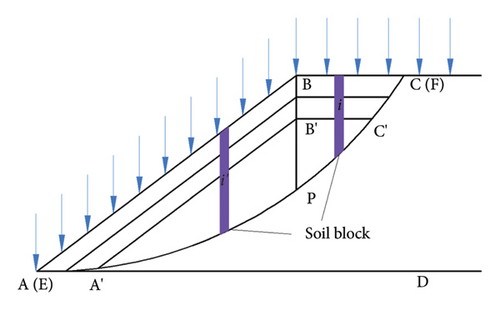
3.3. Solving Method

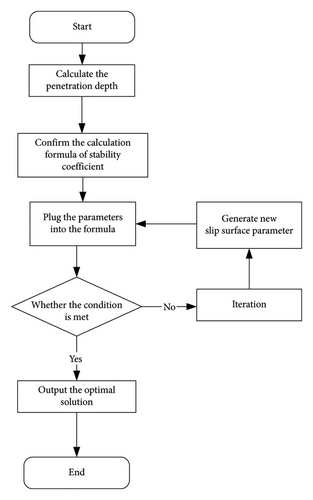
Since the calculation formula is implicit, it is necessary to solve the stability coefficient by iterative calculation, first through the Ferenius method to determine the center of the sliding surface, and then using MATLAB programming, through the substitution of parameters into the program, to solve the stability calculation formula (as shown in Figure 5).

4. Discussion

4.1. Project Case

In order to verify the correctness and accuracy of the formulas in this paper, an engineering example was selected for calculation. A project is a homogeneous loess slope with, slope height of 10 m, slope ratio of 1:1.5, soil cohesion c = 12 kPa, internal friction angle φ = 26°, soil weight γ = 18 kN/m³, initial water content of the soil is 9.55%, saturated water content is 49.8%, and saturation permeability coefficient is 1 × 10 − 6 m/s. The rain intensity was calculated to be 5.75 × 10 − 7 m/s, lasting for 3 days, and the composite soil nail wall was used to support the slope. The calculation diagram is shown in Figure 6.

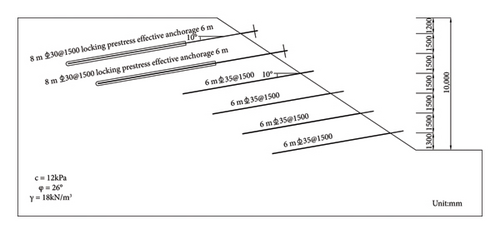
By referring to the data Table 1, the parameters ν₁ and ν₂ required by the Ferenius method are 26° and 35°, respectively, so as to determine the line where the center of the sliding surface is located and create countless centers on the line in order to search the most dangerous sliding surface.

Table 1. Fellenius parameters.

Ratio	Angle	ν₁	ν₂
1:1	45°	28°	37°
1:1.5	33.79°	26°	35°
1:2	26.57°	25°	35°
1:3	18.43°	25°	35°

In order to obtain the instantaneous velocity of raindrops before they fall to the ground, it is necessary to first calculate the total rainfall Q of 24 h and refer to the rainfall grade in Table 2 to confirm that the rainfall in the project is heavy rain. Meanwhile, according to the data, the average diameter of raindrops at this time is 4 mm.

\begin{matrix} Q = 5.7524360049.724 \times 10^{- 7} \times \times = mm / h . \end{matrix}

()

Table 2. Classification of rainfall grades in different periods.

Level	Interval rainfall
Level	12 h rainfall (mm)	24 h rainfall (mm)
Microrainfall	< 0.1	< 0.1
Light rain	0.1∼4.9	0.1∼9.9
Moderate rain	5.0∼14.9	10.0∼24.9
Heavy rain	15.0∼29.9	25.0∼49.9
Intense rain	30.0∼69.9	50.0∼99.9
Rainstorm	70.0∼139.9	100.0∼249.9
Extraordinary rainstorm	≥ 140.0	≥ 250

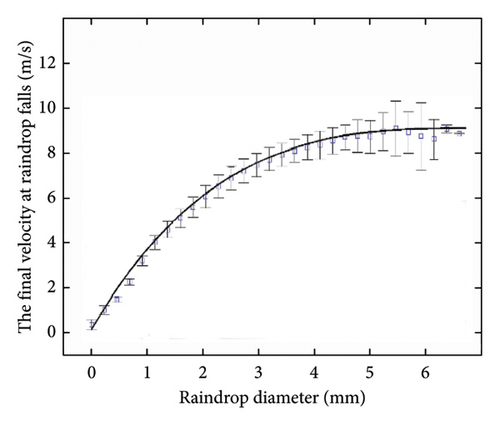
And according to the diameter of raindrops measured by the raindrop spectrometer in Figure 7 and the final velocity of raindrops falling to the ground, it can be seen that the final velocity of raindrops with a diameter of 4 mm is about 8.7 m/s. Thus, all the calculation parameters needed for this project have been obtained.

4.2. Numerical Simulation Analysis

In order to verify the correctness of the formula in this chapter, Seep/W module in GeoStudio series software is selected to simulate rainfall infiltration, then it is replaced by the Slope/W module to solve the overall stability coefficient of composite soil nailing wall support under the action of rainfall.

The seepage field model under rainfall was established according to Figure 6, and the model was divided into quadrilateral grids with a width of 0.5 m. The grid was changed from quadrilateral to triangle at the possible positions of potential fracture surfaces. The model had 1256 nodes and 1181 elements, and the calculation model as shown in Figure 8 was obtained.

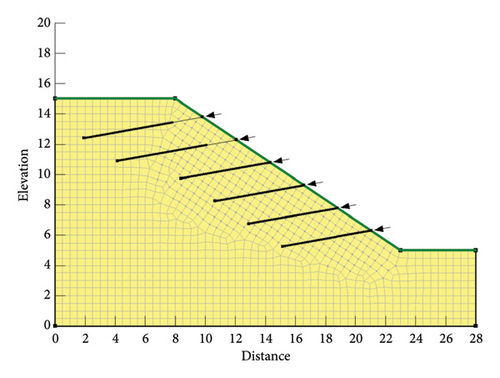
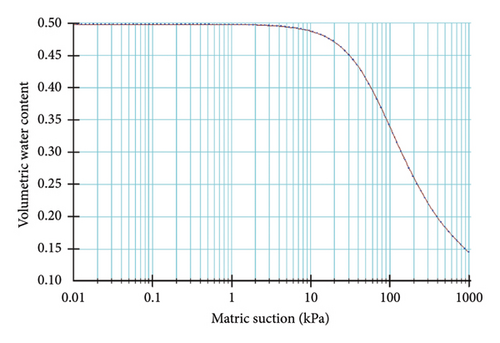
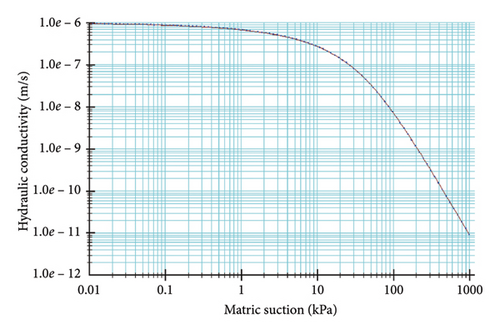
Using the Van Genuchten function, the SWCC and permeability coefficient curve of unsaturated loess in Figure 9 were fitted according to the initial water content, saturated water content, and saturated permeability coefficient of the soil.

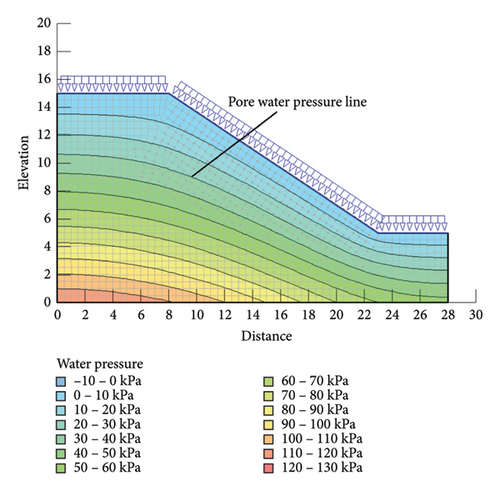
By substituting the water–soil characteristic curve and permeability coefficient curve of unsaturated loess into Seep/W, the slope was rained for 3 days, and the result as shown in Figure 10 was obtained through software iterative calculation. The distribution diagram of the pore water pressure line after 3 days of rainfall can be seen in the figure.

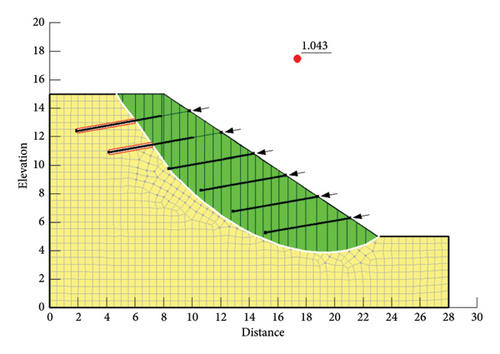
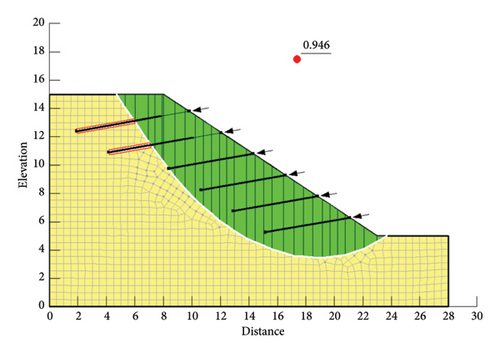
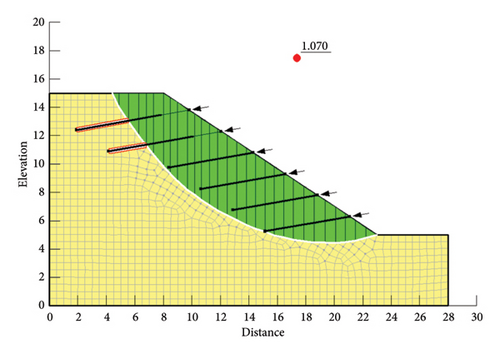
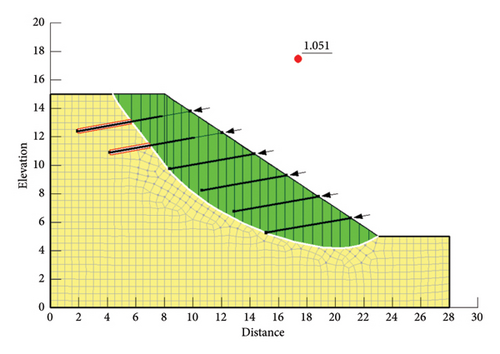
The results of rainfall infiltration were substituted into Slope/W to select the Bishop method, Janbu method, Spencer method, and Morgenstern–Price method, and the stability coefficient was recorded every 12 h, as shown in Figure 11 and Table 3.

Table 3. Calculation results of stability coefficient.

Time (h)	Bishop method	Janbu method	Spencer method	M-P method
0	1.633	1.498	1.635	1.612
12	1.527	1.402	1.515	1.524
24	1.443	1.321	1.441	1.437
36	1.312	1.238	1.354	1.327
48	1.208	1.136	1.260	1.239
60	1.117	1.049	1.165	1.148
72	1.043	0.946	1.070	1.051

It can be seen from Figure 11 that the stability coefficient of slope supported by composite soil nail wall calculated by numerical simulation before rainfall is 1.633 by the Bishop method, 1.498 by the Janbu method, 1.635 by the Spencer method, and 1.612 by the M-P method. After 3 days of rain, the stability coefficients of the composite soil nail wall retaining slope were 1.043 by the Bishop method, 0.946 by the Janbu method, 1.070 by the Spencer method, and 1.051 by the M-P method. The stability coefficient decreases significantly, but only the Janbu method is lower than the safety factor of 1.0, which indicates that the composite soil nail wall has a certain effect on the slope support in the action of rainfall.

4.3. The Formula of This Paper Is Calculated and Analyzed

By using MATLAB to program the calculation formula proposed (see Appendix A) and calculating this example, the final result F_s = 1.165 after 3 days of continuous rainfall is obtained. The variation of stability coefficient during rainfall and the comparison with numerical simulation are shown in Figure 12.

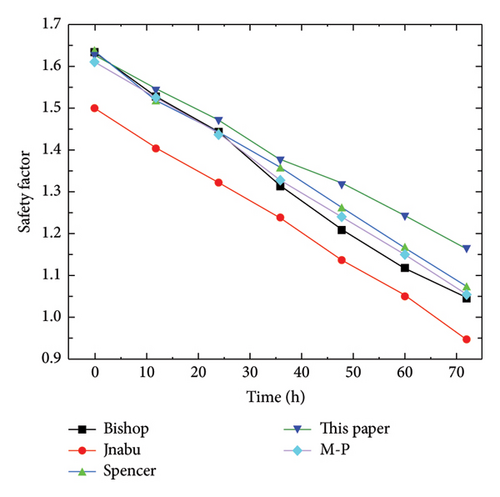
The results obtained by MATLAB when there is no rainfall are basically the same as the numerical simulation results, except for the large difference with the Janbu method because the Janbu method considers more internal forces and is more conservative. Compared with the results after 3 days of rain, the difference between the Spencer method and Janbu method was 0.095 and 0.219, respectively. Because the formula in this chapter is an improvement of Bishop’s method, the difference is 0.122 compared with Bishop’s method. The main reason for the error may be that the cohesion c and internal friction angle φ of unsaturated soil should be reduced under the action of rainfall. However, the formula in this chapter does not consider the weakening of cohesion and internal friction angle when calculating the action of rainfall. No matter how many days of rainfall, the initial value is still used. Although there are some errors, the difference is not large, which can still verify the effectiveness of the formula in this chapter and also provide a basis for slope support under the action of rainfall.

5. Conclusion

To quantitatively analyze the influence of rainfall infiltration on slope stability, based on the traditional Green–Ampt infiltration model, this paper revised this model from the aspects of slope inclination and unsaturated soil seepage. At the same time, the calculation formula of the stability coefficient of the foundation pit supported by composite soil nail wall under the action of rainfall was derived by taking the seepage force and support force into consideration. The following conclusions could be obtained:

1.
The modified model divides the slope into the oblique regions and the vertical regions and considers the permeability characteristics of unsaturated loess and the composite soil nailing wall support well, leading to a more accurate description of the stability calculation method of unsaturated loess slope under the composite soil nailing wall support during rainfall.
2.
For the engineering example, the stability coefficient calculated by the method introduced is 1.165, while the safety factor obtained by the traditional Bishop method is 1.043, with a difference of 0.122. The results can not only verify the correctness of the calculation method in this paper but also reflect the weakening of the stability coefficient caused by rainfall, which makes the calculation more accurate under special conditions. The difference between the method in this paper and the numerical simulation results may be because the formula was derived without considering the weakening effect of rainfall on the soil parameters of unsaturated soil.

Conflicts of Interest

The author declares no conflicts of interest.

Funding

This study was supported by the Technology Project of Gansu Provincial Department of Housing and Urban-Rural Development Construction (Grant no. JK2022-03).

Appendix A: MATLAB Program

function[Fs, x3, y3, R1] = Fmin(b, h, gamma, pi0, c, J1, J2, T)
pi = 3.1415926;
Fs = 100.0;
bet = bet1∗pi/180.0;
F1 = 0; F2 = 0;
pi0 = pi0∗pi/180.0;
a = atan(b);
L = h/sin(a);
m = L∗cos(a);
x0 = m/2;
y0 = h/2;
for theta = 0:a/10:a
for L1=(0.25∗L):(L/10.0):(1.25∗L)
F1 = 0; F2 = 0;
x = x0-cos(pi/2-a + theta)∗L1;
y = y0+sin(pi/2-a+theta)∗L1;
R = sqrt(x^2 + y^2);
x1 = sqrt(R^2-(h-y)^2) + x;
L11 = x1/1000;
for x2 = 0:L11:x1
y2 = y-sqrt(R^2-(x2-x)^2);
be = atan((x2-x)/(y-y2));
n = L11/cos(be);
if x2 ≤ m
y3 = tan(a)∗x2;
h1 = abs(y3-y2);
W1 = gamma∗h1∗L11 + q∗L11+(J1+J2)∗sin(be) + T∗sin(bet);
F1=F1+(m/(m + x2))∗(W1∗tan(pi0)∗cos(be) + c∗n∗cos(be));
F2=F2+(m/(m + x2))∗(W1∗sin(be) + T∗cos(bet+be) + J1+J2);
else
h1 = abs(h-y2);
W1 = gamma∗h1∗L11 + q∗L11 + J1∗sin(be) + T∗sin(bet);
F1=F1+(x2/(m + x2))∗(W1∗tan(pi0)∗cos(be) + c∗n∗cos(be));
F2=F2+(x2/(m + x2))∗(W1∗sin(be) + T∗cos(bet+be) + J1);
end
Fs1 = F1/F2;
disp(Fs1)
if Fs1 < Fs
Fs = Fs1;
end
end
end
end

Open Research

Data Availability Statement

The data of monitoring in the article are not freely available due to legal concerns and commercial confidentiality. Nevertheless, all the concepts and procedures are explained in the presented research, and parts of the research may be available upon request.

References

1 Rahardjo H., Nistor M. M., Gofar N., Satyanaga A., Xiaosheng Q., and Chui Yee S. I., Spatial Distribution, Variation and Trend of Five-Day Antecedent Rainfall in Singapore, Georisk: Assessment and Management of Risk for Engineered Systems and Geohazards. (2019) 14, no. 3, 177–191, https://doi.org/10.1080/17499518.2019.1639196, 2-s2.0-85068590146.
10.1080/17499518.2019.1639196
Google Scholar
2 Guo L., Chen G., Gong S., Sun H., and Chantat K., Analysis of Rainfall-Induced Landslide Using the Extended DDA by Incorporating Matric Suction, Computers and Geotechnics. (2021) 135, https://doi.org/10.1016/j.compgeo.2021.104145.
10.1016/j.compgeo.2021.104145
Web of Science® Google Scholar
3 Satyanaga A., Rahardjo H., Koh Z. H., and Mohamed H., Measurement of a Soil-Water Characteristic Curve and Unsaturated Permeability Using the Evaporation Method and the Chilled-Mirror Method, Journal of Zhejiang University-Science. (2019) 20, no. 5, 368–374, https://doi.org/10.1631/jzus.A1800593, 2-s2.0-85065465346.
10.1631/jzus.A1800593
Google Scholar
4 Satyanaga A. and Rahardjo H., Role of Unsaturated Soil Properties in the Development of Slope Susceptibility Map, Proceedings of the Institution of Civil Engineers-Geotechnical Engineering. (2022) 175, no. 3, 276–288, https://doi.org/10.1680/jgeen.20.00085.
10.1680/jgeen.20.00085
Web of Science® Google Scholar
5 Song J., Wang J., Wang W. et al., Comparison Between Different Infiltration Models to Describe the Infiltration of Permeable Brick Pavement System via a Laboratory-Scale Experiment, Water Science and Technology. (2021) 84, no. 9, 2214–2227, https://doi.org/10.2166/wst.2021.437.
10.2166/wst.2021.437
PubMed Google Scholar
6 Al Maimuri N. M. L. and Najah M. L., Applicability of Horton Model and Recharge Evaluation in Irrigated Arid Mesopotamian Soils of Hashimiya, Iraq, Arabian Journal of Geosciences. (2018) 11, no. 20, https://doi.org/10.1007/s12517-018-3986-4, 2-s2.0-85055081581.
10.1007/s12517-018-3986-4
Web of Science® Google Scholar
7 Ma S., Study on Infinite Slope Stability Based on Green-Ampt Infiltration Model Under Heavy Rainfall Conditions, 2014, Zhejiang University, Hangzhou.
Google Scholar
8 Liu Z., Yan Z., Qiu Z., Wang X., and Li J., Stability Analysis of an Unsaturated Soil Slope Considering Rainfall Infiltration Based on the Green-Ampt Model, Journal of Mountain Science. (2020) 17, no. 10, 2577–2590, https://doi.org/10.1007/s11629-019-5744-9.
10.1007/s11629-019-5744-9
Web of Science® Google Scholar
9 Lei W., Dong H., Chen P., Lv H., and Mei G., Green-Ampt Improved Infiltration Model of Soil Slope Considering Inclination Angle, Journal of Water Conservancy and Transportation Engineering. (2020) no. 6, 101–107, https://doi.org/10.12170/20191027002.
10.12170/20191027002
Google Scholar
10 Pan Y., Jian W., Li L., Lin Y., and Tian P., Study on Rainfall Infiltration Law of Granite Residual Soil Slope Based on Improved Green-Ampt Model, Rock and Soil Mechanics. (2020) 41, no. 8, 2685–2692, https://doi.org/10.16285/j.rsm.2019.1734.
10.16285/j.rsm.2019.1734
Web of Science® Google Scholar
11 Tsai Yi-Z., Wang Y.-Li, Chang L.-C., and Hsu S.-Y., Effects of the Grain Size on Dynamic Capillary Pressure and the Modified Green-Ampt Model for Infiltration, Geofluids. (2018) https://doi.org/10.1155/2018/8946948.
10.1155/2018/8946948
Web of Science® Google Scholar
12 Yao W., Li C., Zhan H., and Zeng J., Time-Dependent Slope Stability During Intense Rainfall With Stratified Soil Water Content, Bulletin of Engineering Geology and the Environment. (2019) 78, no. 7, 4805–4819, https://doi.org/10.1007/s10064-018-01437-3, 2-s2.0-85059639363.
10.1007/s10064-018-01437-3
Web of Science® Google Scholar
13 Stewart R. D., A Dynamic Multidomain GreenAmpt Infiltration Model, Water Resources Research. (2018) 54, no. 9, 6844–6859, https://doi.org/10.1029/2018WR023297, 2-s2.0-85053722521.
10.1029/2018WR023297
Web of Science® Google Scholar
14 Springman S. M., Thielen A., Kienzler P., and Friedel S., A Long-Term Field Study for the Investigation of Rainfall-Induced Landslides, Géotechnique. (2013) 63, no. 14, 1177–1193, https://doi.org/10.1680/geot.11.P.142, 2-s2.0-84892964491.
10.1680/geot.11.P.142
Web of Science® Google Scholar
15 Hou T., Wang X., and Pamukcu S., Geological Characteristics and Stability Evaluation of Wanjia Middle School Slope in Wenchuan Earthquake Area, Geotechnical and Geological Engineering. (2016) 34, no. 1, 237–249, https://doi.org/10.1007/s10706-015-9941-1, 2-s2.0-84957436154.
10.1007/s10706-015-9941-1
CAS Google Scholar
16 Lu N., Wayllace A., and Oh S., Infiltration-Induced Seasonally Reactivated Instability of a Highway Embankment Near the Eisenhower Tunnel, Colorado, USA, Engineering Geology. (2013) 162, 22–32, https://doi.org/10.1016/j.enggeo.2013.05.002, 2-s2.0-84879467838.
10.1016/j.enggeo.2013.05.002
Web of Science® Google Scholar
17 Carey J. M. and Petley D. N., Progressive Shear-Surface Development in Cohesive Materials; Implications for Landslide Behaviour, Engineering Geology. (2014) 177, 54–65, https://doi.org/10.1016/j.enggeo.2014.05.009, 2-s2.0-84902333587.
10.1016/j.enggeo.2014.05.009
Web of Science® Google Scholar
18 Tang G., Huang J., Sheng D., and Sloan S. W., Stability Analysis of Unsaturated Soil Slopes Under Random Rainfall Patterns, Engineering Geology. (2018) 245, 322–332, https://doi.org/10.1016/j.enggeo.2018.09.013, 2-s2.0-85053794759.
10.1016/j.enggeo.2018.09.013
Web of Science® Google Scholar
19 Liang Z., Liu H., Zhao Y. et al., Effects of Rainfall Intensity, Slope Angle, and Vegetation Coverage on the Erosion Characteristics of Pisha Sandstone Slopes Under Simulated Rainfall Conditions, Environmental Science and Pollution Research. (2020) 27, no. 15, 17458–17467, https://doi.org/10.1007/s11356-019-05348-y, 2-s2.0-85066332137.
10.1007/s11356-019-05348-y
PubMed Web of Science® Google Scholar
20 Herrada M. A., Gutierrez-Martin A., and Montanero J. M., Modeling Infiltration Rates in a Saturated/Unsaturated Soil Under the Free Draining Condition, Journal of Hydrology. (2014) 515, 10–15, https://doi.org/10.1016/j.jhydrol.2014.04.026, 2-s2.0-84899949158.
10.1016/j.jhydrol.2014.04.026
Web of Science® Google Scholar
21 Tian W., Peiffer H., Malengier B., Xue S., and Chen Z., Slope Stability Analysis Method of Unsaturated Soil Slopes Considering Pore Gas Pressure Caused by Rainfall Infiltration, Applied Sciences. (2022) 12, no. 21, https://doi.org/10.3390/app122111060.
10.3390/app122111060
Google Scholar
22 Huang W., Loveridge F., and Satyanaga A., Translational Upper Bound Limit Analysis of Shallow Landslides Accounting for Pore Pressure Effects, Computers and Geotechnics. (2022) 148, https://doi.org/10.1016/j.compgeo.2022.104841.
10.1016/j.compgeo.2022.104841
Web of Science® Google Scholar
23 Green W. H. and Ampt G., Studiese on Soil Physics-Part 1, the Flow of Air and Water Through Soils, Journal of Agricultural Science. (1911) 4, 1–24, https://doi.org/10.1017/S0021859600001441, 2-s2.0-84958427998.
10.1017/S0021859600001441
Web of Science® Google Scholar
24 Satyanaga A., Rahardjo H., Zhai Q., Moon S.-W., and Kim J., Modelling Particle-Size Distribution and Estimation of Soil–Water Characteristic Curve Utilizing Modified Lognormal Distribution Function, Geotechnical and Geological Engineering. (2024) 42, no. 3, 1639–1657, https://doi.org/10.1007/s10706-023-02638-8.
10.1007/s10706-023-02638-8
Web of Science® Google Scholar
25 Wen X., Hu Z., Zhang X., Chai S., and Lu X., Study on Improved Infiltration Model and Parameters of Saturated and Unsaturated Loess Based on Green-Ampt Model, Rock and Soil Mechanics. (2020) 41, no. 6, 1991–2000, https://doi.org/10.16285/j.rsm.2019.0821.
10.16285/j.rsm.2019.0821
Web of Science® Google Scholar

All articles

Slope Stability Analysis Considering Rainfall Infiltration Based on Energy Conservation

Abstract

1. Introduction

2. Seepage Force Calculation of Rainfall Infiltration Based on Energy Conservation Equation

2.1. Traditional Green–Ampt Infiltration Model