Structural Control and Health Monitoring

Volume 2025, Issue 1 8868516

Research Article

Open Access

Damage Localization at Steel–Concrete Interface Using Nonlinear Ultrasonic Time Reversal Method

Yi Wen

State Key Laboratory of Coastal and Offshore Engineering , Dalian University of Technology , Dalian , 116024 , China , dlut.edu.cn

Search for more papers by this author

Linsheng Huo,

Corresponding Author

Linsheng Huo

[email protected]

orcid.org/0000-0002-3044-2630

State Key Laboratory of Coastal and Offshore Engineering , Dalian University of Technology , Dalian , 116024 , China , dlut.edu.cn

Search for more papers by this author

Nan Zhao,

Nan Zhao

State Key Laboratory of Coastal and Offshore Engineering , Dalian University of Technology , Dalian , 116024 , China , dlut.edu.cn

Search for more papers by this author

Hongnan Li,

Hongnan Li

State Key Laboratory of Coastal and Offshore Engineering , Dalian University of Technology , Dalian , 116024 , China , dlut.edu.cn

Search for more papers by this author

Yi Wen,

Yi Wen

State Key Laboratory of Coastal and Offshore Engineering , Dalian University of Technology , Dalian , 116024 , China , dlut.edu.cn

Search for more papers by this author

Linsheng Huo,

Corresponding Author

Linsheng Huo

[email protected]

orcid.org/0000-0002-3044-2630

State Key Laboratory of Coastal and Offshore Engineering , Dalian University of Technology , Dalian , 116024 , China , dlut.edu.cn

Search for more papers by this author

Nan Zhao,

Nan Zhao

State Key Laboratory of Coastal and Offshore Engineering , Dalian University of Technology , Dalian , 116024 , China , dlut.edu.cn

Search for more papers by this author

Hongnan Li,

Hongnan Li

State Key Laboratory of Coastal and Offshore Engineering , Dalian University of Technology , Dalian , 116024 , China , dlut.edu.cn

Search for more papers by this author

First published: 23 February 2025

https://doi.org/10.1155/stc/8868516

Academic Editor: Wenai Shen

Share a link

Email
Wechat
Bluesky

Abstract

Steel–concrete composite structures are prevalent in civil engineering, however, due to the temperature variation and fatigue loading, the interface between the steel tube and the core concrete is susceptible to various types of damage, including cracking, delamination, and debonding. Accurate localization of interface damage is crucial to ensure the safety of steel–concrete composite structures. The time-reversal (TR) method is commonly used in nondestructive testing for localizing structural linear damage due to its temporal and spatial focusing characteristics. However, the damage in the steel-concrete interface exhibits complex mechanical behavior and results in localization errors with the traditional TR method. To address this challenge, combined with the advantages of the VAM method, this paper proposes a nonlinear ultrasonic TR method to improve the accuracy of the TR method. This novel approach involves simultaneously exciting low-frequency (LF) and high-frequency (HF) signals using only one lead zirconate titanate (PZT) transducer, extracting the first-order modulation sideband signal, reversing and reemitting this signal, and utilizing the focused signal image to determine the location of damage at the interface. To validate the effectiveness of the proposed method, experiments were conducted on a concrete-filled steel tube with prefabricated interface damage to check its localization accuracy. The results clearly demonstrate an improvement in localization accuracy when using the proposed method compared to the conventional TR method. Specifically, the relative error in the coordinates for damage determined by the conventional TR method was significantly reduced from (25.89%, 18.82%) to (3.53%, 7.06%) with the proposed method. These findings underscore the superior performance of the proposed nonlinear ultrasonic TR method in localizing damage at the steel-concrete interface.

1. Introduction

Steel–concrete composite structures leverage the unique advantages of both steel and concrete, effectively enhancing the load-bearing capacity of the components. These structures are widely used in engineering, such as long-span bridges and high-rise buildings. However, the interface bonding between the steel tube and the core concrete is susceptible to damage, including debonding and delamination, due to construction quality issues, inherent material flaws, and the changes of external loading and environment [1–3]. These damages weaken the confinement of the steel tube against the concrete core, which leads to durability issues and significantly reduce the rigidity of components and pose a threat to the safety of structures. Therefore, precise localization and reinforcement of damage at the steel–concrete interface are essential to prevent potential accidents.

Ultrasonic inspection methods are commonly employed in structural nondestructive testing. These methods include computerized tomography [4, 5], synthetic aperture focusing technique [6], delay-and-sum method [7, 8], and time reversal (TR) method [9, 10]. Among these, the imaging results obtained by the computerized tomography and delay-and-sum method have a low resolution [11]; the synthetic aperture focusing technique has a large amount of data processing and is computationally inefficient. However, the TR method has been widely studied in acoustics and electromagnetics, as well as applications in modern biomedical engineering, underwater communications, and ultrasonic imaging due to its unique ability to focus waves adaptively across a wide detection range without requiring prior knowledge of the transducer properties, which can improve the resolution of damage imaging, and it is not easily disturbed by changes in the detection environment [12–14]. The TR process can be succinctly described as self-adapting and focusing of the probing signals at the excitation location. This involves emitting, receiving, reversing, and reemitting the signals using an array of transducers [9, 15]. Fink [9, 10] proposed a TR mirror and demonstrated its ability to focus an ultrasonic field through inhomogeneous media. Jeong [16] constructed the modular Gaussian beam model, demonstrating that the TR method can be used to generate the spatial and temporal focusing effects in anisotropic solids. The TR theory is well-developed and widely used in monitoring, detecting, and localizing damages in structures. Du et al. [17] proposed a virtual TR method for monitoring bolt preload and demonstrated its effectiveness in both single and multiple bolts. Agrahari and Kapuria [18] proposed a refined TR Lamb wave method for baseline-free damage detection and successfully identified the notch-type damage in an aluminum plate. Wang et al. [19] presented a digital imaging method based on the concept of TR to locate and estimate the size of structural damage. Kannusamy et al. [20] proposed a refined TR method based on Lamb waves to image and localize individual damage in thin isotropic plates. Liu et al. [21] proposed a baseline-free detection method using Lamb waves and the TR method to identify and locate delamination in composite plates. Ciampa and Meo [22] proposed a TR field imaging method for real-time detection of impact damage in anisotropic materials. Mu et al. [23] employed the particle swarm optimization algorithm to address the time-consuming issue of traditional TR localization methods.

However, spurious images can arise with the TR method due to various experimental factors [15], potentially leading to erroneous damage localization. Zhang et al. [24] proposed an approach for compensating signal dispersion in plate structures to improve imaging resolution in regions with multiple target damages. In addition, Zhang et al. [25] integrated the elliptical trajectory algorithm with the probability reconstruction algorithm for TR imaging, with the goal of improving imaging resolution and reducing spurious images. Previous studies have showed that the TR method can effectively localize strong scatterers concealed within a region, mainly due to the alterations in wave propagation caused by linear scattering at material inhomogeneities, such as reflections, refractions, and mode conversions. Unlike the “linear” scattering effect, in which the signal changes only in amplitude without the emergence of new frequency components; however, the damage at the steel–concrete interface exhibits complex nonlinear behavior, and the nonlinear scattering process produces high harmonics and modulated signals, which belong to a nonlinear signal component. These changes in frequency components can be called “nonlinear” scattering effects. Reversing all response signals may lead to the signals to converge on the source of excitation and damage location owing to the temporal and spatial focusing characteristics of the TR method, potentially resulting in erroneous damage localization. Hence, signal processing in TR for the steel–concrete interface should prioritize nonlinear components [26].

Nonlinear ultrasonic inspection methods are widely used in damage detection and localization. Ultrasonic waves interacting with damaged structures, can exhibit nonlinear features in response signals, including subharmonics, frequency mixing, slow dynamics, and modulated vibrations, can be observed. The damage can be detected and evaluated by identifying these distinct nonlinear features [27]. High harmonic wave [28], resonance frequency drift [29], and vibroacoustic modulation (VAM) [30] are commonly used techniques in detecting damages. In particular, VAM is renowned for its robustness against interference and sensitivity to minor damages, rendering it highly effective in detecting fatigue, cracking, and corrosion at the early stage. The VAM involves simultaneously exciting two different signals to the structure: a low frequency (LF) pumping vibration and a high frequency (HF) probing wave. The LF pumping vibration cyclically stretches and compresses the “imperfect” contact interface, causing it to open and close periodically, akin to a “breathing” motion. This introduces perturbation to the HF probing wave. As a result, nonlinear features such as modulation sidebands and high harmonics appear in the spectrum of the received signal. The magnitudes of sidebands and high harmonics indicate the extent of damage [31]. Klepka et al. [32] experimentally studied the fatigue crack identification of aluminum plates using VAM and revealed that energy dissipation is the primary mechanism behind nonlinear modulation. Donskoy et al. [30] revealed the quantitative characterization of modulated damage indicators and interface damages through experiments. Kim et al. [33] successfully identified cracks in wind turbines under operational loads using VAM. Yoder and Adams [34] introduced a scanning detection signal-based VAM and experimentally validated its efficacy on a steel beam in complex environments.

VAM has also been extensively studied for structural damage localization. Pieczonka [35] developed an imaging technique for nonlinear VAM sidebands and tested it on laminated thin composite plates for impact damage localization. Karve and Mahadevan [36] utilized a numerical model to investigate the performance of VAM in localizing hidden, breathing cracks in thick elastic slabs and proved that the method is robust in the presence of measurement noise. In addition, Karve et al. [37] combined VAM with Bayesian probability to localize the through-hole damage of concrete slabs under the action of alkali–carbon dioxide reaction. However, the interface damage in concrete-filled steel tube is different from through-hole damage in concrete slabs, the interface damage in steel–concrete structures exhibits complex nonlinear behavior. When using the conventional TR method to determine the damage location of steel–concrete structures, there will be a significant error. In addition, the previous studies of damage localization have primarily focused on the damage to the material itself. There is a notable lack of research on damage localization at the interfaces of two different materials, such as the steel–concrete interface.

To address this issue, this paper proposes a nonlinear ultrasonic TR method to enhance the accuracy of the conventional TR method. The proposed method involves the simultaneous excitation of LF and HF signals on the damaged structure. Subsequently, the first-order modulated sideband signals extracted from the response signals are reversed and re-excited. The resulting focused signals’ image is then analyzed to determine the damage location in the interface. By selectively reversing only the nonlinear signal which is generated by damage, the signal is precisely focused at the damage location, leveraging the temporal and spatial focusing characteristics of the TR method. As a result, the damage location can be accurately determined. To validate the effectiveness of the proposed method, experiments were conducted for localizing damage in the steel–concrete interface. A comparative experiment with the conventional TR method for damage localization was also designed. In addition, a relative error index is introduced to illustrate the damage localization accuracy.

2. Operation Procedure and Principles of the Proposed Methods

The proposed nonlinear ultrasonic TR localization method mainly includes three modules: the VAM module, the TR module, and the damage imaging module. The workflow of the nonlinear ultrasonic TR method is shown in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The workflow of the nonlinear ultrasonic TR method.

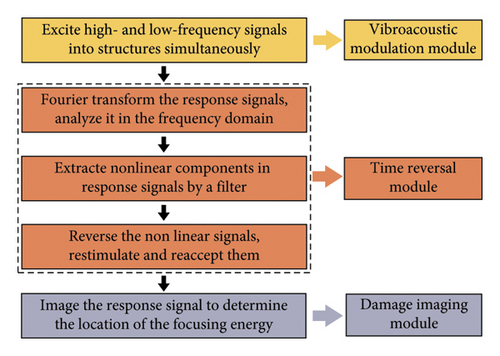
In the VAM module, the structure under investigation is excited with LF and HF signals using optimized parameters to introduce significant nonlinearities in the response signal. In this study, these signals are simultaneously applied to the structure using only one excitation actuator, after which the response signals are captured by a receiving sensor. To facilitate the operation, lead zirconate titanate (PZT) transducers are employed to serve dual roles as both the excitation actuator and the receiving sensor [38–40]. During the experiment, a network with N PZT sensors is used. Each PZT in this network acts as an actuator, with signals being excited sequentially in a numbered order. When one PZT is used as an actuator, the remaining N − 1 PZTs serve as receiving sensors for signal acquisition, resulting in a total of N × (N − 1) groups of data. Since the TR method is independent of the propagation path, that is, half of the data in the sensing path is repeated, so resulting in a total of N × (N − 1)/2 groups of data.

In the TR module, the response signals undergo Fourier transformation and subsequent analysis in the frequency domain. Nonlinear components within these signals are then extracted and utilized for re-exciting the structure. In this study, a filter is designed to extract the first-order modulated sideband signal. This extracted signal exhibits a high signal-to-noise ratio and contains crucial information related to the damage. Subsequently, the extracted nonlinear signal is reversed in the time domain and used to re-excite the structure. During the TR and re-excitation, the excitation process is identical to the signal excitation process in the VAM module.

In the damage imaging module, response signals from all sensing paths are collected, and the damage location is determined by applying the damage imaging algorithm.

The principle of the proposed nonlinear ultrasonic TR method is illustrated in Figure 2. A LF pumping wave and a HF probing wave are simultaneously applied to the steel–concrete composite structures. The frequency of the LF wave is denoted as f_L, and that of the HF wave is denoted as f_H. The resulting response signal contains not only the probing frequency and the pumping frequency but also additional frequency components, including high-order harmonics and sidebands around the probing signal. The amplitudes of these sidebands are directly proportional to the extent of damage, indicating that the more severe the damage corresponds to the stronger nonlinearities, the higher the modulation sidebands. Subsequently, the first-order sideband of the response signal, acting as the TR excitation signal, is extracted, reversed and re-emitted by the original receiving sensor. The response signal is then processed and imaged to identify the location of maximum signal energy, thereby determining the location of damage.

The principle and theoretical background are introduced as follows. For a one-dimensional longitudinal wave propagated in an isotropic solid, its wave equation can be expressed as follows [30, 41]:

(1)

where c denotes the wave velocity, β is the nonlinearity coefficient, u represents the displacement of the particle vibration, x denotes the coordinates of the particle, and t represents time. Assuming that one transducer emits the probe signal, and other transducers receive the response signals in a detection array, the excitation signal composed of the LF pumping vibration and the HF probing signal can be expressed as follows:

(2)

where A₁ and A₂ are the amplitudes of the HF probing wave and the LF pumping vibration, respectively; f_H and f_L are the frequencies of the HF probing wave and the LF pumping vibration, respectively; and τ = t − x/c. The response signal received by a sensor can be expressed as follows [41]:

(3)

where k₁ = f_H/c and k₂ = f_L/c. The third term on the right side of (3) represents the second-order harmonic with the frequencies of 2f_H and 2f_L, and the fourth term of (3) represents the modulated sideband with the frequency of f_H ± f_L.

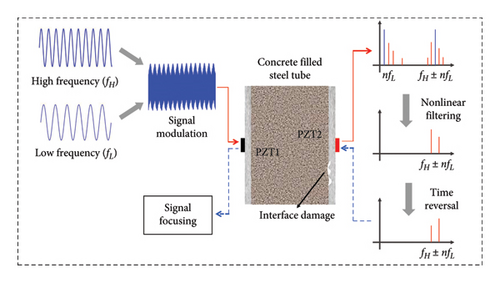
The generation of these nonlinear frequency components is attributed to the microscopically rough contact interface at the steel–concrete interface. Therefore, these contact interfaces can be considered as sources of nonlinear effects, and the energy of nonlinear components will coverage at the damage location after reversing and re-excitation. Prior studies have demonstrated that the amplitude of the first-order sideband signal of nonlinear components can indicate the severity of damage, imaging and localizing damage can be achieved based on the energy distribution of the modulated sideband [26, 42]. Therefore, the first-order sideband signals are extracted through filtering in this study.

The modulated sideband signal, denoted as f_b(t), extracted from the response signal u(x, t), can be expressed as follows:

(4)

Assuming that the number of transducers is L in the detection array, the signal propagated by the nth transducer along the ith propagation path is denoted by f_P and expressed as follows [15]:

(5)

where n denotes the transducers’ number among a total of L, i denotes the initial excitation propagation path number among a total of N, and t_ni is the time delay of the signal propagated by the nth transducer along the ith initial excitation propagation path.

After the TR, the response signal, with the length of the time-window being denoted as T, is denoted by

and expressed as follows [15]:

(6)

The reversed signal is normalized and re-excited at the original receiving sensor and is denoted by f_Q and represented as follows [15]:

(7)

where A^∗ is the maximum amplitude of the response signal.

The total acoustic field generated by the nth sensor at the damage location by the reversed signal is represented as follows:

(8)

where j denotes the reversal excitation propagation path number among a total of N; t_nj is the time delay after the TR of the jth propagation path for the nth sensor.

By exciting all the sensors in the detection array, the total acoustic field generated at the damage location by the reversed signal is represented as follows:

(9)

where u^TR(t) in equation (9) can be separated into individual terms for i = j and i ≠ j, as shown in the following equation:

(10)

where

Substituting equation (4) into equation (10) yields a detailed expression for the u^TR(t):

(11)

where α = βxA₁A₂k₁k₂/4.

The first term on the right side of equation (11) represents the modulated sideband signal f_b(t) that simultaneously arrives at the destination from different actuators and paths, and this term is irrelevant to the value of the i and n. Since the phase differences among these signals are zero, they add up to form a main peak in the frequency domain. The second term on the right side of the equation represents the modulated sideband signals arriving at the different time, indicating that the value of t_ni is not equal to t_nj for i ≠ j. Consequently, they contribute to generate smaller amplitudes and appear on both sides of the main peak in the frequency domain. This equation indicates that by extracting the first-order sideband signal and exciting it after TR, the signals transmitted from different paths can arrive at the damage location simultaneously, thereby achieving the focusing of signal energy and localization of the damage.

The envelope of amplitudes is extracted from all the response signals received by the detection array to establish an image matrix S. Assigning the values of envelope amplitudes using the following formula, an image of the interface damage is constructed [19, 43]:

(12)

where S_{(x, y)} is the pixel value at the location (x, y), N is the number of propagation paths,

is the envelope amplitude of the response signal after reversing and re-excitation; t = (R_i + R_j)/c, c is the propagation velocity of the signal in the structure measured via experiment (c = 5396 m/s in this experiment), R_i and R_j denote the distance from the excitation location and the receiving location to the pixel point (x, y), respectively.

3. Experiments

3.1. Experimental Setup

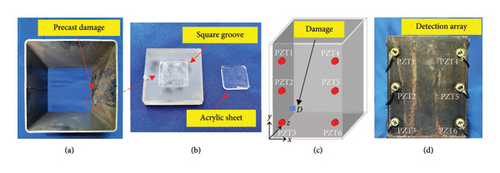
In order to compare the damage localization accuracy of the method proposed in this paper with the conventional TR method, a concrete-filled steel tube specimen with dimensions of 200 × 200 × 250 mm was fabricated. The core concrete had a design strength of C40, and the steel material was Q235. The specimen was created by pouring concrete into a square steel tube with a wall thickness of 3 mm. To simulate the interface damage between the steel tube and the concrete, an acrylic plate with a 10 × 10-mm square groove and a thickness of 1 mm was used. In addition, another acrylic sheet of the same size, thickness, and material as the groove was embedded inside and affixed to the inner wall of the steel tube at the position of (150, 150 mm) in the x and y coordinate system, which is considered as the damage D, as depicted in Figure 3. Six circular PZT transducers, each with a diameter of 15 mm and a thickness of 2 mm are securely attached to the outside surface of the specimen with epoxy to form the detection array. In order to express more clearly the relationship between the position of the PZT and the damage, we established a coordinate system as in Figure 3(c) and use the position of the center of gravity of the PZTs and damage as the value of z in their respective coordinates, respectively, and the x and y coordinates are established at the outside surface of the specimen, the coordinates of the PZT transducers and damage are given in Table 1.

Table 1. Coordinates of transducers.

Transducer no.	Coordinates (x, y, z) (Unit: mm)
PZT 1	(20, 210, −1)
PZT 2	(20, 125, −1)
PZT 3	(20, 40, −1)
PZT 4	(180, 210, −1)
PZT 5	(180, 125, −1)
PZT 6	(180, 40, −1)
D	(150, 150, 0.5)

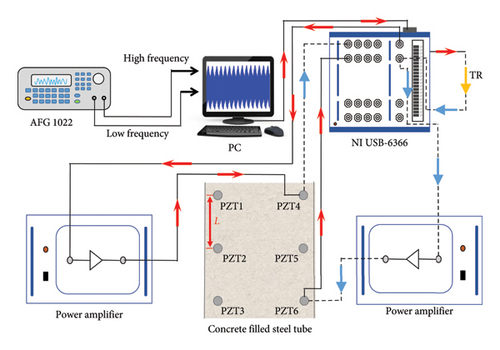
A function generator (Tektronix AFG 1022) was employed to excite the swept sine wave and determine the optimal parameters of frequencies and amplitudes for the excitation signal in each sensing path. Subsequently, the function generator was connected to a power amplifier (Trek 2100 HF-H-CE) to improve the signal strength. A multifunction data acquisition board (NI USB-6366) interfaced with a custom LabVIEW program was used to sample the signals at a frequency of 1 MHz. The experimental instrumentation setup is shown in Figure 4, and the schematic diagram of the experimental process is shown in Figure 5.

3.2. Excitation Technique

The VAM module plays a key role in nonlinear ultrasonic-based damage localization methods. The principle of VAM involves simultaneously exciting two different signals into the damaged structure: a LF pumping vibration and a HF probing wave. Typically, this vibration is provided by an electromagnetic exciter, as depicted in Figure 6(a). However, for damage localization using VAM, a large number of sensors are required to capture the signal of the detection array, which can be inconvenient and uneconomical for experiments. To address this issue, this paper explores a technique that utilizes only one piezoelectric transducer to simultaneously excite LF and HF signals, as illustrated in Figure 6(b).

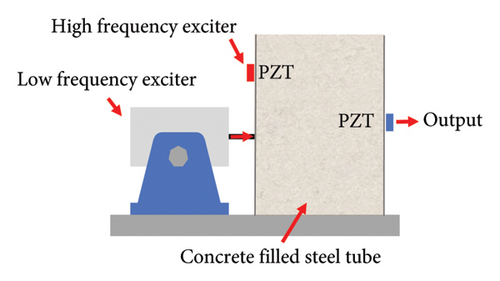
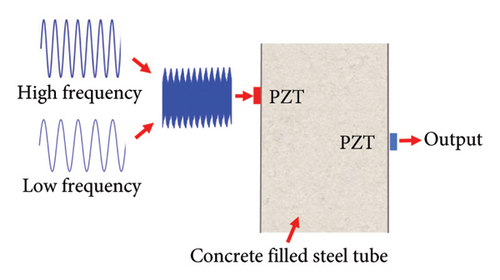
The proposed excitation method operates as follows: initially, the HF and LF signals, each with optimal parameters and the same length are combined. Subsequently, the combined signal is excited by a single transducer and received by other sensors, resulting in the acquisition of the response signal. To illustrate the effect of the proposed excitation method, both the traditional excitation method and the proposed method were respectively utilized to stimulate the HF and LF signals with the same parameters. Taking the PZT 3-PZT 4 sensing path as an example, the response signals in the frequency domain are depicted in Figure 7.

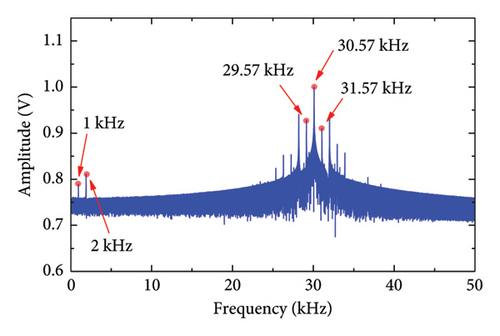
As shown in Figure 7, the spectrum of the response signals obtained using two different excitation methods clearly depicts the LF (1 kHz) and HF (30.57 kHz) components of the excitation signals. The high-order harmonic signal (2 kHz) of the LF can also be observed. In addition, the first-order sideband (29.57 and 31.57 kHz) and other nonlinear components can also be observed on both sides of the HF. These results demonstrate that the proposed excitation method can effectively generate nonlinearity in the ultrasonic response signals. Compared to the traditional excitation method using a shaker, the proposed excitation method is cost-effective and easy to operate, making it an ideal method for excitation.

3.3. Parameters of the Excitation Signal

A continuous sine wave is chosen as the LF excitation signal to ensure the continuous opening and closing of the interface damage. A Hanning window-modulated sine wave with a five-cycle duration and a 0.1-s delay is selected as the HF signal to probe the damage. The expression of the HF excitation signal and LF excitation signal are shown in equations (13) and (14), the synthesized excitation signal with HF and LF is shown in equation (15) [25]:

(13)

(14)

(15)

where A₁₀ is the amplitude of the HF excitation signal, A₂₀ is the amplitude of the LF excitation signal, f_c is the central frequency of the HF signal, φ is the cycle number of sinusoidal signal (φ = 5 in this study), and f₂ is the frequency of the LF signal. The waveform is illustrated in Figure 8.

Previous studies have showed that the choice of the parameters for the excitation signal such as frequency and amplitude greatly impact the cyclic opening and closing of interfaces [44, 45]. Therefore, the parameters of LF and HF signals should be selected carefully to effectively identify the damage. However, the modulation phenomenon is most obvious when the frequency of the excitation signal is the resonant frequency of the structure. Therefore, performing the frequency sweeping test to select the optimal parameters of LF and HF excitation signals. In addition, to quantitatively evaluate the extent of nonlinearity in the response signal under different signals’ parameters, the modulation index MI_D is introduced. Specifically, the larger modulation index corresponds to the stronger nonlinearities. Therefore, the signal parameters corresponding to the maximum MI_D are selected as the optimal signal parameters, the MI_D is expressed as follows [30, 46]:

(16)

where A_m is the amplitude of the HF excitation signal, A_n is the amplitude of the LF excitation signal, and q is the order of modulation sidebands (q = 1 in this study).

The sweeping test was conducted to determine the parameters of excitation signals. Subsequently, the optimal parameters of the excitation signal with maximum MI_D were finally obtained and listed in Table 2.

Table 2. The excitation signal parameters.

HF signal		LF signal
Sampling frequency (MHz)	1	Sampling frequency (MHz)	1
Frequency (kHz)	29.41	Frequency (kHz)	1.05
Amplitude (V)	1	Amplitude (V)	8

4. Experimental Results and Discussion

4.1. Results

After determining all parameters, including frequency and amplitude for LF and HF components, the damage identification experiments were conducted. The frequency spectrum of the response signal is shown in Figure 9(a), illustrating high-order harmonics to the right of the fundamental LF component and first-order modulation sideband around the fundamental HF component. These nonlinear features of the response signal correspond to the interface damage.

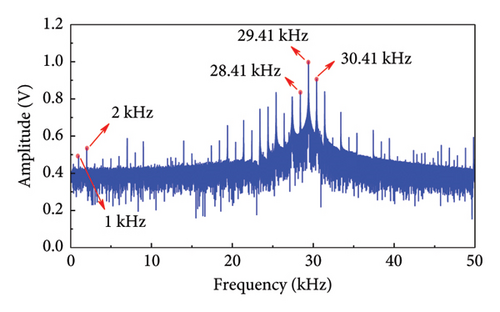
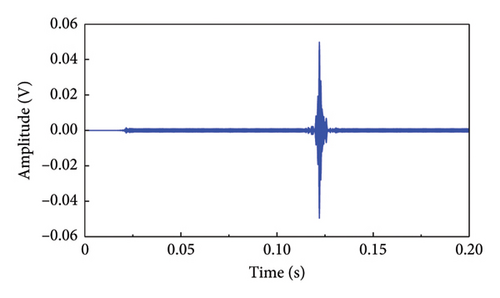
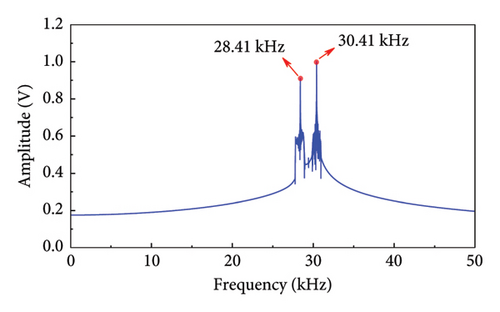
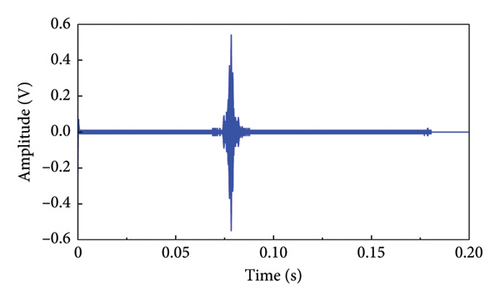
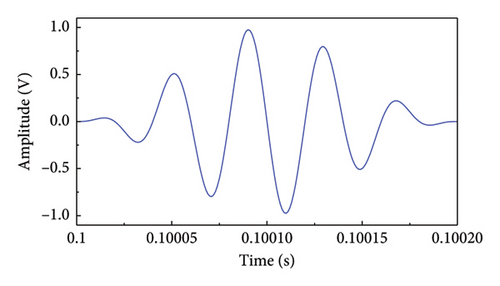
The analysis in this paper focuses on using the first-order modulation sideband around the HF component to identify damage and employing a designed filter for extraction. The key points of the filtering process are as follows: (1) a band-pass filter designed with a Kaiser window was applied to filter the left and right components of the first-order modulation signal, (2) a band-stop filter designed with a Kaiser window was used to remove the frequency components surrounding the fundamental HF component, and (3) the first-order modulation sideband was extracted. The filter parameters are detailed in Table 3. Figures 9(b) and 9(c) illustrate the first-order modulation sideband signal in the time and frequency domains, respectively. Following this, the first-order sideband signal was reversed, propagated back to its original location, and received by the transducer. Finally, the received signal containing damage information is focused, as shown in Figure 9(d), where the amplitude of the focused signal is significantly amplified. The described experimental process was then repeated to acquire the full-path focused signals, which were subsequently imaged according to equation (12).

Table 3. The filter parameters.

Band-pass filter		Band-stop filter
Window function	Kaiser	Window function	Kaiser
Sampling frequency (MHz)	1	Sampling frequency (MHz)	1
Fstop1 (kHz)	28.06	Fpass1 (kHz)	29.11
Fpass1 (kHz)	28.26	Fstop1 (kHz)	29.31
Fpass2 (kHz)	30.56	Fstop2 (kHz)	29.51
Fstop2 (kHz)	30.76	Fpass2 (kHz)	29.71
Order	25,093	Order	18,128
Delay (ms)	12.5	Delay (ms)	9.06

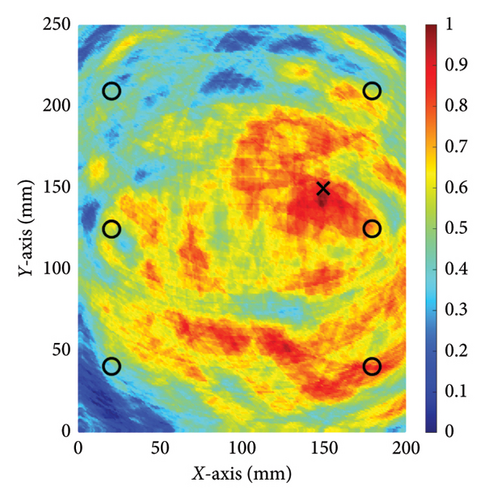
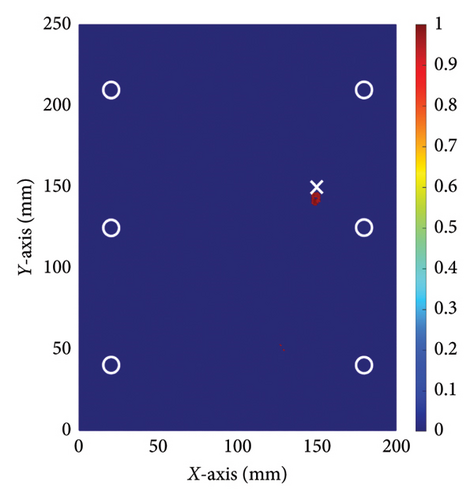
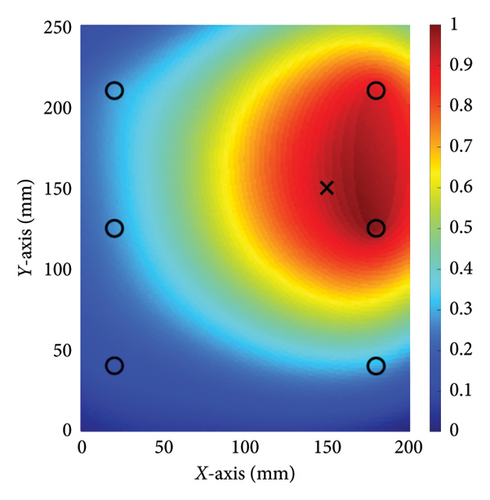
To compare the effectiveness of the damage localization accuracy between the method proposed in this paper and the conventional TR method, experiments were conducted using both methods with the aim of assessing their performance. The identification results were visualized with the normalized pixel values based on equation (12). The Figure 10(b) shows a binary image created from Figure 10(a) by only accounting for image pixels whose intensity is larger than an arbitrary threshold value, which in this study was chosen as 95% of the maximum intensity of the reconstructed damage localization image [8]. In the figure, the symbol ‘○’ denotes the position where piezoelectric transducers were placed, and the symbol ‘×’ indicates the actual location of the damage. In Table 1, we used three-dimensional coordinates to determine the location of the PZT sensors and damage. However, the z coordinates of damage location and PZT location do not belong to the scope of damage localization, so the x and y coordinates are subsequently used to represent the determined damage location and the calculation of positioning errors. It can be observed from Figure 10 that the pixel values around the location (147, 144 mm) display significantly higher values compared to other areas, suggesting that this is the location of the damage. Figure 11 shows the image obtained using the conventional TR method. In this figure, it is evident that the pixel values surrounding the location (172, 134 mm) are significantly larger than those in other areas, indicating that this is the location of the damage.

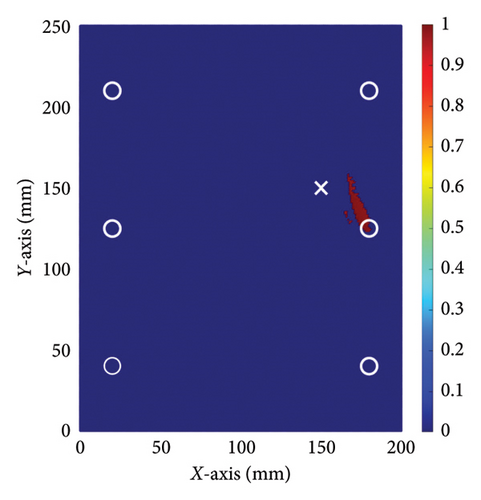
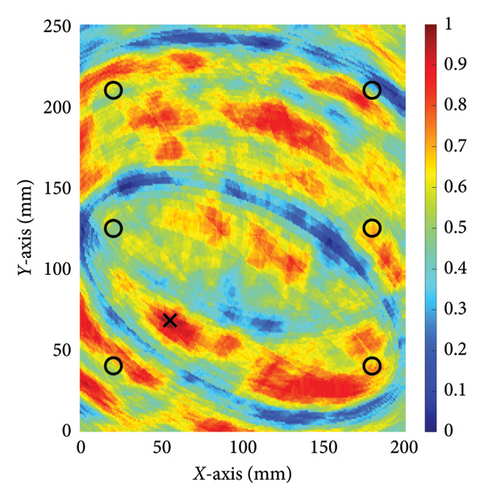
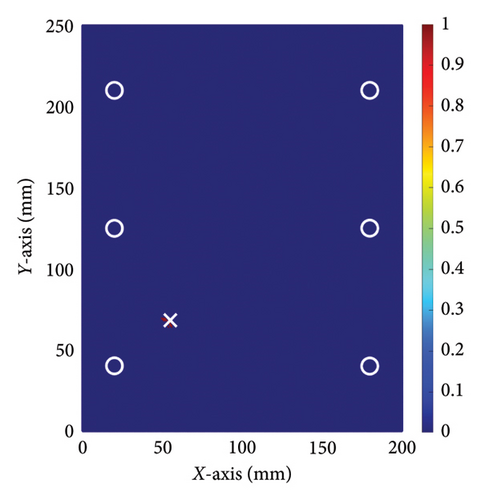
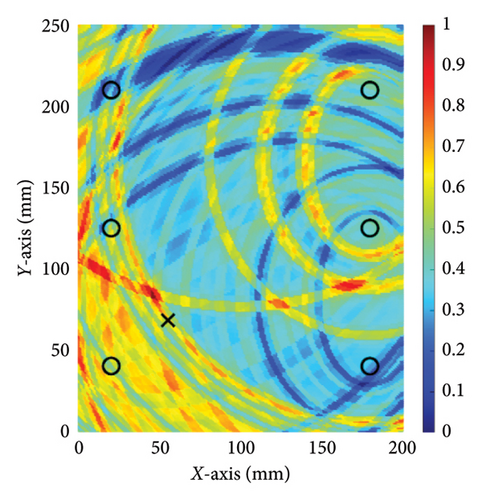
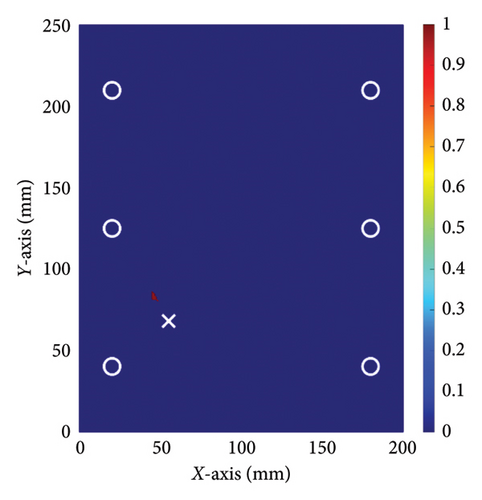
To further validate the effectiveness of the method proposed in this paper, experiments were conducted on another specimen with the same dimension as the previous one, but with the damage located at a different position. In this experiment, the damage was located at coordinates (55, 70 mm), while all other experimental settings remained the same as in the previous one. The experiments followed the same procedure, and a comparative study was also conducted using the conventional TR method. Figures 12 and 13 show the damage imaging for the two methods, respectively. It is evident that the proposed method still performs better than the conventional TR method in locating this damage.

4.2. Discussion

To quantitatively assess the localization performance of the proposed method, the relative error in coordinates is introduced:

(17)

where L represents the minimum distance between sensors, and it is the distance between PZT 1 and PZT 2 in this paper, as shown in Figure 5; x_i and y_i are the coordinates of the damage localized in the ith experiment, and x and y are the coordinates of the actual damage location.

The results of relative errors are listed in Table 4. In the first experiment, the actual location of the interface damage is at (150, 150 mm). The central coordinate of the damage location determined by the conventional TR method is (172, 134 mm), resulting in the relative errors of coordinates of (25.89%, 18.82%). In contrast, the central coordinate of the damage location determined by the proposed method is (147, 144 mm), resulting in relative errors of coordinates of (3.53%, 7.06%). In the second experiment, the relative errors of the damage location determined by the conventional TR method are (11.7%, 15.3%), while the relative errors of the damage location determined by the proposed method are only (2.35%, 4.7%). The results of two experiments show that employing the method proposed in this paper significantly reduces the relative error in damage localization. Compared to the conventional TR method, the proposed approach can more accurately depict the position of damage at the steel-concrete interface. These experimental results suggest that the nonlinear ultrasonic TR method enhances the accuracy of damage localization at the steel–concrete interface and reduces the relative error of damage localization.

Table 4. The results of relative errors.

Experiment no.	Damage location	Coordinates (mm)	Coordinate error d (mm)	Relative error (δ_x, δ_x)
1	Actual (x, y)	(150, 150)	—	—
	Conventional TR (x₁, y₁)	(172, 134)	(22, −16)	(25.89%, 18.82%)
	Proposed method (x₂, y₂)	(147, 144)	(−3, −6)	(3.53%, 7.06%)

2	Actual (x, y)	(55, 70)	—	—
	Conventional TR (x₁, y₁)	(45, 83)	(−10, 13)	(11.7%, 15.3%)
	Proposed method (x₂, y₂)	(57, 66)	(2, −4)	(2.35%, 4.7%)

Note: coordinate error is d = (x₁ − x, y₁ − y).

5. Conclusion and Future Work

In this paper, a damage localization method based on the nonlinear ultrasonic and TR techniques is developed to improve the accuracy of the steel–concrete interface damage localization. To validate the effectiveness of the proposed method, experiments for interface damage localization on concrete-filled steel tubes were conducted using both the proposed method and the conventional TR method. The main contributions of this paper are summarized as follows:

1.
The improved nonlinear ultrasonic TR method differs from the conventional approach by exclusively employing the extracted nonlinear components for damage localization. The temporal and spatial focusing characteristics of this method enhance the concentration of the nonlinear component on the damage area.
2.
The enhanced excitation technique in this study utilizes a single-piezoelectric transducer to simultaneously generate both HF and LF signals, which ensure that the response signal appears significant modulated phenomenon under simple operation, improving the convenience of the VAM method.
3.
Experimental results indicate that the nonlinear ultrasonic TR method exhibits reduced error in damage localization compared to the conventional approach. Specifically, the relative errors in the damage coordinates determined by the conventional method decrease significantly from (25.89%, 18.82%) to (3.53%, 7.06%) with the proposed method.

Currently, the method proposed in this paper is limited to identifying a single damage in the steel–concrete interface. However, considering the diverse-types and severities of interface damages in concrete-filled steel tubes, it is crucial to accurately identify the locations of multiple damage on the steel–concrete interface. Therefore, our future work will focus on applying the proposed method to identify multiple damages on the steel–concrete interface and conducting repeatable experiments to validate its stability. In addition, to guarantee its effectiveness in engineering application, future research will investigate the influence of noise and other variables on experimental results.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This research was supported by the General Project of the Natural Science Foundation of China (Grant No. 52178274).

Open Research

Data Availability Statement

The data used to support the findings of this study are available from the corresponding author upon request.

References

1 Liu H., Liao J. Y., Chen Z. J. et al., Impact Acoustic Inspection of Interfacial Debonding Defects in Concrete-Filled Steel Tubes, Mechanical Systems and Signal Processing. (2023) 200, https://doi.org/10.1016/j.ymssp.2023.110641.
10.1016/j.ymssp.2023.110641
Web of Science® Google Scholar
2 Chen H. B., Zhou M., Gan S. Y., Nie X., Xu B., and Mo Y. L., Review of Wave Method-Based Non-Destructive Testing for Steel-Concrete Composite Structures: Multiscale Simulation and Multi-Physics Coupling Analysis, Construction and Building Materials. (2021) 302, https://doi.org/10.1016/j.conbuildmat.2021.123832.
10.1016/j.conbuildmat.2021.123832
Web of Science® Google Scholar
3 Xue J. Q., Briseghella B., and Chen B. C., Effects of Debonding on Circular CFST Stub Columns, Journal of Constructional Steel Research. (2012) 69, no. 1, 64–76, https://doi.org/10.1016/j.jcsr.2011.08.002, 2-s2.0-80053653786.
10.1016/j.jcsr.2011.08.002
Web of Science® Google Scholar
4 Fröjd P. and Ulriksen P., Continuous Wave Measurements in a Network of Transducers for Structural Health Monitoring of a Large Concrete Floor Slab, Structural Health Monitoring. (2016) 15, no. 4, 403–412, https://doi.org/10.1177/1475921716642139, 2-s2.0-84984801399.
10.1177/1475921716642139
Web of Science® Google Scholar
5 Choi H. and Popovics J. S., NDE Application of Ultrasonic Tomography to a Full-Scale Concrete Structure, IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control. (2015) 62, no. 6, 1076–1085, https://doi.org/10.1109/tuffc.2014.006962, 2-s2.0-84933037306.
10.1109/TUFFC.2014.006962
PubMed Web of Science® Google Scholar
6 Hoegh K. and Khazanovich L., Extended Synthetic Aperture Focusing Technique for Ultrasonic Imaging of Concrete, NDT & E International. (2015) 74, 33–42, https://doi.org/10.1016/j.ndteint.2015.05.001, 2-s2.0-84929629206.
10.1016/j.ndteint.2015.05.001
Web of Science® Google Scholar
7 Michaels J. E., Detection, Localization and Characterization of Damage in Plates With an In Situ Array of Spatially Distributed Ultrasonic Sensors, Smart Materials and Structures. (2008) 17, no. 3, https://doi.org/10.1088/0964-1726/17/3/035035, 2-s2.0-45749126556.
10.1088/0964-1726/17/3/035035
Web of Science® Google Scholar
8 Ng C. T. and Veidt M., A Lamb-Wave-Based Technique for Damage Detection in Composite Laminates, Smart Materials and Structures. (2009) 18, no. 7, https://doi.org/10.1088/0964-1726/18/7/074006, 2-s2.0-68549127121.
10.1088/0964-1726/18/7/074006
Web of Science® Google Scholar
9 Fink M., Time Reversal of Ultrasonic Fields I. Basic Principles, IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control. (1992) 39, no. 5, 555–566, https://doi.org/10.1109/58.156174, 2-s2.0-0026928120.
10.1109/58.156174
CAS PubMed Web of Science® Google Scholar
10 Chakroun N., Fink M. A., and Wu F., Time-Reversal Processing in Ultrasonic Nondestructive Testing, IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control. (1995) 42, no. 6, 1087–1098, https://doi.org/10.1109/58.476552, 2-s2.0-0029410525.
10.1109/58.476552
Web of Science® Google Scholar
11 Martin J., Broughton K. J., Giannopolous A., Hardy M. S. A., and Forde M. C., Ultrasonic Tomography of Grouted Duct Post-Tensioned Reinforced Concrete Bridge Beams, NDT & E International. (2001) 34, no. 2, 107–113, https://doi.org/10.1016/s0963-8695(00)00035-9, 2-s2.0-0035283823.
10.1016/S0963-8695(00)00035-9
Web of Science® Google Scholar
12 Kosmas P. and Rappaport C. M., FDTD-Based Time Reversal for Microwave Breast Cancer Detection-Localization in Three Dimensions, IEEE Transactions on Microwave Theory and Techniques. (2006) 54, no. 4, 1921–1927, https://doi.org/10.1109/tmtt.2006.871994, 2-s2.0-33645952381.
10.1109/TMTT.2006.871994
Web of Science® Google Scholar
13 Yang T. C., Temporal Resolutions of Time-Reversal and Passive-Phase Conjugation for Underwater Acoustic Communications, IEEE Journal of Oceanic Engineering. (2003) 28, no. 2, 229–245, https://doi.org/10.1109/joe.2003.811895, 2-s2.0-0038044856.
10.1109/JOE.2003.811895
Web of Science® Google Scholar
14 Montaldo G., Palacio D., Tanter M., and Fink M., Time Reversal Kaleidoscope: A Smart Transducer for Three-Dimensional Ultrasonic Imaging, Applied Physics Letters. (2004) 84, no. 19, 3879–3881, https://doi.org/10.1063/1.1738186, 2-s2.0-2942574972.
10.1063/1.1738186
CAS Web of Science® Google Scholar
15 Gao W. H., Zhang G. M., Li H. N., Huo L. S., and Song G. B., A Novel Time Reversal Sub-group Imaging Method With Noise Suppression for Damage Detection of Plate-Like Structures, Structural Control and Health Monitoring. (2018) 25, no. 3, https://doi.org/10.1002/stc.2111, 2-s2.0-85041664871.
10.1002/stc.2111
Web of Science® Google Scholar
16 Jeong H., Time Reversal Study of Ultrasonic Waves for Anisotropic Solids Using a Gaussian Beam Model, NDT & E International. (2009) 42, no. 3, 210–214, https://doi.org/10.1016/j.ndteint.2008.09.010, 2-s2.0-61749099098.
10.1016/j.ndteint.2008.09.010
Web of Science® Google Scholar
17 Du F., Xu C., and Zhang J., A Bolt Preload Monitoring Method Based on the Refocusing Capability of Virtual Time Reversal, Structural Control and Health Monitoring. (2019) 26, no. 8, https://doi.org/10.1002/stc.2370, 2-s2.0-85066913910.
10.1002/stc.2370
PubMed Web of Science® Google Scholar
18 Agrahari J. K. and Kapuria S., Active Detection of Block Mass and Notch-Type Damages in Metallic Plates Using a Refined Time-Reversed Lamb Wave Technique, Structural Control and Health Monitoring. (2018) 25, no. 2, https://doi.org/10.1002/stc.2064, 2-s2.0-85026320491.
10.1002/stc.2064
Web of Science® Google Scholar
19 Wang C. H., Rose J. T., and Chang F. K., A Synthetic Time-Reversal Imaging Method for Structural Health Monitoring, Smart Materials and Structures. (2004) 13, no. 2, 415–423, https://doi.org/10.1088/0964-1726/13/2/020, 2-s2.0-2142772678.
10.1088/0964-1726/13/2/020
Web of Science® Google Scholar
20 Kannusamy M., Kapuria S., and Sasmal S., Accurate Baseline-Free Damage Localization in Plates Using Refined Lamb Wave Time-Reversal Method, Smart Materials and Structures. (2020) 29, no. 5, https://doi.org/10.1088/1361-665x/ab8028.
10.1088/1361-665X/ab8028
PubMed Web of Science® Google Scholar
21 Liu Z. H., Zhong X. W., Dong T. C., He C. F., and Wu B., Delamination Detection in Composite Plates by Synthesizing Time-Reversed Lamb Waves and a Modified Damage Imaging Algorithm Based on RAPID, Structural Control and Health Monitoring. (2017) 24, no. 5, https://doi.org/10.1002/stc.1919, 2-s2.0-84979964995.
10.1002/stc.1919
Web of Science® Google Scholar
22 Ciampa F. and Meo M., Impact Detection in Anisotropic Materials Using a Time Reversal Approach, Structural Health Monitoring. (2012) 11, no. 1, 43–49, https://doi.org/10.1177/1475921710395815, 2-s2.0-84855567563.
10.1177/1475921710395815
Web of Science® Google Scholar
23 Mu W. L., Sun J. G., Xin R., Liu G. J., and Wang S. Q., Time Reversal Damage Localization Method of Ocean Platform Based on Particle Swarm Optimization Algorithm, Marine Structures. (2020) 69, https://doi.org/10.1016/j.marstruc.2019.102672.
10.1016/j.marstruc.2019.102672
Web of Science® Google Scholar
24 Zhang M. H., Zhou D. Y., Li X. Q., Yang Z. Q., and Kong Q. Z., A Time-Reversal Assisted Probabilistic Fusion Strategy for Damage Localization in Plate-Like Structures Using Lamb Waves, Structural Health Monitoring. (2023) 22, no. 6, 3579–3603, https://doi.org/10.1177/14759217221151040.
10.1177/14759217221151040
Web of Science® Google Scholar
25 Zhang G. M., Gao W. H., Song G. B., and Song Y., An Imaging Algorithm for Damage Detection With Dispersion Compensation Using Piezoceramic Induced Lamb Waves, Smart Materials and Structures. (2017) 26, no. 2, https://doi.org/10.1088/1361-665x/26/2/025017, 2-s2.0-85011385315.
10.1088/1361-665X/26/2/025017
Web of Science® Google Scholar
26 Bas P. Y. L., Abeele K. V. D., Santos S. D., Goursolle T., and Lille E. C. D., Experimental Analysis for Nonlinear Time Reversal Imaging of Damaged Materials, Applied Physics Letters. (2006) .
Google Scholar
27 Broda D., Staszewski W. J., Martowicz A., Uhl T., and Silberschmidt V. V., Modelling of Nonlinear Crack-Wave Interactions for Damage Detection Based on Ultrasound-A Review, Journal of Sound and Vibration. (2014) 333, no. 4, 1097–1118, https://doi.org/10.1016/j.jsv.2013.09.033, 2-s2.0-84889092832.
10.1016/j.jsv.2013.09.033
Web of Science® Google Scholar
28 Chen J., Xu Z., Yu Y., and Yao Y. P., Experimental Characterization of Granite Damage Using Nonlinear Ultrasonic Techniques, NDT & E International. (2014) 67, 10–16, https://doi.org/10.1016/j.ndteint.2014.06.005, 2-s2.0-84904340638.
10.1016/j.ndteint.2014.06.005
Web of Science® Google Scholar
29 Van Den Abeele K. and De Visscher J., Damage Assessment in Reinforced Concrete Using Spectral and Temporal Nonlinear Vibration Techniques, Cement and Concrete Research. (2000) 30, no. 9, 1453–1464, https://doi.org/10.1016/s0008-8846(00)00329-x, 2-s2.0-0034263067.
10.1016/S0008-8846(00)00329-X
CAS Web of Science® Google Scholar
30 Donskoy D., Sutin A., and Ekimov A., Nonlinear Acoustic Interaction on Contact Interfaces and Its Use for Nondestructive Testing, NDT & E International. (2001) 34, no. 4, 231–238, https://doi.org/10.1016/s0963-8695(00)00063-3, 2-s2.0-0035372331.
10.1016/S0963-8695(00)00063-3
Web of Science® Google Scholar
31 Zhao N., Linsheng H., and Song G. B., Vibration Acoustic Modulation for Bolt Looseness Monitoring Based on Frequency-Swept Excitation and Bispectrum, Smart Materials and Structures. (2023) 32, no. 3, https://doi.org/10.1088/1361-665x/acb579.
10.1088/1361-665X/acb579
Web of Science® Google Scholar
32 Klepka A., Staszewski W. J., Jenal R. B., Szwedo M., Iwaniec J., and Uhl T., Nonlinear Acoustics for Fatigue Crack Detection-Experimental Investigations of Vibro-Acoustic Wave Modulations, Structural Health Monitoring. (2012) 11, no. 2, 197–211, https://doi.org/10.1177/1475921711414236, 2-s2.0-84857669005.
10.1177/1475921711414236
Web of Science® Google Scholar
33 Kim S., Adams D. E., Sohn H. et al., Crack Detection Technique for Operating Wind Turbine Blades Using Vibro-Acoustic Modulation, Structural Health Monitoring. (2014) 13, no. 6, 660–670, https://doi.org/10.1177/1475921714553732, 2-s2.0-84910664992.
10.1177/1475921714553732
Web of Science® Google Scholar
34 Yoder N. C. and Adams D. E., Vibro-Acoustic Modulation Utilizing a Swept Probing Signal for Robust Crack Detection, Structural Health Monitoring. (2010) 9, no. 3, 257–267, https://doi.org/10.1177/1475921710365261, 2-s2.0-77951607895.
10.1177/1475921710365261
Web of Science® Google Scholar
35 Pieczonka L., Zietek L., Klepka A., Staszewski W. J., Aymerich F., and Uhl T., Damage Imaging in Composites Using Nonlinear Vibro-Acoustic Wave Modulations, Structural Control and Health Monitoring. (2018) 25, no. 2, https://doi.org/10.1002/stc.2063, 2-s2.0-85041014400.
10.1002/stc.2063
Web of Science® Google Scholar
36 Karve P. and Mahadevan S., On the Performance of Vibro-Acoustic-Modulation-Based Diagnosis of Breathing Cracks in Thick, Elastic Slabs, Structural Control and Health Monitoring. (2020) 27, no. 3, https://doi.org/10.1002/stc.2470.
10.1002/stc.2470
Web of Science® Google Scholar
37 Karve P., Miele S., Neal K. et al., Vibro-Acoustic Modulation and Data Fusion for Localizing Alkali-Silica Reaction-Induced Damage in Concrete, Structural Health Monitoring. (2020) 19, no. 6, 1905–1923, https://doi.org/10.1177/1475921720905509.
10.1177/1475921720905509
Web of Science® Google Scholar
38 Huo L. S., Chen D. D., Kong Q. Z., Li H. N., and Song G. B., Smart Washer-A Piezoceramic-Based Transducer to Monitor Looseness of Bolted Connection, Smart Materials and Structures. (2017) 26, no. 2, https://doi.org/10.1088/1361-665x/26/2/025033, 2-s2.0-85011361558.
10.1088/1361-665x/26/2/025033
Web of Science® Google Scholar
39 Wang F. R., Chen Z., and Song G. B., Smart Crawfish: A Concept of Underwater Multi-Bolt Looseness Identification Using Entropy-Enhanced Active Sensing and Ensemble Learning, Mechanical Systems and Signal Processing. (2021) 149, https://doi.org/10.1016/j.ymssp.2020.107186.
10.1016/j.ymssp.2020.107186
PubMed Web of Science® Google Scholar
40 Zhang C., Panda G. P., Yan Q. X., Zhang W. L., Vipulanandan C., and Song G. B., Monitoring Early-Age Hydration and Setting of Portland Cement Paste by Piezoelectric Transducers via Electromechanical Impedance Method, Construction and Building Materials. (2020) 258, https://doi.org/10.1016/j.conbuildmat.2020.120348.
10.1016/j.conbuildmat.2020.120348
Web of Science® Google Scholar
41 Zarembo I. K. and Krasil’nikov V. A., Nonlinear Phenomena in the Propagation of Elastic Waves in Solids, Soviet Physics-Uspekhi. (1971) 102, no. 6.
Google Scholar
42 Ulrich T. J., Sutin A. M., Guyer R. A., and Johnson P. A., Time Reversal and Non-Linear Elastic Wave Spectroscopy (TR NEWS) Techniques, International Journal of Non-Linear Mechanics. (2008) 43, no. 3, 209–216, https://doi.org/10.1016/j.ijnonlinmec.2007.12.017, 2-s2.0-39949083754.
10.1016/j.ijnonlinmec.2007.12.017
Web of Science® Google Scholar
43 Croxford A. J., Wilcox P. D., and Drinkwater B. W., Guided Wave SHM with a Distributed Sensor Network, SPIE Proceedings. (2008) 6935, https://doi.org/10.1117/12.776355, 2-s2.0-44349182059.
10.1117/12.776355
Google Scholar
44 He Y., Xiao Y., Su Z. Q., Pan Y. D., and Zhang Z., Contact Acoustic Nonlinearity Effect on the Vibro-Acoustic Modulation of Delaminated Composite Structures, Mechanical Systems and Signal Processing. (2022) 163, https://doi.org/10.1016/j.ymssp.2021.108161.
10.1016/j.ymssp.2021.108161
Web of Science® Google Scholar
45 Houhat N., Tournat V., Ménigot S., Boutkedjirt T., and Girault J. M., Optimal Pump Excitation Frequency for Improvement of Damage Detection by Nonlinear Vibro Acoustic Modulation Method in a Multiple Scattering Sample, Applied Acoustics. (2019) 155, 222–231, https://doi.org/10.1016/j.apacoust.2019.06.010, 2-s2.0-85066981680.
10.1016/j.apacoust.2019.06.010
Web of Science® Google Scholar
46 Dao P. B., Klepka A., Pieczonka L., Aymerich F., and Staszewski W. J., Impact Damage Detection in Smart Composites Using Nonlinear Acoustics-Cointegration Analysis for Removal of Undesired Load Effect, Smart Materials and Structures. (2017) 26, no. 3, https://doi.org/10.1088/1361-665x/aa5744, 2-s2.0-85014606130.
10.1088/1361-665X/aa5744
Web of Science® Google Scholar

All articles

Damage Localization at Steel–Concrete Interface Using Nonlinear Ultrasonic Time Reversal Method

Abstract

1. Introduction

2. Operation Procedure and Principles of the Proposed Methods