Structural Control and Health Monitoring

Volume 2025, Issue 1 1495852

Research Article

Open Access

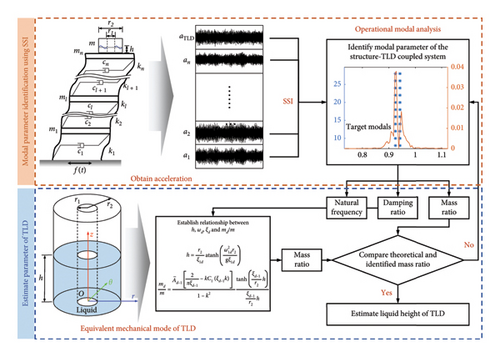
Physics Parameter Identification of Annular Tuned Liquid Damper for the Structure-Damper-Coupled System Using a Mechanics-Enhanced SSI Method

Wenwei Fu

School of Civil Engineering , Suzhou University of Science and Technology , Suzhou , 215009 , China , usts.edu.cn

Future City Laboratory , Innovation Center of Yangtze River Delta , Zhejiang University , Jiaxing , 314100 , China , zju.edu.cn

Search for more papers by this author

Naiwei Kuai,

Naiwei Kuai

School of Civil Engineering , Suzhou University of Science and Technology , Suzhou , 215009 , China , usts.edu.cn

Search for more papers by this author

Xin Chen,

Corresponding Author

Xin Chen

[email protected]

orcid.org/0000-0003-1284-5150

School of Civil Engineering , Suzhou University of Science and Technology , Suzhou , 215009 , China , usts.edu.cn

Search for more papers by this author

Shitang Ke,

Shitang Ke

Department of Civil and Airport Engineering , Nanjing University of Aeronautics and Astronautics , Nanjing , 211106 , China , nuaa.edu.cn

Search for more papers by this author

Tao Liu,

Tao Liu

Jiangsu Provincial Department of Housing and Urban-Rural Development , Nanjing , 210036 , China

Search for more papers by this author

Zhirao Shao,

Zhirao Shao

School of Civil Engineering , Suzhou University of Science and Technology , Suzhou , 215009 , China , usts.edu.cn

Search for more papers by this author

Wenwei Fu,

Wenwei Fu

School of Civil Engineering , Suzhou University of Science and Technology , Suzhou , 215009 , China , usts.edu.cn

Future City Laboratory , Innovation Center of Yangtze River Delta , Zhejiang University , Jiaxing , 314100 , China , zju.edu.cn

Search for more papers by this author

Naiwei Kuai,

Naiwei Kuai

School of Civil Engineering , Suzhou University of Science and Technology , Suzhou , 215009 , China , usts.edu.cn

Search for more papers by this author

Xin Chen,

Corresponding Author

Xin Chen

[email protected]

orcid.org/0000-0003-1284-5150

School of Civil Engineering , Suzhou University of Science and Technology , Suzhou , 215009 , China , usts.edu.cn

Search for more papers by this author

Shitang Ke,

Shitang Ke

Department of Civil and Airport Engineering , Nanjing University of Aeronautics and Astronautics , Nanjing , 211106 , China , nuaa.edu.cn

Search for more papers by this author

Tao Liu,

Tao Liu

Jiangsu Provincial Department of Housing and Urban-Rural Development , Nanjing , 210036 , China

Search for more papers by this author

Zhirao Shao,

Zhirao Shao

School of Civil Engineering , Suzhou University of Science and Technology , Suzhou , 215009 , China , usts.edu.cn

Search for more papers by this author

First published: 28 January 2025

https://doi.org/10.1155/stc/1495852

Academic Editor: Mohamed Ichchou

Share a link

Email
Wechat
Bluesky

Abstract

Tuned liquid damper (TLD) is one of the main technologies for passive control. The fundamental modal parameters of a TLD contain natural frequency and damping ratio, which are primarily related to the liquid height in the TLD device. Although the liquid height of the TLD is calibrated before installation, it is still necessary to identify the physics parameters of the TLD and the main structure during the service period to prevent the detuning of the TLD. A physics parameter identification method for the structure-damper-coupled system based on mechanics-enhanced stochastic subspace identification (SSI) is proposed in this paper, illustrated through annular TLD (ATLD). By extracting the state matrix of the first controlled mode of the main structure, the natural frequency and damping ratio of the ATLD are identified, thereby determining the liquid height of the ATLD. Numerical models of structure-ATLD-coupled systems with different degrees of freedom are constructed, and their simulated acceleration responses under different excitations are obtained. Sensitivity analysis of environmental noise is performed to verify the accuracy and robustness of the proposed parameter identification method. A dynamic test was designed for a steel chimney model to further verify the practicality of this method. The results show that when the noise level of the measurement noise is below 5.0%, the average relative error in identifying the ATLD liquid height does not exceed 10%. The identification error in the damping ratio of the structure-ATLD-coupled system will lead to a decrease in the accuracy of ATLD liquid height estimation. The proposed method can effectively identify changes in the ATLD liquid height within the optimal frequency ratio range by analyzing the experimental data from the chimney model. The proposed method can effectively estimate the modal parameters of the coupled system, providing reliable data support for evaluating the working condition of the ATLD during its service period.

1. Introduction

In modern structural engineering, a passive control strategy for structures is a promising method for vibration control, which can effectively suppress structural dynamic response without external energy [1]. Commonly used passive control strategy contains metal damper [2], viscous damper [3, 4], eddy current damper [5], X-plate damper [6], tuned mass dampers (TMDs) [7–10], tuned liquid dampers (TLDs) [11], and so on. The utilization of TLDs for structural vibration control is becoming increasingly prevalent in engineering practice due to their manufacturing, installation, and maintenance benefits [12]. TLD has been applied across various kinds of structures, including large-span bridges [13, 14] and high-rise buildings [15, 16]. A TLD is generally comprised a rigid tank holding liquid, which capitalizes on the fluid’s dynamic behavior to absorb and dissipate energy, thereby diminishing the dynamic response for the main structure. The principal design objective for TLDs is to match the damper’s frequency with the main structure’s frequency to realize the dissipation of vibrational energy [17]. To achieve specific structural vibration control objectives, tailored optimization methods for TLD design are employed, enabling precise determination of mass, frequency, and damping ratio [18]. Over time, material degradation and the diminution of liquid mass within the TLD may alter its modal parameters, consequently impacting its damping efficacy. Concurrently, advancements in active control technology underscore the importance of accurate modal parameter identification for both the primary structure and the damping devices, which is critical for maintaining active control technology’s effectiveness [19, 20]. Hence, there is a compelling need for research focused on modal parameter identification in structure-TLD-coupled systems to ensure sustained vibration control performance.

In the research of modal parameter identification for coupled systems, the predominant methods include experimental modal analysis (EMA) and operational modal analysis (OMA) to identify the natural frequencies and damping ratios of the structure. OMA is a technique that identifies the modal parameters of a structure solely through measured acceleration responses, without the need for information regarding the input loads. This approach is particularly effective for ascertaining the modal parameters of both the primary structure and its damping devices [21]. Given the complexity of large-scale structures, OMA is well suited for the modal parameter identification of practical structures, offering a more applicable method for real-world applications. The OMA method can generally be divided into time-domain methods [22, 23] and frequency-domain methods [24, 25]. These approaches have been widely utilized in various large-scale civil infrastructure projects [26–28]. Peeters et al. [29] performed a comprehensive study of the OMA method based on the measured data from the Z24 Bridge and compared the modal parameter identification results obtained by different researchers. The stochastic subspace identification (SSI) method has been developed over several decades and is considered one of the most suitable methods for dealing with the OMA problem in civil engineering [30, 31]. They determined that the SSI method has certain advantages in avoiding the randomness and ambiguity that may arise during the OMA process. Similarly, the OMA method is also applied in the structure-damper-coupled systems for modal parameter identification. Weber et al. [32] employed the SSI method for the OMA of a footbridge equipped with TMDs and investigated the influence of seasonal temperature changes on the damping ratio of the main structure. Wang et al. [33] identified TMD parameters in coupled systems based on the SSI method and verified the effectiveness of the method using a numerical example of a three-layer frame. Cho et al. [34] conducted a full-scale field test on a 64-layer concrete building and derived the decoupled equations of the structure motion to identify the dynamic parameters of the secondary mass damper. Due to the influence of the field test environment and excitation equipment, the application of the aforementioned methods is somewhat limited. To account for uncertainties in modal parameter identification, a TMD parameter identification process based on Bayesian theory was proposed and applied to a 183 m-high concrete chimney to verify the reliability of the method [35].

Upon acquiring the modal parameters of the coupled system, it becomes imperative to ascertain the physics parameters of the TLD, including the effective sloshing mass ratio and the height of the liquid. In recent years, extensive research has been undertaken by scholars on the dynamics of structural-TLD-coupled systems. Typically, numerical simulations or equivalent mechanical models are employed to determine the physics parameters of TLD. Sigrist et al. [36] proposed a method for fluid-structure dynamic analysis using ANSYS, focusing on the accurate determination of TLD parameters. They validated this method by applying it to a nuclear reactor, ensuring its reliability for assessing the parameters of TLDs in such critical applications. Vilceanu et al. [37] developed a refined numerical model to assess the dynamic response of high-rise structures equipped with several TLDs. Considering the computational efficiency of numerical simulations, many researchers have used equivalent mechanical models to determine the modal parameters of TLDs. The Housner model represents the classical equivalent mechanical model for simulating liquid sloshing dynamics within a square water tank [38]. Tait et al. [39] developed linear equivalent mechanical models for square TLDs, cylindrical TLDs, and hybrid TLDs to describe the dynamic performance of TLDs. Yu et al. [40] established nonlinear stiffness and damping models using the principle of equivalent energy dissipation to describe the mechanical behavior of coupled systems. In equivalent mechanical models, equations have been formulated to define the natural frequency and damping ratio of a TLD. To calibrate the parameters within these equations, a comprehensive series of experiments was systematically carried out [41]. Determining the TLD parameters through numerical simulations will affect the computational efficiency of parameter identification methods. Explicit calculation formulas based on equivalent mechanical models allow for direct and rapid calculation of damper parameters, making them more suitable for the TLD parameter identification process.

Existing studies have predominantly focused on identifying the natural frequency and damping ratio of TMD, with relatively less research on the parameter identification of TLDs in coupled systems. In addition, TLDs are nonlinear vibration control devices characterized by multimodal and time-varying properties. In light of this, this paper derives the relationship between modal parameters, effective sloshing mass ratio, and liquid height based on the theoretical mechanical model of annular TLD (ATLD). A physics parameter identification method that leverages the mechanics-enhanced SSI method is proposed for the extraction of modal parameters of the ATLD within the coupled system. Numerical simulation methods were used to establish single-degree-of-freedom (SDOF) and multidegree-of-freedom (MDOF) coupled systems considering fluid-structure interaction. The dynamic responses obtained from the numerical coupled system under various excitations were employed to verify the accuracy of the identification method. Environmental noise with different noise levels was introduced to examine the robustness of the method. A dynamic test was conducted on a steel chimney model to analyze the impact of different liquid heights on the accuracy of ATLD parameter identification. The identification results obtained by the proposed method are crucial for ensuring the damping efficiency of the TLD, providing effective data support for the evaluation of the working condition of the TLD during its long-term service stage.

This paper is organized as follows. The theoretical development of the physics parameter identification method for TLD is summarized in Section 2. Section 3 and Section 4 provide the numerical simulation of structure-ATLD-coupled systems with various degrees of freedom for verifying the effectiveness and robustness of the proposed method. Section 5 presents the identification results of vibration response obtained from a high-rise chimney model. Finally, some concluding remarks are presented in Section 6.

2. Theoretical Development of the Parameter Identification Method for ATLD

2.1. Background of Covariance-Driven SSI

The SSI method is a time-domain parameter identification technology for discrete state-space equations of linear systems. It is currently one of the most effective OMA technologies [42]. The dynamic equation of an n degrees-of-freedoms (DOFs) linear system in Figure 1 can be expressed as follows:

()

where M, C, and K denote the mass matrix, damper matrix, and stiffness matrix, respectively; U(t) denotes the displacement vector of the structure; and f(t) denotes the external excitation. According to the state space theory, the dynamic equation in equation (1) can be converted as follows:

()

where x(t) denotes the state-space vector; A_c denotes the state-space matrix of the continue system; B_c denotes the input matrix of the continue system; and subscript c presents the continuous time.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

n DOFs linear system.

In practical engineering applications, it is often the case that not all DOFs of a structure are measured. Assume that a total of l sensors, including accelerometers, velocity sensors, or displacement sensors, are employed for the measurement process. The corresponding observation equation for the system can be obtained as follows:

()

where y(t) denotes the observed variable; and C_a, C_v, and C_d denote the output matrices of the acceleration, velocity, and displacement. The acceleration and velocity can be measured at the same time. Using the defined x(t), equation (4) can be transformed into

()

Equations (2) and (4) collectively constitute a continuous deterministic state-space model.

()

In practical applications, test data are often sampled at discrete time intervals. Accordingly, equation (5) must be discretized to yield a discrete-time state equation as follows:

()

where A denotes the discrete state-space matrix; B_c denotes the discrete input matrix; C denotes the discrete output matrix; D denotes the discrete transformation matrix; and x_k denotes the discrete state-space vector. Combining A and C, the modal parameters corresponding to the system can be calculated as follows:

()

where Λ denotes a diagonal matrix, which consists of the eigenvalues of the state-space matrix as follows:

()

where λ_k denotes the kth eigenvalue of A and is related to the natural frequency and damping ratio of the coupled system. It is assumed that the eigenvectors corresponding to the state matrices of the continuous-time system and the discrete-time system are identical. Moreover, the relationship between the eigenvalues of the state-space matrices for the continuous and discrete-time systems is delineated as follows:

()

where λ_ck denotes the kth eigenvalue of A_c, k = 1, 2, …, n. λ_ck can be obtained as follows:

()

According to equation (11), the natural frequency and damping ratio of the discrete system can be calculated as follows:

()

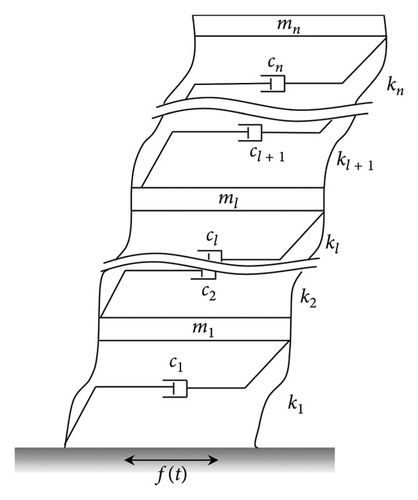
2.2. Modal Parameter Identification for Structure-TLD-Coupled Systems

The placement of the TLD within the primary structure significantly influences its vibration mitigation efficacy. Typically, the TLD is situated in a location that does not disturb the building’s functionality and meets the basic architectural design requirement. Assuming that the TLD is installed at the structure’s nth degree of freedom to manage its dynamic response, the structure and TLD then constitute a coupled system with n + 1 DOFs. The equation of motion for this coupled system is presented as follows:

()

where x₀ is the relative displacement between the nth DOF of the structure and the TLD; δ_n is the position vector of the TLD, which is a column vector with all elements equal to 0 except for the nth element which is 1; and G₁ and G₂ denote the parameters related to the damper. According to the basic theory of SSI, the relationship between the state matrix A, the eigenvalue λ_j, and the eigenvector ϕ_j can be expressed as follows:

()

The natural frequency, damping ratio, and mode shape of the coupled system can be determined as follows:

()

Due to the interaction between the TLD and the primary structure, a pair of peaks emerges close to the natural frequency of the controlled mode within the acceleration spectrum. The TLD is commonly engineered to modulate the first mode. Employing the parameters associated with these modes, the eigenvalue matrix Λ_D and the mode shape matrix Γ_D are established, subsequently deriving the state matrix A^′ for the integrated system. The computations for the abovementioned matrices proceed as follows:

()

According to equations (6) and (7), there is an explicit computational relationship between the modal parameters of the coupled system and the elements in A^′. Consequently, the natural frequency and damping ratio of the main structure and the TLD can be determined. The calculation formulas are as follows:

()

where μ denotes the ratio of the effective sloshing mass within the TLD and the main structure; ω₀ and ω_D denote the first natural frequencies of the main structure and the TLD; and ξ₀ and ξ_D denote the damping ratios of the main structure and the TLD.

2.3. Equivalent Mechanical Model of ATLD

The determination of the modal parameters for the ATLD through the SSI method is the foundation of estimating the liquid height using the ATLD’s equivalent mechanical model. The motion of the liquid within the ATLD can be modeled using the linear potential flow theory. It is assumed that the liquid in the ATLD is incompressible, inviscid, and irrotational. Figure 2 illustrates a schematic representation of the ATLD under these assumptions.

Here, r₁, r₂, and h denote the inner radius, outer radius, and liquid height, respectively. The dynamic response of the liquid in the ATLD can be obtained through linear potential flow theory. When the TLD is subjected to harmonic excitation (x(t) = x₀e^iωt), the horizontal force F_x applied to the inner wall of the tank in the direction of the excitation and the fluid moment M_y at the bottom of the tank can be calculated by the following equations [43]:

()

where m denotes the liquid mass within the ALTD; k denotes the ratio of r₁ and r₂; and ω_1d denotes the angular frequency of the ATLD. The damping ratio of ATLD ξ_1d is the (d + 1)^th root of the following equation:

()

where J₁ and N₁ denote the first-order Bessel functions of the first and the second kinds, respectively. The sloshing natural frequency f_1d of ATLD can be calculated as follows:

()

where d denotes the sloshing order of the effective liquid. The ATLD can be conceptually modeled as a spring-mass-tank system, wherein the total mass of the liquid is decomposed into the following components:

()

When the ATLD is subjected to external excitation, the corresponding equation of motion governing the sloshing dynamics of the liquid is given by

()

where η_d denotes the relative deformation between the tank wall and the sloshing liquid. The general solution of equation (23) can be obtained as follows:

()

According to Newton’s second law, the force that the liquid exerts on the tank wall can be calculated as the product of the liquid’s mass and its acceleration.

()

Upon dividing the aforementioned equation by equation (19), the resultant quotient gives the ratio of the effective sloshing mass of the ATLD liquid to the total mass as follows:

()

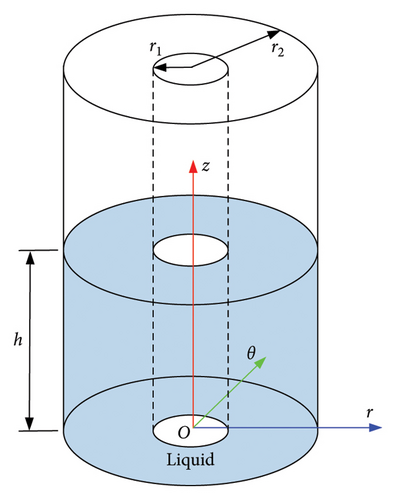
Typically, the first-order sloshing mass of the ATLD is considered with d = 1. Using the aforementioned equivalent mechanical model, the relationship between h, ω_d, and ξ_d is established. The actual ATLD liquid height can be estimated using the identified natural frequency and damping ratio.

2.4. Calculation Procedure for ATLD Parameter Identification

This paper has effectively employed the SSI method to determine the modal parameters of the structure-ATLD-coupled system. By adopting an equivalent mechanical model of the ATLD, the study has established a clear relationship among the TLD’s natural frequency, damping ratio, and liquid height. This approach has facilitated the accurate estimating of the actual liquid height within the ATLD. A visual representation of the calculation process can be referred to Figure 3.

1.
The dynamic structural response under external excitation is obtained from the actual structure and subsequently preprocessed.
2.
The state-space equations of the coupled system are formulated. The SSI method is utilized to identify the natural frequency f_i, damping ratio ξ_j, and mode shapes ψ_j of the coupled system.
3.
The parameters of two modes relevant to the controlled mode are extracted for creating the state-space matrix A^′ reflecting the characteristics of the ATLD based on the eigenvalue matrix Λ^′ and mode shape matrix Γ^′. The TLD natural frequencies ω_D and damping ratios ξ_D are calculated using the elements from A^′.
4.
The correlation between the TLD liquid height h, natural frequency ω_D, and damping ratio ξ_D is established using the equivalent mechanical model. The identified TLD frequency is used to calculate the effective sloshing mass ratio. The theoretical mass ratio of the ATLD is calculated and verified against the identified mass ratio. If convergence requirements are not met, return to Step (2) for reassessment.
5.
The liquid height h in the ATLD is ultimately estimated.

3. Parameter Identification for the Numerical SDOF Structure-ATLD-Coupled System

3.1. Numerical Model of the SDOF Structure-ATLD System

A refined numerical model of the SDOF structure-ATLD-coupled system, depicted in Figure 4, was established and subjected to a nonlinear time history analysis. This process was undertaken to assess the effectiveness and robustness of the proposed parameter identification method in identifying ATLD parameters. Within the coupled system, the mass, stiffness, and damping ratio were set as 950 kg, 40,500 N/m, and 0.5%, respectively. The first natural frequency of the main structure was computed to be 0.91 Hz. Equations (27) and (28) were utilized to determine the optimal frequency and damping ratios of TLD [44].

()

where α_opt denotes the optimal ratio of natural frequency; ζ_opt denotes the optimal damping ratio; and μ denotes the mass ratio. Given a mass ratio of 2.5%, the ATLD tank’s designated mass m₀ is 1 kg. Its inner diameter r₁ and outer diameter r₂ are set as 0.2 m and 0.5 m, respectively, while the height of the tank h₀ is 0.6 m. Optimal ATLD parameters and the geometric dimensions of the tank were inserted into equations (21)–(26), yielding a liquid height of 0.32 m within the tank.

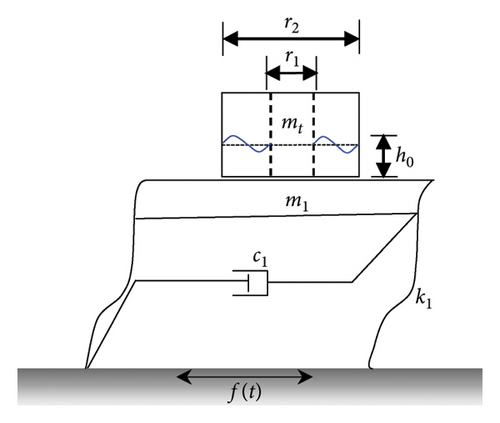
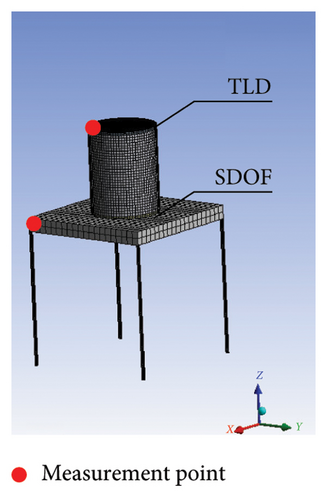
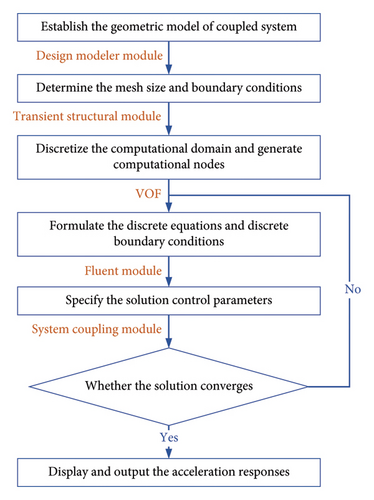
The key point of the numerical simulation for this coupled system is the establishment of the fluid-solid interaction (FSI) model, which is essential for simulating the liquid sloshing in the ATLD tank. The flowchart of FSI is illustrated in Figure 5. To precisely model the mechanical behavior of the coupled system, the mechanical and fluid modules within the workbench are utilized for nonlinear time history analysis and to investigate the liquid sloshing in the ATLD [37]. The geometrical models of the structure and ATLD were established using the design modeler module and imported into the transient structural module to define the material properties, boundary conditions, and mesh size, respectively. The numerical model of ATLD consists of a rigid tank and flexible liquid. The volume of fluid (VOF) model in the FLUENT is utilized for the ATLD’s numerical simulation. The ATLD being partially filled means that the two parts in the VOF model are water and air, with a surface tension coefficient of 0.073 N/m prescribed at the interface. The turbulence within the fluid is modeled using the RNG k-ε turbulence model, and a transient analysis approach is adopted to gain the acceleration response of the structure. No-slip boundary conditions are enforced on both the inner and outer walls and the tank’s base. Thermal transfer phenomena are not considered in this analysis. The interfacial surfaces of FSI are defined within both the FLUENT and transient structural modules, and a bidirectional coupling method is implemented to capture the interactions between the liquid and the tank. The system coupling module integrates the transient structural module and fluent module to enable mutual force transfer, facilitating nonlinear time history analysis of the coupled system.

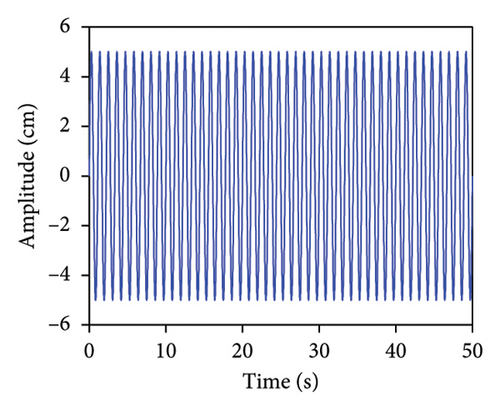
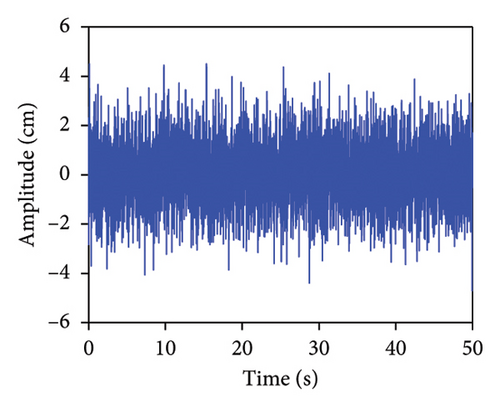
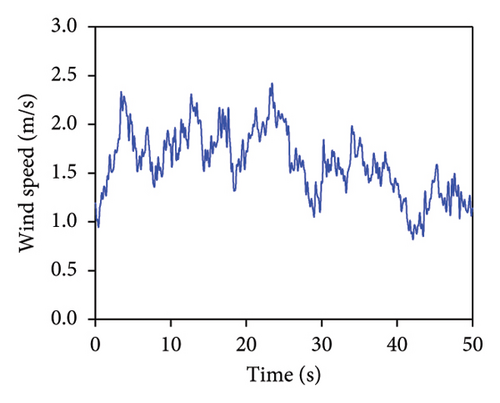
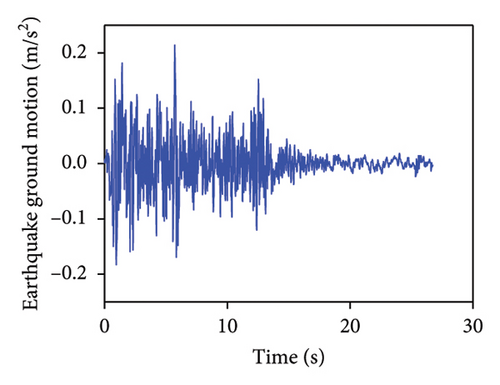
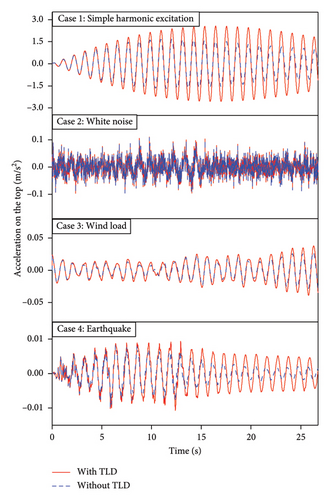
The acceleration responses of the coupled system under different excitations are used for the verification of the proposed method. The external excitations considered were simple harmonic, white noise, wind load, and EI-Centro earthquake. Figure 6 displays the time histories corresponding to these excitations. For the simple harmonic, a sinusoidal excitation with a 5 cm amplitude and a frequency of 100 Hz was employed. Gaussian white noise excitation, characterized by a zero-mean Gaussian distribution, was utilized to simulate random signals. The simulation of wind loads was performed using the harmonic synthesis approach, which characterizes fluctuating wind forces as cross-correlated, zero-mean Gaussian stationary random processes [45]. Lateral wind loads were quantified using the Kamal spectrum, assuming a wind velocity of 8 m/s at the reference height of 10 m. Earthquake simulations employed EI-Centro seismic waves, which were imposed in both the x and y directions of the abovementioned SDOF coupled system. Various excitation types were applied to the system to acquire the acceleration time histories for both the ATLD and the primary structure. Data acquisition for the acceleration was conducted at a frequency of 50 Hz over the sampling duration of 100 s.

3.2. Comparative Analysis for Parameter Identification Under Different Excitations

Figure 7 presents the time histories and spectra of the acceleration responses of the structure-ATLD-coupled system subject to varying excitation. When subjected to the same excitation, the peak acceleration of the coupled system is obviously diminished. Across all cases, the peak acceleration obtained from the SDOF structure-TLD-coupled system is reduced by 25.21% on average. The most pronounced mitigation effect is witnessed under wind load, achieving a peak acceleration reduction of 35.05%. The SSI method is employed to precisely identify the modal parameters of the coupled system, with the model order being determined using equation (29) during the identification phase. The criteria for eliminating spurious modes are set as Δf < 1%, Δξ < 1%, ξ > 0, and MAC > 98% [46].

()

where f_s and f₀ denote the sampling frequency for the acceleration and the first natural frequency of the main structure, respectively, and n_c denotes the number of cycles.

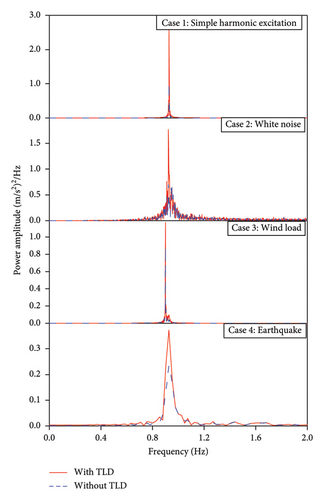
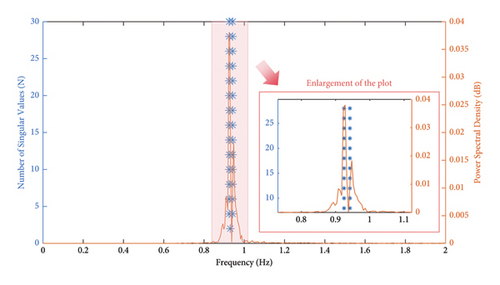
Taking the case with white noise as an example, the stabilization diagram obtained using the SSI method is shown in Figure 8. There are two stable axes in the stabilization diagram under white noise excitation, with identified frequencies of 0.91 Hz and 0.93 Hz. The identified first frequency closely matches the results obtained from numerical simulations, indicating good identification accuracy. Similarly, under the other three types of excitations, the stabilization diagrams also have two stable axes, with identified frequencies of 0.92 and 0.94, 0.93 and 0.93, and 0.91 and 0.94 Hz, respectively.

Using the calculation formulas from Section 2.2, the natural frequencies and damping ratios of the structure and the ATLD are identified based on the eigenvalues and eigenvectors corresponding to the points on the stable axes. According to the theoretical model in Section 2.3, the liquid height in the ATLD device is calculated using the identified f_d and ω_d of the damper. The identification results are shown in Table 1, where the statistical characteristics of the identification results are primarily the relative error and the coefficient of variation (COV) as follows:

()

where μ_y and σ_y denote the average value and covariance of the identified results. The closer the COV is to 0, the lower the dispersion of the identification results. As shown in the table, the identification accuracy of the damper’s natural frequency is relatively high, with an average relative error not exceeding 4.0%. A comparison of the COV indicates that the natural frequency identification results demonstrate the lowest dispersion. In contrast, the TLD damping ratio and liquid level height display significantly higher levels of dispersion. The calculation of the liquid height is related to the natural frequency and damping ratio, so the identification errors of the TLD modal parameters will propagate to the calculation of the liquid height leading to increased identification errors. Upon analyzing the results obtained under various excitations, it was observed that the relative errors associated with the identification of the ATLD liquid height were −4.50%, 6.25%, 3.50%, and −4.00%, respectively. The identification results for the TLD liquid height are generally consistent across different cases, indicating that the proposed method can effectively obtain the liquid height for ATLD.

Table 1. Comparison of estimated TLD parameters under different excitations.

Main parameters		Natural frequency (Hz)	Damping ratio (%)	Liquid height (m)
Theoretical results		0.94	0.064	0.4

Simple harmonic	Identified results	0.97	0.062	0.382
Simple harmonic	Relative errors	3.10%	3.13%	−4.50%

White noise	Identified results	0.98	0.061	0.425
White noise	Relative errors	4.10%	4.69%	6.25%

Wind load	Identified results	0.98	0.062	0.414
Wind load	Relative errors	4.10%	3.12%	3.50%

EI-Centro earthquake	Identified results	0.97	0.068	0.384
EI-Centro earthquake	Relative errors	3.10%	5.88%	−4.00%

Coefficient of variation		0.51%	4.38%	4.65%

3.3. Sensitive Analysis in Noisy Environment

Environmental noise introduces significant uncertainties in both external excitations and structural responses observed during field measurements [47]. To assess the robustness and effectiveness of the parameter identification method, Gaussian white noise of a specified intensity was superimposed on the acceleration responses of the numerical models. The identified results obtained from the acceleration responses with and without noise are similar, indicating the method is robust to noise. The intensity of the noise is quantified by the noise level R, which is calculated based on the ratio of the root mean square (RMS) of the noise signal to the RMS of the noise-free structural response as follows:

()

where

denotes the structural acceleration response with noise;

denotes the calculated structural acceleration response; R denotes the noise level; N_noise denotes the time series of Gaussian white noise with the distribution of N(0,1); and

denotes the covariance of the calculated structural acceleration response. To ascertain the impact of noise on the accuracy of TLD liquid height identification, calculations were performed within a noise range of 0%–8%. To facilitate a more effective comparison between different identification results, two kinds of errors between the identified results and theoretical results are calculated. Figure 9 presents the average absolute and relative errors for each noise level, with the upper and lower sections of the figure depicting absolute and relative errors, respectively. The data in the bar chart reveal a progressive increase in the identification error of the TLD liquid height with escalating noise levels. The line graph shows that the impact of measurement noise is generally consistent across the cases with different excitations. Notably, the precision of identification results for the case with white noise is marginally reduced in comparison to other cases. This discrepancy arises as both the external excitation and the artificially imposed noise conform to a Gaussian distribution. The application of white noise, as described by equation (31), affects the frequency domain characteristics of the acceleration response, thereby compromising the identification accuracy of the damper’s modal parameters. With the elevation of noise levels, the accuracy of identification results for the liquid height gradually decreases. It is found that when the measurement noise surpasses 5.5%, the average relative error for all cases exceeds 10%.

4. Parameter Identification for the Numerical MDOF Structure-ATLD-Coupled System

4.1. Numerical Model of the MDOF Structure-ATLD System

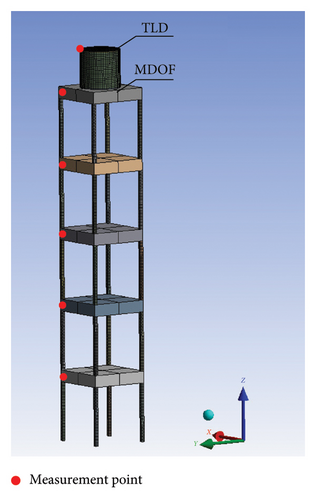
Section 3 addresses the parameter identification for ATLD within SDOF systems. However, real-world engineering structures are typically more complex, exhibiting multiple degrees of freedom, which necessitates validation of the proposed parameter identification theory’s effectiveness and reliability. The numerical examples contain the coupled systems with main structures possessing 3, 5, and 7 degrees of freedom, as illustrated in Figure 10. The red dots on the figure signify the locations from which structural acceleration data are obtained, with the derived acceleration serving to identify further modal parameters. For coupled systems of MDOF structures with ATLDs, variations in the degrees of freedom result in changes to the mass, stiffness, damping ratio, and the first natural frequency. Accordingly, the parameters of the ATLD were tailored to align with the diverse structural parameters, as shown in Table 2.

Table 2. Structural parameters of coupled systems with different DOFs.

Structural system	Main parameter	DOF
Structural system	Main parameter	3	5	7
Main structure	m_i (kg)	1588.1	1638	6392.9
	k_i (kN/m)	366.9	1287.5	4946.1
	Damping ratio (%)	0.5	0.5	0.5
	1^st natural frequency (Hz)	0.51	0.99	0.67

TLD	r₁ (m)	0.1	0.05	0.05
	r₂ (m)	0.3	0.34	0.7
	Liquid height (m)	0.14	0.18	0.29
	Damping ratio (%)	6.4	6.4	6.4
	1^st sloshing frequency (Hz)	0.48	0.97	0.65

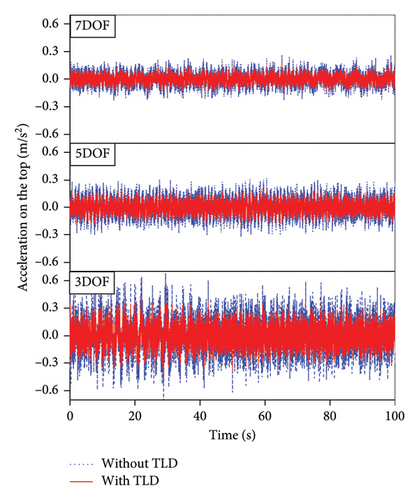
The environmental excitations (simple harmonic, white noise, wind load, and EI-Centro earthquake) were applied to the structure-ATLD-coupled system, and acceleration responses were recorded at the locations marked by red dots, with a sampling frequency of 100 Hz. Utilizing the refined numerical model of the MDOF structure, a nonlinear dynamic time history analysis was performed. This analysis resulted in the acquisition of acceleration responses from the coupled systems, each exhibiting varying degrees of freedom. A comparative analysis was conducted to examine the peak acceleration responses of the structure before and after the implementation of ATLD. Figure 11 presents the time histories of acceleration responses of the coupled systems when subjected to white noise excitation. The peak accelerations under each excitation were extracted, and it was statistically found that the peak accelerations of the coupled systems with different degrees of freedom decreased by 18.15%, 20.23%, and 19.87%, respectively. These results indicate that the TLD effectively reduced the amplitude of the structural dynamic response.

4.2. Comparative Analysis for Parameter Identification Under Different Excitations

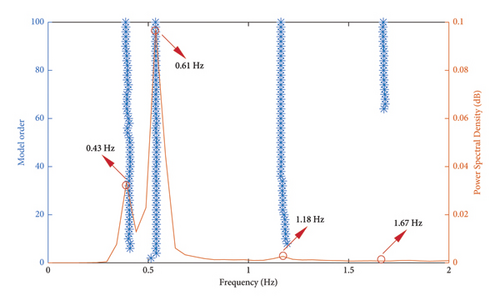
The acceleration of the measurement points shown in Figure 10(b) is extracted as the input of the SSI method for identifying the modal parameters of the structure-damper-coupled system. The parameter settings for the SSI method can be referenced from Section 3.2 for eliminating spurious modes. Taking the white noise excitation condition as an example, the acceleration responses at various points of the 3-DOF system were inputted and a stabilization diagram was plotted as shown in Figure 12. There are four stable axes in the 3-DOF-coupled system, with corresponding natural frequencies of 0.43, 0.61, 1.18, and 1.67 Hz.

The modal parameters of the 5-DOF- and 7-DOF-coupled systems can be obtained by analyzing their acceleration responses using the SSI method. TLDs are typically used to control the first mode of the main structure, so the dynamic characteristics of the first two modes of the coupled system are of primary concern. The identified natural frequencies of the first two modes for the 5-DOF-coupled system are 0.95 and 1.01 Hz, respectively, and they are 0.61 and 0.75 Hz for the 7-DOF-coupled system. The identified modal parameters of the coupled system under various excitations were summarized to further calculate the TLD parameters in Table 3. It is found that the acceleration response includes information about the first two dynamic characteristics of the coupled system under various excitations. The relative deviation between the natural frequencies identified using the SSI method does not exceed 2%. Furthermore, the stable points of the first two modes are extracted. The state matrix reflecting the dynamic characteristics of the TLD is constructed, and the modal parameters of TLD are calculated.

Table 3. OMA results of coupled systems.

Degree of freedom	Orders	Identified natural frequency (Hz)
Degree of freedom	Orders	Simple harmonic	White noise	Wind load	EI-Centro earthquake
3	1st	0.43	0.42	0.43	0.44
3	2^nd	0.61	0.60	0.63	0.60

5	1st	0.95	0.93	0.94	0.92
5	2^nd	1.01	1.03	1.04	1.01

7	1st	0.61	0.62	0.64	0.63
7	2^nd	0.75	0.72	0.73	0.74

Table 4 summarizes the calculated results of TLD parameter identification for each model. The relative error and COV are calculated to verify the efficiency and stability of the identification method. The identification results for MDOF structures are generally consistent with those for SDOF structures. The identification accuracy of the ATLD frequency is relatively high with the absolute value of the relative error not exceeding 2.0%. However, the identification accuracy of the TLD damping ratio and liquid height is relatively low. The main reason is that the TLD’s motion is composed of multiorder liquid sloshing, which has significant nonlinear effects leading to a decrease in the identification accuracy of the TLD damping ratio. According to equation (21), the calculation and identification of the liquid height are related to the frequency and damping ratio, and the identification error of the damping ratio will be transmitted to the identification of h. For coupled systems with different DOFs, the identification accuracy of the main ATLD parameters is generally consistent. By comparing the relative errors and COV of the parameters, the order of identification accuracy can be determined as follows: natural frequency > liquid height≈damping ratio. The results of the numerical examples indicate that this method can effectively estimate the modal parameters of the coupled system and the liquid height of the ATLD under different degrees of freedom and external excitations.

Table 4. Comparison of ATLD parameters under different excitations.

Degree of freedom	Main parameters	Theoretical results	Identified results	Relative errors (%)	Coefficient of variation (%)
3	Natural frequency (Hz)	0.480	0.472	−1.67	1.0
	Damping ratio (%)	0.064	0.068	6.25	3.5
	Liquid height (m)	0.140	0.135	−3.57	2.7

5	Natural frequency (Hz)	0.970	0.962	−0.82	1.5
	Damping ratio (%)	0.064	0.058	−9.38	4.7
	Liquid height (m)	0.180	0.187	3.89	3.4

7	Natural frequency (Hz)	0.650	0.639	−1.69	0.9
	Damping ratio (%)	0.064	0.059	−7.81	3.5
	Liquid height (m)	0.290	0.279	−3.79	3.1

4.3. Sensitive Analysis in Noisy Environment

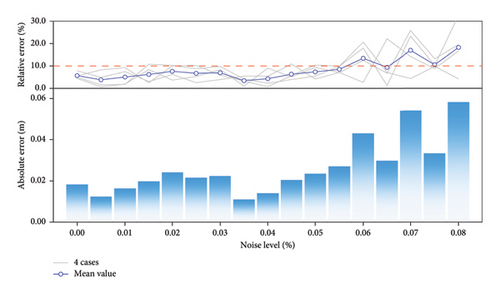
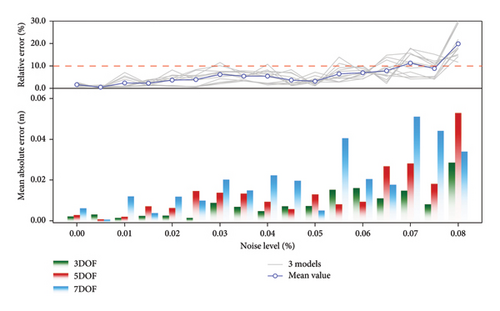
This study investigates the impact of environmental noise on the identification method for coupled systems with different DOFs. The range of noise levels is consistent with Section 3.3. According to equations (31) and (32), environmental noise is added to the simulated acceleration, which is used as input to calculate the dynamic characteristics of the ATLD, and further to determine the ATLD liquid height. The numerical examples contain the acceleration responses of models with three different degrees of freedom under four types of excitations. By analyzing the relative and absolute errors in the identification of the ATLD liquid height, the accuracy and robustness of the proposed method are examined. Figure 13 shows the identification errors of ATLD liquid height identification under different noise levels. The gray lines in the figure represent the relationship between the relative error and noise level for each example. It can be found that the dispersion of the identification results becomes greater as the noise level increases. When the measurement noise reaches 7.0%, the average relative error in TLD liquid height identification exceeds 10%. The main reason for this phenomenon is that environmental noise significantly affects the accuracy of damping ratio identification [48]. According to equation (21), the error in the damping ratio will be transmitted to the identification of the ATLD liquid height. The identification results for coupled systems with different degrees of freedom show a generally consistent trend with identification errors increasing with higher noise levels. Notably, the 7-DOF-coupled system exhibits significant identification errors even at low noise levels (R < 5.0%), with relative errors exceeding 10%. During the parameter identification process, the effectiveness of identifying the ATLD liquid height is determined by verifying the theoretical and identified mass ratios. The identification of the mass ratio in the 7-DOF-coupled system is particularly sensitive to environmental noise, leading to increased errors in the ATLD liquid height identification.

5. Application to Field Measurements on a High-Rise Chimney Model

5.1. Description of the Chimney Model and Dataset

Figure 14 depicts the designed high-rise chimney model. The inner diameter, outside diameter, and height of the chimney are 0.244, 0.25, and 9 m, respectively. The model is split into 9 segments, each 1 m high. The segments are joined by eight high-strength bolts with a diameter of 20 mm, while the bottom segment is attached to the ground transition plate by 4 high-strength bolts with a diameter of 30 mm, which are subsequently fixed to the ground. The modal analysis results suggest that the chimney model’s the first natural frequency without the TLD is 0.85 Hz.

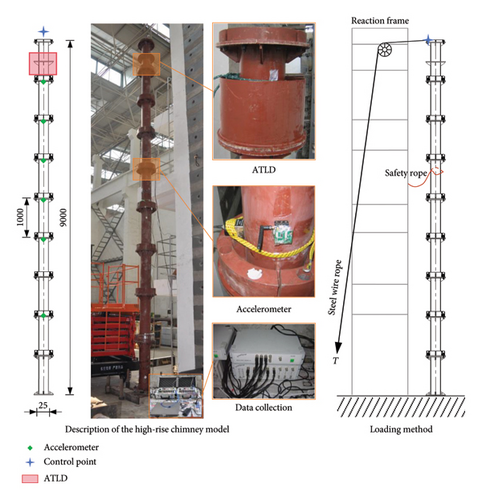
The ATLD is located in the two nodes at the top. In this test, the ATLD is primarily intended to control the chimney model’s the first modal. The ATLD water tank has an inner diameter of 0.135 m, an outside diameter of 0.225 m, an inner-to-outer diameter ratio of 0.6, and a height of 0.3 m. It is located in the center of the top section. Adjusting the liquid height in the tank can modify the ATLD’s natural frequency. To perform dynamic testing for ATLD structural vibration reduction, pure water is added to the designed annular tank and the liquid height is set to vary between 80 and 180 mm. Theoretical ATLD parameters are presented in Table 5. A free decay dynamic test was performed on the structure (Figure 13) to acquire the measured data on the structural dynamic response. When a specific force T is applied to the model’s top, the loading control point’s displacement achieves the preset value. The steel wire rope is released at that moment allowing the model to move freely and decay. The control point’s horizontal extending distance in this test is 5 mm.

Table 5. Liquid height and theoretical natural frequency of the ATLD.

Serial number of model	1	2	3	4	5	6
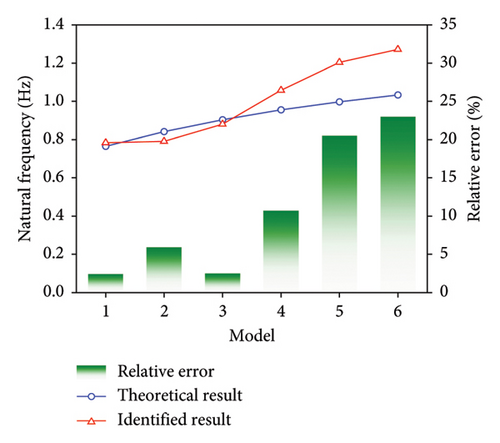
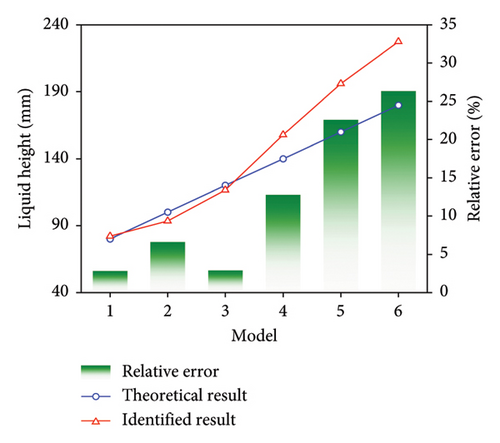
Liquid height (m)	0.08	0.10	0.12	0.14	0.16	0.18
Natural frequency (Hz)	0.765	0.841	0.904	0.956	0.998	1.033

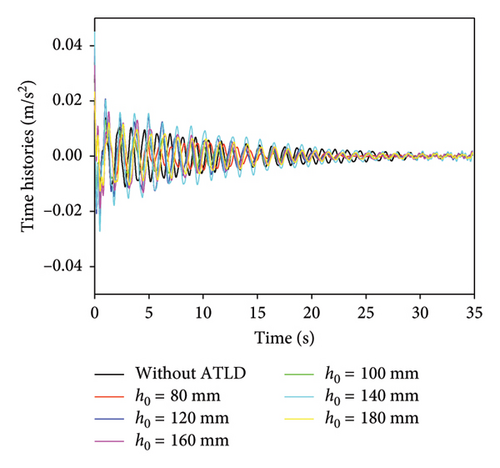
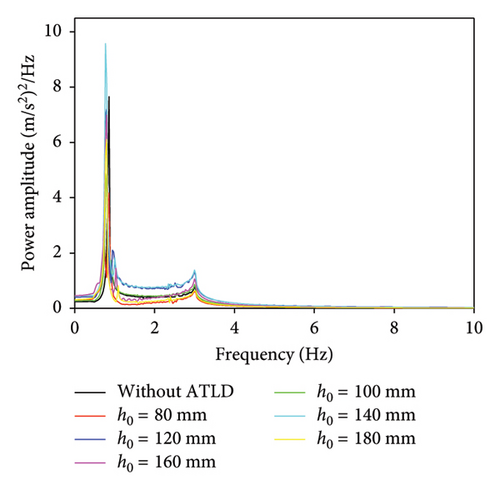
The time histories and analytical results for the acceleration at each chimney model’s middle nodes are displayed in Figure 15. The acceleration response attenuation rate of Models 1∼3 substantially increases. It attenuates to a small value in roughly 20 s as seen in the figure. This suggests that the ATLD in these models has a good control effect. On the other hand, Models 4∼6 do not exhibit an obvious attenuation in its acceleration response. Each model’s spectral peak values of the first mode follow a similar pattern, according to the FFT results. This phenomenon can be explained by the fact that the frequency ratio between the ATLD and the primary structure’s natural frequency should range between 0.9 and 1.1 when the ATLD achieves optimal vibration reduction efficiency. The ATLD frequency exceeds this optimal frequency ratio when the ATLD liquid height is greater than 120 mm, resulting in a detuning and an inability to properly carry out its vibration control.

5.2. Parameter Identification for ATLD in the Chimney Model

The SSI approach was applied to identify the modal parameters of the chimney model. The formulas for eliminating the spurious mode in Section 3.2 can be used to determine the parameters of the SSI approach. Using Model 1 as an example, the stability diagram depicted in Figure 16 was plotted using the acceleration responses at different locations as input.

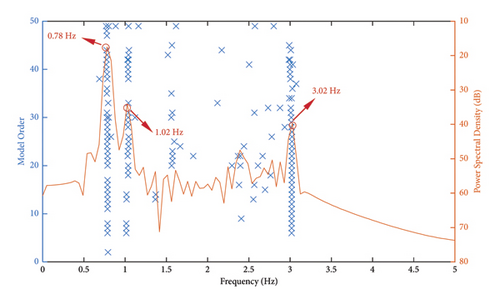
It is evident from the figure that this coupled system has three stable axes, each with a corresponding frequency of 0.78, 1.02, and 3.02 Hz. Using the calculation formulas from Section 1.2, the natural frequencies and damping ratios of the structure and ATLD were identified based on the eigenvalues and eigenvectors corresponding to the points on the stable axes, and the corresponding liquid heights were calculated. The calculation results are shown in Figure 17. It can be seen that the identification accuracy of the ATLD parameters for the first three models is relatively high. The relative errors of the liquid height and the natural frequency are both less than 5.0%. When the liquid height exceeds 120 mm, the identification accuracy of the proposed method rapidly decreases with the rise in the liquid height. The maximum relative error exceeds 25.0%. The rise in liquid height leads to a detuning phenomenon in the ATLD. The vibration energy of the second mode frequency of the coupled system becomes smaller, making it difficult for the SSI method to effectively identify the first two mode frequencies of the coupled system. The experimental results indicate that within the optimal frequency range, the proposed method can effectively identify the main parameters of the ATLD in the coupled system, and the variation in liquid level height has no significant impact on the identification accuracy.

6. Conclusions

This paper addresses the issue of changes in the operational status of TLD during the service stage by proposing a parameter identification method for the structure-ATLD-coupled system based on the enhanced SSI method. This method aims to identify the natural frequency, damping ratio, and liquid height of the ATLD. The approach utilizes the SSI method to identify the modal parameters of the coupled system and constructs the state matrix of the controlled mode to calculate the natural frequency, damping ratio, and mass ratio of the ATLD. Based on the equivalent mechanical model of the ATLD, the relationship between the damping ratio, natural frequency, and liquid height is derived. The difference between the theoretical mass ratio and the identified mass ratio is used as a criterion to ultimately determine the liquid height of the ATLD. Numerical models of structure-ATLD-coupled systems, considering fluid-structure interaction effects, are established to verify the effectiveness and reliability of the proposed method. A steel chimney model was designed to verify the practicality of the proposed method and to analyze the impact of ATLD liquid level height on identification accuracy. The main conclusions of this paper are as follows:

1.
For an SDOF-coupled system, the identification accuracy of the damper’s natural frequency is relatively high, with an average relative error not exceeding 4.0%. It is found that the identification results of the ATLD damping ratio and liquid height have a higher degree of dispersion considering the COV of different parameter identification results. The identification results for the ATLD liquid height are generally consistent under different excitations. When the noise level of environmental noise exceeds 5.5%, the average relative error in identifying the ATLD liquid height exceeds 10%. The parameter identification results of MDOF coupled systems are generally consistent with those of SDOF-coupled systems. The identification accuracy for the ATLD natural frequency is relatively high, with the absolute value of the relative error not exceeding 2.0%. By comparing the relative errors and COV of the identification results of various parameters, the order of identification accuracy can be determined as follows: natural frequency > liquid height≈damping ratio. When the level of measurement noise reaches 7.0%, the average relative error in identifying the ATLD liquid height in MDOF coupled systems exceeds 10%.
2.
The identification results of the various numerical examples indicate that the proposed method can effectively identify the modal parameters of the structure-ATLD-coupled system and accurately estimate the ATLD liquid height. In coupled systems with different DOFs, when the measurement noise level is below 5.0%, the parameter identification results exhibit high accuracy demonstrating the robustness of the proposed method. However, the nonlinear effects of the ATLD can reduce the accuracy of the ATLD damping ratio identification, thereby increasing the identification error of the ATLD liquid height.
3.
The results of the model tests indicate that the proposed method effectively identified the natural frequency and liquid height of the ATLD with a relative error not exceeding 5.0% for the first three models. The frequency ratio between the ATLD and the main structure is one of the main factors affecting identification accuracy. Within the optimal range of frequency ratio, the proposed method can effectively identify the main parameters of the ATLD in the coupled system, and variations in liquid height have no significant impact on identification accuracy.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This work is supported by the National Natural Science Foundation of China (52178294 and 52408200), Natural Science Research Projects of Colleges and Universities in Jiangsu Province (24KJB560022), Science & Technology Program of Suzhou (SYG202113), and Suzhou Science and Technology Plan (Basic Research) Project (SJC2023002).

Acknowledgments

This work was supported by the National Natural Science Foundation of China (52178294 and 52408200), Natural Science Research Projects of Colleges and Universities in Jiangsu Province (24KJB560022), Science & Technology Program of Suzhou (SYG202113), and Suzhou Science and Technology Plan (Basic Research) Project (SJC2023002).

Open Research

Data Availability Statement

All data, models, or codes that support the findings of this study are available from the corresponding author upon reasonable request.

References

1 Zhao Z., Wang Y., Hu X., and Weng D., Seismic Performance Upgrading of Containment Structures Using a Negative-Stiffness Amplification System, Engineering Structures. (2022) 262, https://doi.org/10.1016/j.engstruct.2022.114394.
10.1016/j.engstruct.2022.114394
Google Scholar
2 Lee C. H., Ryu J., Kim D. H., and Ju Y. K., Improving Seismic Performance of Non-ductile Reinforced Concrete Frames through the Combined Behavior of Friction and Metallic Dampers, Engineering Structures. (2018) 172, 304–320, https://doi.org/10.1016/j.engstruct.2018.06.045, 2-s2.0-85048597966.
10.1016/j.engstruct.2018.06.045
Web of Science® Google Scholar
3 Chen X., De Domenico D., and Li C., Seismic Resilient Design of Rocking Tall Bridge Piers Using Inerter-Based Systems, Engineering Structures. (2023) 281, https://doi.org/10.1016/j.engstruct.2023.115819.
10.1016/j.engstruct.2023.115819
Google Scholar
4 Ahmadizadeh M., On Equivalent Passive Structural Control Systems for Semi-active Control Using Viscous Fluid Dampers, Structural Control and Health Monitoring. (2007) 14, no. 6, 858–875, https://doi.org/10.1002/stc.182, 2-s2.0-35348854314.
10.1002/stc.182
Web of Science® Google Scholar
5 Cao L., Li X., Huang Y., Li C., and Pan H., High Robust Eddy Current Tuned Tandem Mass Dampers-Inerters for Structures under the Ground Acceleration, Soil Dynamics and Earthquake Engineering. (2025) 188, https://doi.org/10.1016/j.soildyn.2024.109040.
10.1016/j.soildyn.2024.109040
Web of Science® Google Scholar
6 Bakre S. V., Jangid R. S., and Reddy G. R., Optimum X-Plate Dampers for Seismic Response Control of Piping Systems, International Journal of Pressure Vessels and Piping. (2006) 83, no. 9, 672–685, https://doi.org/10.1016/j.ijpvp.2006.05.003, 2-s2.0-33749529350.
10.1016/j.ijpvp.2006.05.003
Google Scholar
7 Brownjohn J. M. W., Carden E. P., Goddard C. R., and Oudin G., Real-time Performance Monitoring of Tuned Mass Damper System for a 183 M Reinforced Concrete Chimney, Journal of Wind Engineering and Industrial Aerodynamics. (2010) 98, no. 3, 169–179, https://doi.org/10.1016/j.jweia.2009.10.013, 2-s2.0-75849131154.
10.1016/j.jweia.2009.10.013
Web of Science® Google Scholar
8 Pisal A. Y. and Jangid R. S., Dynamic Response of Structure with Tuned Mass Friction Damper, International Journal of Advanced Structural Engineering. (2016) 8, no. 4, 363–377, https://doi.org/10.1007/s40091-016-0136-7, 2-s2.0-84995804420.
10.1007/s40091-016-0136-7
CAS Google Scholar
9 Chen X., Li A., Zhang Z. et al., Improving the Wind-Induced Human Comfort of the Beijing Olympic Tower by a Double-Stage Pendulum Tuned Mass Damper, The Structural Design of Tall and Special Buildings. (2020) 29, no. 4, https://doi.org/10.1002/tal.1704.
10.1002/tal.1704
Google Scholar
10 Li C., Pan H., and Cao L., Pendulum-type Tuned Tandem Mass Dampers-Inerters for Crosswind Response Control of Super-tall Buildings, Journal of Wind Engineering and Industrial Aerodynamics. (2024) 247, https://doi.org/10.1016/j.jweia.2024.105706.
10.1016/j.jweia.2024.105706
Web of Science® Google Scholar
11 Furtmüller T., Di Matteo A., Adam C., and Pirrotta A., Base-isolated Structure Equipped with Tuned Liquid Column Damper: An Experimental Study, Mechanical Systems and Signal Processing. (2019) 116, 816–831, https://doi.org/10.1016/j.ymssp.2018.06.048, 2-s2.0-85050352583.
10.1016/j.ymssp.2018.06.048
Web of Science® Google Scholar
12 Suthar S. J. and Jangid R. S., Design of Tuned Liquid Sloshing Dampers Using Nonlinear Constraint Optimization for Across-Wind Response Control of Benchmark Tall Building, Structures. (2021) 33, 2675–2688, https://doi.org/10.1016/j.istruc.2021.05.059.
10.1016/j.istruc.2021.05.059
Web of Science® Google Scholar
13 Shum K. M. and Xu Y. L., Multiple Tuned Liquid Column Dampers for Reducing Coupled Lateral and Torsional Vibration of Structures, Engineering Structures. (2004) 26, no. 6, 745–758, https://doi.org/10.1016/j.engstruct.2004.01.006, 2-s2.0-16544377323.
10.1016/j.engstruct.2004.01.006
Web of Science® Google Scholar
14 Wang Z., Chai X., Peng S., Wang B., and Zhang L., A Novel Tuned Liquid Mass Damper for Low-Frequency Vertical Vibration Control: Model Experiments and Field Tests, Mechanical Systems and Signal Processing. (2024) 220, https://doi.org/10.1016/j.ymssp.2024.111702.
10.1016/j.ymssp.2024.111702
Google Scholar
15 He X., Li C., Chen L., Yang J., Hu G., and Ou J., Numerical Research on Nonlinear Liquid Sloshing and Vibration Control Performance of Tuned Liquid Damper, Journal of Building Engineering. (2024) 96, https://doi.org/10.1016/j.jobe.2024.110660.
10.1016/j.jobe.2024.110660
Google Scholar
16 Zhou Z., Xie Z., Zhang L., and Zhang L., Optimal Design of Multiple Tuned Liquid Dampers with Paddles for Wind-Induced Vibration Control of High-Rise Buildings, Structures. (2024) 68, https://doi.org/10.1016/j.istruc.2024.107094.
10.1016/j.istruc.2024.107094
Google Scholar
17 Sun J. Q., Jolly M. R., and Norris M. A. T., Passive, Adaptive and Active Tuned Vibration Absorbers—A Survey, Journal of Vibration and Acoustics. (1995) 117, no. B, 234–242, https://doi.org/10.1115/1.2838668, 2-s2.0-0029321567.
10.1115/1.2838668
Google Scholar
18 Soong T. T. and Dargush G. F., Passive Energy Dissipation Systems in Structural Engineering, 1997.
Google Scholar
19 Papadimitriou C., Katafygiotis L. S., and Au S.-K., Effects of Structural Uncertainties on TMD Design: A Reliability-Based Approach, Journal of Structural Control. (2006) 4, no. 1, 65–88, https://doi.org/10.1002/stc.4300040108.
10.1002/stc.4300040108
Google Scholar
20 Wang M., Nagarajaiah S., and Chen L., Adaptive Passive Negative Stiffness and Damping for Retrofit of Existing Tall Buildings with Tuned Mass Damper: TMD-NSD, Journal of Structural Engineering. (2022) 148, no. 11, https://doi.org/10.1061/(asce)st.1943-541x.0003474.
10.1061/(ASCE)ST.1943-541X.0003474
Google Scholar
21 Zou Y., Tong L., and Steven G. P., Vibration-based Model-dependent Damage (Delamination) Identification and Health Monitoring for Composite Structures—A Review, Journal of Sound and Vibration. (2000) 230, no. 2, 357–378, https://doi.org/10.1006/jsvi.1999.2624, 2-s2.0-0033734262.
10.1006/jsvi.1999.2624
Web of Science® Google Scholar
22 Zhang Y., Kurata M., and Lynch J. P., Long-Term Modal Analysis of Wireless Structural Monitoring Data from a Suspension Bridge under Varying Environmental and Operational Conditions: System Design and Automated Modal Analysis, Journal of Engineering Mechanics. (2017) 143, no. 4, https://doi.org/10.1061/(asce)em.1943-7889.0001198, 2-s2.0-85015938437.
10.1061/(ASCE)EM.1943-7889.0001198
Web of Science® Google Scholar
23 Yang X.-M., Yi T.-H., Qu C.-X., and Li H.-N., Modal Identification of Bridges Using Asynchronous Responses through an Enhanced Natural Excitation Technique, Journal of Engineering Mechanics. (2021) 147, no. 12, https://doi.org/10.1061/(asce)em.1943-7889.0002022.
10.1061/(ASCE)EM.1943-7889.0002022
Web of Science® Google Scholar
24 Pan H., Zhang L., and Fu J., Investigation of Dynamic Properties of Tall Buildings under Super Typhoon Mangkhut via Bayesian Method, Journal of Building Engineering. (2023) 65, https://doi.org/10.1016/j.jobe.2022.105807.
10.1016/j.jobe.2022.105807
Google Scholar
25 Can Altunışık A., Sunca F., and Sevim B., Modal Parameter Identification and Seismic Assessment of Historical Timber Structures under Near-Fault and Far-Fault Ground Motions, Structures. (2023) 47, 1624–1651, https://doi.org/10.1016/j.istruc.2022.11.143.
10.1016/j.istruc.2022.11.143
Google Scholar
26 Chen J., Xu Y. L., and Zhang R. C., Modal Parameter Identification of Tsing Ma Suspension Bridge under Typhoon Victor: EMD-HT Method, Journal of Wind Engineering and Industrial Aerodynamics. (2004) 92, no. 10, 805–827, https://doi.org/10.1016/j.jweia.2004.04.003, 2-s2.0-3042594083.
10.1016/j.jweia.2004.04.003
Web of Science® Google Scholar
27 Civera M., Sibille L., Zanotti Fragonara L., and Ceravolo R., A DBSCAN-Based Automated Operational Modal Analysis Algorithm for Bridge Monitoring, Measurement. (2023) 208, https://doi.org/10.1016/j.measurement.2023.112451.
10.1016/j.measurement.2023.112451
Google Scholar
28 Liu X., Wan H. P., Luo Y., and Yang C., A Data-Driven Combined Deterministic-Stochastic Subspace Identification Method for Condition Assessment of Roof Structures Subjected to Strong Winds, Structural Control and Health Monitoring. (2022) 29, no. 10, 1–22, https://doi.org/10.1002/stc.3031.
10.1002/stc.3031
Google Scholar
29 Peeters B. and Lowet G., A New Procedure for Modal Parameter Estimation, Journal of Sound and Vibration. (2004) 38, 24–29.
Google Scholar
30 Reynders E. and Roeck G. De, Reference-based Combined Deterministic–Stochastic Subspace Identification for Experimental and Operational Modal Analysis, Mechanical Systems and Signal Processing. (2008) 22, no. 3, 617–637, https://doi.org/10.1016/j.ymssp.2007.09.004, 2-s2.0-38149097782.
10.1016/j.ymssp.2007.09.004
Web of Science® Google Scholar
31 Zini G., Betti M., and Bartoli G., A Quality-Based Automated Procedure for Operational Modal Analysis, Mechanical Systems and Signal Processing. (2022) 164, https://doi.org/10.1016/j.ymssp.2021.108173.
10.1016/j.ymssp.2021.108173
Web of Science® Google Scholar
32 Weber B. and Feltrin G., Assessment of Long-Term Behavior of Tuned Mass Dampers by System Identification, Engineering Structures. (2010) 32, no. 11, 3670–3682, https://doi.org/10.1016/j.engstruct.2010.08.011, 2-s2.0-77957313193.
10.1016/j.engstruct.2010.08.011
Web of Science® Google Scholar
33 Wang J. F. and Lin C. C., Extracting Parameters of TMD and Primary Structure from the Combined System Responses, Smart Structures and Systems. (2015) 16, no. 5, 937–960, https://doi.org/10.12989/sss.2015.16.5.937, 2-s2.0-84946909111.
10.12989/sss.2015.16.5.937
Web of Science® Google Scholar
34 Cho B., Jo J., Joo S., and Kim H., Dynamic Parameter Identification of Secondary Mass Dampers Based on Full-Scale Tests, Computer-Aided Civil and Infrastructure Engineering. (2012) 27, no. 3, 218–230, https://doi.org/10.1111/j.1467-8667.2011.00740.x, 2-s2.0-84856762026.
10.1111/j.1467-8667.2011.00740.x
Web of Science® Google Scholar
35 Wang X., Zhu Z., and Au S.-K., Bayesian Operational Modal Analysis of Structures with Tuned Mass Damper, Mechanical Systems and Signal Processing. (2023) 182, https://doi.org/10.1016/j.ymssp.2022.109511.
10.1016/j.ymssp.2022.109511
Web of Science® Google Scholar
36 Sigrist J.-F. and Garreau S., Dynamic Analysis of Fluid–Structure Interaction Problems with Modal Methods Using Pressure-Based Fluid Finite Elements, Finite Elements in Analysis and Design. (2007) 43, no. 4, 287–300, https://doi.org/10.1016/j.finel.2006.10.002, 2-s2.0-33846549158.
10.1016/j.finel.2006.10.002
Web of Science® Google Scholar
37 Vîlceanu V., Kavrakov I., and Morgenthal G., Coupled Numerical Simulation of Liquid Sloshing Dampers and Wind–Structure Simulation Model, Journal of Wind Engineering and Industrial Aerodynamics. (2023) 240, https://doi.org/10.1016/j.jweia.2023.105505.
10.1016/j.jweia.2023.105505
Google Scholar
38 Xiao C. Z., Wu Z. H., Chen K., Tang Y., and Yan Y. L., An Experimental Study on the Equivalent Nonlinear Model for a Large-Sized Tuned Liquid Damper, Journal of Building Engineering. (2023) 73, https://doi.org/10.1016/j.jobe.2023.106754.
10.1016/j.jobe.2023.106754
Google Scholar
39 Tait M. J., Modelling and Preliminary Design of a Structure-TLD System, Engineering Structures. (2008) 30, no. 10, 2644–2655, https://doi.org/10.1016/j.engstruct.2008.02.017, 2-s2.0-52749095954.
10.1016/j.engstruct.2008.02.017
Web of Science® Google Scholar
40 Yu J. K., Wakahara T., and Reed D. A., A Non-linear Numerical Model of the Tuned Liquid Damper, Earthquake Engineering & Structural Dynamics. (1999) 28, no. 6, 671–686.
10.1002/(SICI)1096-9845(199906)28:6<671::AID-EQE835>3.0.CO;2-X
Web of Science® Google Scholar
41 Warnitchai P. and Pinkaew T., Modelling of Liquid Sloshing in Rectangular Tanks with Flow-Dampening Devices, Engineering Structures. (1998) 20, no. 7, 593–600, https://doi.org/10.1016/s0141-0296(97)00068-0, 2-s2.0-0032127396.
10.1016/S0141-0296(97)00068-0
Web of Science® Google Scholar
42 Peeters B. and De Roeck G., Reference-based Stochastic Subspace Identification for Output-Only Modal Analysis, Mechanical Systems and Signal Processing. (1999) 13, no. 6, 855–878, https://doi.org/10.1006/mssp.1999.1249, 2-s2.0-0033354387.
10.1006/mssp.1999.1249
Web of Science® Google Scholar
43 Bauer H. F., Theory of the Fluid Oscillations in a Circular Cylindrical Ring Tank Partially Filled with Liquid, 1960, National Aeronautics and Space Administration.
Google Scholar
44 Hartog De J. P., Mechanical Vibrations, 1956, Dover Publications.
Web of Science® Google Scholar
45 Zhao N., Huang G., Kareem A., Li Y., and Peng L., Simulation of Ergodic Multivariate Stochastic Processes: An Enhanced Spectral Representation Method, Mechanical Systems and Signal Processing. (2021) 161, https://doi.org/10.1016/j.ymssp.2021.107949.
10.1016/j.ymssp.2021.107949
Google Scholar
46 Rainieri C. and Fabbrocino G., Operational Modal Analysis of Civil Engineering Structures, 2014.
10.1007/978-1-4939-0767-0
Google Scholar
47 Cao L. and Li C., A High Performance Hybrid Passive Base-Isolated System, Structural Control and Health Monitoring. (2022) 29, no. 3, https://doi.org/10.1002/stc.2887.
10.1002/stc.2887
PubMed Web of Science® Google Scholar
48 Cao Z., Hua X., Wen Q., Chen Z., and Niu H., A State Space Technique for Modal Identification of Coupled Structure–Tuned Mass Damper Systems from Vibration Measurement, Advances in Structural Engineering. (2019) 22, no. 9, 2048–2060, https://doi.org/10.1177/1369433219829807, 2-s2.0-85062477814.
10.1177/1369433219829807
Google Scholar

All articles

Physics Parameter Identification of Annular Tuned Liquid Damper for the Structure-Damper-Coupled System Using a Mechanics-Enhanced SSI Method

Abstract

1. Introduction

2. Theoretical Development of the Parameter Identification Method for ATLD

2.1. Background of Covariance-Driven SSI

2.2. Modal Parameter Identification for Structure-TLD-Coupled Systems

2.3. Equivalent Mechanical Model of ATLD

2.4. Calculation Procedure for ATLD Parameter Identification

3. Parameter Identification for the Numerical SDOF Structure-ATLD-Coupled System

3.1. Numerical Model of the SDOF Structure-ATLD System

3.2. Comparative Analysis for Parameter Identification Under Different Excitations

3.3. Sensitive Analysis in Noisy Environment

4. Parameter Identification for the Numerical MDOF Structure-ATLD-Coupled System

4.1. Numerical Model of the MDOF Structure-ATLD System

4.2. Comparative Analysis for Parameter Identification Under Different Excitations

4.3. Sensitive Analysis in Noisy Environment

5. Application to Field Measurements on a High-Rise Chimney Model

5.1. Description of the Chimney Model and Dataset

5.2. Parameter Identification for ATLD in the Chimney Model

6. Conclusions

Conflicts of Interest

Funding

Acknowledgments

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Physics Parameter Identification of Annular Tuned Liquid Damper for the Structure-Damper-Coupled System Using a Mechanics-Enhanced SSI Method

Abstract

1. Introduction

2. Theoretical Development of the Parameter Identification Method for ATLD

2.1. Background of Covariance-Driven SSI

2.2. Modal Parameter Identification for Structure-TLD-Coupled Systems

2.3. Equivalent Mechanical Model of ATLD

2.4. Calculation Procedure for ATLD Parameter Identification

3. Parameter Identification for the Numerical SDOF Structure-ATLD-Coupled System

3.1. Numerical Model of the SDOF Structure-ATLD System

3.2. Comparative Analysis for Parameter Identification Under Different Excitations

3.3. Sensitive Analysis in Noisy Environment

4. Parameter Identification for the Numerical MDOF Structure-ATLD-Coupled System

4.1. Numerical Model of the MDOF Structure-ATLD System

4.2. Comparative Analysis for Parameter Identification Under Different Excitations

4.3. Sensitive Analysis in Noisy Environment

5. Application to Field Measurements on a High-Rise Chimney Model

5.1. Description of the Chimney Model and Dataset

5.2. Parameter Identification for ATLD in the Chimney Model

6. Conclusions

Conflicts of Interest

Funding

Acknowledgments

Open Research

Data Availability Statement

References

Figures

References

Related

Information