Volume 2025, Issue 1 7359832

Research Article

Open Access

LFQAP: A Lightweight and Flexible Quantum Artificial Intelligence Application Platform

Xin Zhang,

Xin Zhang

orcid.org/0000-0002-7947-916X

College of Intelligence and Computing , Tianjin University , No.135 Ya Guan Road, Tianjin , 300350 , China , tju.edu.cn

Search for more papers by this author

Xiaoyu Li,

Xiaoyu Li

orcid.org/0000-0001-6586-4705

School of Information and Software Engineering , University of Electronic Science and Technology of China , Chengdu , 610054 , Sichuan, China , uestc.edu.cn

Institute of Electronics and Information Industry Technology of Kash , Kash , 844000 , Xinjiang, China

Search for more papers by this author

Yuexian Hou,

Corresponding Author

Yuexian Hou

[email protected]

orcid.org/0000-0002-3238-493X

College of Intelligence and Computing , Tianjin University , No.135 Ya Guan Road, Tianjin , 300350 , China , tju.edu.cn

Search for more papers by this author

Xin Zhang,

Xin Zhang

orcid.org/0000-0002-7947-916X

College of Intelligence and Computing , Tianjin University , No.135 Ya Guan Road, Tianjin , 300350 , China , tju.edu.cn

Search for more papers by this author

Xiaoyu Li,

Xiaoyu Li

orcid.org/0000-0001-6586-4705

School of Information and Software Engineering , University of Electronic Science and Technology of China , Chengdu , 610054 , Sichuan, China , uestc.edu.cn

Institute of Electronics and Information Industry Technology of Kash , Kash , 844000 , Xinjiang, China

Search for more papers by this author

Yuexian Hou,

Corresponding Author

Yuexian Hou

[email protected]

orcid.org/0000-0002-3238-493X

College of Intelligence and Computing , Tianjin University , No.135 Ya Guan Road, Tianjin , 300350 , China , tju.edu.cn

Search for more papers by this author

First published: 19 April 2025

https://doi.org/10.1155/que2/7359832

Academic Editor: Yu-Bo Sheng

Share a link

Email
Wechat
Bluesky

Abstract

Quantum artificial intelligence (AI) is one of the critical research domains in the field of quantum computing and holds significant potential for practical applications in the near future. A quantum AI software platform serves as a fundamental infrastructure for advancing research and facilitating applications in this area. Such a platform supports essential tasks including quantum AI model training, inference, and the deployment of diverse applications. The current quantum AI software platforms prioritize comprehensive functionality; however, they often lack scalability, making it challenging to integrate new features flexibly. Given the broad and evolving research landscape of quantum AI algorithms, it is crucial to develop a software framework that is both user-friendly and capable of autonomous functional extension. In this paper, we present a lightweight, scalable, and open-source quantum AI platform designed to support the training and inference of variational quantum algorithms. This platform employs a hierarchical and structured architecture, enhancing the overall manageability and modularity of the software. Notably, it exhibits improved scalability, incorporating a compiler module for the first time. This module enables support for user-defined quantum devices, including both real physical quantum computers and quantum circuit simulators, as well as custom-defined optimizers. The platform integrates both tensor network simulator and full-amplitude simulator, providing powerful ability for quantum AI research. Utilizing these simulators, we conducted training experiments on three publicly available datasets and compared the results with TensorFlow Quantum. The experimental results validate the reliability and effectiveness of our platform, demonstrating its potential as a powerful tool for quantum AI applications.

1. Introduction

Quantum artificial intelligence (AI) represents a significant class of quantum algorithms and is among the most extensively studied areas in quantum computing. It encompasses a diverse range of algorithms, including quantum neural networks (QNNs) [1–5], quantum approximate optimization algorithm (QAOA) [6], quantum principal component analysis (quantum PCA) [7], and quantum support vector machines (quantum SVMs) [3, 8, 9], among others. In this paper, the term “quantum AI” specifically refers to quantum AI algorithms based on the quantum variational method, with QNNs serving as a prominent representative of this category. In recent years, significant progress has been made in the field of QNNs, including interpretability of QNNs [10, 11], demonstrated advantages [12–15], robustness [16, 17], and quantum generative adversarial networks (quantum GANs) [18–20]. Moreover, due to the relatively shallow circuit depth of quantum AI algorithms, they exhibit strong potential for noise robustness. This characteristic makes quantum AI particularly promising for practical applications in the noisy intermediate-scale quantum (NISQ) era. For instance, research has explored the application of quantum AI in the field of smart manufacturing [21]. As the saying goes, “To do a good job, one must first sharpen one’s tools.” A well-designed quantum AI platform is crucial for advancing quantum AI research, as it serves as the essential bridge between quantum AI algorithms and quantum computers.

Numerous quantum AI software platforms have been developed, many of which originate from large commercial companies. Notable examples include Qiskit [22], TensorFlow Quantum [23], MindSpore Quantum [24], and QPanda [25]. These platforms are typically developed by large quantum computing teams and are often integrated into general-purpose AI software frameworks. These software platforms have a large user base and play an indispensable role in quantum AI research. However, many of them are either not fully open-source or have complex architectures, making secondary development challenging. Recently, several excellent lightweight frameworks, such as TorchQuantum [26] and PennyLaneAI [27], have been open-sourced, contributing significantly to the advancement of quantum AI. Nevertheless, these frameworks also have certain limitations, such as dependencies on third-party packages, which can make it difficult to integrate user-defined quantum simulators or quantum computing hardware seamlessly.

To address the aforementioned challenges, this paper introduces LFQAP, an open-source, lightweight, interface-flexible, and easily extensible quantum AI application platform. The key advantages of LFQAP are as follows. (1) This platform introduces a quantum instruction compiler module for the first time, enabling the transformation of the platform’s instruction set into the instruction sets of any simulator or real quantum computer. This feature significantly enhances scalability, allowing for seamless integration of user-defined quantum circuit executors. (2) The platform adopts a hierarchical and modular architecture, facilitating efficient management and extensibility. This design enables the straightforward addition of computational modules, such as entropy and mutual information. Furthermore, the platform integrates a density matrix tensor network simulator and a full-amplitude simulator, supports user-defined noise simulation, and is adaptable to a wide range of application scenarios.

In order to verify the reliability of this platform, we carried out the verification experimental on three public datasets: Iris dataset, Moon dataset, and Original Wisconsin Breast Cancer dataset. We called the tensor network simulator and the full-amplitude simulator separately and compared the results with TensorFlow Quantum, the results are basically the same, and this confirms the reliability of our platform. The source code of the platform is open sourced on GitHub [28].

2. Our Architecture

Our architecture adopts a hierarchical design, which can enhance the extensibility and scalability of the platform. The overall architecture is illustrated in Figure 1. The top layer consists of quantum algorithms and applications. Quantum algorithms must be written using the instruction specification defined in this work, as detailed in Sections 3.1 and 3.2. The middle layer represents the quantum AI training platform, which is responsible for training the Ansatz parameters of quantum AI models. This layer is composed of three main components: quantum computing part, classical computing part, and compiler part. Quantum computing part is used to calculate gradient, classical part is used to update the parameters by SGD, Adam, and so on, and compiler part is used to transform our platform’s instruction specification to the executor’s specification. The bottom layer comprises the quantum circuit execution platform, which executes quantum circuits and provides feedback on results. Quantum circuits can be executed on either a simulator or a real quantum computer. This platform integrates both a tensor network simulator and a full-amplitude simulator while also supporting the extension to user-defined simulators or physical quantum hardware, ensuring flexibility and adaptability for various research and application scenarios.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Overall architecture of LFQAP.

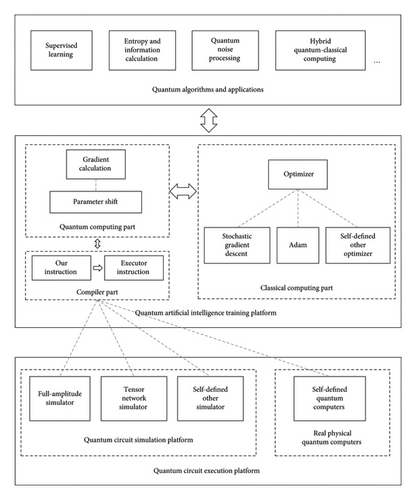
2.1. Compiler

We defined the instruction set of our platform in Section 3.1; however, quantum circuit executes on either a simulation platform or a real quantum computer (collectively referred to as executors), each of which has its own distinct instruction set. To address this discrepancy, we design a compiler module that translates our platform’s instructions into executor-specific instructions. The compiler plays a crucial role in ensuring the scalability of the platform. When integrating a new simulation platform or quantum computer, it is only necessary to modify the compiler to generate the corresponding target instructions.

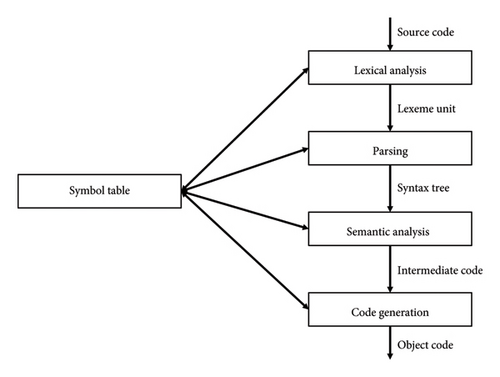
The design of this compiler follows principles similar to those of traditional compilers [29], consisting of four key stages: lexical analysis, parsing, semantic analysis, and code generation. The specific processing modules and intermediate representations are illustrated in Figure 2. In essence, the compiler translates one programming language into another. However, unlike traditional compilers, our compiler does not construct a syntax tree due to the simplicity of the instruction set, which consists of only 11 instructions. Symbol table serves as the key module, providing translation rules. Semantic analysis is performing pattern matching to find the target instruction format based on the keyword. Code generation is to translate the platform instructions to target format line by line and get instructions that can be executed on the running platform. For example, the compiler translates an instruction from our platform, such as RX2 3.14, into the format required by a specific executor, such as Rx3.14 2.

2.2. Gradient Calculation

Classical neural networks typically utilize backpropagation for gradient computation; however, QNNs cannot directly employ backpropagation. Instead, the parameter shift method is commonly used [30]. The parameter shift method is essentially a finite-difference approach that estimates gradients by evaluating the circuit output (i.e., the loss function) at shifted parameter values. By iteratively adjusting the parameters in this manner, the loss function is minimized, leading to model convergence. In the following sections, we introduce the formal definition of the QNN loss function and provide a detailed explanation of the parameter shift method for gradient computation.

Suppose x_i is the i-th sample feature in training dataset and y is the corresponding label (represented by a vector of 0, 1). First, we encode x_i into a quantum state by qubit encoding or amplitude encoding [31]; for the qubit encoding method, each feature corresponds to a rotation gate; for the amplitude encoding method, each feature is mapped to probability amplitudes of quantum states. Then, we evolve the quantum state into = U(θ)|ϕ_i after Ansatz U(θ), and θ represents the trainable parameters of Ansatz. In the end, we get the result after measurement, and the result is h_k(x_i, θ) = <Ψ_i|O_k|Ψ_i> (O_k is the projective measurement, which acts on kth qubit). In this platform, we used the cross-entropy loss function, which can be defined as

()

For the parameter shift method, the gradient is calculated by calculating the difference of the circuit output between the training parameters by adding π/2 and subtracting π/2. The detailed calculation process is as follows.

The gradient can be represented as

()

denotes the measurement results with the parameter θ_j being θ_j ± π; then we calculate the gradient of θ_j of all samples and get their statistical average, and thus we get the real gradient of θ_j. User can define other loss functions and calculate their gradient, such as mean square error.

2.3. Optimizer

After obtaining the gradient, the optimizer is used to update the parameters until the model converges. For gradient descent, the formula for the parameter update is given below:

()

where θ_t represents the parameters at the t-th step and ϵ is the learning rate. In practical applications, we usually choose stochastic gradient descent or Adam for higher training performance [32], and these are variants based on gradient descent. These optimizers are integrated into the platform, and it is also easy to add other types of optimizers.

2.4. Full-Amplitude Simulator

The full-amplitude simulator stores all probability amplitudes of quantum states, and these amplitudes evolve under the action of quantum gates. This approach is particularly advantageous for simulating quantum circuits with a small number of qubits and deep circuit layers.

There are numerous open-source projects for full-amplitude simulators available on GitHub. In our platform, we integrate the Quantum-Computing-Library [33], though we have refactored portions of the original code and removed certain unused functionalities to optimize performance and maintainability. Additionally, previous studies have demonstrated that distributing probability amplitudes across multiple nodes [34] can significantly enhance both the scalability and performance of quantum simulations.

2.5. Tensor Network Simulator Based on Density Matrix

The tensor network simulator is a single-amplitude simulator, which differs from the full-amplitude simulator in that it does not require storing all quantum states. Instead, quantum initialization, gate operations, and measurements are represented as tensors, and the contraction result of the tensor network yields the measurement outcome. Since storing the entire quantum state is unnecessary, the single-amplitude simulator is capable of simulating larger quantum systems more efficiently.

There are various implementation approaches for tensor network simulators. Our platform integrates a density matrix–based tensor network simulator, originally proposed by Markov and Shi [35]. The key advantage of this approach is its ability to simulate quantum noise using Kraus operators, allowing users to define both noise types and intensity. Fried et al. have open-sourced a quantum computing simulator based on this methodology [36], which we have incorporated into our platform with some modifications and optimizations.

In [37], a distributed tensor network simulation scheme was proposed, where large tensor networks are decomposed into multiple smaller tensor networks through tensor network edge cutting. These smaller tensor networks can then be processed in parallel across different computing cores. By leveraging this technique, the authors successfully simulated a 120-qubit QAOA algorithm using a 4096-core supercomputer. This method provides a promising avenue for large-scale quantum AI training using high-performance computing infrastructure.

3. Application Specification

This section describes the instruction specification of this platform and gives an example of how to train a QNN.

3.1. Instruction Set

The instruction set (quantum assembly language) serves as the foundation for writing quantum algorithms, where each quantum gate typically corresponds to a single instruction, and the complete set of instructions constitutes the instruction set. The general format of a quantum instruction follows the structure: Instruction Name + Target Qubit(s) + Parameters; in many cases, some instruction parameters have default values. Table 1 provides an overview of the instruction set used in this platform, which includes single-bit instructions (acting on one bit), double-bit instructions (acting on two bits), and measurement instructions. This project is open-source, allowing users to add, modify, or remove instructions as needed.

Table 1. The instruction set for this platform, including the quantum gate type, the corresponding instruction format, and a description of the parameters in the instruction.

Gate type	Instruction format	Parameter description
X	X n	n is the qubit that X gate acts on.
Y	Y n	n is the qubit that Y gate acts on.
Z	Z n	n is the qubit that Z gate acts on.
H	H n	n is the qubit that H gate acts on.
RX	RX n index/angle/value	n is the qubit that RX gate acts on, index/angle/value is the rotation angle from sample file, random initialization or real rotation angle.
RY	RY n index/angle/value	n is the qubit that RX gate acts on, index/angle/value is the rotation angle from sample file, random initialization or real rotation angle.
RZ	RZ n index/angle/value	n is the qubit that RX gate acts on, index/angle/value is the rotation angle from sample file, random initialization or real rotation angle.
CNOT	CNOT control target	Control is the control qubit, target is the control qubit.
CZ	CZ control target	Control is the control qubit, target is the control qubit.
SWAP	SWAP n1 n2	Swap state of qubits n1 and n2.
MZ	MZ n1 n2 … nx	n1, n2, …, nx represent the qubits that MZ gate acts on. MZ gate is the σ_Z measurement.

3.2. Instruction Identifiers

In order to distinguish the types of parameters, instruction identifiers are added before each instruction, in three categories.

The first type of identifiers: ∗. This identifier involves RX, RY, and RZ. This type of identifier indicates that the angle of the rotation gate is read from a file, and the index shown in the Table 1 represents the position of the feature or parameters in the file, which typically corresponds to the feature data of a sample.
The second type of identifiers: #. This identifier involves RX, RY, and RZ, this type of identifier means that the angle of the rotation gate is random initialization, and it is commonly used for random initialization of training parameters of QNNs.
The third type of identifiers: &. This identifier involves all type of instructions, for RX, RY, and RZ, and this means it is rotated by the specified value. It has no practical effect on the other instructions, just for syntactic consistency.

Table 2 presents examples of three types of identifiers used in our platform. Lines 1 and 2 (∗ identifiers): These indicate that the 0th and 1st qubits read the corresponding feature data (0th and 1st) from a file, enabling sample data loading. Lines 4, 5, 12, and 13 (# identifiers): These are used for initializing the training parameters of the QNN. Lines 8 and 9 (& identifiers): These represent fixed (frozen) trainable parameters, meaning these parameters are set to specific values and are not updated during training. Lines 6, 10, 14, and 16: These are included for syntactic consistency and do not carry special functional significance. Line 16: This specifies a Pauli-Z measurement on the 1st qubit.

Table 2. Example code for three classes of instruction identifiers.

1. ∗ RX 0 0

2. ∗ RX 1 1

4. # RY 0 parameter0

5. # RY 1 parameter1

6. & CNOT 0 1

8. & RX 0 3.14

9. & RX 1 3.14

10. & CNOT 0 1

11.

12. # RY 0 parameter2

13. # RY 1 parameter3

14. & CNOT 0 1

15.

16. & MZ 1

3.3. Platform Operation

This section will illustrate how to train a QNN using our platform, mainly including three steps.

Step 1: initialization. This involves configuring the number of iterations, selecting either a simulator or a real quantum computer, specifying the optimizer, and partitioning the dataset into training and testing sets. Detailed procedures are provided in the platform application description [28]. After initialization, the code is compiled into an executable file.
Step 2: training the QNNs. This is performed using the command ./plt network.dat sample.data, where plt is the executable file generated after compilation, network.dat specifies the structure of the QNNs, and sample.data contains the training samples, with each sample occupying a single row. Table 2 provides a concrete example of this process.
Step 3: result analysis. This step involves analyzing the loss, accuracy, and other relevant metrics recorded during training. Furthermore, advanced statistical or information-theoretic measures, including entropy, can be computed for deeper insights.

4. Test and Analysis

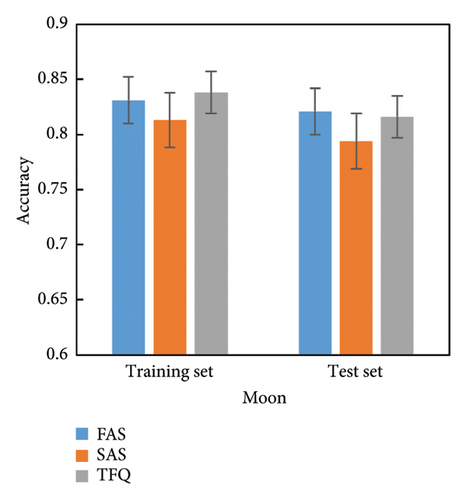
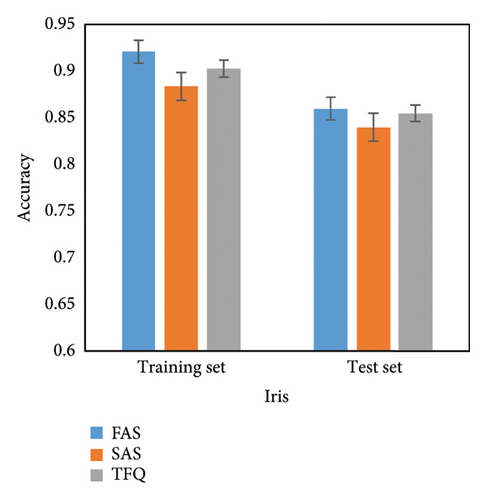
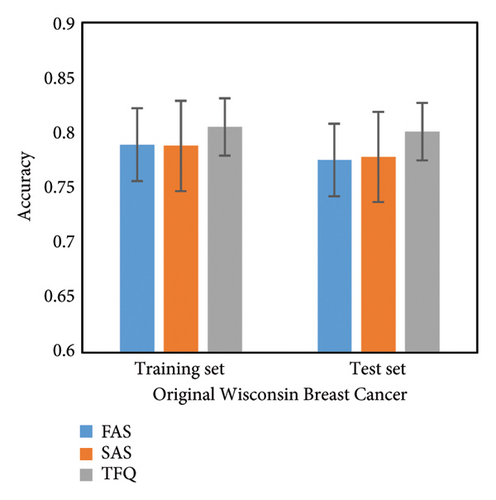
In order to verify the reliability of this platform, we test it on three public datasets: Moon (0.2 noise), Iris [38], and Original Wisconsin Breast Cancer [39]. We adapt break-wall structured QNN Ansatz with depth 4 [11]. We employ the Adam optimizer and set the number of training iterations to 100. We also compare the results with TensorFlow Quantum. The results are shown in Figure 2.

We completed the test on three publicly available datasets, and we statistically find the accuracy of both the training and test sets. Figure 3(a) shows the result of Moon dataset, the maximum difference between our platform and TFQ of training set is 2.5%, and the maximum difference between our platform and TFQ of test set is 2.2%. Figure 3(b) shows the result of Iris dataset, the maximum difference between our platform and TFQ of training set is 2.2%, and the maximum difference between our platform and TFQ of test set is 1.2%. Figure 3(c) shows the result of Original Wisconsin Breast Cancer dataset, the maximum difference between our platform and TFQ of training set is 1.7%, and the maximum difference between our platform and TFQ of test set is 2.6%. We also counted the standard deviation, which did not exceed 0.04 for all datasets, confirming that the platform is stable. The experiment proves the reliability of our platform.

5. Discussion

To accommodate the diverse and evolving needs of quantum AI algorithm research, we have open-sourced a flexible and extensible quantum AI application platform. The platform adopts a hierarchical design and incorporates a compiler module, enabling seamless integration of custom simulators and real quantum computers, as well as additional functionalities.

To evaluate the reliability of our platform, we conducted experiments on three public datasets, utilizing both the full-amplitude simulator and the single-amplitude simulator. We then compared the results with TensorFlow Quantum, and the outcomes were generally consistent within an acceptable range. However, due to the lack of access to a real quantum computer, we have not yet included test results from actual quantum hardware. In the future, we plan to further explore the application of our platform in various scenarios, including incremental learning [40].

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This work was supported in part by the National Natural Science Foundation of China under grant no. 62472072.

Acknowledgments

The authors thank J. Jiang for the comparison experiment with TensorFlow Quantum.

Open Research

Data Availability Statement

The simulation data used to support the findings of this study are included within the article.

References

1 Farhi E. and Neven H., Classification With Quantum Neural Networks on Near Term Processors, 2018, https://arxiv.org/abs/1802.06002.
Google Scholar
2 Schuld M., Bocharov A., Svore K. M., Wiebe N., and Wiebe N., Circuit-Centric Quantum Classifiers, Physical Review A. (2020) 101, no. 3, https://doi.org/10.1103/physreva.101.032308.
10.1103/PhysRevA.101.032308
Web of Science® Google Scholar
3 Schuld M., Supervised Quantum Machine Learning Models Are Kernel Methods, 2021, https://arxiv.org/abs/2101.11020.
Google Scholar
4 Schuld M., Sweke R., Meyer J. J., and Meyer J. J., Effect of Data Encoding on the Expressive Power of Variational Quantum-Machine-Learning Models, Physical Review A. (2021) 103, no. 3, https://doi.org/10.1103/physreva.103.032430.
10.1103/PhysRevA.103.032430
Web of Science® Google Scholar
5 Jerbi S., Fiderer L. J., Nautrup H. P., Kübler J. M., Briegel H. J., and Dunjko V., Quantum Machine Learning beyond Kernel Methods, Nature Communications. (2023) 14, no. 1, https://doi.org/10.1038/s41467-023-36159-y.
10.1038/s41467-023-36159-y
PubMed Web of Science® Google Scholar
6 Farhi E., Goldstone J., and Gutmann S., A Quantum Approximate Optimization Algorithm, 2014, https://arxiv.org/abs/1411.4028.
Google Scholar
7 Lloyd S., Mohseni M., Rebentrost P., and Rebentrost P., Quantum Principal Component Analysis, Nature Physics. (2014) 10, no. 9, 631–633, https://doi.org/10.1038/nphys3029, 2-s2.0-84904520343.
10.1038/nphys3029
CAS Web of Science® Google Scholar
8 Rebentrost P., Mohseni M., and Lloyd S., Quantum Support Vector Machine for Big Data Classification, Physical Review Letters. (2014) 113, no. 13, https://doi.org/10.1103/physrevlett.113.130503, 2-s2.0-84907425976.
10.1103/PhysRevLett.113.130503
PubMed Web of Science® Google Scholar
9 Bartkiewicz K., Gneiting C., Černoch A., Jiráková K., Lemr K., and Nori F., Experimental Kernel-Based Quantum Machine Learning in Finite Feature Space, Scientific Reports. (2020) 10.
10.1038/s41598-020-68911-5
Web of Science® Google Scholar
10 Lloyd S., Schuld M., Ijaz A., Izaac J., and Killoran N., Quantum Embeddings for Machine Learning, 2020, https://arxiv.org/abs/2001.03622.
Google Scholar
11 Shen H., Zhang P., You Y. Z., Zhai H., and Zhai H., Information Scrambling in Quantum Neural Networks, Physical Review Letters. (2020) 124, no. 20, https://doi.org/10.1103/physrevlett.124.200504.
10.1103/PhysRevLett.124.200504
Web of Science® Google Scholar
12 Liu Y., Arunachalam S., and Temme K., A Rigorous and Robust Quantum Speed-Up in Supervised Machine Learning, Nature Physics. (2021) 17, 1013–1017.
10.1038/s41567-021-01287-z
CAS Web of Science® Google Scholar
13 Huang H.-Y., Broughton M., Mohseni M. et al., Power of Data in Quantum Machine Learning, Nature Communications. (2021) 12, no. 1, https://doi.org/10.1038/s41467-021-22539-9.
10.1038/s41467-021-22539-9
Web of Science® Google Scholar
14 Jiang J., Zhao Y., Li R. et al., Strong Generalization in Quantum Neural Networks, Quantum Information Processing. (2023) 22.
10.1007/s11128-023-04095-x
Web of Science® Google Scholar
15 Du Y., Hsieh M. H., Liu T., You S., Tao D., and Tao D., Learnability of Quantum Neural Networks, PRX Quantum. (2021) 2, no. 4, https://doi.org/10.1103/prxquantum.2.040337.
10.1103/PRXQuantum.2.040337
PubMed Web of Science® Google Scholar
16 Du Y., Hsieh M. H., Liu T., Tao D., Liu N., and Liu N., Quantum Noise Protects Quantum Classifiers Against Adversaries, Physical Review Research. (2021) 3, no. 2, https://doi.org/10.1103/physrevresearch.3.023153.
10.1103/PhysRevResearch.3.023153
Web of Science® Google Scholar
17 Ren W., Li W., Xu S. et al., Experimental Quantum Adversarial Learning With Programmable Superconducting Qubits, Nature Computational Science. (2022) 2, 711–717.
10.1038/s43588-022-00351-9
PubMed Web of Science® Google Scholar
18 Lloyd S. and Weedbrook C., Quantum Generative Adversarial Learning, Physical Review Letters. (2018) 121.
10.1103/PhysRevLett.121.040502
Web of Science® Google Scholar
19 Hu L., Wu S.-H., Cai W. et al., Quantum Generative Adversarial Learning in a Superconducting Quantum Circuit, Science Advances. (2019) 5, no. 1, https://doi.org/10.1126/sciadv.aav2761, 2-s2.0-85060785009.
10.1126/sciadv.aav2761
Web of Science® Google Scholar
20 Huang K., Wang Z.-An, Song C. et al., Quantum Generative Adversarial Networks With Multiple Superconducting Qubits, Quantum Information. (2021) 7.
Web of Science® Google Scholar
21 Narwane V. S., Gunasekaran A., Gardas B. B., and Sirisomboonsuk P., Quantum Machine Learning a New Frontier in Smart Manufacturing: A Systematic Literature Review From Period 1995 to 2021, International Journal of Computer Integrated Manufacturing. (2025) 38, no. 1, 116–135, https://doi.org/10.1080/0951192x.2023.2294441.
10.1080/0951192X.2023.2294441
Web of Science® Google Scholar
22 Javadi-Abhari A., Treinish M., Krsulich K. et al., Quantum Computing With Qiskit, 2024, https://arxiv.org/abs/2405.08810.
Google Scholar
23 Broughton M., Verdon G., McCourt T. et al., TensorFlow Quantum: A Software Framework for Quantum Machine Learning, 2020, https://arxiv.org/abs/2003.02989.
Google Scholar
24 Xu X., Cui J., Cui Z. et al., MindSpore Quantum: A User-Friendly, High-Performance, and AI-Compatible Quantum Computing Framework, 2024, https://arxiv.org/abs/2406.17248.
Google Scholar
25 Dou M., Zou T., Fang Y. et al., QPanda: High-Performance Quantum Computing Framework for Multiple Application Scenarios, 2022, https://arxiv.org/abs/2212.14201.
Google Scholar
26 Wang H., Ding Y., Gu J., Lin Y., Pan D. Z., and Chong F. T., QuantumNAS: Noise-Adaptive Search for Robust Quantum Circuits, Proceedings of the 2022 IEEE International Symposium on High-Performance Computer Architecture (HPCA), 2022, Seoul, Republic of Korea.
Google Scholar
27 Bergholm V., Izaac J., Schuld M. et al., PennyLane: Automatic Differentiation of Hybrid Quantum-Classical Computations, 2018, https://arxiv.org/abs/1811.04968.
Google Scholar
28 https://github.com/xzphys/LFQAP.
Google Scholar
29 Aho A. V., Lam M. S., Sethi R., and Ullman J. D., Compilers: Principles, Techniques, and Tools, 2026, 2nd edition, Addison-Wesley Longman Publishing Co., Inc.
Google Scholar
30 Schuld M., Bergholm V., Gogolin C., Izaac J., Killoran N., and Killoran N., Evaluating Analytic Gradients on Quantum Hardware, Physical Review A. (2019) 99, no. 3, https://doi.org/10.1103/physreva.99.032331, 2-s2.0-85063268743.
10.1103/PhysRevA.99.032331
Web of Science® Google Scholar
31 LaRose R. and Coyle B., Robust Data Encodings for Quantum Classifiers, Physical Review A. (2020) 102.
10.1103/PhysRevA.102.032420
Web of Science® Google Scholar
32 Kingma D. P. and Ba J., Adam: A Method for Stochastic Optimization, 2017, https://arxiv.org/abs/1412.6980.
Google Scholar
33 https://github.com/AbeerVaishnav13/Quantum-Computing-Library/tree/master.
Google Scholar
34 De Raedt H., Jin F., Willsch D. et al., Massively Parallel Quantum Computer Simulator, Eleven Years Later, Computer Physics Communications. (2019) 237, 47–61.
10.1016/j.cpc.2018.11.005
CAS Web of Science® Google Scholar
35 Markov I. L. and Shi Y., Simulating Quantum Computation by Contracting Tensor Networks, SIAM Journal on Computing. (2008) 38, no. 3, 963–981, https://doi.org/10.1137/050644756, 2-s2.0-54849416233.
10.1137/050644756
Web of Science® Google Scholar
36 Fried E. S., Sawaya N. P. D., Cao Y. et al., qTorch: The Quantum Tensor Contraction Handler, PLoS One. (2018) 13, no. 12, https://doi.org/10.1371/journal.pone.0208510, 2-s2.0-85058215912.
10.1371/journal.pone.0208510
Web of Science® Google Scholar
37 Zhao Ya-Q., Li R.-G., Jiang J.-Z. et al., Simulation of Quantum Computing on Classical Supercomputers With Tensor-Network Edge Cutting, Physical Review A. (2021) 104.
10.1103/PhysRevA.104.032603
Web of Science® Google Scholar
38 Fisher R. A., The Use of Multiple Measurements in Taxonomic Problems, Annals of Eugenics. (1936) 7, 179–188.
10.1111/j.1469-1809.1936.tb02137.x
PubMed Web of Science® Google Scholar
39 William W., Breast Cancer Wisconsin (Original) [Dataset], UCI Machine Learning Repository. (1990) https://doi.org/10.24432/C5HP4Z.
10.24432/C5HP4Z
Google Scholar
40 Li L., Li J., Song Y., Qin S., Wen Q., and Gao F., An Efficient Quantum Proactive Incremental Learning Algorithm, Science China Physics, Mechanics & Astronomy. (2025) 68.
10.1007/s11433-024-2501-4
Web of Science® Google Scholar

All articles

LFQAP: A Lightweight and Flexible Quantum Artificial Intelligence Application Platform

Abstract

1. Introduction