Volume 2025, Issue 1 8503137

Research Article

Open Access

PID Parameter Optimization of Temperature Control for Plastic Extruder Based on ISA-PSO Algorithm

Corresponding Author

Peng-fei Ji

[email protected]

orcid.org/0009-0008-3513-2392

School of Electronics & Electrical Engineering and Unmanned Aerial Vehicle , Anyang Institute of Technology , Anyang , Henan , China , ayit.edu.cn

Search for more papers by this author

Tian-Peng Zhang,

Tian-Peng Zhang

orcid.org/0000-0003-4984-2594

School of Electronics & Electrical Engineering and Unmanned Aerial Vehicle , Anyang Institute of Technology , Anyang , Henan , China , ayit.edu.cn

Search for more papers by this author

Yang Li,

Yang Li

orcid.org/0009-0000-3934-6963

School of Electronics & Electrical Engineering and Unmanned Aerial Vehicle , Anyang Institute of Technology , Anyang , Henan , China , ayit.edu.cn

Search for more papers by this author

Chao Lu,

Chao Lu

orcid.org/0000-0002-9883-1149

School of Electronics & Electrical Engineering and Unmanned Aerial Vehicle , Anyang Institute of Technology , Anyang , Henan , China , ayit.edu.cn

Search for more papers by this author

Peng-fei Ji,

Corresponding Author

Peng-fei Ji

[email protected]

orcid.org/0009-0008-3513-2392

School of Electronics & Electrical Engineering and Unmanned Aerial Vehicle , Anyang Institute of Technology , Anyang , Henan , China , ayit.edu.cn

Search for more papers by this author

Tian-Peng Zhang,

Tian-Peng Zhang

orcid.org/0000-0003-4984-2594

School of Electronics & Electrical Engineering and Unmanned Aerial Vehicle , Anyang Institute of Technology , Anyang , Henan , China , ayit.edu.cn

Search for more papers by this author

Yang Li,

Yang Li

orcid.org/0009-0000-3934-6963

School of Electronics & Electrical Engineering and Unmanned Aerial Vehicle , Anyang Institute of Technology , Anyang , Henan , China , ayit.edu.cn

Search for more papers by this author

Chao Lu,

Chao Lu

orcid.org/0000-0002-9883-1149

School of Electronics & Electrical Engineering and Unmanned Aerial Vehicle , Anyang Institute of Technology , Anyang , Henan , China , ayit.edu.cn

Search for more papers by this author

First published: 15 April 2025

https://doi.org/10.1155/mse/8503137

Academic Editor: Marco Bonopera

Share a link

Email
Wechat
Bluesky

Abstract

In order to improve the control accuracy of the temperature control system for the plastic extruder and better achieve optimal control between the parameter settings and the temperature of the plastic extruder, an intelligent algorithm combining improved simulated annealing (ISA) algorithm and particle swarm optimization (PSO) algorithm is studied. This algorithm is utilized to achieve automatic optimization of the PID parameters of the temperature control system, thereby making parameter optimization faster and more accurate. The benchmark test function was employed to evaluate the performance of the improved PSO (IPSO) algorithm, genetic algorithm improved PSO (GA-PSO), simulated annealing PSO (SA-PSO), and ISA-PSO. The results demonstrated that the ISA-PSO algorithm possesses stronger global optimization capability and superior convergence performance. Finally, MATLAB simulation and experimental test results indicate that, compared to the control effects of IPSO, GA-PSO, and SA-PSO, the PID controller optimized by the ISA-PSO algorithm exhibits better accuracy and robustness. The temperature fluctuation of the charging barrel is significantly reduced, with the maximum value of the absolute temperature deviation being only 0.6°C and the average value of the absolute temperature deviation being approximately 0.35°C. This effectively enhances the accuracy and robustness of the temperature control system for the plastic extruder.

1. Introduction

Plastic products are widely used in industrial and agricultural production, transportation, building materials, and other fields due to their abundant raw materials, low prices, easy processing, and other characteristics [1]. The plastic extruder is the primary equipment for the production and processing of plastic products [2], and its temperature is the prerequisite condition for promoting the plasticization of molding materials and the flow of plastic melt. The precision of temperature control directly determines the quality and performance of plastic products [3]. Therefore, rapidly and accurately controlling the temperature of the plastic extruder has become a key research focus in the plastic extrusion molding process.

Currently, plastic extruders exhibit characteristics such as large inertia, time delay, and nonlinearity in temperature control of plastic melts during operation, which reduces the system’s ability to quickly adjust and steady-state accuracy, making the control effect achieved by standard PID methods not ideal. For the characteristics of the temperature control system, some researchers have made adaptions. For example, Yang et al. [4] constructed an improved genetic algorithm (IGA) and used it to optimize the PID controller parameters of the control loop for the variable air volume air conditioning system. Compared with the conventional PID method, the IGA PID control system has a certain improvement in control accuracy, response speed, and robustness. Jiang [5] introduced the fuzzy neural network (FNN) algorithm into PID parameter tuning and verified the superiority of the FNN PID algorithm through example simulation in the intelligent control of the plastic extruder. In order to improve the control performance and anti-interference ability of the airborne optoelectronic platform, Wang et al. [6] improved the particle swarm optimization (PSO) algorithm from the two aspects of speed and inertia and adjusted the parameters of the PID controller with the PSO algorithm. The simulation results show that the PSO algorithm has a faster rate of convergence and the control performance of the system has been greatly improved. Zhang et al. [7], Shi et al. [8], Zhan and Su [9], He et al. [10], and Ali et al. [11] used the improved sparrow search algorithm (ISSA), improved PSO (IPSO) algorithms, etc., to optimize PID parameters. The introduction of the above individual algorithms has a certain positive effect on the tuning of PID control parameters, but there are still some aspects that need to be improved, such as the number of neurons and hidden layers of neural network which is difficult to determine, and PSO is prone to premature convergence and local optimality. Zhu et al. [12] used the GA-PSO hybrid method to optimize the initial weights of the BP neural network and achieved good control results in the water and fertilizer control system. However, the GA algorithm is difficult to encode the network weights, and its performance is greatly affected by the selection of genetic operators. Shao et al. [13] used the SA-PSO algorithm to optimize the PID parameters of a quadcopter unmanned aerial vehicle control system. The results showed that the algorithm effectively improved the disadvantage of the PSO algorithm being prone to local optima and enhanced the optimization speed and disturbance resistance. The SA algorithm does not require encoding like the GA algorithm and does not require genetic operator selection, but its search space is greatly affected by the cooling function. Therefore, selecting an appropriate cooling function is particularly important.

With the development of artificial intelligence technology, machine learning methods represented by deep learning have been successfully applied in many fields [14, 15]. Wang et al. [16] utilized deep Q-networks and PID algorithms to achieve effective tracking of moving targets, with stronger robustness and generalization. Yang et al. [17] improved the traditional PID controller based on the deep deterministic policy gradient (DDPG) algorithm to adapt to different road conditions and vehicle acceleration and deceleration situations. Although deep learning has shown its own advantages in the field of control, there are still problems such as low sample efficiency, unstable training, and difficulty in balancing exploration and utilization.

Therefore, this paper proposes an improved simulated annealing PSO (ISA-PSO) algorithm to optimize the parameters of PID controller and applies it to the temperature control system of plastic extruders. The main contributions of this paper are as follows:

1.
By improving the cooling function and adding storage elements, the performance of the SA algorithm can be enhanced. The integration of ISA algorithm and PSO algorithm improves the problem of PSO easily getting stuck in local optima, while enhancing the convergence speed and accuracy of particle optimization at the end.
2.
Applying this algorithm to the temperature control of plastic extruders not only solves the problem of PID controller lag in the temperature control system but also improves the accuracy and speed of PID parameter automatic optimization, achieving precise temperature control of plastic extruders.

2. Temperature Control System for Plastic Extruder

The plastic extruder is mainly composed of transmission unit, extrusion unit, and heating and cooling unit. The structure schematic diagram of its charging barrel is shown in Figure 1. During the working process of the plastic extruder, the heater makes the temperature of the charging barrel rise, and the raw material is transformed from particles to melts. The melts are evenly stirred by the screw in the charging barrel and extruded by the die head, and then processed into plastic products after cooling, trimming, and winding.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Structure schematic diagram of the charging barrel.

The structural characteristics of the plastic extruder determine that its temperature control system is a long delay system [18]. Therefore, the temperature control system of the charging barrel is usually described using a second-order model, which is shown in Equation (1).

(1)

where G(s) is the transfer function of the second-order system, K represents the gain coefficient, τ represents the delay time, and T₁ and T₂ are the undetermined coefficients.

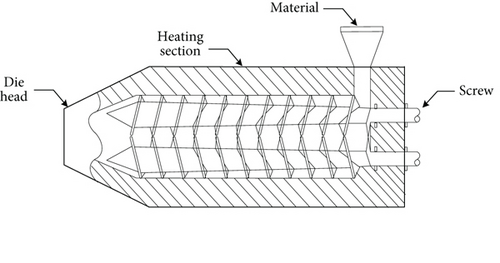
3. SA-PSO Algorithm and Its Improvement

3.1. PSO Algorithm

PSO algorithm is a random search algorithm that seeks for the extreme value in the region by simulating the foraging behavior of birds [19–21]. While the standard PSO algorithm has a fast convergence process, it is easy to reach the local optimal due to the influence of the objective function, resulting in fast convergence speed and low efficiency of the optimization process. In order to speed up the search and reduce the possibility of falling into the local optimal, the weighting factor ω is usually adjusted, and its value is obtained by using the nonlinear adaptive weighting coefficient method, which is shown in Equation (2).

(2)

where f represents the fitness value of the current particles; f_min and f_max are the minimum fitness value and the average fitness value of all current particles, respectively; ω_max represents the maximum of the weighting factor ω; and ω_min represents the minimum of the weighting factor ω.

Even if the value adjusted by using the above method is adopted, the PSO is still easy to fall into the local extremum, so other optimization algorithms need to be adopted to make the PSO jump out of the local optimal.

3.2. SA and Its Improvement

SA algorithm randomly searches to obtain the global optimal solution of the objective function by giving probabilistic jumping in the search process. However, this algorithm also has some shortcomings such as slow convergence speed and difficult parameter adjustment [22, 23]. According to the characteristics of temperature control for the plastic extruder, this study proposes an improved SA algorithm based on the standard SA algorithm.

3.2.1. Improved Cooling Function

The cooling function is one of the main elements in the SA algorithm, which affects the search space of the algorithm. The temperature can make the algorithm conduct global search or local search.

The standard cooling algorithm, as shown in Equation (3), has slow cooling and weak local search ability, which affects the quality of the solution. The rapid cooling algorithm is shown in Equation (4) [24], but the global search time is too short to obtain the global optimal solution.

(3)

(4)

where T₁, T₂ represents the temperature after transformation; T₀ represents the initial annealing temperature; λ represents cooling coefficient; and k represents the number of iteration.

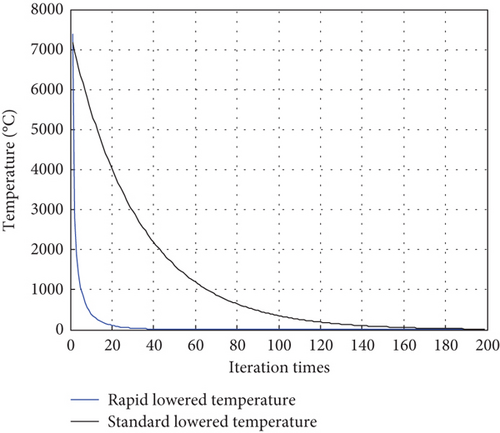
The above two cooling function curves are shown in Figure 2. From the graph, it can be seen that both cooling functions will decrease the quality of the solution.

Therefore, this paper improves the cooling function by introducing a cosine periodic function based on the standard cooling function, adjusting the cooling rate using the cosine function, and achieving tempering during the cooling process. The cosine periodic function is shown as follows:

(5)

where α represents the adjustment coefficient of tempering cycle and gapiter represents the number of floating intervals.

According to the periodic characteristics of cosine function, the period of the function T is as follows:

(6)

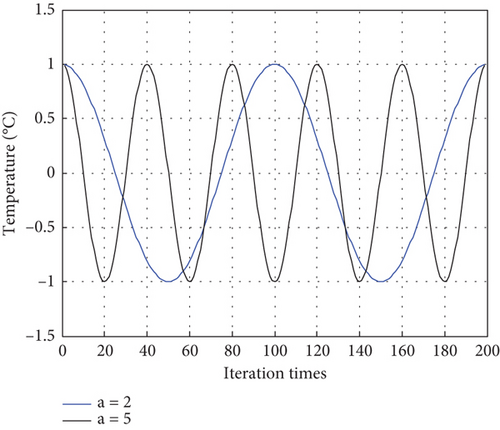
The function curves for different values of α are shown in Figure 3.

Since negative numbers cannot occur during the cooling process, the cosine function has been improved as follows:

(7)

By fusing the cosine function with the standard cooling function, an improved cooling function can be obtained as shown in Equation (8).

(8)

In order to verify the effect of the improved cooling function, standard cooling, rapid cooling, and the cooling function in this paper are selected for comparison, and the cooling curve is shown in Figure 4.

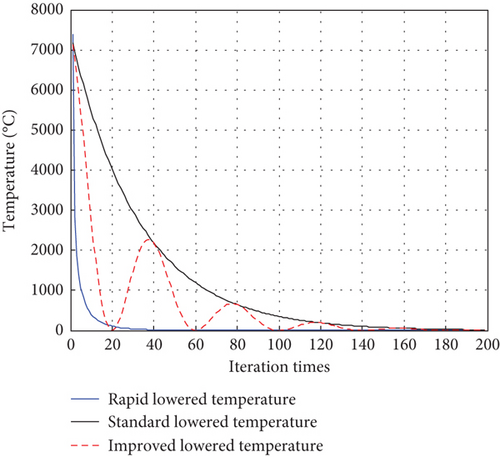
As can be seen from Figure 4, the cooling function in this paper combines the advantages of standard cooling and rapid cooling and adds the tempering process to enhance the global search and local search capabilities of the algorithm. At the same time, the cooling speed and tempering process can be adjusted by adjusting the tempering cycle coefficient.

3.2.2. Add Storage Segment

SA is a heuristic search algorithm that extends local search to global search. This algorithm is based on simulating the solid annealing process, with internal energy simulated as the objective function value f and temperature simulated as the control parameter. During the decreasing process of the algorithm, for each value of temperature T, the solving process is controlled to move towards the optimal direction while accepting inferior solutions with a certain probability, allowing the algorithm to escape from local extremum points. When accepting new solutions, accept them based on probability P_i.

(9)

where f(i) represents the current objective function value and f(i + 1) represents the new objective function value. The algorithm iterates in this way during the search process, effectively avoiding falling into local optima.

In the iterative process of the algorithm, the principle of acceptance criteria may lead to abandoning the optimal solution. Therefore, the memory matrix M and the memory function F are added in the iterative process. At the beginning, the memory matrix M has only element i₀, and F = f(i₀). Each time the new solution j is accepted, F and f(j) are compared. If f(j) < F, then F = f(j), and j is accepted, F will be stored in the memory matrix M. If f(j) > F, then F remains unchanged, and j is accepted, F will not be released into the memory matrix M. After the iteration is completed, the final optimal solution is compared with the historical optimal solution in the memory matrix M to determine the optimal one as the final optimal solution, thereby ensuring that the final solution is in the best state.

Through the above improvements on the traditional SA algorithm, the improved SA algorithm realizes fast cooling in the initial stage and stable cooling in the later stage and includes the tempering process and the memory function, which improves the search accuracy and operation efficiency of the algorithm.

3.2.3. ISA-PSO Algorithm

The PSO algorithm is simple to implement and has strong global search ability. However, during the optimization process, it tends to focus on the current optimal solution, which can lead to getting stuck in local optima. On the other hand, the ISA algorithm is characterized by its heuristic and random search properties, with probabilistic jumping in the search process that helps escape local optima. Taking into account the characteristics of both algorithms comprehensively, this paper proposes the ISA-PSO algorithm, and its flowchart and pseudocode are shown in Figure 5 and Algorithm 1.

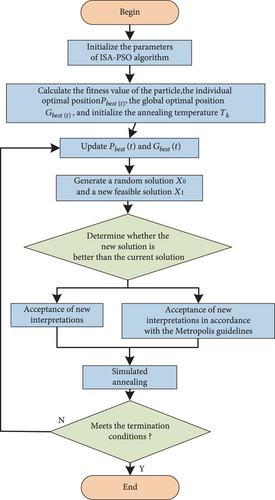
Algorithm 1: ISA-PSO algorithm pseudocode.

Algorithm: ISA-PSO
Input: Initialize the basic parameters of PSO and ISA algorithm, including the Number M, Dimensions D, Iteration times N, Weight factors ω_max and ω_min, Velocity boundary V_max and V_min, and ISA algorithm constants k
Output: Global optimal solution G_best(t)
1 Initialize the basic parameters of PSO and ISA algorithm
2 For i = 1 to M do
3 Initialize position x_i, v_i randomly within range
4 Calculate fitness value f(x_i)
5 Set P_best(t) = x_i
6 end For
7 G_best(t) = min{P_best}
8 For t = 1 to N do
9 For i = 1 to M do
10 Calculate the initial annealing temperature T₀
11 E = f(x_i) − f(x_i+1)
12 if E < 0 or random(0, 1) ≤ P_i then
13 G_best(t) = x_i+1
14 elseG_best(t) = x_i
15 end if
16 Update x_i and v_i
17 Update P_best and G_best
18 end For
19 Update Temperature T
20 t = t + 1
21 end For

The specific steps are as follows:

Step 1: Initialize the position and velocity of each particle in the population.

Step 2: Calculate the fitness value of each particle, and save the individual optimal position in P_best(t) and the global optimal position in G_best(t).

Step 3: Determine the initial annealing temperature T₀.

Step 4: Perform ISA algorithm iteration for P_best(t) of each particle, perform optimal operation, and update P_best(t) of each particle and G_best(t) of the population.

Step 5: Conduct cooling operation according to Equation (5).

Step 6: When the algorithm meets the termination conditions, stop searching, and output the results. Otherwise, return to Step 4 to continue searching.

3.3. PID Controller Design of ISA-PSO Algorithm

The PID controller takes the deviation e(t) between the input value r(t) and the output value y(t) as the input of the controller, as shown in the following equation:

(10)

The control strategy of PID is as follows:

(11)

where K_p is the proportionality coefficient, K_i is the integral time constant, and K_d is the differential time constant.

Let the number of searchers in the population be S, and the position vector of each particle is composed of three control parameters of the PID controller. The population can be represented by a matrix:

(12)

Using the ISA-PSO algorithm, the individual and global extreme values of the searcher are continuously calculated and updated through the fitness function value, ultimately finding the optimal solution for the three parameters K_p, K_i, and K_d to ensure the optimal performance of the temperature control system. The system control structure is shown in Figure 6.

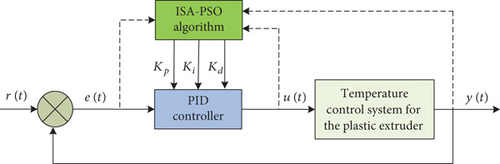
4. System Simulation Test and Experiment

4.1. Algorithm Performance Testing

Before applying the ISA-PSO algorithm to practical engineering, the performance of the algorithm is tested based on four benchmark test functions [25]. Among them, the sphere function is a typical single-peak function with only one extreme point; Rosenbrock has a global minimum point, but it is a pathological function, and it is difficult for the general algorithm to converge to this extreme point; Rastrigin and Griewank are multipeak functions with multiple local minimum points in the solution space. The function expression and parameter range of each test function are shown in Table 1.

Table 1. Standard test functions.

Function name	Displayed formula	Parameter range
Sphere		[−100, 100]
Rosenbrock		[−30, 30]
Rastrigin		[−5.12, 5.12]
Griewank		[−600, 600]

IPSO algorithm [26], GA-PSO [12] algorithm, SA-PSO [13] algorithm, and ISA-PSO algorithm are used as comparison objects for the experiment. The simulation software was MATLAB 2018b, and the computer configuration was Intel Core i7-7700HQ CPU @ 2.80 GHz, the memory is 8 GB, and the operating system is Windows 10. In order to ensure fairness, the parameter settings of each PSO algorithm are basically the same, with the number of particles set to 50 and the number of iterations set to 100. In order to reduce the impact of the randomness of the algorithms on the test results, each algorithm is run independently for each test function for 30 times. The mean and standard deviation based on the error are used to evaluate the convergence accuracy: The mean reflects the optimization ability of the algorithm, while the standard deviation reflects the stability of the algorithm. The running results are shown in Table 2.

Table 2. Algorithm operation results.

Test function	Algorithm	Average value	Standard deviation
Sphere	IPSO	1.22e−02	2.92e−02
	GA-PSO	1.22e+02	2.47e+02
	SA-PSO	8.71e−04	1.89e−04
	ISA-PSO	4.65e−08	2.07e−08

Rosenbrock	IPSO	2.79e−01	4.94e−01
	GA-PSO	1.36e+00	2.57e+00
	SA-PSO	1.42e−02	2.41e−02
	ISA-PSO	6.85e−06	3.04e−06

Rastrigin	IPSO	1.91e+01	2.05e+01
	GA-PSO	7.48e+02	1.28e+02
	SA-PSO	1.46e+00	1.62e+01
	ISA-PSO	8.63e−02	6.59e−02

Griewank	IPSO	2.77e−01	2.06e−01
	GA-PSO	1.92e+00	1.15e+00
	SA-PSO	2.55e−02	2.54e−02
	ISA-PSO	1.24e−03	5.54e−03

As can be seen from Table 2, in the process of optimizing four functions, the optimization performance of ISA-PSO algorithm is superior to the other three algorithms, and the optimization accuracy has been improved by one to four orders of magnitude. The above indicates that ISA-PSO algorithm can effectively overcome the disadvantage of PSO algorithm being prone to falling into local optima, and the optimization ability and efficiency have been effectively improved. In the multipeak complex test function Rastrigin and Griewank, the ISA-PSO algorithm has higher convergence accuracy and more stable iteration results than the other three algorithms, indicating that the ISA-PSO algorithm has stronger global optimization ability and better robustness. So both in single-peak and multipeak functions, the proposed ISA-PSO hybrid algorithm exhibits superior optimization performance compared to the other three algorithms. The convergence of IPSO algorithm, GA-PSO algorithm, SA-PSO algorithm, and ISA-PSO algorithm in solving the test function is shown in Figure 7.

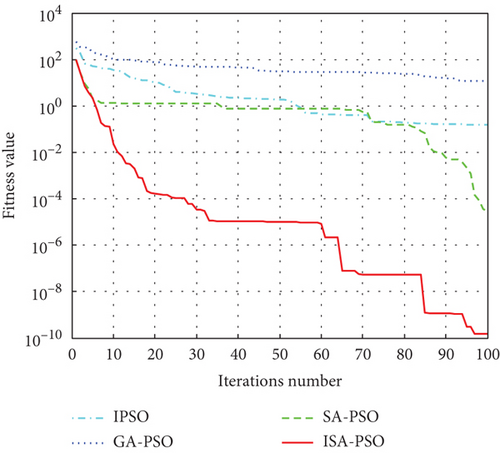
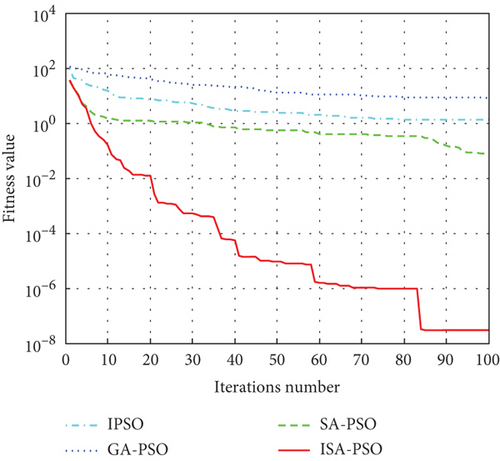
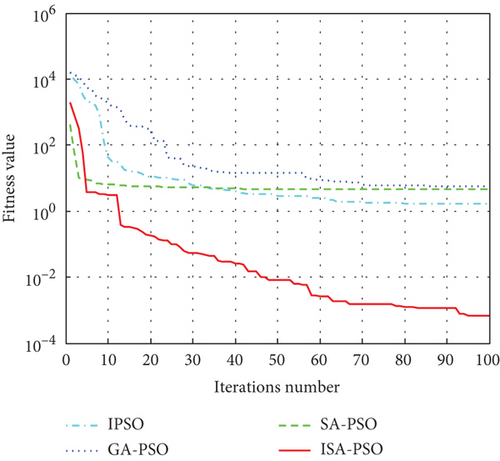
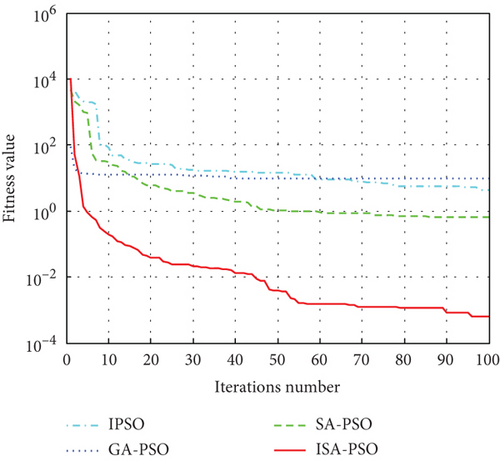
From Figure 7, it can be seen that compared with IPSO algorithm, GA-PSO algorithm, and SA-PSO algorithm, ISA-PSO algorithm can find the solution of the test function quickly and has better convergence performance.

To further evaluate the performance of the ISA-PSO algorithm, different population sizes were used to test the optimization efficiency of the algorithm. Set the population size to 20, 50, 80, and 100, respectively, and use the ISA-PSO algorithm to optimize and solve the four functions. The simulation results are shown in Figure 8.

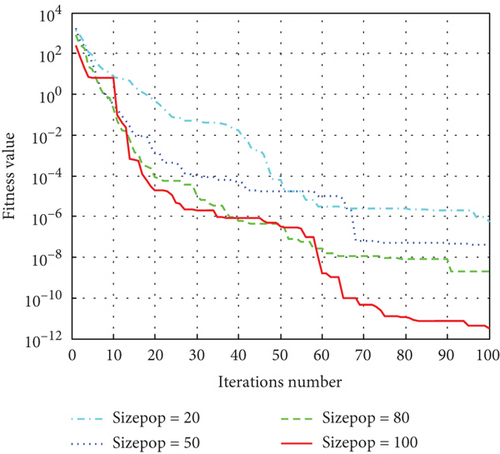
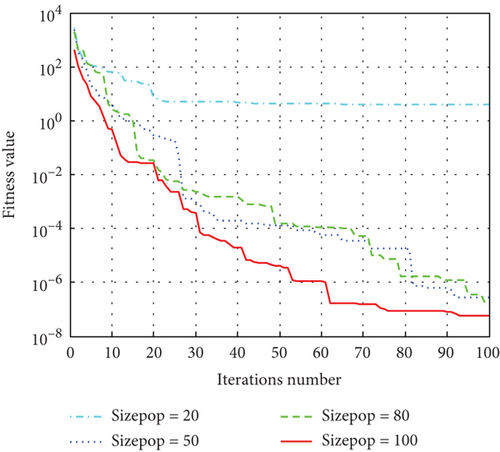
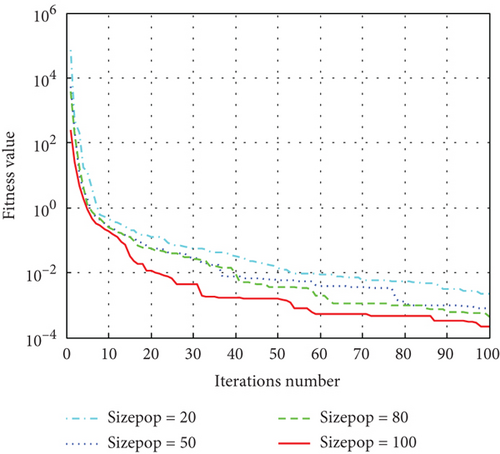
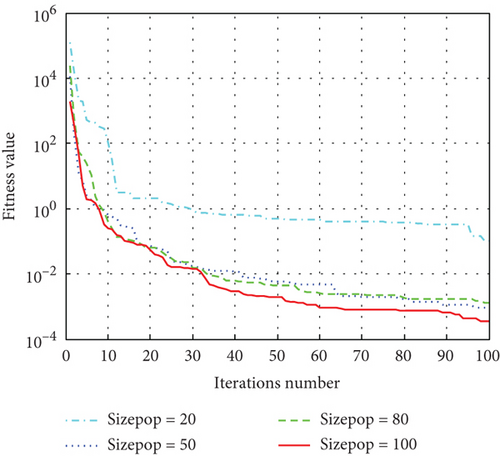
From the Figure 8, it can be seen that ISA-PSO algorithms with different population sizes converge after about 80 iterations. The higher the population size, the more concentrated the convergence curve of the algorithm, indicating that the stability of the algorithm is also higher. Comparing Figures 8a, 8b, 8c, and 8d, it is found that the maximum convergence algebra of the algorithm decreases with the increase of the population size. However, the larger the population size, the longer the convergence time of the algorithm. If the population size is too small, it will reduce the diversity of the population, and there is a risk of falling into local optima. If the problem requires high convergence time for the algorithm, it tends to choose a smaller population size.

4.2. Simulation Test

In order to prove the effectiveness of this research method, it is applied to the temperature control system for the plastic extruder. Using the temperature change data of the integral charging barrel in the SHJ series of twin-screw extruder made by a company [27], the control system transfer function between the temperature of the charging barrel (T) and the power of the electric heater (P) is obtained through the system identification and analysis combined with Equation (1), which is shown in Equation (13).

(13)

Under the control of the traditional PID method, the temperature change curve of the charging barrel is shown in Figure 9, which is mainly divided into heating stage and insulation stage. The temperature rises rapidly in the heating stage and slowly after approaching the set temperature. The system does not have good adjustment ability for environmental changes, and the adjustment time is long. During this period, the system cannot meet the production quality requirements. In order to improve the system performance, it is necessary to continuously adjust the parameters K_p, K_i, and K_d based on experience. The adjustment process is complex, and the accuracy is not high. In addition, the parameters need to be readjusted every time when the production is adjusted, which increases the time and cost of production and maintenance. Therefore, it is necessary to use optimization algorithm to optimize PID parameters.

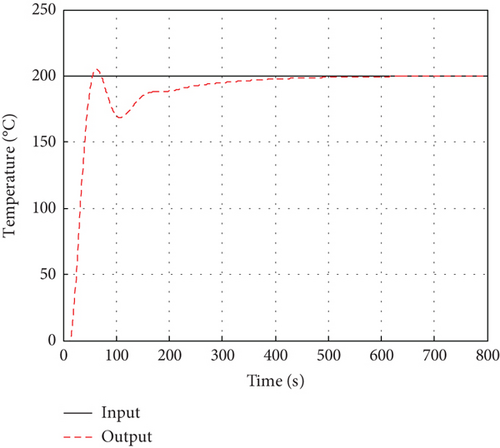
The simulation experiments were carried out in MATLAB software. After multiple tests, the maximum number of iteration in the PSO algorithm was 100, the particle swarm size was 50, the maximum inertia weight was 0.9, and the minimum inertia weight was 0.1.

The initial temperature in ISA algorithm satisfies the following function:

(14)

where P_g represents the global optimum in PSO algorithm and k is a random number, which is selected as 5 after multiple tests.

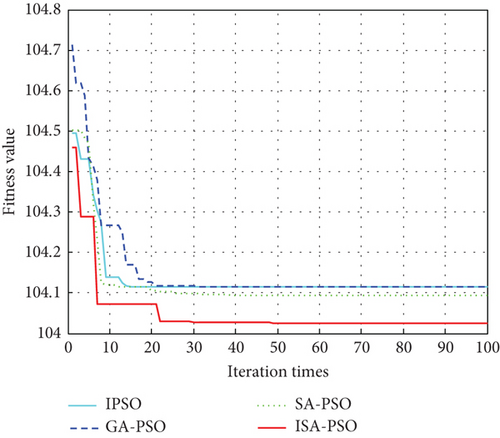
The simulation results of the IPSO, GA-PSO, SA-PSO, and ISA-PSO are compared and analyzed, and the change curves of fitness value are shown in Figure 10. The four algorithms all achieve fast convergence within the number of iteration, but the convergence speed and accuracy of the ISA-PSO algorithm are obviously more advantageous.

Given the step signal for the temperature control system, the steady-state value of the system is set as 200°C according to the actual working condition of the temperature control system for the plastic extruder. The parameters K_p, K_i, and K_d optimized by the three algorithms are, respectively, brought into the control system, and the simulation results are shown in Figure 11.

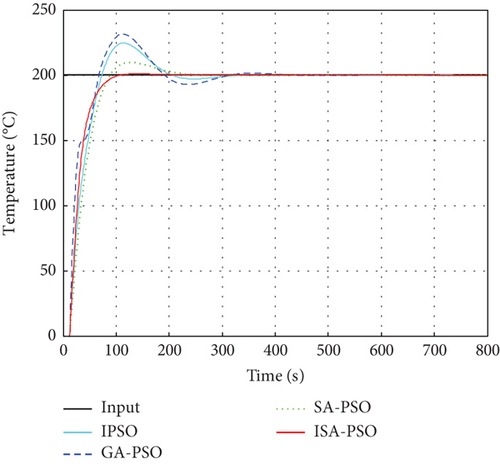
As can be seen from Figure 11, all four algorithms optimized controllers can make the system achieve stable output results: GA-PSO and IPSO algorithms make the control system output response about 15.79% and 12.31% dynamic overshooting, respectively, and reach a stable state in about 280 s; SA-PSO algorithm reduces the dynamic overshooting of the control system output response to about 4.91% and reaches a stable state in about 211 s; and ISA-PSO algorithm can reduce the overshoot response of the control system to only 0.54%, and it can reach a stable state in about 93 s without any shaking phenomenon, greatly improving the output response speed and accuracy of the control system. The performance indicators under different algorithms are shown in Table 3.

Table 3. Performance indicators under different algorithms.

Control algorithm	Rise time t/s	Overshoot σ /%	Settling time t/s
IPSO	61.34	12.31%	268.58
GA-PSO	59.47	15.79%	294.13
SA-PSO	69.35	4.91%	211.46
ISA-PSO	56.12	0.54%	93.88

To further verify the improved anti-interference performance of the ISA-PSO algorithm optimized control system, interference signals with pulse width of 50 s and amplitudes of 10%, 20%, and 30% of the set values were added to the system input at t = 400 s, as shown in Figure 12.

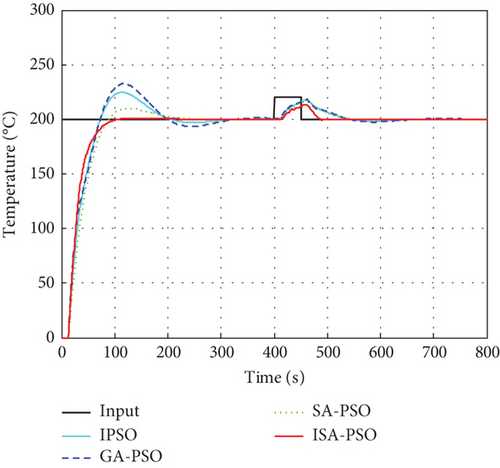
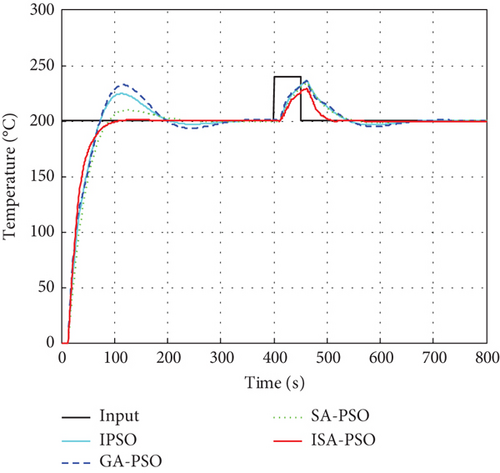
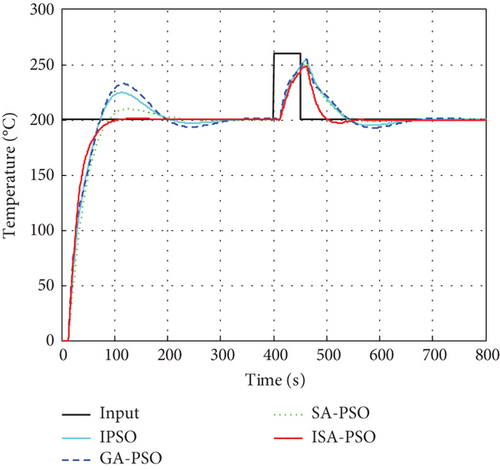
From Figure 12a, it can be seen that the control systems optimized by the four algorithms will produce certain oscillations after being disturbed, resulting in dynamic overshoot in the system output. However, the dynamic overshoot generated by the ISA-PSO algorithm is the smallest among the four methods and can stabilize the system output in 90.27 s. From Figure 12b, it can be seen that under 20% interference, the control effect of the ISA-PSO algorithm optimized control system is still better than the other three algorithms, and the system output can be stabilized in 102.42 s. From Figure 12c, it can be seen that as the amplitude of the interference signal increases, the control effect of the ISA-PSO algorithm oscillates, and the adjustment time further increases. After 136.12 s, the system output tends to stabilize, but the control effect is still the best. The specific performance indicators are shown in Table 4. The above results indicate that the control system optimized by the ISA-SPO algorithm has stronger robustness, which presents a good control effect on the temperature control of plastic extruders.

Table 4. Performance indicators of algorithms under different interferences.

Disturbance signal	Control algorithm	Overshoot σ /%	Settling time t/s
10%	IPSO	9.21%	118.25
	GA-PSO	9.88%	129.53
	SA-PSO	8.61%	124.18
	ISA-PSO	6.77%	90.27

20%	IPSO	18.41%	223.87
	GA-PSO	18.21%	239.51
	SA-PSO	17.22%	138.05
	ISA-PSO	14.55%	102.42

30%	IPSO	27.61%	237.78
	GA-PSO	27.82%	248.93
	SA-PSO	25.82%	173.44
	ISA-PSO	24.32%	136.12

4.3. Algorithm Experiment Test

In order to further verify the effectiveness of the ISA-PSO algorithm, an intelligent PID control platform was established, which could collect the charging barrel temperature by using thermocouple sensor and transmit the collected temperature signal to the acquisition module of the PLC through the transmitter. The PLC controller changes the output signal through the intelligent algorithm according to the difference between the sampling value and the set value of the temperature, thus realizing the control of the charging barrel temperature. The hardware structure diagram of the control system is shown in Figure 13.

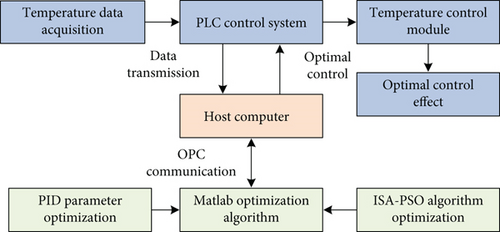
The experimental verification of the selected plastic extruder in the paper was carried out. The charging barrel temperature of the plastic extruder was set at 200.0°C. The temperature was, respectively, controlled by the IPSO algorithm, the GA-PSO algorithm, the SA-PSO algorithm, and the ISA-PSO algorithm. The charging barrel temperature was collected at regular intervals for real-time detection, recording, and comparison. The results are shown in Table 5.

Table 5. Experimental results.

IPSO algorithm		GA-PSO algorithm		SA-PSO algorithm		ISA-PSO algorithm
Actual value	Absolute deviation	Actual value	Absolute deviation	Actual value	Absolute deviation	Actual value	Absolute deviation
201.6	1.6	202.6	2.6	200.6	0.6	200.1	0.1
200.8	0.8	202.9	2.9	201.6	1.6	200.4	0.4
201.7	1.7	198.6	1.4	200.4	0.4	199.7	0.3
202.8	2.8	196.4	3.6	199.3	0.7	199.5	0.5
203.8	3.8	198.9	1.1	198.5	1.5	199.7	0.3
202.8	2.8	203.4	3.4	198.9	1.1	200.6	0.6
201.6	1.6	202.4	2.4	200.5	0.5	200.4	0.4
198.6	1.6	201.8	1.8	201.8	1.8	200.3	0.3
198.3	1.7	198.6	1.4	201.7	1.7	199.7	0.3
198.6	1.4	198.3	1.7	200.5	0.5	200.3	0.3
Average value	1.98	Average value	2.23	Average value	1.04	Average value	0.35

It can be seen from Table 5 that the charging barrel temperature in the GA-PSO and IPSO algorithms fluctuates greatly, the maximum value of the absolute temperature deviation is 3.8°C, and the average value of the absolute temperature deviation is about 2°C. In the SA-PSO algorithm, the temperature fluctuation is slightly improved, and the maximum value and the average value of the absolute temperature deviation are 1.8°C and 1.04°C, respectively. In the ISA-PSO algorithm, the temperature fluctuation becomes significantly smaller, and the maximum value and the average value of the absolute temperature deviation are 0.6 °C and 0.35°C, respectively. This indicates that the temperature control effect of the ISA-PSO algorithm is relatively ideal, which can significantly improve the accuracy of temperature control. For a complete list of symbols and abbreviations, refer to Appendix A.

5. Conclusion

Based on the intelligent algorithm and the temperature control system for the plastic extruder, an optimization control method of PID parameters based on ISA-PSO algorithm is proposed.

1.
The ISA-PSO algorithm effectively combines the strengths of both the ISA and PSO algorithms. This integration enhances the accuracy and timeliness of the PID controller. The proposed method has been validated through simulations in MATLAB and experimental platforms.
2.
The simulation results of the ISA-PSO algorithm were compared with IPSO algorithm, GA-PSO algorithm, and SA-PSO algorithm. The findings indicate that the ISA-PSO algorithm effectively leverages the benefits of ISA and PSO algorithms, significantly improving the optimization process in terms of speed and accuracy. The optimized PID controller can reduce the overshoot response of the plastic extruder temperature control system to only 0.54%, and it can reach a stable state in about 93 s without any shaking phenomenon, which is at least 118 s faster than the other three methods. Under interference, the overshoot was lower than the other three methods, and the adjustment time was shortened by at least 30 s. This reduction effectively mitigates the impact of interference on the control system, further enhances the system’s robustness, and enables precise temperature control of plastic extruders, demonstrating practical value.
3.
With the continuous advancement of intelligent algorithms, the accuracy and stability of PID control systems based on these algorithms can be expected to improve. This will enable better adaptation to diverse application scenarios, further enhancing the performance and reliability of plastic extruder temperature control systems.

In summary, the ISA-PSO algorithm offers significant improvements in PID parameter optimization for plastic extruder temperature control systems, demonstrating superior performance in terms of speed, accuracy, and robustness compared to other algorithms. This approach holds promise for practical applications in the field of plastic extrusion. With the emergence of innovative technologies such as artificial intelligence, cloud computing, and big data, future work will consider using machine learning algorithms to tune the PID parameters of control systems, utilizing the powerful self-learning characteristics of machine learning algorithms to reduce the dependence on system models during the optimization process, thereby achieving better control effects in the optimization control of more complex systems.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This work was supported by the Key Problems in Science and Technology of Henan Provincial (232102210049, 242102240114, and 252102240115) and the Key Discipline of Henan Province (Electronic Information).

Acknowledgments

Appendix A

Table A1. List of symbols and abbreviations with explanations.

Serial number	Symbols and acronyms	Elaboration
1	PSO	Particle swarm optimization
2	SA	Simulated annealing
3	IPSO	Improved particle swarm optimization
4	ISA	Improved simulated annealing
5	GA-PSO	Genetic algorithm improved particle swarm optimization
6	SA-PSO	Simulated annealing particle swarm optimization
7	ISA-PSO	Improved simulated annealing particle swarm optimization
8	IGA	Improved genetic algorithm
9	FNN	Fuzzy neural network
10	ISSA	Improved sparrow search algorithm
11	DDPG	Deep deterministic policy gradient
12	Equation (1)	G(s) is the transfer function of the second order system, K represents the gain coefficient, τ represents the delay time, and T₁ and T₂ are the undetermined coefficients
13	Equation (2)	f represents the fitness value of the current particles; f_min and f_avg are the minimum fitness value and the average fitness value of all current particles, respectively; ω_max represents the maximum of the weighting factor ω; and ω_min represents the minimum of the weighting factor ω
14	Equations (3)–(4)	T₁, T₂ represents the temperature after transformation, T₀ represents the initial annealing temperature, λ represents cooling coefficient, and k represents the number of iteration
15	Equations (5)–(8)	α represents the adjustment coefficient of tempering cycle and gapiter represents the number of floating intervals
16	Equation (9)	f(i) represents the current objective function value and f(i + 1) represents the new objective function value
17	Equation (10)	r(t) is the input value, y(t) is the output value, and e(t) is the deviation
18	Equation (11)	K_p is the proportionality coefficient, K_i is the integral time constant, and K_d is the differential time constant
19	Equation (12)	S is the number of searchers in the population

Open Research

Data Availability Statement

The data that support the findings of this study are available on request from the corresponding author. The data are not publicly available due to privacy or ethical restrictions.

References

1 Wu Z. M., Research on automation control in injection molding, China Plastics Industry. (2019) 47, no. 2, 89–91, https://doi.org/10.3969/j.issn.1005-5770.2019.02.018.
10.3969/j.issn.1005-5770.2019.02.018
Google Scholar
2 Xiao S. C., Zhang Q., and Peng L., Temperature control strategy of plastic extruder based on matrix FIR filter, Plastics Science and Technology. (2022) 48, no. 5, 99–102, https://doi.org/10.15925/j.cnki.issn1005-3360.2020.05.024.
10.15925/j.cnki.issn1005-3360.2020.05.024
Google Scholar
3 Zhang Y. S., Fuzzy PID control of temperature in plastic extruder, China Synthetic Resin and Plastics. (2019) 36, no. 5, 88–90, https://doi.org/10.3969/j.issn.1002-1396.2019.05.021.
10.3969/j.issn.1002-1396.2019.05.021
CAS Google Scholar
4 Yang S. Z., Sun C. G., and Li S. W., Optimization control of VAV air conditioning system based on improved genetic algorithm, Computer Simulation. (2021) 38, no. 11, 230–234, https://doi.org/10.3969/j.issn.1006-9348.2021.11.047.
10.3969/j.issn.1006-9348.2021.11.047
Google Scholar
5 Jiang Z. Y., Application of fuzzy neural network PID algorithm in intelligent control of plastic extruder, China Plastics Industry. (2019) 47, no. 3, 69–72, https://doi.org/10.3969/j.issn.1005-5770.2019.03.016.
10.3969/j.issn.1005-5770.2019.03.016
Google Scholar
6 Wang H. C., Li W., Zhao K. J., and Shen X. Y., Fractional order control of airborne optoelectronic platform based on improved PSO algorithm, Electronics Optics & Control. (2023) 30, no. 4, 83–87, https://doi.org/10.3969/j.issn.1671-637x.2023.04.016.
10.3969/j.issn.1671-637x.2023.04.016
Google Scholar
7 Zhang Z. H., Zhou K. H., and Zhu M. Y., Lower limb rehabilitation robot control based on PID optimized by ISSA, Modern Electronics Technique. (2024) 13, 153–159, https://doi.org/10.16652/j.issn.1004-373x.2024.13.027.
10.16652/j.issn.1004-373x.2024.13.027
Google Scholar
8 Shi L. L., Gong J. H., and Zhai C. J., Application of a hybrid PSO-GA optimization algorithm in determining pyrolysis kinetics of biomass, Fuel. (2022) 323, 124344, https://doi.org/10.1016/j.fuel.2022.124344.
10.1016/j.fuel.2022.124344
CAS Web of Science® Google Scholar
9 Zhan C. S. and Su L. Q., PID control strategy of active suspension based on particle swarm optimization, Science Technology and Engineering. (2022) 10, 4180–4186, https://doi.org/10.3969/j.issn.1671-1815.2022.10.044.
10.3969/j.issn.1671-1815.2022.10.044
Google Scholar
10 He C. L., Xu X. L., Zhang X. W., Zhang Y. B., and Li J. Y., PID parameters tuning of rotary inverted pendulum based on improved particle swarm optimization algorithm, Techniques of Automation and Applications. (2021) 12, 10–15, https://doi.org/10.3969/j.issn.1003-7241.2021.12.003.
10.3969/j.issn.1003-7241.2021.12.003
Google Scholar
11 Ali H. H., Elbasuony G. S., and Kamal N. A., Control of the rated production power of DFIG-wind turbine using adaptive PSO and PI conventional controllers, International Journal of Automation and Control. (2022) 16, no. 2, 219–249, https://doi.org/10.1504/IJAAC.2022.121134.
10.1504/IJAAC.2022.121134
Web of Science® Google Scholar
12 Zhu F. L., Zhang L. X., Hu X., Zhao J. W., and Zheng Y., Research and design of hybrid optimized backpropagation (BP) neural network PID algorithm for integrated water and fertilizer precision fertilization control system for field crops, Agronomy. (2023) 13, no. 5, https://doi.org/10.3390/agronomy13051423.
10.3390/agronomy13051423
Google Scholar
13 Shao K. Y., Liu J. X., and Li M. X., Fractional order PID control of quadrotor UAV based on SA-PSO algorithm, Proceedings of the Third International Conference on Computer Science and Communication Technology (ICCSCT 2022), 2022, Beijing, China, https://doi.org/10.1117/12.2662180.
10.1117/12.2662180
Google Scholar
14 Noorizadegan A., Cavoretto R., Young D. L., and Chen C. S., Stable weight updating: a key to reliable PDE solutions using deep learning, Engineering Analysis with Boundary Elements. (2024) 168, 105933, https://doi.org/10.1016/j.enganabound.2024.105933.
10.1016/j.enganabound.2024.105933
Web of Science® Google Scholar
15 Raissi M., Perdikaris P., and Karniadakis G. E., Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations, Journal of Computational Physics. (2018) 378, 686–707, https://doi.org/10.1016/j.jcp.2018.10.045, 2-s2.0-85057501376.
10.1016/j.jcp.2018.10.045
Google Scholar
16 Wang F., Ren B. M., Liu Y., and Cui B., Tracking moving target for 6 degree-of-freedom robot manipulator with adaptive visual servoing based on deep reinforcement learning PID controller, Review of Scientific Instruments. (2022) 93, no. 4, 045108, https://doi.org/10.1063/5.0087561.
10.1063/5.0087561
CAS PubMed Web of Science® Google Scholar
17 Yang J. R., Peng W. F., and Sun C., A learning control method of automated vehicle platoon at straight path with DDPG-based PID, Electronics. (2021) 10, no. 21, https://doi.org/10.3390/electronics11040617.
10.3390/electronics10212580
PubMed Web of Science® Google Scholar
18 Zhang P., Intelligent Production Technological Parameter Optimization Design of Plastic Extrusion Unit Based on Expert System, 2017, Guangdong University of Technology, https://doi.org/10.7666/d.D01243185.
Google Scholar
19 Lin S. W., Liu A., Wang J. G., and Kong X. Y., An intelligence-based hybrid PSO-SA for mobile robot path planning in warehouse, Journal of Computational Science. (2023) 67, 101938, https://doi.org/10.1016/j.jocs.2023.102183.
10.1016/j.jocs.2022.101938
Web of Science® Google Scholar
20 Yang X. G., Zhang Q. S., Zhang Y. M., and Sheng G. J., Research on cloud computing task scheduling problem based on improved hybrid particle swarm optimization, Acta Scientiarum Naturalium Universitatis Neimongol. (2019) 50, no. 6, 674–678, https://doi.org/10.13484/j.nmgdxxbzk.20190615.
10.13484/j.nmgdxxbzk.20190615
Google Scholar
21 Jing L. and Shi C., Parameter settings in particle swarm optimisation algorithms: a survey, International Journal of Automation and Control. (2022) 16, no. 2, 164–182, https://doi.org/10.1504/ijaac.2022.10044251.
10.1504/IJAAC.2022.121124
Google Scholar
22 Sun J., Liu S. Z., Wu X. X., and Wu S. M., Solving TSP based on spark-based parallel simulated annealing algorithm, Electric Measurement Technology. (2022) 45, no. 4, 53–58, https://doi.org/10.19651/j.cnki.emt.2108429.
10.19651/j.cnki.emt.2108429
Google Scholar
23 Yan Q. M., Ma R. Q., Ma Y. X., and Wang J. J., Adaptive simulated annealing particle swarm optimization algorithm, Journal of Xidian University. (2021) 48, no. 4, 120–127, https://doi.org/10.19665/j.issn1001-2400.2021.04.016.
10.19665/j.issn1001-2400.2021.04.016
Google Scholar
24 Wang J. C., Chen Z. B., and Jiang H. Y., Based on successive very fast simulated annealing and the grid subdivision of micro seismic localization algorithm research, Science Technology and Engineering. (2017) 17, no. 33, 248–252, https://doi.org/10.3969/j.issn.1671-1815.2017.33.037.
10.3969/j.issn.1671-1815.2017.33.037
Google Scholar
25 Cheng R., Jin Y., Olhofer M., and Sendhoff B., Test problems for large-scale multiobjective and many-objective optimization, IEEE Transactions on Cybernetics. (2017) 47, no. 12, 4108–4121, https://doi.org/10.1109/TCYB.2016.2600577, 28113614.
10.1109/TCYB.2016.2600577
PubMed Web of Science® Google Scholar
26 Liu J. J., Wu H. R., and Ji M. X., Multi strategy improvement particle swarm optimization AGV fuzzy PID control, Machine tools & Hydraulics. (2024) 52, no. 9, 44–51, https://doi.org/10.3969/j.issn.1001-3881.2024.09.007.
10.3969/j.issn.1001-3881.2024.09.007
Google Scholar
27 Li Y., Lan W. M., and Zhang M. J., Temperature control algorithm of plastic extruder based on improved lattice joint processor, Plastics Science and Technology. (2020) 48, no. 12, 121–124, https://doi.org/10.15925/j.cnki.issn1005-3360.2020.12.029.
10.15925/j.cnki.issn1005-3360.2020.12.029
Google Scholar

All articles

PID Parameter Optimization of Temperature Control for Plastic Extruder Based on ISA-PSO Algorithm

Abstract

1. Introduction

2. Temperature Control System for Plastic Extruder