This paper introduces a compact dual-band band-pass filter using single multimode (TE₁₀₁, TE₁₀₂, TE₂₀₁, and TE₂₀₂) substrate-integrated waveguide (SIW) cavity with independent controllable fractional bandwidth (FBW) using metallic vias and slot perturbations. A via is placed at the center of the cavity, to shift the TE₁₀₁ mode towards the TE₁₀₂ mode which forms the Passband I with a center frequency (CF) of 16.2 GHz and a FBW of 1.71%. Two vias and slots are positioned and adjusted to shift the TE₂₀₁ mode and TE₂₀₂ mode, respectively, to achieve the Passband II with a CF of 19.1 GHz and an FBW of 3.09%. The measured insertion loss (IL) of the proposed filter is 1.8 dB for the Passband I and 1.9 dB for the Passband II.

1. Introduction

Multiband band-pass filters (BPFs) are indispensable components in advanced wireless communication systems, fulfilling the crucial role of managing signals across diverse frequency bands and addressing the intricate challenges posed by modern communication technologies. Various technologies can be employed to implement these filters, each with its own merits and drawbacks. A waveguide with a high Q-factor can handle high power in high-frequency applications. However, their nonplanar structures present integration challenges with planar circuits. Conversely, microstrip filters offer a compact size and ease of integration with other planar circuits. But, their Q-factor typically lags behind that of waveguide. SIW technology strikes a balance between these approaches featuring a planar structure, facilitating seamless integration with other planar circuits. They offer a moderate Q-factor and the ability to handle moderate power levels exhibiting relatively low losses, particularly in high-frequency ranges.

Various methods are proposed for achieving dual-band filters. One approach combines two separately designed BPFs to produce a dual-band passband response [1]. However, the overall size increases. Multi-BPF is achieved through coupling matrix synthesis techniques [2], and this approach is specifically tailored for BPFs with closely spaced adjacent passbands, potentially resulting in larger sizes.

Complementary split-ring resonators (CSRRs) are introduced in the cavity for dual-band frequency response [3–5]. However, it is important to note that such circuits may incur higher insertion losses (ILs). The SIW square cavity was coupled with an E-shaped slot line resonator to achieve a dual passband [6, 7]. Nevertheless, it is crucial to acknowledge that the inclusion of slot lines introduces radiation losses into the structure. Two defected ground structures (DGSs) were incorporated on the above and below surfaces of the SIW cavity to create a dual-band [8]. DGS introduces an increase in IL.

A wideband BPF is obtained using a comb-slotted SIW cavity using a multimode [9]. The dual-band BPF is achieved based on CSRR and multimode cavity [10, 11]. The dual-band BPF is obtained using multilayer dual-mode [12]. Dual-band SIW using cross-coupling via a half-mode BPF [13].

This paper introduces the dual-band BPF design utilizing the SIW cavity’s multimode property. The perturbation of the fundamental mode (TE₁₀₁) and the next three higher modes (TE₁₀₂, TE₂₀₁, and TE₂₀₂) of the SIW cavity is achieved by placing via-holes where the electric field of TE₁₀₁ and TE₂₀₁ is maximum and slots are placed at TE₂₀₂ where the electric field is minimum. The positions and dimensions of the via-holes and slots are optimized using EM simulations in Ansys HFSS to achieve the desired dual passband response, as briefly explained in the following section.

2. Dual-Band SIW Filter Design

2.1. Filter Specifications

Two center frequencies (CFs) are chosen at f₀₁ = 16.2 GHz (Passband I) and f₀₂ = 19.1 GHz (Passband II) with a fractional bandwidth (FBW) of 1.96% and 3.14%. The return loss for each frequency is set to be at −20 dB. The second-order g-parameters of the low-pass prototype for Chebyshev response are given as

()

Q_e1(Q_e1) is the external quality factor, M₁(M₂) is the coupling coefficients between the modes, and their theoretical values for each passband are Q_e1 (33.8), Q_e2 (20.8), M₁ (0.032), and M₂ (0.053), respectively, which are calculated using (1) [14].

2.2. Filter Design

The dual-band SIW filter, as proposed in this paper, is illustrated in Figure 1, and the coupling topology is presented in Figure 2. The resonant frequency of TE_m0n is determined using the provided relations (2) and (3) [15]:

()

where a_eff and b_eff are the effective width and length of the cavity, p is the pitch distance between the two adjacent vias, and d is the diameter of the via. The cavity is designed at f₁₀₁ = 10 GHz using the dielectric substrate Rogers RT/Duroid 5880 with a dielectric constant of the substrate ε_r = 2.2, height = 0.51 mm, and loss tangent = 0.0009.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Schematic of the proposed dual-band band-pass filter.

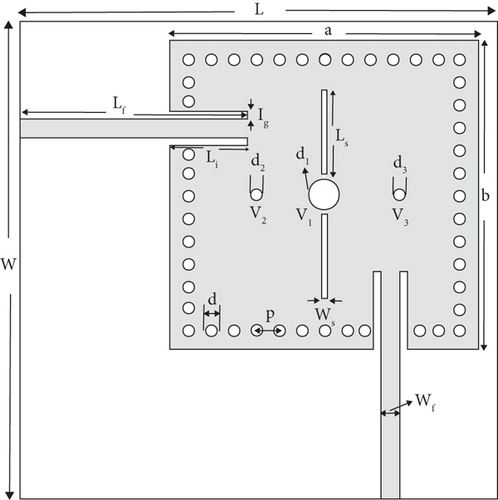
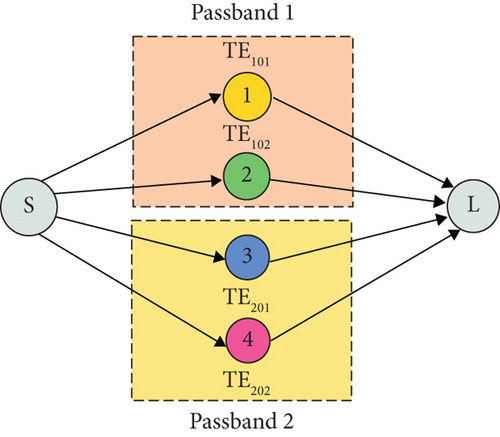
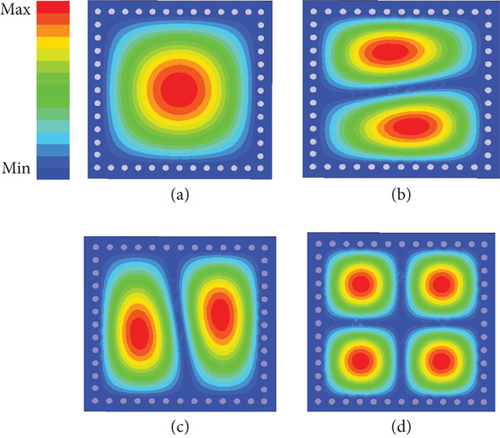
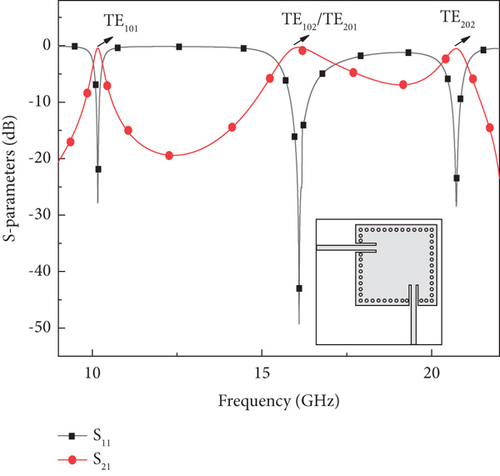
The first four resonating modes in the SIW cavity are considered to achieve second-order dual-band band-pass response. The electric field distribution of the fundamental and higher modes of SIW is presented in Figure 3. The simulated S-parameters of the mutlimode SIW cavity without any perturbation are shown in Figure 4. The resonant frequencies of the fundamental mode TE₁₀₁ (f₁) are observed at 10 GHz, the two degenerate modes TE₁₀₂ (f₂)/TE₂₀₁ (f₃) appear at 16.2 GHz, and a higher-order mode TE₂₀₂ (f₄) occurs at 20.2 GHz.

In the proposed design, Passband I is realized by shifting TE₁₀₁ towards TE₁₀₂. Similarly, Passband II is realized by shifting TE₂₀₁ towards TE₂₀₂. To achieve this initially, via V₁ is placed at the center of the cavity, aligning with the maximum electric field position, to effectively perturb the TE₁₀₁ mode. This placement also slightly affects the TE₁₀₂ and TE₂₀₁ modes, due to their minimal electric field distribution at the center. However, since the electric field is nearly zero at the center for the TE₂₀₂ mode, as illustrated in Figure 3d, via V₁ does not cause any significant perturbation. This is further confirmed by the S-parameters shown in Figure 5. By varying the diameter (d₁) of via V₁ from 0.1 to 0.9 mm, it is observed that the fundamental TE₁₀₁ mode shifts towards the degenerate TE₁₀₂ mode, as shown in Figure 5.

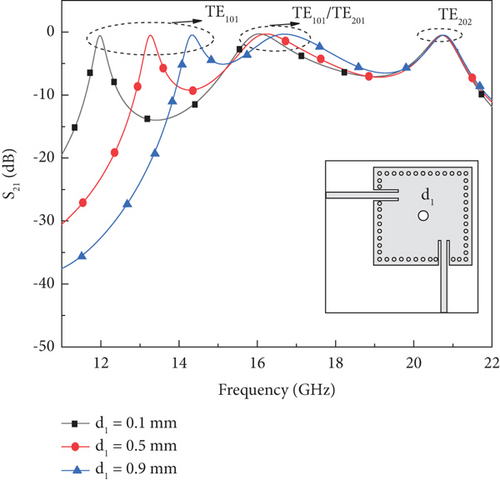
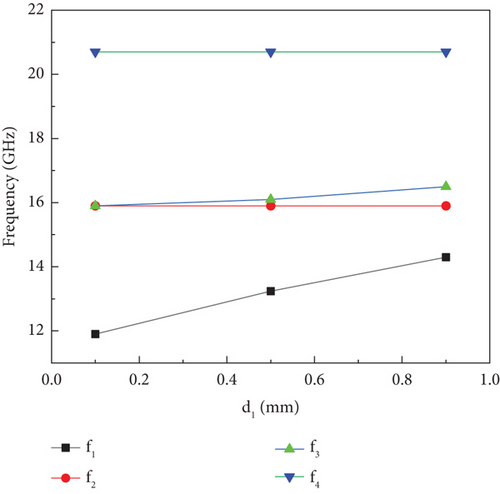
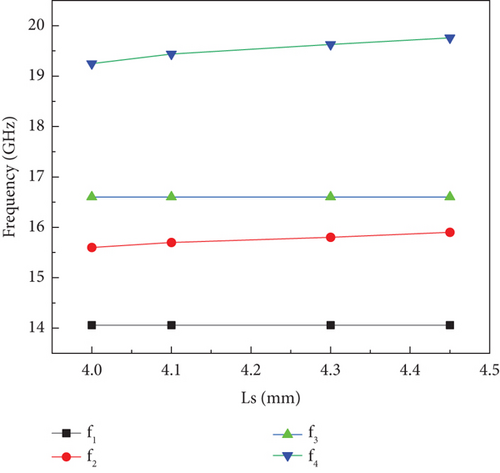
Figure 6 displays the resonant frequencies (f₁, f₂, f₃, and f₄) plotted against the diameter of the center via (d₁). The variation of d₁ from 0.1 to 0.9 mm shows an increase in f₁, while f₂ and f₃ have less effect and no effect on f₄. This indicates a significant perturbation on TE₁₀₁ and minor perturbation of TE₁₀₂ and TE₂₀₁ and no effect on TE₂₀₂.

By analyzing the electric field distribution of the resonant modes in Figure 3c, vias V₂ and V₃ are positioned at the maximum electric field locations (at a distance of P_S) to perturb the TE₂₀₁ mode towards the TE₂₀₂ mode. As P_S increases from 0.1 to 2 mm, as shown in Figures 7 and 8, the TE₂₀₁ mode shifts towards the higher order TE₂₀₂ mode, with slight variations in the TE₁₀₁ mode and no significant effect on the TE₁₀₂ mode. Hence, the influence of vias V₂ and V₃ is also taken into account, along with via V₁, in shifting the TE₁₀₁ mode towards the TE₁₀₂ mode to realize the Passband I. The electric field distributions of the perturbed TE₁₀₁ and TE₁₀₂ modes are shown in Figure 9a,b. These modes exhibit similar electric field patterns, ensuring the formation of Passband I.

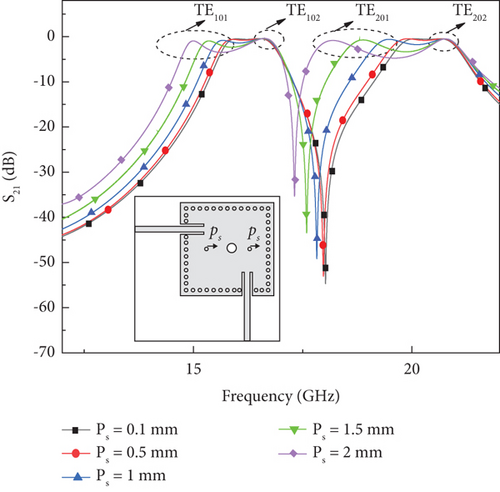
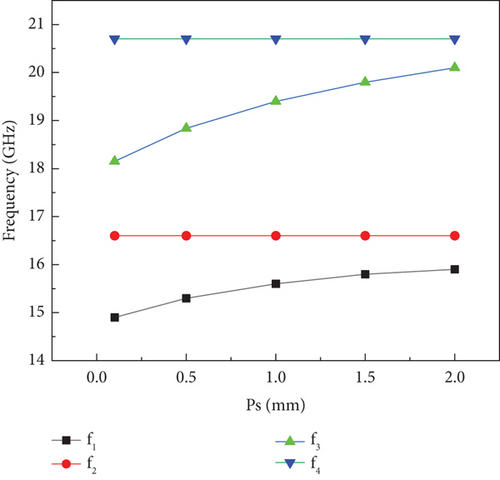
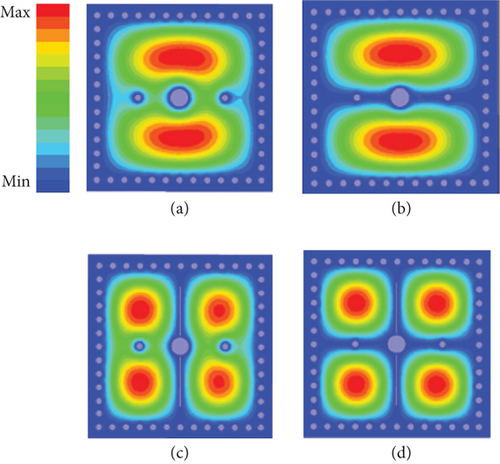
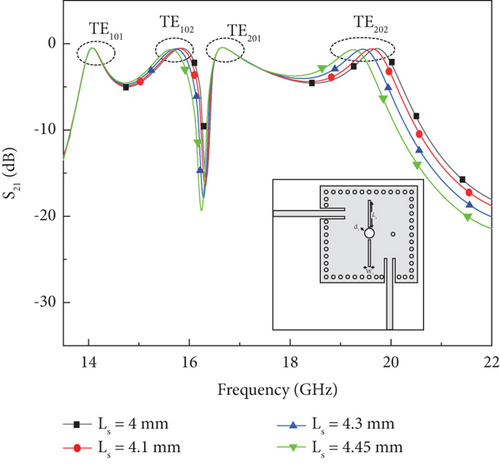
To shift the TE₂₀₂ mode towards the TE₂₀₁ mode, a rectangular slot is placed at the location of the minimum electric field in the TE₂₀₂ mode. When the slot width (W_S) is fixed at 0.1 mm and the slot length (L_S) is varied from 3 to 4 mm, the TE₂₀₂ mode shifts closer to the TE₂₀₁ mode, as illustrated in Figures 10 and 11. Hence, the influence of vias V₂ and V₃, along with the slots, is considered in perturbing the TE₂₀₁ and TE₂₀₂ modes to achieve Passband II.

The electric field distributions of the perturbed TE₂₀₁ and TE₂₀₂ modes, shown in Figure 9c,d, exhibit similar electric field patterns, forming the Passband II.

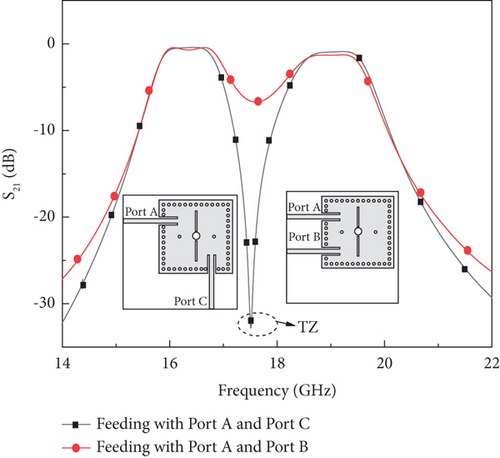
Figure 10 shows a transmission zero (TZ) between the passbands, attributed to the feed alignment, which is carefully designed to enhance isolation between the passbands.

Figure 12 illustrates the electric field distribution of the proposed dual-band filter with the input/output (I/O) feedline arrangements. When Port A and Port B serve as the input and output ports, respectively, the TE₂₀₁ and TE₁₀₂ modes exhibit the same electric field polarity, resulting in no TZ between the passbands. However, when Port A and Port C are used as the input and output ports, the TE₂₀₁ and TE₁₀₂ modes have opposite electric field polarities, creating a TZ between the passbands due to phase cancellation [16].

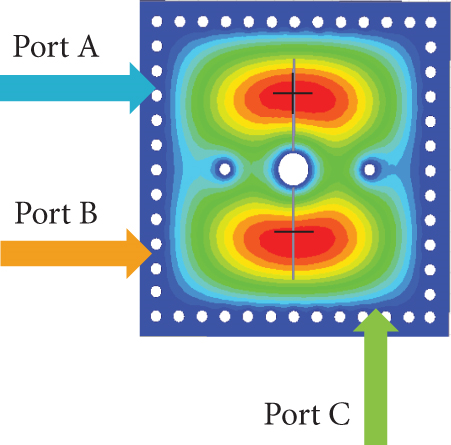
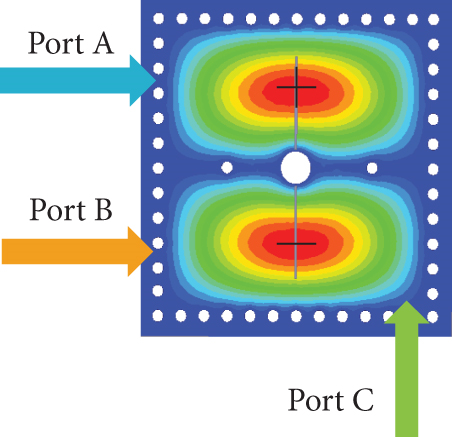
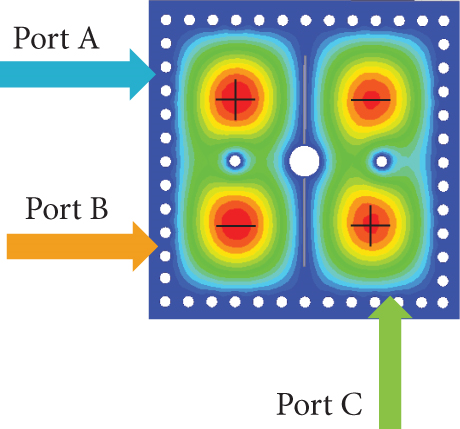
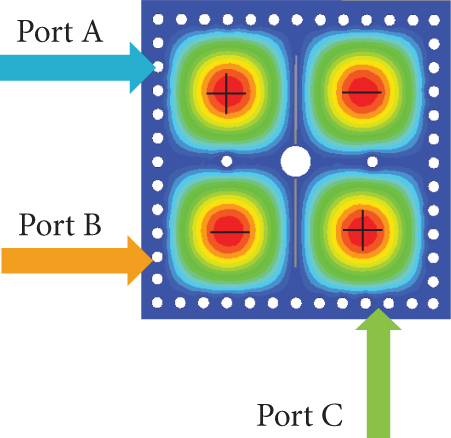
The feedlines are arranged such that the modes of the Passband I (TE₁₀₁ and TE₁₀₂) and the Passband II (TE₂₀₁ and TE₂₀₂) are out of phase, ensuring high isolation between the two passbands. Therefore, in the proposed design, Port A and Port C are selected as the I/O ports to enhance passband selectivity, with the corresponding response shown in Figure 13.

2.3. Extracting Coupling Coefficients

The proposed multimode cavity is weakly coupled to realize the coupling coefficient M₁ for the Passband I and M₂ for the Passband II, which is extracted using (4) and (5) [13]:

()

Figure 14 shows the simulated S-parameters corresponding to the cavity’s first four resonant modes. As the diameter of via V₁ increases, the resonant peak f₁ shifts towards higher frequencies, thereby affecting the bandwidth of the Passband I. When the diameter of via V₁ (d₁) is varied from 0.6 to 0.9 mm, the mutual coupling coefficient M₁ decreases linearly, as illustrated in Figure 15. The desired FBW for Passband I is achieved when d₁ = 0.8 mm.

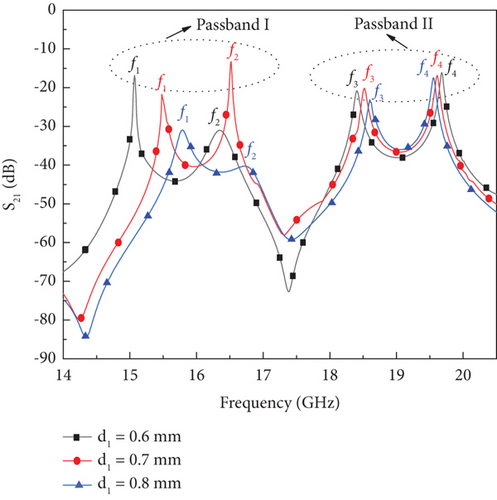
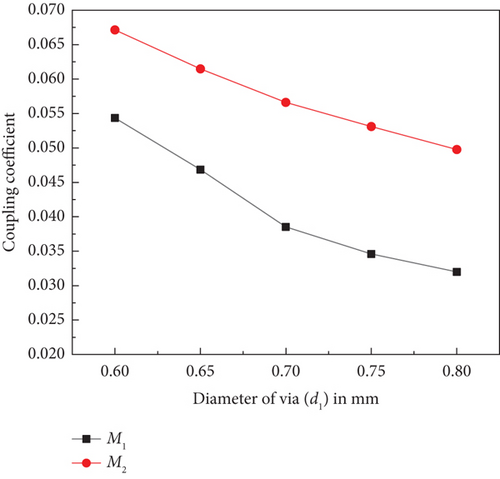
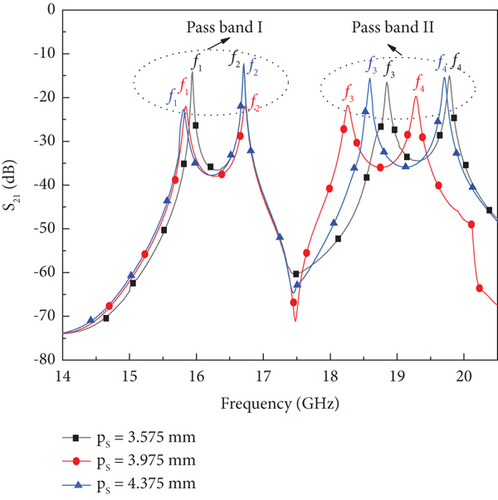
By varying the distance P_S, a shift in the resonant frequency f₃ towards a higher mode is observed, as shown in Figure 16, which affects the bandwidth of the Passband II. The coupling coefficients M₁ and M₂ increase linearly, as illustrated in Figure 17. At P_S = 3.775 mm, the required Passband II with a FBW is achieved.

2.4. Extraction of External Quality Factor

The external quality factor (Q_e1(Q_e2)) can be determined through simulation using the following Equation (6) [17]:

()

where f₀ denotes the peak of the resonator’s response curve, while Δf_3dB symmetrically extends around this frequency, defining the range where the power response remains within 3 dB of its maximum value.

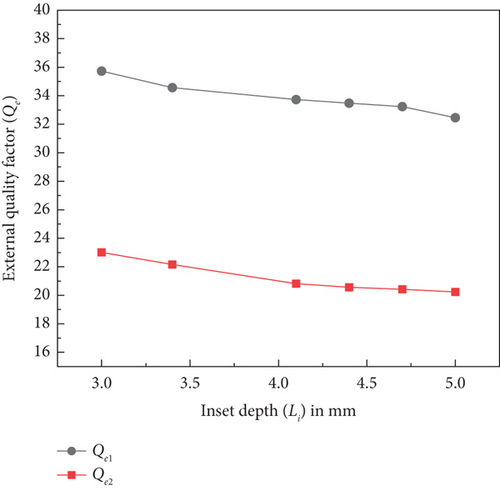
The extracted external quality factor (Q_e) results are illustrated in Figure 18. As the inset depth (L_i) increases from 3 to 5 mm, both Q_e1 and Q_e2 decrease. The parameter L_i is optimized to achieve the required values of Q_e1 and Q_e2.

The procedure for dual-band filter design using the proposed multimode cavity is summarized as follows:

1.
Initially, determine the theoretical coupling parameters (Q_e1(Q_e2) and M₁(M₂) for the desired passbands from the low-pass prototype g-parameters using (1).
2.
Determine the dimensions of the SIW cavity using Equations (2) and (3).
3.
Consider the fundamental mode TE₁₀₁ and the higher mode (TE₁₀₂) for Passband I and the next two higher modes (TE₂₀₁ and TE₂₀₂) for Passband II.
4.
Introduce vias (V₁, V₂, and V₃) and slot perturbations in the SIW cavity to shift the resonance frequencies of modes.
5.
Then, vary the diameter of via V₁ to perturb fundamental mode TE₁₀₁ towards TE₁₀₂ to obtain M₁ for Passband I.
6.
Next, vary the position of vias V₂ and V₃ and length of slots to perturb TE₂₀₁ and TE₂₀₂, respectively, to obtain M₂ for Passband II.
7.
Finally, the inset depth (L_i) and inset gap (I_g) of the feedline is varied to achieve the required Q_e1 and Q_e2 for both the passbands.

3. Fabrication and Measurement

The final dimensions of the proposed dual-band filter shown in Figure 1 are L = 25 mm, W = 25 mm, a = 14.6 mm, d₁ = 0.8 mm, d₂ = 0.3 mm, d₃ = 0.3 mm, L_S = 4.45 mm, W_S = 0.1 mm, L_i = 4.1 mm, I_g = 0.3 mm, W_f = 1 mm, L_f = 12 mm, d = 0.6 mm, and p = 1.2 mm.

The proposed SIW cavity, fabricated on an RT/Duroid 5880 substrate, is measured using an Anritsu MS46524B vector network analyzer (VNA) to obtain the S-parameters. Figure 19 presents the simulated and measured results of the dual-band SIW filter with CFs at 16.2 GHz and 19.1 GHz. The simulated FBWs for the Passband I and Passband II are 1.74% and 3.14%, respectively, with ILs of 0.59 and 0.9 dB and reflection coefficients of −18 and −19.2 dB. The measured FBWs for the Passband I and Passband II are 1.71% and 3.09%, with IL values of 1.8 and 1.9 dB and reflection coefficients of −11 and −14.8 dB.

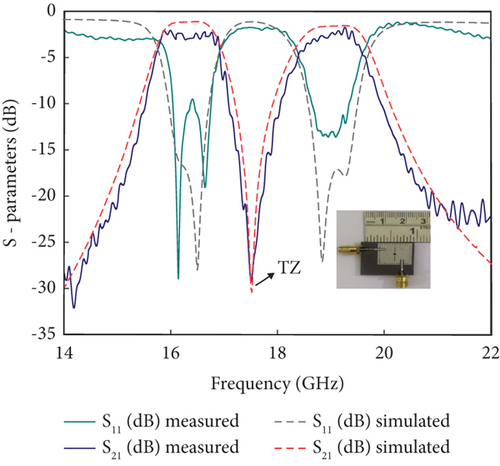
Table 1 compares different dual-band SIW BPFs with their CFs, IL, and size. The proposed design is in agreement with the size and IL.

Table 1. Comparison of the proposed BPF with SIW filters from existing literature.

Ref.	CF (GHz)	IL(dB)	FBW (%)	Size ()
[18]	26.5/31.5	0.48/0.67	3.6/2	1.5∗2.2
[19]	2.51/5.30	1.41/1.88	6.8/5.8	0.23∗0.45
[20]	9.5/15.95	2.77/2.42	2.7/4.9	0.98∗0.98
[21]	6.22/8.24	0.86/1.32	7.7/3.9	0.89∗0.41
[22]	8/11.4	2.26/3.07	3.01/2.46	2.17∗2.17
[23]	9.8/13.5	1.8/1.5	11.8/9.8	1.22∗1.22
[24]	6.0/12.0	0.79/1.39	18.3/29.1	0.92∗0.53
[25]	18.8/19.4	0.68/0.61	NA	1.15∗1.15
[26]	46.7/60	2/2.8	11.7/6.8	1.8∗1.77
[27]	42.8/60.5	1.9/1.4	6.1/7.7	1.14∗1.64
This work	16.2/19.1	1.8/1.9	1.71/3.09	0.41∗0.41

4. Conclusion

This paper presents the design of a compact dual-band BPF using a multimode perturbation within a single SIW cavity resonator. The fundamental TE₁₀₁ mode and the first higher order TE₁₀₂ mode form the Passband I, with a CF of 16.2 GHz, an FBW of 1.71%, and an IL of 1.8 dB. The Passband II is formed by the higher order TE₂₀₁ and TE₂₀₂ modes, with a CF of 19.1 GHz, an FBW of 3.09%, and an IL of 1.9 dB. The proposed filter features a compact size, low IL, and independently controllable FBW.

Conflicts of Interest

The authors disclose that BITS Pilani, Hyderabad Campus, has provided funding and support related to this research. However, this does not affect the integrity or objectivity of the study.

Funding

BITS Pilani, Hyderabad Campus, supported this research. The authors acknowledge the financial and technical support provided.

Open Research

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

1 Dhwaj K., Li X., Shen Z., and Qin S., Cavity Resonators Do the Trick: A Packaged Substrate Integrated Waveguide, Dual-Band Filter, IEEE Microwave Magazine. (2016) 17, no. 1, 58–64, https://doi.org/10.1109/MMM.2015.2487920, 2-s2.0-84961728595.
10.1109/MMM.2015.2487920
Web of Science® Google Scholar
2 Macchiarella G. and Tamiazzo S., Design Techniques for Dual-Passband Filters, IEEE Transactions on Microwave Theory and Techniques. (2005) 53, no. 11, 3265–3271, https://doi.org/10.1109/TMTT.2005.855749, 2-s2.0-28144448109.
10.1109/TMTT.2005.855749
Web of Science® Google Scholar
3 Zhang H., Kang W., and Wu W., Dual-Band Substrate Integrated Waveguide Bandpass Filter Utilising Complementary Split-Ring Resonators, Electronics Letters. (2018) 54, no. 2, 85–87, https://doi.org/10.1049/el.2017.3478, 2-s2.0-85041106768.
10.1049/el.2017.3478
Web of Science® Google Scholar
4 Dong Y., Wu C. T. M., and Itoh T., Miniaturised Multi-Band Substrate Integrated Waveguide Filters Using Complementary Split-Ring Resonators, IET Microwaves, Antennas and Propagation. (2012) 6, no. 6, 611–620, https://doi.org/10.1049/iet-map.2011.0448, 2-s2.0-84862167753.
10.1049/iet-map.2011.0448
Web of Science® Google Scholar
5 Gao H.-Y., Tang Z. X., Cao X., Wu Y. Q., and Zhang B., Compact Dual-Band SIW Filter With CSRRS and Complementary Spiral Resonators, Microwave and Optical Technology Letters. (2016) 58, no. 1, 1–4, https://doi.org/10.1002/mop.29482, 2-s2.0-84948734033.
10.1002/mop.29482
CAS Web of Science® Google Scholar
6 Zhang H., Kang W., and Wu W., Miniaturized Dual-Band SIW Filters Using E-Shaped Slotlines With Controllable Center Frequencies, IEEE Microwave and Wireless Components Letters. (2018) 28, no. 4, 311–313, https://doi.org/10.1109/LMWC.2018.2811251, 2-s2.0-85044295277.
10.1109/LMWC.2018.2811251
Web of Science® Google Scholar
7 Li J., Zheng W., Wei X., Huang Y., and Wen G., Millimeter-Wave Substrate Integrated Waveguide Bandpass Filters Based on Stepped-Impedance E-Shaped Defected Ground Structures, International Journal of RF and Microwave Computer-Aided Engineering. (2022) 32, no. 11, e23340, https://doi.org/10.1002/mmce.23340.
10.1002/mmce.23340
Web of Science® Google Scholar
8 Xu S., Ma K., Meng F., and Yeo K. S., Novel Defected Ground Structure and Two-Side Loading Scheme For Miniaturized Dual-Band SIW Bandpass Filter Designs, IEEE Microwave and Wireless Components Letters. (2015) 25, no. 4, 217–219, https://doi.org/10.1109/LMWC.2015.2400916, 2-s2.0-84927597256.
10.1109/LMWC.2015.2400916
Web of Science® Google Scholar
9 Muchhal N. and Srivastava S., Design of Wideband Comb Shape Substrate Integrated Waveguide Multimode Resonator Bandpass Filter With High Selectivity and Improved Upper Stopband Performance, International Journal of RF and Microwave Computer-Aided Engineering. (2019) 29, no. 9, e21807, https://doi.org/10.1002/mmce.21807, 2-s2.0-85064703819.
10.1002/mmce.21807
Web of Science® Google Scholar
10 Yang Z., You B., and Luo G., Dual-/Tri-Band Bandpass Filter Using Multimode Rectangular SIW Cavity, Microwave and Optical Technology Letters. (2020) 62, no. 3, 1098–1102, https://doi.org/10.1002/mop.32145.
10.1002/mop.32145
Web of Science® Google Scholar
11 Guo H., An X., and Lv Z. Q., Dual-Mode Bandpass Substrate Integrated Waveguide Filter With a Complementary Split Ring Resonator, Microwave and Optical Technology Letters. (2018) 60, no. 3, 735–741, https://doi.org/10.1002/mop.31039, 2-s2.0-85041731647.
10.1002/mop.31039
Google Scholar
12 Liu Q., Zhou D., Lv D., Zhang D., Zhang J., and Zhang Y., Multi-Layered Dual-Mode Substrate Integrated Waveguide Bandpass Filter With Input and Output Ports Located on Same Substrate Layer, IET Microwaves, Antennas & Propagation. (2019) 13, no. 15, 2641–2648, https://doi.org/10.1049/iet-map.2019.0275.
10.1049/iet-map.2019.0275
Web of Science® Google Scholar
13 Liu Q. and Zhu L., Design of Cross-Coupled Bandpass Filters With Flexible Coupling via Half-Mode Substrate-Integrated Waveguide, International Journal of RF and Microwave Computer-Aided Engineering. (2024) 2024, 13, https://doi.org/10.1155/2024/3897878, 3897878.
10.1155/2024/3897878
Google Scholar
14 Hong J.-S. and Lancaster M. J., Microstrip Filters for RF/Microwave Applications, 2001, Wiley, https://doi.org/10.1002/0471221619.
10.1002/0471221619
Google Scholar
15 Shen Y., Wang H., Kang W., and Wu W., Dual-Band SIW Differential Bandpass Filter With Improved Common-Mode Suppression, IEEE Microwave and Wireless Components Letters. (2015) 25, no. 2, 100–102, https://doi.org/10.1109/LMWC.2014.2382683, 2-s2.0-85027919897.
10.1109/LMWC.2014.2382683
Web of Science® Google Scholar
16 Thomas J. B., Cross-Coupling in Coaxial Cavity Filters—A Tutorial Overview, IEEE Transactions on Microwave Theory and Techniques. (2003) 51, no. 4, 1368–1376, https://doi.org/10.1109/TMTT.2003.809180, 2-s2.0-0037398727.
10.1109/TMTT.2003.809180
Web of Science® Google Scholar
17 Pozar D. M., Microwave Engineering, 2005, 3rd edition, Wiley.
Google Scholar
18 Dong K., Mo J., He Y., Ma Z., and Yang X., Design of A Millimeter-Wave Dual-Band Bandpass Filter Using SIW Dual-Mode Cavities, Proceedings of the 2016 IEEE MTT-S International Wireless Symposium (IWS), 2016, IEEE, 1–3, https://doi.org/10.1109/IEEE-IWS.2016.7585456, 2-s2.0-84994337273.
10.1109/IEEE-IWS.2016.7585456
Google Scholar
19 Li M., Chen C., and Chen W., Miniaturized Dual-Band Filter Using Dual-Capacitively Loaded SIW Cavities, IEEE Microwave and Wireless Components Letters. (2017) 27, no. 4, 344–346, https://doi.org/10.1109/LMWC.2017.2678435, 2-s2.0-85017180134.
10.1109/LMWC.2017.2678435
Web of Science® Google Scholar
20 Zhou K., Kang W., and Wu W., Compact Dual-Band Balanced Bandpass Filter Based on Double-Layer SIW Structure, Electronics Letters. (2016) 52, no. 18, 1537–1539, https://doi.org/10.1049/el.2016.1968, 2-s2.0-84983628533.
10.1049/el.2016.1968
Web of Science® Google Scholar
21 Zhang H., Kang W., and Wu W., Miniaturized Dual-Band Differential Filter Based on CSRR-Loaded Dual-Mode SIW Cavity, IEEE Microwave and Wireless Components Letters. (2018) 28, no. 10, 897–899, https://doi.org/10.1109/LMWC.2018.2867082, 2-s2.0-85053143427.
10.1109/LMWC.2018.2867082
Web of Science® Google Scholar
22 Xie H. W., Zhou K., Zhou C. X., and Wu W., Compact SIW Diplexers and Dual-Band Bandpass Filter with Wide-Stopband Performances, IEEE Transactions on Circuits and Systems II: Express Briefs. (2020) 67, no. 12, 2933–2937, https://doi.org/10.1109/TCSII.2020.2992059.
10.1109/TCSII.2020.2992059
Web of Science® Google Scholar
23 Shi L.-F., Sun C. Y., Chen S., Liu G. X., and Shi Y. F., Dual-Band Substrate Integrated Waveguide Bandpass Filter Based on CSRRs and Multimode Resonator, International Journal of RF and Microwave Computer-Aided Engineering. (2018) 28, no. 9, e21412, https://doi.org/10.1002/mmce.21412, 2-s2.0-85047397662.
10.1002/mmce.21412
Web of Science® Google Scholar
24 Fu W., Li Z., Liu P., Cheng J., and Qiu X., Modeling and Analysis of Novel CSRRs-Loaded Dual-Band Bandpass SIW Filters, IEEE Transactions on Circuits and Systems II: Express Briefs. (2021) 68, no. 7, 2352–2356, https://doi.org/10.1109/TCSII.2021.3052574.
10.1109/TCSII.2021.3052574
Web of Science® Google Scholar
25 Zhou X., Zhang G., Zheng J., Tang W., and Yang J., SIW Filter With Adjustable Number of Passbands Using Assembled Multimode Resonant PCBs, IEEE Transactions on Circuits and Systems II: Express Briefs. (2022) 69, no. 8, 3386–3389, https://doi.org/10.1109/TCSII.2022.3157713.
10.1109/TCSII.2022.3157713
Google Scholar
26 Yang X. L., Zhu X. W., and Wang X., Dual-Band Substrate Integrated Waveguide Filters With Perturbed Circular Cavity, IEEE Microwave and Wireless Components Letters. (2022) 32, no. 4, 293–296, https://doi.org/10.1109/LMWC.2021.3125098.
10.1109/LMWC.2021.3125098
Web of Science® Google Scholar
27 Yang X. L., Zhu X. W., and Wang X., Dual-Band Substrate Integrated Waveguide Filters Based on Multi-Mode Resonator Overlapping Mode Control, IEEE Transactions on Circuits and Systems II: Express Briefs. (2023) 70, no. 6, 1971–1975, https://doi.org/10.1109/TCSII.2023.3236365.
10.1109/TCSII.2023.3236365
Google Scholar

All articles

Compact Dual-Band Band-Pass Filter Using Single Multimode SIW Cavity With Independent Controllable Fractional Bandwidth

Abstract

1. Introduction