Predicting Oil Temperature in Electrical Transformers Using Neural Hierarchical Interpolation
Abstract
Effective electricity consumption planning is critical for power distribution. Ensuring the distribution network aligns with expected demand fluctuations is a challenging task influenced by various time-related and seasonal variables. This study focuses on improving transformer oil temperature forecasting, an indicator of transformer health, using the neural hierarchical interpolation for time series (NHITS) model. The NHITS model’s architecture is designed to handle long-term forecasting efficiently, making it ideal for capturing extended trends in transformer oil temperature. It incorporates multirate signal sampling via MaxPool layers and hierarchical interpolation to merge predictions across different time scales. The proposed methodology involves two key phases: data preparation and model development. In the data preparation phase, the electricity transformer temperature (ETT) datasets are used, normalized with a standard scaler, and essential features such as oil temperature and external power load are selected. During the model development phase, the proposed NHITS model is trained and its hyperparameters are optimized for optimal performance. The study evaluates the model’s performance under various conditions, including the comparison of multivariate and univariate time series, the effects of short and long-term forecasting horizons, and the impact of temporal resolution. The model was validated using the ETT dataset, and our results were benchmarked against a previous study that employed the same dataset and used the Informer model. The results indicate that the NHITS model outperforms the Informer model, showing an average decrease of 51.37% in mean squared error (MSE) and 37.83% in mean absolute error (MAE). These findings highlight the model’s ability to capture both long-term and short-term characteristics of time series data, making it a promising solution for forecasting transformer oil temperatures.
1. Introduction
Electric power distribution heavily relies on accurate forecasting of consumption and equipment performance, especially transformer oil temperature. Effective power distribution and consumption planning ensure reliable electricity supply by managing transmission from high-voltage networks to users and maintaining infrastructure like substations and transformers [1]. Electricity consumption planning revolves around forecasting and managing the demand for electricity within a defined region or system. Accurate predictions of electricity consumption are essential for purposes like load balancing, infrastructure planning, and energy resource management [2]. Furthermore, electricity consumption forecasting serves a practical role in predictive maintenance by providing valuable insights into future energy usage patterns. This enables maintenance teams to schedule their activities efficiently, anticipate peak equipment demand, and ultimately minimize unexpected breakdowns while reducing downtime [3]. This practice contributes to the optimization of both electricity transmission and distribution, ensuring the robustness of the power grid while avoiding overloads or shortages [4]. Forecasting transformer oil temperature is important for understanding and managing electricity consumption. Higher temperatures in transformers frequently signify increased electrical load or system stress, which correlates with raised electricity usage. Therefore, predictions of oil temperature serve as an indirect gauge of electrical load and electricity consumption [5].
Numerous studies aim to enhance the accuracy of electricity demand predictions, with a primary focus on short and medium-term forecasts [6]. These forecasts typically span periods from a few hours to several days and often utilize data with low temporal resolution. In this context, one study introduces a method to predict next-day electricity demand and price curves based on historical data [7], offering forecasts for the next 24 h at an hourly resolution. Additionally, another study suggests a long-term forecasting approach for electricity demand in the residential sector spanning two years, but with a monthly temporal resolution [8]. While these models address demand forecasting, there is a need for models capable of predicting equipment-specific indicators, such as transformer oil temperature, which affect power distribution stability. Some other studies are location-specific. Studies [9, 10] present forecasting methods specifically tailored to predict electricity consumption in Pakistan, using advanced ensemble learning and component-based estimation techniques to improve prediction accuracy. While these studies have contributed significantly to improving demand predictions within these time frames, there remains a need for research that addresses long-term forecasting with higher temporal resolution to better capture daily and seasonal variations in electricity consumption [11]. Predicting long-term electricity consumption is a complex task because it is influenced by numerous factors, including economic development, climatic conditions, and the unpredictability of electricity usage patterns [12]. Moreover, forecasting multivariate time series is challenging due to the inherent complexity and high dimensionality of the data. Leveraging these inter-series dependencies has the potential to improve both the model fit and forecast accuracy of multivariate time series models, particularly in the context of long-term predictions [13].
- 1.
Expanded application of NHITS model: We applied the NHITS model to all available subsets within the ETT datasets, including those not covered in previous studies [14, 15]. The performance of NHITS on each subset was compared with other models from the literature, particularly the Informer model.
- 2.
Comprehensive scenario analysis: We conducted a comprehensive analysis of various scenarios, examining the impact of using multivariate and univariate time series, the effects of short and long-term horizon forecasting, and the influence of temporal resolution on each dataset.
The structure of the study is as follows. In Section 2, we present an overview of relevant research, encompassing traditional time series models commonly found in the literature, the use of neural forecasting techniques, and the diverse methodologies applied to long-sequence time series forecasting. Section 3 details our proposed approach and study design, outlining the various steps involved. Section 4 presents the outcomes and findings. Section 5 examines these results and offers an in-depth analysis. Lastly, in Section 6, a conclusion is presented for the study. A list of abbreviations used in this paper is provided in Table 1.
| Abbreviation | Definition |
|---|---|
| ANN | Artificial neural network |
| AR | Autoregressive |
| ARIMA | Autoregressive integrated moving average |
| ETT | Electricity transformer temperature |
| LSTM | Long short-term memory |
| MAE | Mean absolute error |
| MLP | Multilayer perceptron |
| MSE | Mean squared error |
| NHITS | Neural hierarchical interpolation for time series |
| RNN | Recurrent neural network |
| STL | Seasonal and trend decomposition using loess |
2. Related Work
2.1. Traditional Time Series Models
Traditional time series models have been extensively employed for the analysis and prediction of diverse time series data. These models rely on statistical methodologies and mathematical algorithms to capture patterns and trends within the data. Notable examples encompass autoregressive integrated moving average (ARIMA) models, which are widely used for forecasting and analyzing stationary time series data [16]. ARIMA models operate on the premise that future values in a time series can be foretold based on historical values and the model’s errors. Another traditional method involves the use of autoregressive (AR) models, which assume a linear dependence of future time series values on past values [17]. Furthermore, traditional models like exponential smoothing models, state space models, and seasonal and trend decomposition using LOESS (STL) models have been employed for time series analysis and prediction [18–20]. Combining traditional models can effectively capture the complexities of nonlinear and high-variance data. Reference [21] investigates the effectiveness of hybrid combinations of linear and nonlinear models for predicting Brent crude oil prices, demonstrating how decomposing the data into trend and stochastic components allows for more accurate day-ahead forecasts by addressing underlying patterns separately. Ensemble techniques are also highly effective in managing such intricate data patterns. Reference [22] introduces an ensemble approach tailored for electricity demand forecasting in the Peruvian market, where multiple models work together to refine predictions after preprocessing for seasonality, stationarity, and variance. Similarly, reference [23] employs multiple decomposition techniques for forecasting electricity consumption in Pakistan, breaking down time series into trend, seasonal, and stochastic components, each forecasted with optimized models. Building on these decomposition methods, recent studies have demonstrated the effectiveness of functional data analysis (FDA) in forecasting by isolating key data components for individual modeling. This method, which has been applied in various fields, allows each component—whether based on trends or stochastic processes—to be addressed with models tailored to their specific characteristics. Applications have demonstrated this approach in forecasting ozone concentration [24], wind speed [25], and electricity prices [26].
These models serve as a robust framework for comprehending and forecasting time series data and have found utility across various domains, including economics, finance, meteorology, and engineering. However, traditional models often struggle with long-term forecasting and fail to capture the complex, nonlinear dynamics inherent in transformer oil temperature data. Consequently, more advanced approaches, such as neural forecasting, have arisen to tackle these challenges and enhance the accuracy of time series forecasting.
2.2. Neural Forecasting Applications
Neural forecasting encompasses the utilization of neural network models to make predictions and forecasts across diverse domains. This approach has gained popularity due to its ability to capture complex patterns and relationships in data, particularly in tasks related to time series forecasting. The applications of neural forecasting are spanning various fields. In the domain of economics and finance, neural networks have been used to forecast stock prices and earnings per share, GDP, and foreign exchange rates [27–29]. In the energy sector, neural networks find applications in predicting electricity load, wind power generation, and solar wind activity [30–32]. In this context, a study utilized a classification predictive model to assess maintenance requirements for distribution transformers, thereby improving their reliability and cutting costs through predictive maintenance [33]. Another research employed artificial neural networks (ANNs) to predict wind and solar energy production, attaining higher accuracy than traditional models, which helps in balancing energy supply and demand [34]. Moreover, neural forecasting has been adopted in hydrology for the prediction of runoff and water demand [35]. In the transportation sector, neural networks have proven valuable in forecasting traffic patterns and emergency calls [36]. Additionally, neural forecasting has made inroads into the domains of marketing, tourism, and even geomagnetic storm prediction [32, 37, 38]. Although these methods have been successful, they are less suited for long-term forecasting tasks, which NHITS is designed to address more effectively.
2.3. Long-Sequence Time Series Forecasting
Long-sequence time series forecasting refers to predicting extended sequences of time series data with a focus on capturing intricate long-range dependencies. This forecasting challenge arises from the need to efficiently grasp precise long-range relationships between input and output variables [14]. Conventional time series forecasting methods, such as ARIMA models, can encounter difficulties when dealing with lengthy sequences [39]. To address this challenge, researchers have explored the utilization of deep learning models, including recurrent neural networks (RNNs) and transformers, for long-sequence time series forecasting. RNNs, which encompass long short-term memory (LSTM) networks, have demonstrated effectiveness in capturing long-sequence patterns and making multistep forecasts while considering multiple variables [40]. In this context, a bidirectional LSTM neural network was implemented to enhance the prediction of electrical loads. This approach significantly improves accuracy compared to previous models and aids in more effective energy planning and market management [41]. Transformers, which have gained popularity in natural language processing tasks, have been adapted for time series forecasting. Notably, the Informer model extends the transformer architecture to efficiently capture long-range dependencies between input and output variables [14]. DeepAR is another model that leverages AR recurrent networks for probabilistic forecasting, showcasing enhanced accuracy when compared to state-of-the-art methods [42]. In a separate study, a transformer model with attention-based encoder–decoder networks was proposed. This model incorporates attention mechanisms to focus on critical attributes and capture dependencies in multivariate time series prediction [43].
3. Methodology
In this section, we outline the sequence of actions taken in this research and describe the methodology employed. Figure 1 provides the study design, illustrating the stages carried out during both data preparation and model development. Details of each step are in the following sections.
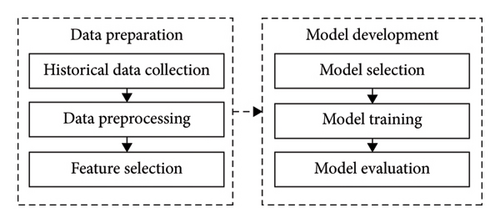
3.1. Historical Data Collection
This study leverages the ETT dataset1, an accessible multivariate time series dataset consisting of four subdatasets containing electric load data and oil temperature records from two different electrical stations located in separate regions [14]. Variations between regions may reflect different operational environments, which could influence the oil temperature trends. The ETT dataset is accessible in two resolutions, either every 15 min or hourly intervals. Table 2 describes the available datasets and their specific attributes.
| Dataset | ETTm1 | ETTm2 | ETTh1 | ETTh2 |
|---|---|---|---|---|
| Region | Region 1 | Region 2 | Region 1 | Region 2 |
| Frequency | 15 min | 15 min | 1 h | 1 h |
| Time series | 7 | 7 | 7 | 7 |
| Length | 69,680 | 69,680 | 17,420 | 17,420 |
3.2. Data Preprocessing
3.3. Feature Selection
The ETT dataset contains different features, including date points, electrical transformer oil temperature, and six distinct categories of external power load features. Features such as electrical load are important to the model as they are directly linked to transformer operation and potential temperature changes. The prediction of electrical transformer oil temperature serves a vital role as an early warning for a predictive maintenance system. As oil temperature rises, it signifies increased demand and stress on the transformer. By forecasting temperature fluctuations, proactive management of maintenance and load distribution becomes possible, averting overheating and optimizing electricity consumption. This approach ensures the reliability and effectiveness of the system [5]. Table 3 outlines the various attributes present within the ETT dataset. This study compares the influence of employing multivariate and univariate time series for predicting the oil temperature of transformers using the ETT datasets. In the multivariate scenario, all dataset features are utilized, whereas in the univariate scenario, only the OT variable serves as the sole input to the model. The aim is to analyze the performance of the model under each scenario.
| Field | Description |
|---|---|
| Date | Recorded date |
| OT | Oil temperature |
| HULL | High UseLess Load |
| HUFL | High UseFul Load |
| MULL | Middle UseLess Load |
| MUFL | Middle UseFul Load |
| LULL | Low UseLess Load |
3.4. Model Selection
The NHITS model was chosen to predict the oil temperature of transformers in the ETT dataset. The model incorporates two key techniques: multirate signal sampling and hierarchical interpolation. The multirate signal sampling of the input signal is achieved by the MaxPool layer, with the sampling rate determined by the kernel size. A larger kernel size tends to highlight the long-term characteristics of the time series, while a smaller kernel size does the opposite. This allows the model to decrease memory consumption and computational demands, thereby improving its performance in long-term forecasting. Additionally, the NHITS model effectively addresses seasonality by isolating seasonal trends through its multirate signal sampling, which captures recurring patterns within different time scales of the transformer oil temperature data. This hierarchical approach ensures that seasonal fluctuations are recognized and interpreted as part of the core patterns rather than as anomalies. The hierarchical interpolation is then utilized to merge the predictions of all stacks, with each stack focusing on a different time scale. This lowers the computational demands by reducing the cardinality of predictions, thereby preventing overfitting and enhancing forecast accuracy. By using this hierarchical approach, the model is able to tackle both short-term and long-term forecasting tasks more effectively.
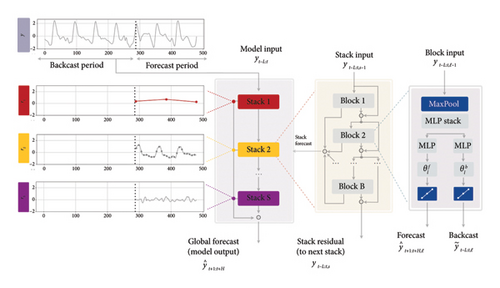
3.5. Model Training and Hyperparameter Optimization
The data are divided into training, validation, and testing subsets, apportioned at a ratio of 60%–20%–20%, respectively. The training set is utilized for training the model parameters, the validation set facilitates hyperparameter tuning, and the test set is employed for model evaluation. Figure 3 illustrates the seasonal trends in the transformer oil temperature, which our model must capture accurately to provide reliable long-term forecasts. The figure presents the time series of the OT variable with the utilized data partitions within the ETTm1 dataset, along with an enlarged section highlighting the variable’s seasonality. The model structure comprises 3 stacks, with a maximum of 2 blocks in each stack. Every block consists of 2 MLP layers, with 512 hidden units. The complete set of hyperparameters used for the NHITS configuration is detailed in Table 4.

| Hyperparameter | Values |
|---|---|
| Maximum training steps | 1000 |
| Learning rate | 1 × 10−3 |
| Validation interval | 100 |
| Stacks | S = 3 |
| Blocks per stack | B ∈{1, 2} |
| MLP layers per block | 2 |
| Hidden unit size | 512 |
| Autoregressive input size | 5 × Horizon |
| Batch size | {1, 3, 7} |
| Window batch size | 256 |
| Pooling kernel size | [k1, k2, k3] ∈ [2, 2, 2] |
| Inverse expressivity ratios | {[24, 12, 1], [1, 1, 1]} |
| Activation | ReLU |
| Interpolation type | Linear |
3.6. Model Evaluation
In this context, yτ and represent the actual and observed values at time τ, with t indicating the initial time index and H denoting the forecast horizon or time steps over which the metric is calculated.
4. Key Results
4.1. Forecasting Accuracy
The NHITS model proposed in this study was evaluated against the Informer model [14]. The Informer model utilizes a ProbSparse Self-Attention Mechanism to lower time complexity and memory consumption by concentrating on essential parts of the sequence. Additionally, it employs Self-Attention Distilling to handle long input sequences more effectively by highlighting important attention areas and reducing cascading layer inputs. This makes the Informer model an efficient transformer-based solution for long-sequence time series forecasting. In this evaluation, ARIMA serves as a baseline for the comparison. The results for both the Informer model and ARIMA are derived from the same study [14].
In the context of the ETT dataset, Table 5 showcases the outcomes of benchmarked models for both univariate and multivariate time series, specifically in the case of short forecasting horizons. On the other hand, Table 6 details the results for long forecasting horizons. The top-performing outcomes are indicated in bold. Lower MSE and MAE values signify superior model performance. The reported metrics represent the averages derived from three separate runs.
| Method | NHITS | Informer [14] | ARIMA [14] | |||||
|---|---|---|---|---|---|---|---|---|
| Dataset | Type | Horizon | MSE | MAE | MSE | MAE | MSE | MAE |
| ETTh1 | Univariate | 24 | 0.008 | 0.077 | 0.098 | 0.247 | 0.108 | 0.284 |
| 48 | 0.014 | 0.095 | 0.158 | 0.319 | 0.175 | 0.424 | ||
| Multivariate | 24 | 0.471 | 0.445 | 0.577 | 0.549 | 0.650 | 0.624 | |
| 48 | 0.443 | 0.425 | 0.685 | 0.625 | 0.702 | 0.675 | ||
| ETTh2 | Univariate | 24 | 0.134 | 0.268 | 0.093 | 0.240 | 3.554 | 0.445 |
| 48 | 0.155 | 0.298 | 0.155 | 0.314 | 3.190 | 0.474 | ||
| Multivariate | 24 | 0.131 | 0.249 | 0.720 | 0.665 | 1.143 | 0.813 | |
| 48 | 0.133 | 0.256 | 1.457 | 1.001 | 1.671 | 1.221 | ||
| ETTm1 | Univariate | 24 | 0.011 | 0.097 | 0.030 | 0.137 | 0.090 | 0.206 |
| 48 | 0.012 | 0.100 | 0.069 | 0.203 | 0.179 | 0.306 | ||
| Multivariate | 24 | 0.110 | 0.275 | 0.323 | 0.369 | 0.621 | 0.629 | |
| 48 | 0.382 | 0.436 | 0.494 | 0.503 | 1.392 | 0.939 | ||
| ETTm2 | Univariate | 24 | 0.002 | 0.036 | — | — | — | — |
| 48 | 0.016 | 0.081 | — | — | — | — | ||
| Multivariate | 24 | 0.058 | 0.180 | — | — | — | — | |
| 48 | 0.081 | 0.198 | — | — | — | — | ||
| Method | NHITS | Informer [14] | ARIMA [14] | |||||
|---|---|---|---|---|---|---|---|---|
| Dataset | Type | Horizon | MSE | MAE | MSE | MAE | MSE | MAE |
| ETTh1 | Univariate | 336 | 0.065 | 0.211 | 0.222 | 0.387 | 0.468 | 0.593 |
| 720 | 0.078 | 0.228 | 0.269 | 0.435 | 0.659 | 0.766 | ||
| Multivariate | 336 | 0.586 | 0.566 | 1.128 | 0.873 | 1.424 | 0.994 | |
| 720 | 0.383 | 0.452 | 1.215 | 0.896 | 1.960 | 1.322 | ||
| ETTh2 | Univariate | 336 | 0.336 | 0.458 | 0.263 | 0.417 | 2.753 | 0.738 |
| 720 | 0.223 | 0.392 | 0.277 | 0.431 | 2.878 | 1.044 | ||
| Multivariate | 336 | 0.416 | 0.457 | 2.723 | 1.340 | 3.434 | 1.549 | |
| 720 | 3.043 | 1.304 | 3.467 | 1.473 | 3.963 | 1.788 | ||
| ETTm1 | Univariate | 288 | 0.086 | 0.214 | 0.401 | 0.554 | 0.462 | 0.558 |
| 672 | 0.067 | 0.209 | 0.512 | 0.644 | 0.639 | 0.697 | ||
| Multivariate | 288 | 0.358 | 0.386 | 1.056 | 0.786 | 1.740 | 1.124 | |
| 672 | 0.540 | 0.604 | 1.192 | 0.926 | 2.736 | 1.555 | ||
| ETTm2 | Univariate | 288 | 0.195 | 0.382 | — | — | — | — |
| 672 | 0.250 | 0.411 | — | — | — | — | ||
| Multivariate | 288 | 0.105 | 0.227 | — | — | — | — | |
| 672 | 0.128 | 0.269 | — | — | — | — | ||
Tables 5 and 6 demonstrate that the NHITS model consistently outperforms the Informer and ARIMA models across various datasets and forecasting horizons. The exception is the ETTh2 dataset for Horizon ∈ {24, 336}, where the Informer model performs marginally better than NHITS. Table 7 highlights the relative improvement in MSE and MAE of the NHITS model over the Informer model. On average, NHITS shows a 51.37% improvement in MSE and a 37.83% improvement in MAE. This significant enhancement underscores NHITS’s superior capability in capturing both short-term and long-term dependencies in the data, facilitated by its hierarchical interpolation mechanism and multirate signal sampling technique.
| Relative improvement (%) | ||||
|---|---|---|---|---|
| Dataset | Type | Horizon | MSE | MAE |
| ETTh1 | Univariate | 24 | 91.83 | 68.82 |
| 48 | 91.13 | 70.21 | ||
| 336 | 70.72 | 45.47 | ||
| 720 | 71.00 | 47.58 | ||
| Multivariate | 24 | 18.37 | 18.94 | |
| 48 | 35.32 | 32.00 | ||
| 336 | 48.04 | 35.16 | ||
| 720 | 68.47 | 49.55 | ||
| ETTh2 | Univariate | 24 | −44.08 | −11.66 |
| 48 | 0.00 | 5.09 | ||
| 336 | −27.75 | −9.83 | ||
| 720 | 19.49 | 9.04 | ||
| Multivariate | 24 | 81.80 | 62.55 | |
| 48 | 90.87 | 74.42 | ||
| 336 | 84.72 | 65.89 | ||
| 720 | 12.22 | 11.47 | ||
| ETTm1 | Univariate | 24 | 63.33 | 29.19 |
| 48 | 82.60 | 50.73 | ||
| 288 | 78.55 | 61.37 | ||
| 672 | 86.91 | 67.54 | ||
| Multivariate | 24 | 65.94 | 25.47 | |
| 48 | 22.67 | 13.32 | ||
| 288 | 66.09 | 50.89 | ||
| 672 | 54.69 | 34.77 | ||
| Average | 51.37 | 37.83 | ||
4.2. Univariate and Multivariate Forecasting
Univariate forecasting and multivariate forecasting represent two distinct methodological approaches applied in the field of predictive modeling and time series analysis. Univariate forecasting entails making predictions based on a single variable, whereas multivariate forecasting involves the simultaneous consideration of multiple variables to inform predictive outcomes [45].
Univariate forecasting typically offers relative simplicity and computational efficiency compared to its multivariate counterpart. It is particularly advantageous when relationships between variables are ill-defined or when there is limited availability of data. In contrast, multivariate forecasting methods address predictive challenges by comprehensively considering the interactions among multiple variables. These techniques excel in capturing dependencies and correlations between variables, leading to more precise forecasts in specific scenarios [46].
In the univariate benchmark for the ETT dataset, the target variable is the OT variable, with all other fields, presented in Table 2, excluded from consideration. Conversely, in the multivariate benchmark, the models generate predictions for every feature within the dataset, and the evaluation metrics are computed as averages across all dataset features.
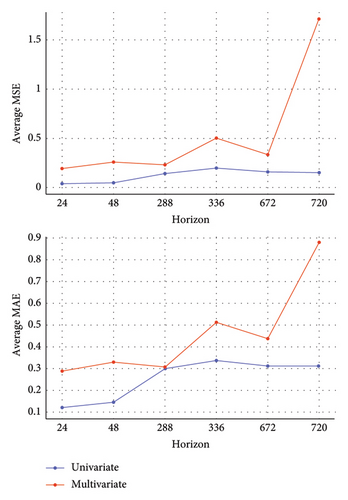
Figure 4 presents the average MSE and MAE for the NHITS model over various forecasting horizons for both univariate and multivariate time series on the ETT datasets. The figure demonstrates that univariate forecasts maintain relatively low and stable MSE and MAE values across different horizons, indicating high accuracy. In contrast, multivariate forecasts start with higher MSE and MAE values than univariate forecasts, and these metrics increase significantly as the forecast horizon extends.
4.3. Forecast Horizon
Long-horizon forecasting and short-horizon forecasting represent distinct temporal prediction approaches that focus on different forecasting time frames. Long-horizon forecasting involves predicting events in the distant future, while short-horizon forecasting focuses on predicting events shortly. Long-horizon forecasting, which involves making predictions for the distant future, is particularly challenging due to the inherent unpredictability of forecasts, increasing uncertainties, and the compounding of errors over time [47].
Tables 5 and 6 display the outcomes of forecasting over short and long-term horizons, respectively, as applied to the ETT dataset. In the case of short-horizon forecasting, we considered horizons of 24 and 48 data points, encompassing 1 day and 2 days for univariate and multivariate time series within the ETTh1,2 datasets, and 6 h and 12 h for the ETTm1,2 datasets. For long-horizon forecasting, we selected horizons of 336 and 720 data points for ETTh1,2, and for ETTm1,2 we selected horizons of 288 and 672. That is equivalent to 14 days and 30 days for ETTh1,2, and 72 h and 168 h for ETTm1,2. This configuration was applied for both the univariate and the multivariate time series.
Figure 4 shows that both MSE and MAE for univariate forecasts remain relatively low and stable across various horizons, indicating high accuracy, especially for shorter horizons (24 and 48 units). As the forecasting horizon extends to 288, 336, and 672 units, both metrics show a slight increase but tend to stabilize beyond 288 units. In contrast, multivariate forecasts display higher MSE and MAE values even at shorter horizons, reflecting the added complexity and potential errors from considering multiple variables simultaneously. For longer horizons (336 and 720 units), there is a significant increase in both MSE and MAE, particularly at the 336-unit mark and a noticeable spike at 720 units, indicating that multivariate forecasts become significantly less accurate over very extended periods.
4.4. Temporal Resolution
ETTm1,2 and ETTh1,2 represent two versions of the same dataset, with different temporal resolutions. Both datasets capture information related to electric load and oil temperature. However, ETTm1,2 maintains a high temporal resolution of 15 min, providing fine-grained insights into fluctuations and patterns over shorter time intervals. In contrast, ETTh1,2 opts for a lower temporal resolution, with data points collected at hourly intervals, offering a broader perspective with less granularity but spanning longer periods.
Table 8 displays the performance metrics for the univariate time series using ETTm1,2 and ETTh1,2 across various periods. The periods under consideration are t ∈ {1, 3, 7} days, corresponding to the horizon H ∈ {76, 288, 672} for ETTm1,2 and H ∈ {24, 72, 168} for ETTh1,2. An analysis of these results reveals distinct patterns for each case. For the 1-day forecast period, ETTm1 shows significantly higher MSE and MAE than ETTh1, with ETTm2 and ETTh2 exhibiting similar patterns. This suggests that the higher temporal resolution of ETTm1 may introduce more variability, leading to greater errors in short-term forecasts. Over a 3-day forecast horizon, the performance of ETTm datasets improves relative to ETTh datasets, with both ETTm1 and ETTm2 demonstrating lower MSE and MAE compared to their ETTh counterparts. This indicates that the higher granularity in ETTm datasets becomes beneficial over medium-term forecasts, possibly due to capturing more detailed fluctuations that aid in improving prediction accuracy. Finally, in the long-term 7-day forecasts, ETTm1 maintains lower error metrics compared to ETTh1, a trend that is also observed in ETTm2 and ETTh2. The reduced error in ETTm datasets for longer horizons suggests that the finer temporal resolution allows the model to maintain accuracy even as the forecast period extends, likely by better capturing underlying trends and periodic patterns.
| Period | 1 day | 3 days | 7 days | |||
|---|---|---|---|---|---|---|
| Dataset | MSE | MAE | MSE | MAE | MSE | MAE |
| ETTh1 | 0.008 | 0.077 | 0.089 | 0.229 | 0.121 | 0.290 |
| ETTm1 | 0.273 | 0.403 | 0.086 | 0.214 | 0.067 | 0.209 |
| ETTh2 | 0.134 | 0.268 | 0.179 | 0.347 | 0.233 | 0.383 |
| ETTm2 | 0.155 | 0.321 | 0.195 | 0.382 | 0.250 | 0.411 |
5. Discussion
The study demonstrates the effectiveness of the NHITS model in forecasting transformer oil temperature. To evaluate its performance, the NHITS model was compared against the Informer model using the same ETT dataset.
5.1. Forecasting Accuracy
The NHITS model demonstrated a notable decrease in both MSE and MAE compared to the Informer model, highlighting its superior capability for long-sequence forecasting. NHITS efficiently captures both long-term and short-term characteristics of time series data using its multirate signal sampling technique. Additionally, its hierarchical interpolation mechanism integrates predictions across various time scales, enhancing forecast accuracy and providing interpretable forecast decompositions. This approach allows for more precise insights into trends and seasonal patterns within the data. The model’s architecture, which includes multiple stacks and blocks operating at different temporal resolutions, effectively manages the diverse patterns and trends present in the data, further distinguishing it from the Informer model.
5.2. Univariate and Multivariate Forecasting
There is a clear performance gap between univariate and multivariate forecasts, with univariate forecasts consistently showing lower MSE and MAE values, highlighting their superior accuracy and stability across different horizons. In contrast, multivariate forecasts exhibit higher variability and error rates, especially for long-term predictions. This trend is observed in the NHITS, Informer, and ARIMA models and can be attributed to the higher dimensionality and complexity of multivariate data, which demand more computational resources and sophisticated handling. In the ETT dataset, the multivariate time series’ dimensionality is seven times greater. The lower error rates in univariate forecasting suggest that focusing on single-variable predictions might be more effective for applications requiring high accuracy, while multivariate forecasts, though potentially more informative, require careful handling.
5.3. Impact of Forecast Horizon
Another key finding is the model’s performance across different forecast horizons. Short-horizon forecasts were consistently more accurate than long-horizon ones, a trend seen in other models as well due to increased uncertainty and error accumulation over longer periods. Although the NHITS model’s hierarchical structure and multirate sampling approach help mitigate these issues, long-term predictions remain challenging. Nonetheless, NHITS still outperformed the Informer model.
5.4. Impact of Temporal Resolution
The performance differences between ETTm and ETTh datasets across different forecast horizons highlight the impact of temporal resolution on the NHITS model’s forecasting accuracy. Higher temporal resolution (15-minute intervals) in ETTm datasets generally leads to better performance in medium to long-term forecasts. In contrast, lower temporal resolution (hourly intervals) datasets might be more suitable for very short-term predictions but tend to lag in accuracy over extended periods. This analysis underscores the importance of selecting appropriate temporal resolutions based on the specific forecasting horizon and application requirements. For applications needing high accuracy over longer forecast periods, utilizing higher temporal resolution data can be advantageous. Conversely, for short-term forecasts, lower temporal resolutions may suffice and potentially reduce computational complexity.
The NHITS model’s ability to efficiently handle long-term dependencies, coupled with its hierarchical interpolation, allows it to outperform traditional models that rely on simpler time series extrapolation techniques. While NHITS shows promising results, its performance in different contexts or with larger datasets warrants further investigation to ensure generalizability. These results highlight the importance of selecting forecasting methods that suit the specific needs of each application, striking a balance between accuracy and computational efficiency.
6. Conclusions
Planning for electricity consumption over an extended period is a complex task that necessitates capturing long-range dependencies within the data. The proposed NHITS model shows superior performance compared to the Informer model in the context of the ETT dataset. This improvement can be attributed to the model’s ability to capture both long-term and short-term characteristics of the time series data through multirate signal sampling and hierarchical interpolation. The study highlights the differences between univariate and multivariate forecasting cases in the ETT dataset and explores the impact of forecast horizon length and temporal resolution on forecasting accuracy.
In conclusion, the NHITS model offers a promising solution for long-sequence and multivariate time series forecasting. By improving the accuracy of oil temperature forecasting, this model holds promise for enhancing predictive maintenance strategies, reducing operational costs, and preventing transformer failures in power distribution networks. Although training the NHITS model, particularly for multivariate time series, demands notable computational power and resources, its encouraging results highlight its potential. With future advancements and optimizations, it could become more suitable for real-time applications and environments with limited computational capacity. Future research could investigate combining NHITS with advanced methods, like ensemble techniques or hybrid models, to further improve its performance. Another area of focus could be implementing NHITS in real-time monitoring systems, allowing for dynamic adjustments to maintenance schedules based on predicted temperature fluctuations. Evaluating the model’s integration into real-time systems and its effectiveness in operational environments would provide valuable insights for practical use.
Conflicts of Interest
The authors declare no conflicts of interest.
Author Contributions
Abdeltif Boujamza: conceptualization, formal analysis, methodology, and writing–original draft. Saâd Lissane Elhaq: supervision, resources, project administration, and writing–review and editing.
Funding
This research did not receive any external funding.
Endnotes
1Data are available at https://github.com/zhouhaoyi/ETDataset.
Open Research
Data Availability Statement
The data that support the findings of this study are openly available on GitHub at https://github.com/zhouhaoyi/ETDataset.




