Volume 2025, Issue 1 5511446

Research Article

Open Access

Frequency Characteristics Analysis of Wind–Storage Joint Frequency Regulation System Taking Into Account the State of Storage Battery

Qihui Yu

Department of Mechanical Engineering , Inner Mongolia University of Science & Technology , Baotou , China , imust.cn

Inner Mongolia Engineering Technology Research Center of Mechatronics System Intelligent Diagnosis & Control Engineering , Baotou , China

Search for more papers by this author

Yuhui Li,

Yuhui Li

Department of Mechanical Engineering , Inner Mongolia University of Science & Technology , Baotou , China , imust.cn

Search for more papers by this author

Jianlong Zhang,

Jianlong Zhang

Inner Mongolia Mingyang North Smart Energy Research and Development Center Co. , Ltd. , Baotou , China

Search for more papers by this author

Ripeng Qin,

Ripeng Qin

orcid.org/0009-0008-7454-5333

Department of Mechanical Engineering , Inner Mongolia University of Science & Technology , Baotou , China , imust.cn

Inner Mongolia Engineering Technology Research Center of Mechatronics System Intelligent Diagnosis & Control Engineering , Baotou , China

Search for more papers by this author

Xueqing Hao,

Xueqing Hao

Department of Mechanical Engineering , Inner Mongolia University of Science & Technology , Baotou , China , imust.cn

Inner Mongolia Engineering Technology Research Center of Mechatronics System Intelligent Diagnosis & Control Engineering , Baotou , China

Search for more papers by this author

Guoxin Sun,

Corresponding Author

Guoxin Sun

[email protected]

orcid.org/0000-0001-7334-3205

Department of Mechanical Engineering , Inner Mongolia University of Science & Technology , Baotou , China , imust.cn

Inner Mongolia Engineering Technology Research Center of Mechatronics System Intelligent Diagnosis & Control Engineering , Baotou , China

Search for more papers by this author

Qihui Yu,

Qihui Yu

Department of Mechanical Engineering , Inner Mongolia University of Science & Technology , Baotou , China , imust.cn

Inner Mongolia Engineering Technology Research Center of Mechatronics System Intelligent Diagnosis & Control Engineering , Baotou , China

Search for more papers by this author

Yuhui Li,

Yuhui Li

Department of Mechanical Engineering , Inner Mongolia University of Science & Technology , Baotou , China , imust.cn

Search for more papers by this author

Jianlong Zhang,

Jianlong Zhang

Inner Mongolia Mingyang North Smart Energy Research and Development Center Co. , Ltd. , Baotou , China

Search for more papers by this author

Ripeng Qin,

Ripeng Qin

orcid.org/0009-0008-7454-5333

Department of Mechanical Engineering , Inner Mongolia University of Science & Technology , Baotou , China , imust.cn

Inner Mongolia Engineering Technology Research Center of Mechatronics System Intelligent Diagnosis & Control Engineering , Baotou , China

Search for more papers by this author

Xueqing Hao,

Xueqing Hao

Department of Mechanical Engineering , Inner Mongolia University of Science & Technology , Baotou , China , imust.cn

Inner Mongolia Engineering Technology Research Center of Mechatronics System Intelligent Diagnosis & Control Engineering , Baotou , China

Search for more papers by this author

Guoxin Sun,

Corresponding Author

Guoxin Sun

[email protected]

orcid.org/0000-0001-7334-3205

Department of Mechanical Engineering , Inner Mongolia University of Science & Technology , Baotou , China , imust.cn

Inner Mongolia Engineering Technology Research Center of Mechatronics System Intelligent Diagnosis & Control Engineering , Baotou , China

Search for more papers by this author

First published: 10 May 2025

https://doi.org/10.1155/je/5511446

Academic Editor: Fabio La Foresta

Share a link

Email
Wechat
Bluesky

Abstract

With the adjustment of the global energy structure, the power system under the penetration of new energy has developed rapidly. In response to the frequency security issues brought by new energy to the power system and the influence of the state of energy storage batteries on the system frequency, this paper constructs a frequency response model for wind–storage joint frequency regulation to analyze the frequency characteristics of the power system under different operating conditions. On this basis, considering the influence of the state of energy storage batteries on the system frequency, a system model under the scenario of additional load disturbance is built; the influence of environmental temperature on the state of energy storage batteries is analyzed to explore the changes in system frequency under high- and low-temperature conditions; finally, the robustness of the system frequency model under different wind speed changes is analyzed. The results show that when the state of energy storage batteries is considered in the wind–storage joint frequency regulation, the system frequency overshoot is reduced by 6.01%, the frequency recovery time is shortened by 3.476 s, and the steady-state frequency error is reduced by 0.004; high- and low-temperature environments will cause the frequency recovery time to be prolonged, with an overshoot of 16.30% in the 45°C high-temperature environment and an overshoot of 52.66% in the −25°C low-temperature environment; the lowest point of the system frequency remains above 49.6 Hz in the wind speed range of 5–15 m/s.

1. Introduction

In a period with a swift spread of globalization economic development, population increase, and technical advancement, there is an unparalleled rise in the world’s energy consumption [1]. Due to changes in the global energy system and the quick growth of clean resources, the share of newly generated power, mostly from wind and solar energy, is steadily rising [2]. Based on the German news agency, citing data from the Federal Network Agency, reported [3], Germany’s renewable energy generation in 2023 accounted for 56%; by the end of 2023, China’s wind power generation amounted to 885.87 billion kWh, and solar power generation amounted to 58.44 billion kWh, with the wind and solar power generation accounting for 25.63% of the total [4, 5]. However, traditional generators are unable to respond quickly enough to mitigate the intermittent power losses caused by new energy generation [6]. Moreover, the intermittent and random nature of new energy sources increases the volatility of grid-connected power generation and raises the frequency of system frequency regulation, leading to widespread concerns about the reliability of the power system [7]. Energy storage is one way to improve the utilization of new energy sources, reduce the impact of intermittent new energy sources on the grid, and provide flexibility and ancillary services to manage future power supply and demand challenges. It does this by having precise, quick, and flexible power response capabilities [8].

Therefore, the study suggests connecting energy storage to the wind power grid–connected system to provide active support, which can meet the grid’s requirement for the inertial response of wind farms and the primary frequency management, depending on the wind power’s inherent capacity for frequency regulation. Sun et al. [9] exploited the fast-ramping characteristics of energy storage systems to provide frequency regulation services using risk minimization techniques to address the uncertainty of frequency deviation and mitigate the problems associated with limited storage capacity. Castillo and Gayme [10] discussed the substantial role of grid-scale energy storage in the transition to an efficient, reliable, and cost-effective power system with renewable penetration rates, potential, and barriers and analyzed and compared different grid-scale storage technologies and battery technologies, showing that lithium battery storage is more suitable for large-scale energy and power services in terms of charge/discharge duration, response time, and efficiency. Wang et al. [11] conducted a comparative analysis of the substitution capability of energy storage and thermal units in power system frequency regulation, the multitimescales of different disturbance scenarios of the substitution ability of energy storage are analyzed under different disturbance scenarios in multiple timescales, and the high substitution ability of battery energy storage for thermal power units is verified. Liu et al. [12] establish the economic benefit model of energy storage batteries supporting conventional units in primary FM by carefully weighing the energy conversion rate and response time of various energy storage batteries when sizing energy storage capacity. This will yield the types of energy storage batteries that are appropriate for various control strategies in primary FM. In order to further analyze the frequency change of the power system when the battery energy storage participates in frequency regulation, scholars at home and abroad have carried out a lot of research on the frequency characteristics of the power system containing a high proportion of new energy sources [13, 14]. Yang et al. [15] use the model analysis method to establish the frequency response model of the power system where the wind–storage participates in frequency regulation and analyze the multidimensional frequency stability through the frequency characteristic transfer function, but they do not explore the internal state of lithium energy storage batteries. Gao et al. [16], after the power step, analyze the frequency response characteristics of the new energy power system and propose a workable method to quantify the common mode frequency characteristics of the system. To quantify the frequency characteristics, two indexes are proposed: a simple fall depth coefficient and a simple fall slope coefficient, but the battery pack state is not included. Zhang and Shi [17] conducted a dynamic modeling of large-scale wind power access to the power system’s frequency control features and examined the effects of wind power access on the power system’s frequency characteristics. Dar, [18] described the power and current response, which gives ideas for the simulation of this paper, based on the power system under high wind power penetration rate, the use of energy storage technology to improve the regional response characteristics of single-area power system, and the introduction of load perturbation.

When the energy storage charge state is at the top and lower limits, there will not be adequate storage power in the actual joint frequency control application. This is due to the fact that the energy storage battery’s internal condition affects how frequently the power system changes frequencies. Zhang et al. [19] proposed a wind–storage joint frequency regulation control strategy considering the state of charge (SOC) of the energy storage, comprehensively considered the frequency regulation demand under the complex working conditions of random changes in the wind speed and the load, and simulated and verified the proposed control strategy to take into account both the frequency regulation effect and the SOC protection. Ma and Yu [20] established the principle of dividing the charge state of energy storage to ensure the long-term stable operation of energy storage and adjusted the output of the energy storage device according to the division of the region, which greatly improved the stability of the frequency. Li et al. and Yan et al. [21, 22] proposed an SOC recovery strategy to ensure the stability of energy storage by considering the power management of the energy storage and taking full advantage of the dead zone of the frequency regulation, based on the base point of the SOC. SOC recovery strategy is proposed to ensure that the energy storage SOC is in a good state for a long time, but this control strategy model is more complex, which is not conducive to practical control. Large-scale battery energy storage systems are typically made up of several storage power plants. As input times increase, variations in the state of health (SOH) of the storage batteries develop gradually. These variations will eventually cause the storage system’s capacity and lifespan to be significantly reduced. Duan et al. [23] proposed an energy storage power allocation strategy that takes into account the consistency of the SOH of the storage batteries and the SOC, by using the optimization algorithm of the adaptive variational particle swarm algorithm, but this control strategy model is more complicated and is not conducive to practical control. To summarize, the majority of scholarly research has concentrated on energy storage SOC and SOH control strategies, largely ignoring the impact of external temperature, cycle times, and other factors on the internal characteristics of the battery in real-world scenarios. Additionally, analysis of the battery’s condition has a bearing on how the energy storage battery is allocated to capacity under wind–storage joint FM and how the power system frequency changes.

The main contributions of this paper are as follows: (1) By taking into account the penetration of new energy sources and the status of the storage battery, a suggested energy storage system frequency response model increases the power system’s frequency stability when compared to previous studies. (2) Dynamic characteristics (frequency recovery time t_r, overshoot M_p) and static characteristics (frequency steady-state error e_ss) are introduced to qualitatively analyze the system frequency characteristics. The formation of rest of the article is organized as follows: A frequency response model of the power system under the combined wind–storage FM is constructed in Section 2. The energy storage system’s capacity is configured in Section 3. In Section 4, the model is validated by simulation, and the outcomes are analyzed. Lastly, the final portion contains the study’s conclusion.

2. Frequency Response Modeling of Power System Under Joint Wind–Storage Frequency Regulation

In order to get the highest output power at the current wind speed, a power electronic converter regulates the rotational speed of the doubly fed induction generator (DFIG) set, which is a wind turbine. The wind turbine’s mechanical power output P_m, in the absence of additive control, is represented as

()

where ρ is the air density, S is the area swept by the blade, v is the value of wind speed, λ is the tip speed ratio, β is the pitch angle of the fan blade, and C_p is the wind energy conversion coefficient, which indicates the energy capture efficiency of the fan. C_p has a certain coupling relationship with λ and β, and its expression is shown in Equation (2):

()

where ω is the rotor speed of the wind turbine, under MPPT control, when the wind turbine output is less than the rated power, the pitch angle is 0, and the wind energy utilization factor can be maximized by the speed adjustment of the generator set.

Equation (3) illustrates the small signal increment expression of the transmission system, which transfers the mechanical power absorbed by the wind turbine to the generator:

()

where P_mw is the mechanical power of the fan, P_e is the electromagnetic power of the fan, H_wind is the fan inertia time constant, and Δω is the fan speed variation of the Mississippi value.

Power electronic control is primarily necessary for the realization of active frequency support in new energy power generation equipment, such as wind power and photovoltaic power generation equipment. Active support falls into two categories: power standby control and virtual inertia control. Wind farm virtual inertia is a control technique that mimics the synchronous generator’s inertia characteristics. It works by adding more virtual inertia to the wind farm, simulating the synchronous generator’s inertia response, which slows down power fluctuations and further improves power system stability. Figure 1 illustrates the control principle of the wind farm.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Principles of wind farm control.

The virtual inertia control participates in FM with an additional active power of

()

The wind turbine active power output value is the sum of additional power and MPPT power, and its small signal increment expression is shown in Equations (5) and (6).

()

where H_w is the virtual inertia coefficient, ΔP_MPPT(s) is the MPPT power, ΔP_e(s) is the additional power, and Δf(s) is the system frequency variation. Wind turbine frequency regulation is mainly through two ways: rotor inertia and variable pitch control. Rotor inertia controls the change of rotor speed by controlling the rotor side converter, which releases or absorbs the kinetic energy stored in the rotating mass of the WTG for a short period of time, in order to respond quickly to the system frequency change [24]. Its frequency characteristic transfer function is shown in Equation (7).

()

where k_df is the inertia response coefficient, T_w is the rotor inertia response time constant, and ΔP_w is the rotor inertia provided power [25]. By altering the windward angle of the wind turbine’s paddles, variable pitch control lowers the wind turbine’s efficiency of wind energy conversion while shifting the operating point of the wind turbine away from the MPPT point and increasing the FM standby capacity. Its frequency characteristic transfer function is shown in Equation (8):

()

where k_pf is the primary FM coefficient, T_β is the pitch response time constant, and ΔP_β is the power provided by pitch control. Equation (9), which illustrates the transfer function of the wind turbine frequency regulation model, shows how the two frequency regulation methods—pitch control and rotor inertia—combine to give the wind turbine a primary ability to regulate frequency:

()

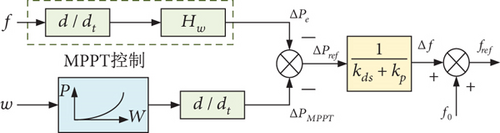
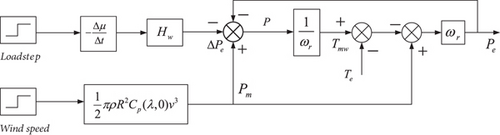
According to the above mathematical model, the wind turbine (DFIG) FM model is built as shown in Figure 2.

The traditional power source includes steam turbine and hydraulic turbine, and the steam turbine can be divided into reheat turbine and non-reheat turbine, whose transfer functions are shown in Equations (10)–(12):

()

where T_CH is the steam volume time constant, T_RH is the reheat time constant, T_W is the water hammer effect constant, and F_HP is the proportion of the work done by the high-pressure cylinder in the work done by the turbine.

The actual power system includes multiple generating units; in order to simplify the model, the common method is to equate various types of generators into a single generating unit and attach the active power to the single system. Literature [26] built an improved SFR analytical calculation equivalent model through the weighted equivalence method; at this time, when the system includes multiple thermal power units, the equivalent turbine-generator aggregation model transfer function obtained is shown in the following equation:

()

where R_TG, T_RHG, and F_HPG, respectively, are expressed as the equivalent thermal unit of the governor coefficient 0.05, reheater time constant 5 s, and high-pressure turbine stage power share of the aggregation parameter 0.3.

Without considering the generating unit governor, the frequency characteristic transfer function of the power system is shown in Equation (14):

()

where M = 2H, H is the inertia constant, and D is the damping constant. When modeling in this paper, the impact of the high percentage of new energy penetration on the frequency characteristics of the grid system is considered, assuming that the new energy penetration rate is α; then, the system frequency characteristic transfer function is shown in Equation (15):

()

where M₁ = (1 − α)M.

Due to the significant influx of new energy into the power system, traditional wind turbine frequency regulation finds it challenging to meet system frequency regulation requirements. However, energy storage offers precise, quick, and adaptable power response capabilities, so its involvement in frequency regulation can accelerate wind turbine frequency regulation’s response time. According to the literature [27], battery energy storage system can be expressed as a first-order transfer function; the frequency response [28] transfer function of the energy storage system is shown in Equation (16):

()

where ΔP_E is the power provided when only energy storage is used, T_E is the energy storage response time constant, and k_df is the inertia response coefficient of the energy storage system.

Due to the unpredictable character of wind speed in real-world application scenarios, the energy storage battery occasionally needs to be continuously charged or discharged, which causes the system’s SOC to exceed its limit. Additionally, the battery’s capacity is limited, and it must be charged and discharged in a way that is appropriate for its SOC. The mathematical model of energy storage battery charging and discharging [28] is shown in Equation (17):

()

where P_E(k) is the power command of energy storage at time k, when P_E(k) > 0 indicates that the energy storage is in a charging state and P_E(k) < 0 indicates that the energy storage is in a discharging state [28]; SOC(k) is the SOC value of the energy storage at time k, C_rated i s the rated capacity of the battery storage, η₁ is the charging efficiency of the battery storage system, and η₂ is the discharging efficiency of the battery storage system, which is calculated as shown in Equation (18):

()

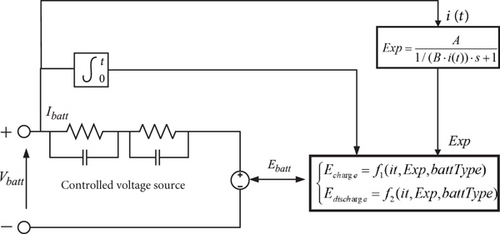
In the equation, η_AC-DC is the energy storage battery [29] AC to DC conversion power, η_DC-AC is the energy storage battery DC to AC conversion power, η_C is the storage battery’s own charging efficiency, and η_d is the storage battery’s own discharge efficiency. As can be seen from the formula, η₁ and η₂ are the value of the approximation, and it is unified to express the storage battery charging and discharging efficiency. The above mathematical models are combined to build a frequency response model of the battery energy storage system considering the efficiency of energy storage charging and discharging, as shown in Figure 3. The diagram controls the charging and discharging modes through logical judgments (such as “yes” and “not”) and describes the dynamic response characteristics of the system using transfer functions (such as 1/(s + 1)). Key parameters include power (P_e), time (3600 s), energy rate (E_rate), and the battery’s SOC and initial energy (E₀).

In the actual grid operation process, three aspects of energy storage system capacity matching, operation strategy, and economic evaluation need to be analyzed, and the decay of battery capacity is one of the indicators for the cost-and-benefit evaluation of energy storage system. The capacity decay of the battery is the result of the combined effect of cyclic aging and calendar aging, in which the calendar aging is mainly affected by temperature, and according to Arrhenius’ law, the effect of temperature on the relative discharge capacity decay is shown in Equations (19) and (20) [30, 31]:

()

where k_temp(T) is the influence factor representing the temperature; k_soc(SOC) is the influence factor representing the SOC;

is the influence factor representing the time; k_ref is the influence factor representing the reference temperature and the SOC; T_ref is the reference temperature; E_a is the activation energy, and the unit is joule per mole (J/mol); and R is the universal gas constant, which takes the value of 8.314 J/(mol K). Cyclic aging refers to the depletion of battery capacity by the increase in the number of battery charging and discharging times, and the effects of the number of cycles on the battery capacity and internal resistance are shown in the following Equations (21) to (23).

()

where k = 1, 2, 3, ⋯, T_h is the half-cycle, and the unit is seconds (s), when the battery is discharging and charging opposite to get a full cycle; ε(n) is the battery aging factor, and the BOL and EOL aging factor is equal to 0 or 1; R_EOL is the internal resistance of the battery at the EOL and the standard temperature (25°C), and the unit is ohms; R_BOL is the internal resistance of the battery, and the unit is ohms; Q_EOL is the battery at the end of the life at the rated ambient temperature of maximum capacity, and the unit is Ah; and Q_BOL is the battery at the beginning of the life of the maximum capacity at the rated ambient temperature, and the unit is Ah. The formula for calculating the battery aging factor is shown below:

()

where N is the maximum number of cycles. Combining the above mathematical models, the dynamic equivalent circuit model of the energy storage battery considering the temperature and life cycle can be built, as shown in Figure 4.

Based on the dynamic equivalent circuit model of the energy storage battery, the internal characteristics of the energy storage battery can be further analyzed, and the frequency response model of the battery energy storage system can be constructed considering the temperature and life cycle:

()

where P_e is the load demand power of the energy storage system, P is the value of grid power output, P_L is the additional load,

is the output power of traditional thermal power units,

is the output power of traditional hydroelectric units, and P_m is the output power of wind turbines. The actual grid battery energy storage system is formed by a number of batteries in series and parallel integration, with the series and parallel number of power requirements by the system, assuming the amount of series for a, parallel number b, and the power of a single storage battery as shown in Equation (26):

()

where P_batt is the power value of a single energy storage battery. When the power of a single battery is greater than 0, this indicates that the battery is in the discharge state, and the equivalent resistance value is calculated; when the power of a single battery is less than 0, this indicates that the battery is in the charging state, and the value of its charging current is calculated. Figure 5 shows the frequency response model of the battery energy storage system considering the temperature and life cycle.

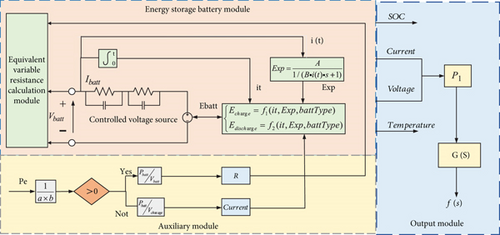
The energy storage system’s capacity can be configured in a way that is both rational and scientific to address the issue of grid frequency that arises from wind power grid integration. In order to analyze the additional load, frequency downward fluctuation of the wind power, and energy storage system to participate in the ratio of the electric power system’s capacity in order to meet the demand of the storage system under the change of wind speed, this section combines the actual wind speed and power data of a wind power plant in the Inner Mongolia Autonomous Region.

When the wind farm participates in FM, the required primary FM power

and capacity

are as shown in Equations (27) and (28):

()

where P_m is the output power of the wind turbine, R is the sag factor 0.05, and T_d is the duration of the energy storage system for 50 s.

The wind turbine provides primary FM through pitch control, the power it provides is shown in Equation (29), the insufficient power is supplemented by the energy storage system, and the power of energy storage is shown in Equation (30):

()

Assuming that the rated capacity of the storage battery is E_rated , the SOC of the storage battery Q_soc can intuitively reflect the remaining capacity of the storage battery as shown in Equation (31):

()

The SOC of the storage battery Q_soc,k at the kth moment is shown in Equation (32):

()

Considering the application effect and the cost of the energy storage battery and other factors, it can be seen that the rated capacity should satisfy

()

The minimum storage battery capacity that can meet the requirements when the above equation takes the equal sign is the rated capacity E_rated ; then, the rated value of the storage battery output power is as shown in Equation (34):

()

where DOD is the depth of discharge.

3. Results

Based on the aforementioned study, a power system frequency response model is constructed on the MATLAB/Simulink simulation platform, as seen in Figure 6, and the system configuration is displayed in Table 1. In the MATLAB/Simulink model, the initial power value is set to P₀ = 100 MW and the initial frequency value is f₀ = 50 Hz. A step load disturbance with an amplitude of ΔP_L = 10 MW is applied to simulate the system’s response to sudden changes in load. The model includes traditional power supply, wind generation, and energy storage. This study sets up four simulation instances with varying operating conditions to show how the wind–storage joint system improves frequency responsiveness while taking the energy storage battery’s condition into account.

Table 1. System configuration parameters.

Parameters	Numerical value	Parameters	Numerical value
Initial Power P₀	100 MW	Initial frequency f₀	50 Hz
New energy penetration α	30%	Inertial response time T_w	0.1 s
System equivalent time constant H	4.5	Sagging factor R	0.05
Damping constants D	2	Energy storage time constant T_E	0.2 s
Wind power inertia factor k_df	20	Primary FM power for wind farms ΔP_β	20 MW
Primary frequency modulation factor k_pf	20	Primary FM capacity of wind farms E	166 KMh
System disturbance P_L	10 MW	The duration of the energy storage system T_d	50 s

Working Condition I: no wind power access, by the traditional power supply for a frequency regulation; Working Condition II: wind power to participate in frequency regulation; Working Condition III: energy storage system access, do not consider the storage battery state of the wind–storage joint frequency regulation; Working Condition IV: energy storage system access, considering the storage battery state of the wind–storage joint frequency regulation.

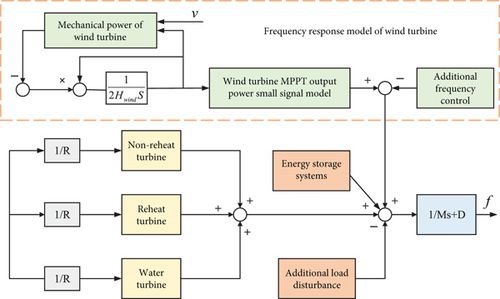
From Figures 7 and 8, it is found that when new energy is connected to the power system, wind power participation in frequency regulation provides inertial response and spare capacity required for frequency regulation so that the lowest point of the system frequency under the additional perturbation is increased, the amount of frequency deviation is reduced, the inertial response of the wind turbine is faster than that of the traditional power source, and the fluctuation is more gentle.

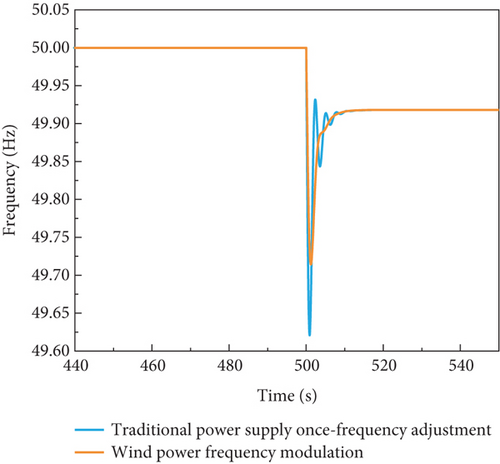
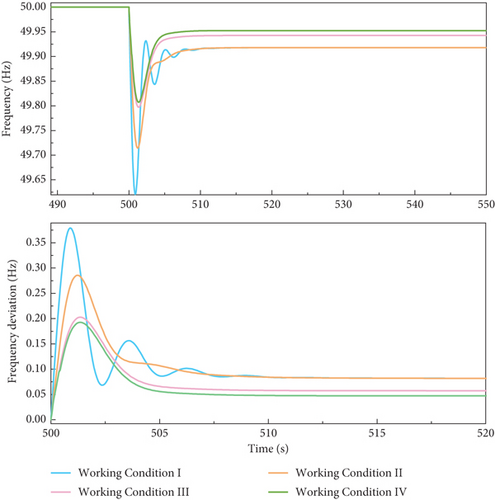
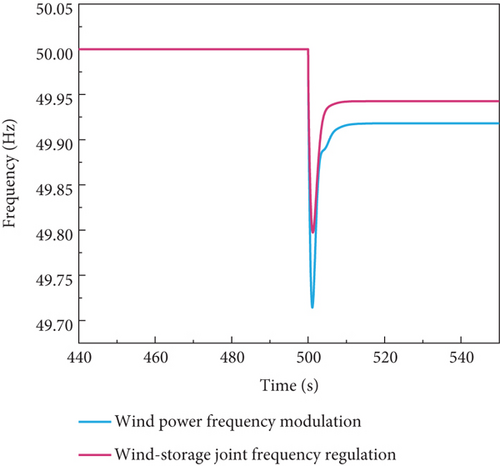
As shown in Figures 8 and 9, the integration of the energy storage system significantly improves the frequency response characteristics of the power system. Specifically, the frequency recovery time under Condition IV is reduced to 10.788 s, which is substantially shorter than that of Condition I (23.5813 s). The energy storage system compensates for the power required by the rotor inertia of the wind turbine and variable pitch control, thereby effectively meeting the system’s frequency regulation demands. The wind–storage joint frequency regulation not only elevates the lowest point of the system frequency but also reduces the rate of frequency change and minimizes frequency deviation, significantly enhancing the stability of the power system. Furthermore, the energy storage system enables peak-shaving and valley-filling, which reduces frequency volatility. Compared to Conditions I and II, the frequency curve under Condition IV is smoother, indicating a more effective reduction in storage capacity requirements.

4. Discussion

The frequency response process is a dynamic process. This paper introduces the dynamic characteristic index to further analyze the frequency characteristics of the proposed model. Frequency recovery time t_r refers to the time required from the frequency fluctuation to the frequency to restore the steady state and is a measure of the system response speed; from what can be seen in Figure 8, the traditional power supply once the frequency recovery time t_r1 for 23.5813 s, wind power to participate in the frequency adjustment frequency recovery time t_r2 for 16.899 s, the wind and storage of the joint frequency adjustment frequency recovery time t_r3 for 14.264 s, and the storage battery state of the wind and storage of the joint frequency adjustment time t_r4 for 10.788 s can be considered The frequency recovery time t_r4 is 10.788 s for wind–storage joint FM when the storage battery state is considered; it can be seen that the frequency recovery time of the system is reduced by 3.476 s when the internal state of the storage battery is considered comprehensively, and the response speed is faster.

The overshoot M_p refers to the extent to which the maximum value of the output signal exceeds the steady-state value when the system undergoes a step input or other sudden change in input. The following Equation (35) shows that ξ represents the damping ratio, which is related to the ambient temperature:

()

From the steady-state characteristic index to analyze the frequency characteristics of the power system in the load disturbance, the frequency steady-state error value is shown in the following Equation (37):

()

Based on the aforementioned equations, Table 2 summarizes the key frequency characteristics under different operating conditions, including frequency overshoot (M_p), frequency recovery time (t_r), and steady-state frequency error (e_ss). The results demonstrate that the wind–storage joint frequency regulation system, especially when considering the state of the storage battery (Condition IV), significantly improves system performance by reducing frequency overshoot by 6.01%, shortening the recovery time by 3.476 s, and decreasing the steady-state error by 0.004 compared to traditional power supply (Condition I).

Table 2. Frequency characteristics under different operating conditions.

Condition	Description	M_p	t_r	e_ss
I	Traditional power supply	10.04%	23.5813 s	0.245
II	Wind power participation	8.02%	16.899 s	0.238
III	Wind–storage joint FM (without battery state)	6.63%	14.264 s	0.232
IV	Wind–storage joint FM (with battery state)	0.62%	10.788 s	0.228

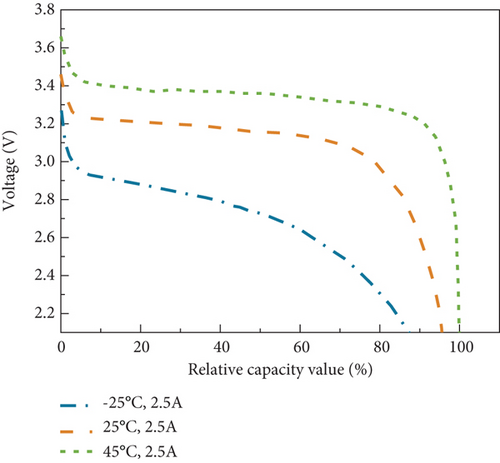
The variation in environmental temperature can directly affect the capacity of the battery. In high-temperature environments, the battery capacity increases, while in low-temperature environments, the battery capacity decreases, as shown in Figure 10. To assess the feasibility of practical application scenarios and considering the unique characteristics of high-temperature deserts or low-temperature polar regions, this study has simulated high-temperature conditions at 45°C and low-temperature conditions at −25°C. As shown in Figure 11, the frequency recovery time in low-temperature environments increases by 5.216 s compared to the standard temperature (25°C), while in high-temperature environments, the frequency recovery time increases by 3.316 s compared to the standard temperature (25°C). The specific frequency stability index calculation results are shown in Table 3.

Table 3. Frequency steady-state index calculation results at high temperature (45°C) and low temperature (−25°C).

Temperature (°C)	Damping ratio ξ	Frequency overshoot M_P
45	0.2	16.30%
−25	0.5	52.66%

In addition to the operating conditions discussed above, the performance of the proposed wind–storage joint frequency regulation system was further evaluated under different wind speeds to assess its robustness in real-world scenarios. Three wind speed conditions were considered: low wind speed (5 m/s), rated wind speed (10 m/s), and high wind speed (15 m/s).

Figure 12 shows the frequency response curves under low wind speed (5 m/s), rated wind speed (10 m/s), and high wind speed (15 m/s). The results indicate that the system maintains stable frequency regulation performance across a wide range of wind speeds. The frequency recovery time is shortest under rated wind speed (10.2 s), while low wind speed (5 m/s) results in a slightly longer recovery time (12.5 s) due to reduced power output. High wind speed (15 m/s) also shows a relatively short recovery time (11.0 s) but with a slightly higher frequency overshoot (0.624%) compared to rated wind speed (0.532%). These findings are summarized in Table 4.

Table 4. Frequency response characteristics under different wind speeds.

Wind speed (m/s)	Frequency lowest point (Hz)	Frequency recovery time (s)	Frequency overshoot (%)
5	49.6	12.5	0.811
10	49.8	10.2	0.532
15	49.7	11.0	0.624

These experimental results demonstrate that the proposed system is robust to variations in wind speed and can effectively stabilize frequency under different operating conditions. This further supports the practical applicability of the wind–storage joint frequency regulation system in real-world power systems with fluctuating wind resources.

5. Conclusions

To address the frequency fluctuations in power systems caused by the integration of renewable energy, this paper proposes a power system frequency response model based on the transfer function of the power system, incorporating the penetration rate of renewable energy. A simulation model is developed to analyze the system’s behavior under a step load disturbance scenario, and the frequency characteristics are evaluated across various operating conditions. For the wind–storage joint frequency regulation system, an in-depth analysis is performed to investigate the influence of the internal state of the storage battery on system frequency dynamics. Furthermore, special operational scenarios, such as those in desert and polar environments, are examined, with a focus on system frequency variations under extreme high and low temperatures. Additionally, a robustness analysis is conducted to assess the system’s performance under varying wind speed conditions. The following conclusions are drawn:

1.
The wind–storage joint frequency regulation method makes full use of the superiority of energy storage, to make up for the rotor inertia of the wind turbine and the power required for pitch control, and improves the lowest point of the system frequency by 0.084 Hz.
2.
The charge state of the storage battery decreases with time, and the internal temperature of the battery increases; when considering the state of the storage battery, the maximum frequency deviation of the system frequency can be reduced by 0.01 Hz, the frequency steady-state error value e_ss is reduced by 0.004, the frequency recovery time t_r is reduced by 3.476 s, and the overshoot in frequency is reduced by 6.01%.
3.
The change in ambient temperature will directly affect battery capacity. Under high-temperature conditions of 45°C, the frequency recovery time increases by 3.316 s, while under low-temperature conditions of −25°C, the frequency recovery time increases by 5.216 s. Moreover, under low-temperature conditions, the frequency overshoot reaches 52.665%, whereas under high-temperature conditions, the frequency overshoot is 16.30%.
4.
Furthermore, the proposed wind–storage joint frequency regulation system demonstrates strong robustness under varying wind speeds (low wind speed: 5 m/s; rated wind speed: 10 m/s; and high wind speed: 15 m/s). Experimental results show that the system performs optimally at rated wind speed, with the shortest frequency recovery time (10.2 s). Under low wind speed, the frequency recovery time increases to 12.5 s due to reduced power output from the wind turbine, but the system still maintains stable frequency regulation. Under high wind speed, the frequency recovery time is slightly longer (11.0 s) with a minor overshoot (0.624%), indicating that the system can effectively handle excess wind power without significant instability.

Although the proposed model demonstrates significant improvements in frequency stability, this study has certain limitations. Specifically, the impact of energy storage capacity on the frequency performance of the model has not been fully explored. Further research could investigate the effects of energy storage capacity on system frequency and propose strategies to mitigate its impact on system frequency stability. Future work will focus on optimizing energy storage capacity, combining experimental and algorithmic studies to further analyze the extent to which the internal state of the battery affects system frequency, and conduct an economic analysis of the system.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

Research is supported by the Foundation for Innovative Research Groups of the National Natural Science Foundation of China (10.13039/501100001809) (52465008), the Basic Scientific Research Fund Projects of Universities Affiliated with Inner Mongolia Autonomous Region (2024QNJS012, 2024QNJS075, 0406082203), and the Natural Science Foundation of Inner Mongolia (2022LHMS05023).

Acknowledgments

The research work presented in this paper is financially supported by a Grant (52465008) of the National Natural Science Foundation of China and a Grant (2022LHMS05023) of the Natural Science Foundation of Inner Mongolia. The authors also acknowledge support from the Basic Scientific Research Fund Project of Universities Directly Under the Jurisdiction of the Inner Mongolia Autonomous Region through grants 0406082203, 2024QNJS075, and 2024QNJS012.

Open Research

Data Availability Statement

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

References

1 Abeg A. I., Islam M. R., Hossain M. A., Ishraque M. F., Islam M. R., and Hossain M. J., Capacity and Operation Optimization of Hybrid Microgrid for Economic Zone Using a Novel Meta-Heuristic Algorithm, Journal of Energy Storage. (2024) 94, 112314, https://doi.org/10.1016/j.est.2024.112314.
10.1016/j.est.2024.112314
Google Scholar
2 Chen C., Duan S., Cai T., Liu B., and Hu G., Optimal Allocation and Economic Analysis of Energy Storage System in Microgrids, IEEE Transactions on Power Electronics. (2011) 26, no. 10, 2762–2773, https://doi.org/10.1109/TPEL.2011.2116808, 2-s2.0-80053618733.
10.1109/TPEL.2011.2116808
Web of Science® Google Scholar
3 Federal Network Agency for Electricity, Gas, Telecommunications, Posts and Railway (BNetzA), [Online]. Available: https://www.bundesnetzagentur.de.
Google Scholar
4 National Energy Administration (NEA), Xi Jinping Presides Over Central Financial and Economic Leadership Group Meeting [EB/OL], 2014, Retrieved from http://www.nea.gov.cn/2014-06/17/c_133413362.htm.
Google Scholar
5 National Energy Administration, China Electricity Statistical Yearbook, 2024, China Statistical Publishing House.
Google Scholar
6 Sepúlveda F. J., Montero I., Barrena F., Miranda M. T., and Arranz J. I., Design and Energy Analysis of Photovoltaic-Battery Prototype Considering Different Voltage Levels, Batteries. (2023) 9, no. 1, https://doi.org/10.3390/batteries9010016.
10.3390/batteries9010016
Google Scholar
7 Mohamad F., Teh J., and Lai C. M., Optimum Allocation of Battery Energy Storage Systems for Power Grid Enhanced With Solar Energy, Energy. (2021) 223, 120105, https://doi.org/10.1016/j.energy.2021.120105.
10.1016/j.energy.2021.120105
Web of Science® Google Scholar
8 Akinyele D. O. and Rayudu R. K., Review of Energy Storage Technologies for Sustainable Power Networks, Sustainable Energy Technologies and Assessments. (2014) 8, 74–91, https://doi.org/10.1016/j.seta.2014.07.004, 2-s2.0-84907163711.
10.1016/j.seta.2014.07.004
Google Scholar
9 Sun Y., Bahrami S., Wong V. W. S., and Lampe L., Application of Energy Storage Systems for Frequency Regulation Service, Proceedings of the 2017 IEEE International Conference on Smart Grid Communications (SmartGridComm), 2017, IEEE, 141–146, https://doi.org/10.1109/SmartGridComm.2017.8340719, 2-s2.0-85050885826.
10.1109/SmartGridComm.2017.8340719
Google Scholar
10 Castillo A. and Gayme D. F., Grid-Scale Energy Storage Applications in Renewable Energy Integration: A Survey, Energy Conversion and Management. (2014) 87, 885–894, https://doi.org/10.1016/j.enconman.2014.07.063, 2-s2.0-84907343531.
10.1016/j.enconman.2014.07.063
Google Scholar
11 Wang K. F., Xie L. R., Qiao Y., Lu Z., and Yang H., Analysis of Frequency Regulation Performance of Power System Improved by Battery Energy Storage, Automation of Electric Power Systems. (2022) 46, no. 1, 174–181.
Google Scholar
12 Liu X., Li X., Tan Z., Huang J., Cui Y., and Zhang B., Economic Comparison of Optimal Strategies Based on Different Types of Energy Storage Batteries Participating in Primary Frequency Regulation, High Voltage Engineering. (2022) 48, no. 4, 1403–1410.
Google Scholar
13 Zeng P., Zhang X. P., Terzija V., Ding Y., and Luo Y., The 37th Annual Conference on Power System and Automation in Chinese Universities (CUS-EPSA), 2023, 1030, Springer Nature, https://doi.org/10.1007/978-981-99-1439-5_18.
10.1007/978-981-99-1439-5
Google Scholar
14 Shu H., Dong H., Wang G., Chen J., Shi B., and Tang Y., Wind-Storage Coordinated Control Strategy for Inertia Enhancement of High Ratio Renewable Energy Power Systems, Journal of Energy Storage. (2024) 97, 112998, https://doi.org/10.1016/j.est.2024.112998.
10.1016/j.est.2024.112998
Google Scholar
15 Yang K., Xie L., Xiong H., Cui Z., Yang X., and Liu Y., Frequency Characteristic Analysis of Smart Grid Considering Wind-Storage Frequency Response, Electrical Measurement. (2024) 61, no. 11, 165–173.
Google Scholar
16 Gao H., Xin H., Huang L., Xu T., Ju P., Qin X., and Huang W., Common Mode Frequency Analysis and Characteristic Quantification of New Energy Power System, Chinese Journal of Electrical Engineering. (2021) 41, no. 3, 890–900.
Google Scholar
17 Sun H. S., Liu J., Wen J. Y., Cheng S. J., Luo C., and Yao L. Z., Participation of Large-Scale Wind Power Generation in Power System Frequency Regulation, Chinese Science Bulletin. (2013) 58, no. 36, 4557–4565, https://doi.org/10.1007/s11434-013-6094-6, 2-s2.0-84888233805.
10.1007/s11434-013-6094-6
Google Scholar
18 Dar S. Z. N., Enhanced Power and Frequency Response Characteristics in Single Area Power System With Superconducting Magnetic Energy Storage, Proceedings of the 2017 International Conference on Intelligent Computing, Instrumentation and Control Technologies (ICICICT), 2017, IEEE, 1551–1555, https://doi.org/10.1109/ICICICT1.2017.8342801, 2-s2.0-85049414554.
10.1109/ICICICT1.2017.8342801
Google Scholar
19 Zhang X., Qin S., Chen C., Hao S., Wu Q., and Zhang J., Wind-Storage Combined Frequency Regulation Control Strategy Considering Charge-Discharge Balance of Energy Storage, Power System Technology. (2024) 48, no. 5, 1938–1946.
Google Scholar
20 Ma Y. and Yu P., Research on Combined Frequency Regulation Control Method of Wind Storage With Storage System Optimized Intervals Considered, Mathematical Problems in Engineering. (2022) 2022, 12, https://doi.org/10.1155/2022/6872799, 6872799.
10.1155/2022/6872799
Google Scholar
21 Li J., Gao Z., Li C., Yan G., Ma D., and Kan Z., Energy Storage-Assisted Wind Power Primary Frequency Modulation Control Strategy Based on Dynamic Task Coefficient, Automation of Electric Power Systems. (2021) 45, no. 19, 52–59.
Google Scholar
22 Yan Q., Wang M., Duan S., Zhang W., Li J., and Cai C., Energy Storage Primary Frequency Modulation Control Strategy Considering Charge State Recovery, Automation of Electric Power Systems. (2022) 46, no. 21, 52–61.
Google Scholar
23 Duan S., Yu H., Liu C., Wang M., Wang S., and Xia B., Power Allocation Strategy for BESS Considering Consistency of Health State and State of Charge in Energy Storage Units, Automation of Electric Power Systems. (2023) 47, no. 5, 65–73.
Google Scholar
24 Miao F., Tang X., and Qi Z., Analysis of Frequency Characteristics of Power System Based on Wind Farm-Energy Storage Combined Frequency Regulation, Gaodianya Jishu/High Voltage Engineering. (2015) 41, no. 7, 2209–2216, https://doi.org/10.13336/j.1003-6520.hve.2015.07.013, 2-s2.0-84939449007.
10.13336/j.1003-6520.hve.2015.07.013
Google Scholar
25 Li J., Xin D., Liu C., Hou X., and Li D., Research on the Frequency Regulation Characteristics and Control Strategy of Wind Power Generation With Energy Storage Synergy, Batteries. (2023) 9, no. 2, https://doi.org/10.3390/batteries9020117.
10.3390/batteries9020117
Google Scholar
26 Li S., Cao R., Lei X., Li Z., and Liu D., Frequency Response Characteristics of Power System With Wind Power Virtual Inertia/Primary Frequency Regulation Based on Improved SFR Model, Renewable Energy Resources. (2019) 37, no. 5, 694–700.
Google Scholar
27 Mishra S., Mallesham G., and Jha A. N., Design of Controller and Communication for Frequency Regulation of a Smart Microgrid, IET Renewable Power Generation. (2012) 6, no. 4, 248–258, https://doi.org/10.1049/iet-rpg.2011.0165, 2-s2.0-84874997459.
10.1049/iet-rpg.2011.0165
Web of Science® Google Scholar
28 Lei C., Wang Q., and Wang S., Optimization of Controlling Parameters of DFIG and Battery Energy Storage Combined Frequency Modulation Based on PSO, Journal of Physics: Conference Series. (2019) 1311, no. 1, 012030, https://doi.org/10.1088/1742-6596/1311/1/012030, 2-s2.0-85074139087.
10.1088/1742-6596/1311/1/012030
Google Scholar
29 Ye Z., Xie Y., and Zhu H., Review on Power System Frequency Regulation With High Wind Power Permeability, Energy and Power Engineering. (2018) 10, no. 8, 366–382, https://doi.org/10.4236/epe.2018.108023.
10.4236/epe.2018.108023
Google Scholar
30 Tran M. K., Mathew M., Janhunen S., Panchal S., Raahemifar K., Fraser R., and Fowler M., A Comprehensive Equivalent Circuit Model for Lithium-Ion Batteries, Incorporating the Effects of State of Health, State of Charge, and Temperature on Model Parameters, Journal of Energy Storage. (2021) 43, 103252, https://doi.org/10.1016/j.est.2021.103252.
10.1016/j.est.2021.103252
Google Scholar
31 Zhang B., Wang Y., Guo Y., Xu W., Jiang X., and Ge C., A Combined Wind-Storage Primary Frequency Regulation Method Considering Low-Speed Shaft Fatigue Loads in Wind Turbine, Electric Power Systems Research. (2024) 235, 110891, https://doi.org/10.1016/j.epsr.2024.110891.
10.1016/j.epsr.2024.110891
Google Scholar

All articles

Frequency Characteristics Analysis of Wind–Storage Joint Frequency Regulation System Taking Into Account the State of Storage Battery

Abstract

1. Introduction

2. Frequency Response Modeling of Power System Under Joint Wind–Storage Frequency Regulation

3. Results

4. Discussion

5. Conclusions

Conflicts of Interest

Funding

Acknowledgments

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Frequency Characteristics Analysis of Wind–Storage Joint Frequency Regulation System Taking Into Account the State of Storage Battery

Abstract

1. Introduction

2. Frequency Response Modeling of Power System Under Joint Wind–Storage Frequency Regulation

3. Results

4. Discussion

5. Conclusions

Conflicts of Interest

Funding

Acknowledgments

Open Research

Data Availability Statement

References

Figures

References

Related

Information