Journal of Computer Networks and Communications

Volume 2024, Issue 1 5541283

Research Article

Open Access

Energy Detector–Based Spectrum Sensing in Cognitive Radios Over Fading Channel

Rahul Kumar,

Rahul Kumar

ECE Department , GLA University , Mathura , India , gla.ac.in

Search for more papers by this author

Jagadeesh Chandra Prasad M.,

Jagadeesh Chandra Prasad M.

ECE Department , G. Narayanamma Institute of Technology and Science (for Women) , Hyderabad , India

Search for more papers by this author

Shweta Singh,

Corresponding Author

Shweta Singh

[email protected]

orcid.org/0000-0002-8094-2289

Department of Electronics and Communication Engineering , Manipal Institute of Technology Bengaluru , Manipal Academy of Higher Education , Manipal , India , manipal.edu

Search for more papers by this author

Nithin Varma Malathkar,

Nithin Varma Malathkar

ECE Department , Malla Reddy Engineering College , Secunderabad , India , mrec.ac.in

Search for more papers by this author

Rahul Kumar,

Rahul Kumar

ECE Department , GLA University , Mathura , India , gla.ac.in

Search for more papers by this author

Jagadeesh Chandra Prasad M.,

Jagadeesh Chandra Prasad M.

ECE Department , G. Narayanamma Institute of Technology and Science (for Women) , Hyderabad , India

Search for more papers by this author

Shweta Singh,

Corresponding Author

Shweta Singh

[email protected]

orcid.org/0000-0002-8094-2289

Department of Electronics and Communication Engineering , Manipal Institute of Technology Bengaluru , Manipal Academy of Higher Education , Manipal , India , manipal.edu

Search for more papers by this author

Nithin Varma Malathkar,

Nithin Varma Malathkar

ECE Department , Malla Reddy Engineering College , Secunderabad , India , mrec.ac.in

Search for more papers by this author

First published: 20 December 2024

https://doi.org/10.1155/jcnc/5541283

Academic Editor: Hesham Elbadawy

Share a link

Email
Wechat
Bluesky

Abstract

Cognitive radios (CRs) are envisioned as a potential solution, to provide spectrum-efficient communication for futuristic wireless communication systems like the Internet of Things (IoT) and others. This article examines the efficiency of CR’s detection performance over the fading channel. The fading model is a generalized fading model intended to collectively quantify channel nonlinearity and shadowing effects. Therefore, the effect of channel nonlinearity and shadowing together on CR detection performance has been studied. New analytical formulas for the average probability of detection (APOD) for a single user and cooperative detection are obtained for energy detection (ED)–based spectrum sensing (SS). Additionally, to provide a deeper understanding of detection characteristics, expression for the area under the receiver operating characteristics is also obtained. The effectiveness of CR detection under various nonlinearity and shadowing effects is investigated using the developed analytical expressions, and the results indicate that performance degrades as channel impairments increase. At last, Monte Carlo simulations are employed to demonstrate that the obtained analytical expressions are valid.

1. Introduction

Cognitive radio (CR)–based systems are a clear approach to the problem of increasing spectral demand as CRs are founded on the core principle of making the best possible use of the spectrum that is already in use. For a CR device to deliver improved quality of service without affecting existing communicating primary users (PUs), it is important to perform spectrum sensing (SS) or find spectrum holes accurately. The energy detection (ED)–based SS, which was first presented by Urkowitz [1], is still recognized as one of the most expedient SS strategies, due to its simple structure and speedy decision capacity without the requirement for any prior knowledge about PU signals. The efficacy of ED-based SS communication systems is degraded severely due to channel fading effects, and hence it is important to characterize these fading channels appropriately to compute the received signal accurately and to implement the CR technology effectively. The performance of communication systems under various short-term fading conditions, including Nakagami, Weibull, and Rayleigh, has been extensively studied in prior works [2–4] and their cited references. Furthermore, various studies have presented the impact of these conventional fading scenarios on the performance of ED; as an illustration, the authors in [5, 6] accounted for Rayleigh, Rician, and Nakagami channels with and without diversity reception.

Recent investigations indicate that traditional fading models do not adequately represent experimental data in certain futuristic communication having nontraditional communication venues like machine-to-machine (M2M), vehicle-to-vehicle (V2V), mobile-to-mobile communications, indoor-to-outdoor propagation in 5G and beyond networks, or communication inside confined areas like trains, buses, and airplanes [7, 8]. It has been observed that to underscore such propagation scenarios, there is a need for a comprehensive and flexible channel model that can capture the diverse fading behaviors and characterize them accurately. Consequently, significant research over the past few decades has focused on developing generalized channel fading models for robust analysis and to better predict the performance of modern communication technologies accounting for nonhomogeneity, nonlinearity, multipath, and shadowing. To account for the multipath and shadowing effects, few research studies have been presented; for instance, a unified technique for determining detection probability under fading conditions with diversity reception has been introduced in [9].

In addition to multipath effects, a wireless signal also experiences shadowing effects. The authors in [10, 11] evaluated ED performance over composite fading channels. Furthermore, line-of-sight (LOS) and non-LOS fading scenarios can be described by κ − μ and η − μ fading models, and the effectiveness of the ED in both scenarios has been studied in [12, 13]. A more generalized variant of the κ − μ and η − μ fading models is the fading α − η − κ − μ model introduced in [14], and ED performance for the channel has been investigated in [15]. Further, the approximation of the linearity and homogeneity in the channel model accounted for in the conventional fading distribution needs to be justified since the diffuse scattering field demonstrates spatial correlations at surfaces creating a nonlinear environment [16]. To investigate this nonhomogeneity, two fading distributions, the κ − μ distribution and η − μ distribution, were introduced in [17–19]. Additionally, the α − μ distribution was recently proposed to further explore the nonlinearity of the propagation medium [20]. The authors in [21] presented a unified model for the composite η − μ/gamma, κ − μ/gamma, and α − μ/gamma distributions based on a mixture gamma distribution mixture gamma distribution. The authors in [22] proposed the κ − μ shadowed fading distribution.

Further, the authors in [23] explored the use of the inverse gamma distribution for characterizing composite fading channels. The α − κ − μ shadowed fading distribution was later proposed as an extension of the κ − μ shadowed fading distribution [24]. The composite distributions introduced in this letter uniquely account for both shadowing effects and the nonlinearity of the propagation medium, offering greater flexibility by encompassing other well-known distributions such as κ − μ/inverse gamma and η − μ/inverse gamma distributions [25]. The authors in [26] presented the and composite fading distributions. The two distributions generalize the two well-known composite fading distributions, namely, the η − μ/inverse gamma and the κ − μ/inverse gamma distributions. The fading distribution is shown to present a versatile fading channel as various well-known fading channels in the literature can be obtained under its special cases. Since the new distributions jointly consider the nonlinearity of the propagation media and shadowing, it is expected that they can provide better flexibility to characterize wireless fading channels compared with other distributions in the literature, such as the α − η − μ [27], α − κ − μ [24, 27], η − μ/inverse gamma, and κ − μ/inverse gamma distributions [25].

The α − η − κ − μ fading channel model [15] is recognized for its ability to provide accurate field measurement data and offers significant flexibility across a wide range of fading environments by adjusting its parameters. The derived expressions are adaptable to various conventional fading models by substituting different parameter values. However, this model falls short of effectively capturing the fluctuations of the LOS component, leading to an unrealistic representation of certain scenarios. By integrating the

Schneider distribution [28], researchers have developed a more accurate model that accounts for LOS fluctuations, resulting in the composite

distribution. This enhanced model better represents channel nonlinearity and shadowing effects, providing a more accurate depiction of real-world conditions [26]. Despite its advantages, the performance evaluation of ED in such environments has received limited attention. This article aims to bridge that gap by assessing and analyzing ED-based SS performance in the

fading environment, offering a more realistic model and critical insights for CR SS and signal detection. The following are the major contributions of this article:

•
We first derive a novel mathematical expression for the average probability of detection (APOD) by considering the PDF expression for the fading.
•
With the aid of a single SU APOD, the detection performance for a cooperative communication scenario is evaluated.
•
Finally, to better understand how various parameters impact ED performance, we derive a novel analytical formulation for the average area under the receiver operating characteristics curve or AUC.

The subsequent sections are organized as follows.

The system model for the ED process and the fading model is described in Section 2. Two performance indicators, i.e., APOD and AUC over the specified fading environment, are deduced in Section 3. Section 4 presents numerical simulation and an associated discussion for different fading situations. Section 5 concludes by summarizing the major findings of the article.

2. System Model

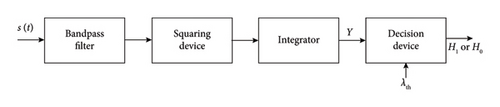
The system model comprises energy detector–based CR SS. This process is sequentially carried out through multiple stages: Firstly, a bandpass filter (BPF) is employed to select the specific frequency band of interest from the received signal s(t) and serve as a prenoise filter. The filtered signal is then passed through a squaring device, where the signal undergoes squaring to emphasize the energy content. Following this, the squared signal is integrated over a predefined time period to compute the total energy within the selected frequency band. Finally, the computed energy Y is compared to a predefined threshold (λ_th) value using a decision device. If the energy exceeds the threshold, the presence of a PU signal is inferred; otherwise, the absence of a PU signal is concluded.

Figure 1 illustrates the procedure for ED-based SS. As shown in (1), the received signal s(t) is distinguished by hypothesis H_o or H₁ corresponds to the received noise or received transmitted signal impaired with noise respectively. As illustrated in (1), the received signal s(t) can be classified into hypothesis H₀ or H₁ which corresponds to received noise or a received PU signal that has been corrupted by noise.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Spectrum sensing procedure.

Let us define x(t) and n(t) as PU transmitted signal and additive white Gaussian noise, respectively; then received signal s(t) is represented as [5]

(1)

where g represents channel gain between PU and SU terminal. Here, the difference between the two hypotheses is tested statistically using the energy of the received signal, s(t), i.e., Y. Therefore for a given decision threshold λ_th, if Y > λ_th, the PU signal is regarded to be present; otherwise, it is assumed to be absent. For the presented system model, two performance indicators, namely, detection and false alarm probability, are provided by (2) and (3), respectively [5].

(2)

and

(3)

where Γ(.), Γ(..), and Q_d(..) represent gamma function, upper incomplete gamma function, and Marcum-Q function, respectively. d is the time-bandwidth product and γ is the instantaneous signal-to-noise ratio (SNR) given as

with E_x, N₀ representing the energy of x(t) and noise power spectral density, respectively.

2.1. The Fading Model

fading model [26] is a versatile fading distribution used to model channel nonlinearity and shadowing effects concurrently. Since the model takes account of both nonlinear and shadowing effects simultaneously, it can be used to describe other channel distribution models like α − η − μ, α − κ − μ, η − μ/inversegamma, and κ − μ/inversegamma distributions. The PDF of SNR for

fading distribution given by

(4)

where

is confluent hypergeometric function

and δ = μ(1 + κ). The parameter ω is defined by

. In the above equation, the parameter α represents the channel nonlinearity, while κ denotes the ratio of the dominant to the specular component. The function

corresponds to the composite Nakagami-m fading distribution, accounting for fluctuations in the composite fading model as described by the Nakagami-m and Fisher-Schneider distributions. The parameter μ signifies the number of multipath components, whereas m_s is the shadowing parameter. Finally,

denotes the average SNR.

3. ED Over Fading Channel

Multipath propagation through the wireless channel results in unpredictable amplitude fluctuations at the receiver terminal, weakening CR detection ability, and hence the receiver characteristics should be studied while taking adequate fading conditions into consideration. This section will analyze two ED-based SS performance metrics in the context of fading scenario: (i) APOD and (ii) average area under the ROC curve (AUC). Here, ROC refers to the receiver operating characteristic, an important performance metric used to evaluate the effectiveness of the ED process. It leads to reduced interference and improved sensing performance.

3.1. Single User Detection

Note that the detection probability stated in (2) overlooks the impacts of channel fading while the received SNR varies randomly due to multipath fading, and hence considering

fading scenario, APOD is evaluated by averaging (2), i.e.,

(5)

where Q_d(..) denotes Marcum-Q function. Using [29], we get

Hence, the Q(.,.) function in (5) is rewritten as .

Now using ([30], eq (8.445)), we expand the modified Bessel function as and rewrite the function as .

Using these mathematical manipulations and using ([30], eq (3.351.2)) and ([30], eq (3.351.3)) with PDF property, i.e.,

, we get (7). Now using integral representation for Marcum function ([29], equation (1)) in (5), we get

(6)

With the help of [29] and ([30], eq (8.445)),

is written as

(7)

where Υ(..) is the lower incomplete gamma function. Now with (7) and (4),

(8)

Observe that a closed-form expression for integral in (8) is difficult to attain as it requires several series approximations. APOD is calculated using the Gauss–Laguerre integral approximation, expressed as follows (8):

(9)

where M represents the number of sampling points, w_m and x_m are Gauss–Laguerre approximation weights and abscissa, and function f(x) is defined as follows:

(10)

3.2. Cooperative SS

In many cases, whenever the available SNR from PUs is relatively low, the single-user SS performs poorly. Although employing cooperative SS, which makes use of the spatial diversity among the SUs, it is possible to further improve the detection performance. The following are the performance metrics applied to the cooperative detection technique [31]:

(11)

(12)

where H_c denotes the number of cooperative users.

Therefore, by plugging (9) into (12), one can simply calculate the APOD for cooperative SS, and by plugging (3) into (11), one can get the corresponding false alarm probability.

(13)

(14)

(15)

3.3. Average Area Under the ROC ()

Given the uncertainty around the p_fa intersection with ROC-based comparisons, AUC is another performance metric that is viewed as a comparative measure for CR and finds its relevance when comparing two CR systems. The performance of the receiver can be better understood by evaluating AUC and recognized as a single figure of merit for the CR system. As λ_th varies from 0 to ∞, the AUC ranges from 0.5 to 1, indicating a progression from poorer to better CR performance, respectively. This is calculated as follows: [32].

(16)

where

(17)

With (9), (16), and (17) and utilizing area property for PDF, (16) is written as

(18)

Using ([30], equation.6.445.2), (18) reduces to

(19)

4. Results and Discussion

This segment evaluates the ED-based SS performance over α − κ − F fading channel, using various numerical simulations of derived mathematical expressions and Monte Carlo recreations. To show the analysis detection performance of various ROCs ( vs. p_fa), vs. SNR and AUC curves are plotted and variants are presented for different channel-related parameters.

Figure 2 depicts the vs. p_fa plots, i.e., ROC for ED-based SS with SNR = 0 dB, d = 1, and with light shadowing (m_s = 50) conditions. An improved APOD is observed with a higher p_fa, as higher p_fa needs a lower detection threshold and therefore enhanced detection performance. APOD is also improved for the increased value of the parameters α, κ, and μ, whereas the relative impact of κ is lower than other parameters on detection probability.

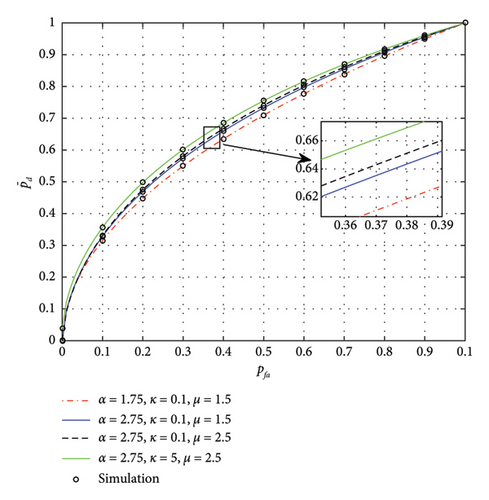
Figure 3 shows vs. SNR plots for collaborative SS over the α − κ − F fading with p_fa = 0.1, m_s = 50, and d = 1. Note that APOD improves with the involvement of collaborative users; however, the effectiveness of collaborative detection is constrained by the severity of channel-related parameters. Moreover, APOD is improving with the increase in SNR as the effect of fading reduces for higher SNRs.

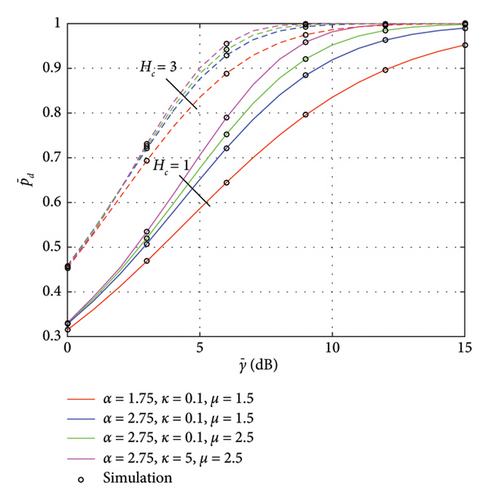
Figure 4 shows AUC vs. d curves with m_s = 50 and at SNR = 0 and +5 dB. As seen in the plot, an improved AUC performance is detected for higher SNRs; this can be related to the fact that at higher SNRs, the impact of the unknown noise power level on the energy detector’s performance is reduced, leading to improved AUC as the signal becomes more distinguishable from the noise. Resultantly, the detector can achieve higher detection accuracy and lower false alarm rates, ultimately enhancing the overall performance as reflected by the AUC curve in Figure 4.

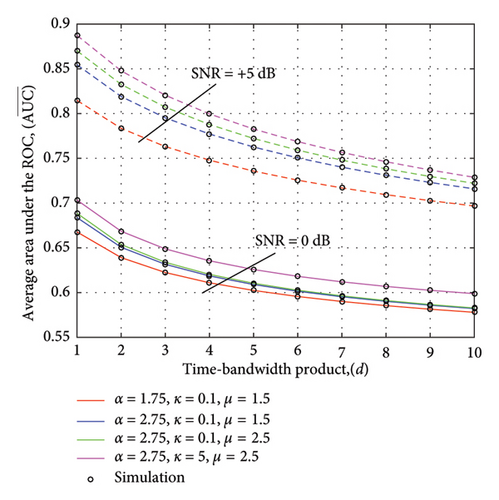
Furthermore, a lowered AUC trend is observed at the larger value time-bandwidth products, and the explanation for the behavior is as follows: With increased time-bandwidth products, both APOD and false alarm probability increase, while false alarm probability increases with a higher rate as compared to APOD variation, leading to a fall in overall AUC performance.

5. Conclusion

The efficacy of ED-based SS has been assessed over the fading environment. New analytical mathematical expressions for APOD and AUC are derived over the given fading channel. Obtained results are generalized and take both channel nonlinearity and shadowing effects into account simultaneously. It has been demonstrated that channel nonlinearity and shadowing effects significantly negatively impact detector performance and that incorporating diversity reception and cooperative SS can boost detection performance. Along with that, diversity reception and cooperative SS also limit the severity of channel nonlinearity effects. A comparative analysis embracing channel nonlinearity and shadowing effects is helpful for quantifying CR detection sensitivity in various wireless propagation conditions and building CR-based communication systems.

Ethics Statement

The authors have nothing to report.

Consent

The authors have nothing to report.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

All the listed authors have made a substantial contribution to the research, and their contributions can be listed as follows.

Rahul Kumar: conceptualization and problem formulation.

Jagadeesh Chandra Prasad M.: analytical development and validation.

Shweta Singh: MATLAB simulations and data analysis.

Nithin Varma Malathkar: revision process and finalization.

Funding

The authors received no specific funding for this work.

Open Research

Data Availability Statement

The result/plot data used to support the findings of this study are included within the article.

References

1 Urkowitz H., Energy Detection of Unknown Deterministic Signals, Proceedings of the IEEE. (1967) 55, no. 4, 523–531.
10.1109/PROC.1967.5573
Web of Science® Google Scholar
2 Zou Y. and Wang G., Intercept Behavior Analysis of Industrial Wireless Sensor Networks in the Presence of Eavesdropping Attack, IEEE Transactions on Industrial Informatics. (2016) 12, no. 2, 780–787.
10.1109/TII.2015.2399691
Web of Science® Google Scholar
3 Jameel F., Wyne S., and Krikidis I., Secrecy Outage for Wireless Sensor Networks, IEEE Communications Letters. (2017) 21, no. 7, 1565–1568.
10.1109/LCOMM.2017.2691347
Web of Science® Google Scholar
4 Shankar R., Bi-Directional LSTM Based Channel Estimation in 5G Massive MIMO OFDM Systems over TDL-C Model With Rayleigh Fading Distribution, International Journal of Communication Systems. (2023) 36, no. 16.
10.1002/dac.5585
Google Scholar
5 Digham F. F., Alouini M. S., and Simon M. K., On the Energy Detection of Unknown Signals Over Fading Channels, IEEE Transactions on Communications. (2007) 55, no. 1, 21–24.
10.1109/TCOMM.2006.887483
Web of Science® Google Scholar
6 Herath S. P., Rajatheva N., and Tellambura C., Energy Detection of Unknown Signals in Fading and Diversity Reception, IEEE Transactions on Communications. (2011) 59, no. 9, 2443–2453.
10.1109/TCOMM.2011.071111.090349
Web of Science® Google Scholar
7 Ibdah Y. and Ding Y., Mobile-to-Mobile Channel Measurements at 1.85 GHz in Suburban Environments, IEEE Transactions on Communications. (2015) 63, no. 2, 466–475.
10.1109/TCOMM.2014.2380314
Web of Science® Google Scholar
8 Hamid S., Al-Dweik A. J., Mirahmadi M., Mubarak K., and Shami A., Inside-Out Propagation: Developing a Unified Model for the Interference in 5G Networks, IEEE Vehicular Technology Magazine. (2015) 10, no. 2, 47–54.
10.1109/MVT.2015.2410812
Google Scholar
9 Annamalai A., Olabiyi O., Alam S., Odejide O., and Vaman D., Unified Analysis of Energy Detection of Unknown Signals Over Generalized Fading Channels, 4, 2011 7th International Wireless Communications and Mobile Computing Conference, July 2011, Istanbul, Turkey, IEEE, 636–641.
Google Scholar
10 Atapattu S., Tellambura C., and Jiang H., Performance of an Energy Detector Over Channels With Both Multipath Fading and Shadowing, IEEE Transactions on Wireless Communications. (2010) 9, no. 12, 3662–3670.
10.1109/TWC.2010.100110.091042
Web of Science® Google Scholar
11 Peppas K. P., Efthymoglou G., Aalo V. A., Alwakeel M., and Alwakeel S., Energy Detection of Unknown Signals in Gamma-Shadowed Rician Fading Environments With Diversity Reception, IET Communications. (2014) 9, no. 2, 196–210.
10.1049/iet-com.2014.0170
Web of Science® Google Scholar
12 Sofotasios P. C., Rebeiz E., Zhang L., Tsiftsis T. A., Cabric D., and Freear S., Energy Detection Based Spectrum Sensing Over κ-μ and κ-μ Extreme Fading Channels, IEEE Transactions on Vehicular Technology. (2012) 62, no. 3, 1031–1040.
10.1109/TVT.2012.2228680
Web of Science® Google Scholar
13 Atapattu S., Tellambura C., and Jiang H., Energy Detection of Primary Signals Over η-μ fading Channels, 2009 International Conference on Industrial and Information Systems (ICIIS), December 2009, Peradeniya, Sri Lanka, 118–122.
Google Scholar
14 Moualeu J. M., da Costa D. B., Lopez-Martinez F. J., and de Souza R. A., On the Performance of α–η–κ–μ Fading Channels, IEEE Communications Letters. (2019) 23, no. 6, 967–970.
10.1109/LCOMM.2019.2910526
Web of Science® Google Scholar
15 Al-Hmood H. and Al-Raweshidy H., On the Effective Rate and Energy Detection Based Spectrum Sensing Over α-η-κ-μ Fading Channels, IEEE Transactions on Vehicular Technology. (2020) .
10.1109/TVT.2020.2998895
PubMed Google Scholar
16 Braun W. R. and Dersch U., A Physical Mobile Radio Channel Model, IEEE Transactions on Vehicular Technology. (May 1991) 40, no. 2, 472–482.
10.1109/25.289429
Web of Science® Google Scholar
17 Yacoub M. D., The η-μ Distribution: A General Fading Distribution, IEEE Boston Fall Vehicular Technology Conference 2000, September 2000, Boston, MA.
Google Scholar
18 Yacoub M. D., The κ-μ Distribution: A General Fading Distribution, IEEE Atlantic City Fall Vehicular Technology Conference 2001, October 2001, Atlantic City, NJ.
Google Scholar
19 Yacoub M. D., The κ-μ Distribution and the η-μ Distribution, IEEE Transactions on Antennas and Propagation. (2006) .
Google Scholar
20 Yacoub M. D., The α-μ Distribution: A General Fading Distribution, IEEE Transactions on Vehicular Technology. (2006) .
Google Scholar
21 Al-Hmood H. and Al-Raweshidy H. S., Unified Modeling of Composite κ-μ/η-μ/ Fading Channels Using a Mixture Gamma Distribution With Applications to Energy Detection, IEEE Antennas and Wireless Propagation Letters. (2017) 16, 104–108.
10.1109/LAWP.2016.2558455
Web of Science® Google Scholar
22 Paris J. F., Statistical Characterization of κ-μ Shadowed Fading, IEEE Transactions on Vehicular Technology. (2014) 63, no. 2, 518–526.
10.1109/TVT.2013.2281213
Web of Science® Google Scholar
23 Ramirez-Espinosa P. and Lopez-Martinez F. J., On the Utility of the Inverse Gamma Distribution in Modeling Composite Fading Channels, 2024 IEEE Global Communications Conference (GLOBECOM), December 2019, Cape Town, South Africa, 1–6.
Google Scholar
24 Ramirez-Espinosa P., Moualeu J. M., da Costa D. B., and Lopez-Martinez F. J., The α-κ-μ Shadowed Fading Distribution: Statistical Characterization and Applications, IEEE Global Communications Conference (GLOBECOM), December 2019, Cape Town, South Africa, 1–6.
Google Scholar
25 Yoo S. K., The κ-μ Gamma Composite Fading Models: Fundamental Statistics and Empirical Validation, IEEE Transactions on Communications. (2017) .
Google Scholar
26 Badarneh O. S., The α-η-F and α-κ-F Composite Fading Distributions, IEEE Communications Letters. (2020) 24, no. 9, 1924–1928.
10.1109/LCOMM.2020.2995113
Web of Science® Google Scholar
27 Fraidenraich G. and Yacoub M. D., The α-η-μ and α-κ-μ Fading Distributions, 2006 IEEE Ninth International Symposium on Spread Spectrum, August 2006, Amazon, Brazil, 16–20.
Google Scholar
28 Yoo S. K., Cotton S. L., Sofotasios P. C., Matthaiou M., Valkama M., and Karagiannidis G. K., The Fisher–Snedecor: A Simple and Accurate Composite Fading Model, IEEE Communications Letters. (2017) 21, no. 7, 1661–1664.
10.1109/LCOMM.2017.2687438
Web of Science® Google Scholar
29 Nuttall A., Some Integrals Involving the Q_M Function (Corresp.), IEEE Transactions on Information Theory. (1975) 21, no. 1, 95–96.
10.1109/TIT.1975.1055327
Web of Science® Google Scholar
30 Gradshteyn I. S., Ryzhik I. M., Jeffrey A., and Zwillinger D., Table of Integrals, Series, and Products, TISP. (2007) .
Google Scholar
31 Ghasemi A. and Sousa E. S., Impact of User Collaboration on the Performance of Sensing-Based Opportunistic Spectrum Access, IEEE Vehicular Technology Conference, September 2006, Melbourne, Australia, 1–6.
Google Scholar
32 Atapattu S., Tellambura C., and Jiang H., Analysis of Area Under the ROC Curve of Energy Detection, IEEE Transactions on Wireless Communications. (2010) 9, no. 3, 1216–1225.
10.1109/TWC.2010.03.091085
Web of Science® Google Scholar

All articles

Energy Detector–Based Spectrum Sensing in Cognitive Radios Over Fading Channel

Abstract

1. Introduction