The performance of a gray-coded dual polarization-16 quadrature amplitude modulation (DP-16 QAM)–based multiple input multiple output (MIMO)-FSO link using coherent detection and digital signal processing (DSP) is investigated. The MIMO link is used to mitigate geometric loss, atmospheric attenuation, and atmospheric turbulence. Additionally, a coherent receiver with DSP algorithms is used to improve channel capacity, receiver performance, and link range. The performance of the system is evaluated by constellation diagrams, RF and optical power spectra, bit error rate (BER), and error vector magnitude (EVM). It is observed that before DSP, the constellation diagrams are distorted, whereas after DSP, distinct constellation symbols are observed. The system possesses a spectral efficiency of around 4.62 b/s/Hz. The longest link range to attain the acceptable BER limit is achieved under 4 × 4 MIMO weak turbulence levels in clear air conditions, which is 11.55 km, while the shortest is achieved under SISO strong turbulence levels in light fog conditions, which is 0.895 km. After the channel impairments are mitigated by DSP, the simulation results show that the MIMO link outperforms the SISO link in all scenarios.

1. Introduction

Recently, there has been a dramatic rise in demand for high-speed data and multimedia services, such as high-speed internet, video conferencing, and live streaming, which has caused the radio frequency (RF) spectrum to become congested. Because of this, an optical carrier is now required instead of an RF carrier [1, 2]. As a result, free-space optical (FSO) communication systems have been a potential solution in recent times due to their various advantages. Some of these are low installation and operating costs, low power consumption, license-free spectrum, large bandwidth, security, flexibility, high speed, small size, and light weight [2–5]. Its applications are found in deep space communication, backhaul for wireless cellular networks, remote sensing, military applications, inter-satellite communications, terrestrial communications, inter-building communications, and disaster recovery [3, 6]. However, its performance is limited by geometric loss, atmospheric attenuation, and atmospheric turbulence, which deteriorate the performance of the link [6, 7]. A variety of mitigation technologies are used to overcome these channel-induced losses, including adaptive optics, aperture averaging, multiple input multiple output (MIMO), hybrid FSO, channel coding, robust modulation formats, and so on [7, 8].

Different research groups conducted diverse studies and reported their findings to increase the capacity and spectral efficiency of FSO systems, with a particular focus on reducing channel-induced impairments. Previously, Kumar and Teixeira [9] presented a 10 Gbps OFDM-FSO link by using a square root device at the receiver to compensate for signal degradation due to nonlinear photodiodes. The authors reported that a maximum link range of 1800 m was achieved in 4-quadrature amplitude modulation (QAM), at this low capacity. Pottoo, Goyal, and Gupta [10] proposed a 128 Gbps single-channel gray-coded dual polarization (DP)-QPSK with balanced homodyne detection and digital signal processing (DSP) in fair weather conditions. The results revealed that homodyne detection systems exhibit a 3 dB greater receiver sensitivity than heterodyne detection systems. But, the atmospheric turbulence effect was not considered.

Moustafa et al. [11] also simulated SISO and 4 × 4 MIMO FSO links using NRZ, CSNRZ, DBNRZ, and MDBNRZ modulation schemes under different weather conditions and reported that NRZ was better in terms of received power under 4 × 4 MIMO links. However, due to the use of direct detection techniques, the system operates at low capacity. Kakati and Sonkar [12] investigated a DSP-assisted gray-coded DP-16 QAM 64-channel Nyquist-DWDM transceiver for a spectrally efficient long-haul optical interconnect. Gray code shows an OSNR improvement of 0.8 dB and a receiver sensitivity improvement of ≥ 4.6 dBm as compared to differential coding. Due to dense channel spacing, crosstalk is very high. Miglani and Malhotra [13] investigated a 1.28 Tbps (32 × 40 Gbps) system using coherent detection and DSP for performance enhancement under adverse weather and turbulence atmospheric conditions. The DSP-aided coherent DWDM-FSO link shows a 760 m link range increment as compared to IM/DD-based DWDM-FSO links in a SISO system.

In other aspects, to improve the transmission performance, Konda et al. [14] demonstrated the comparison of EDFA and SOA on a single-channel IQM-based PM-256 QAM modulation scheme using coherent detection and DSP. The obtained result showed that the received signal quality is better in the case of EDFA as compared to SOA. However, the atmospheric turbulence effect was not considered. Janu Dimpal and Vijay Janyani [15] analyzed the performance of the FSO link at a link range of 0.6 km and a data rate of 125 Gbps using a single polarization-QPSk modulation scheme under the gamma-gamma channel model. Kakatia and Arya [16] observed the performance of a 120 Gbps single-channel coherent transceiver with a target bit error rate (BER) of 2 × 10⁻³ in an FSO link for different weather conditions.

The contributions of the paper are as follows:

•
A gray-coded DP-16 QAM-based MIMO FSO link using coherent detection and DSP is analyzed to transmit a data rate of 120 Gbps and a symbol rate of 15 GBaud. The transmitter uses a DP-16 QAM modulation format for enhanced spectral efficiency, and gray code is used to reduce the BER during symbol recovery. The MIMO system is used to mitigate geometric loss, atmospheric loss, and atmospheric turbulence. Additionally, a coherent receiver with DSP algorithms has been used on the receiver side to mitigate free-space channel loss and improve receiver performance.
•
Due to the DP-16 QAM modulation format, the system is dual-polarized, which leads to polarization mode dispersion (PMD). In addition, component losses, like Mach–Zehnder modulator (MZM) insertion losses, also affect the overall performance of this system. DSP algorithms such as QI compensation are used to mitigate the amplitude and phase imbalance between the IQ electrical signals caused by inappropriate bias voltages of MZM, misalignment of the polarization splitter and polarization combiner, and imperfections in the optical 90° hybrid. Also, an adaptive equalizer (AE) is used to mitigate inter-symbol interference and PMD; frequency offset estimation (FOE) is used to cancel the frequency mismatch between the transmitter and the local oscillator (LO); and carrier phase estimation (CPE) is used to cancel the phase mismatch between the transmitter and the LO.
•
We also made performance comparisons between SISO and 4 × 4 MIMO FSO links under the gamma-gamma channel model in clear air, wet snow, medium rain, and light fog conditions under weak and strong turbulence levels. The system’s reliability has been verified using constellation diagrams, RF and optical power spectra, BER, and error vector magnitude (EVM) as performance metrics.

The rest of this paper is structured as follows. In Section 2, the system model and analysis are described. Simulation results and discussion are described in Section 3. Finally, conclusions are drawn based on the result in Section 4.

2. System Model and Analysis

Figure 1 shows the overall block diagram of the MIMO-FSO link with a DP-16 QAM transmitter, an optical amplifier, a DP-16 QAM coherent receiver, a DSP unit, a decision unit, and a decoding unit.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Block diagram for DP-16 QAM modulated MIMO-FSO link with DSP.

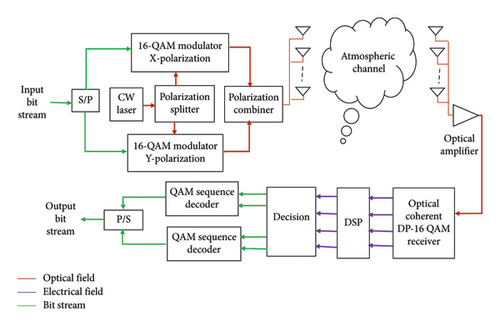
2.1. DP-16 QAM Transmitter

The internal structure of the optical DP-16 QAM transmitter is shown in Figure 2. The instantaneous electric field of the CW laser is given by [17]

(1)

where P_s is the signal power, ω_s is the angular frequency of the signal, φ_s is the initial phase of the signal, and

is the polarization of the signal. The probability density function (PDF) of the laser phase noise is given by [14, 17]

(2)

where Δf denotes the laser linewidth, Δt denotes the time interval, and Δφ is the phase difference between two successive time intervals. It is assumed that the phase difference between two successive time intervals is a Gaussian random variable with a zero mean and a variance is the probability weighted average of the square deviation from the mean, which leads to the variance of 2πΔfΔt.

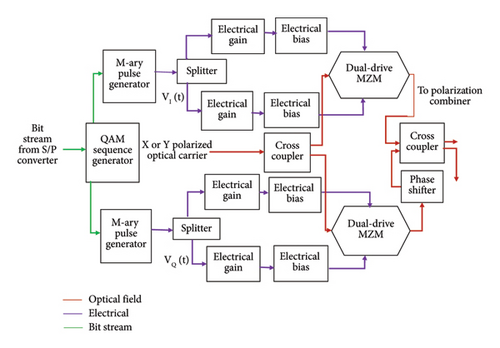
The light wave is split into the X and Y orthogonal polarization components by a polarization splitter, which is used to drive the upper and lower IQM branches. At the input of each IQM section, a cross-coupler with a coupling coefficient of 0.5 is used to send the laser beam along the in-phase and quadrature-phase paths of the IQM [14].

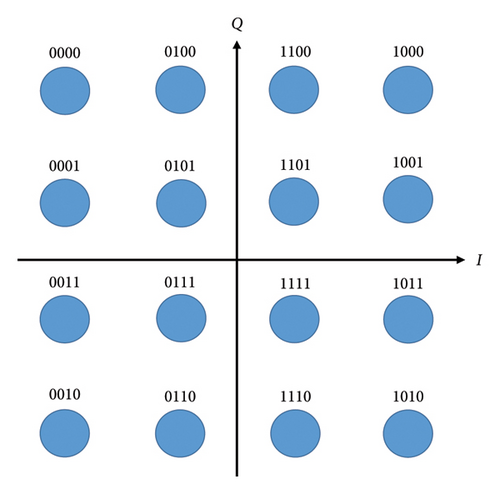
The input bit sequence generated from a PRBS is split into two parallel bit sequences by an S/P converter and sent to the upper and lower IQMs. Two equivalent M-ary symbol sequences are generated from the input binary sequence by 16-QAM sequence generators and sent toward M-ary pulse generators. This bit series is mapped into M symbols in a single bit alteration among any two adjacent symbols as it is shown in Figure 3. This bit mapping is called gray code. Gray code is essential to reducing BER during symbol recovery [10, 12].

The M-ary pulse generator output is applied to the RF plates of the dual-drive MZM, and the DC bias point of the two MZMs is set at the null point with an extinction ratio of 30 dB, a switching voltage of 3 V, and a bias voltage of 0 V [7]. In each quadrature-phase branch of both IQMs, a relative phase shift of π/2 is used to generate the modulated optical QAM signal. Then the modulated optical signals are combined using a polarization combiner to get the DP-16-QAM signal and transmitted over the MIMO-FSO link. The multilevel driving signals at the in-phase and quadrature branches for the ideal case in the perfect modulation process are given by [18]

(3)

where V_π is the driving voltage at a phase shift of π, k is the symbol interval, and T_s denotes the symbol duration, while i_k and q_k are the in-phase and quadrature normalized symbol coordinates and p(t) denotes the pulse shape of the signal. For the practical modulation process, by considering phase errors and the nonlinearity effect, the multilevel driving signals at the in-phase and quadrature branches are modified as

(4)

where Δφ_I and Δφ_Q are the phase errors in the in-phase and quadrature components, respectively, whereas

and

represent the nonlinear distortion in the driving signals for the in-phase and quadrature components, respectively. The data-bearing optical signal at the transmitter output is given by [17, 18]

(5)

where γ₁ is the insertion loss of MZM, I (t) and Q (t) are the in-phase and quadrature components of the transmitted signal, respectively, V_m is the bias voltage of MZM, and m_h1 = π(V_m/V_π) is the modulation index.

In a MIMO link, the transmitter transmits the same signal with the same parameters, and the receiver receives all the transmitted signals and combines them using the equal gain combining (EGC) technique. In this paper, the 4 × 4 MIMO FSO link is used to achieve an optimal balance between performance in mitigating beam divergence loss, geometric loss, and atmospheric turbulence and practical deployment constraints such as hardware complexity and cost.

2.2. FSO Channel

Because of diffraction, the optical beam spreads out as it travels through the atmosphere. The receiver aperture may not be able to collect all transmitted beams as a result, leading to beam divergence loss. The ideal geometric loss for FSO in perfect alignment between the transmitter and receiver and a stable beam divergence angle is calculated as [3]

(6)

where R is the link range, D_T denotes the transmitter aperture diameter, D_R denotes the receiver aperture diameter, and θ is the beam divergence angle. However, the misalignment errors and variations in beam divergence angle due to environmental factors degrade the FSO system performance. By considering misalignment errors and variations in the beam divergence angle, the geometric loss can be modified as

(7)

where θ₀ is nominal beam divergence, Δθ is misalignment error, and Δθ(t) is a random fluctuation in beam divergence due to environmental conditions.

Atmospheric attenuation is the second factor that occurs due to bad weather conditions such as fog, rain, and snowfall, which cause optical signal absorption and scattering. The attenuation of fog is predicted and estimated by the Kruse, Kim, Al Naboulsi, Ijaz, and other models. The Kruse model is the most widely used model to estimate and predict the attenuation in near-infrared and visible-range bands because it is simple and easy to implement. However, the Kruse model is less accurate for low-visibility conditions. The Kim model is an improvement of the Kurse model, which is more accurate and flexible in a wide range of visibility conditions. While the Al Naboulsi and Ijaz models provide better accuracy in certain specific conditions, these models require more complex inputs and empirical data. The Kim model is used in this system as a performance trade-off because it is more accurate than the Kruse model and less complex than the Al Naboulsi and Ijaz models. The attenuation of fog is explained by the Kim model as [19, 20]

(8)

where V (km) is the link visibility, λ is the operating wavelength, and q is the particle size coefficient in the air and expressed as [21]

(9)

Rain attenuation occurs due to rain falling and is a nonselective scattering. Rain attenuation is given by [22]

(10)

where R_r is the rainfall rate in mm/h. The attenuation produced by rainfall increases linearly with the rainfall rate. The parameters a and b are the power law parameters that depend on frequency, raindrop size, humidity, and rain temperature. To determine the power law parameters a and b, Marshal and Charbonneau models are used. The Carbonneau model is more acceptable to use since it depends on using a physical method based on practical measurements. In the Carbonneau model, a and b are equal to 1.076 and 0.67, respectively. The rain attenuation is expressed as

(11)

Attenuation caused by snow depends on snowflake size and snowfall rate. The snow attenuation is expressed as [3, 19]

(12)

where S_r is the snowfall rate in mm/h. The coefficients a and b are dependent on temperature, snow density, humidity, and flake size and vary according to dry or wet snow.

For dry snow, a = 5.42 × 10⁻⁵λ + 5.4958776 and b = 1.38. For wet snow, a = 1.023 × 10⁻⁴λ + 3.7855466 and b = 0.72.

Atmospheric turbulence is another factor that happens due to variations in temperature and pressure in the atmosphere, which result in random fluctuations in the phase and intensity of received optical signals (scintillation). The refractive index structure parameter is expressed as [3]

(13)

where p denotes atmospheric pressure, T denotes atmospheric temperature, and

is the mean square temperature between two points within the link.

The gamma-gamma channel model is used to describe the range of turbulence from weak to strong. Its PDF is given by [23]

(14)

where K_{(α − β)} is the modified Bessel function of the second kind of order α − β and Γ(.) is the gamma function. The parameters α and β are the variances of small and large-scale turbulent eddies, respectively, and are defined by

(15a)

(15b)

where δ² represents the Rytov variance for a plane wave and is defined as

(16)

where K = 2π/λ is the wave number.

EDFA is used in the system as a preamplifier to enhance the transmission over long link ranges because it has a high pump power utilization, is suitable for long-haul applications, has a low noise figure, is polarization independent, has a very high gain, and is low cost [24].

2.3. Coherent DP-16 QAM Receiver

In an ideal case without the effects of phase noise, PMD, and polarization-dependent loss (PDL), the received data-bearing optical signal for the SISO-FSO link after propagating a distance R is given by [7, 17]

(17)

where H(ω) = e^−αRe^−jβ(ω)R is the transfer function of the transmission medium with attenuation coefficient α and propagation constant β(ω), n(t) is the amplifier noise, and

is the received data-bearing optical signal after the SISO-FSO link without considering the effect of EDFA. F{} and F⁻¹{ } are the forward and inverse Fourier transformations, respectively. By considering the effects of laser phase noise, PMD, and PDL, the received data-bearing optical signal for the SISO-FSO link after propagating a distance R is expressed as

(18)

where L_p(ω) is the PDL, e^jφ(t) is the phase noise, and

represents the PMD-induced delay.

The received data-bearing optical signal for the MIMO-FSO link with the effects of practical impairments such as phase noise, PMD, and PDL is expressed as

(19)

where N is the number of receiver apertures in the MIMO-FSO links used.

Figure 4 demonstrates the block diagram of the coherent DP-16 QAM receiver. It consists of CW lasers acting as the LO, polarization splitters for extracting the X and Y polarization components, (2 × 4)90^° optical hybrids, balanced detectors (BDs), and electrical amplifiers (EAs).

The LO signal is given by [25]

(20)

where P_LO is the LO power, ω_LO is the angular frequency of L_O, ψ_LO is the phase of L_O, and e_LO is the polarization of L_O.

After mixing the received optical signal with the LO signal, the output electric fields of the 90^° hybrid coupler are expressed as [7]

(21)

where E (R, t) is the received data-bearing optical signal for SISO/MIMO-FSO link.

After BDs, the IQ-phase currents for both polarizations can be expressed as

(22a)

(22b)

where R_D is the responsivity of the photodetector and I_shI and I_shQ are the photocurrents due to shot noise. Shot noise current is considered in the in-phase and quadrature-phase expressions because shot noise affects the statistical properties of the detected optical signal.

2.4. DSP

In the DSP unit shown in Figure 5, various step-by-step compensation algorithms are implemented to recover the transmitted symbols from the received electrical signals. The preprocessing stage of each DSP unit includes three functions: noise sources within the transmission bandwidth are converted into signals and added to the sampled optical signal; imperfectly biased voltages of the modulators are compensated by DC blocking; and the 16-QAM grid is used to normalize the received signal.

The various steps involved in the signal recovery stages are described as follows:

a.
Low-pass Bessel filter: A 4^th-order low-pass Bessel filter with a bandwidth of 0.75× symbol rate is used to remove the out-of-band noise.
b.
Resampling: Cubic interpolation is used for resampling the received signal, with symbol rate of = bit rate/8.
c.
QI compensation: The Gram–Schmidt orthogonalization procedure (GSOP) is used to mitigate the amplitude and phase mismatch between the IQ electrical signals. Consider r_I(t) and r_Q(t) to be nonorthogonal components of the received signal, and then GSOP produces two orthonormal signals, I^o(t) and Q^o(t), as follows [26]:
(23a)

(23b)

(23c)
where ρ = E{r_I(t), r_Q(t)} is the correlation coefficient, P_I = E{r²(t)}, , and E‹.›denotes expectation operator.
d.
AE: AE is used to mitigate PMD and ISI. The AE is implemented by using a two-stage constant modulus algorithm-radius directed (CMA-RD). The objective of CMA is to minimize the cost function [18].
(24)
where y (k) denotes the AE output and R_P is a constant whose value depends only on the input data symbol a(k).
e.
FOE: FOE is used to cancel the frequency mismatch between the transmitter and the LO. The received signal after proper equalization is expressed as [12]
(25)
where C (k) denotes the data symbols, f denotes the carrier frequency offset, φ_k denotes the carrier phase, T denotes the symbol period, and n(k) denotes the zero-mean Gaussian random variable. The frequency offset can be minimized by maximizing the spectral density of the fourth power S⁴(k) of the received signal as [26]
(26)
where M is the symbol block size.
f.
CPE: CPE using a blind phase search (BPS) algorithm is used to recover and remove the phase noise by trying different test phases until the optimum phase is found. The received signal Z_k is alternated by B test carrier phase angles φ_b [26]:
(27)
with b ε{0, 1, …, B − 1}. All the alternated symbols are fed into the decision circuit, and the distance to the nearest constellation points is calculated in the complex plane as [10]
(28)
where is the decision of .

The electrical signals that are received from the DSP stage are processed by the decision circuit. The output of the decision block is provided to two 16-QAM decoders to decode the sequences for both polarizations. Then, the decoded outputs are combined S/P converter and the output of the S/P converter is again provided as input to a BER tester. A BER tester is used to generate the transmitted bit sequence on the transmitter side and compare it with the received bit sequence.

BER: The BER for a dual-polarization system is given by [27]

(29)

where the errors are counted only on the portions of sequence length outside the guard bits.

EVM: The EVM (%) of the received signals with the symbol sequence of S and its decision of ⌊S⌋_d is given as follows [28]:

(30)

where

indicates the mean value.

3. Results and Discussion

The simulation results are evaluated in terms of constellation diagrams, RF and optical power spectra, BER, and EVM performance metrics.

3.1. Simulation Parameters

As the input signal sequence length increases, the performance of the system becomes more reliable and robust. However, that causes limitations on the computer’s memory and total simulation time. As a performance trade-off, typically a sequence length of 65,536 bits with a sample per bit of 4 and a number of samples of 62,144 is sufficient for this research. In addition to this, a set of 100 guard bits is used to analyze the system. The remaining simulation parameters are summarized in Table 1.

Table 1. Simulation parameters.

Name of the parameters used	Values of the parameters
Data rate	120 Gbps
Symbol rate	15 GBaud
Launch optical power/LO power	15 dBm
Laser linewidth/LO linewidth	0.1 MHz
Lase center wavelength/LO wavelength	1550 nm (C-band)
Transmitter aperture diameter	5 cm
Receiver aperture diameter	20 cm
Beam divergence angle	2 mrad
Atmospheric attenuation	0.233 dB/km (clear air), 6.2 dB/km (wet snow), 9.64 dB/km (medium rain), 15.5 dB/km (light fog)
Refractive index structure constant (C²n)	5 × 10⁻¹³m^−2/3 (strong turbulence) and 5 × 10⁻¹⁷m^−2/3(weak turbulence)
Forward pumping power of EDFA	100 mW at 980 nm pumping laser
EDFA length	5 m
PIN photodiode responsivity	1 A/W
Dark current	10 nA
BER-FEC limit	2 × 10⁻³

Figures 6(a), 7(a), 8(a), and 9(a) show a distorted, overlapping, and rotating constellation diagram obtained at the input of DSP at a link range of 2 km in wet snow conditions. This is because of the information-bearing signal degradation due to atmospheric attenuation, geometric loss, and atmospheric turbulence. Figures 6(b), 7(b), 8(b), and 9(b) show the constellation diagram after the band noise is filtered out using the 4th-order low-pass Bessel filter. Figures 6(c), 7(c), 8(c), and 9(c) show the constellation diagram obtained after resampling. After AE, marginally clear constellation diagrams are shown in Figures 6(d), 7(d), 8(d), and 9(d). Figures 6(e), 7(e), 8(e), and 9(e) show the constellation diagram after QI compensation. Figures 6(f), 7(f), 8(f), and 9(f) show the constellation after FOE. Figures 6(g), 7(g), 8(g), and 9(g) show the constellation diagram after CPE. As a result, the constellation diagrams at 4 × 4 MIMO-weak turbulence levels are less distorted as compared to 4 × 4 MIMO-strong turbulence. Figure 10(a) shows the optical power spectrum of the system at the transmitter output. The center frequency is at 193.414 THz (i.e., 1550 nm), and the peak power observed at this frequency is around −7.9967 dBm. Spectral efficiency is a measure of how efficiently a communication system uses its allocated bandwidth to transmit data. Mathematically, spectral efficiency (in b/s/Hz) = data rate (in bps)/channel bandwidth (in Hz). The transmission bandwidth, or full width at half maximum, is approximately 25.95 GHz, as observed in Figure 10. For a transmitted data rate of 120 Gbps, the system possesses a spectral efficiency of around 4.62 b/s/Hz. The obtained peak power at a center frequency of 193.414 THz under weak turbulence levels in wet snow conditions is around −40.5516 dBm, whereas under strong turbulence levels in wet snow conditions, it is around −41.5524 dBm. Due to this, the impact of atmospheric turbulence on power loss is insignificant. At the same center frequency, the peak power was reduced from −41.5524 dBm to −60.3094 dBm under strong turbulence levels in light fog conditions as compared to strong turbulence levels in wet snow conditions. The result shows that power loss increases as the atmospheric attenuation value increases. After EDFA, the peak power increased from −41.5524 dBm to −4.8903 dBm under strong turbulence levels in wet snow conditions as compared to strong turbulence levels in wet snow conditions.

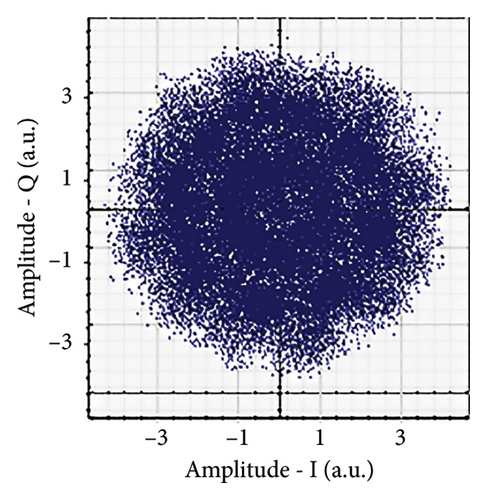
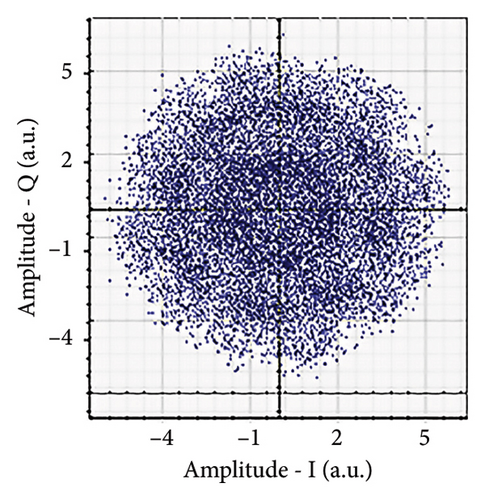
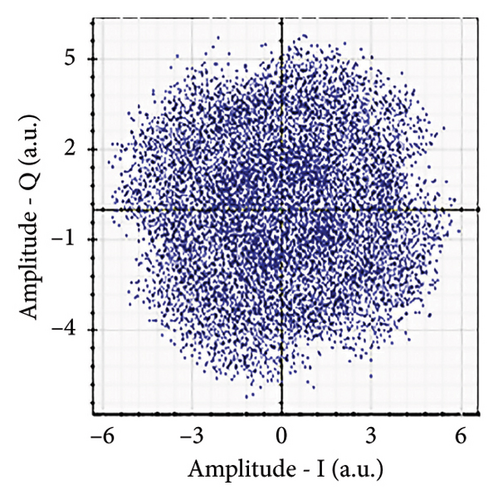
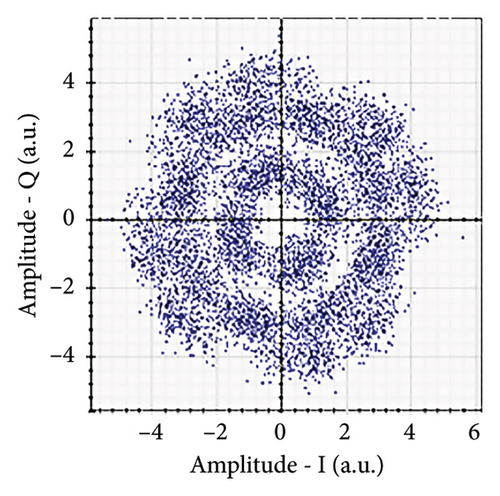
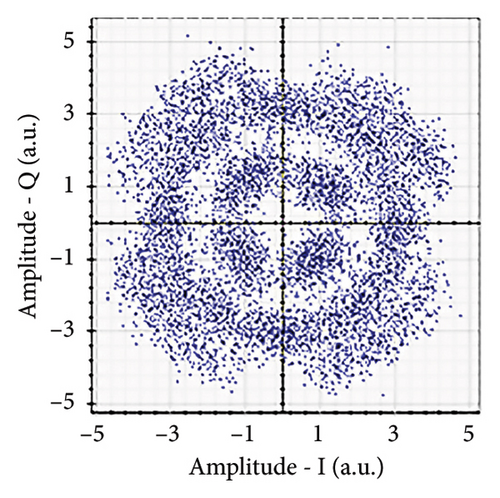
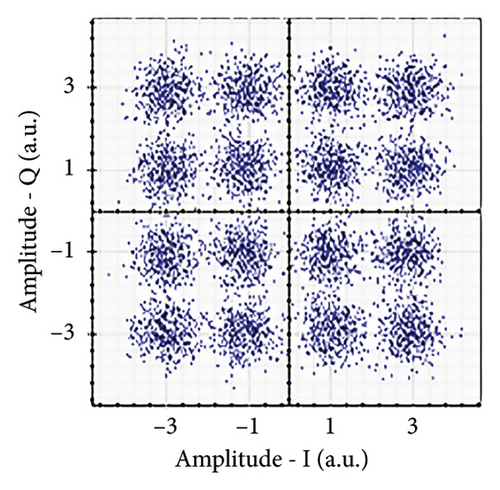
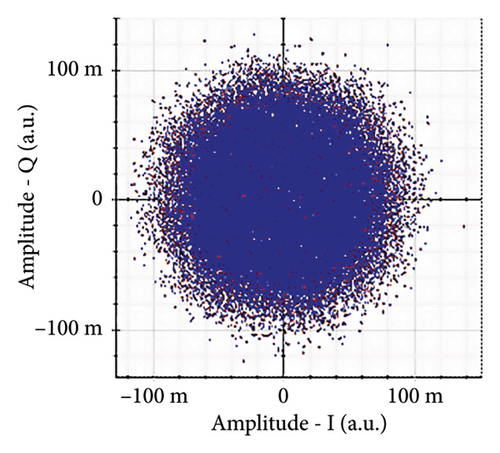
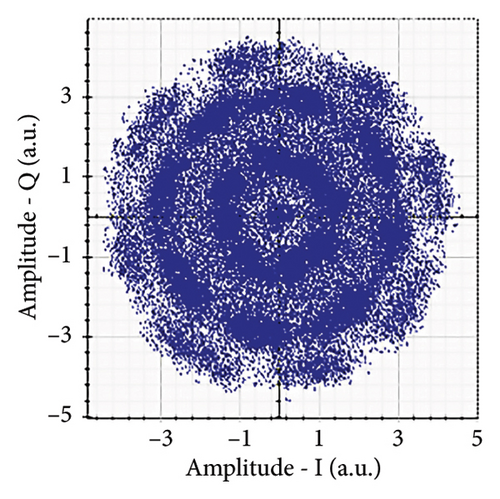
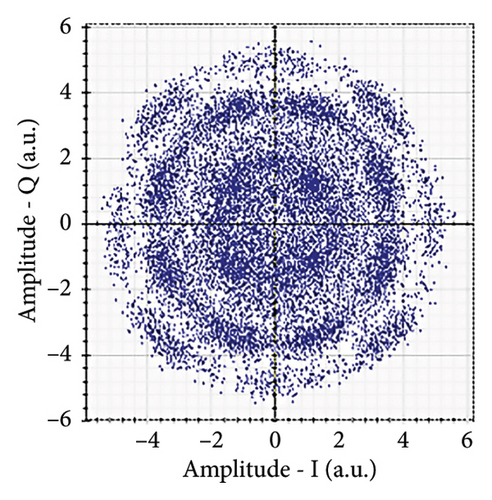
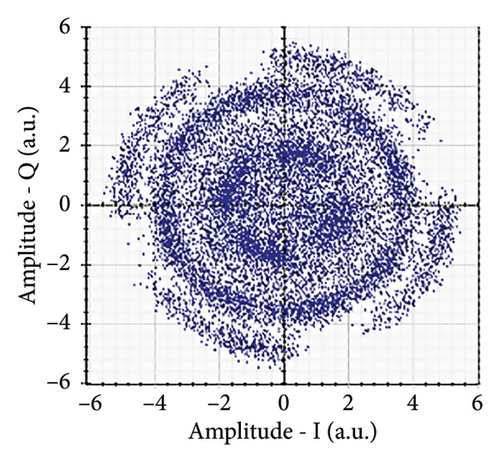
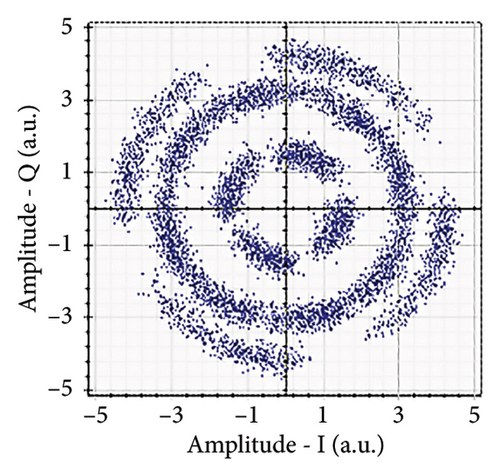
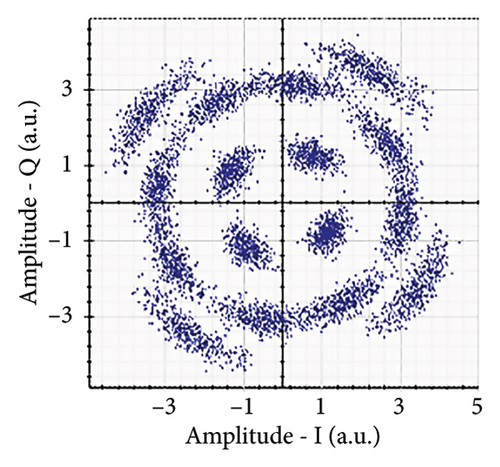
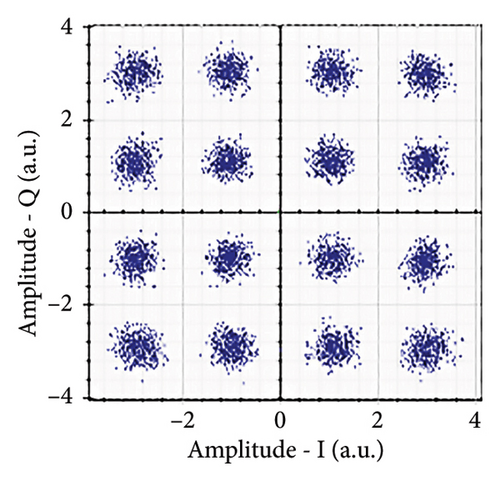
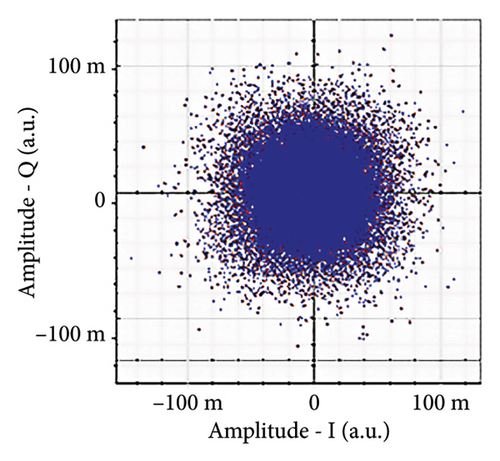
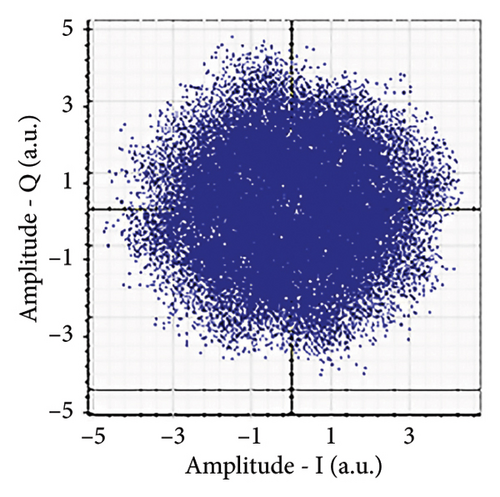
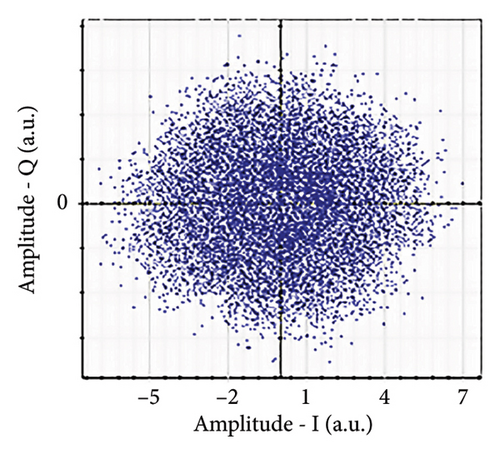
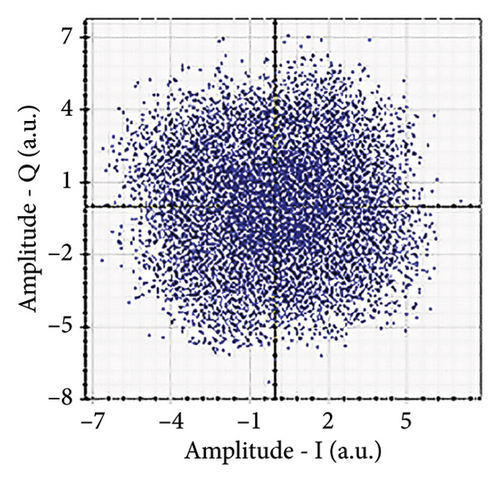
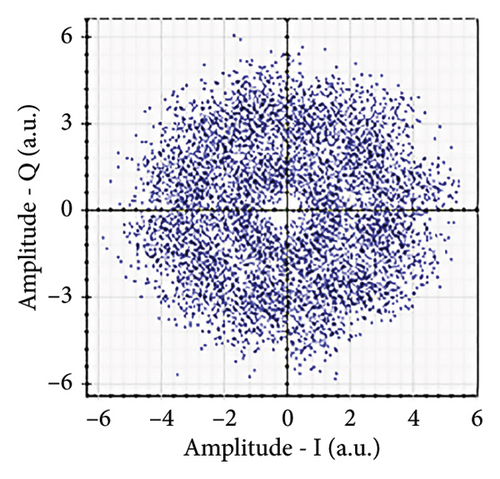
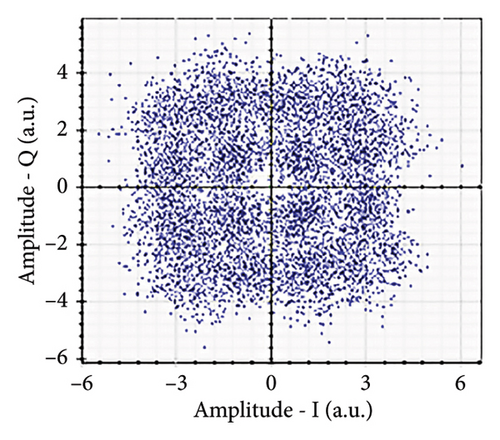
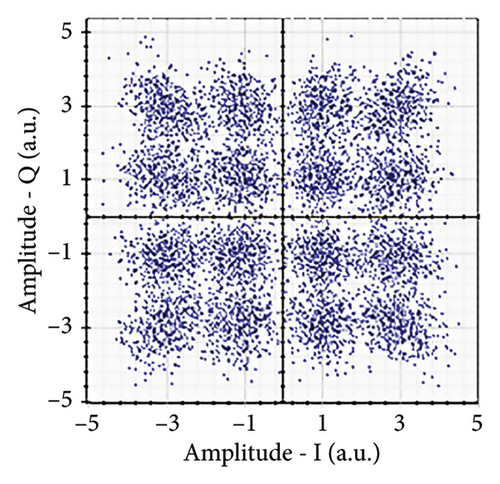
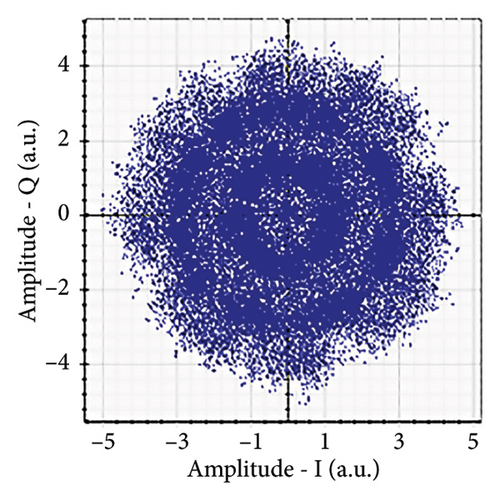
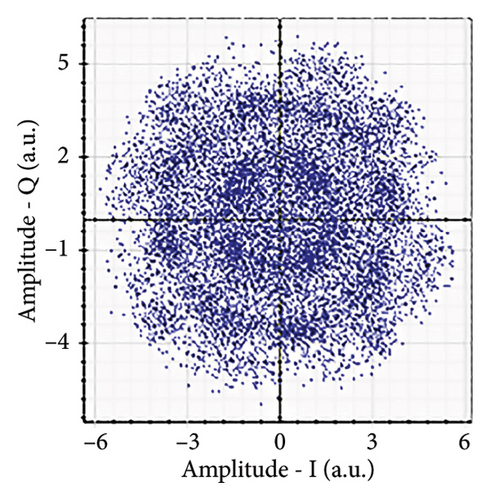
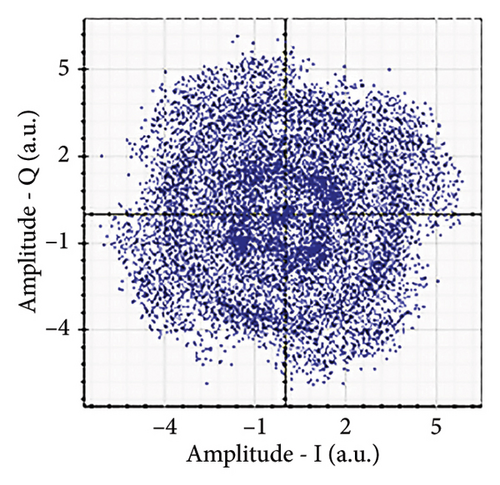
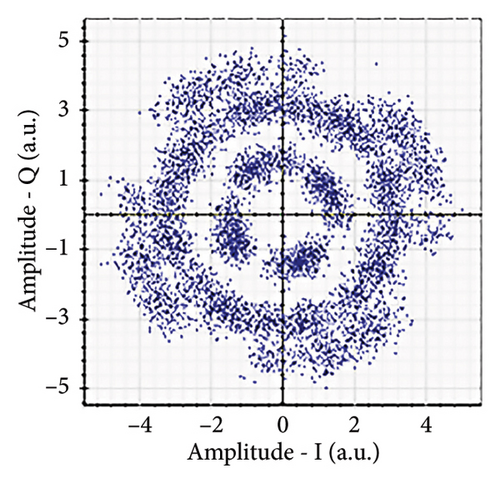
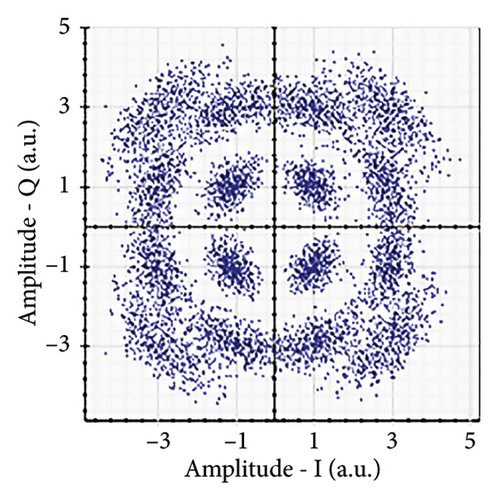
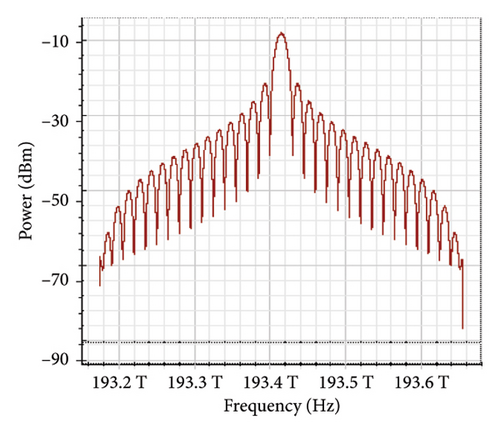
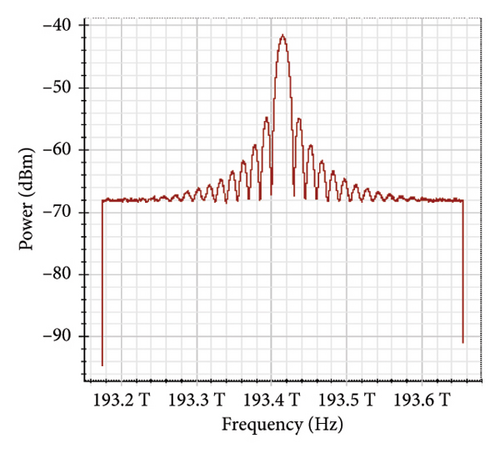
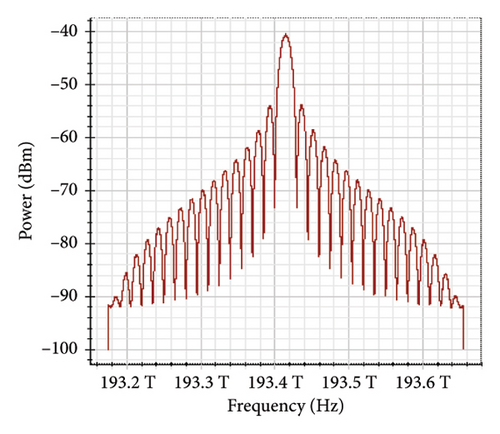
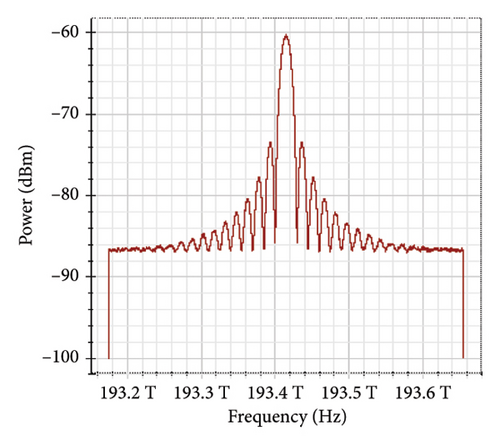
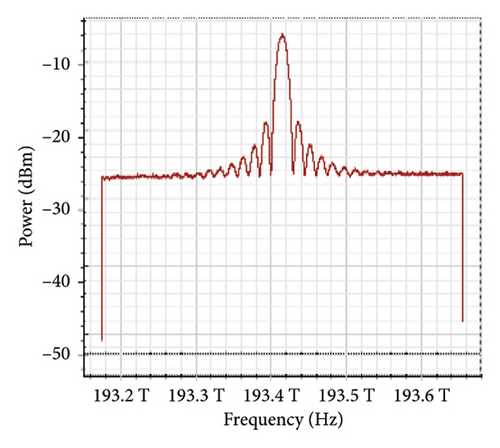
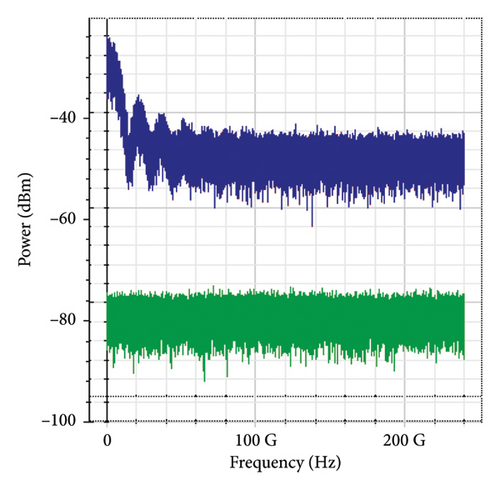
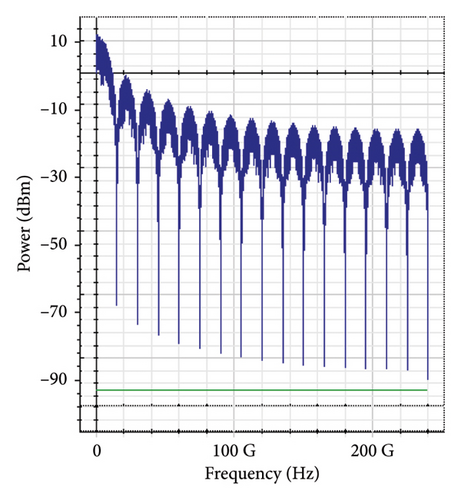
Figure 11 shows the RF power spectrum for strong turbulence levels in wet snow conditions at 2 km in a 4 × 4 MIMO-FSO link. Before DSP, the green color indicates the noise, and blue is the signal; in this case, the signal is weak and has a certain degree of distortion. After DSP, the noise is compensated, and the signal quality has improved.

3.2. Effect of Link Range on the Performance of the System

The BER and EVM results are done after the channel impairments are compensated by the DSP. The results obtained due to the effects of the link range are divided into four parts according to different weather conditions.

3.2.1. Clear Air Conditions

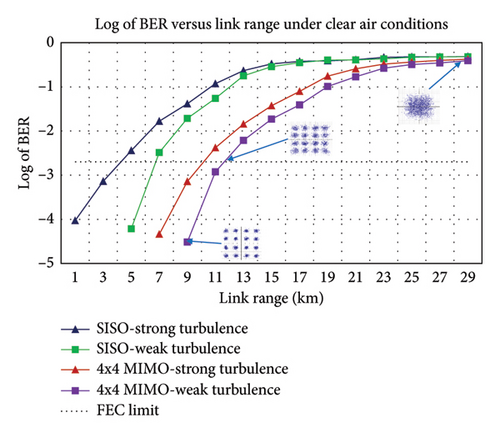
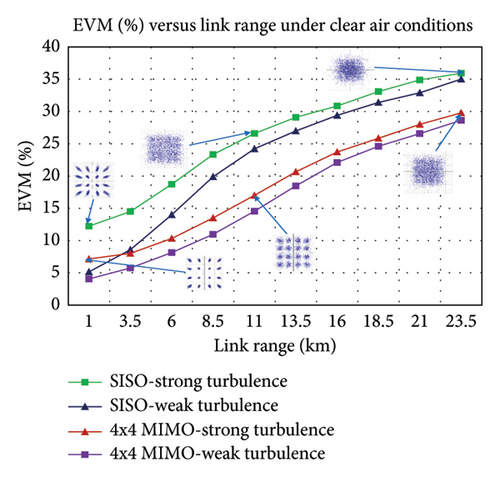
Figure 12(a) shows the BER versus link range plot for clear air conditions. The proposed model can achieve a maximum link range of 4.18 km, 6.6 km, 10.125 km, and 11.55 km in SISO-strong, SISO-weak, 4 × 4 MIMO-strong, and 4 × 4 MIMO-weak turbulence levels, respectively, under acceptable BER-FEC limit. As the link range increases, the BER of the received signal increases due to atmospheric attenuation, geometric loss, and atmospheric turbulence. Figure 12(b) depicts the EVM versus link range plot under clear air conditions. As the link range increases from 1 km to 25 km, the EVM values increase from 12.2348% to 35.9406%, 5.1522% to 35.0269%, 7.15105% to 29.7989%, and 4.05288% to 28.6475% under SISO-strong, SISO-weak, 4 × 4 MIMO-strong, and 4 × 4 MIMO-weak turbulence levels, respectively. As the link range increases, distortion in the constellation diagram increases, due to which information retrieval becomes challenging on the receiver end.

3.2.2. Wet Snow Conditions

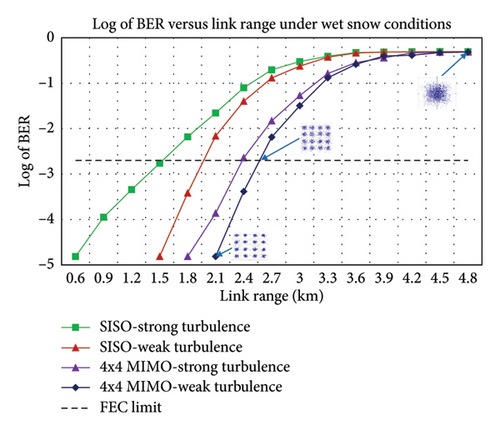
Figure 13(a) shows the BER versus link range plot for wet snow conditions. As the attenuation value increases from 0.233 dB/km to 6.2 dB/km, the maximum link range to achieve the BER-FEC limit decreases to 1.48 km, 1.951 km, 2.378 km, and 2.548 km for SISO-strong, SISO-weak, 4 × 4 MIMO-strong, and 4 × 4 MIMO-weak turbulence levels, respectively.

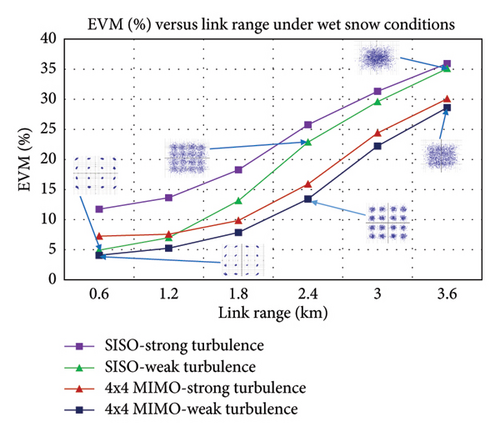
The EVM versus link range graph for wet snow conditions is illustrated in Figure 13(b). Also, at a link range of 1.8 km, the EVM values of 18.2692%, 13.1358%, 9.8594%, and 7.85845% are achieved under SISO-strong, SISO-weak, 4 × 4 MIMO-strong, and 4 × 4 MIMO-weak turbulence levels, respectively.

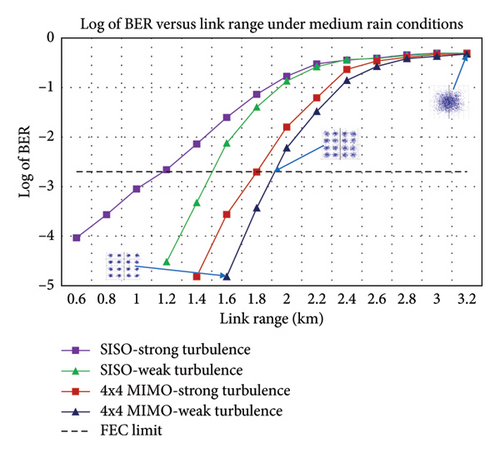
3.2.3. Medium Rain Conditions

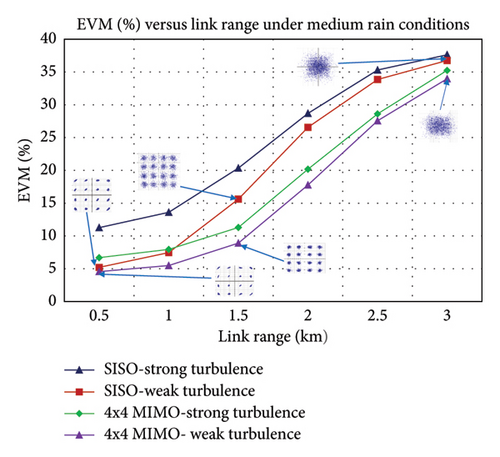
The BER versus link range plot for medium rain conditions is illustrated in Figure 14(a). The BER-FEC limit is obtained at a link range of 1.192 km, 1.499 km, 1.78 km, and 1.906 km under SISO-strong, SISO-weak, 4 × 4 MIMO-strong, and 4 × 4 MIMO-weak turbulence levels, respectively. The EVM versus link range plot for medium rain conditions is shown in Figure 14(b). At a link range of 1 km, the EVM values of 13.6034%, 7.46588%, 7.95825%, and 5.49211% are achieved under SISO-strong, SISO-weak, 4 × 4 MIMO-strong, and 4 × 4 MIMO-weak turbulence, respectively.

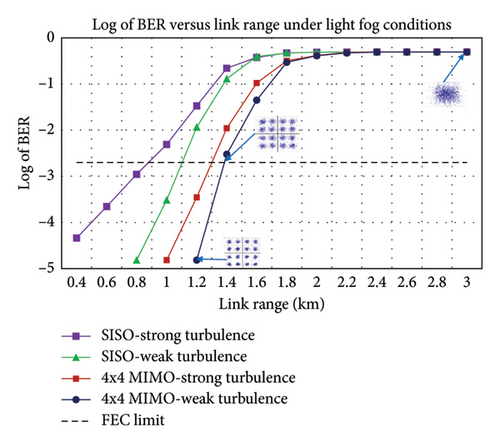
3.2.4. Light Fog Conditions

Figure 15(a) shows the BER versus link range graph for light fog conditions. As the attenuation value increases from clear air conditions to light fog conditions, the maximum link range decreases from 4.14 km, 6.6 km, 10.125 km, and 11.55 km to 0.895 km, 1.101 km, 1.297 km, and 1.37 km in SISO-strong, SISO-weak, 4 × 4 MIMO-strong, and 4 × 4 MIMO-weak turbulence levels, respectively.

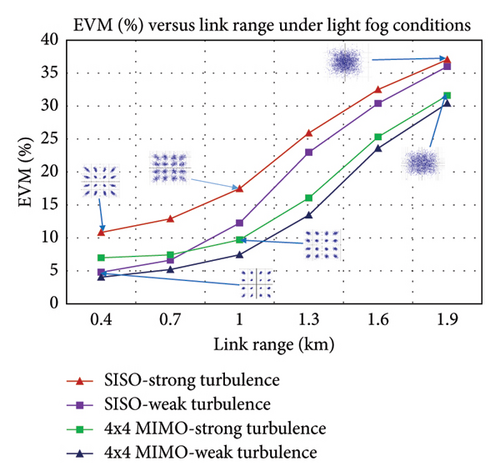
Finally, the EVM versus link range graph for light fog conditions is illustrated in Figure 15(b). The computed values of EVM at a link range of 1 km are 17.4805%, 12.2439%, 9.69993%, and 7.44222% under SISO-strong, SISO-weak, 4 × 4 MIMO-strong, and 4 × 4 MIMO-weak turbulence, respectively. According to the simulation results, the observable tolerance EVM limit to achieve the BER-FEC limit is around 15% for all considered scenarios.

Table 2 shows the performance comparison of SISO and 4 × 4 MIMO-FSO links in terms of the BER at various weather conditions. The 4 × 4 MIMO link improves the link range under different weather conditions as compared to the SISO link. Table 3 also presents performance comparisons with current studies.

Table 2. Comparison between SISO and 4 × 4 MIMO-FSO links in terms of link range in km at a BER-FEC limit of 2 × 10⁻³ under different weather conditions.

Weather condition	SISO-strong turbulence	SISO-weak	4 × 4 MIMO-strong	4 × 4 MIMO-weak
Clear air	4.18	6.6	10.125	11.55
Wet snow	1.48	1.951	2.378	2.548
Medium rain	1.192	1.499	1.78	1.906
Light fog	0.895	1.101	1.297	1.37

Table 3. Performance comparisons with contemporary works.

Authors	Proposed technique	Data rate (Gbps)	Weather conditions	Link range (km)
[9]	4-QAM-OFDM–based FSO link using preamplifier and square root module	10	Clear air	1.8

[10]	Gray-coded DP-QPSK–based FSO link using homodyne detection and DSP	128	Clear air	2.65

[14]	DP-256 QAM-based FSO link using coherent detection and DSP	160	Clear air	3.9

Proposed	Gray-coded DP-16 QAM-based 4 × 4 MIMO FSO link using coherent detection and DSP	120	Clear air, strong turbulence	10.125
Proposed		120	Clear air, weak turbulence	11.55

4. Conclusions

In this paper, the performance of gray-coded DP-16 QAM-based MIMO-FSO links using coherent detection and DSP has been investigated. A coherent receiver with DSP algorithms is used to compensate for amplitude and phase imbalances, PMD, ISI, frequency offset, and phase mismatch, which enhance the transmission range and channel capacity. Further, to mitigate the effects of geometric loss, atmospheric attenuation, and atmospheric turbulence, MIMO links are utilized, which significantly improve the link range. As we have seen from the results, distorted constellation diagrams are observed before DSP, whereas after DSP, distinct constellation symbols are observed. As a result, distinct constellation symbols demonstrate error-free transmission. The system possesses a spectral efficiency of around 4.62 b/s/Hz. The longest link range to attain the BER-FEC limit was achieved under 4 × 4 MIMO weak turbulence levels in clear air conditions, which is 11.55 km, while the shortest was achieved under SISO strong turbulence levels in light fog conditions, which is 0.895 km. The observed tolerable EVM limit to achieve the BER-FEC limit is around 15% for all considered scenarios. Therefore, the combination of MIMO link and DSP is the right candidate to mitigate geometric loss, atmospheric attenuation, and atmospheric turbulence in the FSO system. In MIMO FSO links using coherent detection and DSP, as the MIMO size increases, computational complexity also increases. For the future, this work can be extended to computational complexity reduction.

5. Limitations of the Research Work

The combination of MIMO links and DSP algorithms successfully addresses the challenges of geometric loss, atmospheric attenuation, and atmospheric turbulence in FSO systems. However, this comes at the cost of increased complexity, higher hardware requirements, and potential delays. In order to guarantee optimal performance in practical applications, successful implementation of such systems requires a careful evaluation of their advantages against their limitations.

Disclosure

This paper is already published in the preprint/thesis given in the Faculty of Electrical and Computer Engineering and is archived in BiT-BDU institutional repository system [29] (https://ir.bdu.edu.et/handle/123456789/15801).

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

All authors contributed equally to this work.

Funding

No funding was received to assist with the preparation of this manuscript.

Acknowledgments

The authors wish to thank Bahir Dar Institute of Technology, Bahir Dar University (BiT-BDU), for giving an opportunity and providing the necessary facility to carry out this research.

Open Research

Data Availability Statement

The datasets generated and/or analyzed during the current study are available from the corresponding author on reasonable request.

References

1 Kaushal H. and Kaddoum G., Optical Communication in Space: Challenges and Mitigation Techniques, IEEE communications surveys & tutorials. (2017) 19, no. 1, 57–96, https://doi.org/10.1109/comst.2016.2603518, 2-s2.0-85027695956.
10.1109/COMST.2016.2603518
Web of Science® Google Scholar
2 Odeyemi K. O., Owolawi P. A., and Srivastava V. M., Optical Spatial Modulation with Diversity Combiner in Dual-Hops Amplify-And-Forward Relay Systems over Atmospheric Impairments, Wireless Personal Communications. (2017) 97, no. 2, 2359–2382, https://doi.org/10.1007/s11277-017-4612-6, 2-s2.0-85021156822.
10.1007/s11277-017-4612-6
Web of Science® Google Scholar
3 Kaushal H., Jain V., and Kar S., Free Space Optical Communication, 2017, Springer.
10.1007/978-81-322-3691-7
Google Scholar
4 Alkholidi A. G., Altowij K. S. et al., Free Space Optical Communications: Theory and Practices, 2014, Contemporary Issues in Wireless Communications.
Google Scholar
5 Majumdar A. K. and Ricklin J. C., Free-space Laser Communications: Principles and Advances, Springer Science & Business Media. (2010) 2.
Google Scholar
6 Malik A. and Singh P., Free Space Optics: Current Applications and Future Challenges, International Journal of Optics. (2015) 2015, 1–7, https://doi.org/10.1155/2015/945483, 2-s2.0-84948844330.
10.1155/2015/945483
Web of Science® Google Scholar
7 Patel D. K. and Mandloi A., Investigation of RS Coded DP-16-QAM DWDM FSO Link under Various Atmospheric Conditions, Optical and Quantum Electronics. (2022) 54, no. 1, https://doi.org/10.1007/s11082-021-03412-x.
10.1007/s11082-021-03412-x
Web of Science® Google Scholar
8 Alsharari M., Aliqab K., Ali F., and Armghan A., Integrated Free-Space Optics and Fiber Optic Network Performance Enhancement for Sustaining 5G High Capacity Communications, International Journal of Optics. (2023) 2023, 1–9, https://doi.org/10.1155/2023/8685686.
10.1155/2023/8685686
Web of Science® Google Scholar
9 Kumar N. and Teixeira A. L. J., 10 Gbit/s OFDM Based FSO Communication System Using M-QAM Modulation with Enhanced Detection, Optical and Quantum Electronics. (2016) 48, 9–7, https://doi.org/10.1007/s11082-015-0272-5, 2-s2.0-84949545599.
10.1007/s11082-015-0272-5
Web of Science® Google Scholar
10 Pottoo S. N., Goyal R., and Gupta A., Development of 32-GBaud DP-QPSK Free Space Optical Transceiver Using Homodyne Detection and Advanced Digital Signal Processing for Future Optical Networks, Optical and Quantum Electronics. (2020) 52, no. 11, https://doi.org/10.1007/s11082-020-02623-y.
10.1007/s11082-020-02623-y
PubMed Web of Science® Google Scholar
11 Moustafa S. M., Fayed H. A., Aly M. H., and Mahmoud M., SISO and MIMO FSO Based Links under Different Weather Conditions: System Evaluation, Optical and Quantum Electronics. (2021) 53, no. 12, 674–722, https://doi.org/10.1007/s11082-021-03339-3.
10.1007/s11082-021-03339-3
Web of Science® Google Scholar
12 Kakati D. and Sonkar R. K., Performance of DSP-Assisted Gray-Coded DP-16-QAM Nyquist-DWDM Super-channel Transceiver for High-Speed Long-Haul Optical Interconnects, Photonic Network Communications. (2023) 45, no. 1, 37–48, https://doi.org/10.1007/s11107-022-00988-6.
10.1007/s11107-022-00988-6
Web of Science® Google Scholar
13 Miglani R. and Malhotra J. S., Performance Enhancement of High-Capacity Coherent DWDM Free-Space Optical Communication Link Using Digital Signal Processing, Photonic Network Communications. (2019) 38, no. 3, 326–342, https://doi.org/10.1007/s11107-019-00866-8.
10.1007/s11107-019-00866-8
Web of Science® Google Scholar
14 Konda R. R., Thirunavvukkarasu Velayudham N., and Venkatesan Pg R., Performance Analysis of Coherent Free-Space Optics Transmission Link Using In-phase Quadrature Modulator-Based Polarization Multiplexed-256-Quadrature Amplitude Modulation, Transactions on Emerging Telecommunications Technologies. (2021) 32, no. 9, 42–62, https://doi.org/10.1002/ett.4262.
10.1002/ett.4262
Web of Science® Google Scholar
15 Janu D. and Janyani V., Performance of QPSK Modulation for FSO under Different Atmospheric Turbulence, Optical and Wireless Technologies: Proceedings of OWT 2018, 2020, Springer, 513–520.
10.1007/978-981-13-6159-3_54
Google Scholar
16 Kakati D. and Arya S. C., Performance of 120 GBps Single Channel Coherent DP-16-QAM in Terrestrial FSO Link under Different Weather Conditions, Optik. (2019) 178, 1230–1239, https://doi.org/10.1016/j.ijleo.2018.10.035, 2-s2.0-85055467936.
10.1016/j.ijleo.2018.10.035
Web of Science® Google Scholar
17 Kakati D. and Arya S. C., A 640-Gbps, 15.2344-b/s/Hz Full-Duplex Optical Fiber/wireless Single-Channel Coherent Communication System Using IQM-Based DP-256-QAM and DSP Techniques, Photonic Network Communications. (2020) 39, no. 1, 26–38, https://doi.org/10.1007/s11107-019-00875-7.
10.1007/s11107-019-00875-7
Web of Science® Google Scholar
18 Kakati D. and Arya S. C., A Full-Duplex Optical Fiber/wireless Coherent Communication System with Digital Signal Processing at the Receiver, Optik. (2018) 171, 190–199, https://doi.org/10.1016/j.ijleo.2018.05.140, 2-s2.0-85048534526.
10.1016/j.ijleo.2018.05.140
Web of Science® Google Scholar
19 Anandkumar D. and Sangeetha R., A Survey on Performance Enhancement in Free Space Optical Communication System through Channel Models and Modulation Techniques, Optical and Quantum Electronics. (2021) 53, 5–39, https://doi.org/10.1007/s11082-020-02629-6.
10.1007/s11082-020-02629-6
Web of Science® Google Scholar
20 Algamal A. A., Fayed H. A., Mahmoud M., and Aly M. H., Reliable FSO System Performance Matching Multi-Level Customer Needs in Alexandria City, Egypt, Climate: Sandstorm Impact with Pointing Error, Optical and Quantum Electronics. (2020) 52, no. 7, 349–418, https://doi.org/10.1007/s11082-020-02468-5.
10.1007/s11082-020-02468-5
Web of Science® Google Scholar
21 Singh H. and Mittal N., Analyzing the Impact of Fog and Atmospheric Turbulence on the Deployment of Free-Space Optical Communication Links in India, Arabian Journal for Science and Engineering. (2022) 47, no. 3, 2691–2710, https://doi.org/10.1007/s13369-021-05763-9.
10.1007/s13369-021-05763-9
Web of Science® Google Scholar
22 Paliwal P., Shreemali J., Chakrabarti P., and Poddar S., Performance Optimization of Hybrid RAMAN-EDFA Based WDM-FSO under Adverse Climatic Conditions, Materials Today: Proceedings. (2021) .
10.1016/j.matpr.2020.12.624
Google Scholar
23 Magidi S. and Jabeena A., Free Space Optics, Channel Models and Hybrid Modulation Schemes: A Review, Wireless Personal Communications. (2021) 119, no. 4, 2951–2974, https://doi.org/10.1007/s11277-021-08380-9.
10.1007/s11277-021-08380-9
Web of Science® Google Scholar
24 Singh N., Kumar M., and Verma A., Analysis of Four Wave Mixing in Ultra Dense WDM-Hybrid Optical Amplifier Systems, Journal of Optical Communications. (2022) 43, no. 3, 303–309, https://doi.org/10.1515/joc-2019-0006, 2-s2.0-85061725980.
10.1515/joc-2019-0006
Google Scholar
25 Kumari M., Sheetal A., and Sharma R., Performance Analysis of Symmetrical and Bidirectional 40 Gbps TWDM-PON Employing M-QAM-OFDM Modulation with Multi-Color Lds Based VLC System, Optical and Quantum Electronics. (2021) 53, no. 8, 455–529, https://doi.org/10.1007/s11082-021-03108-2.
10.1007/s11082-021-03108-2
Web of Science® Google Scholar
26 Sharma N., Agrawal S., and Kapoor V., Improved Adaptive Equalization with Fixed Step Size CMA for DP-QPSK DWDM System, Optical and Quantum Electronics. (2020) 52, no. 5, 236–317, https://doi.org/10.1007/s11082-020-02352-2.
10.1007/s11082-020-02352-2
Web of Science® Google Scholar
27 Sharma N., Agrawal S., and Kapoor V., Performance Optimization of OADM Based DP-QPSK DWDM Optical Network with 37.5 GHz Channel Spacing, Optical Switching and Networking. (2021) 40, https://doi.org/10.1016/j.osn.2021.100606.
10.1016/j.osn.2021.100606
Web of Science® Google Scholar
28 Padhy J. B. and Patnaik B., Performance Enhancement of FSO Based Multi Carrier System Using DP-QPSK and Manchester Coding in Weak to Strong Turbulence Regime, Optical and Quantum Electronics. (2022) 54, no. 2, https://doi.org/10.1007/s11082-021-03491-w.
10.1007/s11082-021-03491-w
Web of Science® Google Scholar
29 Libisework Z., Performance Analysis of Gray Coded DP-16 QAM Based MIMO-FSO Link Using Coherent Detection and DSP, 2023, https://ir.bdu.edu.et/handle/123456789/15801.
Google Scholar

All articles

Performance Analysis of Gray-Coded DP-16QAM MIMO-FSO Systems With Coherent Detection and DSP Techniques

Abstract

1. Introduction

2. System Model and Analysis

2.1. DP-16 QAM Transmitter

2.2. FSO Channel

2.3. Coherent DP-16 QAM Receiver

2.4. DSP

3. Results and Discussion

3.1. Simulation Parameters

3.2. Effect of Link Range on the Performance of the System

3.2.1. Clear Air Conditions

3.2.2. Wet Snow Conditions

3.2.3. Medium Rain Conditions

3.2.4. Light Fog Conditions

4. Conclusions

5. Limitations of the Research Work

Disclosure

Conflicts of Interest

Author Contributions

Funding

Acknowledgments

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Performance Analysis of Gray-Coded DP-16QAM MIMO-FSO Systems With Coherent Detection and DSP Techniques

Abstract

1. Introduction

2. System Model and Analysis

2.1. DP-16 QAM Transmitter

2.2. FSO Channel

2.3. Coherent DP-16 QAM Receiver

2.4. DSP

3. Results and Discussion

3.1. Simulation Parameters

3.2. Effect of Link Range on the Performance of the System

3.2.1. Clear Air Conditions

3.2.2. Wet Snow Conditions

3.2.3. Medium Rain Conditions

3.2.4. Light Fog Conditions

4. Conclusions

5. Limitations of the Research Work

Disclosure

Conflicts of Interest

Author Contributions

Funding

Acknowledgments

Open Research

Data Availability Statement

References

Figures

References

Related

Information