Influences of Cattaneo–Christov Heat–Mass Fluxes and Viscous Dissipation on Stagnation Point Casson Hybrid Nanofluid Flow Over a Stretching Sheet With Nonlinear Thermal Radiation
Abstract
This study explores the impact of the Cattaneo–Christov heat and mass fluxes, viscous dissipation, and nonlinear thermal radiation on the stagnation point flow of electrically conductive Casson hybrid nanofluids over a porous material. Employing a similarity transformation, the nonlinear partial differential equations are reduced to nonlinear ordinary differential equations, which are then numerically solved using MATLAB’s bvp4c solver. The results highlight the influence of nanoparticle fraction on velocity, temperature, heat transfer, and drag forces, with hybrid nanofluids outperforming single nanofluids. Increased nanoparticle fraction improves particle interaction and thermal conductivity.
1. Introduction
Models of non-Newtonian fluids have attracted the attention of researchers in the literature. Numerous scholars have examined the non-Newtonian problem for industrial applications in engineering, food production, and storage. The Casson fluid model characterizes a class of non-Newtonian fluids displaying distinctive shear-dependent properties, rendering it notably applicable across diverse industrial and biological systems. This model is characterized by a yield stress, below which the fluid behaves as a solid, and above which it flows like a liquid. Tomato sauce, honey, synovial fluids, sewage sludge, soup, jelly, and human blood are a few examples of Casson fluid. This fluid model illustrates that the fluid flows when the yield stress is lower than the shear stress but acts as a solid when the yield stress surpasses the shear stress. In the chemical and biological industries, understanding and modeling the flow of Casson fluids is crucial for processes involving the handling and transport of these materials, as their viscosity can change significantly under different shear stresses. Gireesha et al. [1] examined melting heat transfer and the Cattaneo–Christov heat flux in dusty Casson fluid flow over a stretching sheet, demonstrating that melting effects elevate temperature distributions in both fluid and particulate phases. Reddy et al. [2] applied the implicit finite difference method to analyze the influence of chemical reaction effects and slip boundary conditions on Casson fluid flow with the Cattaneo–Christov heat flux. Their results revealed that increasing the inclination angle reduces flow velocity. Meanwhile, Khan et al. [3] investigated the role of slip dynamics, convective boundary conditions, and mixed convection in unsteady two-dimensional stagnation point flow of a Casson fluid over contracting and stretching sheets.
Optimizing the thermal transport efficiency of conventional base fluids constitutes a pivotal challenge in advancing contemporary scientific and technological applications. To enhance thermal efficiency and ensure the effective operation, longevity, and optimal thermal performance of systems like radiators and computer cooling systems, energy systems, biotechnology, and chemical engineering, it is essential to focus on these aspects. Because of this, scientists and researchers are increasingly interested in investigating the thermal transfer properties of solid particles compared to traditional base fluids. Nanofluids comprise nanoparticles of metals, oxides, carbides, or carbon nanotubes dispersed in conventional base fluids such as water, ethylene glycol, or oil. Pioneered by Choi and Eastman [4], this class of fluids leverages nanoparticle inclusion to augment thermal conductivity and heat transfer performance. Subsequent research has expanded to diverse applications, including Said et al. [5], who evaluated aluminum oxide (Al2O3) nanoparticles for improving solar collector efficiency; Elnaqeeb et al. [6], who modeled heat transfer enhancement using the Cattaneo heat flux framework; and Shi et al. [7], who analyzed water-based Al2O3 nanofluids in microchannel cooling systems.
Despite the significant potential of nanofluids to enhance heat transfer efficiency, they face several challenges, including material compatibility issues and concerns about long-term stability. A hybrid nanofluid consists of more than one type of nanoparticle in addition to a single primary carrier fluid. Due to its extraordinary properties, researchers have focused a lot of attention on this hybrid nanofluid flow. Hybrid nanofluid flows enhance both the chemical and physical properties of materials. Hybrid nanofluids demonstrate superior performance relative to single-component nanofluids, exhibiting enhanced thermal conductivity, heat transfer efficiency, electrical conductivity, and colloidal stability. Applications for hybrid nanofluids are numerous and span a wide range of industries, such as biomedical engineering, photovoltaic current applications, electronics cooling, lubrication, air conditioning systems, welding, and automatic reactors. Suresh et al. [8] pioneered the synthesis and analysis of water-based Al2O3-Cu hybrid nanomaterials, highlighting their enhanced thermophysical properties. In contrast, Ali et al. [9] investigated convective stagnation point flow dynamics of Al2O3-Cu/H2O hybrid nanofluids over a stretching disk, emphasizing momentum and heat transfer characteristics. Khan et al. [10] employed fractional calculus to model radiative thermal conductivity in Jeffrey fluid-based hybrid nanofluids, revealing nonlinear heat flux dependencies. Ahmad and Priyanka [11, 12] systematically evaluated the thermal behavior of hybrid nanofluid flows across divergent geometric configurations, identifying optimal design parameters. Adnan and Ashraf [13] assessed the thermohydraulic performance of hybrid and ternary hybrid nanofluids under magnetohydrodynamic (MHD) and convective boundary conditions, demonstrating enhanced energy efficiency. Meanwhile, Senthilvadivu et al. [14] explored magnetically driven interactions in blood-based hybrid nanofluids, quantifying variations in thermal conductivity and mass transport phenomena. Higher thermal conductivity often results in improved heat transfer rates. The results can inform the design of more efficient systems utilizing nanofluids, potentially leading to innovations in drug delivery, medical devices, and other technologies.
Stagnation point flow is a fundamental concept in fluid dynamics with wide-ranging applications and significance in various fields, including aerodynamics, biomedical engineering, and chemical processes. Understanding this phenomenon helps engineers and scientists design more efficient systems and improve performance in numerous applications. Stagnation point flow captivates researchers due to its relevance across various scientific disciplines and industries. Many scholars are actively investigating different facets of the flow dynamics near the stagnation point. The applications of stagnation point phenomena are extensive in engineering and industrial sectors, encompassing areas such as particle deposition, material fabrication, metallurgical processing, hybrid reactors, and external plasma aerodynamics. Ijaz Khan and Alzahrani [15] analyzed the electrical conductivity and stagnation point flow of Williamson nanomaterials over a stretched surface, while Anusha et al. [16] studied the effect of hybrid nanofluids on the unstable stagnation point of a non-Newtonian fluid, and Poornima et al. [17] recently investigated the impact of CuO and MgO nanoparticles on stagnation point flow over shrinking and expanding cylinders.
Fourier’s theory of heat conduction, established by Jean-Baptiste Joseph Fourier in the early 19th century, serves as a fundamental principle in heat transfer. It explains how heat energy moves through materials as a result of temperature differences. This theory is encapsulated in Fourier’s law of heat conduction, which lays the groundwork for understanding thermal conduction in solids, liquids, and gases. Fourier’s theory of heat conduction provided a foundational framework for understanding the mechanisms underlying heat transmission [18]. Cattaneo [19] added a thermal relaxation period to the Fourier theory to enhance thermal transmission more effectively. This formulation introduces a temporal component to the classical Fourier heat conduction equation, addressing the noninstantaneous propagation of thermal signals. Consequently, the revised approach yields a hyperbolic heat transport model, diverging from the parabolic formulation inherent to Fourier’s original framework. Christov [20] developed the Cattaneo–Christov heat flow model, a time derivative model that is very useful in convective heat transfer mechanisms. Christov further developed the Cattaneo model to include mass flux equations, reflecting the finite speed of diffusion processes, thereby extending the concept to mass transfer. The Cattaneo–Christov heat and mass flux model represents a substantial advancement in heat and mass transfer, providing a more precise and thorough understanding of complex systems. Its applications extend across multiple disciplines, making it a crucial resource for researchers and engineers aiming to optimize processes and materials in both scientific and industrial settings. Mustafa [21] investigated the rotating flow of a Maxwell fluid over an extended sheet using the Cattaneo–Christov heat flux model, whereas Alshehri and Shah [22] conducted a numerical investigation of nonisothermal Williamson liquid flow over an exponential surface, incorporating the Cattaneo–Christov thermal framework.
Viscous dissipation refers to the transformation of kinetic energy into thermal energy resulting from internal viscous shear stresses between fluid layers. Its understanding is essential across various fields, from engineering to biology, as it impacts the thermal behavior and efficiency of fluid flows in numerous applications. By accounting for viscous dissipation, engineers and scientists can design more effective systems and processes that optimize performance and energy use. Viscous dissipation is often incorporated into the energy equation. Viscous dissipation manifests as a volumetric energy source within the governing equations, enhancing the fluid’s internal energy while modifying its thermal distribution. Das et al. [23] analyzed the interplay between thermal transmission and viscous dissipation on momentum transfer dynamics in MHD flow along an inclined permeable plate. Concurrently, Ali et al. [24] examined the synergistic effects of nanoparticle aggregation phenomena and viscous dissipation during transient MHD nanofluid flow around a translating slender needle.
MHD constitutes a multidisciplinary theoretical framework unifying electromagnetic and fluid dynamic principles across scales, from industrial liquid metal systems to cosmic plasma phenomena. The deliberate integration of magnetic fields into thermal transport mechanisms unlocks transformative potential for engineering applications, particularly in precision manufacturing and materials processing. Such magnetothermal coupling proves critical in advanced industrial operations, including semiconductor crystal cultivation, high-speed paper coating, microstructured polymer extrusion, and ultrathin film deposition technologies. Krishna and Chamkha [25] conducted a parametric investigation of MHD squeezing flow in nanofluids confined between parallel disks, systematically evaluating the interdependencies between governing parameters and flow characteristics. Their analysis revealed that Lorentz force dominance in such configurations is primarily dictated by transverse magnetic field intensity, with negligible Hall current influence a phenomenon particularly pronounced in water-based nanofluids characterized by low electrical conductivity or laminar velocity regimes. Expanding this research trajectory, Krishna et al. [26] further analyzed the Hall current phenomena in peristaltically driven MHD transport of Jeffrey viscoelastic fluids through a vertically stratified porous configuration, elucidating the interplay between non-Newtonian rheology, electromagnetic stresses, and porous matrix anisotropy. Peristaltic flows generally involve periodic motion, which can dominate the flow characteristics. When the periodic motion is strong, the Hall effect may become less significant compared to the inertial and viscous forces in the fluid. This allows for the simplification of the model by neglecting the Hall effect. In flows through porous media, the structure and properties of the medium can significantly reduce the effects of both the induced magnetic field and Hall currents. The resistance of the porous medium can dominate the fluid’s behavior, creating conditions where the Hall effect and induced magnetic fields become negligible. Generally, neglecting the induced magnetic field and Hall effect is justified by considering the relative magnitudes of the forces involved, the nature of the fluid flows, and the focus of the analysis. Simplifying the model in this way allows researchers to gain meaningful insights without compromising result accuracy, especially when the induced effects are small compared to the dominant flow mechanisms. However, it is crucial to validate this assumption for specific parameter ranges and flow conditions relevant to the study. Guedri et al. [27] investigated the MHD flow of an electromagnetic ternary hybrid nanofluid over a stretched permeable surface employing a homotopy analysis technique, demonstrating that coupled electric and magnetic fields critically govern both velocity profiles and thermal boundary layer evolution. Complementing this work, Oweidi et al. and Shamshuddin et al. [28, 29] conducted a computational analysis of thermal-electromagnetic coupling in ternary hybrid nanofluids within a rotating disk configuration, quantifying the synergistic effects of the Hall current phenomena and radiative heat transfer under high-rotation regimes.
Porous media are essential in fields like groundwater management, energy production, and filtration. Understanding fluid behavior in porous structures, including Darcy’s law, is key for advancements in environmental science, engineering, and medicine. Darcy’s law states that flow rate is proportional to pressure difference and inversely proportional to permeability and fluid viscosity. Non-Darcy flow is often described using empirical models such as the Forchheimer equation, which adds a second term to account for inertial effects in addition to the viscous resistance described by Darcy’s law. In porous media systems operating within low-velocity regimes, Darcy’s law serves as the fundamental governing principle, postulating a linear proportionality between viscous drag and flow velocity. The Forchheimer equation extends this framework by incorporating quadratic velocity-dependent inertial drag, though such nonlinear effects gain prominence only under high-velocity conditions or within ultrapermeable matrices. Within the strict Darcy regime, Forchheimer inertia terms are rendered negligible. Crucially, hydromagnetic effects—encompassing magneto–fluidic interactions—often assume hydrodynamic primacy over inertial forces, particularly in dictating momentum transport characteristics. Under strong electromagnetic coupling, the Lorentz force dominance typically overshadows Forchheimer-related inertial contributions, thereby enabling analytical simplification through prioritized MHD coupling. Chamkha [30] conducted a seminal analysis of non-Darcy mixed convection in porous systems with thermal energy generation and magnetoviscous coupling, while Gorla et al. [31] performed a numerical investigation of buoyancy-driven flow along a vertical wedge geometry within nanofluid-impregnated porous media, quantifying synergistic heat transfer enhancement mechanisms.
Recent research has explored Casson hybrid nanofluid dynamics over stretching sheets, employing diverse geometries and methodologies to assess heat and mass transfer. Halim and Kechil [32] analyzed stagnation point flow using a modified Buongiorno model, focusing on linearly stretching surfaces. However, their work omitted critical influences such as viscous dissipation, porous media, non-Newtonian behavior, nonlinear thermal radiation, relaxation times, Joule heating, chemical reactions, and heat generation/absorption. Similarly, You and Cui [33] derived analytical solutions for hybrid nanofluid flow at a Homann stagnation point over flat sheets but excluded the aforementioned parameters. To date, no study has holistically investigated the synergistic impacts of viscous dissipation, nonlinear thermal radiation, Joule heating, relaxation times, chemical reactions, heat generation/absorption, Brownian motion, and thermophoresis on the electrical conductivity of Casson hybrid nanofluids during stagnation point flow over a porous stretching sheet. This work addresses this gap by examining these interconnected phenomena in a Casson hybrid nanofluid composed of copper (Cu) and alumina Al2O3 nanoparticles dispersed in ethylene glycol. Such fluids find utility in biomedical engineering, thermal management systems, electronics cooling, and automotive radiators. A finite-speed Cattaneo–Christov heat flux model is incorporated to minimize entropy generation. The governing partial differential equations are converted into ordinary differential equations (ODEs) via similarity transformations and solved numerically using MATLAB’s bvp4c solver. Graphical and tabular analyses elucidate the effects of key parameters on velocity, temperature, concentration profiles, skin friction, and heat/mass transfer rates. This comprehensive approach advances understanding of multifactor interactions in hybrid nanofluid systems, offering insights for optimizing industrial and engineering applications.
2. Problem Formulation
This study investigates a two-dimensional, steady, laminar, incompressible flow of a Casson hybrid nanofluid (comprising ethylene glycol as the base fluid with suspended Cu and Al2O3 nanoparticles) near a stagnation point. The flow occurs over a linearly stretching porous sheet (y = 0) bounded at y > 0. A uniform transverse magnetic field B0 is applied along the y-axis, with negligible induced magnetic field due to a low magnetic Reynolds number. The sheet exhibits constant surface temperature (Tw) and concentration (Cw), both exceeding their ambient counterparts (T∞, C∞). The surface velocity is defined as uw(x) = ax (stretching rate a), while the external boundary layer velocity follows ue(x) = bx, where b > 0 quantifies the stagnation flow strength. Key assumptions include spherical nanoparticle morphology, incorporation of nonlinear thermal radiation, viscous dissipation, and Joule heating; the Cattaneo–Christov heat–mass flux model to account for finite thermal relaxation; negligible Hall effect; Darcy–Forchheimer influences; applied electric fields; constant porosity; and uniform fluid properties. The Casson fluid model governs the rheology, incorporating yield stress and non-Newtonian viscosity to characterize flow and heat transfer dynamics. Thermal equilibrium is assumed, simplifying energy equations while retaining viscous dissipation effects. Magnetic dissipation and constant porosity of the porous medium are also considered. A schematic of the configuration is provided in Figure 1.

The hybrid nanofluid is modeled as a homogenized suspension, neglecting internal density or velocity gradients a simplification prevailing in conventional analyses of heat transfer and porous media fluid dynamics. The assumption of local thermal equilibrium (LTE) between the nanofluid and porous matrix is retained, as commonly adopted in such studies. This simplification is validated by the nanofluid’s enhanced thermal conductivity, nanoscale particle dimensions, the porous medium’s permeability and effective thermal diffusivity, and the dominant conductive and convective mechanisms governing energy transport. While this assumption may not hold in every scenario, it provides a valuable simplification for analyzing heat transfer processes in many practical applications involving nanofluids in porous media.
3. Method of Solution
This section outlines the numerical methodology for solving the coupled nonlinear ODE system (Equations (12)–(14)) subject to boundary conditions (15), implemented via MATLAB’s bvp4c boundary value problem (BVP) solver. BVPs for ODEs are better solved by bvp4c since it is accessible in commonly used numerical computing programs like MATLAB since it is robust, accurate, efficient, and flexible.
- •
Governing equation formulation: The governing partial differential equations for the nanofluid system are reformulated as a coupled system of first-order ODEs.
- •
Define the boundary conditions: The boundary conditions for the nanofluids model are specified at the endpoints of the domain η = 0 and η = ηmax.
- •
Provide an initial guess: An initial guess for the solution is required to start the numerical process.
- •
Solve the BVP using bvp4c: The BVP is solved using the bvp4c function.
- •
Extract and analyze the solution: The solution is extracted and analyzed.
- •
Validate the numerical method: To validate the accuracy of the bvp4c numerical scheme, the results are rigorously benchmarked against canonical analytical and numerical solutions from established literature. This comparative analysis ensures fidelity in convergence rates, boundary layer profiles, and dimensionless parameter dependencies, confirming the solver’s robustness for the nonlinear BVP under study. Perform a grid independence test by varying the number of mesh points and observing the convergence of the solution. Check the residuals of the governing equations and boundary conditions to ensure they are satisfied within a small tolerance.
The shooting technique has been utilized, which converts the system of Equations (12)–(14) into a first-order system that is equal to it in terms of f, θ, and Φ.
Using Table 1, the BVP is numerically solved in MATLAB using the bvp4c function, configured with a step size of 0.1 and a mesh of 101 grid points. The shooting method, implemented with a stringent tolerance of 10−7, achieves enhanced precision compared to earlier approaches. As demonstrated in Table 2, our results exhibit excellent agreement with prior studies, validating the accuracy of the proposed methodology.
| Physical properties | (C2H6O2)(f) | (Cu(ϕnp1)) | (Al2O3(ϕnp2)) |
|---|---|---|---|
| ρ | 1115 | 3970 | 8933 |
| Cp | 2430 | 385 | 765 |
| κ | 0.253 | 40 | 400 |
| σ | 0.107 | 3.5 × 107 | 5.96 × 107 |
| Pr | Halim and Kechil [32] | Ishfaq et al. [40] | S.U. Devi and S.P.A. Devi [41] | Senthilvadivu et al. [14] | Present study |
|---|---|---|---|---|---|
| 0.7 | 0.45392 | 0.4539 | — | — | 0.45392 |
| 1 | — | — | — | 0.582010509 | 0.58197 |
| 2 | 0.91136 | 0.9114 | 0.91135 | 0.911352752 | 0.91136 |
| 6.13 | — | — | 1.75968 | 1.759681708 | 1.75968 |
| 7 | 1.89540 | 1.8954 | 1.89540 | 1.895400400 | 1.89540 |
| 10 | — | — | — | 2.308001329 | 2.30800 |
| 20 | 3.35390 | 3.3539 | 3.35390 | 3.353901837 | 3.35390 |
4. Results and Discussion
This section presents the numerical solutions for local skin friction, Nusselt number, Sherwood number, and velocity, heat, and mass transfer under the influence of various physical parameters, all shown in graphical and tabular formats. For numerical simulations, the following fixed parameter values are adopted unless otherwise specified in individual figures: Pr = 4, δ = 0.1, Sc = 2, Nb = Nt = β1 = β2 = Q = 0.1, K = 3, β = 0.3, M = 2, R = 1.5, θw = 1.2, and Ec = H = 0.2. The nanoparticle volume fractions ϕ1 and ϕ2 are varied within the range 0.0 ≤ (ϕ1, ϕ2) ≤ 0.45. The parameters in this study were selected according to their physical significance, material attributes, flow dynamics, thermal transfer conditions, and insights drawn from existing literature. This careful selection ensures the model’s predictive accuracy and real-world applicability, yielding more dependable simulations and a deeper comprehension of the system’s underlying behavior.
4.1. Analysis of Velocity Distributions
Figures 2, 3, 4, and 5 illustrate the impact of various factors on the scaled velocity (f′(η)). Figure 2 shows the effect of the stagnation parameter (δ) on the scaled velocity profile (f′(η)). Growing values of the stagnation parameter could be responsible for a bigger increase in the velocity profile. When it comes to fluid flow scenarios, the stagnation parameter is typically associated with boundary conditions. As a result of this stretching, the fluid particles are drawn toward the direction of the stretch, increasing the velocity profile. The fluid particles are impacted by a stronger force due to the bigger stagnation parameter, which essentially results in larger degrees of surface deformation and accelerated motion. This directly leads to an improvement in the hybrid nanofluids velocity profile, shown by the observation of greater velocities throughout the flow field. Figure 3 shows the shifts in the velocity profile resulting from changes to the magnetic parameter (M) for the hybrid nanofluid. For 0 < δ < 1, as the magnetic field strength increases, the Lorentz force, acting perpendicular to both the magnetic field and the fluid motion, dampens the flow. At δ = 1, increasing the magnetic field helps maintain flow stability. The effects of stretching and magnetic damping balance out, resulting in a well-defined velocity profile. The magnetic field may not significantly alter the velocity profile at this point, allowing for efficient energy transfer. With strong stretching (δ > 1) and an increasing magnetic field, the initial response of the fluid is to exhibit higher velocities and steeper gradients due to the strong stretching. However, as the magnetic field increases, it dampens these effects, potentially limiting the velocity increases. This can lead to a scenario where the velocity profile no longer increases proportionally with stretching. The interplay between stretching and magnetic effects creates a dynamic where higher magnetic fields can stabilize the flow, possibly resulting in a more uniform velocity profile but at the cost of reduced maximum velocities compared to the scenario without magnetic influence. Figure 4 shows that the velocity profiles decrease as the porosity parameter increases. Since porosity is a property of a porous surface, it allows fluid particles to flow through the surface’s pores, which leads to a reduction in the fluid’s velocity. Figure 5 illustrates the effect of the Casson parameter (β) on the velocity profile. It is observed that the velocity distributions become smaller as the β value rises. The reason for this is that when β rises, the Casson fluid parameter’s yield stress decreases, accelerating the pace at which plastic dynamic fluid flow occurs. As the absolute viscosity of the plastic rises, fluid flow resistance results in a diminish in velocity.
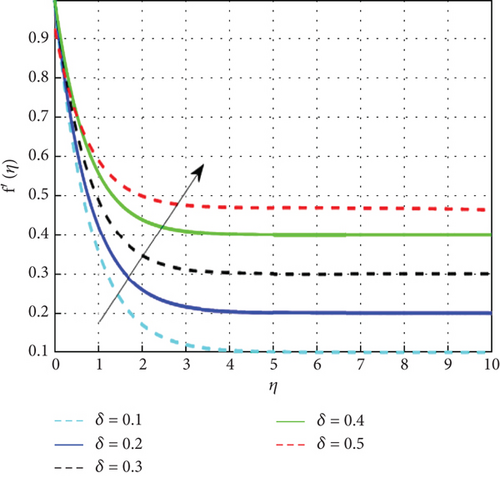
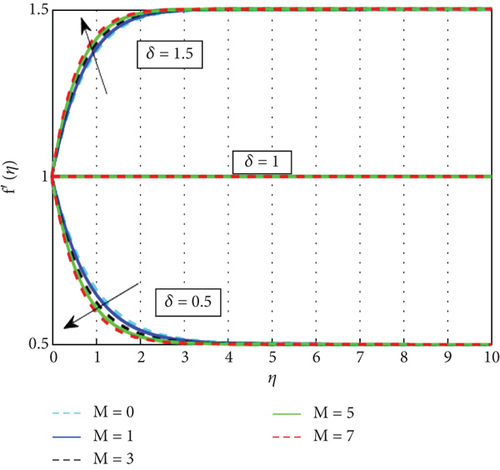
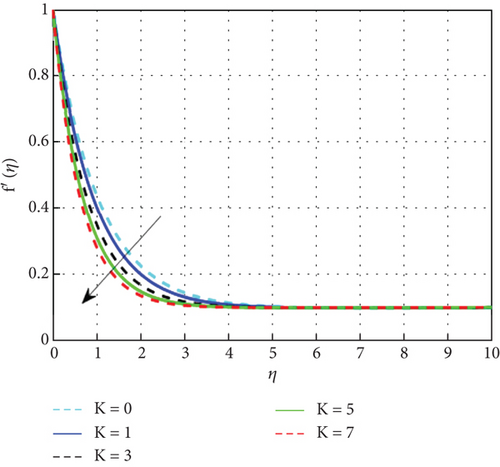
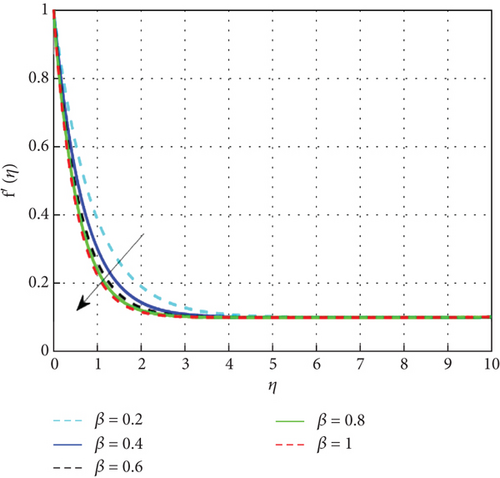
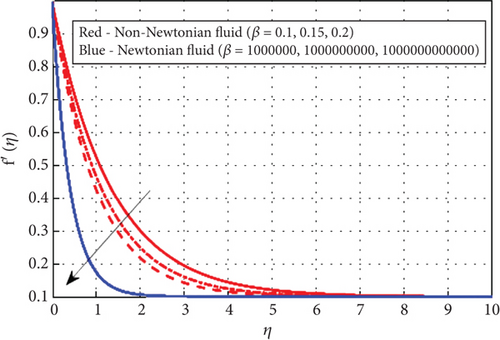
Figure 6 depict the comparison between the Casson hybrid nanofluid and Newtonian nanofluid with β on velocity profile. When the Casson parameter is small, the fluid exhibits strong non-Newtonian behavior with a significant yield stress. This makes the fluid resist deformation, resulting in a thicker velocity boundary layer. The slower adjustment of the fluid’s velocity from the surface to the free stream causes the boundary layer to remain thicker, since the fluid needs more time and distance to flow freely. On the other hand, as the Casson parameter increases toward infinity, the fluid transitions to Newtonian behavior, characterized by the absence of yield stress. In this regime, the velocity boundary layer thickness decreases as the fluid flows with reduced resistance and adapts more rapidly from the no-slip boundary condition to the free-stream velocity. This diminished flow resistance accelerates velocity stabilization, resulting in a thinner boundary layer.
4.2. Analysis of Temperature Characteristics
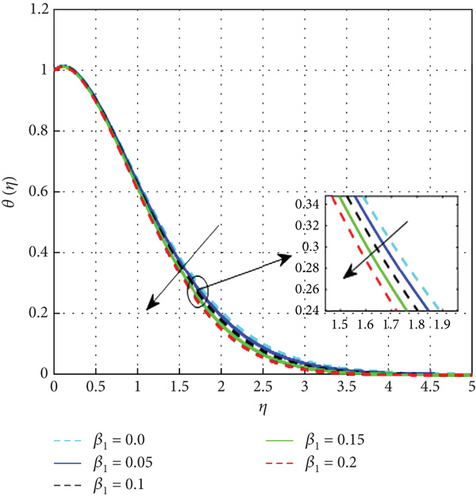
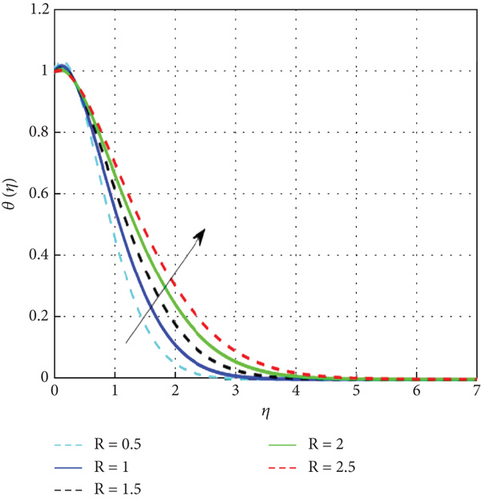
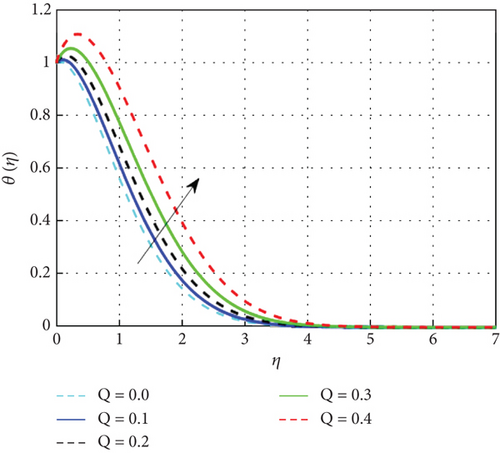
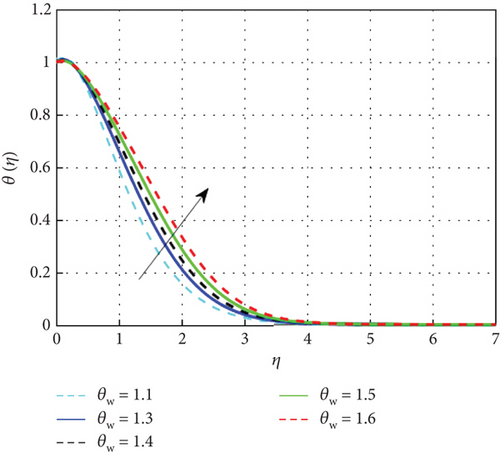
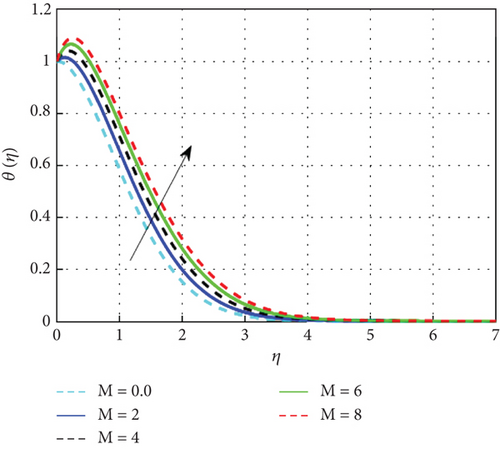
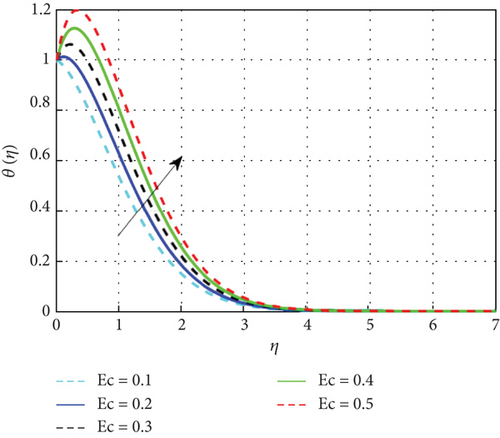
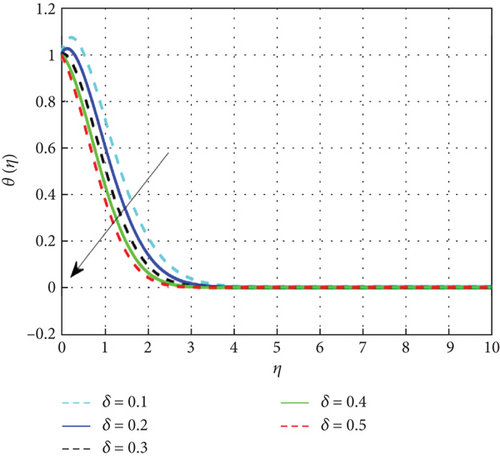
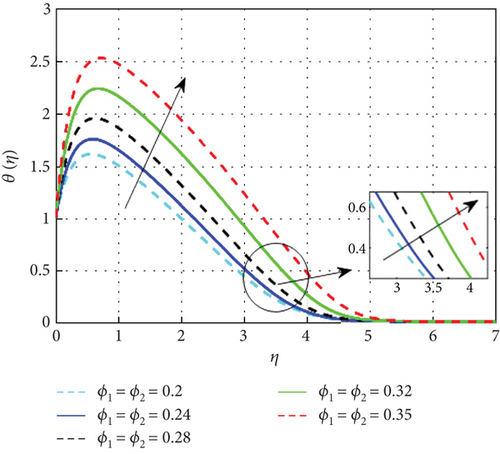
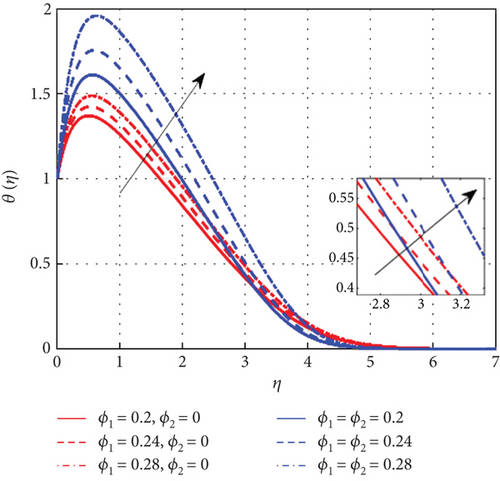
Figure 7 examines the effect of the thermal relaxation parameter on the profile of thermal distributions. The temperature distributions decline as the thermal relaxation parameter rises. Physically, the thermal relaxation time factor increased with the amount of time the material’s particles needed to transport heat to their nearby nanoparticles. The result of R on θ(η) is expressed in Figure 8. This is because when R is added to the system, the nanoparticle’s random motion gets more pronounced. As a result of the ongoing collision, more heat is generated. Therefore, θ(η) rises. Figure 9 shows the effect of the heat generation parameter (Q) across temperature (θ(η)). As we can see from this graph, the θ(η) improves as Q rises. Figure 10 exhibits the effect of the temperature ratio factor (θw) on the thermal profiles. θw represents the ratio of the surface temperatures of the medium to the ambient temperature values. The increase in θw leads to an increase in thermal flow at the medium’s surface, which reinforces the thermal layer at the boundaries. Therefore, the increased values of θw lead to rise in thermal profile values. Figure 11 shows that as the magnetic parameter (M) increases, the Lorentz force enhances friction, thickening the thermal boundary layers and boosting the temperature profile. Figure 12 shows that a higher Eckert number (Ec) leads to a higher temperature, as increased Ec indicates fluid flow dominated by kinetic energy, raising the temperature profile. Figure 13 shows that as the stagnation parameter (δ) increases, the temperature profiles decrease due to enhanced stretching, better fluid mixing, and higher heat transfer rates, which remove more heat from the boundary surface. Figure 14 shows that increasing the thermophoresis parameter (Nt) raises the temperature profile by causing nanoparticles to move from hot to colder areas, thickening the boundary layer and enhancing the temperature. Figure 15 depicts the temperature profile for increasing values of Casson parameter (β). As β increases, the yield stress of the Casson fluid diminishes, enhancing its flow rate. At elevated β values, the fluid progressively adopts Newtonian behavior. Notably, increasing the Casson parameter correlates with a thickening of the thermal boundary layer. Temperature profiles under increasing nanoparticle volume fractions (ϕ1 and ϕ2) are shown in Figures 16, 17, and 18. As nanoparticle concentration increases, the fluid becomes more viscous, leading to higher intermolecular friction and an increase in temperature, as seen with higher nanoparticle volume fractions. Figure 19 shows that hybrid nanofluids have a thicker thermal boundary layer than mono nanofluids, as the addition of Cu and Al2O3 nanoparticles enhances particle collision and improves thermal conductivity. Finally, after a comparative analysis, it was discovered that hybrid nanofluids is more effective than mono nanofluids on the temperature profile.
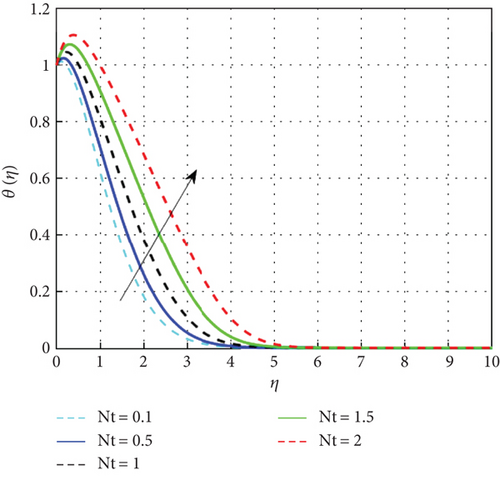
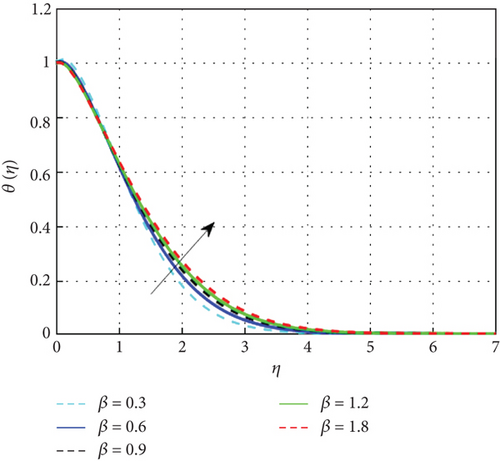
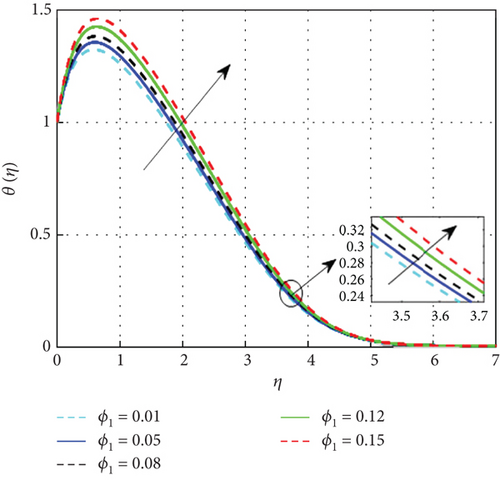
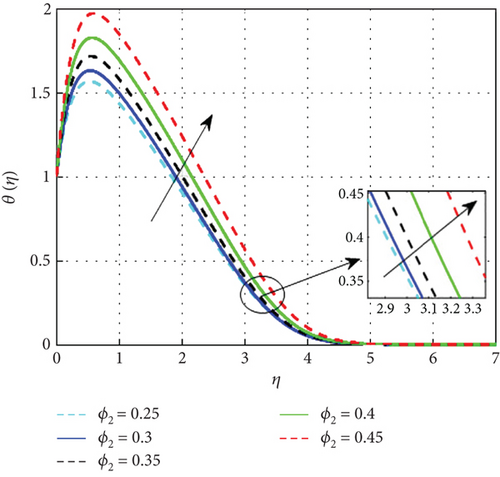
4.3. Analysis of Concentration Characteristics
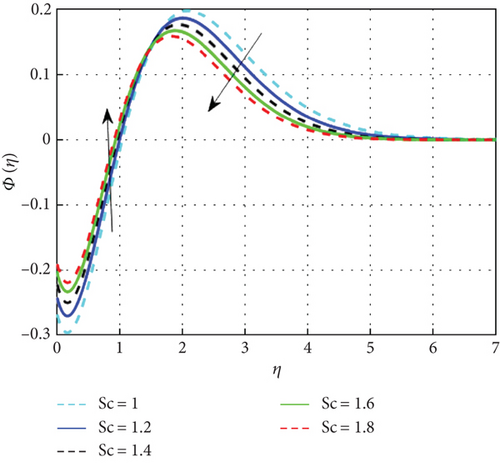
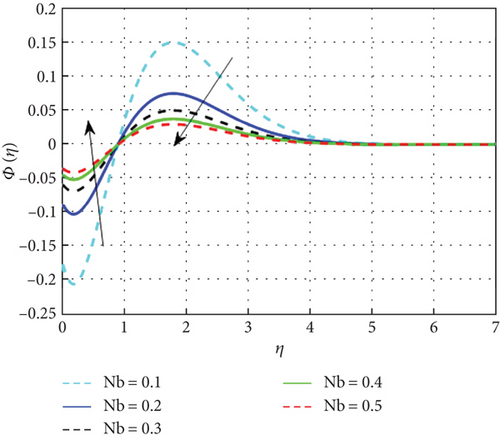
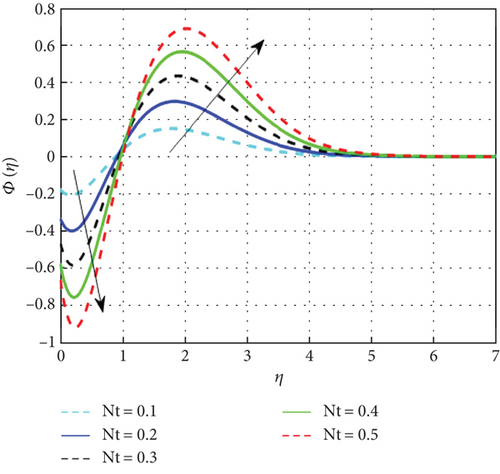
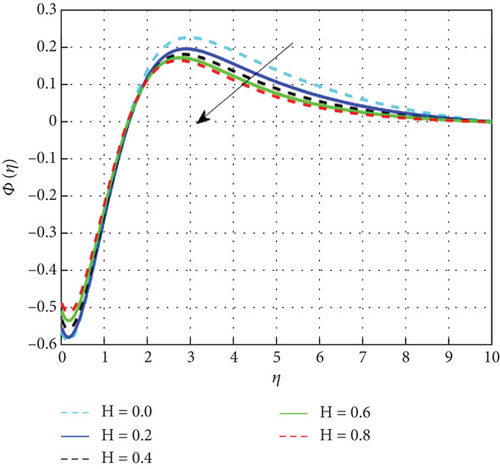
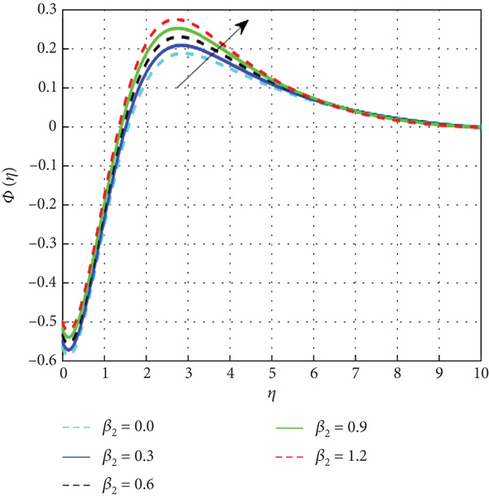
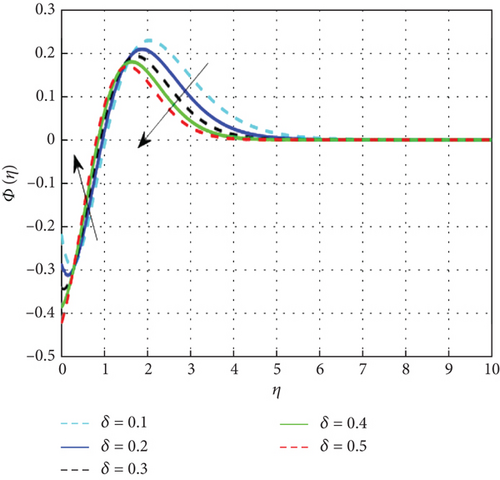
Figure 20 displays the concentration pattern in relation to the Schmidt number (Sc). The mass transfer rate diminishes with increasing Schmidt number (Sc), as Sc is inversely proportional to mass diffusivity and directly related to the fluid’s kinematic viscosity. Figure 21 demonstrates the corresponding decline in the concentration profile with higher Brownian motion parameter values. Brownian motion refers to the random nanoparticle movement caused by persistent collisions with base fluid molecules. Increased Nb indicates more frequent collisions, which cause the particle displacements to grow and, as a result, reduce the fluid concentration. On the other hand, the process known as thermophoresis explains how particles spread when a temperature gradient is present. Figure 22 displays the concentration pattern in relation to the thermophoresis parameter. A greater temperature gradient encourages mass diffusion and raises the fluid’s concentration. The distribution of concentration is negatively impacted by the chemical reaction parameter, as presented in Figure 23. An increase in the chemical reaction parameter reduces both nanoparticle concentration and solutal boundary layer thickness. Near the surface, nanoparticle concentration is suppressed by chemical reactions, as reflected in the negative correlation with concentration distribution. Figure 24 displays the results of studying the effect of the parameter β2 against concentration profiles of hybrid nanofluids. The concentration profile enhanced as increase the concentration relaxation time parameter (β2) because higher β2 implies that slows down the diffusion of solute particles due to a concentration gradient. Thus, the concentration profile rises. Figure 25 shows that the hybrid nanofluid concentration profiles decrease as the stagnation parameter values improve.
4.4. Analysis of Coefficient of Skin Friction, Local Nusselt, and Sherwood Numbers
This section includes calculations of skin friction, the Nusselt number, and the Sherwood number to help researchers and engineers make educated decisions regarding heat, mass transfer augmentation, and fluid flow management strategies. The perception of various physical factors on skin friction along the x-direction, as well as the local Sherwood number and Nusselt number of mono and hybrid nanofluids, are covered in Table 3. It is evident from the results that, in the direction of the stretching sheet, a rise in ϕ1 and ϕ2 causes a rises in Nusselt number and skin friction in all mono and hybrid nanofluid values. This occurs because increasing the nanoparticle volume fraction elevates fluid viscosity and thermal conductivity. Skin friction in the x-direction intensifies with the magnetic field, while higher values of the Casson parameter and stagnation parameter reduce it. Elevated stagnation values lower velocity gradients near the surface, enhancing heat transfer efficiency. Nusselt numbers decrease with increases in magnetic field (M), temperature ratio (θw), chemical reaction (H), concentration relaxation time (β2), and the Eckert number (Ec), while they increase with higher Casson parameter (β), nonlinear thermal radiation (R), stagnation parameter (δ), thermal relaxation time (β1), and nanoparticle volume fractions (ϕ1, ϕ2). Finally, the Sherwood numbers rise when magnetic field (M), the Eckert number (Ec), temperature ratio (θw), nonlinear thermal radiation (R), concentration relaxation time (β2), and chemical reaction (H) values grow, whereas they fall when the Casson parameter (β), stagnation parameter (δ), and thermal relaxation time (β1) values enhance. Additionally, the rate of heat transfer and momentum flow rates in a mono nanofluid and hybrid nanofluid flow are enhanced.
| β | M | δ | ϕ1 | ϕ2 | R | Ec | θw | β1 | β2 | H | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.2 | 2.868185 | 0.312058 | −0.123357 | ||||||||||
| 0.3 | 2.438048 | 1.119964 | −0.442724 | ||||||||||
| 0.4 | 2.191669 | 1.122109 | −0.443572 | ||||||||||
| 0.1 | 2.359769 | 1.177529 | −0.465479 | ||||||||||
| 0.2 | 2.438048 | 1.123075 | −0.443954 | ||||||||||
| 0.3 | 2.514011 | 1.070323 | −0.423101 | ||||||||||
| 0.01 | 2.522615 | 1.041824 | −0.411835 | ||||||||||
| 0.1 | 2.438048 | 1.123075 | −0.443954 | ||||||||||
| 0.12 | 2.419928 | 1.147199 | −0.453490 | ||||||||||
| 0 | 0.01 | 2.342988 | 1.143853 | −0.452164 | |||||||||
| 0 | 0.03 | 2.464666 | 1.239171 | −0.478261 | |||||||||
| 0 | 0.05 | 2.591623 | 1.358531 | −0.511730 | |||||||||
| 0.01 | 0.01 | 2.438048 | 1.123075 | −0.443954 | |||||||||
| 0.03 | 0.03 | 2.753822 | 1.178917 | −0.455035 | |||||||||
| 0.05 | 0.05 | 3.083087 | 1.243571 | −0.468512 | |||||||||
| 1.2 | 2.438048 | 1.086540 | −0.487301 | ||||||||||
| 1.5 | 2.438048 | 1.119964 | −0.442724 | ||||||||||
| 1.8 | 2.438048 | 1.172439 | −0.414332 | ||||||||||
| 0.1 | 2.438048 | 1.378672 | −0.544991 | ||||||||||
| 0.2 | 2.438048 | 1.123075 | −0.443954 | ||||||||||
| 0.3 | 2.438048 | 0.866877 | −0.342678 | ||||||||||
| 1.2 | 2.438048 | 1.123075 | −0.443954 | ||||||||||
| 1.4 | 2.438048 | 0.899156 | −0.355438 | ||||||||||
| 1.6 | 2.438048 | 0.728100 | −0.287819 | ||||||||||
| 0.01 | 2.438048 | 1.086445 | −0.429474 | ||||||||||
| 0.05 | 2.438048 | 1.102637 | −0.435875 | ||||||||||
| 0.1 | 2.438048 | 1.123075 | −0.443954 | ||||||||||
| 0.01 | 2.438048 | 1.123120 | −0.443971 | ||||||||||
| 0.05 | 2.438048 | 1.123109 | −0.443967 | ||||||||||
| 0.1 | 2.438048 | 1.123075 | −0.443954 | ||||||||||
| 0.1 | 2.438048 | 1.123075 | −0.443954 | ||||||||||
| 0.2 | 2.438048 | 1.121498 | −0.443330 | ||||||||||
| 0.3 | 2.438048 | 1.119964 | −0.442724 |
The analysis of stagnation point flow in the Casson hybrid nanofluids over a stretching sheet, incorporating the Cattaneo–Christov heat/mass fluxes, viscous dissipation, and nonlinear thermal radiation, holds significant implications for industrial thermal management. In sectors such as electronics and automotive engineering, where precise cooling is paramount, leveraging these nanofluids can optimize the efficiency and reliability of heat exchangers, radiators, and advanced thermal management systems. The findings can be applied in processes like extrusion or polymer processing, where controlling temperature and flow properties is vital for product quality. In solar thermal systems, understanding how hybrid nanofluids behave under thermal radiation can enhance the efficiency of solar collectors, leading to improved energy capture and conversion. The findings from this study offer optimization pathways for mixing processes in chemical reactors, particularly in systems utilizing yield-stress-dependent non-Newtonian fluids. In biomedical contexts, the enhanced thermal characteristics of hybrid nanofluids could improve the precision and efficacy of thermal therapies or targeted drug delivery systems.
5. Conclusion
- •
The velocity profile increases with the stagnation parameter while decreasing with higher values of the magnetic field, porosity parameter, and Casson parameter.
- •
The temperature profile improves with enhancing values of the R, θw, heat generation (Q0 > 0), Nt, M, and Ec. The temperature profile decreases with increasing thermal relaxation parameter, Casson parameter, and stagnation parameter.
- •
The temperature of the fluid rises with the increase in nanoparticle volume fractions (ϕ1, ϕ2).
- •
The concentration of the hybrid nanofluids declines with enhancing values of the Schmidt number, Brownian diffusion, chemical reaction, and stagnation parameter but improves with an increase in the concentration relaxation parameter and thermophoresis diffusion parameter.
- •
Skin friction rises as the magnetic field parameter and nanoparticle volume fraction rise.
- •
The local Nusselt number increases with higher values of the Casson parameter, stagnation parameter, nonlinear thermal radiation, thermal relaxation parameter, and nanoparticle volume fraction. Conversely, it decreases with stronger magnetic fields, larger Eckert numbers, elevated temperature ratio parameters, and increased chemical reaction rates.
- •
The Sherwood number exhibits an inverse trend compared to the Nusselt number across all parameters, highlighting a distinct inverse correlation between mass transfer efficiency and heat transfer performance.
- •
In conclusion, after a comparative analysis, it was found that hybrid nanofluids are more effective than mono nanofluids in enhancing the temperature profile, with the addition of Cu and Al2O3 nanoparticles increasing particle collisions and improving fluid thermal conductivity.
Future research could expand on this study by considering other non-Newtonian fluids with different physical parameters and methods.
Nomenclature
-
- Py
-
- yield stress
-
- B0
-
- uniform magnetic field
-
- Cp
-
- specific heat
-
- u, v
-
- velocity components
-
- Tw
-
- wall temperature
-
- Ec
-
- Eckert number
-
- Cw
-
- wall concentration
-
- M
-
- magnetic field parameter
-
- C∞
-
- ambient concentration
-
- Nux
-
- Nusselt number
-
- Cf
-
- skin friction
-
- R
-
- nonlinear thermal radiation parameter
-
- K
-
- porosity parameter
-
- H
-
- chemical reaction
-
- T∞
-
- ambient temperature
-
- Sc
-
- Schmidt number
-
- x, y
-
- space coordinates
-
- DB
-
- Brownian diffusion
-
- DT
-
- thermophoresis diffusion
-
- Nt
-
- thermophoresis parameter
-
- T
-
- fluid temperature
-
- qr
-
- nonlinear radiative heat flux
-
- C
-
- fluid concentration
-
- Nb
-
- Brownian diffusion parameter
-
- Pr
-
- Prandtl number
-
- Rex
-
- local Reynolds number
-
- β
-
- Casson parameter
-
- δ
-
- stagnation parameter
-
- Shx
-
- local Sherwood number
-
- κf
-
- thermal conductivity
-
- uw
-
- velocity of stretching sheet along x-axis
-
- ue
-
- free stream velocity
-
- μ∞
-
- limiting viscosity at infinite
-
- Q0
-
- heat generation (Q0 > 0) and absorption (Q0 < 0)
-
- κ∗
-
- Rosseland mean absorption coefficient
-
- θw
-
- ratio temperature
-
- Γ
-
- time constant
-
-
- heat capacity
-
- θ
-
- dimensionless temperature
-
- Φ
-
- dimensionless concentration function
-
- νhnf
-
- hybrid nanofluid of kinematic viscosity
-
- f′
-
- primary dimensionless velocity
-
-
- heat capacity of a nanoparticle
-
- σhnf
-
- hybrid nanofluid of electrical conductivity
-
- ∞
-
- ambient condition
-
- κ
-
- thermal conductivity
-
- η
-
- similarity variable
-
- αhnf
-
- hybrid nanofluid of thermal diffusivity
-
- μf
-
- dynamic viscosity
-
- σ∗
-
- Stefan–Boltzmann constant
-
- μhnf
-
- hybrid nanofluid dynamic viscosity
-
- κhnf
-
- hybrid nanofluid of thermal conductivity
-
- ρf
-
- density of base fluid
-
- ρhnf
-
- density of hybrid nanofluid
-
- ϕ1
-
- nanoparticle volume fraction of Al2O3
-
- μ0
-
- limiting viscosity at zero shear rate
-
-
- hybrid nanofluid heat capacitance
-
- β1
-
- thermal relaxation parameter
-
- β2
-
- concentration relaxation parameter
-
- λe
-
- energy relaxation factor
-
- λc
-
- concentration relaxation factor
-
- τ
-
- ratio of heat capacity
-
- ϕ3
-
- nanoparticle volume fraction of TiO2
-
- σf
-
- base fluid of electrical conductivity
-
- ϕ2
-
- volume fraction of copper
Conflicts of Interest
The authors declare no conflicts of interest.
Author Contributions
Asfaw Tsegaye Moltot: writing–review and editing, conceptualization, methodology, formal analysis, validation, and writing the original draft. Eshetu Haile Gorfie: writing the review, editing, supervision, conceptualization, and resources. Gurju Awgichew Zergaw: writing the review, editing, supervision, and resources. Hunegnaw Dessie Assres: writing the review, editing, supervision, and resources.
Funding
This research work does not have any financial support.
Acknowledgments
No AI tools were used in the preparation of this manuscript.
Open Research
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.




