Volume 2025, Issue 1 2241780

Research Article

Open Access

Modelling Population Dynamics of Substance Abuse in the Presence of Addicted Immigrant With Real Data of Rehabilitation Cases

Jamiu Adeyemi Ademosu

orcid.org/0009-0007-6076-946X

Department of Pure and Applied Mathematics , Ladoke Akintola University of Technology , Ogbomoso , Nigeria , lautech.edu.ng

Department of Mathematical Sciences , Lagos State University of Science and Technology , Ikorodu , Nigeria

Search for more papers by this author

Samson Olaniyi,

Corresponding Author

Samson Olaniyi

[email protected]

orcid.org/0000-0001-6492-1405

Department of Pure and Applied Mathematics , Ladoke Akintola University of Technology , Ogbomoso , Nigeria , lautech.edu.ng

Search for more papers by this author

Sulaimon Femi Abimbade,

Sulaimon Femi Abimbade

orcid.org/0000-0002-1992-9560

Department of Pure and Applied Mathematics , Ladoke Akintola University of Technology , Ogbomoso , Nigeria , lautech.edu.ng

Search for more papers by this author

Furaha Michael Chuma,

Furaha Michael Chuma

orcid.org/0000-0002-6672-3039

Department of Physics , Mathematics and Informatics , Dar es Salaam University College of Education , Dar es Salaam , Tanzania , duce.ac.tz

Search for more papers by this author

Richard Chinedu Ogbonna,

Richard Chinedu Ogbonna

Department of Computer Science and Mathematics , Evangel University Akaeze , Akaeze , Ebonyi State , Nigeria

Search for more papers by this author

Ramoshweu Solomon Lebelo,

Ramoshweu Solomon Lebelo

orcid.org/0000-0002-8051-1569

Department of Applied Physical Sciences , Vaal University of Technology , Vanderbijlpark , South Africa , vut.ac.za

Search for more papers by this author

Kazeem Oare Okosun,

Kazeem Oare Okosun

Department of Mathematics , University of Kansas , Lawrence , Kansas , USA , ku.edu

Search for more papers by this author

Jamiu Adeyemi Ademosu,

Jamiu Adeyemi Ademosu

orcid.org/0009-0007-6076-946X

Department of Pure and Applied Mathematics , Ladoke Akintola University of Technology , Ogbomoso , Nigeria , lautech.edu.ng

Department of Mathematical Sciences , Lagos State University of Science and Technology , Ikorodu , Nigeria

Search for more papers by this author

Samson Olaniyi,

Corresponding Author

Samson Olaniyi

[email protected]

orcid.org/0000-0001-6492-1405

Department of Pure and Applied Mathematics , Ladoke Akintola University of Technology , Ogbomoso , Nigeria , lautech.edu.ng

Search for more papers by this author

Sulaimon Femi Abimbade,

Sulaimon Femi Abimbade

orcid.org/0000-0002-1992-9560

Department of Pure and Applied Mathematics , Ladoke Akintola University of Technology , Ogbomoso , Nigeria , lautech.edu.ng

Search for more papers by this author

Furaha Michael Chuma,

Furaha Michael Chuma

orcid.org/0000-0002-6672-3039

Department of Physics , Mathematics and Informatics , Dar es Salaam University College of Education , Dar es Salaam , Tanzania , duce.ac.tz

Search for more papers by this author

Richard Chinedu Ogbonna,

Richard Chinedu Ogbonna

Department of Computer Science and Mathematics , Evangel University Akaeze , Akaeze , Ebonyi State , Nigeria

Search for more papers by this author

Ramoshweu Solomon Lebelo,

Ramoshweu Solomon Lebelo

orcid.org/0000-0002-8051-1569

Department of Applied Physical Sciences , Vaal University of Technology , Vanderbijlpark , South Africa , vut.ac.za

Search for more papers by this author

Kazeem Oare Okosun,

Kazeem Oare Okosun

Department of Mathematics , University of Kansas , Lawrence , Kansas , USA , ku.edu

Search for more papers by this author

First published: 25 March 2025

https://doi.org/10.1155/jama/2241780

Academic Editor: Manzoor Hussain

Share a link

Email
Wechat
Bluesky

Abstract

Excessive intake or injection of substances, namely, medications, alcohol, and other harmful drugs, has resulted into unimaginable serious consequences, including mental health and social problems. In an attempt to understand the dynamics of substance abuse and forestall its potential spread in the population, a novel model based on nonlinear system of ordinary differential equations is formulated and analysed in this study. The model takes into account, among other important features, the influx of addicted immigrant and rehabilitation of individuals affected by substance abuse. Least squares method with minimization-constrained function is employed to fit the model with the real data of substance-induced mental cases under rehabilitation. Conditions that guarantee the existence and global asymptotic stability of steady states are established, and a key threshold quantity which measures the potential spread of substance abuse influence in a community comprising susceptible and prudent populations is determined. Sensitive parameters of the model are identified, and their effects on the dynamics of substance abuse transmission are investigated with a view to suggesting possible effective measures against the harmful spread of substance abuse in the population.

1. Introduction

Substance or drug abuse refers to misuse or excessive consumption of substance for either therapeutic or nontherapeutic effects on the mind or body of the users. Some of the psychoactive substances usually misused include but not limited to alcohol and medications such as analgesics and cough syrups, as well as some illegal narcotic drugs such as cocaine, cannabis, and heroin. Following the report by the World Health Organization (WHO) [1], at a global scale, an estimated 3.3 million deaths each year are due to harmful consumption of alcohol. In addition, between 129 and 190 million people use cannabis in the world, making it the most abused psychoactive substance. It is most frequently used in the African Region with consumption rates between 5.2% and 13.5%, especially in West and Central Africa.

In response to the difficult experiences of life, people often resort to using psychoactive substances to placate their emotions. In the process, individuals become continuously dependent on the substances, since emotional needs cannot be completely satisfied. This eventually leads to the problem of addiction and a wide range of negative consequences, including health problems, social problems, legal cases, and mental health issues. Particularly, addiction to psychoactive substances can cause damages to organs such as the lung, liver, kidney, and heart and may lead to multiorgan system failure [2, 3]. Injection of these substances through shared syringes has been reported to contribute to a high risk of contracting some deadly viruses like HIV, hepatitis B, and hepatitis C. Social problems associated with substance abuse include increased risk of motor vehicle accidents, heavy financial burden, job loss, and relationship issues. Mental disorders like depression, anxiety, psychosis, or schizophrenia are the prominent negative byproducts of substance abuse [1–3].

The need to nip the indiscriminate use of psychoactive substances in the bud is, therefore, imperative in order to avert the myriad of dangerous consequences experienced by members of the society. To do this, some attempts have been made by researchers in constructing mathematical models to analyse the dynamics of substance abuse transmission and other related studies (see, for example, [4–10]). Sharomi and Gumel [11] qualitatively studied public health’s impact of smoking dynamics by designing and analysing a compartmental model that described subpopulations of individuals based on their smoking status and incorporated mild and chain smoking populations as well as the impact of smoking-related illnesses in the community. Public-oriented intervention strategies and policies were provided for minimizing the problematics drug abuse in a population through a dynamic modelling study presented by Rossi [12]. In a bid to establish the effect of policing in the control of drug epidemic, Njagarah and Nyabadza [13] investigated how drug barons contribute to the prevalence of drug abuse circulation in the population and showed how law enforcement could be used to reduce the prevalence using mathematical modelling approach. Similarly, authors in [14] developed and analysed a drug abuse transmission model incorporating criminal law with optimal control measures. It was shown that the criminal law gives a significant decrease in the sizes of mild and heavy drug addicts in the population.

Moreover, in the study by Memarbashi and Pourhossieni [15], a model that described the spread of illicit drug in a population structured by education status of heroin users was proposed and analysed to assess the significance of educational programs on drug abuse control. Islam and Biswas [16] applied optimal control theory to study the dynamics of drug abuse and showed that educational programs and proper medical treatment as well as family-based care could be effective in reducing the negative effects of drug addiction in the shortest period of time. Akanni et al. [17] studied a model for illicit drug use in a population using dynamical system theory and suggested measures to mitigate the spread of the menace in the population. A model for the spread of drug addiction with counseling and imprisonment as preventive strategies was proposed and studied in [18]. Similarly, Abidemi [19] incorporated triple time-dependent optimal control measures, namely, treatment, corrective measure, and enlightenment campaign, into a nonlinear model of illicit drug use dynamics based on optimal control theory framework. In [20], a model on smoking dynamics was framed and incorporated the effects of media awareness with optimal control measures to achieve smoking cessation. Isa et al. [21] considered a model for drug use dynamics capturing the assumption that recovered individuals may not remain resistant to the illicit drug use. In [22], the authors framed a mathematical model to investigate the dynamics of addiction to substance abuse among women population with optimal control and showed the significance of parameters on the addict generation number. Djilali et al. [23] proposed and analysed a spatiotemporal model incorporating distributed delay to explore the consumption of heroin in a heterogeneous environment. In Zhang et al.’s [24] study, deterministic and stochastic smoking epidemic models were used to examine social interactions among different smoking levels of individuals in the population, and it was shown that proper monitoring of initial sizes of smoking population could be an effective strategy to control smoking prevalence. In an attempt to understand the influence of one of the most dangerous among drug abuse—methamphetamine (MPT) misuse—on society and restrict the surge in the population of MPT users, Abbas et al. [25] introduced cases of four-dimensional models to describe the dynamics of MPT abuse using harmonic mean type incidence term and taking relapse and the effects of migrants into consideration. The formulated models were analysed to explore the future dynamics of MPT usage in the population.

In the present study, a new model fitted to the real data of substance-induced mental cases under rehabilitation and which incorporates the influx of immigrants addicted to substance abuse is designed. The model is qualitatively and quantitatively assessed to provide insightful findings arising from the asymptotic dynamics of the substance abuse transmission and show how some key estimated parameters affect the behaviours of psychoactive substance users in the population. Throughout this study, substance and drug will be used interchangeably. The full description of the model formulation is given in Section 2. Conditions for existence and stability of substance abuse–free and substance abuse–present steady states are established in Section 3. Model-data fitting and analysis of sensitive parameters with simulations are carried out in Section 4, while in Section 5, concluding remarks are provided.

2. Model Formulation

Six classes of individuals in a population are considered depending on their behavioural status, these include the susceptible class, denoted by S(t); light psychoactive substance users, denoted by L(t); heavy user population, denoted by H(t); mentally ill class, denoted by M(t); substance abuse–induced mental cases under rehabilitation, denoted by R(t); and prudent or stayers class (individuals who choose to stay away from psychoactive substance use due to proper education), denoted by P(t). Therefore, the total population of individuals at any time t is given by

The susceptible class is assumed to increase at a recruitment rate by birth or immigration, denoted by Π, excluding fractions, a and b, of recruitment rate for immigrant addicted to substance abuse and recruitment rate for prudent class, respectively, keeping in mind that 0 ≤ a + b ≤ 1. Since susceptible individuals are not drug users themselves, they can be negatively influenced by subpopulations of light and heavy substance users. Hence, the susceptible class is decreased by the standard force of influence, β(L + ρH)/N, where β is the effective substance abuse influence rate and ρ ≥ 1 denotes modification parameter for a higher level of influence by the heavy users compared to the light users. The population of susceptible can also be reduced at the per capita natural death rate, μ. It follows that the time evolution of susceptible population is given by

()

The population of light drug users is generated by standard force of influence, β(L + ρH)S/N, and increased by reactivation of individuals under rehabilitation with standard force of influence, denoted by β_r(L + ρH)/N, where β_r is the effective substance abuse reactivation rate. Due to unsuccessful rehabilitation, the population is further increased by a fraction, (1 − θ) > 0, of some individuals who exit the rehabilitation class at exit rate ω. The population is decreased at the rates α, γ, and τ, due to transition to populations of heavy users, mentally ill individuals, and rehabilitation class, respectively. The population can also be reduced at the per capita natural death rate, μ. Hence, the population dynamics of the light drug abuse users is described by

()

Heavy substance abuse class is populated by immigration of addicted users at recruitment rate aΠ and by progression of light users at a rate α. The population of heavy users is reduced by transition to mentally ill class and rehabilitation class at rates σ and ε, respectively. The population is further decreased at natural and substance abuse–induced mortality rates μ and δ, respectively. Thus, the rate of change of this population is given by

()

Mentally ill class becomes populated by transition of light and heavy users at rates γ and σ, respectively. The class is reduced due to per capita natural and substance abuse–induced death rates μ and δ, respectively. Therefore, the rate of change of mentally ill population is given by

()

The population of individuals under rehabilitation is generated by light and heavy users at rehabilitation rates τ and ε, respectively. The population is decreased by reactivation of force of substance abuse influence β_r(L + ρH)/N and further decreased by exit from rehabilitation at a rate ω and natural death rate μ. The time evolution of the rehabilitation class is given by

()

Finally, the prudent population is generated at both recruitment rate bΠ and successful fraction θ of some individuals exiting the rehabilitation class at the exit rate ω. The natural death rate for prudent class is also μ. Hence, the dynamics of the prudent population over time is given by

()

Following the aforementioned assumptions and putting all the above equations together, the time evolution of the overall population dynamics of the substance abuse transmission is described by the following six-dimensional system of nonlinear ordinary differential equations. The full descriptions of the variables and parameters associated with the system are provided in Table 1. The schematic diagram depicting the flow of the system is given in Figure 1.

()

with the state variables at instant of time t = 0 given by

()

Table 1. Variables and parameters of the substance abuse transmission model (7).

Variable	Description
S	Susceptible population liable to be influenced
L	Light drug users
H	Heavy drug users
M	Mentally ill population due to drug abuse
R	Population under rehabilitation
P	Prudent population who abstains from drug abuse
Parameter
Π	Recruitment rate
a	Fraction of recruits who are heavy users by immigration
b	Fraction of recruits who are prudent
β	Effective substance abuse influence rate
ρ	Modification parameter for higher level of influence
β_r	Effective substance abuse reactivation rate
ω	Exit rate due to rehabilitation
θ	Successful fraction of exit rate due to rehabilitation
1 − θ	Unsuccessful fraction of exit rate due to rehabilitation (recidivist rate)
α	Progression rate of light users to heavy users
γ, σ	Transition rates of light and heavy users to mentally ill class
τ, ε	Rehabilitation rates for light and heavy users, respectively
μ	Natural death rate
δ	Substance abuse–induced death rate

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Schematic diagram for the population dynamics of substance abuse transmission with Λ = Π(1 − (a + b)), f₁ = β(L + ρH)/N, and f₂ = β_rf₁/β.

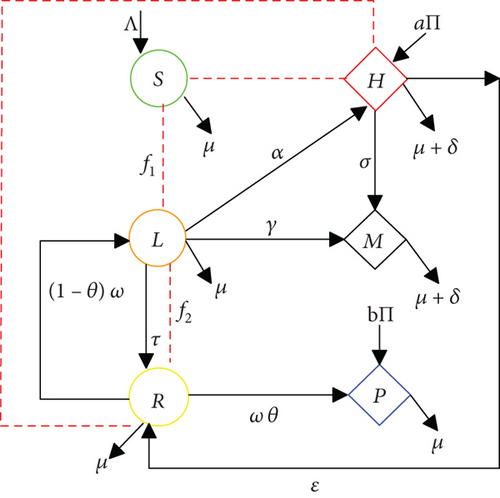
2.1. Well-Posedness of the Model

It should be mentioned that the nonnegativity of the parameters of the model (7) is valid since the model represents the dynamics of substance abuse among human population. Thus, it is necessary to verify the well-posedness of the model. To do this, the following positivity, boundedness, existence, and uniqueness results are established.

2.1.1. Nonnegativity of Solutions

Theorem 1. Given the positive initial conditions (8), the solutions S(t), L(t), H(t), M(t), R(t), and P(t) of the substance abuse model (7) are positive for all t > 0.

Proof 1. Employing the approach used in [26–28], one sees from the model (7) that

()

It is clear from (9) that all the rates of change on the bounding cone ℝ⁶ are nonnegative. As a consequence, nonnegativity of solutions of the substance abuse model (7) is established since the vector field is directed inward on all the bounding planes.

2.1.2. Invariant Region

Theorem 2. The region Δ, given by

is positively invariant with respect to the substance abuse model (7).

Proof 2. Adding all the equations in the system (7) yields

so that

It follows that

Taking the limsup as t⟶∞ gives N(t) ≤ Π/μ. Further, if N(0) ≤ Π/μ, then N(t) ≤ Π/μ. Hence, the region Δ is positively invariant.

2.1.3. Existence and Uniqueness of Solutions

The substance abuse model (7) with initial conditions (8) can be written as an initial valued system of the form

()

where w = (S, L, H, M, R, P)^⊺ and

Definition 1. F(w) is Lipschitz continuous in w if there exists a constant L > 0 such that

()

Theorem 3. There exists a unique solution w(t) of the system (10) analogous to the substance abuse model (7).

Proof 3. It suffices to show that F(w) satisfies the Lipschitz condition given in Definition 1. Considering the first equation of the model (7) and keeping in mind that N ≤ Π/μ in the positively invariant region Δ, one can show that

Similarly, considering other equations of the model (7), it can be shown that

As a consequence, F(w) satisfies the Lipschitz condition

where L = max{(β(1 + ρ) + μ), (β + β_r + b), (σ + ε + μ + δ), (μ + δ), (β_r(1 + ρ) + ω + μ), μ}.

3. Existence and Stability of Steady States

In this section, conditions for existence and stability of substance abuse–free and substance abuse–present steady states are analysed.

3.1. Substance Abuse–Free Steady State

Substance abuse–free steady state is obtained by simultaneously solving System (7) at equilibrium, such that the light and heavy users of psychoactive substance are absent in the population (i.e., L = 0, H = 0). By this, it also follows that the fraction of recruitment rate for addicted immigrant must vanish (i.e., a = 0), while the fraction of recruitment rate for prudent population exists (i.e., b ≠ 0). In this case, the substance abuse–free steady state of the system (7), denoted by

, is given by

()

where S⁰ = Π(1 − b)/μ, L⁰ = 0, H⁰ = 0, M⁰ = 0, R⁰ = 0, and P⁰ = bΠ/μ.

The condition for local stability of the substance abuse–free steady state can be determined based on the effective reproduction number of the model. In the context of substance abuse population dynamics, the effective reproduction number, denoted by

, is defined as the average number of secondary psychoactive substance users that are influenced by either one light or heavy user in the population consisting susceptible and prudent individuals (see [29]). Using the next-generation operator approach [30] and considering only the last five equations of the system (7), the matrices F (for the substance abuse incidence terms) and V (of the transition terms), evaluated at

, are given, respectively, by

()

where K₁ = α + γ + τ + μ, K₂ = σ + ε + μ + δ, K₃ = μ + δ, and K₄ = ω + μ. Therefore, the effective reproduction number, which is the maximum eigenvalue of FV⁻¹, denoted by

, is obtained as

()

It must be mentioned that K₁K₂K₄ > (1 − θ)ω(αε + τK₂) by algebraic simplifications and since 1 − b > 0, thereby making both numerator and denominator of in (15) positive. This ensures the positivity of the effective reproduction number of the model. Hence, the following local stability result is claimed, using Theorem 2 of [30].

Theorem 4. The substance abuse–free steady state, denoted by (12), of the model (7) is locally asymptotically stable if and unstable if .

The practical implication of Theorem 4 is that the incidence of substance abuse can be effectively curbed in the population if the effective reproduction number .

3.2. Substance Abuse–Present Steady State

Here, the existence of substance abuse–present steady state of the system (7) is explored in the presence of psychoactive substance users in the population. Let the substance abuse–present steady state be designated by

and the substance abuse standard force of influence be represented by λ^∗∗ = β(L^∗∗+ρH^∗∗)/N^∗∗, where N^∗∗ = Π/μ at steady state. Thus, the resulting solution after solving the system (7) as a function of λ^∗∗ simultaneously gives

()

and the cubic polynomial

()

where

It is observed that the coefficient A₁ of the cubic polynomial is positive since K₁K₂ > (τK₂ + αε) by algebraic simplification. Then, invoking the spirit of Descartes’ sign rule [31], the number of positive roots of the cubic polynomial (17) depending on the threshold quantity is summarized in Table 2.

Table 2. Descartes’ rule conditions for maximum of two positive real roots based on

Cases	A₁	A₂	A₃	A₄	Number of positive roots	Steady states existence
(i)	+	+	+	+	0	exists
(ii)	+	+	+	−	1	exists
(iii)	+	+	−	−	1	exists
(iv)	+	+	−	+	2	and coexist
(v)	+	−	−	+	2	and coexist

The existence of only one positive root in both Cases (ii) and (iii) of Table 2 indicates that Model (7) has unique substance abuse–present steady state if the associated effective reproduction number exceeds unity, that is,

. In addition, the existence of two positive roots appearing in Cases (iv) and (v) of Table 2 is pointing to the bistability of substance abuse–free and substance abuse–present steady states at

, where both coexist. This bistability makes the control of drug abuse problem difficult as long as immigrant heavy drug users are present in the population (a > 0), even when

is below unity. However, in the absence of immigrant heavy drug users (a = 0), it follows that A₄ = 0 and the cubic polynomial (17) is reduced to the quadratic equation of the form

()

where A₂ and A₃, respectively, now become

As a consequence of the absence of immigrant heavy drug users fraction, it can be seen that A₂ > 0 and A₃ > 0 if , and by Descartes’ rule, only exists. In this case, bistability of both steady states and will no longer occur at , where may be globally asymptotically stable as would be shown in the next subsection. However, if when a = 0, only substance abuse–present steady state exists, regardless of the sign of A₂.

3.3. Global Stability Analysis

In accordance with the fact that global asymptotic dynamics is an important performance metric for dynamical systems, this subsection seeks to examine how the dynamics of the substance abuse system (7) behaves around the substance abuse–free and substance abuse–present steady states.

3.3.1. Global Stability of Substance Abuse–Free Steady State

The global asymptotic stability of the substance abuse model (7) around the substance abuse–free equilibrium point (12) of the model is explored using the method adopted in [32, 33]. This is done by rewriting the substance abuse model (7) in a compact form as follows:

()

where

and

It should be noted that

represents the non–drug user class, while ℤ = (L, H, M) is the drug user class of the model. For convenience, let the substance abuse–free equilibrium be represented by

, so that its global asymptotic stability is examined under the condition that the following properties are preserved.

P₁. For , is globally asymptotically stable

P₂. , , for where is a Metzler matrix evaluated at .

Theorem 5. The substance abuse–free equilibrium of the system (7) is globally asymptotically stable provided Conditions P₁ and P₂ are met.

Proof 4. The functions and are obtained from (19) as follows:

()

Since evaluated at gives

()

then

means that

()

Solving System (23) simultaneously yields

()

One sees that (S, R, P)⟶(S⁰, R⁰, P⁰) as t⟶∞, satisfying Property P₁, and that is globally asymptotically stable. It remains to establish Property P₂.

The M-matrix whose off-diagonal entries are nonnegative is obtained as

()

Then, solving for gives

()

It can be seen that despite 0 ≤ S ≤ S⁰ and 0 ≤ R ≤ R⁰, indicating that Property P₂ is not satisfied. However, one can only achieve except that a = 0, satisfying Property P₂. Therefore, it suffices to say that the equilibrium point, , of the substance abuse model is globally asymptotically stable in the absence of addicted immigrant drug users. This completes the proof.

Practically, Theorem 5 is suggesting that the eradication of substance abuse dynamics in the population cannot be possible as long as immigrant psychoactive drug users are present in the population. As a consequence, controlling substance abuse transmission in the population can only be possible if strict measures can be placed on the immigration of addicted psychoactive drugs users into the population.

3.3.2. Global Stability of Substance Abuse–Present Steady State

It has been shown that regardless of the presence or absence of the addicted immigrant drug users (i.e., whether a = 0 or a ≠ 0), the substance abuse–present steady state exists at . Hence, the investigation of the global asymptotic stability of the substance abuse model (7) around is carried out as follows.

Theorem 6. The substance abuse–present steady state, , of the system (7) is globally asymptotically stable provided the associated effective reproduction number exceeds unity, .

Proof 5. Using the following positive definite Lyapunov function of quadratic type (see [34–36]),

()

It is should be noted that N = S + L + H + M + R + P and N^∗∗ = S^∗∗ + L^∗∗ + H^∗∗ + M^∗∗ + R^∗∗ + P^∗∗. Therefore, the Lyapunov function (27) becomes

()

Since the time derivative of (27) is given by

()

where

, therefore, it follows that

()

Recall that dN/dt = Π − μN − δ(H + M); then, (30) becomes

Consequently, implying that the time derivative of the Lyapunov function is negative semidefinite. Furthermore, provided S = S^∗∗, L = L^∗∗, H = H^∗∗, M = M^∗∗, R = R^∗∗ and P = P^∗∗. Then, the largest invariance set for which is the singleton In the spirit of LaSalle’s invariance principle [37], it follows that the substance abuse–present steady state is globally asymptotically stable.

4. Data Fitting and Sensitivity Analysis

Here, the substance abuse model (7) is fitted to real data of mental cases under rehabilitation due to psychoactive substance abuse. Yearly data of cases spanning 10 years from 2013 to 2022 are collected from a rehabilitation health facility, Neuro-Psychiatric Hospital, Lagos, Nigeria. The least squares fitting method with minimization-constrained function, fmincon, implemented in MATLAB is used to fit the substance abuse model (7) to the cumulative cases under rehabilitation. This is achieved by minimizing the sum of squared errors, as in [38–42], given by

()

where

is the solution associated with the rehabilitation class of the model at time t and

, denoting unknown parameters to be fitted.

represents the real data of cases under rehabilitation, and the total number of data points is given by n = 10. According to the 2022 data on Lagos State of Nigeria [43], the total population and the average life expectancy are estimated as N = 15,387,600 and 53 years, respectively. Hence, the natural death rate μ = 1/53 per year. The recruitment rate is estimated as Π = μN, so that Π = 290,332 humans per year. To minimize

subject to the substance abuse model (7), the initial condition for rehabilitation class is obtained from the real data as R₀ = 308, while the initial conditions for the remaining state variables are chosen as S₀ = 12,000,000; L₀ = 1,411,924; H₀ = 0; M₀ = 0; and P₀ = 5,000,000. Following the algorithm for fitting deterministic model to real data as provided in [38, 41], the result for data fitting of the substance abuse model (7) is displayed in Figure 2, while Table 3 gives the corresponding fitted values of the parameters, so that the effective reproduction number

. The fitted parameter values obtained in this study differ from the similar parameter estimates obtained from previous studies that involved data fitting in drug abuse modelling due to different data collections (see, for example of such previous related studies, [44–47]).

Table 3. Values of the parameters for the substance abuse model (7).

Parameter	Value	Source
Π	290,332	Estimated [43]
a	0.01	Assumed
b	0.1472	Fitted
β	0.0183	Fitted
ρ	1.5	Assumed
β_r	0.001	Assumed
ω	0.0006	Assumed
θ	0.5606629	Fitted
α	0.00750351	Fitted
σ	0.009001	Fitted
γ	0.0011	Assumed
τ	0.0000953025	Fitted
ε	0.002649	Fitted
μ	0.01887	Estimated [43]
δ	0.0002	Assumed

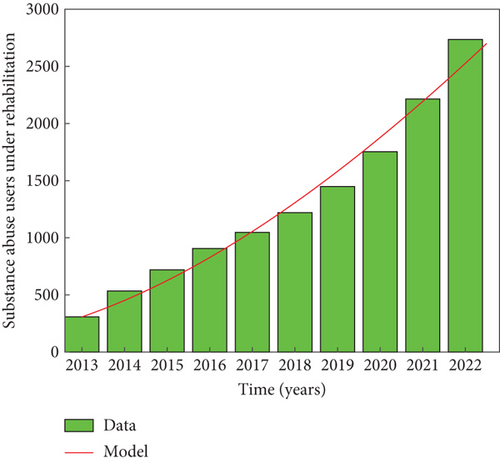
4.1. Analysis of Sensitive Parameters

Since the value of the effective reproduction number of the substance abuse model fitted to the real data is estimated to be less than one, that is, , this implies that substance abuse problem in Lagos, Nigeria, is not endemic yet, but caution should be taken to ensure that is not greater than one. Hence, it is imperative to perform the sensitivity analysis of the model in order to know how changes in the parameters of the model affect the effective reproduction number. With sensitivity analysis, the impact of some critical parameters on the dynamics of the substance abuse transmission model (23) can be determined, providing deeper insights into prevention and control efforts for mitigating the influence of substance abuse. Thus, sensitivity analysis will help guide against the outbreak of substance abuse problem in the population. To achieve this, the use is made of the forward sensitivity index defined as follows [27, 48].

Definition 2. The normalized forward sensitivity index of any variable, , depending on such parameter, p, is defined as

()

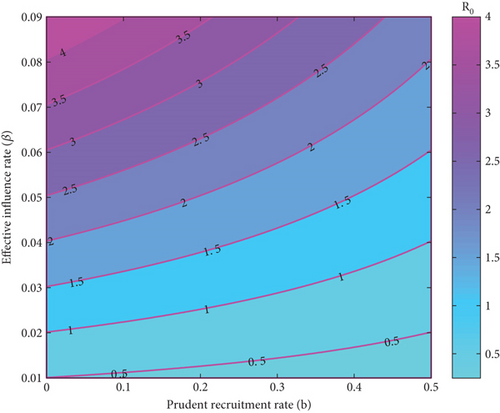
Consequently, the sensitivity indices of all parameters associated with the effective reproduction number, , given in (15), are shown in Table 4, using (32). The parameters with positive sensitivity index signal that any rise (fall) in their values will cause a rise (fall) in the value of . On the contrary, the parameters with negative sensitivity index signal that any increase (decrease) in their values will lead to decrease (increase) in . For example, indicates that increasing the prudent fraction of the recruitment rate by 100% will cause the effective reproduction number to decrease by 17.26%. This means that the problem of substance abuse can be abated in the community if there are more prudent individuals or stayers who abstain from the use of psychoactive substance. This result is corroborated in Figure 3, where effects of increasing other parameters are also displayed with respect to the effective reproduction number. As shown in Figure 3a, as the effective substance abuse influence rate increases through the interval 0.01 ≤ β ≤ 0.09, the reproduction number increases through . This shows that the problem of substance abuse can escalate in the population if the influences of light and heavy drug users on the susceptible population and individuals under rehabilitation are not prevented.

Table 4. Sensitivity indices of parameters of the substance abuse model (7).

Parameter	Value	Sensitivity indices
b	0.1472	−0.1726
β	0.0183	+1.0000
ρ	1.5	+0.0353
ω	0.0006	+0.0328
θ	0.5606629	−0.0001
α	0.00750351	−0.0007
σ	0.009001	−0.0104
γ	0.0011	−0.0529
τ	0.0000953025	−0.0045
ε	0.002649	−0.0030
μ	0.01887	−0.9285
δ	0.0002	−0.0002

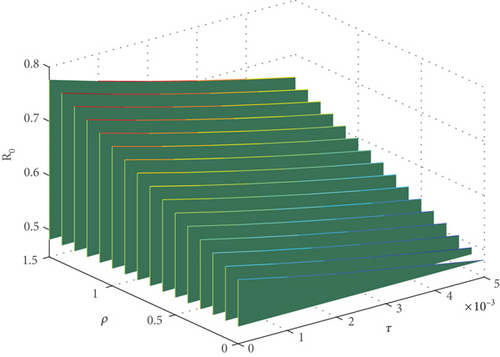
Similarly, in Figure 3b, increase in the modification parameter, ρ, for higher influence of heavy drug users will cause a rise in the value of the reproduction number , while it can also be seen that decreases with increase in the value of rehabilitation rate, τ.

4.2. Simulations and Discussion

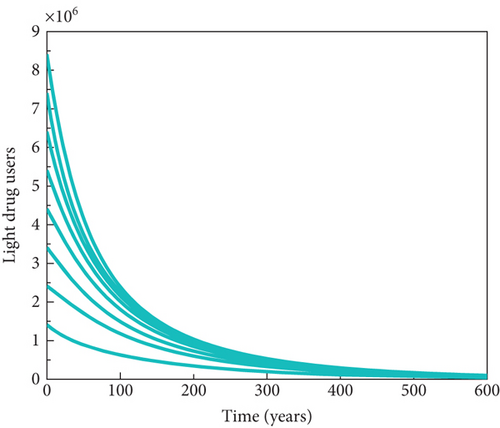
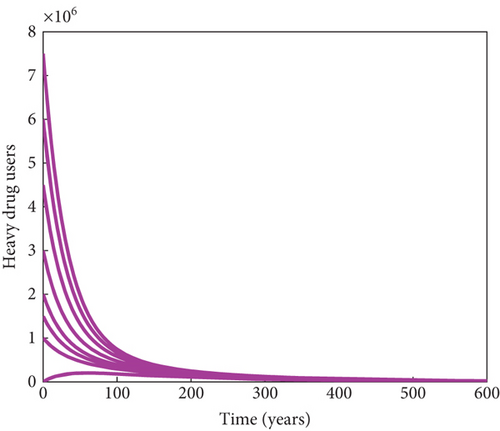
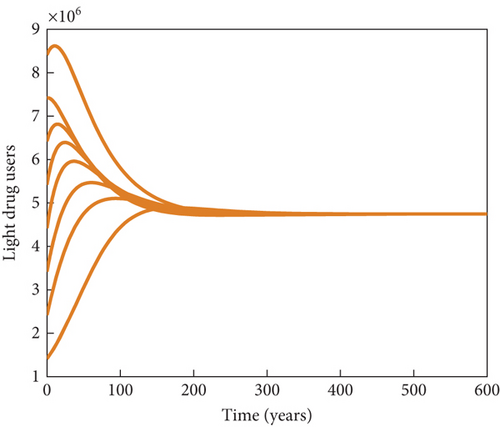
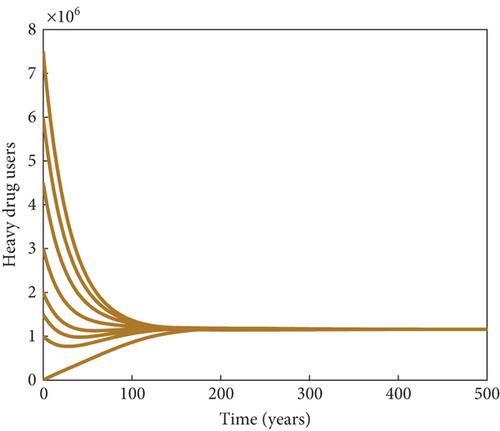
Here, further simulations of the substance abuse model (7) are done to support the theoretical global stability results earlier obtained in Theorem 5 and Theorem 6. Using the same values of parameters as given in Table 3 in the absence of the immigrant heavy drug users (a = 0), it can be observed in Figure 4a and Figure 4b, respectively, that the trajectories of light drug users and heavy drug users converge asymptotically to the substance abuse–free equilibrium point, regardless of the initial conditions of the state variables. This establishes that the problem of substance abuse in the population can be curtailed whenever the effective reproduction number in the absence of immigrant heavy drug users, corroborating the global asymptotic stability result for the drug abuse–free equilibrium point in Theorem 5. Similarly, using the values given in Table 3, except that β = 0.05, so that , the solutions of the system converge to the substance abuse–present equilibrium point irrespective of the initial conditions of the light and heavy drug users in the population, as shown in Figure 4c and Figure 4d, respectively, corroborating the global asymptotic stability result for the drug abuse–present equilibrium point in Theorem 5.

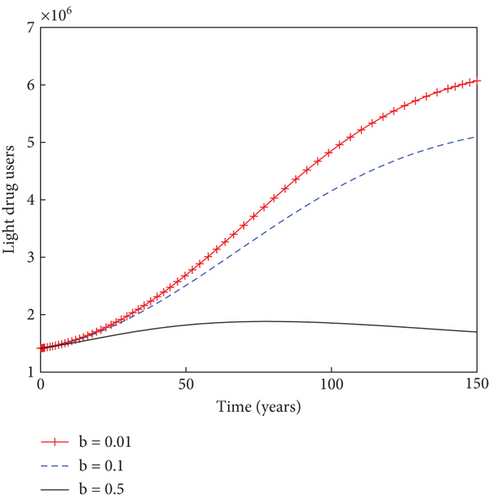
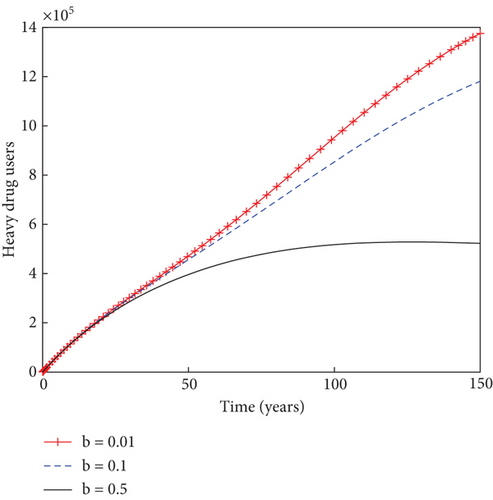
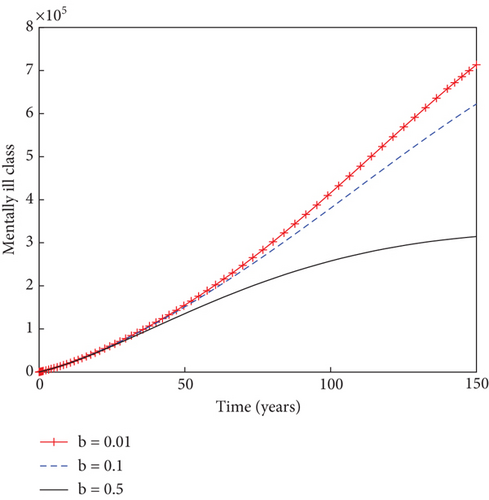
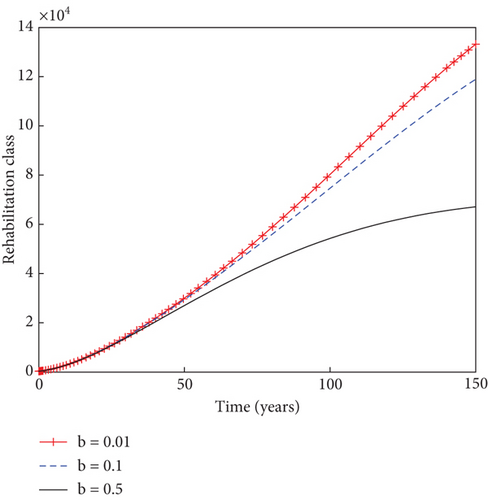
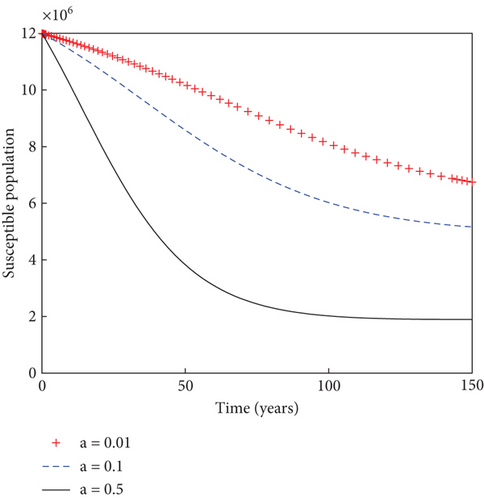
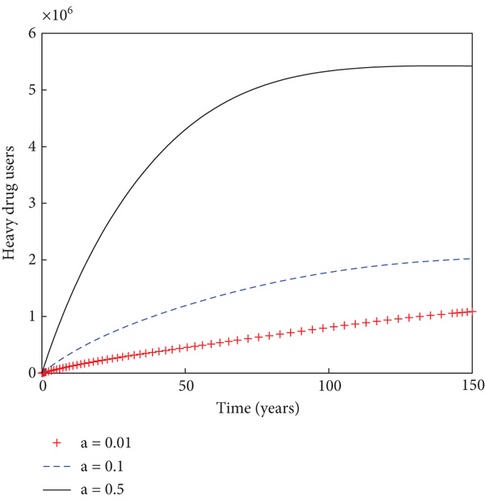
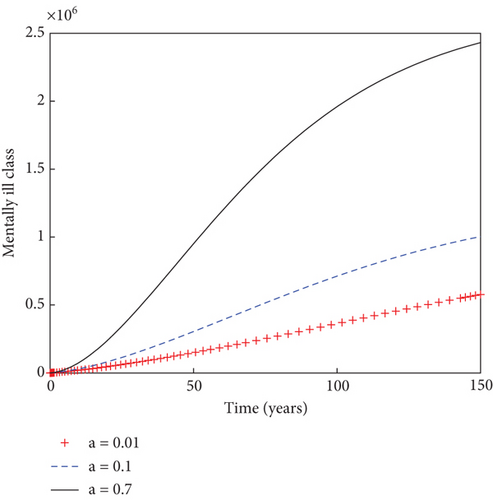
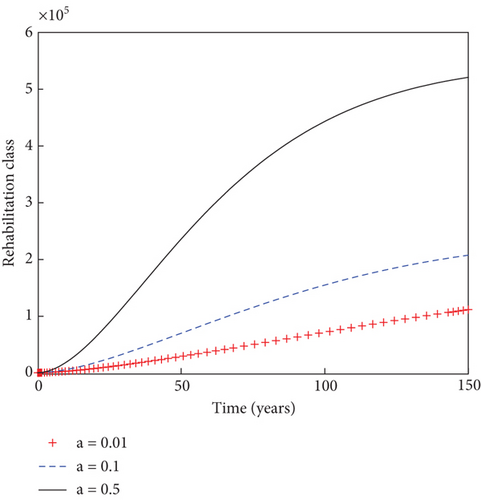
In another sense, the impact of the prudent fraction, b, of the recruitment rate is examined on the dynamics of individuals in the population, as indicated in Figure 5. It is observed that the sizes of light drug users, heavy drug users, mentally ill class, and individuals under rehabilitation reduce with time as the prudent fraction increases from 1% to 50%. This result stresses the need for increased presence of prudent individuals in the community in order to minimize the menace of substance abuse and ultimately bringing the population into a substance abuse–free state. Figure 6 shows how the system behaves in the presence of immigrant drug users. It is shown that the sizes of susceptible individuals reduces with time in the population, as the fraction for immigrant drug users rises from 1% to 50%. This increase in the value of immigrant drug users results into the increase in the numbers of heavy drug users, mentally ill class, and individuals under rehabilitation in the population. This result suggests that thorough scrutiny of immigrants could be necessary in order to stem down the spread of drug abuse in the population.

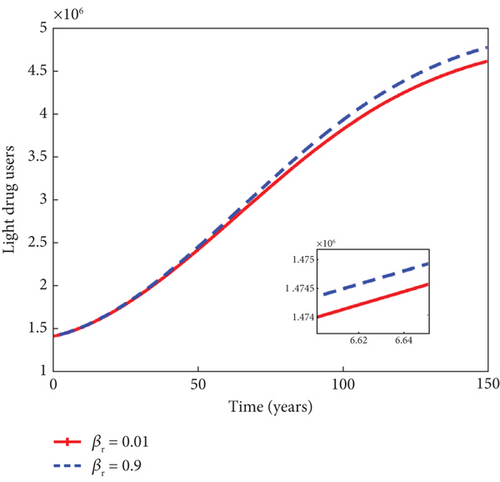
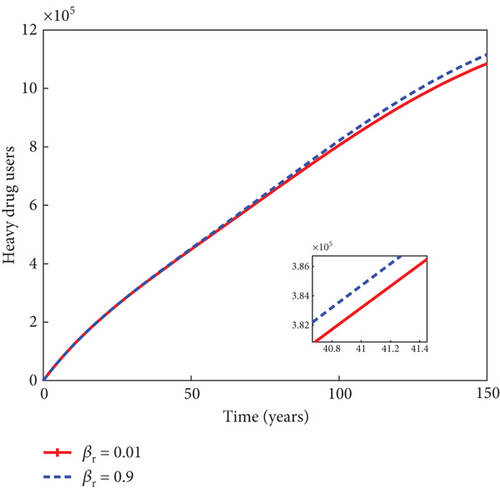
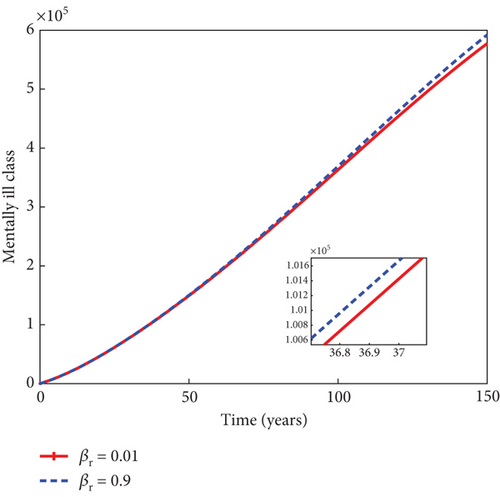
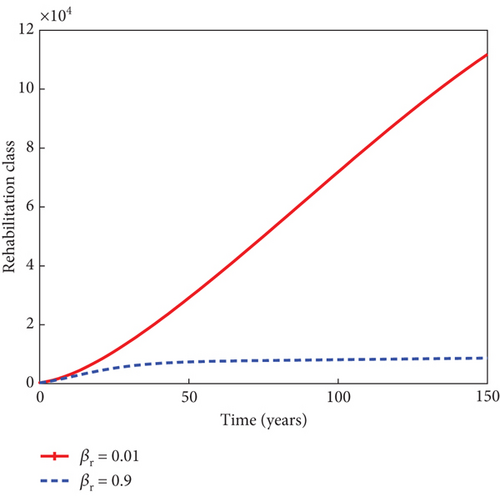
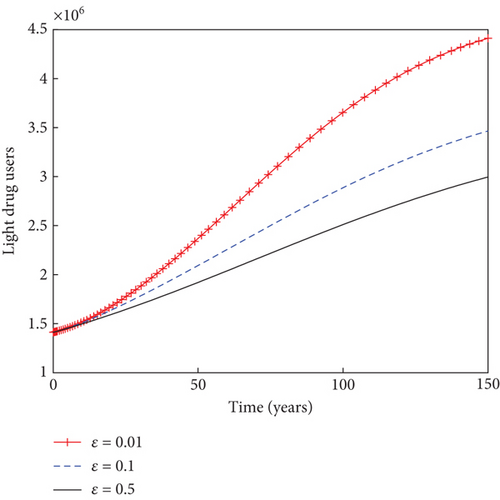
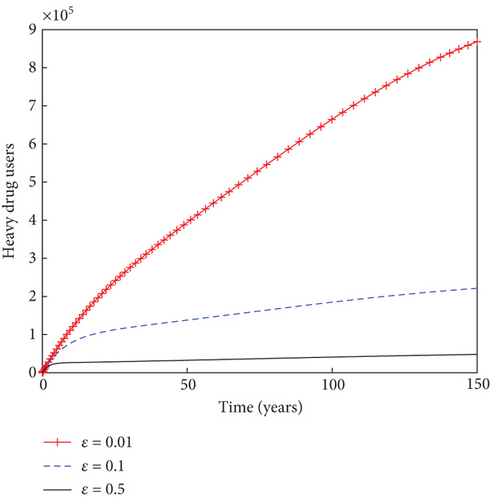
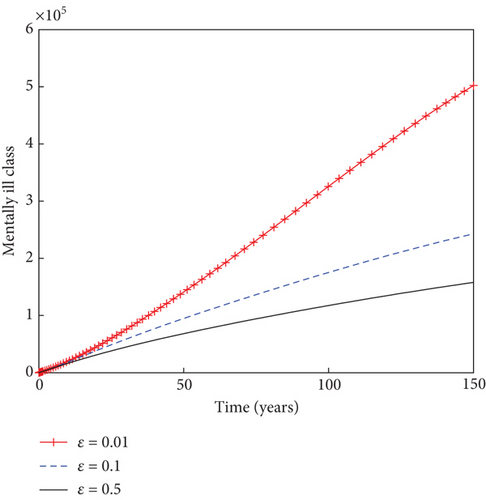
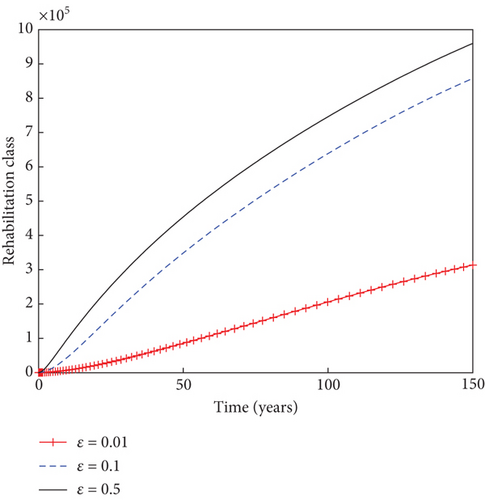
In Figure 7, it can be seen that increase in the reactivation rate of substance abuse influence, denoted by β_r, from 1% to 90% slightly increases the populations of light and heavy drug users, as well as mentally ill population. This in turn decreases the sizes of individuals under rehabilitation. As the rate of rehabilitating heavy drug users increases from 1% to 50% in Figure 8, the populations of light drug users, heavy drug users, and mentally ill individuals decrease in sizes, while there is an increase in the number of individuals under rehabilitation. This result underscores the importance of rehabilitation in the fight against the negative influence of psychoactive substance abuse in the population.

5. Conclusion

In an attempt to stem down the rising menace of substance abuse and its associated harmful consequences in the community, a mathematical model fitted to the real data of substance-induced mental cases under rehabilitation has been proposed in this study. The model describes how substance abuse affects total human population subdivided into six compartments, including susceptible class, light and heavy psychoactive substance users, mentally ill population, rehabilitation patients, and prudent class. Theoretically, the model is shown to be well-posed following the existence of positive, bounded, and unique solution through Lipschitz continuity approach. An important threshold quantity called the effective reproduction number, which quantifies the average population of secondary substance abuse cases influenced by a single light or heavy drug user during his influence period in a population where some individuals are susceptible and prudent, is calculated based on fitted parameter values obtained from data of drug-induced cases in a neuropsychiatric rehabilitation facility in Lagos, Nigeria. Further findings of this work are enumerated hereunder:

i.
The model has substance abuse–free and substance abuse–present steady state solutions that coexist at the effective reproduction number less than unity, thereby making the control of drug abuse problem difficult.
ii.
The coexistence of the aforesaid two steady states is caused by the unhindered influx of immigrants who are heavy drug users in the population.
iii.
In the absence of immigrant heavy drug users, when the effective reproduction number is below one, the model is shown to have a globally asymptotically stable substance abuse–free steady state.
iv.
A globally asymptotically stable substance abuse–present equilibrium point exists when the effective reproduction number is greater than unity.
v.
The increased presence of prudent fraction of the recruitment of human population reduces the sizes of light drug users, heavy drug users, and substance abuse–induced mental cases in the community.
vi.
The model’s most sensitive parameter with respect to the effective reproduction number is the influence rate of the substance abuse from both light and heavy drug users.

Overall, this study contributes to our understanding of the population dynamics of substance abuse in the presence of immigrant drug abusers and prudent individuals. Building on the aforementioned findings, future studies might investigate, via optimal control modelling approach, the optimum interventions for hampering the influence of drug users on the susceptible population and for checking the immigration of drug users with a view to further nipping the problem of drug abuse in the bud.

Conflicts of Interest

The authors declare no conflicts of interest.

Author Contributions

S.O. conceptualized the problem; S.O., J.A.A., and S.F.A. did the formal analysis; J.A.A. and S.F.A. wrote the original draft; F.M.C., R.C.O., R.S.L., and K.O.O. investigated and validated results. All authors reviewed and edited the manuscript.

Funding

This research received no external funding.

Open Research

Data Availability Statement

The data that support the findings of this study are available within the article, as obtained from Neuro-Psychiatric Hospital, Yaba, Lagos, Nigeria.

References

1 World Health Organization (WHO), Health Topics: Substance Abuse, Accessed July 4, 2024 https://www.afro.who.int/health-topics/substance-abuse.
Google Scholar
2 Malakooti M., Friedman M., and Smith C., 1127: Multi-Organ Failure Associated With Ingestion of Synthetic Street Drug “25I”(25I-NBOME), Critical Care Medicine. (2013) 41, no. 12, https://doi.org/10.1097/01.ccm.0000440361.58922.cf.
10.1097/01.ccm.0000440361.58922.cf
Google Scholar
3 National Institute on Drug Abuse (NIDA) Report 2022, Addiction and Health, Accessed July 4, 2024, Retrieved from https://nida.nih.gov/publications/drugs-brains-behavior-science-addiction/addiction-health.
Google Scholar
4 Nyabadza F. and Coetzee L., A Systems Dynamic Model for Drug Abuse and Drug-Related Crime in the Western Cape Province of South Africa, Computational and Mathematical Methods in Medicine. (2017) 2017, no. 1, 4074197, https://doi.org/10.1155/2017/4074197, 2-s2.0-85019618929, 28555161.
10.1155/2017/4074197
PubMed Web of Science® Google Scholar
5 Wangari I. M. and Stone L., Analysis of a Heroin Epidemic Model With Saturated Treatment Function, Journal of Applied Mathematics. (2017) 2017, no. 1, https://doi.org/10.1155/2017/1953036, 2-s2.0-85029809268, 1953036.
10.1155/2017/1953036
Google Scholar
6 Akanni J. O., Akinpelu F. O., Olaniyi S., Oladipo A. T., and Ogunsola A. W., Modelling Financial Crime Population Dynamics: Optimal Control and Cost-Effectiveness Analysis, International Journal of Dynamics and Control. (2020) 8, no. 2, 531–544, https://doi.org/10.1007/s40435-019-00572-3, 2-s2.0-85073951123.
10.1007/s40435-019-00572-3
Google Scholar
7 Goswami N. K., Athithan S., and Shanmukha B., Modeling and Optimal Control: The Role of Media on the Dynamics of the Spread of Crime, Nonlinear Studies. (2022) 29.
Google Scholar
8 Olaniyi S., Akanni J. O., and Adepoju O. A., Optimal Control and Cost-Effectiveness Analysis of an Illicit Drug Use Population Dynamics, Journal of Applied Nonlinear Dynamics. (2023) 12, no. 1, 133–146, https://doi.org/10.5890/JAND.2023.03.010.
10.5890/JAND.2023.03.010
Web of Science® Google Scholar
9 Ibrahim O. M., Okuonghae D., and Ikhile M. N. O., A Mathematical Model of Criminal Gang Rivalry: Understanding the Dynamics and Implications, Results in Control and Optimization. (2024) 14, 100398, https://doi.org/10.1016/j.rico.2024.100398.
10.1016/j.rico.2024.100398
Web of Science® Google Scholar
10 Gutema T. W., Wedajo A. G., and Koya P. R., A Mathematical Analysis of the Corruption Dynamics Model With Optimal Control Strategy, Frontiers in Applied Mathematics and Statistics. (2024) 10, 1387147, https://doi.org/10.3389/fams.2024.1387147.
10.3389/fams.2024.1387147
Web of Science® Google Scholar
11 Sharomi O. and Gumel A. B., Curtailing Smoking Dynamics: A Mathematical Modeling Approach, Applied Mathematics and Computation. (2008) 195, no. 2, 475–499, https://doi.org/10.1016/j.amc.2007.05.012, 2-s2.0-37349018244.
10.1016/j.amc.2007.05.012
Web of Science® Google Scholar
12 Rossi C., The Role of Dynamic Modelling in Drug Abuse Epidemiology, Bulletin on Narcotics. (2012) 54, no. 1, 33–44.
Google Scholar
13 Njagarah J. B. H. and Nyabadza F., Modelling the Role of Drug Barons on the Prevalence of Drug Epidemics, Mathematical Biosciences and Engineering. (2013) 10, no. 3, 843–860, https://doi.org/10.3934/mbe.2013.10.843, 2-s2.0-84877011595, 23906152.
10.3934/mbe.2013.10.843
PubMed Web of Science® Google Scholar
14 Hafiruddin M., Fatmawati F., and Miswanto M., Mathematical Model Analysis of a Drug Transmission With Criminal Law and Its Optimal Control, AIP Conference Proceedings. (2019) 2192, no. 1, 060010, https://doi.org/10.1063/1.5139156.
10.1063/1.5139156
Google Scholar
15 Memarbashi R. and Pourhossieni M., Global Dynamic of Heroin Epidemic Model, UPB Science Bulletin Series A. (2019) 81, no. 3, 115–126.
Google Scholar
16 Islam M. A. I. and Biswas A. M. H., Optimal Control Strategy Applied to Dynamic Model of Drug Abuse Incident for Reducing Its Adverse Effects, 2020, med Rxiv, https://doi.org/10.1101/2020.05.02.20088468.
Google Scholar
17 Akanni J. O., Olaniyi S., and Akinpelu F. O., Global Asymptotic Dynamics of a Nonlinear Illicit Drug Use System, Journal of Applied Mathematics and Computation. (2021) 66, no. 1-2, 39–60, https://doi.org/10.1007/s12190-020-01423-7.
10.1007/s12190-020-01423-7
Web of Science® Google Scholar
18 Memarbashi R. and Ebadi Z., An Epidemic Model for Drug Addiction, Computational Methods in Difference Equations. (2022) 10, no. 4, 876–893, https://doi.org/10.22034/cmde.2021.47532.1989.
10.22034/cmde.2021.47532.1989
Web of Science® Google Scholar
19 Abidemi A., Optimal Cost-Effective Control of Drug Abuse by Students: Insight From Mathematical Modeling, Modeling Earth Systems and Environment. (2023) 9, no. 1, 811–829, https://doi.org/10.1007/s40808-022-01534-z.
10.1007/s40808-022-01534-z
Web of Science® Google Scholar
20 Sofia I. R., Bandekar S. R., and Ghosh M., Mathematical Modeling of Smoking Dynamics in Society With Impact of Media Information and Awareness, Results in Control and Optimization. (2023) 11, 100233, https://doi.org/10.1016/j.rico.2023.100233.
10.1016/j.rico.2023.100233
Web of Science® Google Scholar
21 Isa R. S., Emmanuel S., Danat N. T., Abubakar S. S., Hwere T. S., and Garba U., Mathematical Modeling of Illicit Drug Use Dynamics Examining the Impact of Recycling Recovered Individuals Into the Population, Applied Mathematics and Computational Intelligence. (2024) 13, no. 2, 74–99, https://doi.org/10.58915/amci.v13i2.226.
10.58915/amci.v13i2.226
Google Scholar
22 Divya G., Athithan S., and Jan R., Modeling and Stability Analysis of Substance Abuse in Women With Control Policies, Partial Differential Equations and Applied Mathematics. (2024) 9, 100650, https://doi.org/10.1016/j.padiff.2024.100650.
10.1016/j.padiff.2024.100650
Google Scholar
23 Djilali S., Chen Y., and Bentout S., Dynamics of a Delayed Nonlocal Reaction-Diffusion Heroin Epidemic Model in a Heterogenous Environment, Mathematical Methods in Applied Science. (2025) 48, no. 1, 273–307, https://doi.org/10.1002/mma.10327.
10.1002/mma.10327
Web of Science® Google Scholar
24 Zhang S., Meng Y., Chakraborty A. K., and Wang H., Controlling Smoking: A Smoking Epidemic Model With Different Smoking Degrees in Deterministic and Stochastic Environments, Mathematical Biosciences. (2024) 368, 109132, https://doi.org/10.1016/j.mbs.2023.109132, 38128645.
10.1016/j.mbs.2023.109132
PubMed Web of Science® Google Scholar
25 Abbas S., Gómez-Aguilar J. F., Rahman G., and Asif M., Modeling the Mechanisms of Methamphetamine Abuse Transmission With Immigration Impact and Relapse, European Physical Journal Plus. (2023) 138, no. 6, https://doi.org/10.1140/epjp/s13360-023-04122-x.
10.1140/epjp/s13360-023-04122-x
Web of Science® Google Scholar
26 Srivastav A. K. and Ghosh M., Assessing the Impact of Treatment on the Dynamics of Dengue Fever: A Case Study of India, Applied Mathematics and Computation. (2019) 362, 124533, https://doi.org/10.1016/j.amc.2019.06.047, 2-s2.0-85068497668.
10.1016/j.amc.2019.06.047
Web of Science® Google Scholar
27 Goswami N. K., Olaniyi S., Abimbade S. F., and Chuma F. M., A Mathematical Model for Investigating the Effect of Media Awareness Programs on the Spread of COVID-19 With Optimal Control, Healthcare Analytics. (2024) 5, 100300, https://doi.org/10.1016/j.health.2024.100300.
10.1016/j.health.2024.100300
Google Scholar
28 Mamo D. K., Kinyanjui M. N., Teklu S. W., and Hailu G. K., Mathematical Modeling and Analysis of the Co-Dynamics of Crime and Drug Abuse, Scientific Reports. (2024) 14, no. 1, https://doi.org/10.1038/s41598-024-75034-8, 39488534.
10.1038/s41598-024-75034-8
PubMed Web of Science® Google Scholar
29 Falowo O. D., Olaniyi S., and Oladipo A. T., Optimal Control Assessment of Rift Valley Fever Model With Vaccination and Environmental Sanitation in the Presence of Treatment Delay, Modeling Earth Systems and Environment. (2023) 9, no. 1, 457–471, https://doi.org/10.1007/s40808-022-01508-1.
10.1007/s40808-022-01508-1
Web of Science® Google Scholar
30 van den Driessche P. and Watmough J., Reproduction Numbers and Sub-Threshold Endemic Equilibria for Compartmental Models of Disease Transmission, Mathematical Biosciences. (2002) 180, no. 1-2, 29–48, https://doi.org/10.1016/S0025-5564(02)00108-6, 2-s2.0-0036845274, 12387915.
10.1016/S0025-5564(02)00108-6
CAS PubMed Web of Science® Google Scholar
31 Polyanin A. D. and Manzhirov A. V., Handbook of Mathematics for Engineers and Scientists, 2006, Chapman and Hall/CRC, https://doi.org/10.1201/9781420010510.
10.1201/9781420010510
Google Scholar
32 Olaniyi S., Kareem G. G., Abimbade S. F., Chuma F. M., and Sangoniyi S. O., Mathematical Modelling and Analysis of Autonomous HIV/AIDS Dynamics With Vertical Transmission and Nonlinear Treatment, Iranian Journal of Science. (2024) 48, no. 1, 181–192, https://doi.org/10.1007/s40995-023-01565-w.
10.1007/s40995-023-01565-w
Web of Science® Google Scholar
33 Abimbade S. F., Chuma F. M., Sangoniyi S. O., Lebelo R. S., Okosun K. O., and Olaniyi S., Global Dynamics of a Social Hierarchy-Stratified Malaria Model: Insight From Fractional Calculus, Mathematics. (2024) 12, no. 10, https://doi.org/10.3390/math12101593.
10.3390/math12101593
Web of Science® Google Scholar
34 Ademosu J. A., Olaniyi S., and Adewale S. O., Stability Analysis and Optimal Measure for Controlling Eco-Epidemiological Dynamics of Prey-Predator Model, Advances in Systems Science and Applications. (2021) 21, no. 2, 83–103, https://doi.org/10.25728/assa.2021.21.2.1064.
10.25728/assa.2021.21.2.1064
Google Scholar
35 Olaniyi S., Falowo O. D., Okosun K. O., Mukamuri M., Obabiyi O. S., and Adepoju O. A., Effect of Saturated Treatment on Malaria Spread With Optimal Intervention, Alexandria Engineering Journal. (2023) 65, 443–459, https://doi.org/10.1016/j.aej.2022.09.024.
10.1016/j.aej.2022.09.024
Web of Science® Google Scholar
36 Rois M. A., Fatmawati C., Alfiniyah S., Martini D. A., and Nyabadza F., Modeling and Optimal Control of COVID-19 With Comorbidity and Three-Dose Vaccination in Indonesia, Journal of Biosafety and Biosecurity. (2024) 6, no. 3, 181–195, https://doi.org/10.1016/j.jobb.2024.06.004.
10.1016/j.jobb.2024.06.004
Google Scholar
37 Lasalle J. P., The Stability of Dynamical Systems, 1976, SIAM, https://doi.org/10.1137/1.9781611970432.
10.1137/1.9781611970432
Google Scholar
38 Fatmawati U. D. P. and Nainggolan J., Parameter Estimation and Sensitivity Analysis of Malaria Model, Journal of Physics: Conference Series. (2020) 1490, no. 1, 012039, https://doi.org/10.1088/1742-6596/1490/1/012039.
10.1088/1742-6596/1490/1/012039
Google Scholar
39 Olaniyi S., Obabiyi O. S., Okosun K. O., Oladipo A. T., and Adewale S. O., Mathematical Modelling and Optimal Cost-Effective Control of COVID-19 Transmission Dynamics, European Physical Journal Plus. (2020) 135, no. 11, https://doi.org/10.1140/epjp/s13360-020-00954-z, 33262923.
10.1140/epjp/s13360-020-00954-z
PubMed Web of Science® Google Scholar
40 Moore S. E., Nyandjo-Bamen H. L., Menoukeu-Pamen O., Asamoah J. K. K., and Jin Z., Global Stability Dynamics and Sensitivity Assessment of COVID-19 With Timely-Delayed Diagnosis in Ghana, Computational and Mathematical Biophysics. (2022) 10, no. 1, 87–104, https://doi.org/10.1515/cmb-2022-0134.
10.1515/cmb-2022-0134
Google Scholar
41 Das H. K., Exploring the Dynamics of Monkeypox Transmission With Data-Driven Methods and a Deterministic Model, Frontiers in Epidemiology. (2024) 4, 1334964, https://doi.org/10.3389/fepid.2024.1334964, 38840980.
10.3389/fepid.2024.1334964
PubMed Google Scholar
42 Goswami N. K. and Athithan S., Global Stability and Optimal Control Analysis of COVID-19 Transmission, Journal of Biological Systems. (2025) 33, no. 1, 1–31, https://doi.org/10.1142/S0218339025300015.
10.1142/S0218339025300015
Web of Science® Google Scholar
43 Lagos Population and Life Expectancy in 2022, Accessed July 9, 2024, https://www.statista.com.
Google Scholar
44 Mushanyu J., Nyabadza F., and Stewart A. G. R., Modelling the Trends of Inpatient and Outpatient Rehabilitation for Methamphetamine in the Western Cape Province of South Africa, BMC Research Notes. (2015) 8, no. 1, https://doi.org/10.1186/s13104-015-1741-4, 2-s2.0-84950252162, 26681295.
10.1186/s13104-015-1741-4
PubMed Google Scholar
45 Mushanyu J., Nyabadza F., Muchatibaya G., and Stewart A. G. R., Modelling Multiple Relapses in Drug Epidemics, Ricerche di Matematica. (2016) 65, no. 1, 37–63, https://doi.org/10.1007/s11587-015-0241-0, 2-s2.0-84937144114.
10.1007/s11587-015-0241-0
Google Scholar
46 Mushanyu J., Nyabadza F., Muchatibaya G., and Stewart A. G. R., On the Role of Imitation on Adolescence Methamphetamine Abuse Dynamics, Acta Biotheoretica. (2017) 65, no. 1, 37–61, https://doi.org/10.1007/s10441-016-9302-3, 2-s2.0-85006511650, 27990591.
10.1007/s10441-016-9302-3
CAS PubMed Web of Science® Google Scholar
47 Mushanyu J., Nyabadza F., Mafuta P., and Ngarakana-Gwasira E. T., Modelling Gender Differences in Drug Abuse Epidemics, International Journal of Applied and Computational Mathematics. (2018) 4, 1–21, https://doi.org/10.1007/s40819-017-0477-3, 2-s2.0-85062692042.
10.1007/s40819-017-0477-3
Google Scholar
48 Chitnis N., Hyman J. M., and Cushing J. M., Determining Important Parameters in the Spread of Malaria Through the Sensitivity Analysis of a Mathematical Model, Bulletin of Mathematical Biology. (2008) 70, no. 5, 1272–1296, https://doi.org/10.1007/s11538-008-9299-0, 2-s2.0-47349102730, 18293044.
10.1007/s11538-008-9299-0
PubMed Web of Science® Google Scholar

All articles

Modelling Population Dynamics of Substance Abuse in the Presence of Addicted Immigrant With Real Data of Rehabilitation Cases

Abstract

1. Introduction