International Journal of Intelligent Systems
Volume 2025, Issue 1 9253392
Research Article
Open Access

Gradient Reconstruction Protection Based on Sparse Learning and Gradient Perturbation in IoV

Jia Zhao, 

Jia Zhao

School of Cyberspace Science and Technology , Beijing Jiaotong University , Beijing , 100044 , China , njtu.edu.cn

Xinjiang Production and Construction Corps Key Laboratory of Computing Intelligence and Network Information Security , Xinjiang , 832003 , China

Beijing Key Laboratory of Security and Privacy in Intelligent Transportation , Beijing Jiaotong University , 3 Shangyuancun, Beijing , 100044 , China , njtu.edu.cn

Search for more papers by this author
Xinyu Rao, 

Xinyu Rao

School of Cyberspace Science and Technology , Beijing Jiaotong University , Beijing , 100044 , China , njtu.edu.cn

Beijing Key Laboratory of Security and Privacy in Intelligent Transportation , Beijing Jiaotong University , 3 Shangyuancun, Beijing , 100044 , China , njtu.edu.cn

Search for more papers by this author
Bokai Yang, 

Corresponding Author

Bokai Yang

School of Cyberspace Science and Technology , Beijing Jiaotong University , Beijing , 100044 , China , njtu.edu.cn

Beijing Key Laboratory of Security and Privacy in Intelligent Transportation , Beijing Jiaotong University , 3 Shangyuancun, Beijing , 100044 , China , njtu.edu.cn

Search for more papers by this author
Yanchun Wang, 

Yanchun Wang

School of Cyberspace Science and Technology , Beijing Jiaotong University , Beijing , 100044 , China , njtu.edu.cn

Beijing Key Laboratory of Security and Privacy in Intelligent Transportation , Beijing Jiaotong University , 3 Shangyuancun, Beijing , 100044 , China , njtu.edu.cn

Search for more papers by this author
Jiaqi He, 

Jiaqi He

School of Cyberspace Science and Technology , Beijing Jiaotong University , Beijing , 100044 , China , njtu.edu.cn

Beijing Key Laboratory of Security and Privacy in Intelligent Transportation , Beijing Jiaotong University , 3 Shangyuancun, Beijing , 100044 , China , njtu.edu.cn

Search for more papers by this author
Hongliang Ma, 

Corresponding Author

Hongliang Ma

Xinjiang Production and Construction Corps Key Laboratory of Computing Intelligence and Network Information Security , Xinjiang , 832003 , China

Search for more papers by this author
Wenjia Niu, 

Wenjia Niu

School of Cyberspace Science and Technology , Beijing Jiaotong University , Beijing , 100044 , China , njtu.edu.cn

Beijing Key Laboratory of Security and Privacy in Intelligent Transportation , Beijing Jiaotong University , 3 Shangyuancun, Beijing , 100044 , China , njtu.edu.cn

Search for more papers by this author
Wei Wang, 

Wei Wang

Beijing Key Laboratory of Security and Privacy in Intelligent Transportation , Beijing Jiaotong University , 3 Shangyuancun, Beijing , 100044 , China , njtu.edu.cn

Ministry of Education Key Lab for Intelligent Networks and Network Security , aka MOE KLINNS Lab , Xi’an Jiaotong University , 28 West Xianning Road, Xi’an , 710049 , China , xjtu.edu.cn

Search for more papers by this author
First published: 04 March 2025
https://doi.org/10.1155/int/9253392
Academic Editor: Konglin Zhu

Abstract

Existing research indicates that original federated learning is not absolutely secure; attackers can infer the original training data based on reconstructed gradient information. Therefore, we will further investigate methods to protect data privacy and prevent adversaries from reconstructing sensitive training samples from shared gradients. To achieve this, we propose a defense strategy called SLGD, which enhances model robustness by combining sparse learning and gradient perturbation techniques. The core idea of this approach consists of two parts. First, before processing training data at the RSU, we preprocess the data using sparse techniques to reduce data transmission and compress data size. Second, the strategy extracts feature representations from the model and performs gradient filtering based on the l2 norm of this layer. Selected gradient values are then perturbed using Von Mises–Fisher (VMF) distribution to obfuscate gradient information, thereby defending against gradient reconstruction attacks and ensuring model security. Finally, we validate the effectiveness and superiority of the proposed method across different datasets and attack scenarios.

1. Introduction

Connected vehicle technology provides strong support for intelligent transportation services through communication with roadside infrastructure. This technology enables vehicles to collect and analyze key data such as location, speed, direction of travel, real-time road conditions, weather conditions, and driving behavior. The goals are to enhance road safety, improve operational efficiency, reduce energy consumption and environmental pollution, and optimize the driving experience and comfort of passengers. To achieve these objectives, connected vehicle technology widely employs deep learning (DL) algorithms to process multimodal data, including images, speech, text, and video. For example, models such as YOLO and Mask R-CNN assist vehicles in recognizing the road environment using sensors such as cameras or radars, enabling autonomous driving and collision avoidance. Voice interaction systems such as Alexa and Siri provide services such as entertainment, navigation, and information. Wireless communication models, such as V2X and DSRC, enable vehicles to exchange data with other vehicles or roadside equipment, enhancing safety and operational efficiency.

However, the adoption of DL algorithms raises privacy and security concerns, as sensitive data used for training may inadvertently be exposed. For instance, if a criminal suspect identification system’s training data are compromised, it could leak images of individuals included in the dataset. Addressing these concerns requires protecting sensitive data while preserving its utility.

To address these challenges, federated learning (FL) provides a solution. FL allows multiple participants to collaborate on learning without sharing raw data by exchanging model parameters [1]. This enables effective knowledge sharing while protecting data privacy. Applying FL to the Internet of Vehicles (IoVs) is a wise choice for safeguarding user privacy and promoting multiparty cooperation, further advancing intelligent transportation services. However, recent research indicates that FL does not always provide sufficient privacy and robustness guarantees. Although private data remain with its owner, exchanged model parameters may inadvertently leak information from private training datasets. Sensitive information about vehicle owners could be inferred through attack methods such as gradient inversion, gradient reconstruction attacks (GRAs) [2], membership inference attacks (MIAs) [3], and property inference attacks (PIAs) [4]. These attacks not only threaten personal privacy but also raise legal, ethical, and societal concerns. Therefore, addressing these model attacks and protecting user privacy in the IoV remain urgent research problems.

Our research focuses on gradient reconstruction attacks, which are privacy attacks against FL systems. These attacks exploit shared gradient information to infer or reconstruct original training data. Although FL aims to protect data privacy, gradients may contain sensitive information such as labels, attributes, or images. Therefore, when building privacy-centric systems, the system’s defense against privacy leakage is crucial. Gradient reconstruction attacks pose a threat to both centralized and decentralized FL systems, potentially leading to data privacy breaches.

To address these issues, we propose the following approaches:
  • •

    We proposed a defense strategy called sparse learning and gradient disturbance (SLGD) that combines sparse learning and gradient disturbance techniques to process the original data through sparseization, reduce the data transmission volume, and achieve data compression.

  • •

    When executing global model training in multiaccess edge computing (MEC), our strategy extracts the representation layer of the model, calculates the gradient screen based on the l2 norm of the representation layer, applies the screen to confuse the information in the gradient, and finally disturbs the gradient by adding von Mises–Fisher (VMF) noise.

  • •

    Experimental verification shows that the defense strategy proposed by us can effectively resist gradient reconstruction attacks while maintaining model performance.

2. Related Work

FL protects user privacy and data security. However, it inevitably introduces privacy risks inherent to FL itself. As Yang et al. pointed out [5], defending against gradient reconstruction attacks requires further research. Currently, two main defense methods are commonly used: adding Gaussian noise to gradients and implementing cryptographic-based approaches. However, the former comes at the cost of model accuracy, and finding the right balance remains challenging. The latter not only requires modifying the model structure but also consumes significant bandwidth and storage resources during global model updates. Regarding defense strategies against gradient reconstruction, several approaches exist:
  • 1.

    Adding noise to gradients: techniques such as differential privacy and homomorphic encryption add noise to gradients before sharing them. However, this approach reduces gradient effectiveness and impacts model training performance.

  • 2.

    Gradient compression: methods such as quantization, sparsification, and low-rank approximation aim to compress gradients. While they make gradient reconstruction more difficult, they do not completely prevent it.

  • 3.

    Gradient masking: techniques such as gradient pruning and filtering alter gradients to protect privacy. However, this may lead to loss of critical gradient information and degrade model performance.

  • 4.

    Gradient obfuscation: approaches such as gradient perturbation and mixing introduce additional computational overhead but help protect against attacks.

The idea behind gradient pruning-based defenses is to trim gradients during FL to reduce the risk of gradient reconstruction. Pruning methods include pruning, alignment, and filtering. While these approaches effectively reduce gradient sensitivity, they may impact gradient effectiveness and model performance. In addition, some pruning techniques introduce extra computational or communication costs.

In 2023, PriPrune [6] was proposed, which is a defense method combining gradient pruning and quantization aimed at improving the privacy protection of user data. The basic idea of the method is as follows: in each round of FL, the user device first prunes its own local model to remove some unimportant parameters or connections; then, the user device quantizes the pruned model, i.e., it maps the values of the parameters to some discrete values, which further reduces the accuracy and sensitivity of the model; finally, the user device uploads the quantized model to the server, which uploads different. Finally, the user device uploads the quantized model to the server, and the server aggregates the models of different users to get a global model and sends it back to the user device. The disadvantage is that it requires the user device to have certain computing power and storage space because both pruning and quantization need to be carried out on the user device, and the information of pruning and quantization needs to be saved. And it also requires a certain level of trust between the server and the user device because the server needs to know the parameters and methods of the user device’s pruning and quantization in order to correctly aggregate the model, and the user device needs to trust that the server will not misuse or disclose its model.

In 2023, Zhang et al. [7] proposed a defense method based on gradient large-scale pruning, which can protect data privacy while improving the efficiency of FL. Specifically, the authors propose two defense mechanisms, the first is a strict large-gradient pruning mechanism, which sorts the gradients of each layer in descending order of absolute magnitude and prunes the gradients larger than a threshold to zero. This reduces the amount of private data information contained in the gradients, thus preventing the adversary from utilizing gradient matching to reconstruct the data. The selection of the threshold can be automatically adjusted based on some metrics, such as PSNR, to meet the privacy protection requirements. The second loose large gradient pruning mechanism, instead of directly pruning the large gradient to zero, prunes the large gradient to different degrees based on the l2-paradigm value of each layer of gradient. If the l2-paradigm value is greater than one, then the large gradient will be divided by that value to reduce its size; if the l2-paradigm value is less than or equal to one, then the large gradient will still be pruned to zero. This avoids an unstable training process for some models with fewer parameters. The defense method in this thesis requires choosing an appropriate pruning threshold, but this threshold may affect the effectiveness of the model and the degree of privacy protection, and this threshold may need to be adjusted according to different datasets and models, without giving a general method.

The main idea of gradient perturbation based defense method is to perturb the gradient in FL to reduce the risk of gradient reconstruction. The ways of perturbation include adding noise, rotation, and transformation. The advantage of it is that it can effectively increase the uncertainty of the gradient and thus improve the level of privacy protection. The disadvantage is that the perturbation may affect the direction of the gradient, thus reducing the performance of the model. In addition, the perturbation may also introduce additional computational or communication overhead.

In 2021, Soteria [8] was proposed, a privacy defense method in FL that reduces the reconfigurability of the data by adding a perturbation to one of the layers of the neural network while maintaining the training of the model. Let H be a neural network with L layers, each of size n1, …, nL, and n0 input layers. Let X and denote the original and reconstructed inputs of H, respectively, and denotes the mapping function between the i th layer of H and the j th layer. For a selected defense layer l, denote the intermediate representations of X and X′ in this layer by r = h0,l−1(X) and r′ = h0,l−1(X′), respectively, and solve the following optimization problem: . The goal of the problem is to find a minimal perturbation r′ − r that maximizes the difference between the reconstructed input X′ and the original input X. Since the attacker cannot directly observe r and r′, this is equivalent to generating a gradient of the perturbation on the defense layer l. Therefore, instead of sending the original gradient ∇W, Soteria’s client sends the perturbed gradient ∇W′, where ∇Wl′ is computed from the intermediate representation of the perturbation r′.

In 2023, Yongqi et al. [9] proposed a novel privacy-preserving FL method with a dual perturbation strategy. First, a feature extractor and a fuzzy function are added to the objective function of the conditional generative adversarial network to improve the quality and diversity of the generated data. Then, the generated data are mixed with real data to form false training data for updating the central model, thus reducing the risk of leakage of real data. Second, the gradient of the fully connected layer is perturbed by performing a Hadamard product with a matrix of the same dimension as the gradient. This matrix is generated based on an objective function that aims to make the inferred feature representations as close as possible to the true feature representations and the reconstructed data as far away from the true data as possible. With this approach, inferred attacks can be effectively resisted while maintaining a high accuracy rate. More perturbation schemes are also proposed by Wang, Hugh, and Li [10] of Outpost, Yang et al. [11] proposed by Federated Learning Mode Perturbation Method.

The core idea of data transformation based defense methods is to reduce the possibility of gradient reconstruction by performing different forms of transformations on the data during FL. These transformations include operations such as decomposing, transforming, and expanding the data. The advantage of this method is that it can effectively enhance the diversity of data and thus enhance the effect of privacy protection. However, there are some limitations of this approach, such as the transformations may compromise the quality of the data, leading to a decrease in the performance of the model. In addition, some transformations may also increase the cost of computation or communication. For example, Gao et al. [12] proposed a scheme called ATS, which utilizes a stochastic search method to select the best transformation strategy from a data enhancement library. On the other hand, Lin, Zhang, and Yu [13] used sparse dictionary learning or orthogonal triangulation decomposition techniques for privacy-preserving treatment of the original data. PRECODE [14] employs variational modeling by adding a randomly sampled bottleneck layer to one of the layers of the model, thus effectively blocking the pathway of gradient reconstruction. Ma et al. [15] designed a privacy-preserving collaborative learning scheme based on image transformation and autoencoder, which is capable of multiple data sources sharing a prediction task among multiple data sources, while improving the performance of machine learning models and preventing sensitive data from being leaked by gradient reconstruction attacks. The scheme randomizes the training images by adjusting the block size, which destroys the spatial structure and semantic information of the images. Self-encoders are then used to learn useful feature representations from the transformed images for classification tasks on high-dimensional images.

3. Proposed Strategies

Gradient Inversion (GradInv) attacks are a form of attack against machine learning models, especially those in FL environments. In FL, multiple participants collaborate to train a shared model while keeping their respective data private. To accomplish this, it is common practice to have clients share only the gradient information of model updates rather than the raw data itself. This design assumes that the gradient information is secure enough not to be used to infer the original data. However, gradient reconstruction attacks exploit a potential weakness in this assumption. The attacker tries to infer the original dataset used for local training by analyzing the gradient update information exposed by the client. The attacker may generate some random data and feed these data into the model as a way to compute the model’s gradient. The attacker then compares these computed gradients with the client’s publicly available gradients and adjusts its own input data through an optimization algorithm to make the generated gradients as close as possible to the client’s gradients. In this way, the attacker can gradually approximate and eventually reconstruct the client’s original data. This attack poses a serious threat to the protection of user privacy, as it potentially undermines the fundamental assumption of data privacy in FL. To defend against gradient reconstruction attacks, researchers have proposed a variety of strategies including, but not limited to, using differential privacy to add noise to the gradient or designing more sophisticated models and update strategies to resist such attacks. These defenses aim to make it more difficult for attackers to reconstruct the data, thus protecting data privacy. According to Zhang et al. [16], existing gradient reconstruction attacks can be categorized into two paradigms: iteration based and recursion based. We focus on defending against iterative gradient reconstruction-based attacks in FL. In the “honest but curious” attacker scenario, the attacker may be a central server or other entity involved in distributed training. These attackers have the ability to capture the victim’s gradient information at a specific point in time and may attempt to use this information to recover the data x(t) or the label y(t). This type of attack is often referred to as a GradInv attack. The core goal of a GradInv attack is to minimize the difference between the generated gradient and the true gradient. The attacker constructs an iterative optimization problem to recover the original private data by generating virtual gradients and treating their differences as errors. Imagine a scenario where the attacker can only observe the gradient g and tries to infer the generated input x from g. The attacker can be viewed as a function f : Rk⟶X whose input is the gradient information and whose output is the reconstructed x. There exists a neural network hθ : X⟶Y that maps x in the input space X⊆Rd to y in the labeling space Y using the parameter θ. A given input (x,  y) follows a distribution D with marginal distribution p(x). In a FL-based Telematics system consisting of n RSUs, each RSU has a loss function L1, ⋯, Ln, which together solve the following optimization:
()
In each round of training, RSU i first computes the gradient ∇θLi(hθ(xi), yi) on the dataset (xi, yi) and sends it to the MEC. MEC updates the parameters θ′ by gradient descent , where α is the learning rate. Assuming that (x,  g) follows the joint distribution (x,  g), reconstruction of f(g) leads to a loss L′(x, f(g)). A binary loss function is usually used, which is 0 only if the attacker’s reconstruction is very close to the original input, and 1 otherwise. If the purpose of the attack is to fully recover the input x, the loss can be defined as , where O is the indicator function. If the purpose of the attack is to find the input x in a δ-neighborhood, the more suitable loss is , where d is the l2 distance. The risk of attacking R(f) is as follows.
()

Consider a defense mechanism where instead of the true gradient, each RSU reports a gradient g with noise drawn from the distribution p(g|x). The purpose of this mechanism is to introduce noise in the gradient to hide sensitive information about the user while retaining enough information for effective training. Thus, given a noisy gradient g, the MEC will update the parameters to Common defense strategies include adding Gaussian or Laplace noise to the original gradient or randomly masking certain components of the gradient. Together, p(x) and p(g|x) form the joint distribution p(x, g). Note that the undefended network corresponds to the distribution p(g|x) and focuses only on the true gradient at x.

We aim to introduce the proposed sparse learning and gradient perturbation based gradient reconstruction protection scheme, abbreviated as SLGD, and provide its architecture (see Figure 1). In FL, multiple participants train models using local data and send model parameters or updates to a central server. This process may expose information in the data representation layer due to leakage of model parameters or updates. To address this problem, Gao et al. [12] proposed an image transformation-based privacy-preserving strategy, which ensures the model’s performance while significantly reducing the gradient information reconstruction risk. However, this approach has a drawback: it may set certain perturbed gradient values to zero, thus affecting the accuracy of model training. Therefore, we propose a gradient defense scheme that combines sparse matrix and VMF perturbation with the aim of achieving more efficient and secure privacy protection. We define r and r′ as the unperturbed and perturbed data representations, respectively, and x and x′ as the original inputs and the inputs reconstructed through the perturbed data representations. The goal of the study is to maximize the l2-parameter between x and x′ if the following two conditions are satisfied:
  •  

    Goal 1: the distance between x and x′ should be as large as possible to increase the difficulty and error of reconstruction.

  •  

    Goal 2: the distance between r and r′ should be bounded to ensure that model performance is maintained in the perturbed data.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Architecture diagram of gradient leakage protection scheme based on sparse learning and gradient perturbation.

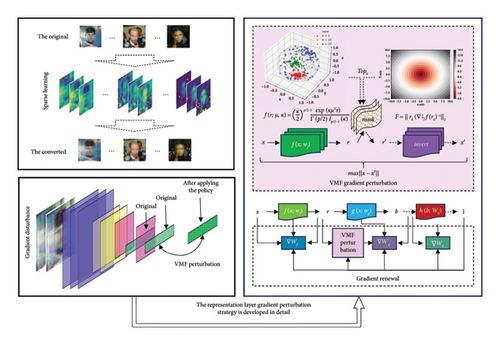
3.1. VMF-Based Gradient Perturbation

To achieve the optimization objective, assume that there exists a feature extractor f : x⟶r that maps the original input to the data representation layer and its inverse function f−1 maps the data representation layer back to the original input. Assume that f−1 is differentiable on r and that f−1(r′) exists for any r′ satisfying . By the chain rule, ∇rf−1 = ∇xf−1. Therefore, the objective function simplifies to
()

When adding a perturbation, the perturbation is based on the angle of deviation from the original gradient. For any two vectors v,  v′ in RK space, the angular distance between them is defined as dθ(v, v′) = arccos(vTv′)/(|v||v′|). The angular distance dθ can be used as a metric to quantify the angular difference between vectors when v and v′ lie on a unit K dimensional sphere.

Definition 1. ((ε, dθ)-directional differential privacy [9]). Assuming > 0, there is the mechanism and for all v,  v′ and :

()

The mechanism is said to satisfy (ε, dθ)-direction differential privacy if the abovementioned condition is satisfied.

The directional privacy theorem shows that when the mechanism perturbs the vectors ,  v′, the probability that the perturbed vectors fall in the measurable set Z differs by a factor . This means that the smaller the angular distance between v and v′, the more indistinguishable they become, thus providing a high degree of indistinguishability.

The VMF mechanism takes advantage of this property by perturbing input vectors while preserving their proximity on the unit sphere. For instance, if v = (1, 0) and v′ = (0.98, 0.2), the angular distance dθ(v, v′) is small, ensuring high indistinguishability after perturbation.

Definition 2. ((ε, dθ)-differential privacy [9]). Let ϵ >  0 and SK−1 denote the K-dimensional unit sphere. If for all x, x′ ∈ SK−1 and all measurable Y⊆SK−1, there are

()

Then, the VMF mechanism is said to satisfy (ϵ, d2)-differential privacy, where d2 denotes the Euclidean metric.

When constructing convex combinations of m mutually orthogonal vectors in n-dimensional space, considering m vectors, the mechanism is usually applied independently to each vector. The differential privacy guarantee can be specified by the parameter m. Let v and v′ be two vectors on the unit sphere, denoted as a linear combination of m orthogonal vectors u1, …, um on the unit sphere. The mechanism constructs the perturbation vectors by applying the VMF mechanism independently to each vector ui. For the perturbation vectors and , it is necessary to compute the differential privacy measure between them. Since ui is orthogonal, the Euclidean distance between and can be converted to the angular distance dθ between them. Thus, there is

()

On the unit sphere, since the relationship between d2 (Euclidean distance) and dθ (angular distance) is d2 ≤ dθ, it follows

()

From the fact that the absolute value of each λi and does not exceed 1,

()

Combining the above inequalities and taking into account that is an extension mechanism for , it follows

()

Next, it is necessary to compare the probability of the output vector Y under v and v′ after applying the mechanism . To do this, the property of orthogonal vectors on the unit sphere is utilized, as well as the relationship between d2 (Euclidean distance) and dθ (angular distance). For any two neighboring inputs v and v′, differential privacy ensures that the ratio between the output probabilities is constrained by ε. Specifically, for each vector ui and there are

()

Since the mechanism is applied independently, it is possible to multiply the probabilities of each vector to obtain the total probability of v and v′, leading to the following form:

()

Applying the above inequality for the probability ratios to each vector and multiplying them together gives

()

Since ui is orthogonal, one can utilize the property on the unit sphere that . Combining the trigonometric inequality of d2 with , we get

()

Based on the above theoretical framework, we propose an innovative approach to perturb the FC layer in the model. The core of the method lies in identifying and utilizing the key elements of the gradient to guide the perturbation to be applied. Specifically, for the set , the largest ϵ elements are found and a mask is constructed, which replaces the values corresponding to these largest elements with the corresponding VMF probability values to be perturbed, as detailed in the Algorithm 1 shown. Specifically, during model training, the l2 norm of the gradient of each representation layer is computed and the largest ϵ element is selected (lines 11–13 of the algorithm). The layer masks are then computed, each of which is a tensor of the same shape as its corresponding layer, and all of which are set to an initial value of 1. This initialization strategy means that at the beginning, each element is “activated,” i.e., all features are taken into account, and maskk denotes the mask of the k th layer (line 14 of the algorithm). The maskk denotes the mask of the k th layer (line 14 of the algorithm). In the process of updating the mask, the position corresponding to the largest ϵ element will be set to 0 in the mask and the remaining positions will be kept as 1. The largest ϵ element will then be filled with the corresponding VMF distribution value. In this way, the mask will effectively perturb those features that contribute most to the model’s performance (line 15 of the algorithm).

In this way, not only are perturbations introduced in the representation layer but it is also ensured that the perturbations are purposeful, i.e., they are chosen based on the VMF distribution, helping to maintain the model performance while making the attack more difficult. Finally, this method is extended to all representation layers of the model, thus avoiding the failure of defense strategies caused by gradient freezing.

3.2. Privacy Policy Based on Sparse Learning

In the communication process between vehicles and RSUs, the direct transmission of raw data may lead to an excessive amount of data, which triggers the problems of inefficient transmission and waste of bandwidth resources. To address this challenge, we propose a strategy based on sparse learning theory, whose core idea is to streamline the data by identifying and retaining the most important features and removing redundant and unimportant information. This approach can not only significantly reduce the amount of data required for transmission but also improve the speed and efficiency of data processing while ensuring data quality. By applying the sparse learning strategy, the data transmission between vehicles and RSUs can be optimized without sacrificing the value of the data. This strategy is important for realizing efficient communication in intelligent transportation systems. In addition, sparse learning can also improve the scalability and reliability of the system and provide strong support for the development of intelligent transportation systems. As shown in Figure 2, the training sample matrix X (of size M × N) can be expressed as the product of the dictionary matrix D (of size M × K) and the sparse matrix L (of size K × N), i.e., Y = D × L. The Karhunen–Loève singular value decomposition (KSVD) algorithm can effectively improve the quality of image data through sparse representation, which in turn provides purer training data for DL models. The algorithm solves the following optimization problem, where li denotes the i th row vector of L and T_0 is a threshold that limits the number of nonzero elements.
()
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Privacy policy flowchart based on sparse learning.
    Algorithm 1: SLGD algorithm.
  •  

    Require: data matrix X, loss function ∇θLi(hθ(X), Y), learning rate required for the i th iteration ηi, group size . Feature extractor before defense layer f : RM×N⟶RL, clean data representation r ∈ RL, perturbation boundaries ϵ, initialization θ0

  • 1.

    for each i ∈ 1, ⋯, N do

  • 2.

     Randomize under sampling probability .

  • 3.

     for each do

  • 4.

      

  • 5.

      

  • 6.

     end for

  • 7.

     for each j ∈ Size(gi) do

  • 8.

    Extract the representation layer in gi, assign index k.

  • 9.

      compute

  • 10.

      computes the gradient inverse matrix

  • 11.

      computes

  • 12.

      Find the largest ϵ element in set F to form indexed set S

  • 13.

      initialize mask

  • 14.

      maskk⟵(maskk − selectϵ(S))⊙VMF(rk, ϵ)

  • 15.

      rk⟵rk⊙maskk

  • 16.

     end for

  • 17.

     θt+1 = θi − ηigi

  • 18.

    end for

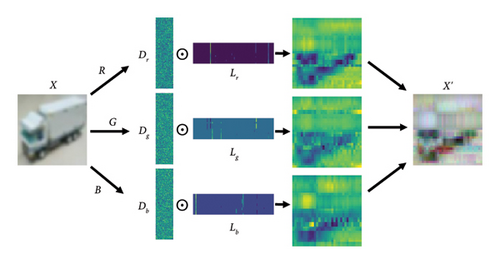
Specifically, the image dataset to be trained is partitioned into chunks and each chunk is converted into a column vector of length p. Next, an appropriate dictionary D ∈ Rp×m is chosen, which can be a randomly selected image chunk or a predefined dictionary. For each image block vector x, the dictionary D and the sparse coding algorithm are utilized to find its sparse representation α that satisfies x = Dα, where α is a sparse vector containing only s nonzero elements. By iteratively updating the dictionary D using the KSVD algorithm, it is able to better adapt it to the properties of the data. In each iteration, the algorithm adjusts certain column vectors and corresponding sparse coding coefficients in the dictionary with the aim of reducing the reconstruction error. Using the updated dictionary D and sparse coding α, each image block is reconstructed to obtain the refined image blocks x′ = Dα. These refined image blocks will be used to train DL models.

4. Experimental Setup and Implementation Details

4.1. Dataset and Model

In order to verify the effectiveness and sophistication of the proposed scheme, experiments were conducted on three types of datasets and a classical deep neural network model. These two types of datasets are (1) natural image datasets, including CIFAR10 [17], CIFAR100 [17], MNIST, and Fashion MNIST [18], which contain different image classes and complexity and can be used to test the model’s classification ability and robustness; (2) the face image dataset Labeled Faces in the Wild (LFW) dataset [19], containing different angles and expressions of multiple faces, which can be used to test the model’s recognition ability and antagonism; and (3) the vehicle dataset Stanford Cars, which was developed by Stanford University’s Artificial Intelligence Laboratory. LeNet is chosen as the deep neural network model, a simple but effective convolutional neural network widely used in image processing. A side-by-side comparison of the proposed SLGD method with other methods on these datasets and models is performed to demonstrate the advantages and limitations of SLGD. To ensure the fairness of the experiments, all the datasets are divided into training and testing sets in the ratio of 8:2.

4.2. Training Configuration

The experimental environment is an Ubuntu server with specific parameters of a CPU with 18 physical cores and 36 logical cores, a TITAN RTX graphics card with 24 GB of GDDR6 video memory, and 128 GB of RAM. We use the SGD optimizer to train the deep neural network, a commonly used optimization algorithm that effectively reduces the loss function of the model.

We set some technical parameters for the SGD optimizer to improve the convergence speed and stability of the model. The momentum is 0.9 to accelerate the convergence direction of the model and avoid falling into local optimums; the weight decay is 2 · 10−3 to prevent overfitting of the model and to regularize the complexity of the model; and the learning rate is 0.01, and it decays to 0.1 of the original rate every 50 rounds, which can be used dynamically according to the training progress of the model. The size of the learning rate can be dynamically adjusted according to the training progress of the model to balance the convergence speed and accuracy of the model.

We set the batch size to 200, which means that 200 samples are randomly selected from the training set as input for each training. Different numbers of training rounds were set according to different experimental purposes; specifically, 300 rounds were set for the experiment on gradient reconstruction defense to test the model’s defense against privacy protection and 50 rounds were set for the experiment on image classification to test the model’s classification ability.

4.3. Attack Realization

In order to effectively evaluate the performance of SLGD in privacy protection, the experiments use a gradient reconstruction attack technique based on optimizer and distance metric. This attack is able to accurately reconstruct the original input data through the gradient information of the model. Specifically, DLG (LBFGS+ l2) [20] is used as the attack model. In this model, LBFGS is chosen as the optimizer, which significantly improves the efficiency of the optimization process by utilizing historical gradient information to dynamically adjust the gradient direction and step size. Meanwhile, the l2-paradigm is chosen as the distance metric, which can effectively measure the similarity between two vectors and thus accurately assess the quality of reconstructed data. Through this attack model, the effectiveness of the proposed privacy protection method can be comprehensively evaluated to ensure its security and reliability in practical applications.

4.4. Evaluation Metrics and Influencing Factors

We used three evaluation metrics to assess the effectiveness of the defense strategy, including peak signal-to-noise ratio (PSNR), pixel-level inverse attack index (IIP-pixel), and structural similarity index (SSIM). These metrics measure the quality of the reconstructed image and the defense effectiveness from different perspectives, and all three have lower numerical values, indicating that the reconstructed image is more different from the original image, thus implying a better defense.

4.4.1. PSNR

PSNR measures the clarity of an image by comparing the ratio of the maximum possible power of the image signal to the power of the noise. The PSNR value is measured in decibels (dB), with higher values indicating better image quality and less distortion. For a grayscale image, the mean squared error (MSE) is first calculated, see (15), and then the PSNR value is obtained, see (16), where the size of the clean image I is m × n, K represents the noisy image, and MAXI is the maximum possible pixel value of the image.
()
()

4.4.2. SSIM

SSIM is a measure of the similarity between two images. The structural similarity between two images is measured by a perception-based model that treats image degradation as a perceptual change, see (17), where μx and represent the average luminance of the two images, respectively. and represent the corresponding variances. σxy is the covariance. and are constants introduced to ensure the stability of the division operation. L is the dynamic range of the pixel values. By default, k1 = 0.01 and k2 = 0.03 are constants.
()

4.4.3. IIP-Pixel

The IIP-pixel is used to measure the ability of DL models to withstand inverse attacks. The index focuses on pixel-level security analysis, i.e., evaluating whether an attacker is able to deduce the original input image (e.g., the original unprocessed image) from the model’s output (e.g., a processed image) in reverse. Such attacks are typically executed by meticulously analyzing subtle differences between model outputs and inputs, with the underlying goal of exposing the inner workings of the model or recovering sensitive raw data [21]. In our case, the approach adopted is to invert a pixel point of the image to which the defense scheme is applied and then compute its average absolute error with respect to the original picture as a quantitative metric for evaluating the robustness of the defense scheme.

5. Experimental Results and Analysis

5.1. Evaluation of the Effectiveness of the Strategy

Figure 3 demonstrates a comparison of the variability with and without the use of strategic image reconstruction techniques when applying a DLG attack on the CIFAR10, Fashion MNIST, and Stanford Car datasets. Specifically, in the scenario where no defense strategy is employed (corresponding to rows 3, 6, and 9 in the figure), the attacker is able to effectively recover the original image with high fidelity. However, when the SLGD defense mechanism is introduced (corresponding to rows 2, 5, and 8 in figure), the attacker’s ability to extract useful information from the recovered image is significantly reduced, and no meaningful data can be obtained. To provide comprehensive validation, experiments conducted on other datasets (see Figure 4) replicate this finding, further validating the effectiveness of the SLGD defense strategy. Figure 4 now emphasizes the role of KSVD decomposition in preprocessing data, highlighting its stronger effect on grayscale images compared with color images. This is attributed to KSVD’s dimensionality reduction capabilities, which are particularly effective for simpler grayscale images but face challenges with complex multichannel color data.

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Visualization results of gradient attacks with and without defense methods on CIFAR10, Fashion MNIST, and Stanford cars datasets.
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Comparison results of SLGD and other defense methods on multiple datasets.

In order to comprehensively evaluate the performance of SLGD defense strategies on different datasets, SLGD is compared with four other mainstream defense techniques: differential privacy techniques (including DP-Laplace and DP-Gaussian), pruning techniques (GC), and the Sotria method. The experimental results are presented in Figure 4 and Table 1 on four datasets: LFW, MNIST, CIFAR-100, and Stanford Cars were presented on four datasets. In Figure 4, the first column on the left side shows the original image, while the subsequent columns show the image after several rounds of iterative attacks. By visual comparison, it is found that SLGD is effective against image reconstruction attacks on all test datasets, making the original image content difficult to be recognized by the naked eye, and its visual defense effect is comparable with that of the Gaussian noise differential privacy scheme. In contrast, the pruning technique fails to effectively hide the original image on all four datasets after 100 rounds of iterations, making it one of the worst performing defense strategies. Although the Laplace differential privacy approach demonstrates excellent defense on the other three datasets, it fails to successfully defend against the attack on the MNIST dataset. The Sotria scheme, although slightly better than the pruning technique, also fails to effectively prevent the recognition of the original image after 100 rounds of iterations. Table 1 provides a comparative analysis of the performance of different defense strategies on four datasets, namely, LFW, MNIST, CIFAR-100, and Stanford Cars, using the three key evaluation metrics, namely, PSNR, IIP-pixel, and SSIM key evaluation metrics for quantitative assessment. The results show that the SLGD defense policy exhibits excellent performance on most of the datasets, especially on the LFW dataset, where SLGD achieves the optimal results for all three metrics. In addition, the lowest PSNR value of SLGD on the CIFAR-100 dataset also indicates that it is very effective in terms of defense performance. In contrast, the DP-Laplace method outperforms SLGD in some values on the MNIST dataset and the CIFAR-100 dataset but does not match SLGD’s performance on the other datasets. The DP-Gaussian method outperforms SLGD on two datasets (CIFAR-100, Stanford Cars) in terms of IIP-pixel values. It outperforms SLGD on two datasets (CIFAR-100, Stan Cars) but fails to fully outperform SLGD on the other two evaluation metrics. Considering these evaluation metrics together, the SLGD method is the best in terms of the overall performance and is able to fully outperform both Sotria and GC (the pruning method) and slightly outperforms the differential privacy method. In particular, it excels in improving image security. Furthermore, the visualization in Figure 4 supports this conclusion. Although other methods perform in specific aspects, the SLGD method demonstrates its position as the most effective defense strategy in general.

Table 1. Numerical comparison of the defense method in this section with other defense methods on multiple data sets (take the last round of results).
  LFW MNIST CIFAR-100 Stan Cars
SLGD PSNR 10.620 10.175 8.132 6.605
IIP-pixel 0.318 0.478 0.387 0.473
SSIM 0.431 0.510 0.358 0.297
  
Sotria PSNR 12.957 10.150 11.176 12.543
IIP-pixel 0.343 0.553 0.491 0.376
SSIM 0.480 0.652 0.579 0.535
  
DP-L PSNR 10.809 9.422 7.014 9.754
IIP-pixel 0.320 0.510 0.462 0.338
SSIM 0.434 0.626 0.346 0.355
  
GC PSNR 18.609 9.469 12.404 15.097
IIP-pixel 0.369 0.515 0.522 0.405
SSIM 0.598 0.635 0.624 0.724
  
DP-G PSNR 10.577 10.301 9.001 9.880
IIP-pixel 0.320 0.479 0.381 0.334
SSIM 0.432 0.513 0.448 0.351
  • Note: The bold values represent the optimal experimental results under the given experimental conditions.

5.2. Model Performance Evaluation

The accuracy of SLGD is evaluated on both MNIST and CIFAR-10 datasets, and as revealed in Figures 5 and 6, the method achieves the optimal performance when dealing with the single-channel grayscale images of the MNIST dataset whereas on the multichannel color images of the CIFAR-10 dataset on the CIFAR-10 dataset is relatively weak.

Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Experimenting on the MNIST dataset.
Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
Experiment on the CIFAR10 dataset.

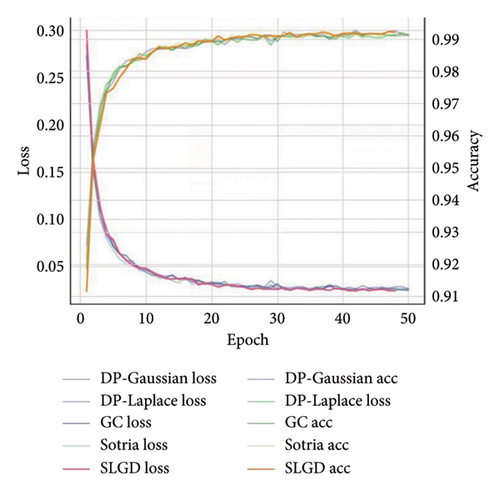
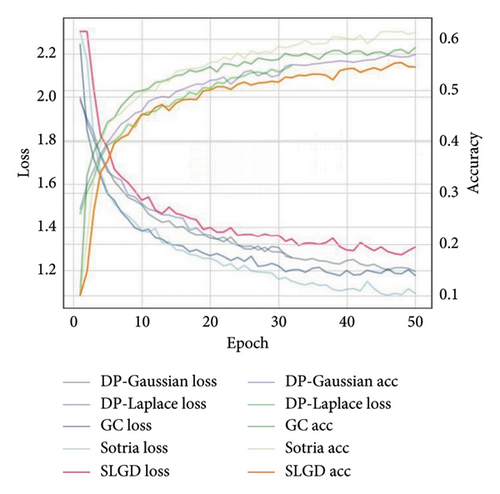
The reason for this phenomenon, which is consistent with expectations, is that the SLGD method employs a unique data preprocessing step: a KSVD decomposition is performed for each channel before the model receives the input data, and the data are resynthesized for use by the model. In contrast, other privacy-preserving strategies typically do not involve preprocessing of the data but rather protect the gradient directly. The introduction of KSVD decomposition may provide an additional advantage for privacy preservation, which is particularly effective in grayscale images due to the low dimensionality of the data; however, in color images, due to the complexity of the image and the increased number of channels, KSVD decomposition may face more challenges, which may be one of the reasons for the performance degradation. This finding emphasizes the importance of considering data preprocessing steps when designing privacy-preserving strategies and points to KSVD decomposition as a potential technical tool that can improve privacy preservation under certain conditions.

5.3. Model Performance Evaluation

Finally, the experiment also considers the evaluation framework proposed by Wei et al. [22] for gradient leakage attacks in FL. According to the thesis, the success rate of the attack is affected by a variety of factors, including the initialization strategy of the virtual attack seed data, the selection of the gradient loss function, and the optimization strategy during the attack. In addition, some key hyperparameter configurations in FL also have an impact on the effectiveness and cost of the attack, including the batch size, the resolution of the training data, the selection of the activation function, and whether to use a baseline communication protocol or a more efficient communication method to upload the data to the FL server during the gradient update process. Given the importance of these factors, this experiment will systematically explore their specific effects on DLG effectiveness in different settings, aiming to evaluate and compare the actual effects of different defense strategies in diverse FL environments.

Figure 7 evaluates the performance of the proposed defense scheme under different combinations of attack loss functions and optimization algorithms. To specifically measure the efficacy, the mean square error value between the reconstructed image and the original image after each iteration is calculated, and it is ensured that all the experiments are conducted based on the same image. The experimental results reveal significant differences in the MSE performance of different optimization algorithms (e.g., L-BFGS, Adam, SGD, and RMSprop) with different loss functions for different numbers of iterations. The left part concentrates on comparing the optimization algorithms, with all experiments using NLLLoss as the loss function, while the right part concentrates on comparing the loss functions, with all experiments using RMSprop as the optimizer. Each row of the graph represents an algorithm, and each column corresponds to a different number of iterations (0, 2000, 4000, 6000, and 8000). Each subfigure presents the reconstructed image as a color plot with text labels to visualize the specific MSE values under each condition. Notably, the lowest MSE value (0.36) was obtained after 8000 iterations using the Adam optimizer, while the MSE value for the L-BFGS optimizer increased with the number of iterations. In terms of optimization algorithms, MSELoss produced the best defense. This finding suggests that the choice of optimization and loss function has a significant impact on the difficulty of reconstruction, but our proposed scheme is effective in providing full protection.

Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
Defense performance under multiple attack losses and optimization strategies.

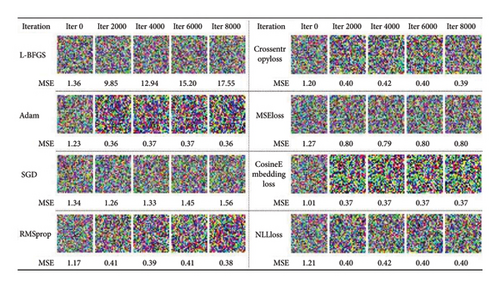
Figure 8 shows the performance of the proposed defense scheme under multiple attack initialization strategies and different image sizes. On the left part, when using the pattern initialization method, 1/4 region of the feature space is initialized with a random seed, and this pattern is subsequently replicated throughout the feature space to form the initialization conditions. While the Dark initialization method reconstructs the data by means of a specific Dark seed, the RGB initialization method specifically chooses a red seed as the starting point for initialization. In the right part, the defense effect is evaluated for different image sizes.

Details are in the caption following the image
Figure 8
Open in figure viewerPowerPoint
Defense performance under multiple initialization algorithms and image sizes.

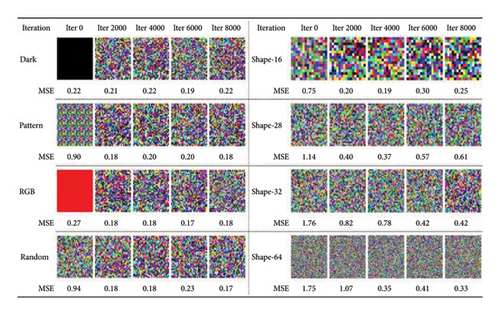
The results show that, despite the existence of multiple initialization strategies, their impact on defense performance is relatively limited. Even after up to 8000 rounds of iterative attacks, the mean-square error only stays at about 0.18. This indicates that the impact of different attack initialization conditions on defense effectiveness is not significant. In contrast, the image size has a more important impact on the defense effect. As the number of image pixels increases, the attacker’s difficulty in recovering the image also increases, which is clearly reflected in the figure. This finding reveals that in defending against gradient inversion attacks, in addition to relying on well-designed privacy protection strategies, the security of the model can be enhanced by adjusting the parameters affected by the attack, such as the image size.

6. Conclusion

We have thoroughly explored the gradient reconstruction problem in DL models and proposed a privacy protection strategy that combines sparse learning and gradient perturbation, aiming to effectively defend against gradient reconstruction attacks. By introducing sparse learning methods in the model training phase, our proposed strategy converts raw data into sparse representations, which reduces the sensitivity and identification of the data. Meanwhile, by perturbing the gradient of the fully connected layer in a targeted manner, our proposed strategy enhances the model’s resistance to attacks while maintaining its performance. In the experimental part, we use a variety of datasets and attack scenarios. The experimental results show that our proposed SLGD strategy excels in both privacy protection and model performance impact compared with other popular defense schemes. In particular, in terms of image security, the SLGD approach is able to effectively defend against gradient reconstruction attacks while maintaining the high accuracy and generalization ability of the model. We also analyze in detail the impact of different attack initialization conditions and image sizes on the defense effect and find that image size is an important factor affecting the defense effect. In addition, our proposed VMF-based gradient perturbation strategy not only introduces perturbations at the representation layer through well-designed perturbations but also ensures that the perturbations are targeted and effective and effectively avoids the gradient freezing problem, thus improving the robustness of the model. Our proposed privacy protection strategy based on sparse learning and gradient perturbation provides a new solution for data privacy protection in FL systems. Future research can further explore how to optimize the strategy and combine it with other privacy protection techniques to achieve efficient and balanced privacy protection across a wider range of data types and application scenarios.

Conflicts of Interest

The authors declare no conflicts of interest.

Funding

This work was supported in part by the National Key R&D Program of China under Grant 2023YFB2703801, the National Natural Science Foundation of China under Grants U21A20463 and U22B2027, the Beijing Natural Science Foundation under Grant L221014, and the Xinjiang Production and Construction Corps Key Laboratory of Computing Intelligence and Network Information Security under Grant CZ002702-04.

Acknowledgments

This work was supported in part by the National Key R&D Program of China under Grant 2023YFB2703801, the National Natural Science Foundation of China under Grants U21A20463 and U22B2027, the Beijing Natural Science Foundation under Grant L221014, and the Xinjiang Production and Construction Corps Key Laboratory of Computing Intelligence and Network Information Security under Grant CZ002702-04.

    Data Availability Statement

    The datasets used in this study are publicly available and can be accessed through the following sources:

    Natural Image Datasets: CIFAR-10 and CIFAR-100 contain 60,000 32 × 32 color images from 10 and 100 different classes, respectively. These datasets provide a variety of image classes and complexities, enabling the evaluation of model classification performance and robustness. These datasets are available at https://www.cs.toronto.edu/%7Ekriz/cifar.html.

    MNIST and Fashion MNIST consist of 28 × 28 grayscale images, representing handwritten digits (MNIST) and fashion items (Fashion MNIST), which are commonly used benchmarks for assessing classification models in terms of accuracy and generalization. These datasets can be accessed at http://yann.lecun.com/exdb/mnist/ and https://github.com/zalandoresearch/fashion-mnist, respectively.

    Face Image Dataset: the LFW dataset contains 13,000 labeled images of faces collected from the wild, covering various angles and facial expressions. This dataset is designed to evaluate the model′s ability to recognize faces and its robustness to variations such as pose, illumination, and expression. This dataset is available at http://vis-www.cs.umass.edu/lfw/.

    Vehicle Dataset: the Stanford Cars dataset, developed by Stanford University’s Artificial Intelligence Laboratory, includes 16,185 images of 196 car models, spanning a wide range of makes and models. This dataset is used to assess the model’s ability to recognize and classify different vehicle types. This dataset can be accessed at https://ai.stanford.edu/%7Ejkrause/cars/car_dataset.html.

    These datasets are publicly available for research purposes and can be downloaded from their respective sources.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.